圆锥曲线讲义(带答案)

个性化辅导授课教案
学员姓名 : 辅导类型(1对1、小班): 年 级: 辅 导 科 目 : 学 科 教 师 : 课 题 圆锥曲线专题
课 型 □ 预习课 □ 同步课 □ 复习课 □ 习题课 授课日期及时段
年 月 日 时间段
教 学 内 容
圆锥曲线知识点总结
1、平面内与两个定点1F ,2F 的距离之和等于常数(大于12F F )的点的轨迹称为椭圆. 即:|)|2(,2||||2121F F a a MF MF >=+。
这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距. 2、椭圆的几何性质:
焦点的位置
焦点在x 轴上
焦点在y 轴上
图形
标准方程
()22
2210x y a b a b +=>> ()22
2210y x a b a b
+=>> 范围
a x a -≤≤且
b y b -≤≤ b x b -≤≤且a y a -≤≤ 顶点
()1,0a A -、()2,0a A
()10,b B -、()20,b B
()10,a A -、()20,a A ()1,0b B -、()2,0b B 轴长 短轴的长2b = 长轴的长2a =
焦点 ()1,0F c -、()2,0F c
()10,F c -、()20,F c
焦距 ()222122F F c c a b ==-
对称性 关于x 轴、y 轴、原点对称
离心率
()2
2101c b e e a a
==-<<
3、平面内与两个定点1F ,2F 的距离之差的绝对值等于常数(小于12
F F )的点的轨迹称为双曲线.即:|)|2(,2||||||2121F F a a MF MF <=-。
这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
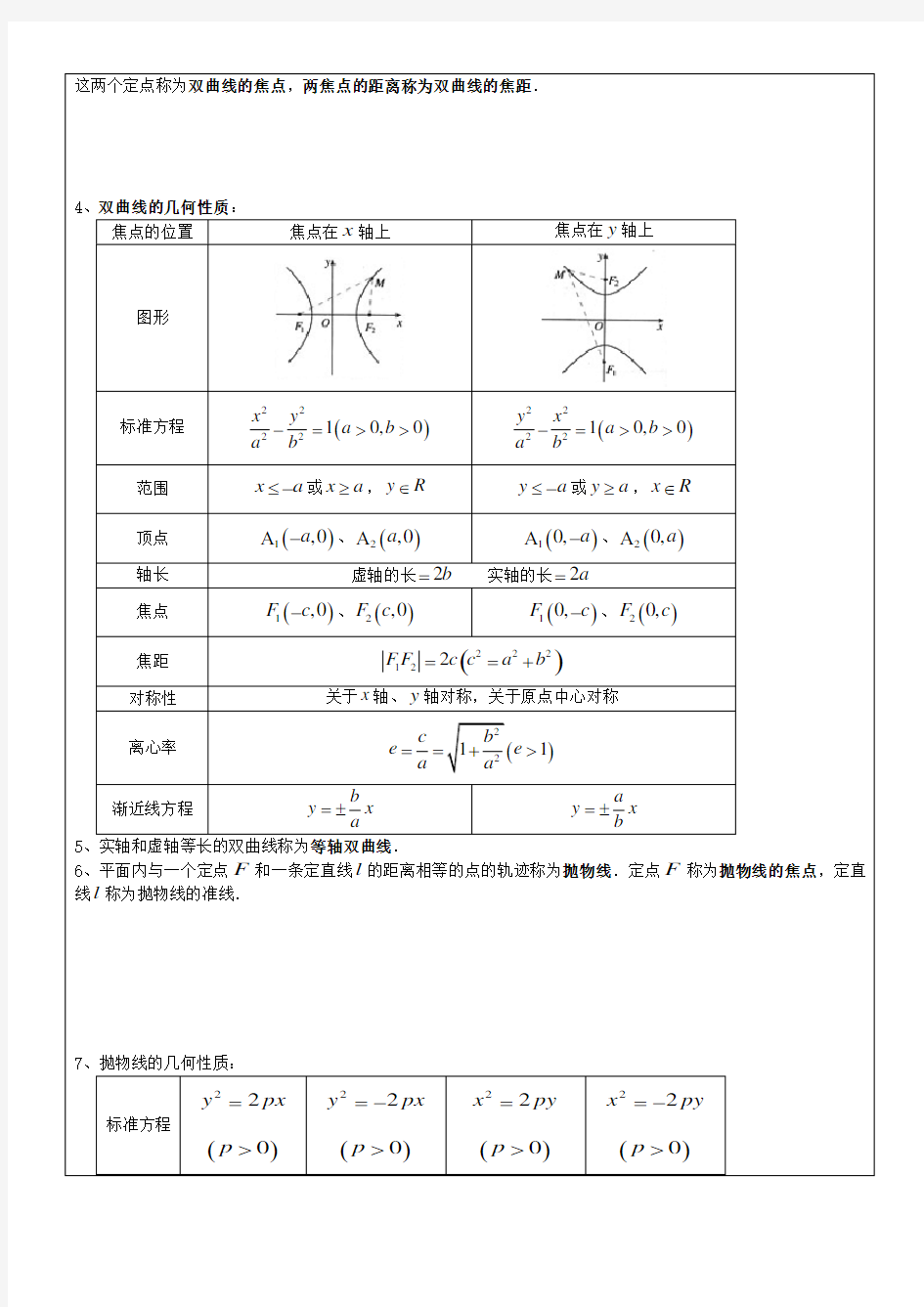
4、双曲线的几何性质:
焦点的位置 焦点在x 轴上
焦点在y 轴上 图形
标准方程
()22
2210,0x y a b a b -=>> ()22
2
210,0y x a b a b
-=>> 范围 x a ≤-或x a ≥,y R ∈ y a ≤-或y a ≥,x R ∈
顶点 ()1,0a A -、()2,0a A ()10,a A -、()20,a A 轴长 虚轴的长2b = 实轴的长2a =
焦点 ()1,0F c -、()2,0F c
()10,F c -、()20,F c
焦距 ()222122F F c c a b ==+
对称性 关于x 轴、y 轴对称,关于原点中心对称
离心率
()2
211c b e e a a
==+>
渐近线方程
b y x a
=±
a y x b
=±
5、实轴和虚轴等长的双曲线称为等轴双曲线.
6、平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线.定点F 称为抛物线的焦点,定直线l 称为抛物线的准线.
7、抛物线的几何性质:
标准方程
22y px =
()0p > 22y px =- ()0p > 22x py = ()0p > 22x py =-
()0p >
图形
顶点
()0,0
对称轴
x 轴
y 轴
焦点
,02p F ??
??? ,02p F ??
- ???
0,2p F ?
? ??
?
0,2p F ?
?- ??
?
准线方程
2
p
x =-
2
p x =
2
p y =-
2
p y =
离心率
1e =
范围
0x ≥ 0x ≤ 0y ≥ 0y ≤
8、过抛物线的焦点作垂直于对称轴且交抛物线于A 、B 两点的线段AB ,称为抛物线的“通径”,即2p AB =. 9、焦半径公式:
若点()00,x y P 在抛物线()2
20y px p =>上,焦点为F ,则02p
F x P =+
; 若点()00,x y P 在抛物线()2
20x py p =>上,焦点为F ,则02
p F y P =+
1. 值范围。
圆锥曲线的方程与性质 常用结论
A .常见结论:
1.与椭圆22221x y a b
+=(a>b>0)共焦点的椭圆方程可设为:22
2
21x y a k b k +=++ 中心在原点,坐标轴为对称轴的椭圆、双曲线方程可设为
(m>0,n>0)
2.与22221x y a b -=共渐近线的双曲线方程22
a
x -22y b λ=(0λ≠).
与22221x y a b
-=有相同焦点的双曲线方程22x a k --2
2
1y b k =+(2k a <且2k b ≠-) 3.抛物线:抛物线的通径为2P ,焦准距为P,径是所有焦点弦(过焦点的弦)中最短的弦
若抛物线的焦点弦为AB,,则①,
若OA、OB是过抛物线顶点O的两条互相垂直的弦,则直线AB恒经过定点
B.直线与曲线方程的位置关系:
1.方法一是方程的观点,即把曲线方程和直线的方程联立成方程组,利用判别式Δ来讨论位置关系.
(1)相交:直线与椭圆相交;
直线与双曲线相交,但直线与双曲线相交不一定有,当直线与双曲线的渐近线平行时,
直线与双曲线相交且只有一个交点,故是直线与双曲线相交的充分条件,但不是必要条
件;
直线与抛物线相交,但直线与抛物线相交不一定有,当直线与抛物线的对称轴平行时,
直线与抛物线相交且只有一个交点,故也仅是直线与抛物线相交的充分条件,但不是必
要条件
(2)相切:直线与椭圆相切;直线与双曲线相切;直线与抛物线相切;
(3)相离:直线与椭圆相离;直线与双曲线相离;直线与抛物线相离。
【注:a.直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形:相切和相交。如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;
b.过双曲线=1外一点的直线与双曲线只有一个公共点的情况如下:
①P点在两条渐近线之间且不含双曲线的区域内,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线共四条;
②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;
③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;
④P为原点时不存在这样的直线;
c.过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线。】
2.方法二是几何的观点
a.遇到中点弦问题常用“韦达定理”或“点差法”求解。
在椭圆中,以为中点的弦所在直线的斜率k=-;在双曲线中,以
为中点的弦所在直线的斜率k=;在抛物线中,以为中点的弦所在直
线的斜率k=
b.在求直线与曲线的相交弦的弦长时,要分开讨论:直线与圆相交充分运用垂径定理,即先求出圆心到直线的距离d 和半径R 解出弦长;而直线与其他曲线方程相交通过联立方程应用韦达定理来求解2121AB k x x =+- 若12,y y 分别为A 、B 的纵坐标,则2
1211()AB y y k
=+-
四、常规题型及解题的技巧方法 A:常规题型方面 (1)中点弦问题
具有斜率的弦中点问题,常用设而不求法(点差法):设曲线上两点为,
,代入方程,
然后两方程相减,再应用中点关系及斜率公式,消去四个参数。 典型例题 给定双曲线。过A (2,1)的直线与双曲线交于两点
及
,求线段
的中
点P 的轨迹方程。 分析:设,
代入方程得
,
。
两式相减得
。
又设中点P (x,y ),将
,
代入,当
时得
。
又,
代入得。
当弦
斜率不存在时,其中点P (2,0)的坐标也满足上述方程。
因此所求轨迹方程是
说明:本题要注意思维的严密性,必须单独考虑斜率不存在时的情况。
