matlab练习题和答案
MATLAB习题及参考答案经典.doc
习题：1， 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
2， 对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。
3， 已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。
4， 角度[]604530=x ，求x 的正弦、余弦、正切和余切。
(应用sin,cos,tan.cot)5， 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵： （1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546， 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
(应用poly,polyvalm)7， 求解多项式x 3-7x 2+2x +40的根。
(应用roots)8， 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
(应用poly,polyvalm)9， 计算多项式9514124234++--x x x x 的微分和积分。
(应用polyder,polyint ，poly2sym)10， 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。
(应用x=a\b)11， 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。
(应用pinv) 12， 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。
(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。
matlab复习题标准答案
matlab复习题标准答案# MATLAB复习题标准答案一、选择题1. MATLAB中的矩阵默认是按什么顺序存储的？- A. 行主序- B. 列主序- C. 随机序- D. 行主序2. 下列哪个函数用于计算矩阵的行列式？- A. `det`- B. `diag`- C. `trace`- A. `det`3. MATLAB中如何创建一个5x5的单位矩阵？- A. `eye(5,5)`- B. `zeros(5,5)`- C. `ones(5,5)`- A. `eye(5,5)`4. 下列哪个命令用于生成0到1之间的随机数？- A. `rand()`- B. `randi()`- C. `randn()`- A. `rand()`5. MATLAB中如何计算向量的范数？- A. `norm(vector)`- B. `abs(vector)`- C. `sum(vector)`- A. `norm(vector)`二、填空题1. MATLAB中的`%`符号用于______。
- 答案：注释2. 要创建一个从10到1的递减向量，可以使用______。
- 答案：`1:-1:10`3. MATLAB中，`zeros(3,4)`会生成一个______。
- 答案：3行4列的全零矩阵4. 函数`max(A)`会返回矩阵A中的______。
- 答案：最大值5. `plot(x,y)`函数在MATLAB中用于______。
- 答案：绘制x和y的数据点的图形三、简答题1. 请简述MATLAB中矩阵的基本操作有哪些？- 答案：矩阵的基本操作包括矩阵的创建、转置、求逆、矩阵乘法、矩阵加法、矩阵减法等。
2. MATLAB中如何实现循环结构？- 答案：MATLAB中实现循环结构主要有两种方式，一种是使用`for`循环，另一种是使用`while`循环。
3. 请解释MATLAB中的函数文件和脚本文件的区别。
- 答案：函数文件通常包含返回值和参数，可以被其他脚本或函数调用；而脚本文件主要用于执行一系列命令，不包含返回值。
matlab考试题目及答案
matlab考试题目及答案1. 题目：编写一个MATLAB函数，实现计算并返回一个向量中所有元素的平方和。
答案：以下是一个简单的MATLAB函数，用于计算并返回一个向量中所有元素的平方和。
```matlabfunction sumOfSquares = calculateSumOfSquares(vector)sumOfSquares = sum(vector.^2);end```2. 题目：给定一个3x3的矩阵A，使用MATLAB编写代码，求出矩阵A 的转置。
答案：可以通过简单的转置操作来求得矩阵A的转置。
```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = A';```3. 题目：编写一个MATLAB脚本，实现对一个二维数组进行排序，并返回排序后的数组。
答案：以下是一个MATLAB脚本，用于对一个二维数组进行排序，并返回排序后的数组。
```matlabfunction sortedArray = sort2DArray(array)sortedArray = sort(array(:));end```4. 题目：给定一个向量x，使用MATLAB编写代码，计算并返回向量x的元素个数。
答案：可以通过内置函数`numel`来计算向量x的元素个数。
```matlabx = [1, 2, 3, 4, 5];numElements = numel(x);```5. 题目：编写一个MATLAB函数，实现计算并返回两个向量元素的点积。
答案：以下是一个简单的MATLAB函数，用于计算两个向量的点积。
```matlabfunction dotProduct = calculateDotProduct(vector1, vector2)dotProduct = dot(vector1, vector2);end```6. 题目：给定一个矩阵B，使用MATLAB编写代码，求出矩阵B的行列式。
matlab试题及答案
matlab试题及答案# MATLAB试题及答案一、选择题1. MATLAB的基本数据单位是：A. 矩阵B. 向量C. 标量D. 数组答案：A2. 下列哪个命令可以用来绘制函数图形？A. `plot`B. `graph`C. `draw`D. `chart`答案：A3. MATLAB中，以下哪个是正确的矩阵转置操作？A. `transpose(A)`B. `A'`C. `A^T`D. `flip(A)`答案：B二、简答题1. 简述MATLAB中矩阵的基本操作。
答案：在MATLAB中，矩阵是最基本的数据结构，可以进行加、减、乘、除等基本运算。
矩阵的创建可以使用方括号`[]`，例如`A = [1 2;3 4]`。
矩阵的转置使用单引号`'`，例如`A'`。
矩阵的求逆使用`inv`函数，例如`inv(A)`。
2. MATLAB中如何实现循环结构？答案：MATLAB中实现循环结构主要有两种方式：`for`循环和`while`循环。
`for`循环用于已知迭代次数的情况，例如：```matlabfor i = 1:5disp(i);end````while`循环用于迭代次数未知的情况，例如：```matlabi = 1;while i <= 5disp(i);i = i + 1;end```三、计算题1. 给定矩阵A和B，请计算它们的乘积C，并求C的行列式。
A = [1 2; 3 4]B = [5 6; 7 8]答案：首先计算矩阵乘积C：```matlabC = A * B;```然后计算C的行列式：```matlabdetC = det(C);```结果为：```matlabC = [19 22; 43 50]detC = -16```2. 编写一个MATLAB函数，计算并返回一个向量的范数。
答案：```matlabfunction norm_value = vector_norm(v)norm_value = norm(v);end```四、编程题1. 编写一个MATLAB脚本，实现以下功能：- 随机生成一个3x3的矩阵。
matlab20道试题及解答
试题1．“数学黑洞”：任意一个4位自然数，将组成该数的各位数字重新排列，形成一个最大数和一个最小数，之后两数相减，其差仍为一个自然数。
重复进行上述运算，最终会出现一个神秘的数，请编程输出这个神秘的数。
clear;a=input('请输入一个四位正整数：');str_a=num2str(a); %将a转化为一个字符串b_min=str2double(sort(str_a)); %形成最小数b_max=str2double(sort(str_a,'descend')); %形成最大数b=b_max-b_min; %求最大数与最小数之差while (b~=a)a=b;str_a=num2str(a); %将a转化为一个字符串b_min=str2double(sort(str_a)); %形成最小数b_max=str2double(sort(str_a,'descend')); %形成最大数b=b_max-b_min; %求最大数与最小数之差endb试题2．将数字1、2、3、4、5、6填入一个2行3列的表格中，要使得每一列右边的数字比左边的数字大，每一行下面的数字比上面的数字大。
请编写程序求出按此要求可有几种填写方法。
a(1)=1;a(6)=6;count=0; %用来计数b=perms('2345'); %产生2345的全排列[m,n]=size(b);for i=1:mtemp=b(i,:);a(2)=str2double(temp(1));a(3)=str2double(temp(2));a(4)=str2double(temp(3));a(5)=str2double(temp(4));if ((a(4)>a(2))&&(a(4)>a(3))&&(a(5)>a(3)))count=count+1;c=reshape(a,2,3); %将a向量转化为2*3矩阵输出disp(c);endenddisp(['共有',num2str(count),'种填写方法']); %输出填写方法的种数试题3．编写成绩排序程序。
matlab开卷考试题及答案
matlab开卷考试题及答案MATLAB开卷考试题及答案一、选择题（每题2分，共20分）1. MATLAB中用于创建一个3x3的单位矩阵的命令是：A. `eye(3)`B. `ones(3)`C. `zeros(3)`D. `identity(3)`答案：A2. 下列哪个函数用于计算矩阵的逆？A. `inv()`B. `det()`C. `eig()`D. `trace()`答案：A3. MATLAB中，用于绘制二维图形的函数是：A. `plot()`B. `surf()`C. `mesh()`D. `bar()`答案：A4. 如何在MATLAB中计算向量的范数？A. `norm()`B. `abs()`C. `length()`D. `size()`答案：A5. MATLAB中，用于创建一个随机数矩阵的函数是：A. `rand()`B. `randi()`C. `randn()`D. `randperm()`答案：A6. 下列哪个命令用于在MATLAB中求解线性方程组？A. `solve()`B. `fsolve()`C. `fzero()`D. `linsolve()`答案：A7. MATLAB中，用于计算矩阵的行列式的函数是：A. `det()`B. `trace()`C. `eig()`D. `inv()`答案：A8. 如何在MATLAB中创建一个全1的3x3矩阵？A. `ones(3,3)`B. `eye(3,3)`C. `zeros(3,3)`D. `rand(3,3)`答案：A9. MATLAB中，用于计算矩阵的特征值的函数是：A. `eig()`B. `eigs()`C. `svd()`D. `qr()`答案：A10. 下列哪个函数用于计算矩阵的奇异值分解？A. `eig()`B. `svd()`C. `qr()`D. `lu()`答案：B二、填空题（每题3分，共30分）1. MATLAB中，用于创建一个3x3的零矩阵的命令是 `____`。
(完整版)matlab基础练习题(带答案)
Matlab 基础练习题常量、变量、表达式1、 MATLAB 中，下面哪些变量名是合法的？（ ）（A ）_num （B ）num_ （C ）num- （D ）-num 2、 在MA TLAB 中，要给出一个复数z 的模，应该使用（ ）函数。
（A ）mod(z) （B ）abs(z) （C ）double(z) （D ）angle(z) 3、 下面属于MATLAB 的预定义特殊变量的是？（ ）（A ）eps （B ）none （C ）zero （D ）exp4、 判断：在MA TLAB 的内存工作区中，存放一个英文字符 'a' 需要占用1个字节，存放一个中文字符‘啊’需要占用2个字节。
（ 错，都是2个字节 ）5、 判断：MA TLAB 中，i 和j （ 对 ）6、 判断：MA TLAB 中，pi 代表圆周率，它等于3.14。
（ 错，后面还有很多位小数 ）7、 在MA TLAB 中，若想计算的51)3.0sin(21+=πy 值，那么应该在MA TLAB 的指令窗中输入的MA TLAB 指令是__y1=2*sin(0.3*pi)/(1+sqrt(5))_。
8、 在MA TLAB 中，a = 1，b = i ，则a 占_8__个字节，b 占_16_个字节，c 占________字节。
9、 在MA TLAB 中，inf 的含义是__无穷大__，nan 的含义是__非数（结果不定）___。
数组1、 在MA TLAB 中，X 是一个一维数值数组，现在要把数组X 中的所有元素按原来次序的逆序排列输出，应该使用下面的（ ）指令。
（A ）X[end:1] （B ）X[end:-1:1] （C ）X (end:-1:1) （D ）X(end:1) 2、 在MA TLAB 中，A 是一个字二维数组，要获取A 的行数和列数，应该使用的MATLAB的命令是（ ）。
（A ）class(A) （B ）sizeof(A) （C ）size(A) （D ）isa(A)3、 在MATLAB 中，用指令x=1:9生成数组x 。
matlab简单编程21个题目及答案
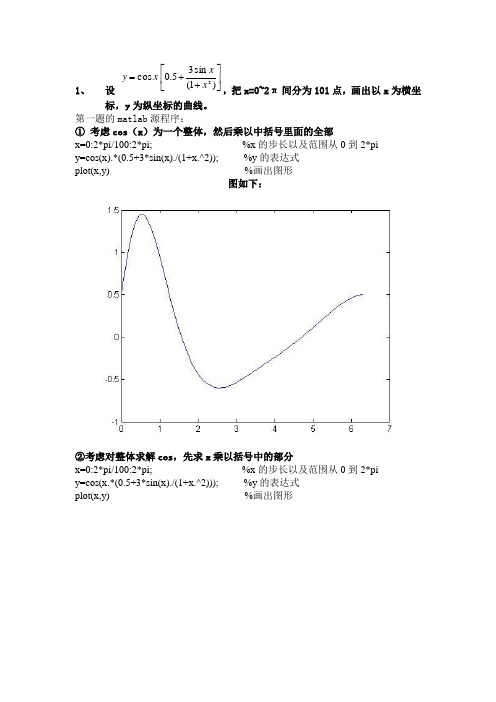
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy，把x=0~2π间分为101点，画出以x为横坐标，y为纵坐标的曲线。
第一题的matlab源程序：①考虑cos（x）为一个整体，然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下：②考虑对整体求解cos，先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下：2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下：R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4，画出参数t=0~10区间生成的x~y 曲线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
matlab练习题和答案控制系统仿真实验Matlab部分实验结果目录实验一 MATLAB基本操作 ..................................................................... ....................... 1 实验二 Matlab编程 ..................................................................... ............................... 5 实验三 Matlab底层图形控制 ..................................................................... ..................... 6 实验四控制系统古典分析...................................................................... .......................12 实验五控制系统现代分析 ..................................................................... . (15)实验六 PID控制器的设计 ..................................................................... ......................19 实验七系统状态空间设计...................................................................... .......................23 实验九直流双闭环调速系统仿真 ..................................................................... . (25)实验一 MATLAB基本操作1 用MATLAB可以识别的格式输入下面两个矩阵1233，，1443678，i，，,,2357,,,,2335542，i,,,, A,1357B,,,2675342，i,,3239,,,,189543，，,,1894，，再求出它们的乘积矩阵C，并将C矩阵的右下角2×3子矩阵赋给D矩阵。
赋值完成后，调用相应的命令查看MATLAB工作空间的占用情况。
A=[1,2,3,3;2,3,5,7;1,3,5,7;3,2,3,9;1,8,9,4];B=[1+4i,4,3,6,7,8;2,3,3,5,5,4+2i;2,6+7i,5,3,4,2;1,8,9,5,4,3];C=A*B;D=C(4:5,4:6);whosName Size Bytes Class AttributesA 5x4 160 doubleB 4x6 384 double complexC 5x6 480 double complexD 2x3 96 double complex 2 选择合适的步距绘制出下面的图形，其中 sin(/)1tt,,(,)11t=[-1:0.1:1];y=sin(1./t);plot(t,y)13 对下面给出的各个矩阵求取矩阵的行列式、秩、特征多项式、范数、特征根、特征向量和逆矩阵。
5765753500..，，，，,,,,71087833410.,,,,， B,A,,,,,681090910315,.,,,,579100037193..，，，，12343324,,，，，，,,,,56785518,,,,,， C,D,,,,,910111211857,,,,,131415165131,,,，，，，A=[7.5,3.5,0,0;8,33,4.1,0;0,9,103,-1.5;0,0,3.7,19.3];B=[5,7,6,5;7,10,8,7;6,8,10,9;5,7,9,10]; C=[1:4;5:8;9:12;13:1rtf6];D=[3,-3,-2,4;5,-5,1,8;11,8,5,-7;5,-1,-3,-1];det(A);det(B);det(C);det(D);rank(A);rank(B);rank(C);rank(D);a=poly(A);b=poly(B);c=poly(C);d=poly(D);norm(A);2norm(B);norm(C);norm(D);[v,d]=eig(A,'nobalance');[v,d]=eig(B,'nobalance');[v,d]=eig(C,'nobalance');[v,d]=eig(D,'nobalance');m=inv(A);n=inv(B);p=inv(C);q=inv(D);4 求解下面的线性代数方程，并验证得出的解真正满足原方程。
72124,1321390，，，，，，，，,,,,,,,,721264,915327,,,,,,,,,(a)，(b)X,X,,,,,,,,,91532117,,,,221151,,,,,,,,,,,,2211521132130，，，，，，，，(a)A=[7,2,1,-2;9,15,3,-2;-2,-2,11,5;1,3,2,13];B=[4;7;-1;0];X=A\B;C=A*X;(b)A=[1,3,2,13;7,2,1,-2;9,15,3,-2;-2,-2,11,5];B=[9,0;6,4;11,7;-2,-1];X=A\B;C=A*X;5.(1) 初始化一10*10矩阵，其元素均为1 ones(10,10);(2) 初始化一10*10矩阵，其元素均为0 zeros(10,10);(3) 初始化一10*10对角矩阵v=[1:10];diag(v);(4) 输入A=[7 1 5;2 5 6;3 1 5]，B=[1 1 1; 2 2 2; 3 3 3]，执行下列命令，理解其含义A(2, 3) 表示取A矩阵第2行、第3列的元素;3A(:,2) 表示取A矩阵的第,列全部元素;A(3,:) 表示取A矩阵第,行的全部元素;A(:,1:2:3)表示取A矩阵第1、3列的全部元素;A(:,3).*B(:,2)表示A矩阵第3列的元素点乘B矩阵第2列的元素A(:,3)*B(2,:)表示A矩阵第3列的元素乘以B矩阵第2行 A*B 矩阵AB相乘A.*B矩阵A点乘矩阵BA^2矩阵A的平方A.^2矩阵表示求矩阵A的每一个元素的平方值B/A 表示方程AX=B的解XB./A表示矩阵B的每一个元素点除矩阵A的元素6在同一坐标系中绘制余弦曲线y=cos(t-0.25)和正弦曲线y=sin(t-0.5)，t?[0，2π]，用不同颜色，不同线的类型予以表示，注意坐标轴的比例控制。
t=[0:0.01:2*pi];y1=cos(t-0.25);plot(t,y1,'r--')hold ony2=sin(t-0.5);plot(t,y2,'k')4实验二 Matlab编程1分别用for和while循环结构编写程序，求出63i236263 K,,，，，，，，2122222？,,i0并考虑一种避免循环的简洁方法来进行求和。
(a)j=1;n=0;sum=1; for n=n+1:63for i=1:nj=j*2;endsum=sum+j;j=1;endsum(b)j=1;n=1;sum=1;while n~=64i=1;while i<n+1j=j*2;i=i+1;endn=n+1;sum=sum+j;j=1;endSum(c)i=0:63;k=sum(2.^i);2计算1+2+…+n<2000 时的最大 n 值s=0;m=0;while(s<=2000),m=m+1;s=s+m;end,m3 用MATLAB语言实现下面的分段函数,hxD,,, yfxhDx,,()/,xD,,,,,,hxD,,存放于文件ff.m中，令D=3，h=1求出，f(-1.5), f(0.5), f(5).D=3;h=1;x=-2*D:1/2:2*D;y=-h*(x<-D)+h/D./x.*((x>=-D)&(x<=D))+h*(x>D);5plot(x,y);grid onf1=y(find(x==-1.5))f2=y(find(x==0.5))f3=y(find(x==5))实验三 Matlab底层图形控制 1 在MATLAB命令行中编程得到y=sin(t)和y1=cos(t)函数, plot(t,y);figure(10);plot(t,y1);>> t=[-pi:0.05:pi];>> y=sin(t);>> y1=cos(t);>> plot(t,y)>> figure(10);>> plot(t,y1)2 在MATLAB命令行中键入h=get(0)，查看根屏幕的属性，h此时为根屏幕句柄的符号表示，0为根屏幕对应的标号。
>> h=get(0)h =BeingDeleted: 'off'BusyAction: 'queue'ButtonDownFcn: ''CallbackObject: []Children: [2x1 double]Clipping: 'on'CommandWindowSize: [89 27]CreateFcn: ''CurrentFigure: 1DeleteFcn: ''Diary: 'off'DiaryFile: 'diary'Echo: 'off' FixedWidthFontName: 'Courier New' Format: 'short'FormatSpacing: 'loose' HandleVisibility: 'on'HitTest: 'on'Interruptible: 'on'Language: 'zh_cn.gbk' MonitorPositions: [1 1 1440 900] More: 'off'6Parent: []PointerLocation: [1048 463] PointerWindow: 0RecursionLimit: 500 ScreenDepth: 32 ScreenPixelsPerInch: 96 ScreenSize: [1 1 1440 900] Selected: 'off' SelectionHighlight: 'on' ShowHiddenHandles: 'off'Tag: ''Type: 'root'UIContextMenu: []Units: 'pixels'UserData: []Visible: 'on'3 h1=get(1);h2=get(10), 1, 10分别为两图形窗口对应标号，其中1为Matlab自动分配，标号10已在figure(10)中指定。