种-面积曲线的绘制

姓名：洪俊班级：2013级生物基地学号：201300140030

植物群落种-面积曲线的绘制

一．实验目的

1．学会统计一定面积内不同种群的数量

1.初步认识群落种类组成、生活型类型与群落结构的关系。

二．实验原理

种类组成是指一个群落内的植物成分，即乔木树种、灌木以及其他林下植物各有哪些种类，这是群落结构的主要特征之一。

表现面积是在一个最小地段内，对一个特定群落类型能够提供足够的环境空间或能保证展现出该群落类型的种类组成和结构的真实特征的群落面积或“能包括群落绝大多数种类，并表现出群落一般结构特征的最小面积”，也称为群落的最小面积。不同的群落类型和环境条件下，群落的最小面积会有所差别。

附：常用方法巢式小区几何系统法

图式Ⅰ的方式扩大，则是：

1——第一次取样面积为2m×2m；

1+2——第二次取样累计面积为2m×4m;

1+2+3——第三次取样累计面积为4m×4m;

1+2+3+4——第四次取样累计面积为4m×8m；其余类推。按图式Ⅱ的方式扩大，则是：

1——第一次取样面积为2m×2m； 1+2——第二次取样面积为4m×4m；

1+2+3——第三次取样面积为8m×8m；其余类推

三．实验器材

皮尺，花杆，记录板，细绳

四．实验步骤

1.根据植物群落中的优势种、外貌特征和地形部位的变化选择典型调查地段。

2.因为再浇水所以不能用巢式法。

在距草坪边缘1m的地方拉一条绳，每隔1m一格，每人一格找出格子中除优势物种外的其他物种

3.在不断地扩大累计取样面积的同时，应记载相应出现的新种名称、生活型和

累计种数，记入“结果1”中

4.以直角坐标系的X轴代表累计的取样面积，而以Y轴代表有小到大累计的取

样面积上所发现的累计植物种数，绘制出种类-面积曲线（结果2）。

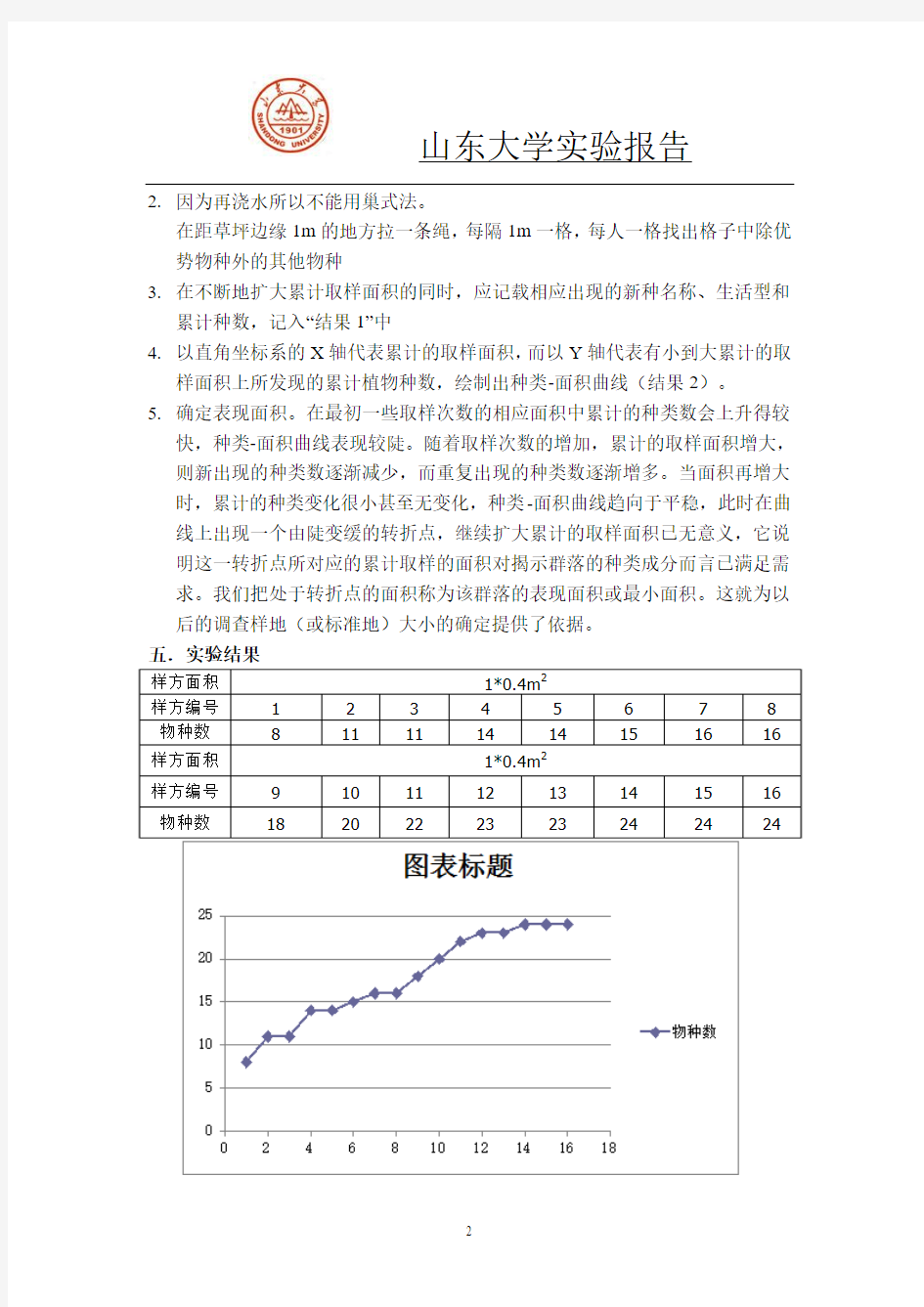
5.确定表现面积。在最初一些取样次数的相应面积中累计的种类数会上升得较

快，种类-面积曲线表现较陡。随着取样次数的增加，累计的取样面积增大，则新出现的种类数逐渐减少，而重复出现的种类数逐渐增多。当面积再增大时，累计的种类变化很小甚至无变化，种类-面积曲线趋向于平稳，此时在曲线上出现一个由陡变缓的转折点，继续扩大累计的取样面积已无意义，它说明这一转折点所对应的累计取样的面积对揭示群落的种类成分而言已满足需求。我们把处于转折点的面积称为该群落的表现面积或最小面积。这就为以后的调查样地（或标准地）大小的确定提供了依据。

五．实验结果

六．注意事项

1．如果调查的是森林群落，单株林木占的面积很大，而树冠下又很少有植物种，因此开始取样的面积应大些，可以2m×2m、5m×5m或10m×10m为开始样方的起点。如果调查的是草木植物群落，则开始样方的面积可为1m×1m。

2．应当根据该群落的特征、分布状况选择在有代表性的地段取样调查。

3．在扩大面积时，不要超出该群落所固有的特征之外，这可以比较容易地由优势树种、地形部位等方面加以确定。

4．调查过程中对一些灌木、草本种类不能在野外定名时，应立即采集标本，在标本上编注号码，并在“结果1”中记载相应的编号，以便查对种名。