实验2 空间曲线曲面图形的绘制

实验二空间曲线曲面图形的绘制
一、实验目的
熟练掌握使用Mathematica软件绘制空间曲线曲面图形的方法.
二、实验内容与Mathematica命令
1.基本三维图形
函数(,)
=的图形为三维空间的一个曲面,Mathematica中,绘制三维曲面图形的
z f x y
基本命令格式为
Plot3D[f,{x,xmin,xmax},{y,ymin,ymax},Options]
其中,f为一个二元显函数. 该命令有众多可供使用的选项,可执行命令“Options[Plot3D]”查询.
1)绘制曲面的基本方法
运行t1=Plot3D[Sin[x+y]*Cos[x+y],{x,0,4},{y,0,4}]
图1
2)用PlotRange 设定曲面的表面的变化范围
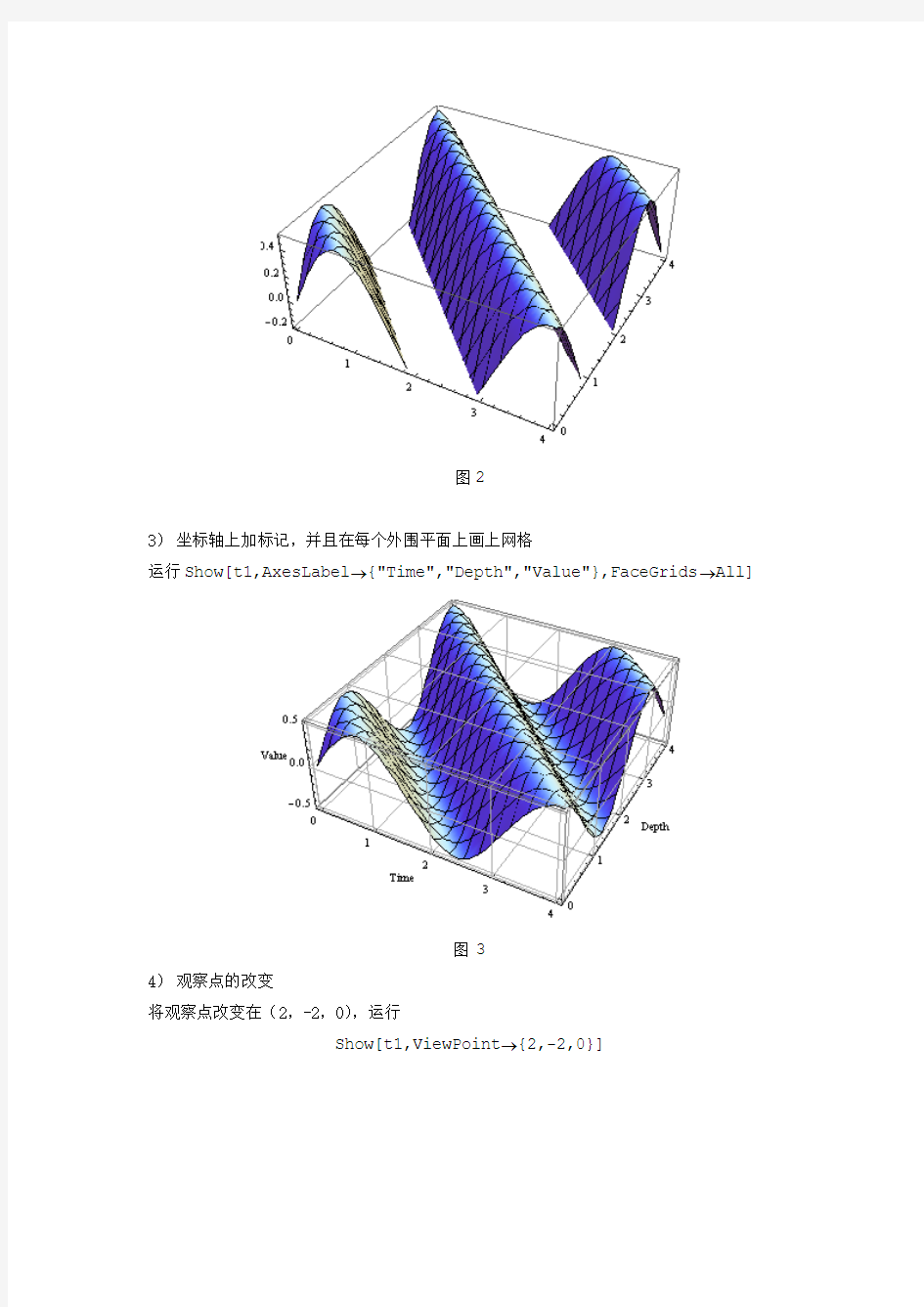
运行Show[t1,PlotRange→{-0.2,0.5}]
图2
3)坐标轴上加标记,并且在每个外围平面上画上网格
运行Show[t1,AxesLabel→{"Time","Depth","Value"},FaceGrids→All]
图 3
4)观察点的改变
将观察点改变在(2,-2,0),运行
Show[t1,ViewPoint→{2,-2,0}]
图4
也可用鼠标拖动改变视点。
5)无网格和立体盒子的曲面
运行 Show[t1,Mesh→False,Boxed→False]
图 5
6)没有阴影的曲面
利用Shading取消曲面的阴影运行 Show[t1,Shading→False]
图 6
7)给曲面着色
Show[t1,Lighting→False
图 7 Show[t1,Lighting→None]
图 8
Show[t1,Lighting→"Neutral"]
图 9
Show[t1,Lighting→{{"Directional",RGBColor[1,.7,.1],{{5,5,4},{5,5,
0}}}}]
图 10
2.离散数据的绘制
ListPlot3D[{y1,y2,…..},{z1,z2…},…]
mytable:=Table[Sin[x*y],{x,0,3Pi/2,Pi/15},{y,0,3Pi/2,Pi/1 5}];
ListPlot3D[mytable]
图 11
3.三维空间参数方程的绘制
1)空间曲线的绘制
pp1=ParametricPlot3D[{3Cos[4t+1],Cos[2t+3],4Cos[2t+5]},{t,0,2Pi}]
图 12
pp2=ParametricPlot3D[{Cos[t],Sin[t],t/10.0},{t,0,10Pi}]
ParametricPlot3D[{Cos[t],Sin[t],t/10.0},{t,0,10Pi},PlotStyle {Thi ckness[0.02],RGBColor[1,0,1]}]
图 13
图 14
2)参数曲面的绘制
ParametricPlot3D[{Cos[u] Sin[v],Cos[u] Cos[v],Sin[u]},{u,0,2 Pi},{v,-Pi,Pi},Boxed→False,Axes→False]
图 15
绘制椭圆抛物面
22
35
x y
z=+,双曲抛物面
22
35
x y
z=-的图形.
Plot3D[x^2/3+y^2/5,{x,-2,2},{y,-2,2},BoxRatios->{1,1,1}, ViewPoint->{1.6,-3.,1.}];
Plot3D[x^2/3-y^2/5,{x,-2,2},{y,-3,3},BoxRatios->{1,1,1}, ViewPoint->{1.6,1.6,1.}];
这里,选项“BoxRatios->{1,1,1}”表示图形边框的长、宽、高的比例为1:1:1,选
项“ViewPoint
->{1.6,-3,1}”观察图形的视点为{1.6,-3,1}. 命令执行后得到下面的图形.
图16 图17
空间曲线与曲面
实验七空间曲线与曲面 实验目的 1.掌握空间直线、平面的画法。 2.了解常见的空间曲线与曲面的画法。 与本实验相关的理论 最基本的空间作图函数是Plot3 ,用于作所有二元函数的三维立方体图形,其格式是: Plot3D[f,{x,xmin,xmax},{y,ymin,ymax},可选项] 由于很多曲面和绝大多数曲线都不能用显函数的形式表示。Mathematica 还提供了Parametric Plot3D参数作图函数,其格式是:Parametric Plot3D[{x[u,v],y[u,v] ,z[u,v]} ,{u,umin,umax},{v,vmin,vmax},可选项] Mathematica作三维图形的机理是先在XOY坐标面给定区域内计算出一系列格点的值,再用矩形“小瓦片”拟合张在上面的曲面上。因而如果曲面的表面变化复杂,可通过设置更细的“瓦片”分割来改善。这时候可增加选项PlotPoint―>n 来说明分割数n。 实验步骤 一、画空间曲线 注意空间曲线的参数方程只有一个参变量,如果要画出螺旋线 x=10cost , y=10sint , z=2t 的图形,只要输入: Parametric Plot3D[{10cos[t],10sin[t],2t} ,{t,0,20}] 空间直线也类似地处理。 例1:求过A(3,5,-2),B(3,5,-2)的直线方程,并画图。 分析:空间直线方程可由点向式写出,再改成参数式
) 2(4)2(535313----=--=--z y x 化为参数式是:t x 23-=,t y 25-=,t z 62+-= 输入:Parametric Plot3D[{3-2t ,5-2t ,-2+6t} ,{t ,0,1}] 二、画空间曲面 例2:求过A (1,0,0),B (0,2,0),C (0,0,3),的平面方程,并画图。 分析:平面方程可由截距式写出,y x z 2 333--=。 输入:Parametric Plot3D[{3-3x-3y/2} ,{x ,-1,1},{y ,-1,1}] 例3:画出二元函数22),(y x y x f +=的图形。 输入:Parametric Plot3D[{x^2+y^2} ,{x ,-4,4},{y ,-4,4}] 例4:画出椭球心在原点,3=a ,4=b ,5=c 的椭球面。 输入:Parametric Plot3D[{3*Cos[u] Cos[v], 4*Sin[u] Cos[v],5*Sin[v]} ,{u ,0,2Pi},{v ,-Pi/2,Pi/2}] 例5:画出以x y cos =为准线,母线平行于Z 轴的柱面。 输入:Parametric Plot3D[{x,Cos[x],z} ,{x ,-4,4},{z ,-4,4}] 例6:画出由平面曲线z x cos 1+=绕Z 轴放转而成的旋转面。 输入:Parametric Plot3D[{(1+Cos[u])Cos[v] ,(1+Cos[u])Sin[v] ,u} ,{u ,-Pi ,Pi},{v ,0,2Pi}] 例7:画单叶双曲面。 输入:Parametric Plot3D[{Sec[u]Cos[v] ,Sec[u]Sin[v] ,Tan[u]} ,{u ,-Pi/2+0.5,Pi/2-0.5},{v ,0,2Pi}]
实验2-空间曲线曲面图形的绘制
实验二空间曲线曲面图形的绘制 一、实验目的 熟练掌握使用Mathematica软件绘制空间曲线曲面图形的方法. 二、实验容与Mathematica命令 1.基本三维图形 函数(,) 的图形为三维空间的一个曲面,Mathematica中,绘制三维曲面图形的 z f x y 基本命令格式为 Plot3D[f,{x,xmin,xmax},{y,ymin,ymax},Options] 其中,f为一个二元显函数. 该命令有众多可供使用的选项,可执行命令“Options[Plot3D]”查询. 1)绘制曲面的基本方法 运行t1=Plot3D[Sin[x+y]*Cos[x+y],{x,0,4},{y,0,4}] 图1 2)用PlotRange 设定曲面的表面的变化围 运行Show[t1,PlotRange{-0.2,0.5}]
图2 3)坐标轴上加标记,并且在每个外围平面上画上网格 运行Show[t1,AxesLabel{"Time","Depth","Value"},FaceGrids All] 图 3 4)观察点的改变 将观察点改变在(2,-2,0),运行 Show[t1,ViewPoint{2,-2,0}]
图 4 也可用鼠标拖动改变视点。 5)无网格和立体盒子的曲面 运行 Show[t1,Mesh False,Boxed False] 图 5 6)没有阴影的曲面 利用Shading取消曲面的阴影运行 Show[t1,Shading False]
图 6 7)给曲面着色 Show[t1,Lighting False 图 7 Show[t1,Lighting None]
计算机图形学试题及答案(汇总)
一、 判断题(10x1=10分) 1、 构成图形的要素可分为两类:刻画形状的点、线、面、体的非几何要素(集合要素)与反映物体表面属性或材质 的明暗、色彩等的(非几何要素)几何要素。( 错误 ) 2、 参数法描述的图形叫图形;点阵法描述的图形叫图像。( 正确 ) 3、 EGA (增强图形适配器)/VGA (视频图形阵列)为增强图形显示效果的一种图形处理软件的名称。( 错误 ) 4、 对山、水等不规则对象进行造型时,大多采用过程式模拟方法。( 正确 ) 5、 若两个图形是拓扑等价的,则一个图形可通过做弹性运动与另一个图形相重合。( 正确 ) 6、 0阶参数连续性和0阶几何连续性的定义是相同的。( 正确 ) 7、 Bezier 曲线可做局部调整。( 错误 ) 8、 字符的图形表示分为点阵和矢量两种形式。( 正确 ) 9、 LCD 表示(液晶显示器)发光二极管显示器。( 错误 ) 10、 使用齐次坐标可以将n 维空间的一个点向量唯一的映射到n+1维空间中。( 错误 ) 二、 填空题(15x2=30分) 1、目前常用的PC 图形显示子系统主要由3个部件组成:(1)帧缓冲存储器、(2)显示控制器、(3)ROM BIOS 。 2、 图形的输入设备有(4)键盘、鼠标、光笔(至少写三种);图形的显示设备有(5)CRT 显示器、LCD 、投影仪(至少写三种)。 3、常用坐标系一般可以分为:建模坐标系、用户坐标系、(6观察坐标系、(7)规格化设备坐标系、(8)设备坐标系。 4、在多边形的扫描转换过程中,主要是通过确定穿越多边形区域的扫描线的覆盖区间来填充,而区域填充则是从(9)给定的位置开始涂描直到(10)指定的边界条件为止。 5、一个交互式计算机图形系统应具有(11)计算 、(12)存储、(13)对话、(14)输入和输出等五个方面的功能。 三、 简答题(5x6=30分) 1、 请列举常用的直线段裁减算法(四种)。 答:答:直接求交算法、编码算法、中点再分算法、Cyrus-Beck 算法。 2、 考虑三个不同的光栅系统,分辨率依次为480640?,10241280?,20482560?。欲存储每个像素12位, 这些系统各需要多大的帧缓冲器(字节数)? 答:480640?需要的帧缓存为KB 4508/12480640=?? 10241280?需要的帧缓存为KB 19208/1210241280=?? 20482560 ?需要的帧缓存为KB 76808/1220482560=?? 3、 什么叫做走样?什么叫做反走样?反走样技术包括那些? 答:走样指的是用离散量表示连续量引起的失真。 为了提高图形的显示质量。需要减少或消除因走样带来的阶梯形或闪烁效果,用于减少或消除这种效果的方法称为反走样。 其方法是①前滤波,以较高的分辨率显示对象;②后滤波,即加权区域取样,在高于显示分辨率的较高分辨率下用点取样方法计算,然后对几个像素的属性进行平均得到较低分辨率下的像素属性。 4、 试说明一致缩放(s x =s y )和旋转形成可交换的操作对。 答:????? ??? ??-=???????? ??-????????? ??=1000cos sin 0sin cos 1000cos sin 0sin cos 10 00 001θθθθ θθθθ y y x x y x s s s s s s T ???? ???? ? ?-=??????????????????? ??-=10 00cos sin 0sin cos 10 000010 00cos sin 0sin cos 2θθθθθθ θθ y x y x y x s s s s s s T
空间曲线的切线与空间曲面的切平面doc资料
第六节 空间曲线的切线与空间曲面的切平面 一、空间曲线的切线与法平面 设空间的曲线C 由参数方程的形式给出:?? ? ??===)()()(t z z t y y t x x ,),(βα∈t . 设),(,10βα∈t t ,)(),(),((000t z t y t x A 、))(),(),((111t z t y t x B 为曲线上两点,B A ,的连线AB 称为曲线C 的割线,当A B →时,若AB 趋于一条直线,则此直线称为曲线C 在点A 的切线. 如果)()()(t z z t y y t x x ===,,对于t 的导数都连续且不全为零(即空间的曲线C 为光滑曲线),则曲线在点A 切线是存在的.因为割线的方程为 ) ()() ()()()()()()(010010010t z t z t z z t y t y t y y t x t x t x x --=--=-- 也可以写为 010********)()() ()()()()()()(t t t z t z t z z t t t y t y t y y t t t x t x t x x ---=---=--- 当A B →时,0t t →,割线的方向向量的极限为{})(),(),(000t z t y t x ''',此即为切线的方向向量,所以切线方程为 ) () ()()()()(000000t z t z z t y t y y t x t x x '-='-='-. 过点)(),(),((000t z t y t x A 且与切线垂直的平面称为空间的曲线C 在点 )(),(),((000t z t y t x A 的法平面,法平面方程为 ))(())(())((00'00'00'=-+-+-z z t z y y t y x x t x 如果空间的曲线C 由方程为 )(),(x z z x y y == 且)(),(0' 0'x z x y 存在,则曲线在点)(),(,(000x z x y x A 的切线是 ) () ()()(100000x z x z z x y x y y x x '-= '-=- 法平面方程为
计算机图形学
《计算机图形学》思考练习题 第一章计算机图形学概论 1.比较计算机图形学与图象处理技术相同点和不同点。 计算机图形学是研究怎样用数字计算机生成、处理和显示图形的一门学科。 图像处理技术研究如何对连续图像取样、量化以产生数字图像,如何对数字图像做各种变换以方便处理,如何滤去图像中的无用噪声,如何压缩图像数据以便存储和传输,图像边缘提取,特征增强和提取。 2.列举三个计算机图形的应用实例。 勘探、绘制地形地貌,系统模拟,虚拟现实。辅助教学设计。 3.简述计算机图形学发展动向。 造型技术—真实图形生成技术—人机交互技术—基于网络的图形技术 第二章计算机图形系统概述 1.叙述计算机图形系统的基本功能。 输入、输出、计算、存储、对话 他的基本功能是帮助人们设计、分析、采集、存贮图形、视频甚至音乐等信息。 2.输入设备可有哪几种逻辑功能?请举出各自对应的物理设备。 .定位(locator): 指定一个坐标点。对应的物理设备有鼠标器、键盘、数字化仪、触摸屏等。.笔划(stroke): 指示一个坐标点系列, 如指定一条曲线的控制点等。主要物理设备有数字化仪。.送值(valuator): 输入一个数值。最常用的物理设备是键盘的数字键。 .字符串(string):输入一个字符串。键盘字母键 .拾取(pick):各种定位设备 .选择(choise): 鼠标器,数字化仪,键盘功能键等 3.画出图形软件的层次结构及主要组成。 ------------------------------------ | 应用程序| | ---------------------------- | | 图形支撑软件| | | ------------------- | | | 高级语言| | | | ------------ | | | | 操作系统| ------------------------------------ 主要部分:图形核心系统GKS 计算机图形元文件CGM 计算机图形设备接口CGI 程序员层次结构图形系统PHIGS 4.颜色查找表的概念及实现原理。 颜色查找表是一维线性表,其每一项的内容对应一种颜色,它的长度由帧缓存单元的位数决定。实现原理:把颜色码放在一个独立的表中,帧缓存存放的是颜色表中各项的索引值,这样在帧缓存单元的位数不增加的情况下,具有了大范围挑选颜色的能力。 5.光栅扫描显示器结构与工作原理。
数学实验教程实验6(空间曲线与曲面
实验6 空间曲线与曲面 实验目的 1.学会利用软件命令绘制空间曲线和曲面 2.通过绘制一些常见曲线、曲面去观察空间曲线和曲面的特点 3.绘制多个曲面所围成的区域以及投影区域。 实验准备 1.复习常见空间曲线的方程 2.复习常见空间曲面的方程 实验内容 1.绘制空间曲线 2.绘制空间曲面:直角坐标方程、参数方程 3.旋转曲面的生成 4.空间多个曲面的所围成的公共区域以及投影区域 软件命令 表6-1 Matlab 空间曲线及曲面绘图命令 实验示例 【例6.1】绘制空间曲线 绘制空间曲线sin ,cos ,x at t y at t z ct ===,在区间09t π≤≤上的图形,这是一条锥面螺旋线,取a=10,c=3。
【程序】: t=0:pi/30:9*pi; a=10; c=3; x=a*t.*sin(t); y=a*t.*cos(t); z=c*t; plot3(x,y,z,’mo ’) 【输出】:见图6-1。 图6-1 空间曲线的绘制 【例6.2】利用多种命令绘制空间曲面 绘制二元函数 22 2 2 sin x y z x y += +在区域:99,99D x y -≤≤-≤≤上的图形。 【程序】:参见Exm06Demo02.m 。 【输出】:见图6-2。 图 6-2 绘制空间曲面 【例6.3】绘制Mobius 带 Mobius 带的参数方程为 122122 cos sin cos ,[0,2],[,] sin u u x r u y r u r c v u v a b z v π=??==+∈∈??=?,, 其中,,a b c 为常数,绘制其图形。
曲面与空间曲面的归纳
曲面与空间曲线的总结
曲面与空间曲线一.曲面及其方程: 1.曲面方程的一般概念: 定义:若曲面上的点的坐标(x,y,z) 都满足方程F(x,y,z)=0, 而满足此方程的点都在曲面上,则称此方程为 该曲面的方程,而曲面称为此方程的‘图形’。 例1:求与A(2,3,1)和B(4,5,6)等距离的点的运动规迹。 解: 设M(x,y,z)为动点的坐标,动点应满足的条件是 |AM|=|BM|由距离公式得 此即所求点的规迹方程,为一平面方程。 2.坐标面及与坐标面平行的平面方程: ①坐标平面xOy 的方程:z=0 ②过点(a,b,c)且与xOy 面平行的平面方程:z=c 222222)6()5()4()1()3()2(-+-+-=-+-+-z y x z y x 整理得 631044=-++z y x
③坐标面yOz 、坐标面zOx 以及过(a,b,c)点且分别与之平行的平面方程:x=0; y=0; x=a; y=b 3. 球面方程: ①球面的标准方程:以M0(x0,y0,z0)为球心,R 为半径 的球面方程为 (x-x0)2+(y-y0)2+(z-z0)2=R2 ②球面的一般方程: x2+y2+z2+Ax+By+Cz+D=0 球面方程的特点:平方项系数相同;没有交叉项。 例2:求x2+y2+z2+2x-2y-2=0表示的曲面 解:整理得: (x+1)2+(y-1)2+z2=22 故此为一个球心在(-1,1,0),半径为2的球。 4.母线平行于坐标轴的柱面方程: 一般我们将动直线l 沿定曲线c 平行移动所形成的轨迹 称为柱面。其中直线l 称为柱面的母线,定曲线c 称为柱面 的准线。本章中我们只研究母线平行于坐标轴的柱面方程。 此时有以下结论: 若柱面的母线平行于z 轴,准线c 是xOy 面上的一条曲线,其方程为F(x,y)=0,则该柱面的方程为F(x,y)=0; 同理,G(x,z)=0,H(y,z)=0在空间中分别表示母线平行于y 轴和x 轴的柱面。 分析:母线平行于坐标轴的柱面的特点为:平行于某轴,则在其方程中无此坐标项。其几何意义为:无论z 取何值,只要满足F(x,y)=0,则总在柱面上。 几种常见柱面:x+y=a 平面; 2 22a y x =+圆柱面
曲面与空间曲线的方程
第 2 章曲面与空间曲线的方程 本章教学目的:通过本章学习,使学生理解空间坐标系下曲面与空间曲线方程之定义及 表示,熟悉空间中一些特殊曲面、曲线的方程。 本章教学重点:空间坐标系下曲面与空间曲线方程的定义。 本章教学难点:(1)空间坐标系下母线平行于坐标轴的柱面方程与平面坐标系下有关平面 曲线方程的区别; ( 2)空间坐标系下,空间曲线一般方程的规范表示。 本章教学内容: § 1 曲面的方程 普通方程: 1 定义:设工为一曲面,F(x, y, z) =0为一三元方程,空间中建立了坐标系以后, 若工上任一点P(x,y,z)的坐标都满足F(x,y, z)=0,而且凡坐标满足方程的点都在曲 面工上,则称F (x, y, z) =0为工的普通方程,记作 2:F (x, y, z) =0. 不难看出,一点在曲面2上〈一〉该点的坐标满足工的方程,即曲面上的点与其 方程的解之间是一一对应的???》的方程的代数性质必能反映出2的几何性质。 2 三元方程的表示的几种特殊图形:空间中任一曲面的方程都是一三元方程,反之,是否任一三 元方程也表示空间中的一个曲面呢?一般而言这是成立的,但也有如下特殊情况 1 ° 若F( x, y, z) =0 的左端可分解成两个(或多个)因式F1( x, y, z) 与F2 (x, y, z)的乘积,即 F (x, y, z)= F i (x, y, z) F2 (x, y, z),贝U F (x , y , z) =0〈一〉F i (x , y , z) =0 或F2 (x , y , z) =0 ,此时 F( x y z) =0 表示两叶曲面1与 2 它们分别以F1( x y z) =0 F2( x y z) =0 为其方程此时称F(x y z)=0 表示的图形为变态曲面。如 F(x,y,z) xyz 0 即为三坐标面。 2 0方程F(x,y,z) (x2 y2 z2) x i2 y 2 2 (z 3)2 0 仅表示坐标原点和点( i 2 3) 3 °方程F(x, y,z) 0可能表示若干条曲线如 F(x, y,z) (x2 y2)(y2 z2) 0 即表示z 轴和x 轴 °方程F(x, y,z) 0不表示任何实图形如 4
空间曲线与曲面的绘制
空间曲线与曲面的绘制 本实验的目的是:利用数学软件Mathematica 绘制三维图形来观察空间曲线和空间曲面图形的特 点,以加强几何的直观性。 1. 空间曲线的绘制 绘制空间曲线时一般使用曲线的参数方程,利用命令“ParametricPlot3D ”如画出参数方程「x =x(t) * y = y(t) , h Et “2所确定的空间曲线的命令格式为: Z =z(t) ParametricPlot3D[{x[t],y[t],z[t]},{t,tmi n, tmax}, 选项] 例1 画出旋转抛物面z = x2y2与上半球面z = 1亠:1 - x2- y2交线的图形。 X = cost 解:它们的交线为平面z=1上的圆x2+y2=1,化为参数方程为*y = sint,t"O,勿],下面的 z = 1 mathematica命令就是作出它们的交线并把它存在变量p中: p ParametricPlot3D Cos t , Sin t , 1 , t, 0, 2 Pi 运行即得曲线如图1所示。 在这里说明一点,要作空间曲线的图形,必须先求出该曲线的参数 乍(x, y, z) =0 方程。如果曲线为一般式,其在xOy面上的投影柱面的 面及其方程 一曲面方程的概念 空间曲面可看做点的轨迹,而点的轨迹可由点的坐标所满足的方程来表达。因此,空间曲面可由方程来表示,反过来也成立。 为此,我们给出如下定义: 若曲面 S与三元方程 F x y z (,,) 0 (1) 有下述关系: 1、曲面 S上任一点的坐标均满足方程(1); 2、不在曲面 S上的点的坐标都不满足方程(1)。 那么,方程(1)称作曲面 S的方程,而曲面S称作方程(1)的图形。 下面,我们来建立几个常见的曲面方程。 【例1】球心在点 ) , , ( z y x M ,半径为R的球面方程。 解:设M x y z (,,)是球面上的任一点,那么M M R 0=, 即: ()()()x x y y z z R -+-+-=020202 ()()()x x y y z z R -+-+-=0202022 (2) (2)式就是球面上任一点的坐标所满足的方程。 反过来,不在球面上的点 ''''M x y z (,,),'M 到M 0的距离M M R 0'≠, 从而点 'M 的坐标不适合于方程(2)。 故方程(2)就是以 M x y z 0000(,,)为球心,R 为半径的球面方程。 若球心在原点,即 M x y z O 0000000(,,)(,,)=,其球面方程为 x y z R 2222++= 【例2】设有点A (,,)123和B (,,)214-,求线段AB 垂直平分面π 的方程。 解:所求平面π是与A 和B 等距离的点的几何轨迹,设M x y z (,,)是所求平面上任意 的一点,则 AM BM = 即: ()()()()()()x y z x y z -+-+-=-+++-123214222222 第2章 曲面与空间曲线的方程 本章教学目的:通过本章学习,使学生理解空间坐标系下曲面与空间曲线方程之定 义及表示,熟悉空间中一些特殊曲面、曲线的方程。 本章教学重点:空间坐标系下曲面与空间曲线方程的定义。 本章教学难点:(1)空间坐标系下母线平行于坐标轴的柱面方程与平面坐标系下有 关平面曲线方程的区别; (2)空间坐标系下,空间曲线一般方程的规范表示。 本章教学内容: §1 曲面的方程 一 普通方程: 1 定义:设Σ为一曲面,F (x ,y ,z )=0为一三元方程,空间中建立了坐标系以后, 若Σ上任一点P (x ,y ,z )的坐标都满足F (x ,y ,z )=0,而且凡坐标满足方程的点都在曲面Σ上,则称F (x ,y ,z )=0为Σ的普通方程,记作 Σ:F (x ,y ,z )=0. 不难看出,一点在曲面Σ上〈═〉该点的坐标满足Σ的方程,即曲面上的点与其方程的解之间是一一对应的 ∴Σ的方程的代数性质必能反映出Σ的几何性质。 2 三元方程的表示的几种特殊图形: 空间中任一曲面的方程都是一三元方程,反之,是否任一三元方程也表示空间中的 一个曲面呢?一般而言这是成立的,但也有如下特殊情况 1° 若F (x ,y ,z )=0的左端可分解成两个(或多个)因式F 1(x ,y ,z ) 与F 2(x ,y ,z )的乘积,即F (x ,y ,z )≡F 1(x ,y ,z )F 2(x ,y ,z ),则 F (x ,y ,z )=0〈═〉F 1(x ,y ,z )=0或F 2(x ,y ,z )=0,此时 F (x ,y ,z )=0表示两叶曲面1∑与2∑,它们分别以F 1(x ,y ,z )=0,F 2(x ,y ,z )=0为其方程,此时称F (x ,y ,z )=0表示的图形为变态曲面。如 0),,(=≡xyz z y x F 即为三坐标面。 20方程()()[] 0)3(21)(),,(222222=-+-+-++≡z y x z y x z y x F 仅表示坐标原点和点(1,2,3) 3°方程0),,(=z y x F 可能表示若干条曲线,如 0))((),,(2 222=++≡z y y x z y x F 即表示z 轴和x 轴 4°方程0),,(=z y x F 不表示任何实图形,如 §7.4空间曲面和空间曲线 本节以两种方式来讨论空间曲面: (1)已知曲面的形状,建立这曲面的方程; (2)已知一个三元方程,研究这方程的图形。 7.4.1球面与柱面 (一)球面 空间中与一定点等距离的点的轨迹叫球面。 求球心在点),,( z y x M ,半径为R 的球面方程。 设),,(z y x M 为球面上的任一点,则有R M M = ,即 R z z y y x x =-+-+-222)()()( ,化简得: 2222)()()(R z z y y x x =-+-+- 。 ① 满足方程①,因此,方程①是球面的方程。 当0=== z y x 时,即球心在原点的球面方程为 2 222R z y x =++。 ② 例1.指出方程05642222=+--+++z y x z y x 表示何种曲面。 解:9415964412222+++-=+-++-+++z z y y x x , 22223)3()2()1(=-+-++z y x ,方程表示以)3 ,2 ,1(-为球心,3为半径的球面。 (二)柱面 动直线L 沿给定曲线C 平行移动所形成的曲面,称为柱面。动直线L 称为柱面的母线,定曲线C 称为柱面的准线。 y 现在来建立以xoy 面上的曲线C :? ??== . 0, 0),(z y x F 为准线,平行于L z 轴的直线 设) ,,( z y x M 为柱面上任一点,过 M 作平行于轴的直线 z ,交xoy 面于点 ) 0 , ,( y x M ,由柱面定义可知点上必在准线C M 。故有0),(= y x F 。由于 M M 与点点有相同的横坐标和纵坐标,故的坐标点 M 也必满足方程 0),(=y x F 。反之,如果空间一点) ,,( z y x M 满足方程0),(=y x F ,即0 ),(= y x F ,故 ) ,,( z y x M 且与轴平行的直线 z 必通过 上的点准线C ) 0 , ,( y x M ,即) 0 , ,( y x M 在过) 0 , ,( y x M 的母线上,于是) ,,( z y x M 必在柱面上,因此方程0),(=y x F 表示平行于轴的柱面 z 。 一般地 方程0) ,(=y x F 表示母线轴的柱面平行于 z ; 方程0) ,(=z y H 表示母线轴的柱面平行于 x ; 方程0) ,(=z x G 表示母线轴的柱面平行于 y 。 以二次曲线为准线的柱面称为二次柱面。 例如:方程2 2 2 a y x =+表示圆柱面;方程 12 22 2=+ b y a x 表示椭圆柱面; 方程12 2 22 =- b x a y 表示双曲柱面;方程Py x 22=表示抛物柱面。 y 22 a y = x x y 1 2 2=b y 北方工业大学 计算机图形学课程实验报告 题目:实验五曲线曲面 学院:计算机学院 专业:数字媒体技术 指导教师:蔡兴泉 学生班级: 学生学号: 学生姓名: 教师评定: 实验报告5 曲线曲面 一.实验目的 1.熟悉OpenGL图形库; 2.掌握曲线曲面实现算法。 二.实验环境 1.软件环境: 操作系统:WinXp 应用软件:VC6.0,OpenGL 2.硬件环境(查看自己的机子) CPU: Intel PIV 2.80GHz 内存RAM: 1GB 显卡:NVIDIA GeForce7650,256M显存 三.实验内容 1. 写程序实现Bezier曲线 2. 写程序实现绘制3个半径不同、颜色不同的小球 3. 写程序实现一个场景,绘制1个立方体、1个圆锥、1个圆柱、1个茶壶 四.程序及结果 1. Bezier曲线实现关键程序及注释 void RenderScene(void) { int i; glClear(GL_COLOR_BUFFER_BIT) //设置贝塞尔曲线 glMap1f(GL_MAP1_VERTEX_3, //生成的数据类型 0.0f, //u值的下界 100.0f, / //u值的上界 3, //顶点在数据中的间隔,x,y,z所以间隔是 3 nNumPoints, //u方向上的阶,即控制点的个数 &ctrlPoints[0][0]); //指向控制点数据的指针 glEnable(GL_MAP1_VERTEX_3);// //必须在绘制顶点之前开启 glBegin(GL_LINE_STRIP); //使用画线的方式来连接点 for(i = 0; i <= 100; i++) { glEvalCoord1f((GLfloat) i); //求的点坐标 } glEnd(); 第六节空间曲线的切线与空间曲面 的切平面 欧阳光明(2021.03.07) 一、空间曲线的切线与法平面 设空间的曲线C 由参数方程的形式给出:?? ???===)()()(t z z t y y t x x ,),(βα∈t . 设),(,10βα∈t t ,)(),(),((000t z t y t x A 、))(),(),((111t z t y t x B 为曲线上两点,B A ,的连线AB 称为曲线C 的割线,当A B →时,若AB 趋于一条直线,则此直线称为曲线C 在点A 的切线. 如果)()()(t z z t y y t x x ===,,对于t 的导数都连续且不全为零(即空间的曲线C 为光滑曲线),则曲线在点A 切线是存在的.因为割线的方程为 也可以写为 当A B →时,0t t →,割线的方向向量的极限为{})(),(),(000t z t y t x ''',此即为切线的方向向量,所以切线方程为 )()()()()()(000000t z t z z t y t y y t x t x x '-='-='-. 过点)(),(),((000t z t y t x A 且与切线垂直的平面称为空间的曲线C 在点)(),(),((000t z t y t x A 的法平面,法平面方程为 如果空间的曲线C 由方程为 且)(),(0'0'x z x y 存在,则曲线在点)(),(,(000x z x y x A 的切线是 法平面方程为 如果空间的曲线C 表示为空间两曲面的交,由方程组 确定时,假设在),,(000z y x A 有0),(),(≠??=A z y G F J ,在),,(000z y x A 某邻域内满足隐函数组存在定理条件,则由方程组 ? ??==0),,(0),,(z y x G z y x F ,在点),,(000z y x A 附近能确定隐函数 有)(),(0000x z z x y y ==,) ,(),(1,),(),(1x y G F J dx dz z x G F J dx dy ??-=??-=。于是空间的曲线C 在 点),,(000z y x A 的切线是 即 法平面方程为 类似地,如果在点),,(000z y x A 有0),(),(≠??A y x G F 或0),(),(≠??A x z G F 时,我们得到的切线方程和法平面方程有相同形式。 所以,当向量 时,空间的曲线C 在),,(000z y x A 的切线的方向向量为r 例6.32 求曲线θθθb z a y a x ===,sin ,cos 在点()πb a ,0,-处的切线方程. 解 当πθ=时,曲线过点()πb a ,0,-,曲线在此点的切线方向向量为 {}{}b a b a a ,,0|,cos ,sin -=-=πθθθ, 所以曲线的切线方程为 b t z z a t y y t x x )()(0)(000-=--=-.空间曲面与空间曲线学习总结
曲面与空间曲线的方程
§7.4.1-3空间曲面和空间曲线
计算机图形学曲线曲面
空间曲线的切线与空间曲面的切平面之欧阳光明创编
