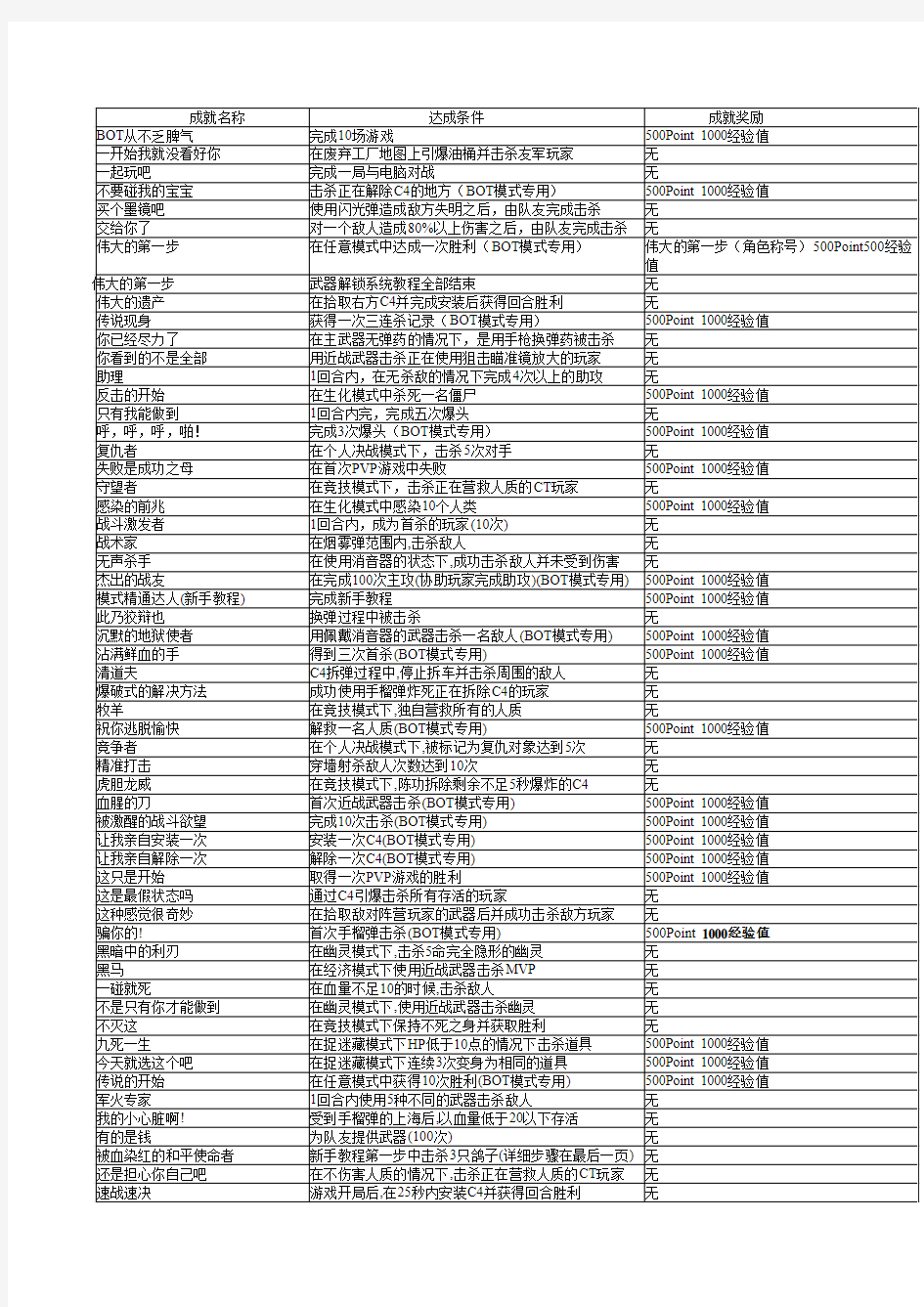
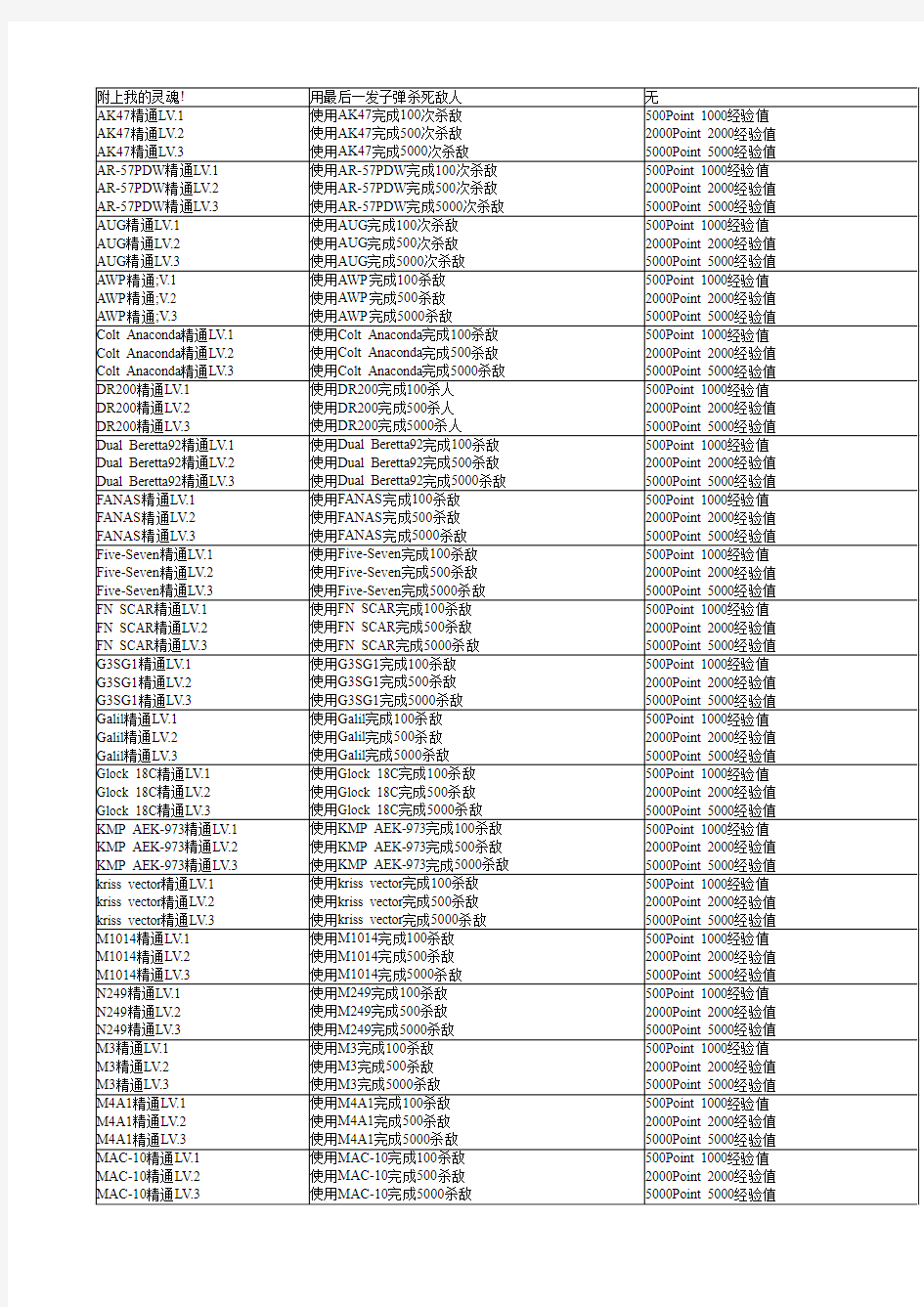
CSOL2成就表

体育高考成绩对照表(完整)

体育高考成绩对照表（女） 100米铅球立定跳远800米 分值成绩分值成绩分值成绩分值成绩 25 12〞8 25 9.6 25 2.4 25 145〞00 2ˊ25 24.68 12〞9 24.67 9.5 24.73 2.39 24.75 145〞98 2ˊ26 24.37 13〞0 24.33 9.4 24.48 2.38 24.5 146〞892ˊ27 24.07 13〞1 24 9.3 24.22 2.37 24.25 147〞84 2ˊ28 23.75 13〞2 23.67 9.2 23.97 2.36 24 148〞79 2ˊ29 23.43 13〞3 23.33 9.1 23.7 2.35 23.75 149〞73 2ˊ30 23.12 13〞4 23 9 23.45 2.34 23.5 150〞68 2ˊ31 22.8 13〞5 22.67 8.9 23.18 2.33 23.25 151〞63 2ˊ32 22.5 13〞6 22.32 8.8 22.93 2.32 23 152〞58 2ˊ33 22.18 13〞7 21.98 8.7 22.68 2.31 22.75 153〞52 2ˊ34 21.87 13〞8 21.65 8.6 22.42 2.3 22.5 154〞47 2ˊ35 21.55 13〞9 21.32 8.5 22.17 2.29 22.25 155〞42 2ˊ36 21.23 14〞0 20.98 8.4 21.92 2.28 22 156〞37 2ˊ37 20.93 14〞1 20.65 8.3 21.67 2.27 21.75 157〞32 2ˊ38 20.61 14〞2 20.32 8.2 21.4 2.26 21.5 158〞27 2ˊ39 20.3 14〞3 19.98 8.1 21.15 2.25 21.25 159〞21 2ˊ40 19.98 14〞4 19.65 8 20.9 2.24 21 160〞16 2ˊ41 19.68 14〞5 19.32 7.9 20.65 2.23 20.75 161〞11 2ˊ42 19.36 14〞6 18.98 7.8 20.4 2.22 20.5 162〞06 2ˊ43 19.05 14〞7 18.65 7.7 20.15 2.21 20.25 163〞01 2ˊ44 18.73 14〞8 18.32 7.6 19.9 2.2 20 163〞96 2ˊ45 18.43 14〞9 17.98 7.5 19.65 2.19 19.75 164〞91 2ˊ46 18.11 15〞0 17.65 7.4 19.4 2.18 19.5 165〞86 2ˊ47 17.8 15〞1 17.33 7.3 19.15 2.17 19.25 166〞81 2ˊ48 17.5 15〞2 17 7.2 18.9 2.16 19 167〞76 2ˊ49 17.18 15〞3 16.67 7.1 18.65 2.15 18.75 168〞71 2ˊ50 16.87 15〞4 16.33 7 18.42 2.14 18.5 169〞71 2ˊ51 16.55 15〞5 16 6.9 18.17 2.13 18.25 170〞62 2ˊ52 16.25 15〞6 15.67 6.8 17.92 2.12 18 171〞57 2ˊ53 15.93 15〞7 15.33 6.7 17.67 2.11 17.75 172〞52 2ˊ54 15.62 15〞8 15 6.6 17.43 2.1 17.5 173〞47 2ˊ55 15.32 15〞9 14.64 6.5 17.18 2.09 17.25 174〞42 2ˊ56 15 16〞0 14.33 6.4 16.93 2.08 17 175〞38 2ˊ57 14.68 16〞1 14 6.3 16.7 2.07 16.75 176〞33 2ˊ58 14.38 16〞2 13.67 6.2 16.45 2.06 16.5 177〞28 2ˊ59 14.07 16〞3 13.35 6.1 16.2 2.05 16.25 178〞23 2ˊ25 13.75 16〞4 13.02 6 15.97 2.04 16 179〞19 2ˊ26 13.45 16〞5 15.72 2.03 15.75 180〞14 3ˊ00〞13.13 16〞6 15.48 2.02 15.5 181〞09 3ˊ01 12.82 16〞7 15.23 2.01 15.25 182〞05 3ˊ02 12.52 16〞8 15 2 15 183〞00 3ˊ03 12.05 16〞9 14.77 1.99 14.75 183〞95 3ˊ04 11.9 17〞0 14.52 1.98 14.5 184〞91 3ˊ05 11.58 17〞1 14.28 1.97 14.25 185〞86 3ˊ06

期望 方差公式的证明全集

期望与方差的相关公式的证明 -、数学期望的来由 早在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目，题目是这样的：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，赢家可以获得100法郎的奖励。当比赛进行到第三局的时候，甲胜了两局，乙胜了一局，这时由于某些原因中止了比赛，那么如何分配这100法郎才比较公平？ 用概率论的知识，不难得知，甲获胜的概率为1/2+(1/2)*(1/2)=3/4，或者分析乙获胜的概率为(1/2)*(1/2)＝1/4。因此由此引出了甲的期望所得值为100*3/4=75法郎，乙的期望所得值为25法郎。 这个故事里出现了“期望”这个词，数学期望由此而来。 定义1 若离散型随机变量ξ可能取值为i a （i =1，2，3 ，…），其分布列为i p （i =1，2，3， …），则当i i i p a ∑ ∞ =1 <∞时， 则称ξ存在数学期望，并且数学期望为E ξ=∑∞ =1 i i i p a ， 如果i i i p a ∑ ∞ =1 =∞，则数学期望不存在。 [] 1 定义2 期望：若离散型随机变量ξ，当ξ=x i 的概率为P （ξ=x i ）=P i （i =1，2，…，n ，…），则称E ξ=∑x i p i 为ξ的数学期望，反映了ξ的平均值. 期望是算术平均值概念的推广，是概率意义下的平均.E ξ由ξ的分布列唯一确定. 二、数学期望的性质 （1）设C 是常数，则E(C )=C 。 （2）若k 是常数，则E (kX )=kE (X )。 （3）)E(X )E(X )X E(X 2121+=+。 三、 方差的定义 前面我们介绍了随机变量的数学期望，它体现了随机变量取值的平均水平，是随机变量一个重要的数字特征。但是在一些场合下，仅仅知道随机变量取值的

数学期望的计算及应用

数学期望的计算及应用 数学与应用数学111 第四小组 引言： 我们知道，随机变量的概率分布是随机变量的一种最完整的数学描述，而数学期望又是显现概率分布特性的最重要的特征数字之一。因此，掌握数学期望的计算并应用他来分析和解决实际问题显得尤为重要。在学习了概率论以后，我们计算数学期望一般有三种方法：1.从定义入手，即∑∞ == 1 )(k k k p x X E ；2. 应用随机变量函数的期望公式 ∑∞ ==1 )())((k k k p x q x q E 3. 利用期望的有关性质。但是还是会碰到许多麻烦，这里我们将 介绍一些解决这些难题的简单方法。在现实生活中，许多地方都需要用到数学期望。如果我们可以在学会怎么解决数学期望的计算之后，将数学期望应用到现实生活中。就可以解决许多问题，例如农业上，经济上等多个方面难以解决的难题。 下面就让我们来看看，除了最常用的三种计算方法之外还有哪些可以计算较为棘手的数学期望的方法。 1. 变量分解法 ] 1[ 如果可以把不易求得的随机变量X 分解成若干个随机变量之和,应用)(...)()()...(2121n n X E X E X E E E X E ++=++再进行求解得值， 这种方法就叫做变量分解法。这种方法化解了直接用定义求数学期望时的难点问题，因为每一种结果比较好计算，分开来计算便可以比较简单的获得结果。 例题1 ： 从甲地到乙地的旅游车上载有20位旅客，自甲地开出，沿途有10个车站，如到达一个车站没有旅客下车，就不停车，以X 表示停车次数，求E(X).(设每位旅客在各个车站下车是等可能的) 分析 ： 汽车沿途10站的停车次数X 所以可能取值为0，1，….，10，如果先求出X 的分布列，再由定义计算E(X)，则需要分别计算{X=0}，{X=1}，…，{X=10}等事件的概率，计算相当麻烦。注意到经过每一站时是否停车，只有两种可能，把这两种结果分别与0，1对应起来，映入随机变量i X 每一种结果的概率较易求得。把X 分解成若干个随机变量i X 之和，然后应用公式)(...)()()...(2121n n X E X E X E E E X E ++=++就能最终求出E(X)。

条件数学期望及其应用

条件数学期望及其应用 The ways of finding the inverse matrix and it ’s application Abstract ：The passage lists the ways of calculating the first type of curvilinear integral,and discusses it ’s application in geometry and in physical. Keywords ：Curvilinear integral;Continuous;Integrable; Lateral area. 0前言 在曲线积分中，被积函数可以是标量函数或向量函数.积分的值是路径各点上的函数值乘上相应的权重（一般是弧长，在积分函数是向量函数时，一般是函数值与曲线微元向量的标量积）后的黎曼和.带有权重是曲线积分与一般区间上的积分的主要不同点.物理学中的许多公式在推广之后都是以曲线积分的形式出现.曲线积分是物理学中重要的工具. 1条件数学期望 1.1条件数学期望的定义 定义1 设X 是一个离散型随机变量，取值为},,{21 x x ，分布列为},,{21 p p .又事件A 有0)(>A P ，这时 ,2,1,) ()}({)|(|=?====i A P A x X P A x X P P i i A i 为在事件A 发生条件下X 的条件分布列.如果有 ∞<∑A i i i p x | 则称 A i i i p x A X E |]|[∑=． 为随机变量X 在条件A 下的条件数学期望（简称条件期望）． 定义2 设X 是一个连续型随机变量，事件A 有0)(>A P ，且X 在条件A 之

条件数学期望及其应用

实用文档 文案大全条件数学期望及其应用 The ways of finding the inverse matrix and it's application Abstract：The passage lists the ways of calculating the first type of curvilinear integral,and discusses it's application in geometry and in physical. Keywords：Curvilinear integral;Continuous;Integrable; Lateral area. 0前言 在曲线积分中，被积函数可以是标量函数或向量函数.积分的值是路径各 点上的函数值乘上相应的权重（一般是弧长，在积分函数是向量函数时，一般是函数值与曲线微元向量的标量积）后的黎曼和.带有权重是曲线积 分与一般区间上的积分的主要不同点.物理学中的许多公式在推广之后都 是以曲线积分的形式出现.曲线积分是物理学中重要的工具. 1条件数学期望 1.1条件数学期望的定义 定义1设X是一个离散型随机变量，取值为},,{21?xx，分布列 为},,{21?pp.又事件A有0)(?AP，这时 ,2,1,)()}({)|(|??????iAPAxXPAxXPP iiAi

为在事件A发生条件下X的条件分布列.如果有 ???Aiii px| 则称 ??． Aiii pxAXE|]|[ 为随机变量X在条件A下的条件数学期望（简称条件期望）． 定义2设X是一个连续型随机变量，事件A有0)(?AP，且X在条件A 之 实用文档 ??????dxAXxf)|(称为随机变量文案大全下的条件分布密度函数为)|(Axf．若 X在条件A下的条件数学期望． 定义3设),(YX是离散型二维随机变量，其取值全体为 },2,1,),,{(??jiyx ii， 联合分布列为 ?,2,1,),,(????jiyYxXPp iiij， 在i yY?的条件下X的条件分布列为?,2,1),|(|????iyYxXPp iiji若 ???jiii px|， 则 ??? jiiii pxyYXE|]|[ 为随机变量X在i yY?条件下的条件数学期望． 定义4 设),(YX是连续型二维随机变量，随机变量X在yY?的条件下的条件密度函数为)|(|yxp YX，若 ??????dxyxpx YX)|(|， 则称

体育高考成绩对照表完整

精品文档 体育高考成绩对照表（女） 100米铅球立定跳远800米 成绩分值 成绩成绩分值分值成绩分值 00 9.6 2.4 25 〞12〞8 145 2ˊ25 25 25 25 2ˊ26 24.67 9.5 9 24.68 1452.39 24.75 〞98 24.73 12〞 2ˊ27 14624.48 2.38 13〞0 〞8924.37 24.5 24.33 9.4 224.07 24.22 2.37 9.3 24 1 〞24.25 ˊ147〞84 28 13 2148〞24 79 23.75 ˊ13〞2 23.97 2.36 9.2 23.67 29 2149〞9.1 23.33 23.7 〞3 2.35 23.43 73 ˊ23.75 30 13 2ˊ 23.5 〞68 31 4 13〞15023.45 2.34 23 23.12 9 2ˊ32 8.9 22.8 22.67 151〞5 23.18 2.33 23.25 〞63 13 2ˊ152〞2.32 58 〞1322.5 6 23 33 8.8 22.32 22.93 222.75 ˊ8.7 21.98 〞7 22.68 2.31 52 34 22.18 15313〞 222.42 21.87 2.3 ˊ8 13〞22.5 47 35 8.6 21.65 154〞 28.5 21.32 ˊ155〞21.55 22.17 2.29 22.25 42 9 13〞36 2ˊ〞140 〞37 8.4 20.98 37 21.23 22 15621.92 2.28 2ˊ21.75 21.67 2.27 38 15714〞1 〞8.3 20.65 20.93 32 21588.2 20.61 20.32 〞21.5 27 2.26 21.4 ˊ39 2 14〞 221.15 2.25 3 14〞ˊ20.3 21 8.1 19.98 159〞21.25 40

概率、期望与方差的计算和性质

概率与统计 知识点一：常见的概率类型与概率计算公式； 类型一：古典概型； 1、 古典概型的基本特点： （1） 基本事件数有限多个； （2） 每个基本事件之间互斥且等可能； 2、 概率计算公式： A 事件发生的概率()A P A = 事件所包含的基本事件数 总的基本事件数 ; 类型二：几何概型； 1、 几何概型的基本特点： （1） 基本事件数有无限多个； （2） 每个基本事件之间互斥且等可能； 2、 概率计算公式： A 事件发生的概率()A P A = 构成事件的区域长度（或面积或体积或角度） 总的区域长度（或面积或体积或角度） ； 注意： （1） 究竟是长度比还是面积比还是体积比，关键是看表达该概率问题需要几个变量，如 果需要一个变量，则应该是长度比或者角度比；若需要两个变量则应该是面积比；当然如果是必须要三个变量则必为体积比； （2） 如果是用一个变量，到底是角度问题还是长度问题，关键是看谁是变化的主体，哪 一个是等可能的； 例如：等腰ABC ?中，角C= 23 π ，则： （1） 若点M 是线段AB 上一点，求使得AM AC ≤的概率； （2） 若射线CA 绕着点C 向射线CB 旋转，且射线CA 与线段AB 始终相交且交点是M ，求 使得AM AC ≤的概率； 解析：第一问中明确M 为AB 上动点，即点M 是在AB 上均匀分布，所以这一问应该是长度 之比，所求概率： 13P =; 而第二问中真正变化的主体是射线的转动，所以角度的变化是均匀的，所以这一问应该是角度之比的问题，所以所求的概率：2755 = =1208 P ?； 知识点二：常见的概率计算性质； 类型一：事件间的关系与运算； A+B （和事件）：表示A 、B 两个事件至少有一个发生； A B ?（积事件） ：表示A 、B 两个事件同时发生； A （对立事件） ：表示事件A 的对立事件；

托福阅读分数对照表

常常有考友询问，为什么托福阅读明明有42个题，总分却只有30分，分数如何计算的呢？其实，每每看到这种问题，小编的内心是疼痛的。 大家准备一个考试，却不看考试指导手册，考得不太理想，简直太正常了。就算天生神勇，也应该有个作战纲领呀！ 打开OG，第一部分就是托福阅读的介绍，编者首先给出了评分标准的表格。 紧接着给出了各类题型的题型解析，这些就是托福阅读的考察内容，众位考友一定要反复研究，在准备考试时，下意识的按照出题者的思路去解题。 那么托福阅读有些什么考察类型？应该怎么解题？

在iBT阅读中，甚至可以扩展到ETS所有考试的阅读题目中，无论是题干还是正确选项，大都能在原文中找出一句话来与之相对应。即题目是原文的意译。这种意译是通过同义词来完成的。即题干中多用近义词来对原文中的句子进行替换，来达到提出问题或者提出正确答案的意思。准确把握意译，是多数题目中准确在原文中定位信息、或者在迷惑选项中选出正确的那个，都有着重要的作用。 1、词汇题 解题方法：若认识，直接解题，没得说；若不认识，就只能推断了。 但是备考阶段最重要的一点。背单词！首先，考托福没有一定的词汇量等于直接酱油了，所以词汇量是一切的基础。 2、指代题 考点：句子直接词之间的关系 解题方法： （1）代词 a. 从句的主语指代主句的主宾语(使用属性判断,不用含义) b. 关系代词指代先行词(插入结构不影响指代关系) c. 重复概念指代: Tom and his cat(就近原则) d. some 和 others （2）名词 a. 优先选择题干的上下意词 m is a kind of M, M是m的上意词 b. 若上下意词不唯一则当作代词指代处理 注意: a.被指代对象往往在代词之前出现 b. 从句开头往后找答案 c. 代词和被指代对象的数性和性质必须一致 d. 指代的传递现象 3、句子简化题 解题方法： （1）确定题干句子中的逻辑成分 逻辑成分主要包括：关联词，动词，状语 而托福最爱考的逻辑主要是：因果，比较、最高级，否定 （2）确定与逻辑相关的语义 要依据最简化原则，抓句子中的逻辑要素。 因果的逻辑要素是：原因结果 比较的逻辑要素是：比较三要素 最高级 否定的逻辑要素是：作用对象 （3）选择与题干逻辑语义一致的选项 先主后次，从逻辑到语义（千万要保证逻辑正确） 很多时候，光凭逻辑关系，就能选出正确选项。越复杂越长的句子，更需要很快地抓住句内的逻辑关系。然后快速看选项，找出逻辑一致的选项。 4、句子插入题

体育高考四项成绩表格模板

100米立定跳远 成绩(S)分值2成绩(m)分值2 12.825.00 2.4025.00 12.924.68 2.3924.73 13.024.37 2.3824.48 13.124.07 2.3724.22 13.223.75 2.3623.97 13.323.43 2.3523.70 13.423.12 2.3423.45 13.522.80 2.3321.52 13.622.50 2.3222.93 13.722.18 2.3122.68 13.821.87 2.3022.42 13.921.55 2.2922.17 14.021.23 2.2821.92 14.120.93 2.2721.67 14.220.62 2.2621.40 14.320.30 2.2521.15 14.419.98 2.2420.90 14.519.68 2.2322.32 14.619.37 2.2220.40 14.719.05 2.2120.15 14.818.73 2.2019.90 14.918.43 2.1919.65 15.018.12 2.1819.40 15.117.80 2.1719.15 15.217.50 2.1618.90 15.317.18 2.1518.65 15.416.87 2.1418.42 15.516.55 2.1318.17 15.616.25 2.1217.92 15.715.93 2.1117.67 15.815.62 2.1017.37 15.915.32 2.0917.18 16.015.00 2.0816.93 16.114.68 2.0716.70 16.214.38 2.0415.87 16.314.07 2.0315.72 16.413.75 2.0215.48 16.513.45 2.0115.23 16.613.13 2.0015.00 16.712.82 1.9914.77

各科学习成绩分析表[1]

各科学习成绩分析表 第四步，有针对性地提出改进措施。 第五步，制定周学习计划，具体落实。 第周学习计划表 最后，教师总结。可选择好的学习计划组织交流，亦可举行展览，组织讨论、评价，然后总结。 [过程二] 探讨有效的学习方法 第一步，简要说明学习方法的重要性，然后将下述三种不同的学习方法写在黑板上，或用投影仪打在屏幕上，请同学们分析A和B哪种学习方法更好、更有效，并填写在题后的括号内。 1．学习英语单词( ) A. 反复读B．边读、边听 2．上课听讲( )

A．注意听B．注意听，重点记 3．课后作业( ) A. 翻开书就做题 B．先复习后做题 第二步，给10分钟，要求学生以语文、数学和外语为例，写出自己的学习方法。 第三步，分组交流，选出代表准备发言。 第四步，全班交流，共同评价。 最后，教师总结，要求小学生根据交流的结果，补充、完善和改进自己的学习方法。 [过程三] 养成良好的学习习惯 第一步，将学习习惯检查表印发给学生，人手一份。 第二步，指导小学生阅读、填写。 指导语：请同学们仔细阅读表中的每一个问题，结合自己的具体情况，想想看，认为符合自己的实际，就在题号后面的括号里打上“√”号，不符合的就打“×”号，并举例演示。然后问：懂了吗？会不会做？好，懂了就从第一题开始做，不要漏题，做好了再检查一遍，50个题是不是都做了，开始。 小学生学习习惯检查表 *1．上课时，必要的学习用品都带齐了。 ( ) 2．经常迟到。 ( ) *3．总是在前一天备齐学习用品。 ( ) *4．课堂上能积极提问或回答问题。 ( ) 5．上课时，在笔记本上乱写乱画。 ( ) *6．能爱护教科书和参考书。 ( )

等级制与百分制成绩对应表

深圳大学 Shenzhen University 课程等级成绩、绩点与综合基本成绩的对照说明 Conversion of Grade, Grade Point and Integrated Score 我校本科生课程成绩评定采用等级制。非设计和实践类的专业课程期末考试设附加题，其等级成绩由平时成绩、期末基本题成绩和附加题成绩综合评定；期末考试不设附加题的其他课程，等级成绩由平时成绩和基本题成绩综合评定。 Grade system is adopted in Shenzhen University for undergraduate students. Extra score questions are included in the final examination paper for specialized courses without design task or practice work, and the finalized grade is given on the basis of the continuous assessment, final examination score and extra score. The grade for other courses without extra score questions is based on the continuous assessment and final examination score. 注：1.非设计和实践类的专业课程成绩最高等级为A+，其他课程的成绩最高等级为A。 2.综合基本成绩由平时成绩和期末基本题成绩按一定比例计算。 Note： 1.The highest grade for non-design and non-practice specialized courses is A+. For the rest courses, the highest grade is capped at A. 2.Integrated score is composed of continuous assessment and final examination score at a certain proportion. 深圳大学教务部 Department of Academic Affairs Shenzhen University

数学期望的计算方法探讨

数学期望的计算方法探讨 X 覃光莲 (华中农业大学理学院数学与信息科学系, 湖北武汉430070) 摘要本文探讨了各种简化计算随机变量数学期望的方法: 利用一些特殊求和与积分公 式、利用数学期望定义的不同形式、利用随机变量分布的对称性、全期望公式以及特征函数等, 以期对该内容的学习和教学有所启发。 关键词数学期望全期望公式特征函数 中图分类号G642 文献标识码 A 随机变量的数学期望是反映随机变量取值的集中位置的一个重要数字特征, 随机变量的其它 数字特征都是通过数学期望来定义的, 因此数学期望的计算问题显得非常重要。求随机变量的数 学期望从模型本身来讲, 无非是计算EX = Σ ∞ i = 1 x i P( X = x i) 或EX =∫+ ∞ - ∞ x p ( x ) dx ,但涉及到随 机变量分布的各具体场合,其计算又有很多变化和技巧。下面结合具体场合, 介绍一些简化计算数 学期望的不同方法。 一、利用一些特殊的求和与积分公式 (一) X 是离散型随机变量时, EX = Σ ∞ i =1 x i P( X = x i) 在计算离散型随机变量的数学期望时,常常会用到一些特殊的无穷级数的求和公式,如Σ ∞ k = 0 x k k ! = e x 、Σ ∞ k =0 x k = 1 1 - x (| x | < 1) 等,熟悉这些求和公式以及它们的各种变形往往会使计算变得简 单。

例设X 服从参数为P 的几何分布,求EX , E X2 解: EX = Σ ∞ i =1 i P( x = i) = Σ ∞ i = 1 i P(1 - p) i - 1 = PΣ∞ i =1 i (1 - p) i - 1 为了求级数Σ ∞ i = 1 i (1 - p) i - 1 ,可作如下考虑:由于Σ ∞ k = 0 x k = 1 1 - x (| x | < 1) 利用和函数的可微性对此级数逐项求导,得 d dx (Σ ∞ k =0 x k) = Σ ∞ k = 0 d dx ( x k) = Σ ∞ k = 1 k x k - 1 ,因此Σ ∞ k = 1 k x k - 1 = d dx ( 1 1 - x ) = 1

期望公式

期望公式 弗鲁姆认为，人们采取某项行动的动力或激励力取决于其对行动结果的价值评价和预期达成该结果可能性的估计。换言之，激励力的大小取决于该行动所能达成目标并能导致某种结果的全部预期价值乘以他认为达成该目标并得到某种结果的期望概率。用公式可以表示为： M = ∑ V × E M 表示激发力量，是指调动一个人的积极性，激发人内部潜力的强度。V 表示效价，是指达到目标对于满足个人需要的价值。E 是期望值，是人们根据过去经验判断自己达到某种目标或满足需要的可能性是大还是小，即能够达到目标的主观概率。 期望理论的公式为：激励（motivation）取决于行动结果的价值评价（即“效价”valence）和其对应的期望值（expectancy）的乘积： M=∑V×E 效价（V）——工作态度 效价，是指达到目标对于满足他个人需要的价值。同一目标，由于各个人所处的环境不同，需求不同，其需要的目标价值也就不同。同一个目标对每一个人可能有三种效价：正、零、负。如果个人喜欢其可得的结果，则为正效价；如果个人漠视其结果，则为零值；如果不喜欢其可得的结果，则为负效价。效价越高，激励力量就越大。 该理论指出，效价受个人价值取向、主观态度、优势需要及个性特征的影响。可以根据行为的选择方向进行推测，假如个人可以自由地选择X结果和Y结果的任一个，在相等的条件下：如果选择X，即表示X比Y具有正效价；如果选择Y，则表示Y比X具有正效价。也可以根据观察到的需求完成行为来推测。例如有人认为有价值的事物，另外的人可能认为全无价值。如1000元奖金对生活困难者可能很有价值，而对百万富翁来说意义不大。一个希望通过努力工作得到升迁机会的人，在他心中，“升迁”的效价就很高；如果他对升迁漠不关心，毫无要求，那么升迁对他来说效价就等于零；如果这个人对升迁不仅毫无要求，而且害怕升迁，那么，升迁对他来说，效价就是负值。再例如，吃喝的数量和质量可以表明需求完成的情况，如果吃得多、吃得快，说明食品具有正效价。 期望值（E）——工作信心 期望值，是人们判断自己达到某种目标或满足需要的可能性的主观概率。目标价值大小直接反映人的需要动机强弱，期望概率反映人实现需要和动机的信心强弱。弗鲁姆认为，人总是渴求满足一定的需要并设法达到一定的目标。这个目标在尚未实现时，表现为一种期望，期望的概念就是指一个人根据以往的能力和经验，在一定的时间里希望达到目标或满足需要的一种心理活动。 对于目标的期望值怎样才算适合？有人把它形容为摘苹果。只有跳起来能摘到苹果时，人才最用力去摘。倘若跳起来也摘不到，人就不跳了。如果坐着能摘到，无需去跳，便不会使人努力去做。由此可见，领导者给员工制订工作定额时，要让员工经过努力就能完成，再努力就能超额，这才有利于调动员工的积极性。定额太高使员工失去完成的信心，他就不努力去做；太低，唾手可得，员工也不会努力去做。因为期望概率太高、太容易的工作会影响员工的成就感，失去目标的内在价值。所以领导者制订工作、生产定额，以及使员工获得奖励的可能性都有个适度问题，只有适度才能保持员工恰当的期望值。

期望_方差公式

期望与方差的相关公式 -、数学期望的来由 早在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目，题目是这样的：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，赢家可以获得100法郎的奖励。当比赛进行到第三局的时候，甲胜了两局，乙胜了一局，这时由于某些原因中止了比赛，那么如何分配这100法郎才比较公平？ 用概率论的知识，不难得知，甲获胜的概率为1/2+(1/2)*(1/2)=3/4，或者分析乙获胜的概率为(1/2)*(1/2)＝1/4。因此由此引出了甲的期望所得值为100*3/4=75法郎，乙的期望所得值为25法郎。 这个故事里出现了“期望”这个词，数学期望由此而来。 定义1 若离散型随机变量ξ可能取值为i a （i =1，2，3 ，…），其分布列为i p （i =1，2，3， …），则当i i i p a ∑∞ =1 <∞时，则称ξ存在数学期望，并且数学期望为E ξ=∑∞ =1 i i i p a ， 如果i i i p a ∑∞ =1 =∞，则数学期望不存在。[]1 定义2 期望：若离散型随机变量ξ，当ξ=x i 的概率为P （ξ=x i ）=P i （i =1， 2，…，n ，…），则称E ξ=∑x i p i 为ξ的数学期望，反映了ξ的平均值. 期望是算术平均值概念的推广，是概率意义下的平均.E ξ由ξ的分布列唯一确定. 二、数学期望的性质 （1）设C 是常数，则E(C )=C 。 （2）若k 是常数，则E (kX )=kE (X )。 （3）)E(X )E(X )X E(X 2121+=+。 三、 方差的定义 前面我们介绍了随机变量的数学期望，它体现了随机变量取值的平均水平，

全能成绩(得分)换算查分表

总分成绩分数成绩分数成绩分数成绩分数成绩分数成绩分数成绩分数成绩分数成绩分数成绩分数100米跳远铅球跳高400米110米栏铁饼撑竿跳高标枪 1500米 100 11.7 711 6.00 587 12.0 607 1.75 585 51.0 769 16.5 677 28.0 425 3.15 393 47.0 545 4.50.0 619 5918 98 711 5.95 576 11.9 601 1.72 560 51.5 747 16.6 667 27.5 416 3.10 381 46.2 533 4.52.0 607 5799 96 711 5.90 565 11.8 595 52.0 725 16.7 656 27.0 426 46.0 530 4.54.0 595 5744 94 11.8 691 5.85 554 11.7 589 1.69 536 52.5 703 16.8 645 26.5 396 3.05 369 45.8 527 4.56.0 583 5593 92 691 5.80 544 11.6 583 53.0 682 16.9 635 26.0 387 45.4 521 4.58.0 571 5519 90 11.9 671 5.75 533 11.5 576 1.66 512 53.5 660 17.0 624 25.5 377 3.00 357 45.0 516 5.00.0 560 5386 88 671 5.70 523 11.4 570 54.0 640 17.1 614 25.0 367 44.4 507 5.02.0 548 5309 86 12.0 651 5.65 512 11.3 564 1.63 488 54.5 619 17.2 604 24.5 358 2.95 345 43.8 498 5.04.0 537 5176 84 651 5.60 502 11.2 558 55.0 599 17.3 593 24.0 348 43.2 489 5.06.0 526 5099 82 12.1 631 5.55 492 11.1 552 1.60 464 55.5 579 17.4 583 23.5 339 2.90 333 42.6 480 5.08.0 515 4968 80 631 5.50 481 11.0 546 56.0 559 17.5 573 23.0 329 42.0 472 5.10.0 504 4892 78 12.2 612 5.45 471 10.8 534 1.57 441 56.5 540 17.6 563 22.5 319 2.85 321 41.2 460 5.12.0 493 4754 76 612 5.40 461 10.6 522 57.0 521 17.7 553 22.0 310 40.4 448 5.14.0 482 4671 74 12.3 593 5.35 451 10.4 510 1.54 419 57.5 502 17.8 543 21.5 301 2.80 309 39.6 437 5.16.0 471 4536 72 593 5.30 441 10.2 498 58.0 484 17.9 534 21.0 291 38.8 425 5.18.0 461 4455 70 12.4 573 5.25 431 10.0 486 1.51 396 58.5 466 18.1 515 20.5 282 2.75 298 38.0 414 5.20.0 450 4311 68 573 5.20 421 9.8 474 59.0 448 18.3 496 20.0 272 37.0 400 5.22.0 440 4218 66 12.5 556 5.15 411 9.6 462 1.48 374 59.5 430 18.5 477 19.5 263 2.70 286 36.0 385 5.24.0 429 4073 64 12.6 538 5.10 402 9.4 450 1.00.0 413 18.7 459 19.0 254 35.0 371 5.26.0 419 3966 62 12.7 520 5.05 392 9.2 438 1.45 352 1.01.0 380 18.9 441 18.5 244 2.65 275 34.0 357 5.28.0 409 3808 60 12.8 502 5.00 382 9.0 426 1.02.0 348 19.1 424 18.0 235 33.0 342 5.30.0 399 3685 58 13.1 451 4.95 373 8.8 424 1.42 331 1.02.5 332 19.4 398 17.5 226 2.60 264 31.0 314 5.35.0 375 3478 56 13.2 434 4.90 363 8.8 424 1.03.0 317 19.6 381 17.0 217 30.0 300 5.37.0 366 3384 54 13.3 418 4.85 354 8.7 418 1.39 310 1.03.5 302 19.8 365 16.5 208 2.55 253 29.0 286 5.39.0 356 3280 52 13.4 402 4.80 345 8.7 418 302 20.0 349 16.0 198 28.0 272 5.41.0 347 3203 50 13.5 387 4.75 335 8.6 402 1.36 290 1.04.0 287 20.2 334 15.5 189 2.50 242 27.0 258 5.43.0 338 3062 48 13.7 356 4.70 326 8.6 399 1.04.5 273 20.4 318 15.0 180 26.5 251 5.45.0 329 2964 46 13.8 341 4.65 317 8.5 396 1.33 270 1.05.0 259 20.6 303 14.8 177 2.45 231 26.0 244 5.47.0 320 2858 44 13.9 327 4.60 308 8.5 393 1.05.5 245 20.8 289 14.6 173 25.5 237 5.49.0 311 2794 42 14.0 312 4.55 299 8.4 390 1.30 250 1.06.0 232 21.0 274 14.4 169 2.40 220 25.0 230 5.51.0 302 2678 40 14.1 298 4.50 290 8.4 387 1.06.5 219 21.2 261 14.2 166 24.5 223 5.53.0 293 2607 38 14.2 284 4.45 281 8.3 385 1.27 231 1.07.0 206 21.4 247 14.1 164 2.35 210 24.0 216 5.55.0 285 2509 36 14.3 271 4.40 273 8.3 381 1.07.5 194 21.6 234 14.0 162 23.5 209 5.57.0 276 2441

数学期望的计算方法及其应用

数学期望的计算方法及其应用 摘要：在概率论中，数学期望是随机变量一个重要的数字特征，它比较集中的反映了随机变量的某个侧面的平均性，而且随机变量的其他数字特征都是由数学期望来定义的，因此对随机变量的数学期望的计算方法的研究与探讨具有很深的实际意义。本论文着重总结了随机变量的数学期望在离散型随机变量分布与连续型随机变量分布下的一些常用的计算方法，如利用数学期望的定义和性质，利用不同分布的数学期望公式等等，并通过一些具体的例子说明不停的计算方法在不同情况下的应用，以达到计算最简化的目的。本文还通过介绍了一些随机变量数学期望的计算技巧，并探讨了各种简化计算随机变量数学期望的方法，利用一些特殊求和与积分公式，利用数学期望定义的不同形式，利用随机变量分布的对称性、重期望公式以及特征函数等，并通过例题使我们更加了解和掌握这些计算技巧，已达到学习该内容的目的。 关键词：离散型随机变量 连续型随机变量 数学期望 计算方法 ABSTRACT ： 第一节 离散型随机变量数学期望的计算方法及应用 1.1 利用数学期望的定义，即定义法[1] 则随机变量Ｘ的数学期望E(X)=)(1 i n i i x p x ∑=

学期望不存在[]2 例1 某推销人与工厂约定，永川把一箱货物按期无损地运到目的地可得佣金10元，若不按期则扣2元，若货物有损则扣5元，若既不按期又有损坏则扣16元。推销人按他的经验认为，一箱货物按期无损的的运到目的地有60﹪把握，不按期到达占20﹪，货物有损占10﹪，不按期又有损的占10﹪。试问推销人在用船运送货物时，每箱期望得到多少？ 按数学期望定义，该推销人每箱期望可得 =)(X E 10×0.6＋8×0.2＋5×0.1－6×0.1＝7.5元 1.2 公式法 对于实际问题中的随机变量，假如我能够判定它服从某重点性分布特征（如二项分布，泊松分布，超几何分布等），则我们就可以直接利用典型分布的数学期望公式来求此随机变量的期望。 （1） 二点分布： X ~??? ? ??-p p 101 ，则()p X E = （2） 二项分布：),(~p n B X ，10 p ，则np X E =)( （3） 几何分布：)(~p G X ,则有p X E 1)(= （4） 泊松分布：)(~λP X ，有λ=)(X E （5） 超几何分布： ),,(~M N n h X ,有N M n X E =)( 例2 一个实验竞赛考试方式为：参赛者从6道题中一次性随机抽取3道题,按要求独立完成题目.竞赛规定：至少正确完成其中2题者方可通过,已知6道备选题中参赛者甲有4题能正确 分别求出甲、乙两参赛者正确完成题数的数学期望. 解 设参赛者甲正确完成的题数为X ,则X 服从超几何分布,其中 6,4,3N M n ===, 设参赛者乙正确完成的题数为Y ,则 )32,3(~B Y ,23 2 3)(=?==np Y E 1.3 性质法

期望-方差公式

盛年不重来，一日难再晨。及时宜自勉，岁月不待人。 盛年不重来，一日难再晨。及时宜自勉，岁月不待人。 期望与方差的相关公式 -、数学期望的来由 早在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目，题目是这样的：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，赢家可以获得100法郎的奖励。当比赛进行到第三局的时候，甲胜了两局，乙胜了一局，这时由于某些原因中止了比赛，那么如何分配这100法郎才比较公平？ 用概率论的知识，不难得知，甲获胜的概率为1/2+(1/2)*(1/2)=3/4，或者分析乙获胜的概率为(1/2)*(1/2)＝1/4。因此由此引出了甲的期望所得值为100*3/4=75法郎，乙的期望所得值为25法郎。 这个故事里出现了“期望”这个词，数学期望由此而来。 定义1 若离散型随机变量ξ可能取值为i a （i =1，2，3 ，…），其分布列为i p （i =1，2，3， …），则当i i i p a ∑∞ =1 <∞时，则称ξ存在数学期望，并且数学期望为E ξ=∑∞ =1 i i i p a ， 如果i i i p a ∑∞ =1 =∞，则数学期望不存在。[]1 定义2 期望：若离散型随机变量ξ，当ξ=x i 的概率为P （ξ=x i ）=P i （i =1，2，…，n ，…），则称E ξ=∑x i p i 为ξ的数学期望，反映了ξ的平均值. 期望是算术平均值概念的推广，是概率意义下的平均.E ξ由ξ的分布列唯一确定. 二、数学期望的性质 （1）设C 是常数，则E(C )=C 。 （2）若k 是常数，则E (kX )=kE (X )。 （3）)E(X )E(X )X E(X 2121+=+。 三、 方差的定义