拉普拉斯变换和Z变换表
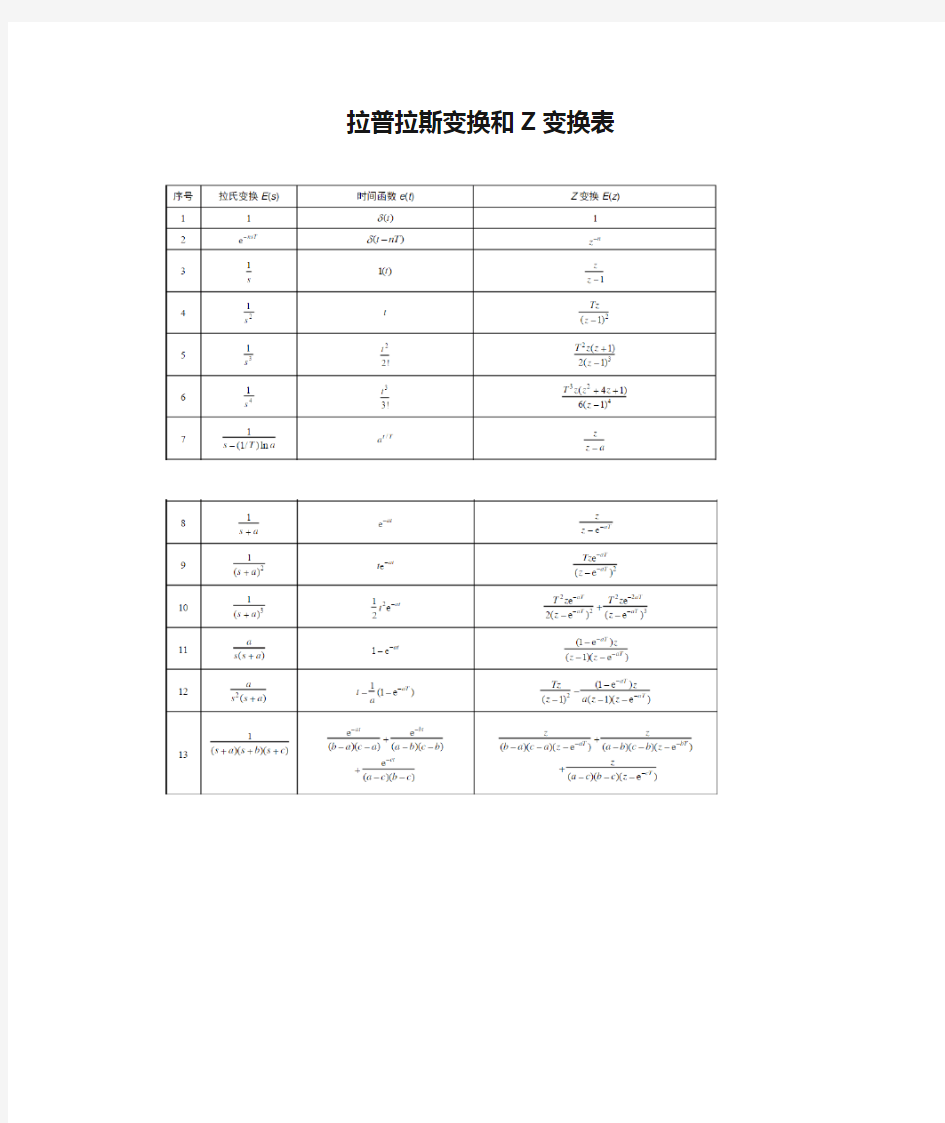
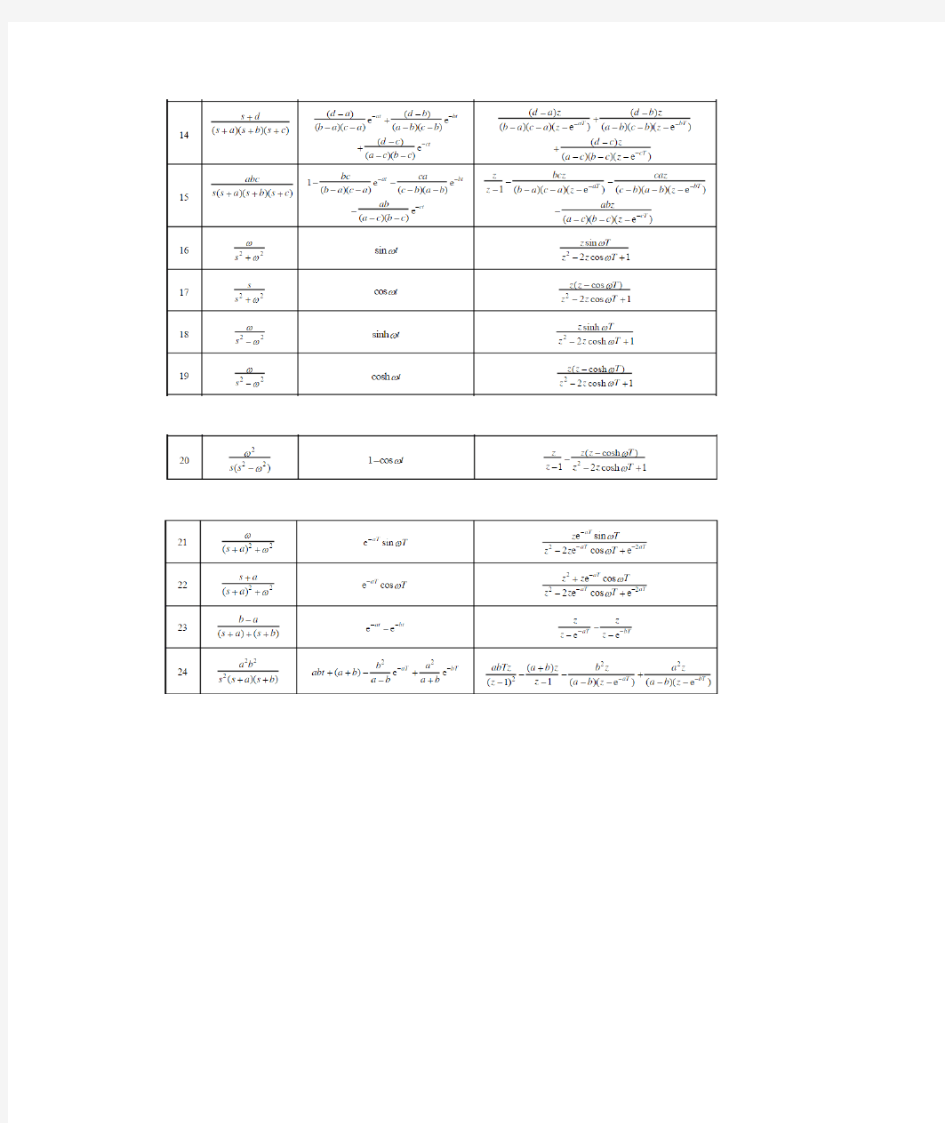
拉普拉斯变换和Z变换表
拉氏变换、传递函数、数学模型18页word文档
拉普拉斯变换的数学方法 一、拉氏变换与拉氏及变换的定义 1、拉氏变换:设有时间函数()t F ,其中0t ≥,则f(t)的拉氏变换记作: 称L —拉氏变换符号;s-复变量; F(s)—为f(t)的拉氏变换函数,称为象函数。 f(t)—原函数 拉氏变换存在,f(t)必须满足两个条件(狄里赫利条件): 1)在任何一有限区间内,f(t)分断连续,只有有限个间断点。 2)当∞→t 时,at Me )t (f ≤,M ,a 为实常数。 2、拉氏反变换:将象函数F (s )变换成与之相对应的原函数f(t)的过程。 1L -—拉氏反变换符号 关于拉氏及变换的计算方法,常用的有:①查拉氏变换表;②部分分式展开法。 二、典型时间函数的拉氏变换 在实际中,对系统进行分析所需的输入信号常可化简成一个成几个简单的信号,这些信号可用一些典型时间函数来表示,本节要介绍一些典型函数的拉氏变换。 1.单位阶跃函数 2.单位脉冲函数 3.单位斜坡函数 4.指数函数at e 5.正弦函数sinwt 由欧拉公式:wt sin j wt cos e jwt += 所以,)e e (j 21wt sin jwt jwt --= 6.余弦函数coswt 其它的可见表2-1:拉氏变换对照表
三、拉氏变换的性质 1、线性性质 若有常数k 1,k 2,函数f 1(t),f 2(t),且f 1(t),f 2(t)的拉氏变换为F 1(s),F 2(s), 则 有 : F k )s (F k )]t (f k )t (f k [L 2112211+=+,此式可由定义证明。 2、位移定理 ?? ?复数域的位移定理实数域的位移定理 (1)实数域的位移定理 若f(t)的拉氏变换为F(s),则对任一正实数a 有 ) s (F e )]a t (f [L as -=-, 其中,当t<0时,f(t)=0,f(t-a)表 f(t)延迟时间a. 证明:?∞ --=-0st dt e )a t (f )]a t (f [L ,
元器件对照表
protues元件库中英文对照表,对初学者找不到元件的很有用元件名称中文名说明 7407 驱动门 1N914 二极管 74Ls00 与非门 74LS04 非门 74LS08 与门 74LS390 TTL 双十进制计数器 7SEG 4针BCD-LED 输出从0-9 对应于4根线的BCD码7SEG 3-8译码器电路BCD-7SEG转换电路ALTERNATOR 交流发电机 AMMETER-MILLI mA安培计 AND 与门 BATTERY 电池/电池组 BUS 总线CAP 电容 CAPACITOR 电容器 CLOCK 时钟信号源 CRYSTAL 晶振 D-FLIPFLOP D触发器 FUSE 保险丝 GROUND 地 LAMP 灯
LED-RED 红色发光二极管 LM016L 2行16列液晶可显示2行16列英文字符,有8位数据总线D0-D7,RS,R/W,EN三个控制端口(共14线),工作电压为5V。没背光,和常用的1602B功能和引脚一样(除了调背光的二个线脚) LOGIC ANALYSER 逻辑分析器 LOGICPROBE 逻辑探针 LOGICPROBE[BIG] 逻辑探针用来显示连接位置的逻辑状态 LOGICSTATE 逻辑状态用鼠标点击,可改变该方框连接位置的逻辑状态LOGICTOGGLE 逻辑触发 MASTERSWITCH 按钮手动闭合,立即自动打开 MOTOR 马达 OR 或门 POT-LIN 三引线可变电阻器 POWER 电源 RES 电阻 RESISTOR 电阻器 SWITCH 按钮手动按一下一个状态 SWITCH-SPDT 二选通一按钮 VOLTMETER 伏特计 VOLTMETER-MILLI mV伏特计 VTERM 串行口终端 Electromechanical 电机Inductors 变压器
拉普拉斯变换在求解微分方程中的应用
目录 拉普拉斯变换在求解微分方程中的应用 物理系0801班学生岳艳林 指导老师韩新华 摘要:拉普拉斯变换在求解微分方程中有非常重要的作用,本文首先介绍拉普拉斯变换的定义及性质; 其次给出拉普拉斯变换求解微分方程的一般步骤;然后重点举例拉普拉斯变换在求解常微分方程(初值问题与边 函数的常微分方程、常微分方程组、拉普拉斯变换在求解微分方程值问题、常系数与变系数常微分方程、含 特解中的应用、拉普拉斯变换在求解高阶微分方程的推广)与典型偏微分方程(齐次与非齐次偏微分方程、有界 与无界问题)中的应用举例;最后综合比较、归纳总结拉普拉斯变换在求解微分方程中的优势以及局限性。 关键词:拉普拉斯变换;拉普拉斯逆变换;常微分方程;偏微分方程;特解
引言 傅里叶变换和拉普拉斯变换是常用的积分变换,但对函数进行傅里叶变换时必须满足狄里希利和在+∞<<∞-t 内绝对可积,但是在物理、无线电技术等实际应用中,许多以时间t 为自变量的函数通常在0t <时不需要考虑或者没有意义,像这样的函数不能取傅里叶变换。为避免上述两个缺点,将函数进行适当改造,便产生了拉普拉斯变换[1]。 1 拉普拉斯变换以及性质 拉普拉斯变换的定义 设函数()f t 当0t ≥时有定义,而且积分 ()st f t e dt +∞ -? (s 是一个复参量)在s 的某一区域内收 敛,则此积分所确定的函数可写为0 ()()st F s f t e dt +∞ -= ? .我们称上式为函数()f t 的Laplace 变换 式.记为()[()]F s L f t =,()F s 称为()f t 的Laplace 变换(或称为象函数). 若()F s 是()f t 的Laplace 变换,则称()f t 为()F s 的Laplace 逆变换(或称为象原函数),记为1()[()]f t L F s -=[2]. Laplace 变换的存在定理 若函数()f t 满足下列条件: 1?在0t ≥的任一有限区间上分段连续; 2?当t →+∞时,()f t 的增长速度不超过某一指数函数,亦即存在常数0M >及0c ≥,使得c ()0f t Me t ≤≤<+∞t,成立(满足此条件的函数,称它的增大是不超过指数级的,c 为它的增长指数). 则()f t 的Laplace 变换0 ()st F f t e dt +∞ -?(s )=在半平面Re()s c >上一定存在,右端的积分在1Re()s c c ≥>的半平面内,()F s 为解析函数[2]. 拉普拉斯变换的性质 ⑴线性性质 若αβ,是常数,11[()]()L f t F s =, 22[()]()L f t F s =, 则有1212[()()][(t)]+[()]L f t f t L f L f t αβαβ+=, 1111212[()()][(s)]+[()]L F s F s L F L F s αβαβ---+=. ⑵微分性质 若[()]()L f t F s =,则有'[()]()(0)L f t sF s f =-. 高阶推广 若[()]()L f t F s =,则有2'[()]()(0)(0)L f t s F s sf f ''=--.
拉普拉斯变换在求解微分方程中的应用
目录 引言 (1) 1 拉普拉斯变换以及性质 (1) 1.1拉普拉斯变换的定义 (1) 1.2拉普拉斯变换的性质 (2) 2 用拉普拉斯变换求解微分方程的一般步骤 (3) 3 拉普拉斯变换在求解常微分方程中的应用 (4) 3.1初值问题与边值问题 (4) 3.2常系数与变系数常微分方程 (5) 3.3含 函数的常微分方程 (6) 3.4常微分方程组 (7) 3.5拉普拉斯变换在求解非齐次微分方程特解中的应用 (7) 3.6拉普拉斯变换在求解高阶微分方程中的推广 (11) 4 拉普拉斯变换在求解偏微分方程中的应用 (12) 4.1齐次与非齐次偏微分方程 (12) 4.2有界与无界问题 (15) 5 综合比较,归纳总结 (19) 结束语 (20) 参考文献 (20) 英文摘要 (21) 致谢 (21)
拉普拉斯变换在求解微分方程中的应用 物理系0801班 学 生 岳艳林 指导老师 韩新华 摘 要:拉普拉斯变换在求解微分方程中有非常重要的作用,本文首先介绍拉普拉斯 变换的定义及性质;其次给出拉普拉斯变换求解微分方程的一般步骤;然后重点举例拉普拉斯变换在求解常微分方程(初值问题与边值问题、常系数与变系数常微分方程、含δ函数的常微分方程、常微分方程组、拉普拉斯变换在求解微分方程特解中的应用、拉普拉斯变换在求解高阶微分方程的推广)与典型偏微分方程(齐次与非齐次偏微分方程、有界与无界问题)中的应用举例;最后综合比较、归纳总结拉普拉斯变换在求解微分方程中的优势以及局限性。 关键词:拉普拉斯变换;拉普拉斯逆变换;常微分方程;偏微分方程;特解 引言 傅里叶变换和拉普拉斯变换是常用的积分变换,但对函数进行傅里叶变换时必须满足狄里希利和在+∞<<∞-t 内绝对可积,但是在物理、无线电技术等实际应用中,许多以时间t 为自变量的函数通常在0t <时不需要考虑或者没有意义,像这样的函数不能取傅里叶变换。为避免上述两个缺点,将函数进行适当改造,便产生了拉普拉斯变换[1]。 1 拉普拉斯变换以及性质 1.1 拉普拉斯变换的定义 设函数()f t 当0t ≥时有定义,而且积分 ()st f t e dt +∞ -? (s 是一个复参量)在s 的 某一区域内收敛,则此积分所确定的函数可写为0 ()()st F s f t e dt +∞ -= ? .我们称上式 为函数()f t 的Laplace 变换式.记为()[()]F s L f t =,()F s 称为()f t 的Laplace 变换(或称为象函数). 若()F s 是()f t 的Laplace 变换,则称()f t 为()F s 的Laplace 逆变换(或称为象原函数),记为1()[()]f t L F s -=[2]. Laplace 变换的存在定理 若函数()f t 满足下列条件:
变焕世界-傅立叶、拉普拉斯、Z变换 汇总对比
变焕世界-傅立叶、拉普拉斯、Z变换 1、傅里叶变换简单通俗理解就是把看似杂乱无章的信号考虑成由一定振幅、相位、频率的基本正弦(余弦)信号组合而成,傅里叶变换的目的就是找出这些基本正弦(余弦)信号中振幅较大(能量较高)信号对应的频率,从而找出杂乱无章的信号中的主要振动频率特点。 2、拉普拉斯变换 定义式:设有一时间函数f(t) [0,∞] 或 0≤t≤∞单边函数 ,其中,S=σ+jω是复参变量,称为复频率。左端的定积分称为拉普拉斯积分,又称为f(t)的拉普拉斯变换; 右端的F(S)是拉普拉斯积分的结果,此积分把时域中的单边函数f(t)变换为以复频率S为自变量的复频域函数F(S),称为f(t)的拉普拉斯象函数。 以上的拉普拉斯变换是对单边函数的拉普拉斯变换,称为单边拉普拉斯变换。 如f(t)是定义在整个时间轴上的函数,可将其乘以单位阶跃函数,即变为f(t)ε(t),则拉普拉斯变换为F(s),=mathcal left =int_ ^infty f(t),e^ ,dt 其中积分下标取0-而不是0或0+ ,是为了将冲激函数δ(t)及其导函数纳入拉普拉斯变换的范围。 z变换可将分散的信号(现在主要用于数字信号)从时域转换到频域。作用和拉普拉斯变换(将连续的信号从时域转换到频域)是一样的。 拉普拉斯变换是将时域信号变换到“复频域”,与傅里叶变换的“频域”有所区别。 FT[f(t)]=从负无穷到正无穷对[f(t)exp(-jwt)]积分 ,LT[f(t)]=从零到正无穷对[f(t)exp(-st)]积分 ,(由于实际应用,通常只做单边拉普拉斯变换,即积分从零开始) .具体地,在傅里叶积分变换中,所乘因子为exp(-jwt),此处,-jwt显然是为一纯虚数;而在拉普拉斯变换中,所乘因子为exp(-st),其中s为一复数:s=D+jw,jw是为虚部,相当于Fourier变换中的jwt,而D则是实部,作为衰减因子,这样就能将许多无法作Fourier变换的函数(比如exp(at),a>0)做域变换。拉普拉斯变换主要用于电路分析,作为解微分方程的强有力工具(将微积分运算转化为乘除运算)。但随着CAD的兴起,这一作
拉普拉斯变换在求解微分方程中的应用总结归纳
精心整理 目录 引言 (1) 1 拉普拉斯变换以及性质 (1) 1.1拉普拉斯变换的定义 (1) 1.2拉普拉斯变换的性质 (1) 2 用拉普拉斯变换求解微分方程的一般步骤 (3) 3 拉普拉斯变换在求解常微分方程中的应用 (3) 3.1初值问题与边值问题 (3) 3.2常系数与变系数常微分方程 (4) 3.3含 函数的常微分方程 (5) 3.4常微分方程组 (6) 3.5拉普拉斯变换在求解非齐次微分方程特解中的应用 (6) 3.6拉普拉斯变换在求解高阶微分方程中的推广 (9) 4 拉普拉斯变换在求解偏微分方程中的应用 (10) 4.1齐次与非齐次偏微分方程 (10) 4.2有界与无界问题 (11) 5 综合比较,归纳总结 (14) 结束语 (15) 参考文献 (15) 英文摘要 (21) 致谢 (16) 拉普拉斯变换在求解微分方程中的应用 物理系0801班学生岳艳林 指导老师韩新华
摘 要:拉普拉斯变换在求解微分方程中有非常重要的作用,本文首先介绍拉普拉斯变换的定义及性质; 其次给出拉普拉斯变换求解微分方程的一般步骤;然后重点举例拉普拉斯变换在求解常微分方程(初值问题与边值问题、常系数与变系数常微分方程、含δ函数的常微分方程、常微分方程组、拉普拉斯变换在求解微分方程特解中的应用、拉普拉斯变换在求解高阶微分方程的推广)与典型偏微分方程(齐次与非齐次偏微分方程、有界与无界问题)中的应用举例;最后综合比较、归纳总结拉普拉斯变换在求解微分方程中的优势以及局限性。 关键词:拉普拉斯变换;拉普拉斯逆变换;常微分方程;偏微分方程;特解 引言 傅里叶变换和拉普拉斯变换是常用的积分变换,但对函数进行傅里叶变换时必须满足狄里希利和在+∞<<∞-t 内绝对可积,但是在物理、无线电技术等实际应用中,许多以时间t 为自变量的函数通常在0t <时不需要考虑或者没有意义,像这样的函数不能取傅里叶变换。为避免上述两个缺点,将函数进行适当改造,便产生了拉普拉斯变换[1]。 1 拉普拉斯变换以及性质 1.1 拉普拉斯变换的定义 设函数()f t 当0t ≥时有定义,而且积分 ()st f t e dt +∞ -? (s 是一个复参量)在s 的某一区域内收敛, 则此积分所确定的函数可写为0 ()()st F s f t e dt +∞ -= ? .我们称上式为函数()f t 的Laplace 变换式.记为 ()[()]F s L f t =,()F s 称为()f t 的Laplace 变换(或称为象函数). 若()F s 是()f t 的Laplace 变换,则称()f t 为()F s 的Laplace 逆变换(或称为象原函数),记为 1()[()]f t L F s -=[2]. Laplace 变换的存在定理 若函数()f t 满足下列条件: 1?在0t ≥的任一有限区间上分段连续; 2?当t →+∞时,()f t 的增长速度不超过某一指数函数,亦即存在常数0M >及0c ≥,使得 c ()0f t Me t ≤≤<+∞t,成立(满足此条件的函数,称它的增大是不超过指数级的,c 为它的增长指数). 则()f t 的Laplace 变换0 ()st F f t e dt +∞ -?(s )=在半平面Re()s c >上一定存在,右端的积分在1Re()s c c ≥>的半平面内,()F s 为解析函数[2]. 1.2 拉普拉斯变换的性质 ⑴线性性质 若αβ,是常数,11[()]()L f t F s =, 22[()]()L f t F s =,
元件对照表详细
proteus常用元件中英文对照表元件名称中文名说明 7407 驱动门 1N914 二极管 74Ls00 与非门 74LS04 非门 74LS08 与门 74LS390 TTL 双十进制计数器 7SEG 4针BCD-LED 输出从0-9 对应于4根线的BCD码 7SEG 3-8译码器电路BCD-7SEG转换电路 ALTERNATOR 交流发电机 AMMETER-MILLI mA安培计 AND 与门 BATTERY 电池/电池组 BUS 总线 CAP 电容 CAPACITOR 电容器 CLOCK 时钟信号源 CRYSTAL 晶振 D-FLIPFLOP D触发器 FUSE 保险丝 GROUND 地 LAMP 灯 LED-RED 红色发光二极管 LM016L 2行16列液晶可显示2行16列英文字符,有8位数据总线D 0-D7,RS,R/W,EN三个控制端口(共14线),工作电压为5V。没背光,和常用的1602B功能和引脚一样(除了调背光的二个线脚) LOGIC ANALYSER 逻辑分析器 LOGICPROBE 逻辑探针 LOGICPROBE[BIG] 逻辑探针用来显示连接位置的逻辑状态 LOGICSTATE 逻辑状态用鼠标点击,可改变该方框连接位置的逻辑状态 LOGICTOGGLE 逻辑触发 MASTERSWITCH 按钮手动闭合,立即自动打开 MOTOR 马达 OR 或门 POT-LIN 三引线可变电阻器 POWER 电源
RES 电阻 RESISTOR 电阻器 SWITCH 按钮手动按一下一个状态 SWITCH-SPDT 二选通一按钮 VOLTMETER 伏特计 VOLTMETER-MILLI mV伏特计 VTERM 串行口终端 Electromechanical 电机 Inductors 变压器 Laplace Primitives 拉普拉斯变换 Memory Ics Microprocessor Ics Miscellaneous 各种器件 AERIAL-天线;ATAHDD;ATMEGA64;BATTERY;CELL;CRYSTAL-晶振;FUSE;METER-仪表; Modelling Primitives 各种仿真器件是典型的基本元器模拟,不表示具体型号,只用于仿真,没有PCB Optoelectronics 各种发光器件发光二极管,LED,液晶等等 PLDs & FPGAs Resistors 各种电阻 Simulator Primitives 常用的器件 Speakers & Sounders Switches & Relays 开关,继电器,键盘 Switching Devices 晶阊管 Transistors 晶体管(三极管,场效应管) TTL 74 series TTL 74ALS series TTL 74AS series TTL 74F series TTL 74HC series TTL 74HCT series TTL 74LS series TTL 74S series Analog Ics 模拟电路集成芯片 Capacitors 电容集合 CMOS 4000 series Connectors 排座,排插 Data Converters ADC,DAC Debugging Tools 调试工具
拉普拉斯变换在求解微分方程中的应用
目录 引言 ............................................... 错误!未定义书签。 1 拉普拉斯变换以及性质 (1) 拉普拉斯变换的定义 ...................................................................................... 错误!未定义书签。拉普拉斯变换的性质 ...................................................................................... 错误!未定义书签。 2 用拉普拉斯变换求解微分方程的一般步骤 ........................... 错误!未定义书签。 3 拉普拉斯变换在求解常微分方程中的应用 ........................... 错误!未定义书签。初值问题与边值问题 ...................................................................................... 错误!未定义书签。常系数与变系数常微分方程........................................................................ 错误!未定义书签。含 函数的常微分方程.................................................................................. 错误!未定义书签。常微分方程组 .................................................................................................... 错误!未定义书签。拉普拉斯变换在求解非齐次微分方程特解中的应用 ........................ 错误!未定义书签。拉普拉斯变换在求解高阶微分方程中的推广 ...................................... 错误!未定义书签。 4 拉普拉斯变换在求解偏微分方程中的应用 ........................... 错误!未定义书签。齐次与非齐次偏微分方程............................................................................. 错误!未定义书签。有界与无界问题................................................................................................ 错误!未定义书签。 5 综合比较,归纳总结 ............................................................... 错误!未定义书签。结束语 ........................................................................................... 错误!未定义书签。参考文献 ....................................................................................... 错误!未定义书签。英文摘要 (21) 致谢 ............................................................................................... 错误!未定义书签。
常用傅里叶_拉普拉斯_Z变换表
时域信号 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移, 变换2的频域对应4 如果值较大,则会收缩 到原点附近,而会扩 散并变得扁平. 当 | a | 趋向 无穷时,成为 Delta函数。 5 傅里叶变换的二元性性质。通过 交换时域变量和频域变量 得到. 6 傅里叶变换的微分性质 7 变换6的频域对应 8 表示和的卷积—这
附录A 拉普拉斯变换及反变换 1.拉氏变换的基本性质 2.常用函数的拉氏变换和z变换表 附表A-2 常用函数的拉氏变换和z变换表
3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式,即 1110 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++= =---- (m n >) 式中,系数n n a a a a ,,...,,110-和011,,,,m m b b b b - 都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 (1)0)(=s A 无重根:这时,F(s)可展开为n 个简单的部分分式之和的形式,即 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)( (F-1) 式中,n s s s ,,,21 是特征方程A(s)=0的根;i c 为待定常数,称为()F s 在i s 处的留数,可按下列两式计算:
