有限差分法
有限差分法
一、单变量函数:
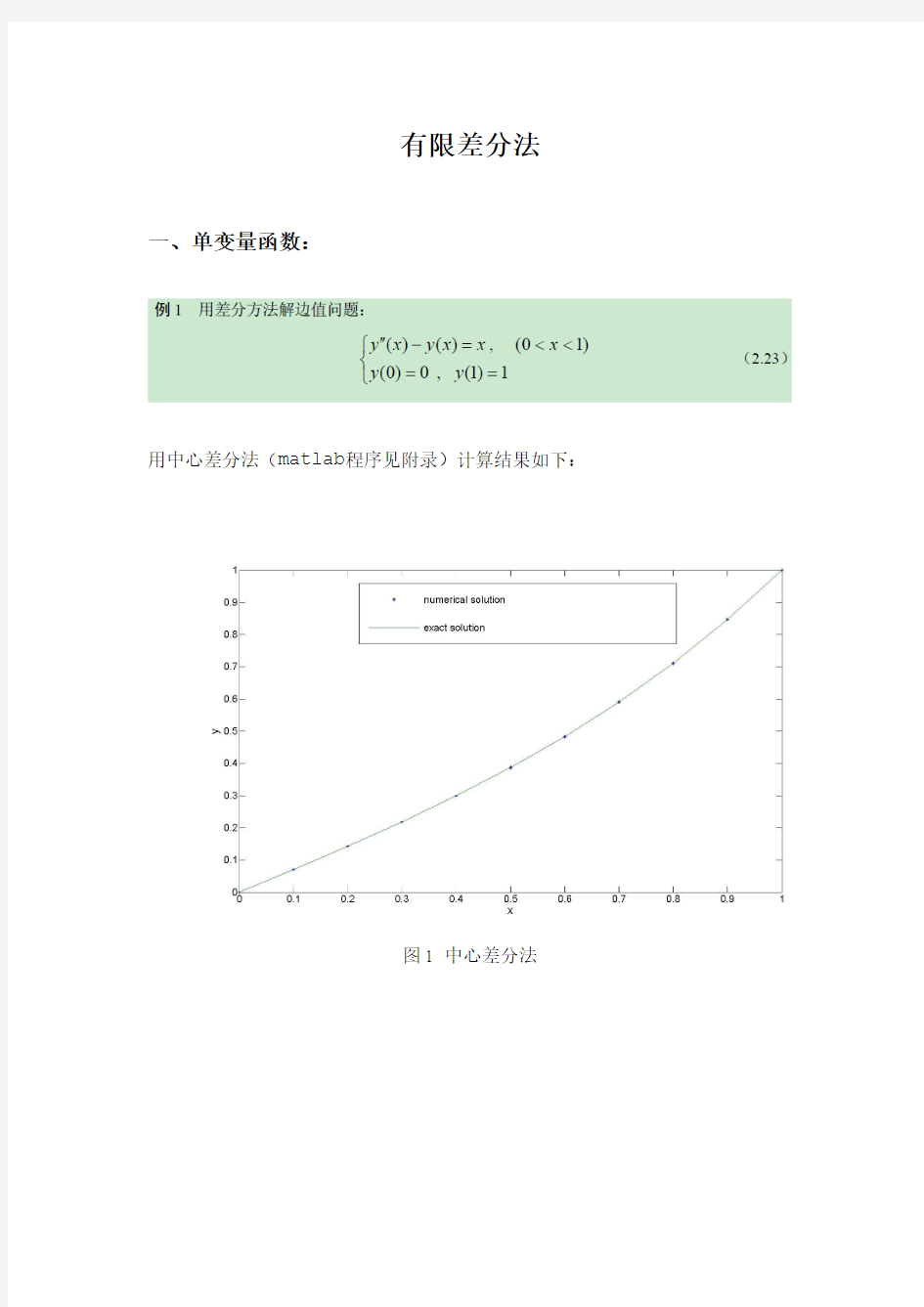
用中心差分法(matlab程序见附录)计算结果如下:
图1 中心差分法
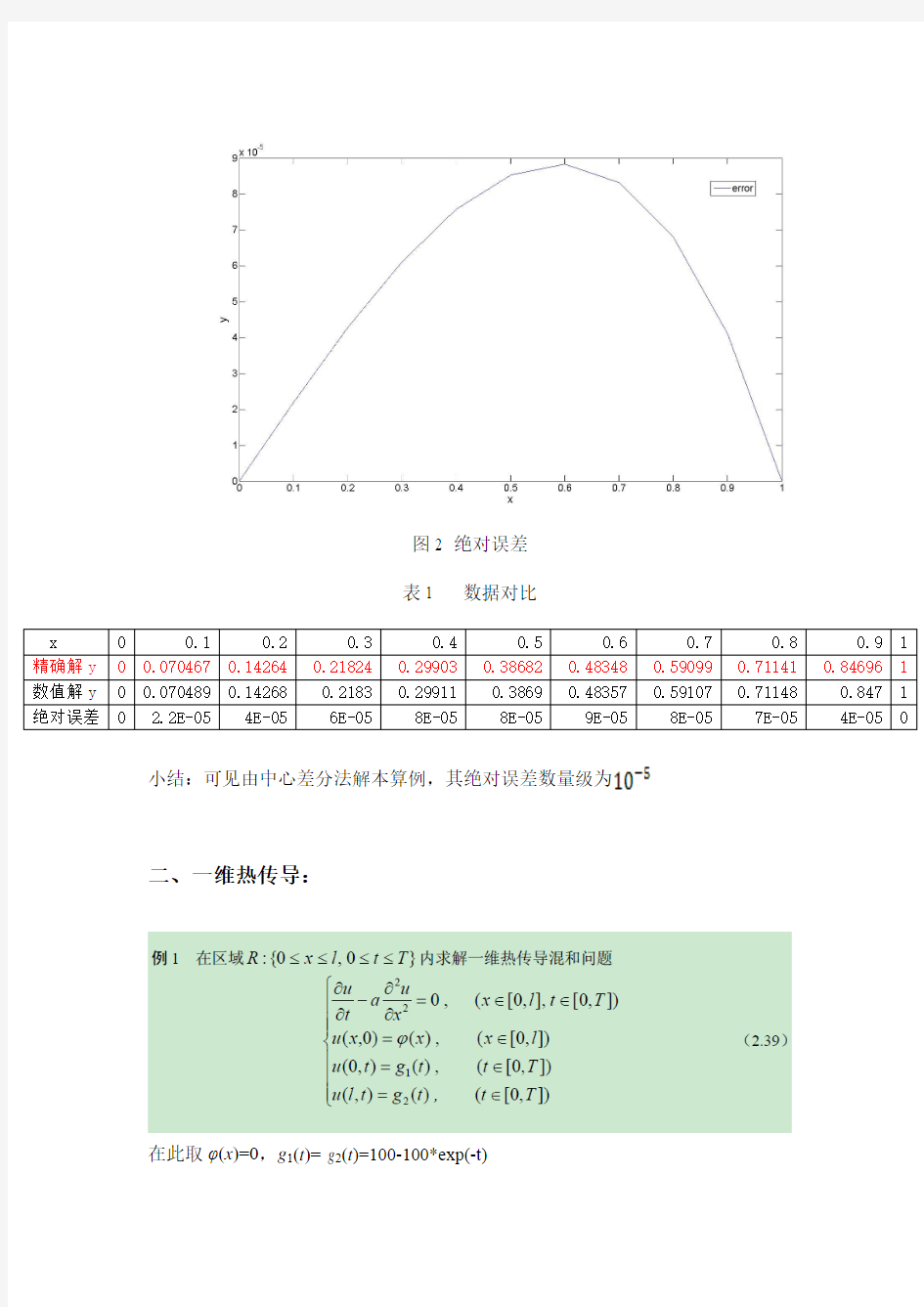
表1 数据对比
二、一维热传导:
在此取φ(x)=0,g1(t)= g2(t)=100-100*exp(-t)
问题描述:
已知厚度为l的无限大平板,初温0度,初始瞬间将其放于温度为100度的流体中,流体与板面间的表面传热系数为一常数。
试确定在非稳态过程中板内的温度分布。
(1)显式差分法:
图3 显式差分法
(2)隐式差分法:
图4 隐式差分法
小结:显式格式仅当时格式是稳定的。(其中称为网格比)
隐式格式从k层求k+1层时,需要求解一个阶方程组。而且隐式格式的稳定性对网格比没有要求,即为绝对稳定的。
三、Possion方程:
取f=1,R=1
图5差分法
图6 误差小结:观察误差曲面,其绝对误差数量级为
附Matlab程序:
第1题:
%===========================Boundary Value Problem 1
clear;clc;
A=[-2.01 1 0 0 0 0 0 0 0;
1 -2.01 1 0 0 0 0 0 0;
0 1 -2.01 1 0 0 0 0 0;
0 0 1 -2.01 1 0 0 0 0;
0 0 0 1 -2.01 1 0 0 0;
0 0 0 0 1 -2.01 1 0 0;
0 0 0 0 0 1 -2.01 1 0;
0 0 0 0 0 0 1 -2.01 1;
0 0 0 0 0 0 0 1 -2.01;];
c1=[0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9];
C=0.01*c1-1*[0;0;0;0;0;0;0;0;1];
y=A\C;
x=0:0.1:1;
yn=[0;y;1];
ye=2*(exp(x)-exp(-x))/(exp(1)-exp(-1))-x;
figure(1);
plot(x,yn,'*',x,ye);
legend('numerical solution','exact solution')
xlabel('x','fontsize',20);
ylabel('y','fontsize',20);
set(gca,'fontsize',18);
figure(2);
err=abs(ye'-yn);
plot(x,err);
legend('error')
xlabel('x','fontsize',20);
ylabel('y','fontsize',20);
set(gca,'fontsize',18);
第2题:
%========================Boundary Value Problem 1_Explicit %显式
clear;clc
l=20;%板厚
h=1;%步长
J=l/h;
T=50;%时间
tao=2.5;%步长
N=T/tao;
%下面组合A矩阵
a=0.2;
lamda=tao/(h^2);
zhu=1-2*a*lamda;
ce=a*lamda;
a00=ones(1,J-1);
a0=diag(a00);
A0=zhu*a0;
a01=ones(1,J-2);
a1=diag(a01,1);
A1=ce*a1;
a2=diag(a01,-1);
A2=ce*a2;
A=A0+A1+A2;
u(:,1)=0; %板的初始温度
for i=2:N+1
u(1,i)=100-100*exp(-(i-1)*tao); %边界条件
u(J+1,i)=100-100*exp(-(i-1)*tao); %边界条件
end
% g01=u(:,1);
% g02=u(:,J);
for k=1:N
% g01=ce*g1(1,k);
% g02=ce*g2(1,k);
oo=zeros(J-3,1);
g(:,k)=[ce*u(1,k);oo;ce*u(J+1,k)];
u(2:end-1,k+1)=A*u(2:end-1,k)+g(:,k);
end
t=0:h:l;
x=0:tao:T;
mesh(x,t,u)
xlabel('t','fontsize',20);
ylabel('x','fontsize',20);
zlabel('T','fontsize',20);
set(gca,'fontsize',18);
%========================Boundary Value Problem 1_2Implicit %隐式
clear;clc
l=20;%板厚
h=1;%步长
J=l/h;
T=50;%时间
tao=2.5;%步长
N=T/tao;
%下面组合A矩阵
a=0.2;
lamda=tao/(h^2);
zhu=1+2*a*lamda;
ce=-a*lamda;
a00=ones(1,J-1);
a0=diag(a00);
A0=zhu*a0;
a01=ones(1,J-2);
a1=diag(a01,1);
A1=ce*a1;
a2=diag(a01,-1);
A2=ce*a2;
A=A0+A1+A2;
u(:,1)=0; %板的初始温度
for i=2:N+1
u(1,i)=100-100*exp(-(i-1)*tao); %边界条件
u(J+1,i)=100-100*exp(-(i-1)*tao); %边界条件
end
% g01=u(:,1);
% g02=u(:,J);
for k=1:N
% g01=ce*g1(1,k);
% g02=ce*g2(1,k);
oo=zeros(J-3,1);
g(:,k)=[ce*u(1,k);oo;ce*u(J+1,k)];
u(2:end-1,k+1)=inv(A)*u(2:end-1,k)-inv(A)*g(:,k);
end
t=0:h:l;
x=0:tao:T;
mesh(x,t,u)
xlabel('t','fontsize',20);
ylabel('x','fontsize',20);
zlabel('T','fontsize',20);
set(gca,'fontsize',18);
第3题:
%=============================used by centered difference clear;
function pdemodel
[pde_fig,ax]=pdeinit;
pdetool('appl_cb',1);
set(ax,'DataAspectRatio',[1 1 1]);
set(ax,'PlotBoxAspectRatio',[1.5 1 1]);
set(ax,'XLim',[-1.5 1.5]);
set(ax,'YLim',[-1 1]);
set(ax,'XTickMode','auto');
set(ax,'YTickMode','auto');
% Geometry description:
pdecirc(0,0,1,'C1');
set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','C1')
% Boundary conditions:
pdetool('changemode',0)
pdesetbd(4,...
'dir',...
1,...
'1',...
'0')
pdesetbd(3,...
'dir',...
1,...
'1',...
'0')
pdesetbd(2,...
'dir',...
1,...
'1',...
'0')
pdesetbd(1,...
'dir',...
1,...
'1',...
'0')
% Mesh generation:
setappdata(pde_fig,'Hgrad',1.3);
setappdata(pde_fig,'refinemethod','regular');
pdetool('initmesh')
pdetool('refine')
% PDE coefficients:
pdeseteq(1,...
'1.0',...
'0.0',...
'1',...
'1.0',...
'0:10',...
'0.0',...
'0.0',...
'[0 100]')
setappdata(pde_fig,'currparam',...
['1.0';...
'0.0';...
'1 ';...
'1.0'])
% Solve parameters:
setappdata(pde_fig,'solveparam',...
str2mat('0','1524','10','pdeadworst',...
'0.5','longest','0','1E-4','','fixed','Inf'))
% Plotflags and user data strings:
setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 0 1 0 0 1 0 0 1]); setappdata(pde_fig,'colstring','');
setappdata(pde_fig,'arrowstring','');
setappdata(pde_fig,'deformstring','');
setappdata(pde_fig,'heightstring','');
% Solve PDE:
pdetool('solve')
有限差分法及其应用
有限差分法及其应用 1有限差分法简介 有限差分法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。该方程将解域划分为差分网格,用有限个网络节点代替连续的求解域。有限差分法通过泰勒级数展开等方法,把控制方程中的导数用网格节点上的函数值得差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。该方法是一种直接将微分问题变为代数问题的近似值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。 2有限差分法的数学基础 有限差分法的数学基础是用差分代替微分,用差商代替微商而用差商代替微商的意义是用函数在某区域内的平均变化率来代替函数的真是变化率。而根据泰勒级数展开可以看出,用差商代替微商必然会带来阶段误差,相应的用差分方程代替微分方程也会带来误差,因此,在应用有限差分法进行计算的时候,必须注意差分方程的形式,建立方法及由此产生的误差。 3有限差分解题基本步骤 有限差分法的主要解题步骤如下: 1)建立微分方程 根据问题的性质选择计算区域,建立微分方程式,写出初始条件和边界条件。 2)构建差分格式 首先对求解域进行离散化,确定计算节点,选择网格布局,差分形式和步长;然后以有限差分代替无线微分,以差商代替微商,以差分方程代替微分方程及边界条件。 3)求解差分方程 差分方程通常是一组数量较多的线性代数方程,其求解方法主要包括两种:精确法和近似法。其中精确法又称直接发,主要包括矩阵法,高斯消元法及主元素消元法等;近似法又称间接法,以迭代法为主,主要包括直接迭代法,间接迭代法以及超松弛迭代法。4)精度分析和检验 对所得到的数值进行精度与收敛性分析和检验。 4商用有限差分软件简介 商用有限差分软件主要包括FLAC、UDEC/3DEC和PFC程序,其中,FLAC是一个基于显式有限差分法的连续介质程序,主要用来进行土质、岩石和其他材料的三维结构受力特性模拟和塑性流动分析;UDEC/3DEC是针对岩体不连续问题开发,用于模拟非连续介质在静,动态载荷作用下的反应;PFC是利用显式差分算法和离散元理论开发的微、细观力学程序,它是从介质的基本粒子结构的角度考虑介质的基本力学特性,并认为给定介质在不同应力条件下的基本特征主要取决于粒子之间接粗状态的变化,适用于研究粒状集合体的破裂和破裂发展问题,以及颗粒的流动(大位移)问题。
时域有限差分法的Matlab仿真
时域有限差分法的Matlab仿真 关键词: Matlab 矩形波导时域有限差分法 摘要:介绍了时域有限差分法的基本原理,并利用Matlab仿真,对矩形波导谐振腔中的电磁场作了模拟和分析。 关键词:时域有限差分法;Matlab;矩形波导;谐振腔 目前,电磁场的时域计算方法越来越引人注目。时域有限差分(Finite Difference Time Domain,FDTD)法[1]作为一种主要的电磁场时域计算方法,最早是在1966年由K. S. Yee提出的。这种方法通过将Maxwell旋度方程转化为有限差分式而直接在时域求解,通过建立时间离散的递进序列,在相互交织的网格空间中交替计算电场和磁场。经过三十多年的发展,这种方法已经广泛应用到各种电磁问题的分析之中。 Matlab作为一种工程仿真工具得到了广泛应用[2]。用于时域有限差分法,可以简化编程,使研究者的研究重心放在FDTD法本身上,而不必在编程上花费过多的时间。 下面将采用FDTD法,利用Matlab仿真来分析矩形波导谐振腔的电磁场,说明了将二者结合起来的优越性。 1FDTD法基本原理 时域有限差分法的主要思想是把Maxwell方程在空间、时间上离散化,用差分方程代替一阶偏微分方程,求解差分方程组,从而得出各网格单元的场值。FDTD 空间网格单元上电场和磁场各分量的分布如图1所示。 电场和磁场被交叉放置,电场分量位于网格单元每条棱的中心,磁场分量位于网格单元每个面的中心,每个磁场(电场)分量都有4个电场(磁场)分量环绕。这样不仅保证了介质分界面上切向场分量的连续性条件得到自然满足,而且
还允许旋度方程在空间上进行中心差分运算,同时也满足了法拉第电磁感应定律和安培环路积分定律,也可以很恰当地模拟电磁波的实际传播过程。 1.1Maxwell方程的差分形式 旋度方程为: 将其标量化,并将问题空间沿3个轴向分成若干网格单元,用Δx,Δy和Δz 分别表示每个网格单元沿3个轴向的长度,用Δt表示时间步长。网格单元顶点的坐标(x,y,z)可记为: 其中:i,j,k和n为整数。 同时利用二阶精度的中心有限差分式来表示函数对空间和时间的偏导数,即可得到如下FDTD基本差分式: 由于方程式里出现了半个网格和半个时间步,为了便于编程,将上面的差分式改写成如下形式:
《有限差分法在微分方程中的应用》课程论文
课程论文
有限差分法在微分方程中的应用 本学期学习了《微分方程数值解》,本书中有限差分法给我留下的印象比较深刻,下边说说自己在方面的一点理解,请老师指正。 1.有限差分法的基本思想: 当系统的数学模型建立后,我们面对的主要问题就是微分积分方程的求解。基本思想是用离散的只含有限个未知量的差分方程组去近似地代替连续变量的微分方程和定解条件,并把差分方程组的解作为微分方程定解问题的近似解。将原方程及边界条件中的微分用差分来近似,对于方程中的积分用求和或及机械求积公式来近似代替,从而把原微分积分方程和边界条件转化成差分方程组。 2.有限差分法求解偏微分方程的步骤: 区域离散,即把所给偏微分方程的求解区域细分成由有限个格点组成的网格,这些离散点称作网格的节点; 近似替代,即采用有限差分公式替代每一个格点的导数。 逼近求解,换而言之,这一过程可以看作是用一个插值多项式及其微分来代替偏微分方程的解的过程。 从原则上说,这种方法仍然可以达到任意满意的计算精度。因为方程的连续数值解可以通过减小独立变量离散取值的间格,或者通过离散点上的函数值进行插值计算来近似得到。理论上,当网格步长趋近于零时,差分方程组的解应该收敛于精确解,但由于机器字节的限制,网格步长不可能也没有必要取得无限小,那么差分法的收敛性或者说算法的稳定性就显得至关重要。因此,在运用有限差分法时,除了要保证精度外,还必须要保证其收敛性。 3.构造差分法的几种形式: 主要草用的是泰勒级数展开的方法。其基本差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等。其中前两种形式为一阶计算精度,后一种为二阶计算精度。
有限差分法
利用有限差分法分析电磁场边界问题 在一个电磁系统中,电场和磁场的计算对于完成该系统的有效设计师极端重要的。例如,在系统中,用一种绝缘材料是导体相互隔离是,就要保证电场强度低于绝缘介质的击穿强度。在磁力开关中,所要求的磁场强弱,应能产生足够大的力来驱动开关。在发射系统中进行天线的有效设计时,关于天线周围介质中电磁场分布的知识显然有实质性的意义。 为了分析电磁场,我们可以从问题所涉及的数学公式入手。依据电磁系统的特性,拉普拉斯方程和泊松方程只能适合于描述静态和准静态(低频)运行条件下的情况。但是,在高频应用中,则必须在时域或频域中求解波动方程,以做到准确地预测电场和磁场,在任何情况下,满足边界条件的一个或多个偏微分方程的解,因此,计算电池系统内部和周围的电场和磁场都是必要的。 对电磁场理论而言,计算电磁场可以为其研究提供进行复杂的数值及解析运算的方法,手段和计算结果;而电磁场理论则为计算电磁场问题提供了电磁规律,数学方程,进而验证计算结果。常用的计算电磁场边值问题的方法主要有两大类,其每一类又包含若干种方法,第一类是解析法;第二类是数值法。对于那些具有最简单的边界条件和几何形状规则的(如矩形、圆形等)问题,可用分离变量法和镜像法求电磁场边值问题的解析解(精确解),但是在许多实际问题中往往由于边界条件过于复杂而无法求得解析解。在这种情况下,一般借助于数值法求解电磁场的数值解。 有限差分法,微分方程和积分微分方程数值解的方法。基本思想是把连续的定解区域用有限个离散点构成的网络来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。 差分运算的基本概念: 有限差分法是指用差分来近似取代微分,从而将微分方程离散成为差分方程组。于是求解边值问题即转换成为求解矩阵方程[5]。 对单元函数 ()x f而言,取变量x的一个增量x?=h,则函数()x f的增量可以表示为 ()x f? = ()h x f+-()x f 称为函数()x f 的差分或一阶差分。函数增量还经常表示为 ()x f? = ? ? ? ? ? + 2 h x f - ? ? ? ? ? - 2 h x f
时域有限差分法发展综述
时域有限差分法发展综述 潘忠 摘要:时域有限差分法(FDTD)是解决复杂电磁问题的有效方法之一,目前FDTD 法的许多重要问题得到了很好的解决,已经发展成为一种成熟的数值计算方法。随着计算机数据处理性能的快速提高和计算机价格的下降,使得FDTD法的应用范围越来越广,而FDTD法本身在应用中又有新的发展.本文介绍并分析了时域有限差分法,对各种条件的应用进行了比较和分析,给出了具有一定参考价值的结论。 关键词:时域有限差分法;研究与发展;比较;分析 A Summary of FDTD and Development at Home and Abroad Zhong Pan Abstract: The finite difference time-domain (FDTD) method is one of the most effective methods to solve electromagnetic problems. Many important questions of FDTD method have been solved well through many scientists’ effort. Now, FDTD method is a mature numerical method. Especially in few years, the range of using FDTD method is becoming wider and wider because of the faster data processing and processing and cheaper price of computer. FDTD method has also been developed during using. FDTD method is introduced and discussed in this paper. The applications of various conditions are compared and analyzed. Finally, some valuable conclusions are drawn. Key words: FDTD; Research and Development; Comparison; Analysis 1966年,K.S.Yee首次提出电磁场数值计算的新方法—时域有限差分法(Finite Difference- Time Domain,简称FDTD)。经历了二十年的发展FDTD法才逐渐走向成熟。上世纪80年代后期以来FDTD法进入了一个新的发展阶段,即由成熟转为被广泛接受和应用的阶段。FDTD法是解决复杂问题的有效方法之一,是一种直接基于时域电磁场微分方程的数值算法,它直接在时域将Maxwell旋度方程用二阶精度的中心差分近似,从而将时域微分方程的求解转换为差分方程的迭代求解。是电磁场和电磁波运动规律和运动过程的计算机模拟。原则上可以求解任意形式的电磁场和电磁波的技术和工程问题,并且对计算机内存容量要求较低、计算速度较快、尤其适用于并行算法。现在FDTD法己被广泛应用于天线的分析与设计、目标电磁散射、电磁兼容、微波电路和光路时域分析、生物电磁剂量学、瞬态电磁场研究等多个领域。
有限差分法
班级:通信13-4 姓名: 学号: 指导教师:徐维 成绩: 电子与信息工程学院 信息与通信工程系
求解金属槽的电位分布 1.实验原理 利用有限差分法和matlab软件解决电位在金属槽中的分布。 有限差分法基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解.然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解.在采用数值计算方法求解偏微分方程时,若将每一处导数由有限差分近似公式替代,从而把求解偏微分方程的问题转换成求解代数方程的问题。 2.有限差分法 方程的定解问题就是在满足某些定解条件下求微分方程的解。在空间区域的边界上要满足的定解条件称为边值条件。如果问题与时间有关,在初始时刻所要满足的定解条件,称为初值条件。不含时间而只带边值条件的定解问题,称为边值问题。与时间有关而只带初值条件的定解问题,称为初值问题。同时带有两种定解条件的问题,称为初值边值混合问题。 定解问题往往不具有解析解,或者其解析解不易计算。所以要采用可行的数值解法。有限差分方法就是一种数值解法,它的基本思想是先把问题的定义域进行网格剖分,然后在网格点上,按适当的数值微分公式把定解问题中的微商换成差商,从而把原问题离散化为差分格式,进而求出数值解。此外,还要研究差分格式的解的存在性和唯一性、解的求法、解法的数值稳定性、差分格式的解与原定解问题的真解的误差估计、差分格式的解当网格大小趋于零时是否趋于真解(即收敛性),等等。 有限差分方法具有简单、灵活以及通用性强等特点,容易在计算机上实现。 2.1有限差分法原理
LED-FDTD LED时域有限差分方法
Efficiency enhancement of homoepitaxial InGaN/GaN light-emitting diodes on free-standing GaN substrate with double embedded SiO2 photonic crystals Tongbo Wei,* Ziqiang Huo, Yonghui Zhang, Haiyang Zheng, Yu Chen, Jiankun Yang, Qiang Hu, Ruifei Duan, Junxi Wang, Yiping Zeng, and Jinmin Li Semiconductor Lighting Technology Research and Development Center, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China *tbwei@https://www.360docs.net/doc/3212722913.html, Abstract: Homoepitaxially grown InGaN/GaN light emitting diodes (LEDs) with SiO2 nanodisks embedded in n-GaN and p-GaN as photonic crystal (PhC) structures by nanospherical-lens photolithography are presented and investigated. The introduction of SiO2 nanodisks doesn’t produce the new dislocations and doesn’t also result in the electrical deterioration of PhC LEDs. The light output power of homoepitaxial LEDs with embedded PhC and double PhC at 350 mA current is increased by 29.9% and 47.2%, respectively, compared to that without PhC. The corresponding light radiation patterns in PhC LEDs on GaN substrate show a narrow beam shape due to strong guided light extraction, with a view angle reduction of about 30°. The PhC LEDs are also analyzed in detail by finite-difference time-domain simulation (FDTD) to further reveal the emission characteristics. ?2014 Optical Society of America OCIS codes: (230.0230) Optical devices; (230.3670) Light-emitting diodes; (160.5298) Photonic crystals; (220.4241) Nanostructure fabrication. References and links 1. B. Monemar and B. E. Sernelius, “Defect related issues in the “current roll-off” in InGaN based light emitting diodes,” Appl. Phys. Lett. 91(18), 181103 (2007). 2. G. Verzellesi, D. Saguatti, M. Meneghini, F. Bertazzi, M. Goano, G. Meneghesso, and E. Zanoni, “Efficiency droop in InGaN/GaN blue light-emitting diodes: Physical mechanisms and remedies,” J. Appl. Phys. 114(7), 071101 (2013). 3. K. Akita, T. Kyono, Y. Yoshizumi, H. Kitabayashi, and K. Katayama, “Improvements of external quantum efficiency of InGaN-based blue light-emitting diodes at high current density using GaN substrates,” J. Appl. Phys. 101(3), 033104 (2007). 4. Y. Yang, X. A. Cao, and C. H. Yan, “Rapid efficiency roll-off in high-quality green light-emitting diodes on freestanding GaN substrates,” Appl. Phys. Lett. 94(4), 041117 (2009). 5. C.-L. Chao, R. Xuan, H.-H. Yen, C.-H. Chiu, Y.-H. Fang, Z.-Y. Li, B.-C. Chen, C.-C. Lin, C.-H. Chiu, Y.-D. Guo, J.-F. Chen, and S.-J. Cheng, “Reduction of Efficiency Droop in InGaN Light-Emitting Diode Grown on Self-Separated Freestanding GaN Substrates,” IEEE Photon. Technol. Lett. 23(12), 798–800 (2011). 6. M. J. Cich, R. I. Aldaz, A. Chakraborty, A. David, M. J. Grundmann, A. Tyagi, M. Zhang, F. M. Steranka, and M. R. Krames, “Bulk GaN based violet light-emitting diodes with high efficiency at very high current density,” Appl. Phys. Lett. 101(22), 223509 (2012). 7. X. A. Cao, S. F. LeBoeuf, M. P. D’Evelyn, S. D. Arthur, J. Kretchmer, C. H. Yan, and Z. H. Yang, “Blue and near-ultraviolet light-emitting diodes on free-standing GaN substrates,” Appl. Phys. Lett. 84(21), 4313 (2004). 8. Y. J. Zhao, J. Sonoda, C.-C. Pan, S. Brinkley, I. Koslow, K. Fujito, H. Ohta, S. P. DenBaars, and S. Nakamura, “30-mW-class high-power and high-efficiency blue (1011) semipolar InGaN/GaN light-emitting diodes obtained by backside roughening technique,” Appl. Phys. Express 3, 102101 (2010). 9. Y.-K. Fu, B.-C. Chen, Y.-H. Fang, R.-H. Jiang, Y.-H. Lu, R. Xuan, K.-F. Huang, C.-F. Lin, Y.-K. Su, J.-F. Chen, and C.-Y. Chang, “Study of InGaN-based light-emitting diodes on a roughened backside GaN substrate by a chemical wet-etching process,” IEEE Photon. Technol. Lett. 23(19), 1373–1375 (2011). #209568 - $15.00 USD Received 4 Apr 2014; revised 23 May 2014; accepted 26 May 2014; published 2 Jun 2014 (C) 2014 OSA30 June 2014 | Vol. 22, No. S4 | DOI:10.1364/OE.22.0A1093 | OPTICS EXPRESS A1093
时域有限差分法(姚伟)介绍
伊犁师范学院硕士研究生 ————期末考核 科目:电磁波有限时域差分方法 姓名:姚伟 学号:1076411203009 学院:电子与信息工程学院 专业:无线电物理
时域有限差分法 1 选题背景 在多种可用的数值方法中,时域有限差分法(FDTD)是一种新近发展起来的可选方法。1966年,K.S.Yee 首次提出电磁场数值计算的新方法—时域有限差分法(Finite Difference- Time Domain ,简称FDTD)。经历了二十年的发展FDTD 法才逐渐走向成熟。上世纪80年代后期以来FDTD 法进入了一个新的发展阶段,即由成熟转为被广泛接受和应用的阶段。FDTD 法是解决复杂问题的有效方法之一,是一种直接基于时域电磁场微分方程的数值算法,它直接在时域将Maxwell 旋度方程用二阶精度的中心差分近似,从而将时域微分方程的求解转换为差分方程的迭代求解。是电磁场和电磁波运动规律和运动过程的计算机模拟。原则上可以求解任意形式的电磁场和电磁波的技术和工程问题,并且对计算机内存容量要求较低、计算速度较快、尤其适用于并行算法。现在FDTD 法己被广泛应用于天线的分析与设计、目标电磁散射、电磁兼容、微波电路和光路时域分析、生物电磁剂量学、瞬态电磁场研究等多个领域[1]。 2 原理分析 2.1 FDTD 的Yee 元胞 E,H 场分量取样节点在空间和时间上采取交替排布,利用电生磁,磁生电的原理 t t ??=??=??E D H ε t t ??-=??-=??H B E μ 图1 Yee 模型 如图1所示,Yee 单元有以下特点[2]: 1)E 与H 分量在空间交叉放置,相互垂直;每一坐标平面上的E 分量四周由H 分量环绕,H 分量的四周由E 分量环绕;场分量均与坐标轴方向一致。 2)每一个Yee 元胞有8个节点,12条棱边,6个面。棱边上电场分量近似相等,用棱边的中心节点表示,平面上的磁场分量近似相等,用面的中心节点表示。 3)每一场分量自身相距一个空间步长,E 和H 相距半个空间步长 4)每一场分量自身相距一个时间步长,E 和H 相距半个时间步长,电场取n 时刻的值,磁场取n+0.5时刻的值;即:电场n 时刻的值由n-1时刻的值得到,磁场n+0.5时刻的值由n-0.5时刻的值得到;电场n 时刻的旋度对应n+0.5时刻的磁场值,磁场n+0.5时刻的
有限差分法
有限差分法 有限差分法(Finite Differential Method, FDM ) 什么是有限差分法 有限差分法是指用泰勒技术展开式将变量的导数写成变量,在不同时间或空间点值的差分形式的方法。 按时间步长和空间步长将时间和空间区域剖分成若干网格,用未知函数在网格结(节)点上的值所构成的差分近似代替所用偏微分方程中出现的各阶导数,从而把表示变量连续变化关系的偏微分方程离散为有限个代数方程,然后解此线性代数方程组,以求出溶质在各网格结(节)点上不同时刻的浓度。 有限差分法的基本步骤 (1)剖分渗流区,确定离散点。将所研究的水动力弥散区域按某种几何形状(如矩形、任意多边形等)剖分成网络系统。 (2)建立水动力弥散问题的差分方程组。 (3)求解差分方程组。采用各种迭代法,如点逐次超松驰方法(SOR)、线逐次超松驰方法(LSOR)、迭代的交替方向隐式方法(IADI)及强隐式方法(SID)等。 (1) 现在分别对时间(从0时刻到到期日)和股票价格(S max )为可达到的足够高的股票价格) 进行分割,即\triangle S=S_{max}/M,\triangle T/N,这样就分别有N+1个时间段和M+1个股票价格,建立如图(所示的坐标方格,将定解区域网格化,坐标方格上的点(i,j )对应时刻 和股票价格 ,用变量f i ,j 表示(i,j )点的期权价格。 2.建立差分格式 (1)内含的有限差分方法 其步骤可分为以下几步:
(1)求前向差分近似:(2) 后向差分格式:(3) 将(2),(3)式平均可更加对称地求出的近似,即 (4) (2)求用前向差分近似: (5) (3)求 (6) (4)将(4),(5),(6)式代入(1)式可得到内含有限差分公式: + b j f i,j?c j f i,j + 1 = f i + 1,j(7) a j f i,j? 1 其中: i=0,1,…,N-1。j=0,1…,M-1 针对看跌期权和看涨期权可分别求出方程的边界条件: 看跌期权: 看涨期权: (5)利用边界条件和(7)式可以给出M-1个联立方程组: + b j f N? 1,j + c j f N? 1,j + 1j=1,2…,M-1 a j f N? 1,j? 1
有限元法与有限差分法的主要区别
有限元法与有限差分法的主要区别 有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。有限差分法以Taylor级数展开等方法,把控制方程中的导数用网格节点上的函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。从差分的空间形式来考虑,可分为中心格式和逆风格式。考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。其基本的差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等,其中前两种格式为一阶计算精度,后两种格式为二阶计算精度。通过对时间和空间这几种不同差分格式的组合,可以组合成不同的差分计算格式。有限元方法的基础是变分原理和加权余量法,其基本求解思想是把计算域划分为有限个互不重叠的单元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。采用不同的权函数和插值函数形式,便构成不同的有限元方法。有限元方法最早应用于结构力学,后来随着计算机的发展慢慢用于流体力学的数值模拟。在有限元方法中,把计算域离散剖分为有限个互不重叠且相互连接的单元,在每个单元内选择基函数,用单元基函数的线形组合来逼近单元中的真解,整个计算域上总体的基函数可以看为由每个单元基函数组成的,则整个计算域内的解可以看作是由所有单元上的近似解构成。在河道数值模拟中,常见的有限元计算方法是由变分法和加权余量法发展而来的里兹法和伽辽金法、最小二乘法等。根据所采用的权函数和插值函数的不同,有限元方法也分为多种计算格式。从权函数的选择来说,有配置法、矩量法、最小二乘法和伽辽金法,从计算单元网格的形状来划分,有三角形网格、四边形网格和多边形网格,从插值函数的精度来划分,又分为线性插值函数和高次插值函数等。不同的组合同样构成不同的有限元计算格式。对于权函数,伽辽金(Galerkin)法是将权函数取为逼近函数中的基函数;最小二乘法是令权函数等于余量本身,而内积的极小值则为对代求系数的平方误差最小;在配置法中,先在计算域内选取N个配置点。令近似解在选定的N个配置点上严格满足微分方程,即在配置点上令方程余量为0。插值函数一般由不同次幂的多项式组成,但也有采用三角函数或指数函数组成的乘积表示,但最常用的多项式插值函数。有限元插值函数分为两大类,一类只要求插值多项式本身在插值点取已知值,称为拉格朗日(Lagrange)多项式插值;另一种不仅要求插值多项式本身,还要求它的导数值在插值点取已知值,称为哈密特(Hermite)多项式插值。单元坐标有笛卡尔直角坐标系和无因次自然坐标,有对称和不对称等。常采用的无因次坐标是一种局部坐标系,它的定义取决于单元的几何形状,一维看作长度比,二维看作面积比,三维看作体积比。在二维有限元中,三角形单元应用的最早,近来四边形等参元的应用也越来越广。对于二维三角形和四边形电源单元,常采用的插值函数为有La grange插值直角坐标系中的线性插值函数及二阶或更高阶插值函数、面积坐标系中的线性插值函数、二阶或更高阶插值函数等。对于有限元方法,其基本思路和解题步骤可归纳为(1)建立积分方程,根据变分原理或方程余量与权函数正交化原理,建立与微分方程初边值问题等价的积分表达式,这是有限元法的出发点。(2)区域单元剖分,根据求解区域的形状及实际问题的物理特点,将区域剖分为若干相互连接、不重叠的单元。区域单元划分是采用有限元方法的前期准备工作,这部分工作量比较大,除了给计算单元和节点进行编号和确定相互之间的关系之外,还要表示节点的位置坐标,同时还需要列出自然边界和本质边界的节点序号和相应的边界值。(3)确定单元基函数,根据单元中节点数目及对近似解精度的要求,选择满足一定插
FDTD(时域有限差分法)算法的Matlab源程序
% 3-D FDTD code with PEC boundaries %*********************************************************************** % % Program author: Susan C. Hagness % Department of Electrical and Computer Engineering % University of Wisconsin-Madison % 1415 Engineering Drive % Madison, WI 53706-1691 % 608-265-5739 % hagness@https://www.360docs.net/doc/3212722913.html, % % Date of this version: February 2000 % % This MATLAB M-file implements the finite-difference time-domain % solution of Maxwell's curl equations over a three-dimensional % Cartesian space lattice comprised of uniform cubic grid cells. % % To illustrate the algorithm, an air-filled rectangular cavity % resonator is modeled. The length, width, and height of the % cavity are 10.0 cm (x-direction), 4.8 cm (y-direction), and % 2.0 cm (z-direction), respectively. % % The computational domain is truncated using PEC boundary % conditions: % ex(i,j,k)=0 on the j=1, j=jb, k=1, and k=kb planes % ey(i,j,k)=0 on the i=1, i=ib, k=1, and k=kb planes % ez(i,j,k)=0 on the i=1, i=ib, j=1, and j=jb planes % These PEC boundaries form the outer lossless walls of the cavity. % % The cavity is excited by an additive current source oriented % along the z-direction. The source waveform is a differentiated % Gaussian pulse given by % J(t)=-J0*(t-t0)*exp(-(t-t0)^2/tau^2), % where tau=50 ps. The FWHM spectral bandwidth of this zero-dc- % content pulse is approximately 7 GHz. The grid resolution % (dx = 2 mm) was chosen to provide at least 10 samples per % wavelength up through 15 GHz. % % To execute this M-file, type "fdtd3D" at the MATLAB prompt. % This M-file displays the FDTD-computed Ez fields at every other % time step, and records those frames in a movie matrix, M, which % is played at the end of the simulation using the "movie" command. %
有限差分法
有限差分法 有限差分法有限差分法 finite difference method 微分方程和积分微分方程数值解的方法。基本思想是把连续的定解区域用有限个离散 点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函 数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似, 积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差 分方程组,解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值方法便 可以从离散解得到定解问题在整个区域上的近似解。 有限差分法的主要内容包括:如何根据问题的特点将定解区域作网格剖分;如何把原 微分方程离散化为差分方程组以及如何解此代数方程组。此外为了保证计算过程的可行和 计算结果的正确,还需从理论上分析差分方程组的性态,包括解的唯一性、存在性和差分 格式的相容性、收敛性和稳定性。对于一个微分方程建立的各种差分格式,为了有实用意义,一个基本要求是它们能够任意逼近微分方程,这就是相容性要求。另外,一个差分格 式是否有用,最终要看差分方程的精确解能否任意逼近微分方程的解,这就是收敛性的概念。此外,还有一个重要的概念必须考虑,即差分格式的稳定性。因为差分格式的计算过 程是逐层推进的,在计算第n+1层的近似值时要用到第n层的近似值,直到与初始值有关。前面各层若有舍入误差,必然影响到后面各层的值,如果误差的影响越来越大,以致 差分格式的精确解的面貌完全被掩盖,这种格式是不稳定的,相反如果误差的传播是可以 控制的,就认为格式是稳定的。只有在这种情形,差分格式在实际计算中的近似解才可能 任意逼近差分方程的精确解。关于差分格式的构造一般有以下3种方法。最常用的方法是 数值微分法,比如用差商代替微商等。另一方法叫积分插值法,因为在实际问题中得出的 微分方程常常反映物理上的某种守恒原理,一般可以通过积分形式来表示。此外还可以用 待定系数法构造一些精度较高的差分格式。 有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。该方法 将求解域划分为差分网格,用有限个网格节点代替连续的求解域。有限差分法以Taylor 级数展开等方法,把控制方程中的导数用网格节点上的函数值的差商代替进行离散,从 而建立以网格节点上的值为未知数的代数方程组。该方法是一种直接将微分问题变为代数 问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。 对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。从差分 的空间形式来考虑,可分为中心格式和逆风格式。 考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。目 前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。差分 方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
时域有限差分法论文
时域有限差分法 1 选题背景 在多种可用的数值方法中,时域有限差分法(FDTD)是一种新近发展起来的可选方法。1966年,K.S.Yee 首次提出电磁场数值计算的新方法—时域有限差分法(Finite Difference- Time Domain ,简称FDTD)。经历了二十年的发展FDTD 法才逐渐走向成熟。上世纪80年代后期以来FDTD 法进入了一个新的发展阶段,即由成熟转为被广泛接受和应用的阶段。FDTD 法是解决复杂问题的有效方法之一,是一种直接基于时域电磁场微分方程的数值算法,它直接在时域将Maxwell 旋度方程用二阶精度的中心差分近似,从而将时域微分方程的求解转换为差分方程的迭代求解。是电磁场和电磁波运动规律和运动过程的计算机模拟。原则上可以求解任意形式的电磁场和电磁波的技术和工程问题,并且对计算机内存容量要求较低、计算速度较快、尤其适用于并行算法。现在FDTD 法己被广泛应用于天线的分析与设计、目标电磁散射、电磁兼容、微波电路和光路时域分析、生物电磁剂量学、瞬态电磁场研究等多个领域[1]。 2 原理分析 2.1 FDTD 的Yee 元胞 E,H 场分量取样节点在空间和时间上采取交替排布,利用电生磁,磁生电的原理 t t ??=??=??E D H ε t t ??-=??-=??H B E μ 图1 Yee 模型 如图1所示,Yee 单元有以下特点[2]: 1)E 与H 分量在空间交叉放置,相互垂直;每一坐标平面上的E 分量四周由H 分量环绕,H 分量的四周由E 分量环绕;场分量均与坐标轴方向一致。 2)每一个Yee 元胞有8个节点,12条棱边,6个面。棱边上电场分量近似相等,用棱边的中心节点表示,平面上的磁场分量近似相等,用面的中心节点表示。 3)每一场分量自身相距一个空间步长,E 和H 相距半个空间步长 4)每一场分量自身相距一个时间步长,E 和H 相距半个时间步长,电场取n 时刻的值,磁场取n+0.5时刻的值;即:电场n 时刻的值由n-1时刻的值得到,磁场n+0.5时刻的值由n-0.5时刻的值得到;电场n 时刻的旋度对应n+0.5时刻的磁场值,磁场n+0.5时刻的旋度对应(n+0.5)+0.5时刻的电场值,逐步外推。 5)3个空间方向上的时间步长相等,
有限差分法
有限差分法有限差分法 finite difference method 微分方程和积分微分方程数值解的方法。基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。 有限差分法的主要内容包括:如何根据问题的特点将定解区域作网格剖分;如何把原微分方程离散化为差分方程组以及如何解此代数方程组。此外为了保证计算过程的可行和计算结果的正确,还需从理论上分析差分方程组的性态,包括解的唯一性、存在性和差分格式的相容性、收敛性和稳定性。对于一个微分方程建立的各种差分格式,为了有实用意义,一个基本要求是它们能够任意逼近微分方程,这就是相容性要求。另外,一个差分格式是否有用,最终要看差分方程的精确解能否任意逼近微分方程的解,这就是收敛性的概念。此外,还有一个重要的概念必须考虑,即差分格式的稳定性。因为差分格式的计算过程是逐层推进的,在计算第n+1层的近似值时要用到第n层的近似值,直到与初始值有关。前面各层若有舍入误差,必然影响到后面各层的值,如果误差的影响越来越大,以致差分格式的精确解的面貌完全被掩盖,这种格式是不稳定的,相反如果误差的传播是可以控制的,就认为格式是稳定的。只有在这种情形,差分格式在实际计算中的近似解才可能任意逼近差分方程的精确解。关于差分格式的构造一般有以下3种方法。最常用的方法是数值微分法,比如用差商代替微商等。另一方法叫积分插值法,因为在实际问题中得出的微分方程常常反映物理上的某种守恒原理,一般可以通过积分形式来表示。此外还可以用待定系数法构造一些精度较高的差分格式。 有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛
