信号与系统公式+常用的连续傅里叶变换
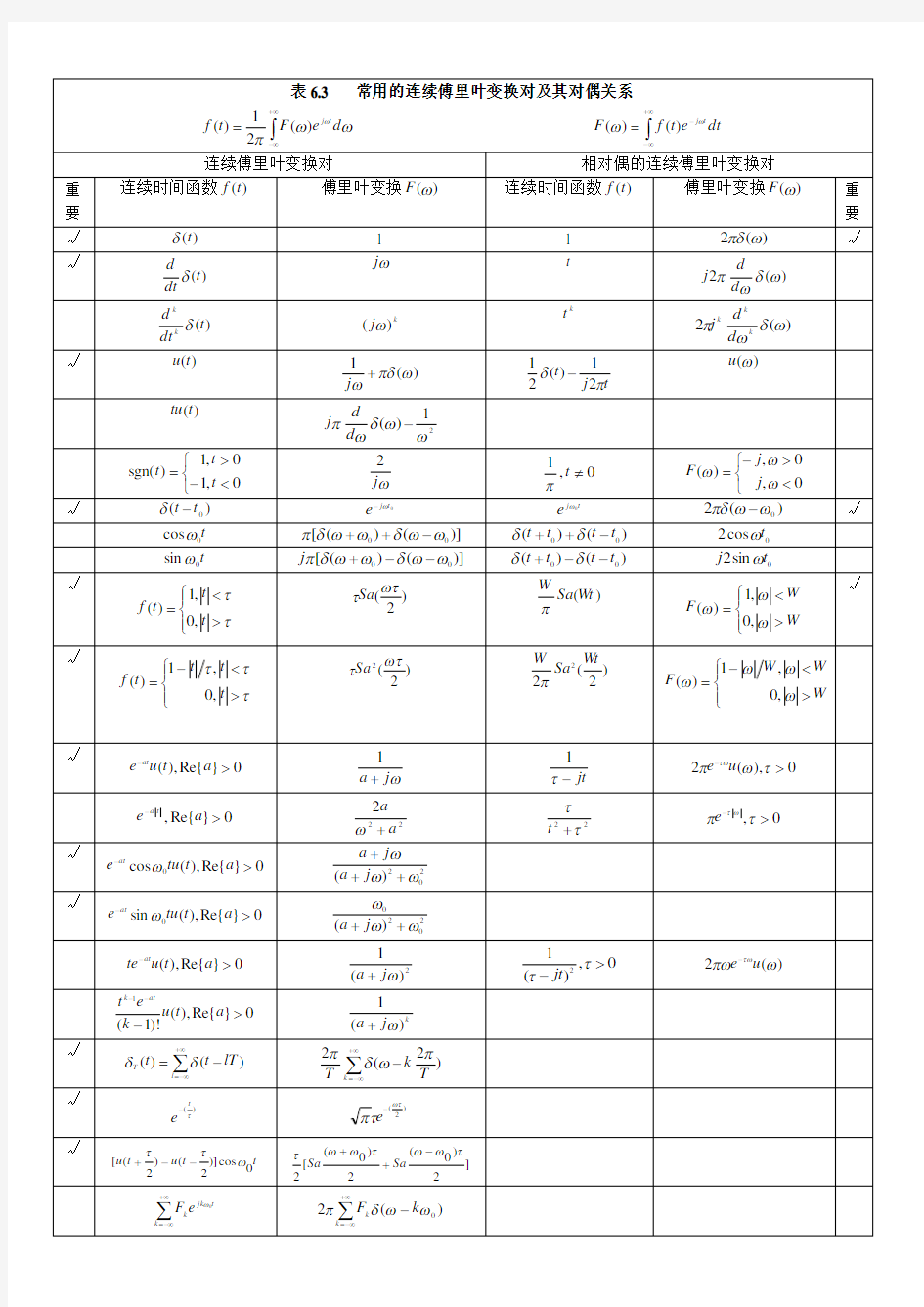
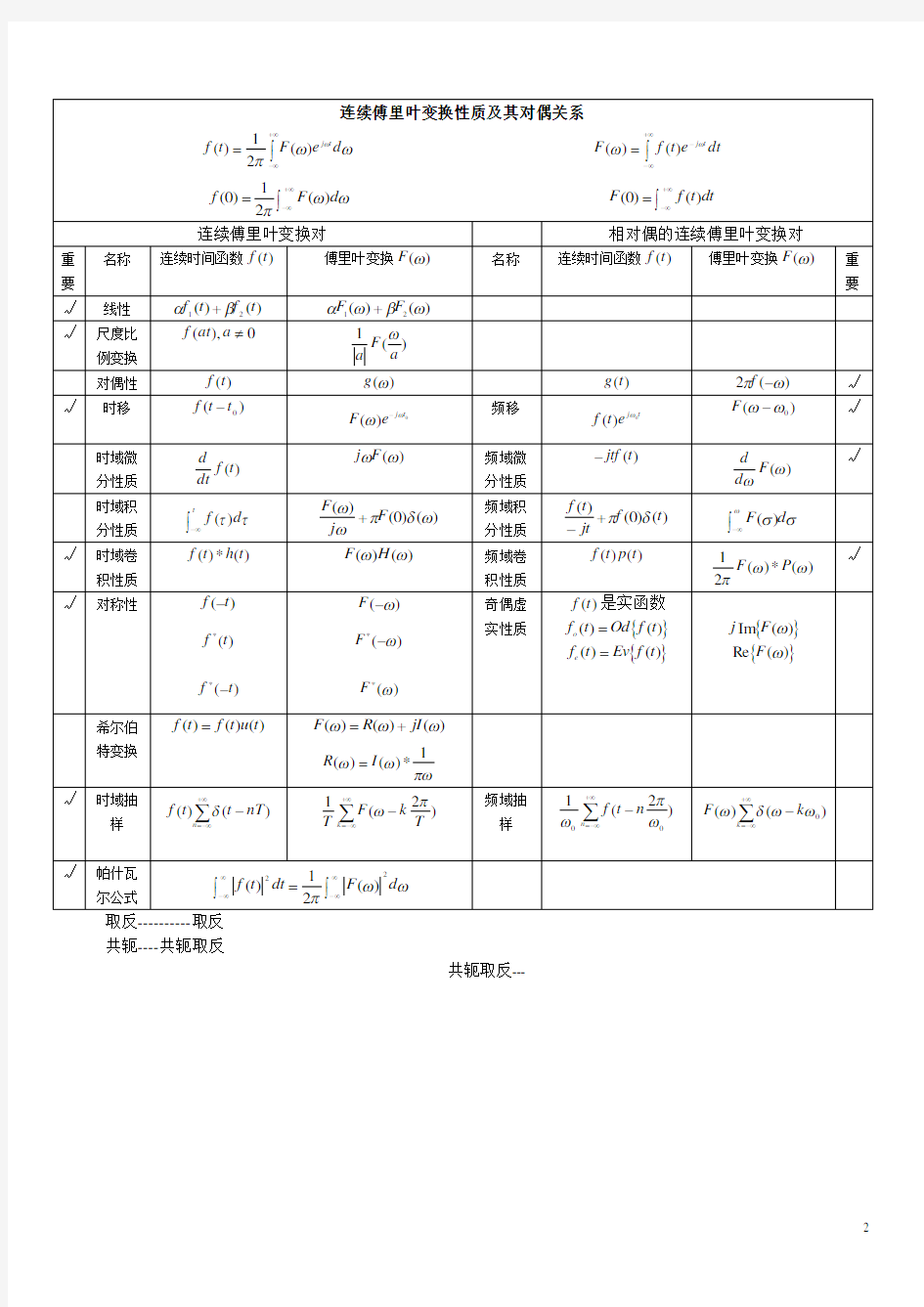
取反----------取反
共轭----共轭取反
共轭取反---
2
傅里叶变换在信号处理中的应用
傅里叶变换在信号处理中的应用 姓名董柱班级电气工程及其自动化学号1109141013 摘要: 傅里叶变换是一种特殊的积分变换。通过傅里叶变换把信号的从时域变换到频域研究,采用频域法较之经典时域的方法有很多突出的优点,虽然傅里叶分析不是信息科学与技术领域中唯一的变换域方法,但是不得不承认,在此领域中,傅里叶变换分析始终有着广泛的应用,通过傅里叶变换实现信号的滤波,调制,抽样是傅里叶变换在信号处理中最主要的作用。通过对信号的调制可以将信号的低频成分调制到高频,实现频谱搬移,减少马间串扰,提高抗噪声新能,有利于信号的远距离传输,另外,对信号采样可以使连续信号离散化,有利于用计算机对信号进行处理,总之,傅里叶变换在信号处理中有着非常重要的作用。傅里叶变换是学习其他频域变换的基础。 关键词: 傅里叶变换,时域,频域,信号处理,信息科学与技术,滤波,调制,抽样。 一傅里叶变换 1.定义 f(t)是t的函数,如果t满足狄里赫莱条件:具有有限个间断点;具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换, ②式的积分运算叫做F(ω)的傅立叶逆变换。F(ω)叫做f(t)的像函数,f(t)叫做 F(ω)的像原函数。F(ω)是f(t)的像。f(t)是F(ω)原像。 ① 傅里叶变换 傅里叶逆变换 2.分类 连续傅立叶变换:一般情况下,若“傅立叶变换”一词的前面未加任何限定语,则指的是“连续傅立叶变换”。“连续傅立叶变换”将平方可积的函数f(t) 表示成复指数函数的积分或级数形式。 f(t) = \mathcal^[F(ω)] = \frac{\sqrt{2π}} \int\limits_{-\infty}^\infty F(ω)e^{iωt}\,dω.
傅里叶(Fourier)级数的指数形式与傅里叶变换
傅里叶(Fourier )级数的指数形式与傅里叶变换 专题摘要:根据欧拉(Euler )公式,将傅里叶级数三角表示转化为指数表示,进而得到傅里叶积分定理,在此基础上给出傅里叶变换的定义和数学表达式。 在通信与信息系统、交通信息与控制工程、信号与信息处理等学科中,都需要对各种信号与系统进行分析。通过对描述实际对象数学模型的数学分析、求解,对所得结果给以物理解释、赋予其物理意义,是解决实际问题的关键。这种数学分析方法主要针对确定性信号的时域和频域分析,线性时不变系统的描述以及信号通过线性时不变系统的时域分析与变换域分析。所有这些分析方法都离不开傅里叶变换、拉普拉斯变换和离散时间系统的z 变换。而傅里叶变换的理论基础是傅里叶积分定理。傅里叶积分定理的数学表达式就是傅里叶级数的指数形式。 不但傅里叶变换依赖于傅里叶级数,就是纯数学分支的调和分析也来源于函数的傅里叶级数。因此,傅里叶级数无论在理论研究还是在实际应用中都占有非常重要的地位。我们承认满足狄里克莱(Dirichlet )条件下傅里叶级数的收敛性结果,不去讨论和深究傅里叶展式的唯一性问题。 傅里叶级数的指数形式 一个以T 为周期的函数)(t f ,在]2 ,2[T T 上满足狄里克莱条件:1o
)(t f 连续或只有有限个第一类间断点;2o 只有有限个极值点。那么)(t f 在]2 ,2[T T - 上就可以展成傅里叶级数。在连续点处 ∑∞ =++=1 )sin cos (2)(n n n t n b t n a a t f ωω, (1) 其中 T πω2= , ),2,1,0(,cos )(2 22Λ==?-n dt t n t f T a T T n ω, (2) ),3,2,1(,sin )(2 22 Λ==?-n dt t n t f T b T T n ω, (3) 根据欧拉(Euler )公式:θθθsin cos j e j +=,(1)式化为 ∑∞=--?? ????-+++=10222)(n t jn t jn n t jn t jn n j e e b e e a a t f ωωωω ∑∞=-?? ? ???++-+=10222n t jn n n t jn n n e jb a e jb a a ωω, (4) 若令 dt t f T c T T ?-=22 0)(1 Λ,3,2,1,)(1 ]sin )[cos (1 sin )(1cos )(1222 2222 22==-=-=-=????-----n dt e t f T dt t n j t n t f T dt t n t f T j dt t n t f T jb a c T T t jn T T T T T T n n n ωωωωω Λ,3,2,1,)(1 22 ==?--n dt e t f T c T T t jn n ω 综合n n c c c -,,0,可合并成一个式子 Λ,2,1,0,)(1 22 ±±==?--n dt e t f T c T T t jn n ω, (5)
傅里叶变换定律-傅里叶变换定义定律
第2章信号分析 本章提要 信号分类 周期信号分析--傅里叶级数 非周期信号分析--傅里叶变换 脉冲函数及其性质 信号:反映研究对象状态和运动特征的物理量信号分析:从信号中提取有用信息的方法 和手段 §2-1 信号的分类 两大类:确定性信号,非确定性信号 确定性信号:给定条件下取值是确定的。 进一步分为:周期信号, 非周期信号。
质量M 弹簧 刚度K t x (t ) o x 0 质量-弹簧系统的力学模型 x (t ) ? ?? ? ??+=0cos )(?t m k A t x 非确定性信号(随机信号):给定条件下取值是不确定的 按取值情况分类:模拟信号,离散信号 数字信号:属于离散信号,幅值离散,并用二进制表示。 信号描述方法 时域描述 如简谐信号
频域描述 以信号的频率结构来描述信号的方法:将信号看成许多谐波(简谐信号)之和,每一个谐波称作该信号的一个频率成分,考察信号含有那些频率的谐波,以及各谐波的幅值和相角。
?- = 2 2 0)(1T T dt t x T a ?- = 2 2 0cos )(2T T n tdt n t x T a ω ? - = 2 2 0sin )(2T T n tdt n t x T b ω 式中 T--周期;0--基频, 0=2 /T 。 三角函数展开式的另一种形式: ) cos()(1 00∑∞ =++=n n n t n A a t x ?ωN 次谐波 N 次谐波的相角 N 次谐波的频率 N 次谐波的幅值 信号的均值,直流分量
Chirp信号的傅里叶变换的特征比较.
Chirp信号的傅里叶变换的特征比较 Chirp信号即线性调频信号是瞬时频率在某个范围内随时间变化的正弦波,因其良好的频带利用率,具有较强的抗干扰、抗多途效应和抗多普勒衰减以及良好的频带利用率等优点,因此在通信、声呐、雷达等领域具有广泛的应用。本文就瞬时频率范围(信号的调频宽度)和信号的持续时间(信号的周期)对傅里叶变换后的chirp函数的频谱函数的影响做出讨论,运用MATLAB仿真分析比较。 一.信号的调频宽度上下限对频谱函数的影响 1)高频宽度300情况下的频谱函数。信号的采样频率为43000,扫描时间为0.05,初始频率设为19700,结束频率位置为20000。 2)低频宽度300情况下的频谱函数。信号的采样频率为2000,信号的持续时间为0.05,初始频率设为40,结束频率设置为340。 由上面两幅图可以看出,当它们满足,幅度谱的大小基本都在 0.01和0.015之间,这是因为它们的调频上下限之差相同都是300,且时间周 期都为0.05。由公式可知,幅度与信号的调频宽度(表示傅里叶变换后的频带宽度)和时间周期有关。 二.信号的调频宽度对频谱函数的影响 1)高频宽度10000情况下的频谱函数。信号的采样频率为48000,扫描时间为0.05,初始频率设为10000,结束频率位置为20000。
2)低频宽度80情况下的频谱函数。信号的采样频率为1000,信号的持续时间为0.05,初始频率设为40,结束频率设置为120。 上面两图在频带宽度内的幅度谱差异很明显,这是因为只有当时,近似程度才更高。 三.信号的持续时间对频谱函数的影响 1)低频宽度80情况下的频谱函数。信号的采样频率为1000,chirp 脉冲为0.05,信号的持续时间为2,初始频率设为40,结束频率设置为120。 上图的信号周期是2,发射脉冲长度为0.05与之前其它参数相同的图4比较可知,频带宽度基本相同,在频带宽度内的幅度谱没有太大变化,只是频点上的曲线多了些波动。
连续时间信号傅里叶变换及调制定理
乐山师范学院学生实验报告 实验课程名称: matlab 与信号系统实验 实验日期:2014年 月 日 姓名 学号 同组人 班级 系(院) 专业 级 班 指导老师 一、实验项目名称 连续时间信号傅里叶变换及调制定理 二、实验目的 1.学会用MA TLAB 求符号运算法的傅立叶正反变换; 2. 理解调制对信号频谱的影响 三、实验主要仪器设备仪器、器材、软件等 PC 机与matlab 软件 四、实验原理 见指导书 五、实验内容、步骤 1.求信号)()(t e t f t ε-=的频谱函数,并分别作出原函数与频谱函数的波形。 2.求信号2 )1(2)(ωω ωj j F += 的原函数,并分别作出原函数与频谱函数的波形。 3.设信号)100sin()(t t f π=,载波)(t y 为频率为400Hz 的余弦信号。试用MATLAB 实现调幅信号)(t y ,并观察)(t y 的频谱和)(t f 的频谱,以及两者在频域上的关系。 4.设),10cos( )()(),1()1()(1t t f t f t u t u t f π=--+=,试用MATLAB 画出)(),(1t f t f 的时域波形及其频谱,并观察傅里叶变换的频移特性。 六、实验记录(数据、现象、报表、软件、图象等) 1、 syms t w; f=exp(-1*t).*heaviside(t); y=fourier(f);
y=simplify(y); subplot(121); ezplot(f,[-3,3]); subplot(122); ezplot(w,y,[-2,2]); -2 02 0.10.20.30.40.50.60.70.80.9t exp(-t) heaviside(t) -2 -1 01 2 -3-2 -101 2 34 x y x = w, y = 1/(1+i w) 2、 syms t w ; ft=ifourier((2*w/(1+i*w)^2),t); y=ifourier(ft); y=simplify(y); subplot(121); ezplot(real(ft)); subplot(122); ezplot(imag(ft)); -5 05 -1 -0.8-0.6-0.4-0.200.20.40.60.81 t i exp(-t) heaviside(t) (t-1)-i conj(exp(-t) heaviside(t) (t-1))0 2 4 6 -0.6 -0.5-0.4-0.3-0.2-0.100.10.20.3 t -1/2 i (2 i exp(-t) heaviside(t) (t-1)+2 i conj(exp(-t) heaviside(t) (t-1)))
常用函数傅里叶变换
信号与系统的基本思想:把复杂的信号用简单的信号表示,再进行研究。 怎么样来分解信号?任何信号可以用Delta 函数的移位加权和表示。只有系统是线性时不变系统,才可以用单位冲激函数处理,主要讨论各个单位冲激函数移位加权的响应的叠加能得到总的响应。 线性系统(齐次性,叠加定理) 时不变系统 对一个系统输入单位冲激函数,得到的响应为h(t).表征线性时不变系统的非常重要的东西,只要知道了系统对单位冲击函数的响应,就知道了它对任何信号的响应,因为任何信号都可以表示为单位冲激函数的移位加权和。 例如:d(t)__h(t) 那么a*d(t-t0)__a*h(t-t0) -()= ()(t-)d f t f τδττ∝∝? 的响应为-y()=()(-)t f h t d τττ∝ ∝ ? 记为y(t)=f(t)*h(t),称为f(t)和h(t)的卷积 总结为两点:对于现行时不变系统,任何信号可以用单位冲激信号的移位加权和表示,任何信号的响应可以用输入函数和单位冲激函数响应的卷积来表示 连续时间信号和系统的频域分析 时域分析的重点是把信号分解为单位冲激函数的移位加权和,只讨论系统对单位冲激函数的响应。而频域的分析是把信号分解为各种不同频率的正弦函数的加权和,只讨论系统对sinwt 的响应。都是把信号分解为大量单一信号的组合。
周期函数可以展开为傅里叶级数,将矩形脉冲展开成傅里叶级数,得到傅里叶级数的系数 n A sin F = T x x τ 其中0=2 nw x τ。 取样函数sin ()=x S a x 。产生一种震荡,0点的值最大,然后渐渐衰减直至0 第一:对于傅里叶级数的系数,n 是离散的,所以频谱也是离散状的每条谱线都出现在基波频率的整数倍上,其包络是取样函数。 第二:谱线的间距是0w .。零点是0=2nw x τ,02w =T π是谱的基波频率。如果τ不变,T 增大,那么0w 减小,当T 非常大的时候,0w 非常小,谱线近似连续,越来越密,幅度越来越小。 傅里叶变换:非周期函数 正变换:--F jw)= ()iwt f t e dt ∝ ∝?( 反变换:-1()=()2jnwt f t F jw e dw π ∝∝ ? 常用函数的傅里叶变换(典型非周期信号的频谱)
常用傅立叶变换表
时域信号 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移, 变换2的频域对应4 如果值较大,则会收缩 到原点附近,而会扩 散并变得扁平. 当 | a | 趋向 无穷时,成为 Delta函数。 5 傅里叶变换的二元性性质。通过 交换时域变量和频域变量 得到. 6 傅里叶变换的微分性质 7 变换6的频域对应 8 表示和的卷积—这
9 矩形脉冲和归一化的sinc 函数 10 变换10的频域对应。矩形函数是理想的低通滤波器,sinc 函数是这类滤波器对反因果冲击的响应。 11 tri 是三角形函数 12 变换12的频域对应 13 高斯函数 exp( ? αt 2) 的傅里叶变换是他本身. 只有当 Re(α) > 0时,这是可积的。 14 15 16 a>0 17 变换本身就是一个公式
18 δ(ω) 代表狄拉克δ函数分布. 这 个变换展示了狄拉克δ函数的重要 性:该函数是常函数的傅立叶变换 19 变换23的频域对应 20 由变换3和24得到. 21 由变换1和25得到,应用了欧拉公 式: cos(at) = (e iat + e?iat) / 2. 22 由变换1和25得到 23 这里, n是一个自然数. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。这 个变换是根据变换7和24得到的。 将此变换与1结合使用,我们可以变 换所有多项式。 24 此处sgn(ω)为符号函数;注意此变 换与变换7和24是一致的. 25 变换29的推广. 26 变换29的频域对应. 27 此处u(t)是单位阶跃函数; 此变换 根据变换1和31得到.
傅里叶变换_百度文库.
傅里叶变换,拉普拉斯变换和Z 变换的意义来源:于理扬的日志 傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中, 傅里叶变换的典型用途是将信号分解成幅值分量和频率分量。 傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数或者它们的积分的线性组合。在不同的研究领域, 傅里叶变换具有多种不同的变体形式, 如连续傅里叶变换和离散傅里叶变换。 傅里叶变换是一种解决问题的方法,一种工具,一种看待问题的角度。理解的关键是:一个连续的信号可以看作是一个个小信号的叠加, 从时域叠加与从频域叠加都可以组成原来的信号,将信号这么分解后有助于处理。 我们原来对一个信号其实是从时间的角度去理解的,不知不觉中,其实是按照时间把信号进行分割, 每一部分只是一个时间点对应一个信号值, 一个信号是一组这样的分量的叠加。傅里叶变换后, 其实还是个叠加问题, 只不过是从频率的角度去叠加, 只不过每个小信号是一个时间域上覆盖整个区间的信号, 但他确有固定的周期,或者说,给了一个周期,我们就能画出一个整个区间上的分信号,那么给定一组周期值(或频率值,我们就可以画出其对应的曲线,就像给出时域上每一点的信号值一样,不过如果信号是周期的话,频域的更简单,只需要几个甚至一个就可以了,时域则需要整个时间轴上每一点都映射出一个函数值。 傅里叶变换就是将一个信号的时域表示形式映射到一个频域表示形式;逆傅里叶变换恰好相反。这都是一个信号的不同表示形式。它的公式会用就可以,当然把证明看懂了更好。 对一个信号做傅里叶变换,可以得到其频域特性,包括幅度和相位两个方面。幅度是表示这个频率分量的大小, 那么相位呢, 它有什么物理意义?频域的相位与时域的相位有关系吗?信号前一段的相位(频域与后一段的相位的变化是否与信号的频率成正比关系。
连续信号的傅里叶变换及matlab显示
(1)f(t)=u(t+6)-u(t-6) (2)f1(t)=f(-2t) (3)f2(t)=f(t-2) (4)f3(t)=f(t)· 以上四个式子的Matlab编程求其傅里叶变换与幅频特性,相频特性图 dt=0.001 t=-15:dt:15; f=(t>=-6)-(t>=6); k=-600:600; w1=2*pi*k/600; F=f*exp(-j*t'*w1)*dt; subplot(4,3,1); plot(t,f); axis([-15,15,-0.1,1.1]);grid; subplot(4,3,2); plot(w1,abs(F)); axis([-7,7,-1,13]);grid; subplot(4,3,3); plot(w1,angle(F)); axis([-10,10,-5,5]);grid; dt=0.001 t=-15:dt:15; f=(t<=6)-(t<=-3); k=-600:600; w1=2*pi*k/600; F=f*exp(-j*t'*w1)*dt; subplot(4,3,4); plot(t,f); axis([-15,15,-0.1,1.1]);grid; subplot(4,3,5); plot(w1,abs(F)); axis([-7,7,-1,10]);grid;
subplot(4,3,6); plot(w1,angle(F)); axis([-10,10,-5,5]);grid; dt=0.001 t=-15:dt:15; f=(t>=-4)-(t>=8); k=-600:600; w1=2*pi*k/600; F=f*exp(-j*t'*w1)*dt; subplot(4,3,7); plot(t,f); axis([-15,15,-0.1,1.1]);grid; subplot(4,3,8); plot(w1,abs(F)); axis([-7,7,-1,13]);grid; subplot(4,3,9); plot(w1,angle(F)); axis([-8,8,-5,5]);grid; dt=0.001; t=-15:dt:15; f=((t>=-6)-(t>=6)).*exp(-j*5*t); k=-600:600; w1=2*pi*k/600; F=f*exp(-j*t'*w1)*dt; subplot(4,3,10); plot(t,f); axis([-10,10,-1.2,1.2]);grid; subplot(4,3,11); plot(w1,abs(F)); axis([-7,7,-1,13]);grid; subplot(4,3,12); plot(w1,angle(F)); axis([-8,8,-5,5]);grid;
傅里叶变换公式
第2 章信号分析 本章提要 ?信号分类 ?周期信号分析--傅里叶级数 ?非周期信号分析--傅里叶变换 ?脉冲函数及其性质信号:反映研究对象状态和运动特征的物理量信号分析:从信号中提取有用信息的方法和手段 §2 -1 信号的分类 ?两大类:确定性信号,非确定性信号确定性信号:给定条件下取值是确定的。 进一步分为:周期信号,非周期信号。
质量-弹簧系 统的力学模型x(t) = A cos k t +0 非确定性信号(随机信号:给定条件下取值是不确定的 ?按取值情况分类:模拟信号,离散信号数字信号:属于离散信号,幅值离散,并用二进制表示。 ?信号描述方法 时域描述如简谐信号
简谐信号及其三个要素 频域描述 以信号的频率结构来描述信号的方法: 将信号看成许多谐波(简谐信号)之和,每一个谐波称作该信号的一个频率成分,考察信号含有那些频率的谐波,以及各谐波的幅值和相角。
T :周期。注意n 的取值:周期信号“无始无 终” # ? 傅里叶级数的三角函数展开式 x (t ) = a + (a cos n t + b sin n t ) n =1 (n =1, 2, 3 ,…) 傅立叶系数: T a 0 = 1 x (t )dt - 2 T x (t )cos n tdt 2 T 2 x (t ) sin n tdt 2 式中 T--周 期;0--基频, 0=2/T 。 ? 三角函数展开式的另一种形式: 2 a n = b n =2
信号处理中傅里叶变换简介
傅里叶变换 一、傅里叶变换的表述 在数学上,对任意函数f(x),可按某一点进行展开,常见的有泰勒展开和傅里叶展开。泰勒展开为各阶次幂函数的线性组合形式,本质上自变量未改变,仍为x,而傅里叶展开则为三角函数的线性组合形式,同时将自变量由x变成ω,且由于三角函数处理比较简单,具有良好的性质,故被广泛地应用在信号分析与处理中,可将时域分析变换到频域进行分析。 信号分析与处理中常见的有CFS(连续时间傅里叶级数)、CFT (连续时间傅里叶变换)、DTFT(离散时间傅里叶变换)、DFS(离散傅里叶级数)、DFT(离散傅里叶变换)。通过对连续非周期信号x c(t)在时域和频域进行各种处理变换,可推导出以上几种变换,同时可得出这些变换之间的关系。以下将对上述变换进行简述,同时分析它们之间的关系。 1、CFS(连续时间傅里叶级数) 在数学中,周期函数f(x)可展开为 由此类比,已知连续周期信号x(t),周期为T0,则其傅里叶级数为 其中,
为了简写,有 其中, 为了与复数形式联系,先由欧拉公式e j z=cos z+jsin z得 故有
令 则 对于D n,有 n≤0时同理。 故 CFS图示如下:
Figure 1 理论上,CFS对于周期性信号x(t)在任意处展开都可以做到无误差,只要保证n从-∞取到+∞就可以。在实践中,只要n取值范围足够大,就可以保证在某一点附近对x(t)展开都有很高的精度。 2、CFT(连续时间傅里叶变换) 连续非周期信号x(t),可以将其看成一连续周期信号的周期T0→∞。当然,从时域上也可以反过来看成x(t)的周期延拓。将x(t)进行CFS展开,有 若令 则 有
连续时间傅里叶变换
2 奇偶信号的FS: (i) 偶信号的FS: 2 a n f (t)cosn T] T 1 Fn 弘 1tdt ; bn 2 T1 f (t)sin n 1tdt c n d n a n (ii ) jbn an 2 2 偶的周期信号的 奇信号的FS: F n ( Fn 实, 偶对称);n FS 系数只有直流项和余弦项。 2 T f(t)sinn 1tdt ; 5 dn T| 11 1 Fn F n jbn ( Fn 纯虚,奇对称); a a n 0 ; b n b n 2jFn 第二章连续时间傅里叶变换 1周期信号的频谱分析 一一傅里叶级数FS (1) 狄义赫利条件:在同一个周期 T1内,间断点的个数有限;极大值和极小值的数目有限;信号绝 为T i ,角频率为 ,2 f ,—。 Ti (3)任何满足狄义赫利条件周期函数都可展成傅里叶级数。 ⑷三角形式的FS: (i) 展开式:f(t) a 0 (ancon it bn sin n ,t) n 1 (ii) 系数计算公式: (a) 直流分量: ao f (t)dt T 1 T 1 (b) n 次谐波余弦分量: a n - f (t) cosn 1tdt, n N T1 T 1 2 (c) n 次谐波的正弦分量: bn — f (t)sinn 1tdt, n N T1 T 1 (iii) 系数an 和bn 统称为三角形式的傅里叶级数系数,简称傅里叶系数。 (iv) 称f1 1/T1为信号的基波、基频; nf1为信号的n 次谐波。 (V) 合并同频率的正余弦项得: n 和n 分别对应合并后 门次谐波的余弦项和正弦项的初相位。 (vi) 傅里叶系数之间的关系: (5)复指数形式的FS: (i) 展开式:f (t) Fne jn 1t n (ii) 系数计算:Fn 丄 f(t)e jn 1t dt, n Z T] T 1 (iii) 系数之间的关系: (iv) Fn 关于 n 是共扼对称的,即它们关于原点互为共轭。 (v) 正负n (n 非零)处的Fn 的幅度和等于Cn 或dn 的幅度。 对可积 丁 f(t)dt 。 (2)傅里叶级数:正交函数线性组合。 正交函数集可以是三角函数集 {1,cosn *,sinn 1t :n N}或复指数函数集 {e jn 术:n Z},函数周期
傅里叶变换公式
连续时间周期信号傅里叶级数:?= T dt t x T a )(1 ??--= = T t T jk T t jk k dt e t x T dt e t x T a π ω2)(1 )(1 离散时间周期信号傅里叶级数:[][]()∑∑= - =-= = N n n N jk N n n jkw k e n x N e n x N a /21 1 0π 连续时间非周期信号的傅里叶变换:()? ∞∞ --=dt e t x jw X jwt )( 连续时间非周期信号的傅里叶反变换:()dw e jw X t x jwt ? ∞ ∞ -=π 21 )( 连续时间周期信号傅里叶变换:∑+∞ -∞ =??? ? ? ? -=k k k w a jw X T 22)(πδπ 连续时间周期信号傅里叶反变换:()dw e w w t x jwt ? ∞ ∞ --=0221 )( πδπ 离散时间非周期信号傅里叶变换:∑∞ -∞ =-= n n j e n x e X ωω j ][)( 离散时间非周期信号傅里叶反变换:? = π 2d e )(e π 21][ωωωn j j X n x 离散时间周期信号傅里叶变换:∑+∞ -∞ =-= k k k a X )(π2)e (0 j ωωδω 离散时间周期信号傅里叶反变换:[]ωω ωδωd e n n j ?--=π 20 πl)2(π2π 21][x 拉普拉斯变换:()dt e t s X st -∞ ∞ -? =)(x 拉普拉斯反变换:()()s j 21 t x j j d e s X st ?∞ +∞ -= σσ π Z 变换:∑∞ -∞ =-=n n z n x X ][)z ( Z 反变换: ??-== z z z X r z X n x n n d )(πj 21d )e ()(π21][1j π2ωω
快速傅里叶变换(FFT)的原理及公式
快速傅里叶变换(FFT)的原理及公式 原理及公式 非周期性连续时间信号x(t)的傅里叶变换可以表示为 式中计算出来的是信号x(t)的连续频谱。但是,在实际的控制系统中能够得到的是连续信号x(t)的离散采样值x(nT)。因此需要利用离散信号x(nT)来计算信号x(t)的频谱。 有限长离散信号x(n),n=0,1,…,N-1的DFT定义为: 可以看出,DFT需要计算大约N2次乘法和N2次加法。当N较大时,这个计算量是很大的。利用WN的对称性和周期性,将N点DFT分解为两个N/2点 的DFT,这样两个N/2点DFT总的计算量只是原来的一半,即(N/2)2+(N/2)2=N2/2,这样可以继续分解下去,将N/2再分解为N/4点DFT等。对于N=2m点的DFT都可以分解为2点的DFT,这样其计算量可以减少为(N/2)log2N 次乘法和Nlog2N次加法。图1为FFT与DFT-所需运算量与计算点数的关系曲线。由图可以明显看出FFT算法的优越性。 将x(n)分解为偶数与奇数的两个序列之和,即
x1(n)和x2(n)的长度都是N/2,x1(n)是偶数序列,x2(n)是奇数序列,则 其中X1(k)和X2(k)分别为x1(n)和x2(n)的N/2点DFT。由于X1(k)和X2(k)均以N/2为周期,且WN k+N/2=-WN k,所以X(k)又可表示为: 上式的运算可以用图2表示,根据其形状称之为蝶形运算。依此类推,经过m-1次分解,最后将N点DFT分解为N/2个两点DFT。图3为8点FFT的分解流程。 FFT算法的原理是通过许多小的更加容易进行的变换去实现大规模的变换,降低了运算要求,提高了与运算速度。FFT不是DFT的近似运算,它们完全是等效的。 关于FFT精度的说明: 因为这个变换采用了浮点运算,因此需要足够的精度,以使在出现舍入误差时,结果中的每个组成部分的准确整数值仍是可辨认的。为了FFT的舍入误差,应该允许增加几倍log2(log2N)位的二进制。以256为基数、长度为N字节的数
实验六傅里叶变换及其反变换
实验六 傅里叶变换及其反变换 6.1实验目的 1.学会运用MATLAB 求连续时间信号的傅里叶变换; 2.学会运用MATLAB 求连续时间信号的傅里叶反变换; 3.学会运用MATLAB 求连续时间信号的频谱图。 6.2实验原理及实例分析 1.连续时间信号傅里叶变换----CTFT 傅里叶变换在信号分析中具有非常重要的意义,它主要是用来进行信号的频谱分析的。傅里叶变换和其逆变换定义如下: ?∞ ∞--= dt e t x j X t j ωω)()( 6.1 ?∞∞-=ωωπωd e j X t x t j )(21)( 6.2 连续时间傅里叶变换主要用来描述连续时间非周期信号的频谱。按照教材中的说法,任意非周期信号,如果满足狄里克利条件,那么,它可以被看作是由无穷多个不同频率(这些频率都是非常的接近)的周期复指数信号e j ωt 的线性组合构成的,每个频率所对应的周期复指数信号e j ωt 称为频率分量(frequency component ),其相对幅度为对应频率的|X(j ω)|之值,其相位为对应频率的X(j ω)的相位。 X(j ω)通常为关于的复函数,可以按照复数的极坐标表示方法表示为: X(j ω)=| X(j ω)|e j ∠ X(j ω) 其中,| X(j ω)|称为x(t)的幅度谱,而∠X(j ω)则称为x(t)的相位谱。 给定一个连续时间非周期信号x(t),它的频谱也是连续且非周期的。对于连续时间周期信号,也可以用傅里变换来表示其频谱,其特点是,连续时间周期信号的傅里叶变换时有冲激序列构成的,是离散的——这是连续时间周期信号的傅里叶变换的基本特征。 2.用MATLAB 实现CTFT 的计算 MATLAB 进行傅里叶变换有两种方法,一种利用符号运算的方法计算,另一种是数值计算。 1) MATLAB 符号运算求解法 MATLAB 符号数学工具箱提供了直接求解傅里叶变换与傅里叶反变换的函数fourier( )及ifourier( )。常用的是:F=fourier(f) 默认返回值是关于ω的函数。 f=fourier(F,t) 返回值是关于t 的函数 例:利用MATLAB 求单边指数信号f(t) = e -2t u(t)的傅里叶变换,画出f(t)及其幅度谱和相位谱图。 syms t v w x phase im re ; %定义符号变量 f = exp(-2*t)*sym('Heaviside(t)'); %f(t)=exp(-2*t)*u(t) Fw = fourier(f); %求傅里叶变换 subplot(311); ezplot(f); %绘制f(t)的时域波形 axis([-1 2.5 0 1.1]); subplot(312); ezplot(abs(Fw)); %绘制幅度谱 im = imag(Fw); %计算F(w)的虚部
用Matlab对信号进行傅里叶变换实例
目录 用Matlab对信号进行傅里叶变换 (2) Matlab的傅里叶变换实例 (5) Matlab方波傅立叶变换画出频谱图 (7)
用Matlab对信号进行傅里叶变换 1.离散序列的傅里叶变换DTFT(Discrete Time Fourier Transform) 代码: 1 N=8; %原离散信号有8点 2 n=[0:1:N-1] %原信号是1行8列的矩阵 3 xn=0.5.^n; %构建原始信号,为指数信号 4 5 w=[-800:1:800]*4*pi/800; %频域共-800----+800 的长度(本应是无穷,高频分量很少,故省去) 6 X=xn*exp(-j*(n'*w)); %求dtft变换,采用原始定义的方法,对复指数分量求和而得 7 subplot(311) 8 stem(n,xn); 9 title('原始信号(指数信号)'); 10 subplot(312); 11 plot(w/pi,abs(X)); 12 title('DTFT变换') 结果: 分析:可见,离散序列的dtft变换是周期的,这也符合Nyquist采样定理的描述,连续时间信号经周期采样之后,所得的离散信号的频谱是原连续信号频谱的周期延拓。 2.离散傅里叶变换DFT(Discrete Fourier Transform)
与1中DTFT不一样的是,DTFT的求和区间是整个频域,这对 结果图:
分析:DFT只是DTFT的现实版本,因为DTFT要求求和区间无穷,而DFT只在有限点内求和。 3.快速傅里叶变换FFT(Fast Fourier Transform) 虽然DFT相比DTFT缩减了很大的复杂度,但是任然有相当大的计算量,不利于信息的实时有效处理,1965年发现的DFT解决了这一问题。 实现代码: 1 N=64; %原离散信号有8点 2 n=[0:1:N-1] %原信号是1行8列的矩阵 3 xn=0.5.^n; %构建原始信号,为指数信号 4 Xk=fft(xn,N); 5 subplot(221); 6 stem(n,xn); 7 title('原信号'); 8 subplot(212); 9 stem(n,abs(Xk)); 10 title('FFT变换') 效果图: 分析:由图可见,fft变换的频率中心不在0点,这是fft算法造成的,把fft改为fftshift可以将频率中心移到0点。
常用傅里叶变换
时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移,变换2 的频域对应 4 如果值较大,则 会收缩到原 点附近,而 会扩 散并变得扁平.当 | a | 趋向无穷 时,成为狄拉克δ 函数。 5 傅里叶变换的二元 性性质。通过交换 时域变量和频域 变量得到. 6 傅里叶变换的微分 性质
7 变换6的频域对应8 表示和 的卷积—这就是卷 积定理 9 变换8的频域对应。[编辑]平方可积函数 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 10 矩形脉冲和归一 化的sinc函数 11 变换10的频域对 应。矩形函数是理 想的低通滤波器, sinc函数是这类 滤波器对反因果 冲击的响应。
12 tri是三角形函数 13 变换12的频域对应 14 高斯函数exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。 15 光学领域应用较多 16 17 18 a>0 19 变换本身就是一个公式
20 J0(t)是0阶第一 类贝塞尔函数。 21 上一个变换的推 广形式; T n(t)是第 一类切比雪夫多 项式。 22 U n (t)是第二类切 比雪夫多项式。[编辑]分布 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 23 δ(ω)代表狄拉克δ函数 分布.这个变换展示了狄 拉克δ函数的重要性:该 函数是常函数的傅立叶 变换 24 变换23的频域对应
25 由变换3和24得到. 26 由变换1和25得到,应用了欧拉公式: cos(at) = (e iat + e?iat) / 2. 27 由变换1和25得到 28 这里, n是一个自然数.δ(n)(ω)是狄拉克δ函数分布的n阶微分。这个变换是根据变换7和24得到的。将此变换与1结合使用,我们可以变换所有多項式。 29 此处sgn(ω)为符号函数;注意此变换与变换7和24是一致的. 30 变换29的推广. 31 变换29的频域对应. 32 此处u(t)是单位阶跃函数;此变换根据变换1和31得到.
常用傅里叶变换
常用傅里叶变换 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT
时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移,变换2 的频域对应 4 如果值较大, 则会收缩 到原点附近,而 会扩 散并变得扁平.当 |?a?|?趋向无穷 时,成为。 5 傅里叶变换的二元 性性质。通过交换 时域变量和频域 变量得到. 6 傅里叶变换的微分 性质 7 变换6的频域对应
8 表示和 的卷积—这就是9 变换8的频域对 应。 []平方可积函数 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 10 和归一化的 11 变换10的频域对 应。矩形函数是 理想的低通滤波 器,是这类滤波 器对冲击的响 应。 12 tri?是 13 变换12的频域对 应
14 exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。 15 领域应用较多 16 17 18 a>0 19 变换本身就是一个公式 20 J0(t)?是。 21 上一个变换的推广形式;?T n(t)?是。 22 ???? U n?(t)是。
[]分布 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 23 δ(ω)代表分布.这个变换 展示了狄拉克δ函数的 重要性:该函数是常函 数的傅立叶变换 24 变换23的频域对应 25 由变换3和24得到. 26 由变换1和25得到,应 用了:?cos(at) = (e iat?+?e???iat) / 2. 27 由变换1和25得到 28 这里,?n是一个.δ(n)(ω)是 狄拉克δ函数分布的n 阶微分。这个变换是根 据变换7和24得到的。 将此变换与1结合使 用,我们可以变换所 有。
实验四连续信号的傅立叶变换
实验4非周期信号的傅立叶变换分析 一、实验目的 (1)熟悉连续非周期信号频谱特点及其分析方法; (2)掌握用MATLAB 实现傅立叶变换的两种方法; (3)了解常用傅立叶变换性质的MATLAB 实现方法; 二、实验原理 1、傅里叶变换和其逆变换定义如下: ?∞ ∞--= dt e t x j X t j ωω)()( 4.1?∞∞-=ωωπωd e j X t x t j )(1)( 4.2 连续时间傅里叶变换主要用来描述连续时间非周期信号的频谱。按照教材中的说法,任意非周期信号,如果满足狄里克利条件,那么,它可以被看作是由无穷多个不同频率(这些频率都是非常的接近)的周期复指数信号e j ωt 的线性组合构成的,每个频率所对应的周期复指数信号e j ωt 称为频率分量(frequency component),其相对幅度为对应频率的|X(j ω)|之值,其相位为对应频率的X(j ω)的相位。 X(j ω)通常为复函数,可以按照复数的极坐标表示方法表示为: X(j ω)=|X(j ω)|e j ∠X(j ω) 其中,|X(j ω)|称为x(t)的幅度谱,而∠X(j ω)则称为x(t)的相位谱。 给定一个连续时间非周期信号x(t),它的频谱也是连续且非周期的。 2、用MATLAB 实现方法 MATLAB 进行傅里叶变换有两种方法,一种利用符号运算的方法计算,另一种是数值计算。 2.1采用数值计算的方法来进行傅里叶变换的计算 严格来说,用数值计算的方法计算连续时间信号的傅里叶变换需要有个限定条件,即信号是时限信号(Time limited signal),也就是当时间|t|大于某个给定时间时其值衰减为零或接近于零,这个条件与前面提到的为什么不能用无限多个谐波分量来合成周期信号的道理是一样的。计算机只能处理有限大小和有限数量的数。 采用数值计算算法的理论依据是: ()()j t X j x t e dt ωω∞ --∞= ?∑∞-∞=-→=k T jk T T e kT x ω)(lim 0
快速傅里叶变换的通俗解释
一、傅立叶变换的由来 关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解,最近,我偶尔从网上看到一个关于数字信号处理的电子书籍,是一个叫Steven W. Smith, Ph.D.外国人写的,写得非常浅显,里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换,虽然是英文文档,我还是硬着头皮看完了有关傅立叶变换的有关内容,看了有茅塞顿开的感觉,在此把我从中得到的理解拿出来跟大家分享,希望很多被傅立叶变换迷惑的朋友能够得到一点启发. 要理解傅立叶变换,确实需要一定的耐心,别一下子想着傅立叶变换是怎么变换的,当然,也需要一定的高等数学基础,最基本的是级数变换,其中傅立叶级数变换是傅立叶变换的基础公式。 二、傅立叶变换的提出 让我们先看看为什么会有傅立叶变换?傅立叶是一位法国数学家和物理学家的名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807 年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的工作,幸运的是,傅立叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。 谁是对的呢?拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅立叶是对的。 为什么我们要用正弦曲线来代替原来的曲线呢?如我们也还可以用方波或三角波来代替呀,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。 三、傅立叶变换分类
