初中三角函数知识点总结及典型习题(含答案)

初三下学期锐角三角函数知识点总结及典型习题

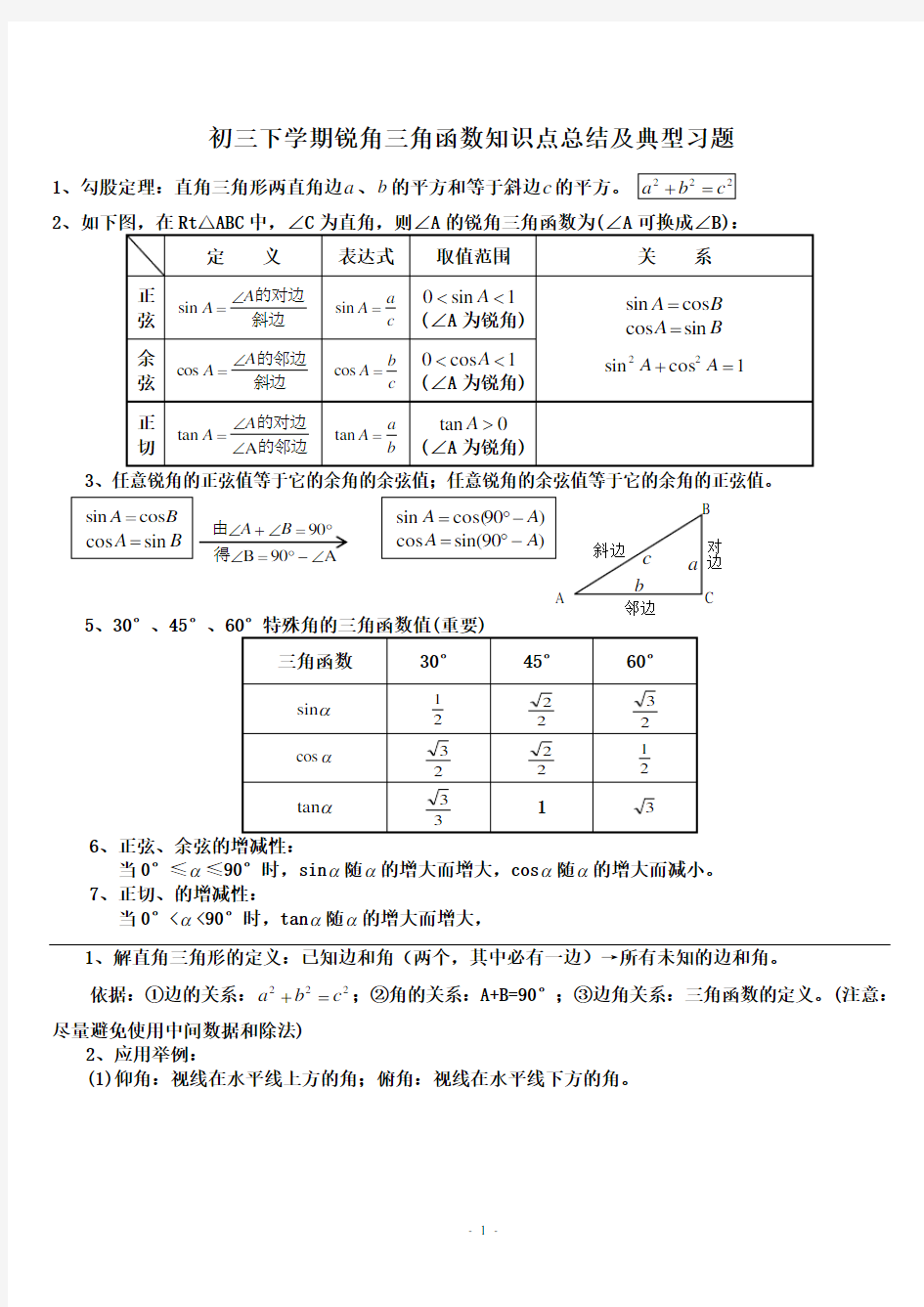
1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

5、30°、45°、 6 当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。 7、正切、的增减性：

当0°<α<90°时，tan α随α的增大而增大，

1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。(注意：尽量避免使用中间数据和除法)

2、应用举例：

(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

A 90

B 90∠-?=∠?

=∠+∠得由B A

对边

邻边

(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。用字母i 表示，即h i l

=。坡度一般写成1:m 的形式，如1:5i =等。

把坡面与水平面的夹角记作α(叫做坡角)，那么tan h

i l

α=

=。 3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。

4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。

例1：已知在Rt ABC △中，3

90sin 5

C A ∠==°，，则tan B 的值为（）

A ．43

B ．45

C ．54

D ．

【解析】本题考查三角函数的定义和勾股定理，在RT ΔABC 中，∠C=90°，则sin a A c =

，tan b

B a

=和222a b c +=；由3s i n 5A =知，如果设3a x =，则5c x =，结合222a b c +=得4b x =；∴44

tan 33

b x B a x ===，

所以选A ．

例2

：104cos30sin 60(2)2008)-??+--=______．

【解析】本题考查特殊角的三角函数值．零指数幂．负整数指数幂的有关运算，

104cos30sin 60(2)2008)-??+--

=134122

??--= ???，故填3

2．

1. 某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（ C ）

A ．8米 B

． C

米

:i h l =h

2. 一架5米长的梯子斜靠在墙上，测得它与地面的夹角是40°，则梯子底端到墙的距离为（ B ）

A．5sin40°B．5cos40°C．

tan40°

D．

cos40°

3. 如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB、CD分别表示一楼、二楼地面的水平

线，∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（ B ）

m B．4 m

．m D．8 m

4. 河堤横断面如图所示，堤高BC=5米，迎水坡AB的坡比是

面的铅直高度BC与水平宽度AC之比），则AC的长是（ A ）

．米 B． 10米

C．15米 D

．

5．如图，在矩形ABCD中，DE⊥AC于E，∠EDC∶∠EDA=1∶3，且AC=10，则DE的长度是（ D ）

A．3 B．5 C．2

5D．

6. 如图所示,小明在家里楼顶上的点A处，测量建在与小明家楼房同一水平线上相邻的电梯楼的高，在点A处看电梯楼顶部点B处的仰角为60°，在点A处看这栋电梯楼底部点C处的俯角为45°，两栋楼之间的距离为30m，则电梯楼的高BC为 82.0 米（精确到

0.1）.

1.414

1.732）

7. 如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯

角为30°，看这栋大楼底部C的俯角为60°，热气球A的高度为240米，求这栋大楼的高度.

解：过点A作直线BC的垂线，垂足为点D.

则90

CDA

∠=°，60

CAD

∠=°，30

BAD

∠=°，CD=240米.

在Rt ACD

△中，tan

CAD

∠=，

tan60

∴===

在Rt ABD

△中，tan

BAD

∠=，

tan3080

BD AD

∴===

·°.

∴BC CD BD

=-=240-80=160.

答：这栋大楼的高为160米.

8. 如图所示，城关幼儿园为加强安全管理，决定将园内的滑滑板的倾斜角由45°降为30°，已知原滑滑板AB的长为4米，点D、B、C在同一水平面上．

（1）改善后滑滑板会加长多少米？

（2）若滑滑板的正前方能有3米长的空地就能保证安全，原滑滑板的前方有6米长的空地，像这样改造是否可行？请说明理由．

（参考数据：141

2=，732

3=，449

6=，以上结果均保留到小数点后两位．）解：（1）在Rt△ABC中，∠ABC=45°

∴AC=BC=AB·sin45°=2

在Rt△ADC中，∠ADC=30°

∴AD= 2

sin

∴AD-AB=66

4≈

∴改善后滑滑板会加长约1.66米.

（2）这样改造能行，理由如下：

∵989

tan

≈

∴07

2≈

=BC

∴6-2.07≈3.93＞3

∴这样改造能行.

．求值

2|20093tan30

+--+

° 1.解：原式

= 2133

-++6

10. 计算：

2009

2sin603tan30(1)

-++-

°°

2.原式

=2311

?-?+-=0．

集合的简单练习题并集合的知识点归纳

必修1 集合复习知识框架： 1.1.1 集合的含义与表示 1．下列各组对象 ①接近于0的数的全体；②比较小的正整数全体；③平面上到点O 的距离等于1的点的全体； ④正三角形的全体；⑤2的近似值的全体．其中能构成集合的组数有( ) A ．2组 B ．3组 C ．4组 D ．5组 2．设集合M ＝{大于0小于1的有理数}，N ＝{小于1050的正整数}， P ＝{定圆C 的内接三角形}，Q ＝{所有能被7整除的数}，其中无限集是( ) A ．M 、N 、P B ．M 、P 、Q C ．N 、P 、Q D ．M 、N 、Q 3．下列命题中正确的是( ) A ．{x ｜x 2＋2＝0}在实数范围内无意义 B ．{(1，2)}与{(2，1)}表示同一个集合 C ．{4，5}与{5，4}表示相同的集合 D ．{4，5}与{5，4}表示不同的集合 4．直角坐标平面内，集合M ＝{(x ，y )｜xy ≥0，x ∈R ，y ∈R }的元素所对应的点是( ) A ．第一象限内的点 B ．第三象限内的点 C ．第一或第三象限内的点 D ．非第二、第四象限内的点 5．已知M ＝{m ｜m ＝2k ，k ∈Z }，X ＝{x ｜x ＝2k ＋1，k ∈Z }，Y ＝{y ｜y ＝4k ＋1，k ∈Z }，则( ) A ．x ＋y ∈M B ．x ＋y ∈X C ．x ＋y ∈Y D ．x ＋y ?M 6．下列各选项中的M 与P 表示同一个集合的是( ) A ．M ＝{x ∈R ｜x 2＋0.01＝0}，P ＝{x ｜x 2＝0} B ．M ＝{(x ，y )｜y ＝x 2＋1，x ∈R }，P ＝{(x ，y )｜x ＝y 2＋1，x ∈R } C ．M ＝{y ｜y ＝t 2＋1，t ∈R }，P ＝{t ｜t ＝(y －1)2＋1，y ∈R } D ．M ＝{x ｜x ＝2k ，k ∈Z }，P ＝{x ｜x ＝4k ＋2，k ∈Z } 7．由实数x ，－x ，｜x ｜所组成的集合，其元素最多有______个． 8．集合{3，x ，x 2－2x }中，x 应满足的条件是______． 9．对于集合A ＝{2，4，6}，若a ∈A ，则6－a ∈A ，那么a 的值是______． 10．用符号∈或?填空： ①1______N ，0______N ．－3______Q ，0.5______Z ，2______R ． ②2 1______R ，5______Q ，｜－3|______N ＋，｜－3｜______Z ． 11．若方程x 2＋mx ＋n ＝0(m ，n ∈R )的解集为{－2，－1}，则m ＝______，n ＝______． 12．若集合A ＝{x ｜x 2＋(a －1)x ＋b ＝0}中，仅有一个元素a ，则a ＝______，b ＝______． 13．方程组?? ???=+=+=+321x z z y y x 的解集为______． 14．已知集合P ＝{0，1，2，3，4}，Q ＝{x ｜x ＝ab ，a ，b ∈P ，a ≠b }，用列举法表示集合Q ＝______． 15．用描述法表示下列各集合：

上海高一反三角函数典型例题

反三角函数典型例题例1：在下列四个式子中，有意义的为__________：解：（4）有意义。（1）（2）arcsin 4 π ；（3）sin(arcsin 2)；（4）arcsin(sin 2)。点评：arcsin x ——x [1,1]∈-。例2：求下列反正弦函数值（1）= 解：3 π （2）arcsin 0= 解：0 （3）1arcsin()2-= 解：6π- （4）arcsin1= 解：2 π 点评：熟练记忆：0，1 2 ±、，，1±的反正弦值。思考：1sin(arcsin )24 π +该如何求？例3：用反正弦函数值的形式表示下列各式中的x (1)sin x = ，x [,]22ππ ∈- 解：x ＝变式：x [,]2 π ∈π? 解：x [,]2π ∈π时，π－x [0,]2 π∈，sin(π－x)＝sinx ∴π－x ＝，则x ＝π－变式：x [0,]∈π? 解：x ＝x ＝π－(2)1sin x 4=-，x [,]22ππ∈- 解：1 x arcsin 4 =- 变式：1 sin x 4=-，3x [,2]2π∈π 解：3x [,2]2π∈π时，2π－x [0,]2 π∈，sin(2π－x)＝－sinx ＝1 4 ∴2π－x ＝arcsin 14，则x ＝2π－arcsin 1 4 点评：当x [,]22ππ ∈-时，x arcsin a =；而当x [,]22ππ?-，可以将角转化到区间[,]22 ππ-上，

再用诱导公式处理对应角之三角比值即可。练习： (1)sin x = ，x [,]22ππ ∈- 解：x 3π= (2)sin x =，x [0,]∈π 解：x arcsin =x =π-(3)3sin x 5=-，3x [,]22ππ∈ 解：3 x arcsin 5 =π+ 例4：求函数y 2arcsin(52x)=-的定义域和值域。解：由152x 1-≤-≤，则x [2,3]∈，arcsin(52x)[,]22ππ-∈-，则y [,]∈-ππ。变式：y sin x arcsin x =+ 解：x [1,1]∈-，y [sin1,sin1]22 ππ ∈--+ 思考：当3x [,]44 ππ ∈-时，求函数y arcsin(cos x)=的值域。解：当3x [, ]44ππ∈-时t cos x [=∈，而y arcsin t =为增函数，则y [,]42 ππ∈-。例5：求下列函数的反函数 (1) y sin x =，x [,]2 π∈π 解：y [0,1]∈，x [,0]2 π-π∈-且sin(x )sin x y -π=-=-，则x arcsin(y)-π=-，则x arcsin y =π-，则反函数是1f (x)arcsin x -=π-，x [0,1]∈。 (2) y arcsin x =，x [0,1]∈ 解：y [0,]2π∈，x sin y =，则反函数是1f (x)sin x -=，x [0,]2 π∈。

高一三角函数题型总结

1.已知角范围和其中一个角的三角函数值求任意角三角函数值方法：①画直角三角形 ②利用勾股定理先算大小后看正负例题：1.已知α∠为第二象限角，13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角，3tan -=α求αcos 、αsin 、αcot 的值 2. 2. 3. 4.利用“加减πk 2”大角化小角，负角化正角，求三角函数值例题：求值：sin(-236π)+cos 137π·tan4π -cos 133 π= ;

1.已知sin α=4 5 ，且α为第二象限角，那么tan α的值等于（） (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α=8 1,且4π<α<2π ，则cos α－sin α的值为（） 33 (D)± 3 3.) 4. ） 5.） * 6.）

三角函数诱导公式诱导公式可概括为把 απ ±?k 2 的三角函数值转化成角α的三角函数值。（k 指奇数或者偶数， α相当锐角）口诀“奇变偶不变，符号看象限。”其中奇偶是指2 π 的奇数倍还是偶数倍，变与不变指函数名称的变化。公式一：=+)2sin(απk =+)2c o s (απk =+)2t a n (απk

三角函数诱导公式练习题 1．若(),2,5 3 cos παππα<≤= +则()πα2sin --的值是（） A ． 53 B ． 53- C ． 54 D ． 5 4 - 2．sin （－6 π 19）的值是（） A 3 6 )= . 10.α是第四象限角,,则αsin 等于________． 13 12 cos =α

三角函数经典例题

经典例题透析类型一：锐角三角函数本专题主要包括锐角三角函数的意义、锐角三角函数关系及锐角三角函数的增减性和特殊角三角函数值，都是中考中的热点．明确直角三角形中正弦、余弦、正切的意义，熟记30°、45°、60°角的三角函数值是基础，通过计算器计算知道正弦、正切随角度增大而增大，余弦随角度增大而减小． 1．在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，已知，BC=2，那么( ) A．B．C．D．思路点拨：由于∠ABC在Rt△ABC和Rt△BCD中，又已知AC和BC，故只要求出AB或CD即可．解析：解法1：利用三角形面积公式，先用勾股定理求出，∴． ∴．解法2：直接利用勾股定理求出，在Rt△ABC中，．答案：A 总结升华：求直角三角形中某一锐角三角函数值，利用定义，求出对应两边的比即可． 2．计算：(1)________； (2)锐角A满足，则∠A=________．答案：(1)；(2)75°. 解析：(1)把角转化为值．(2)把值转化为角即可． (1)．

(2)由，得， ∴．∴A=75°．总结升华：已知角的三角函数，应先求出其值，把角的关系转化为数的关系，再按要求进行运算．已知一个三角函数值求角，先看看哪一个角的三角函数值为此值，在锐角范围内一个角只对应着一个函数值，从而求出此角． 3．已知为锐角，，求．思路点拨：作一直角三角形，使为其一锐角，把角的关系转化为边的关系，借助勾股定理，表示出第三边，再利用三角函数定义便可求出，或利用求出，再利用，使可求出．解析：解法1：如图所示，Rt△ABC中，∠C=90°，∠B=，由，可设，．则， ∴．解法2：由，得， ∴．总结升华：知道一锐角三角函数值，构造满足条件的直角三角形，根据比的性质用一不为0的数表示其两边，再根据勾股定理求出第三边，然后用定义求出要求的三角函数值．或利用，来求．

高考集合知识点总结与典型例题

集合一．【课标要求】 1．集合的含义与表示（1）通过实例，了解集合的含义，体会元素与集合的“属于”关系；（2）能选择自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题，感受集合语言的意义和作用； 2．集合间的基本关系（1）理解集合之间包含与相等的含义，能识别给定集合的子集；（2）在具体情境中，了解全集与空集的含义； 3．集合的基本运算（1）理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集；（2）理解在给定集合中一个子集的补集的含义，会求给定子集的补集；（3）能使用Venn图表达集合的关系及运算，体会直观图示对理解抽象概念的作用二．【命题走向】有关集合的高考试题，考查重点是集合与集合之间的关系，近年试题加强了对集合的计算化简的考查，并向无限集发展，考查抽象思维能力，在解决这些问题时，要注意利用几何的直观性，注意运用Venn图解题方法的训练，注意利用特殊值法解题，加强集合表示方法的转换和化简的训练。考试形式多以一道选择题为主。预测高考将继续体现本章知识的工具作用，多以小题形式出现，也会渗透在解答题的表达之中，相对独立。具体三．【要点精讲】 1．集合：某些指定的对象集在一起成为集合 a∈；若b不是集合A的元素，（1）集合中的对象称元素，若a是集合A的元素，记作A b?；记作A （2）集合中的元素必须满足：确定性、互异性与无序性；确定性：设A是一个给定的集合，x是某一个具体对象，则或者是A的元素，或者不是A的元素，两种情况必有一种且只有一种成立；

互异性：一个给定集合中的元素，指属于这个集合的互不相同的个体（对象），因此，同一集合中不应重复出现同一元素；无序性：集合中不同的元素之间没有地位差异，集合不同于元素的排列顺序无关；（3）表示一个集合可用列举法、描述法或图示法；列举法：把集合中的元素一一列举出来，写在大括号内；描述法：把集合中的元素的公共属性描述出来，写在大括号{}内。具体方法：在大括号内先写上表示这个集合元素的一般符号及取值（或变化）范围，再画一条竖线，在竖线后写出这个集合中元素所具有的共同特征。注意：列举法与描述法各有优点，应该根据具体问题确定采用哪种表示法，要注意，一般集合中元素较多或有无限个元素时，不宜采用列举法。（4）常用数集及其记法：非负整数集（或自然数集），记作N ；正整数集，记作N *或N +；整数集，记作Z ；有理数集，记作Q ；实数集，记作R 。 2．集合的包含关系：（1）集合A 的任何一个元素都是集合B 的元素，则称A 是B 的子集（或B 包含A ），记作A ?B （或B A ?）；集合相等：构成两个集合的元素完全一样。若A ?B 且B ?A ，则称A 等于B ，记作A =B ；若A ?B 且A ≠B ，则称A 是B 的真子集，记作A B ；（2）简单性质：1）A ?A ；2）Φ?A ；3）若A ?B ，B ?C ，则A ?C ；4）若集合A 是n 个元素的集合，则集合A 有2n 个子集（其中2n －1个真子集）； 3．全集与补集：（1）包含了我们所要研究的各个集合的全部元素的集合称为全集，记作U ；（2）若S 是一个集合，A ?S ，则，S C =}|{A x S x x ?∈且称S 中子集A 的补集；（3）简单性质：1）S C (S C )=A ；2）S C S=Φ，ΦS C =S 4．交集与并集：

反三角函数典型例题

精品文档 5 5 (1) sin x 解: (2) sin x [0,] 解: (3) sin x 处］解: 3 ?胚或 arcs in 或 x 3 .3 arcsin .3 arcsin - 3 反三角函数典型例题例2:求下列反正弦函数值 1 sin( arcs in )该如何求? 2 4 用反正弦函数值的形式表示下列各式中的变式：x ［一，］? 2 解: x [2,] 时，n —x 【°,2]， sin( n — x) =sinx = ￡ ? n — x = arcsin —3 ，贝U x = n — arcsin — 3 5 5 解: x = arcsin — 3 或 x = n — arcsin —3 5 例1:在下列四个式子中，有意义的为解：（4）有意义。 (1) arcs in . 2 ； (2) arcsin _ ； (3) 点评：arcsinx 4 1,1]。 sin( arcs in 2) ； ( 4) arcsin(sin2)。 (1) arcsin - 2 (2) arcsin0 解：0 (3) arcsin(-) 2 点评: 1 熟练记忆：0,- 2 解：- 6 2， (4) arcs ini 1的反正弦值。思考: (1)sinx ￡，x [ -,^] 解: .43 x = arcs in 5 变式：x ［0, ]? ⑵ sin x - 4 变式：si nx 2 2 x [—,2 ] 2 解: .1 arcs in 4 3 解：x [ ,2 2 ]时，2 - x [0,2]， 1 sin( 2 n — x) = — sinx =— 4 2 n — x = 1 山 arcs in ，贝U x = 2 n — arcs in — 点评：当 x ［ 2, 2 ］时， x arcsina ；而当处理对应角之三角比值即可。［舊］，可以将角转化到区间［形］上，再用诱导公式练习:

三角函数题型学霸总结(含答案)-

三角函数题型学霸总结（含答案）阳光老师：祝你学业有成一、选择题（本大题共30小题，共150.0分） 1.点在函数的图象上，则m等于 A. 0 B. 1 C. D. 2 【答案】C 【解析】【分析】本题主要考查了正弦函数的性质，属于基础题由题意知，求得m 的值．【解答】解：由题意知，所以，所以． 2.用五点法画，的图象时，下列哪个点不是关键点 A. B. C. D. 【答案】A 【解析】【分析】本题考查三角函数图象的作法，属于基础题．熟练掌握五点法作图即可．【解答】解：用“五点法”画，的简图时，横坐标分别为，纵坐标分别为0，1，0，，0，故选A． 3.函数y x，x的大致图象是

A. B. C. D. 【答案】B 【解析】【分析】本题主要考查三角函数的图像，属于基础题利用“五点法”画出函数图像即可得出答案．【解答】解：“五点法”作图： x0 0100 10121 故选B． 4.用“五点法”作出函数的图象，下列点中不属于五点作图中的五个关键点的是 A. B. C. D. 【答案】A 【解析】【分析】本题考查三角函数图象的画法以及余弦函数的性质，属于基础题．分别令，，，，得，3，4，3，2，即可得到五点，再对照选项，即可得到答案．【解答】解：，分别令，，，，得，3，4，3，2，

所以五个关键点为，，，，，可知A不属于．故选A． 5.已知函数的图象与直线恰有四个公共点，，，，其中，则 A. B. 0 C. 1 D. 【答案】A 【解析】【分析】本题考查了三角函数图象的作法及利用导数求函数图象的切线方程，属于较难题．由三角函数图象及利用导数求函数图象的切线方程可得：切点坐标为，切线方程为：，又切线过点，则，即，得解．【解答】解：由得其图象如图所示，

三角函数典型例题剖析与规律总结00

学科: 数学任课教师：黄老师授课时间：2013年3月日(星期) 1 :00-1 :00 姓名年级：教学课题三角函数典型例题剖析与规律总结阶段基础（√）提高（）强化（）课时计划共次课第次课课前检查作业完成情况：__________________ 建议_________________________________________________________ 教学过程一：函数的定义域问题 1.求函数1 sin 2+ =x y的定义域。分析：要求1 sin 2+ = y的定义域，只需求满足0 1 sin 2≥ + x的x集合，即只需求出满足 2 1 sin- ≥ x的x 值集合，由于正弦函数具有周期性，只需先根据问题要求，求出在一个周期上的适合条件的区间，然后两边加上πk2()Z k∈即可。解：由题意知需0 1 sin 2≥ + x，也即需 2 1 sin- ≥ x①在一周期? ? ? ?? ? - 2 3 , 2 π π 上符合①的角为? ? ? ?? ? - 6 7 , 6 π π ,由此可得到函数的定义域为? ? ? ?? ? + - 6 7 2, 6 2 π π π πk k()Z k∈ 小结:确定三角函数的定义域的依据：（1）正、余弦函数、正切函数的定义域。（2）若函数是分式函数，则分母不能为零。（3）若函数是偶函数，则被开方式不能为负。（4）若函数是形如()()1 ,0 log≠ > =a a x f y a 的函数，则其定义域由()x f确定。（5）当函数是有实际问题确定时，其定义域不仅要使解析式有意义同时还要使实际问题有意义。二．函数值域及最大值，最小值（1）求函数的值域例。求下列函数的值域（1）x y2 sin 2 3- =（2）2 sin 2 cos2- + =x y x 分析：利用1 cos≤ x与1 sin≤ x进行求解。解：（1） 1 2 sin 1≤ ≤ -x∴[]5,1 5 1∈ ∴ ≤ ≤y y （2） ()[].0,4 ,1 sin 1 1 sin 1 sin 2 sin 2 sin 22 2 2 cos- ∈ ∴ ≤ ≤ - - - = - + - = - + =y x x x x x x y 评注：一般函数的值域求法有：观察法，配方法判别式法，反比例函数法等，而三角函数是函数的特殊形式，其一般方法也适用，只不过要结合三角函数本身的性质罢了。

集合知识点+练习题

第一章集合 §1．1集合基础知识点： ⒈集合的定义：一般地，我们把研究对象统称为元素，一些元素组成的总体叫集合，也简称集。 2.表示方法：集合通常用大括号{ }或大写的拉丁字母A,B,C…表示，而元素用小写的拉丁字母a,b,c…表示。 3.集合相等：构成两个集合的元素完全一样。 4.常用的数集及记法：非负整数集（或自然数集），记作N；正整数集，记作N*或N+；N内排除0的集. 整数集，记作Z；有理数集，记作Q；实数集，记作R； 5.关于集合的元素的特征 ⑴确定性：给定一个集合，那么任何一个元素在不在这个集合中就确定了。如：“地球上的四大洋”（太平洋,大西洋，印度洋，北冰洋）。“中国古代四大发明”（造纸，印刷，火药，指南针）可以构成集合，其元素具有确定性；而“比较大的数”，“平面点P周围的点”一般不构成集合，因为组成它的元素是不确定的. ⑵互异性：一个集合中的元素是互不相同的，即集合中的元素是不重复出现的。. 如:方程(x-2)(x-1)2=0的解集表示为{1, 2},而不是{1, 1, 2} ⑶无序性：即集合中的元素无顺序,可以任意排列、调换。练1：判断以下元素的全体是否组成集合，并说明理由： ⑴大于3小于11的偶数；⑵我国的小河流； ⑶非负奇数；⑷方程x2+1=0的解； ⑸徐州艺校校2011级新生；⑹血压很高的人； ⑺著名的数学家；⑻平面直角坐标系内所有第三象限的点 6.元素与集合的关系：(元素与集合的关系有“属于∈”及“不属于?”两种) ⑴若a是集合A中的元素，则称a属于集合A，记作a∈A； ⑵若a不是集合A的元素，则称a不属于集合A，记作a?A。例如，（1）A表示“1~20以内的所有质数”组成的集合，则有3∈A，4?A，等等。（2）A={2，4，8，16}，则4∈A，8∈A，32?A.

(完整word版)反三角函数典型例题.docx

反三角函数典型例题例 1：在下列四个式子中，有意义的为 __________：解：（ 4）有意义。（ 1） arcsin 2 ；（ 2） arcsin ；（ 3） sin(arcsin 2) ；（ 4） arcsin(sin 2) 。 4 点评： arcsin x —— x [ 1,1]。例 2：求下列反正弦函数值（ 1） arcsin 3 解：（ 2） arcsin0 解： 0 2 3 （ 3） arcsin( 1) 解：（4） arcsin1 解： 2 6 2 点评：熟练记忆： 0， 1 2 3 、，，的反正弦值。 2 2 2 1 思考： sin(arcsin 1 4) 该如何求？ 2 例 3：用反正弦函数值的形式表示下列各式中的 x (1) sin x 3 ， x [ , ] 3 5 解： x ＝ arcsin 2 2 5 变式： x [ , ] ? 2 解： x [ , ] 时， π－ x [0, 3 ] ， sin(π－ x)＝ sinx ＝ 2 2 5 ∴ π－ x ＝ arcsin 3 ，则 x ＝π－ arcsin 3 5 5 变式： x [0, ] ? 解： x ＝arcsin 3 或 x ＝ π－arcsin 3 5 5 (2) sin x 1 ， x [ , ] 解： x arcsin 1 4 2 2 4 变式： sin x 1 ， x [ 3 ,2 ] 4 2 解： x [ 3 ] 时， 2π－ x [0, ] ， sin(2π－ x)＝－ sinx ＝ 1 ,2 4 2 2 ∴ 2π－ x ＝ arcsin 1 ，则 x ＝2π－ arcsin 1 4 4 点评：当 x [ , ] 时， x arcsina ；而当 x [ , ] ，可以将角转化到区间 [ , ] 上，再用诱导公式 2 2 2 2 2 2 处理对应角之三角比值即可。练习： (1) sin x 3 [ , ] 解： x ， x 3 2 2 2 (2) sin x 3 [0, ] 解： x arcsin 3 3 ， x 或 x arcsin 3 3 3 (3) sin x 3 ， x [ , 3 ] 解： x arcsin 3

初中三角函数知识点题型总结+课后练习

锐角三角函数知识点 1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)： 3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。 4 5、0 锐角三角函数题型训练类型一：直角三角形求值 1．已知Rt △ABC 中，,12,4 3 tan ,90== ?=∠BC A C 求AC 、AB 和cos B ． 2．已知：如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，?= ∠4 3sin AOC 求：AB 及OC 的长． 3．已知：⊙O 中，OC ⊥AB 于C 点，AB ＝16cm ，?=∠5 3sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ； (2)求cos ∠AOC 及tan ∠AOC ． 4.已知A ∠是锐角，17 8 sin = A ，求A cos ，A tan 的值类型二. 利用角度转化求值：

1．已知：如图，Rt △ABC 中，∠C ＝90°．D 是AC 边上一点，DE ⊥AB 于E 点． DE ∶AE ＝1∶2．求：sin B 、cos B 、tan B ． 2. 如图4，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．已知8AB =，10BC =,则 tan EFC ∠的值为 ( ) Ａ．34 Ｂ．43 Ｃ．35 Ｄ． 4 5 3. 如图6，在等腰直角三角形ABC ?中，90C ∠=?，6AC =，D 为AC 上一点，若1tan 5 DBA ∠= ，则AD 的长为( )A ．2 C ．1 D ．4. 如图6，在Rt △ABC 中，∠C =90°，AC =8，∠A 的平分线AD = 3 16求∠ B 的度数及边B C 、AB 的长. 例2．已知：如图，△ABC 中，AC ＝12cm ，AB ＝16cm ，?=3 sin A (1)求AB 边上的高CD ； (2)求△ABC 的面积S ； (3)求tan B ．例3．已知：如图，在△ABC 中，∠BAC ＝120°，AB ＝10，AC ＝5．求：sin ∠ABC 的值．对应训练 1．（2012?重庆）如图，在Rt △ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号） 2．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ．类型四：利用网格构造直角三角形对应练习： 1．如图，△ABC 的顶点都在方格纸的格点上，则sin A =_______. 特殊角的三角函数值例1．求下列各式的值 ?-?+?30cos 245sin 60tan 2=. 计算：3－1+(2π－1)0－ 3 3 tan30°－tan45°= 0 30tan 2345sin 60cos 221 ??? ? ???-?+?+= ?-?+?60tan 45sin 230cos 2 tan 45sin 301cos 60?+? -? = B

集合知识点总结及习题培训资料

集合知识点总结及习题

集合 123412n x A x B A B A B A n A ∈??? ????? ∈?∈?（）元素与集合的关系：属于（）和不属于（）（）集合中元素的特性：确定性、互异性、无序性集合与元素（）集合的分类：按集合中元素的个数多少分为：有限集、无限集、空集（）集合的表示方法：列举法、描述法（自然语言描述、特征性质描述）、图示法、区间法子集：若，则，即是的子集。、若集合中有个元素，则集合的子集有个，注关系集合集合与集合{}00(2-1)23,,,,.4/n A A A B C A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ??????????? ???????????≠∈?????=???=∈∈?=??=??=???真子集有个。、任何一个集合是它本身的子集，即、对于集合如果，且那么、空集是任何集合的（真）子集。真子集：若且（即至少存在但），则是的真子集。集合相等：且定义：且交集性质：，，，运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ????????=????=∈∈???=??=?=????????=???=+?=∈?=?=??==?=?，定义：或并集性质：，，，，，定义：且补集性质：，，，， ()()()U U U C A B C A C B ????? ?? ?? ???? ?????????? ???????? ?????????????????????? ??????????????????????=??????? 一、集合有关概念 1. 集合的含义 2. 集合的中元素的三个特性： (1)元素的确定性如：世界上最高的山 (2)元素的互异性如：由HAPPY 的字母组成的集合{H,A,P,Y} (3)元素的无序性: 如：{a,b,c}和{a,c,b}是表示同一个集合 3．元素与集合的关系——（不）属于关系（1）集合用大写的拉丁字母A 、B 、C …表示

反三角函数及最简三角方程.docx

标准实用反三角函数及最简三角方程一、知识回顾： 1、反三角函数：概念：把正弦函数y sin x ， x,时的反函数，成为反正弦函数，记作 22 y arcsin x . y sin x( x R) ，不存在反函数. 含义： arcsin x 表示一个角；角,；sin x . 22 反余弦、反正切函数同理，性质如下表. 名称函数式定义域值域奇偶性单调性反正弦函数y arcsin x1,1 增, 2奇函数增函数 2 y arccosx arccos( x)arccosx 反余弦函数1,1 减0,减函数非奇非偶反正切函数y arctanx R增, 2奇函数增函数 2 y arc cot x arc cot( x)arc cot x 反余切函数R减0,减函数非奇非偶其中：（）．符号 arcsin x 可以理解为－， ] 上的一个角弧度，也可以理解为 1[ 2 () 2 区间[－， ] 上的一个实数；同样符号 arccos x 可以理解为 [0 ，π 上的一个角2 ] 2

(弧度 )，也可以理解为区间 [0 ，π]上的一个实数；（2）． y ＝arcsin x 等价于 sin y＝x, y∈ [－，], y＝ arccos x 等价于 cos y 22 ＝x, x ∈[0, π], 这两个等价关系是解反三角函数问题的主要依据；（3）．恒等式 sin(arcsin x)＝x, x∈ [－ 1, 1] , cos(arccos x)＝x, x∈ [－1, 1], tan(arctanx)=x,x ∈ R arcsin(sin x) ＝ x, x ∈ [ －，], arccos(cos x) ＝ x, x ∈ [0, 22 π],arctan(tanx)=x, x∈（－，）的运用的条件； 22 （4）．恒等式 arcsin x＋arccos x＝, arctan x＋arccot x＝的应用。 22 2、最简单的三角方程方程方程的解集 a1x | x2k arcsin a, k Z sin x a a1x | x k 1 k arcsin a, k Z a1x | x2k arccos a, k Z cos x a a1x | x2k arccos a, k Z tan x a x | x k arctana, k Z cot x a x | x k arc cot a, k Z 其中：（1 ）．含有未知数的三角函数的方程叫做三角方程。解三角方程就是确定三角方程是否有解，如果有解，求出三角方程的解集；（2）．解最简单的三角方程是解简单的三角方程的基础，要在理解三角方程的

三角函数题型分类总结

专题三角函数题型分类总结三角函数公式一览表 ............................................................................................................... 错误！未定义书签。一求值问题 ........................................................................................................................................................... - 1 - 练习 ................................................................................................................................................................. - 1 - 二最值问题 ........................................................................................................................................................... - 2 - 练习 ................................................................................................................................................................. - 3 - 三单调性问题 ....................................................................................................................................................... - 3 - 练习 ................................................................................................................................................................. - 3 - 四.周期性问题 ........................................................................................................................................................ - 4 - 练习 ................................................................................................................................................................. - 4 - 五对称性问题 ....................................................................................................................................................... - 5 - 练习 ................................................................................................................................................................. - 5 - 六.图象变换问题 .................................................................................................................................................... - 6 - 练习 ................................................................................................................................................................. - 7 - 七．识图问题 ......................................................................................................................................................... - 7 - 练习 ................................................................................................................................................................. - 9 - 一求值问题类型1 知一求二即已知正余弦、正切中的一个，求另外两个方法：根据三角函数的定义，注意角所在的范围（象限），确定符号；例 4 s i n 5 θ=，θ是第二象限角，求cos ,tan θθ 类型2 给值求值例1 已知2tan =θ，求（1） θ θθθsin cos sin cos -+；（2）θθθθ2 2cos 2cos .sin sin +-的值. 练习 1、sin 330?= tan 690° = o 585sin = 2、（1）α是第四象限角，12 cos 13 α=，则sin α= （2）若4 sin ,tan 05 θθ=- >，则cos θ= . （3）已知△ABC 中，12 cot 5 A =-，则cos A = . (4) α是第三象限角，2 1)sin(=-πα，则αcos = )25cos(απ += 3、(1) 已知5 sin ,5 α= 则44sin cos αα-= .

初中三角函数知识点总结及典型习题)

锐角三角函数知识点总结及典型习题 1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2 5、30°、45°、 6 当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。 7、正切、的增减性：当0°<α<90°时，tan α随α的增大而增大， 1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。(注意：尽量避免使用中间数据和除法) 2、应用举例： (1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。 A 90 B 90∠-?=∠? =∠+∠得由B A 对边邻边

仰角铅垂线水平线视线视线俯角 (2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。用字母i 表示，即h i l = 。坡度一般写成1:m 的形式，如1:5i =等。把坡面与水平面的夹角记作α(叫做坡角)，那么tan h i l α= =。 3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。 4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。例1：已知在Rt ABC △中，3 90sin 5 C A ∠==°，，则tan B 的值为（）A ．43 B ．45 C ．54 D ．34 例2：104cos30sin 60(2)(20092008)-??+---=______． 1. 某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（）A ．8米 B ．83米 C ． 83 3 米 D ． 43 3 米 2. 一架5米长的梯子斜靠在墙上，测得它与地面的夹角是40°，则梯子底端到墙的距离为（） A ．5sin 40° B ．5cos 40° C ．5tan 40° D ．5 cos 40° 3. 如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB 、CD 分别表示一楼、二楼地面的水平线，∠ABC =150°，BC 的长是8m ，则乘电梯从点B 到点C 上升的高度h 是（） A ． 8 33 m B ．4 m C ．43m D ．8 m 4. 河堤横断面如图所示，堤高BC=5米，迎水坡AB 的坡比是1:3（坡比是坡面的铅直高度BC 与水平宽度AC 之比），则AC 的长是（） A ．53 米 B ． 10米 C ．15米 D ．103米 5．如图，在矩形ABCD 中，D E ⊥AC 于E ，∠EDC ∶∠EDA=1∶3，且AC=10，则 DE 的长度是（）A ．3 B ．5 C ．25 D ． 2 2 5 6. 如图所示,小明在家里楼顶上的点A 处，测量建在与小明家楼房同一水平线上相邻的电梯楼的高，在点 :i h l =h l α A B C D 1 h B C A A B

人教版初中数学锐角三角函数的经典测试题及答案解析

人教版初中数学锐角三角函数的经典测试题及答案解析一、选择题 1．如图，在Rt ABC V 中，90ACB ∠=?，3tan 4B = ，CD 为AB 边上的中线，CE 平分ACB ∠，则AE AD 的值（） A ．35 B ．34 C ．45 D ．67 【答案】D 【解析】【分析】根据角平分线定理可得AE ：BE ＝AC ：BC ＝3:4，进而求得AE ＝37 AB ，再由点D 为AB 中点得AD ＝ 12AB ，进而可求得AE AD 的值．【详解】解：∵CE 平分ACB ∠， ∴点E 到ACB ∠的两边距离相等，设点E 到ACB ∠的两边距离位h ，则S △ACE ＝12AC·h ，S △BCE ＝12 BC·h ， ∴S △ACE ：S △BCE ＝ 12AC·h ：12 BC·h ＝AC ：BC ，又∵S △ACE ：S △BCE ＝AE ：BE ， ∴AE ：BE ＝AC ：BC ， ∵在Rt ABC V 中，90ACB ∠=?，3tan 4B = ， ∴AC ：BC ＝3:4， ∴AE ：BE ＝3:4 ∴AE ＝37 AB ， ∵CD 为AB 边上的中线， ∴AD ＝12 AB ，

∴3 6 7 17 2 AB AE AD AB ==，故选：D．【点睛】本题主要考查了角平分线定理的应用及三角函数的应用，通过面积比证得AE：BE＝AC：BC 是解决本题的关键． 2．如图，为了加快开凿隧道的施工进度，要在小山的两端同时施工．在AC上找一点B，取145 ABD ∠=o，500 BD m =，55 D ∠=o，要使A，C，E成一直线，那么开挖点E离点D的距离是（） A．500sin55m o B．500cos55m o C．500tan55m o D． 500 cos55 m o 【答案】B 【解析】【分析】根据已知利用∠D的余弦函数表示即可．【详解】在Rt△BDE中，cosD= DE BD ， ∴DE=BD?cosD=500cos55°．故选B．【点睛】本题主要考查了解直角三角形的应用，正确记忆三角函数的定义是解决本题的关键．3．在半径为1的O e中，弦AB、AC32，则BAC ∠为（）度．A．75B．15或30C．75或15D．15或45 【答案】C 【解析】【分析】根据题意画出草图，因为C点位置待定，所以分情况讨论求解．【详解】利用垂径定理可知： 32 AE．