临界状态是解题的突破口

临界状态是解题的突破口
南平三中郑书光
物理解题过程,要认真分析物理过程变化,有些复杂的过程,要寻找临界状态这一解题突破口,临界状态一旦分析好了,一切问题就会迎刃而解.本文通过一例加以说明.
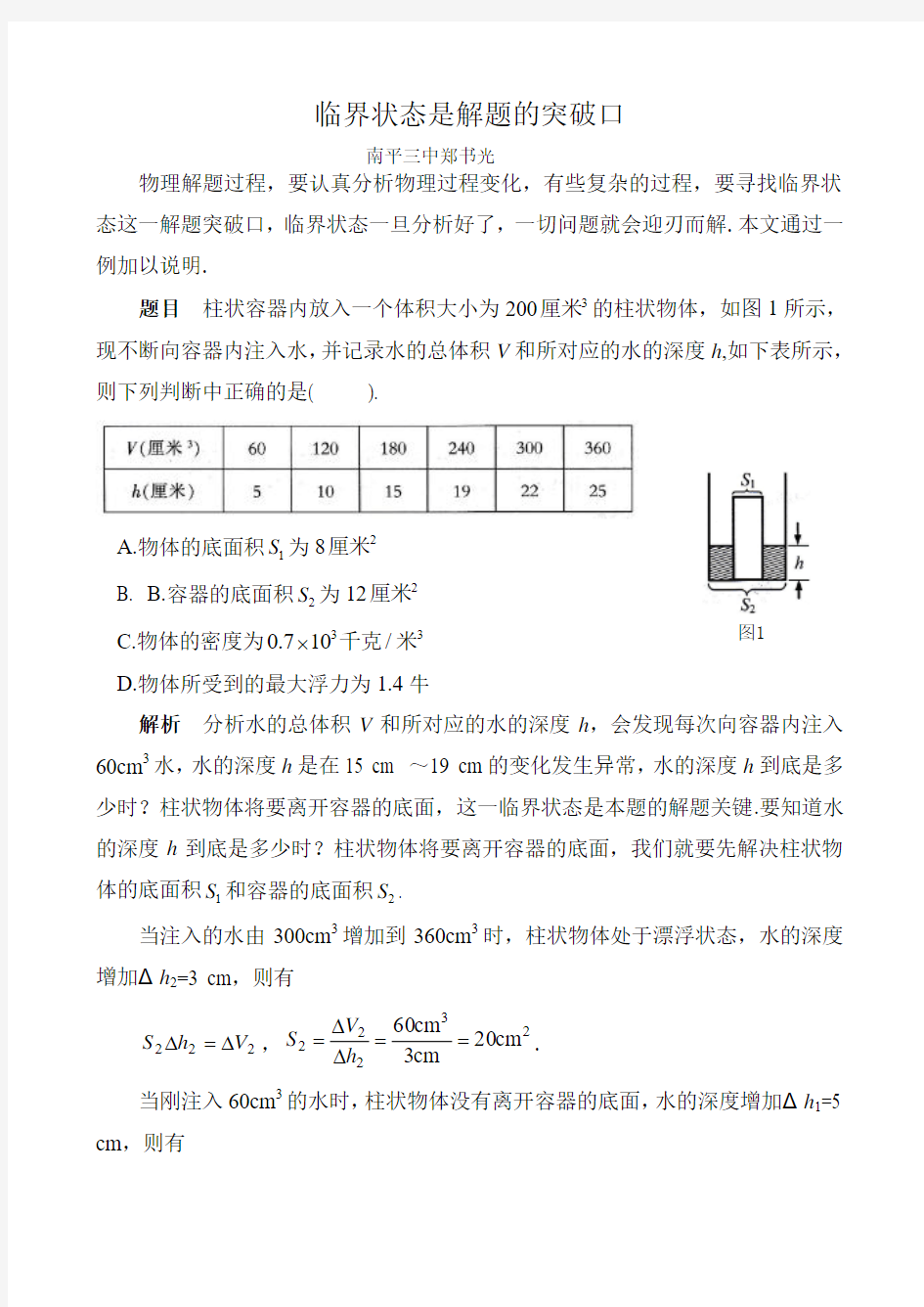
题目 柱状容器内放入一个体积大小为2003厘米的柱状物体,如图1所示,现不断向容器内注入水,并记录水的总体积V 和所对应的水的深度h ,如下表所示,则下列判断中正确的是(
).
A.物体的底面积1S 为82厘米
B. B.容器的底面积2S 为122厘米
C.物体的密度为330.710/?千克米
D.物体所受到的最大浮力为1.4牛
解析 分析水的总体积V 和所对应的水的深度h ,会发现每次向容器内注入60cm 3水,水的深度h 是在15 cm ~19 cm 的变化发生异常,水的深度h 到底是多少时?柱状物体将要离开容器的底面,这一临界状态是本题的解题关键.要知道水的深度h 到底是多少时?柱状物体将要离开容器的底面,我们就要先解决柱状物体的底面积1S 和容器的底面积2S .
当注入的水由300cm 3增加到360cm 3时,柱状物体处于漂浮状态,水的深度增加Δh 2=3 cm ,则有 222V h S ?=?,23
222cm 20cm
3cm 60==??=h V S . 当刚注入60cm 3的水时,柱状物体没有离开容器的底面,水的深度增加Δh 1=5 cm ,则有 图1
(完整word)高中化学极限法
专题7·极限法 极限判断是指从事物的极端上来考虑问题的一种思维方法。该思维方法的特点是确定了事物发展的最大(或最小)程度以及事物发生的范围。 例1 :在120℃时分别进行如下四个反应: A.2H2S+O2=2H2O+2S B.2H2S+3O2=2H2O+2SO2 C.C2H4+3O2=2H2O+2CO2D.C4H8+6O2=4H2O+4CO2 (l)若反应在容积固定的容器内进行,反应前后气体密度(d)和气体总压强(P)分别符合关系式d前=d后和P前>P后的是;符合关系式d前=d后和P前=P后的是(请填写反应的代号)。 (2)若反应在压强恒定容积可变的容器内进行,反应前后气体密度(d)和气体体积(V)分别符合关系式d前>d后和V前
方法:采用极值法或平均分子量法。 解析:[解法一]:(极值法) 假设95mg全为MgCl2,无杂质,则有:MgCl2 ~ 2AgCl 95mg2×143.5mg 生成沉淀为287mg,所以假设95mg全部为杂质时,产生的AgCl沉淀应大于300mg。 总结:极值法和平均分子量法本质上是相同的,目的都是求出杂质相对分子量的区间值,或者杂质中金属元素的原子量的区间值,再逐一与选项比较,筛选出符合题意的选项。 例3 :在一个容积固定的反应器中,有一可左右滑动的密封隔板,两侧分别进行如图所示的可逆反应.各物质的起始加入量如下:A、B和C均为4.0mol、D为6.5 mol、F为2.0 mol,设E为x mol.当x在一定范围内变化时,均可以通过调节反应器的温度,使两侧反应都达到平衡,并且隔板恰好处于反应器的正中位置.请填写以下空白:
拉法尔喷管
1、临界状态 在一个恰当的压强比下,气流在收缩段内加速,至喉部马赫数 ,然后在扩张段内减速,至出口,且,这种流动状态称为拉伐尔尾喷管的临界状态。气流的静压沿喷管轴线的变化如图 7.12 中的曲线所示。临界状态的特点是: ,,(完全膨胀),喷管内无激波,如果不计 摩擦,管内的整个流动可视为等熵流动。记临界状态下的压强比为,可 见当时,尾喷管的流动为临界状态。临界状态下的有关参数计算如下: 喷管出口马赫数:由面积比公式( 7.16a )可计算得到,即 () 出口静压与进口总压之比 由于 ( 7.17 ) 所以是面积比的函数。 通过尾喷管的质量流量
( 7.18 )2.亚临界状态 尾喷管内的流动全部为亚声速时,称为亚临界状态。例如当 时,整个喷管内无流动,静压等于总压且沿尾喷管不变,如图 7.12 中的平行于轴的直线所示,这是亚临界状态的一种极限情况。 当时,气流在喷管收缩段内加速,至喉部仍然是,之后 在扩张管内减速,至出口,,如图 7.12 中的曲线 a 属于亚临界的流动状态。 因此亚临界状态的特点是:,,,气流在喷管内得到完全膨胀,整个喷管为亚声速流动。亚临界状态的有关参数计算如下:出口马赫数可按下式计算: 出口静压 通过喷管的流量 ( 7.19 )3.超临界状态
当时,尾喷管内的流动称为超临界状态。气流在喷管收缩段加 速,至喉部,之后在扩张管内的流动根据的大小不同可能有如下几种情况: (1)气流在扩张管内继续加速,至出口,同时气流在喷管出口达到完 全膨胀,,整个扩张管内无激波,出口外也无激波和膨胀波,静压沿喷 管的变化如图 7.12 中的曲线所示。这种情况即是所谓的设计状态,记该状 态下的压强比,可见当时,尾喷管的流动为超临界状态,且气流在喷管出口达到完全膨胀。 其特点是:,,,因此喷管出口的马赫数可用等熵面积比公式(7.16a)计算,即 () 出口静压: ( 7.20 ) 通过喷管的流量:由于,所以流量达到最大值,仍可用式( 7.18 )计算 (2)当时,气流在扩张段加速直到出口的,气流在喷 管内没有得到完全膨胀,即,因此超声速气流在喷管出口产生膨胀波束。在这个压强比范围内,反压的变化不会影响喷管内的流动,因为外界的扰动是以声速传播的,而喷管出口为超声速流动。其流动特点为
拉伐尔喷管的设计
拉伐尔喷管的设计 Prepared on 24 November 2020
拉伐尔喷管的设计 摘 要:本文针对拉伐尔喷管的几何条件和力学条件进行了推导。建立了喷管截面积变化与流速、压强、密度、温度等流动性能参数间的关系,分析了喷管出口截面下游的外界反压对拉伐尔喷管工作过程的影响。推导建立了拉伐尔喷管主要性能参数的计算方法。针对实际流动损失的存在,为得到喷管的实际流动性能,对理论性能参数提出了修正方法。本文研究内容为拉伐尔喷管的设计提供依据。 关键词:变截面;力学条件;性能参数;流动损失 1.引言 拉伐尔喷管是火箭发动机和航空发动机最常用的构件,由两个锥形管构成,如图1所示,其中一个为收缩管,另一个为扩张管。拉瓦尔喷管是推力室的重要组成部分。喷管的前半部是由大变小向中间收缩至喷管喉部。喉部之后又由小变大向外扩张。燃烧室中的气体受高压流入喷嘴的前半部,穿过喉部后由后半部逸出。这一架构可使气流的速度因喷截面积的变化而变化,使气流从亚音速到音速,直至加速至超音速。所以,人们把这种喷管叫跨音速喷管。瑞典工程师De Laval 在1883年首先将它用于高速,现在这种喷管广泛应用于喷气发动机和火箭发动机。 图1 拉伐尔喷管结构图 2.拉伐尔喷管的几何条件 2.1变截面一维定常等熵流动 在变截面一维定常流动中只考虑截面积变化这一种驱动势,忽略摩擦、传热、重力等其他驱动势,因此流动是绝热无摩擦的,即等熵流动,变截面定常等熵流动模型如图2所示。 变截面一维定常等熵流动的控制方程组为: Const m VA ρ== (1) 0dp VdV ρ+= (2) 2102d h V ? ?+= ?? ? (3) 2.2截面积变化对流动特性的影响 管道的形状变化可以用截面积变化dA 来表示。 图2 变截面一维定常等熵流动 模型
数学分析求极限的方法
求极限的方法 具体方法 ⒈利用函数极限的四则运算法则来求极限 定理1①:若极限)(lim 0 x f x x →和)(lim x g x x →都存在,则函数)(x f ±)(x g ,)()(x g x f ? 当0x x →时也存在且 ①[])()()()(lim lim lim 0 .0 x g x f x g x f x x x x x →→→±=± ②[])()()()(lim lim lim 0 x g x f x g x f x x x x x x →→→?=? 又若0)(lim 0 ≠→x g x x ,则 ) () (x g x f 在0x x →时也存在,且有 )()()() (lim lim lim 0 x g x f x g x f x x x x x x →→→= 利用极限的四则运算法则求极限,条件是每项或每个因子极限存在,一般所给的变量都不满足这个条件,如 ∞ ∞、00 等情况,都不能直接用四则运算法则,必须要对变量进行变形,设法消去分子、分母中的零因子,在变形时,要熟练掌握饮因式分解、有理化运算等恒等变形。 " 例1:求24 22 lim ---→x x x 解:原式=()()()022 22lim lim 22 =+= -+-- - →→x x x x x x ⒉用两个重要的极限来求函数的极限 ①利用1sin lim =→x x x 来求极限 1sin lim 0 =→x x x 的扩展形为: 令()0→x g ,当0x x →或∞→x 时,则有
()()1sin lim 0=→x g x g x x 或()()1sin lim =∞ →x g x g x 例2:x x x -→ππ sin lim 解:令t=x -π.则sinx=sin(-π t)=sint, 且当π→x 时0→t 故 1sin sin lim lim 0 ==-→→t t x x t x ππ ~ 例3:求() 11 sin 21 lim --→x x x 解:原式=()()()()()()()211sin 1111sin 1221 21lim lim =--?+=-+-+→→x x x x x x x x x ②利用e x x =+∞→)1 1(lim 来求极限 e x x =+∞ →)1 1(lim 的另一种形式为e =+→α α α1 )1(lim .事实上,令 .1 x =α∞→x .0→?α所以=+=∞ →x x x e )11(lim e =+→ααα1 0)1(lim 例4: 求x x x 1 )21(lim +→的极限 解:原式=221 210)21()21(lim e x x x x x =?? ?+????+→ 利用这两个重要极限来求函数的极限时要仔细观察所给的函数形式只有形式符合或经过变化符合这两个重要极限的形式时才能够运用此方法来求极限。一般常用的方法是换元法和配指数法。 ⒊利用等价无穷小量代换来求极限 所谓等价无穷小量即.1) () (lim =→x g x f x x 称)(x f 与)(x g 是0x x →时的等价无穷小量,记作)(x f )(~x g .)(0x x →.
数学分析中求极限的方法总结
数学分析中求极限的方 法总结 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
数学分析中求极限的方法总 结 1 利用极限的四则运算法则和简单技巧 极限的四则运算法则叙述如下: 定理:如果0 x x lim f x =,lim g x =x x →→A B ()() (1)[]0 lim ()()lim ()lim ()x x x x x x f x g x f x g x →→→±=±=A ±B (2)[]0 x x lim f x g x =lim f x)lim ()x x x x g x →→→??=A?B ()()( (3)若B ≠0 (4)0 x lim c ()lim ()x x x f x c f x c →→?=?=A (5) [] 0lim ()lim ()n n n x x x x f x f x →→??==A ????(n 为自然数) 上述性质对于,,x x x →∞→+∞→-∞也同样成立i 由上述的性质和公式我们可以看书函数的和、差、积、商的极限等于函数极限的和、差、积、商。 例1. 求225 lim 3x x x →+-的极限 解:由定理中的第三式可以知道 例2. 求3 2 lim 3x x →-的极限 式子经过化简后就能得到一个只有分母含有未知数的分式,直接求极限即可 例3. 已知 ()1111223 1n x n n = +++ ??-?,求lim n n x →∞ 解: 观察 11 =112 2- ? 111=2323-?
因此得到 ()1111223 1n x n n = +++ ??-? 所以 1lim lim 11n n n x n →∞→∞ ?? =-= ??? 2 利用导数的定义求极限 导数的定义:函数f(x)在0x 附近有定义,χ??,则 如果 存在, 则此极限值就称函数f(x)在点0x 的导数记为 () 0'f x 。 即 在这种方法的运用过程中,首先要选好f(x)。然后把所求极限都表示成f(x)在定点0 x 的导数。 例4. 3 利用两个重要极限公式求极限 两个极限公式: (1 (2)1lim 1x x e x →∞ ?? += ??? 但我们经常使用的是它们的变形: (1,
拉伐尔喷管的设计
拉伐尔喷管的设计 摘要:本文针对拉伐尔喷管的几何条件和力学条件进行了推导。建立了喷管截面积变化及流速、压强、密度、温度等流动性能参数间的关系,分析了喷管出口截面下游的外界反压对拉伐尔喷管工作过程的影响。推导建立了拉伐尔喷管主要性能参数的计算方法。针对实际流动损失的存在,为得到喷管的实际流动性能,对理论性能参数提出了修正方法。本文研究内容为拉伐尔喷管的设计提供依据。 关键词:变截面;力学条件;性能参数;流动损失 1.引言 拉伐尔喷管是火箭发动机和航空发动机最常用的构件,由两个锥形管构成,如图1所示,其中一个为收缩管,另一个为扩张管。拉瓦尔喷管是推力室的重要组成部分。喷管的前半部是由大变小向中间收缩至喷管喉部。喉部之后又由小变大向外扩张。燃烧室中的气体受高压流入喷嘴的前半部,穿过喉部后由后半部逸出。这一架构可使气流的速度因喷截面积的变化而变化,使气流从亚音速到音速,直至加速至超音速。所以,人们把这种喷管叫跨音速喷管。瑞典工程师De Laval在1883年首先将它用于高速汽轮机,现在这种喷管广泛应用于喷气发动机和火箭发动机。 图1 拉伐尔喷管结构图 2.拉伐尔喷管的几何条件 2.1变截面一维定常等熵流动 在变截面一维定常流动中只考虑截面积变化这一种驱动势,忽略摩擦、传热、重力等其他驱动势,因此流动是绝热无摩擦的,即等熵流动,变截面定常等熵流动模型如图2所示。
变截面一维定常等熵流动的控制方程组为: (1) (2) (3) 2.2截面积变化对流动特性的影响 管道的形状变化可以用截面积变化dA 来表示。 (a) 截面积变化对流速的影响 对连续方程(1)取对数微分,得 (4) 将(2)两边同除以,得 (5) 由声速公式及马赫数定义,得 (6) 这就是截面积变化及流速变化之间的关系。 (b) 截面积变化对压强的影响 将(2)代入(6),由理想声速公式得到 (7) (c) 截面积变化对密度、温度、声速、马赫数的影响 联立(4)式及(6)式,消去速度项,得 (8) 控制体 p +dp dx ρ+d ρ V +dV T +dT A +dA p T A 图2 变截面一维定常等熵流动模型
拉伐尔喷管的设计
拉伐尔喷管的设计 摘 要:本文针对拉伐尔喷管的几何条件和力学条件进行了推导。建立了喷管截面积变化与流速、压强、密度、温度等流动性能参数间的关系,分析了喷管出口截面下游的外界反压对拉伐尔喷管工作过程的影响。推导建立了拉伐尔喷管主要性能参数的计算方法。针对实际流动损失的存在,为得到喷管的实际流动性能,对理论性能参数提出了修正方法。本文研究内容为拉伐尔喷管的设计提供依据。 关键词:变截面;力学条件;性能参数;流动损失 1.引言 拉伐尔喷管是火箭发动机和航空发动机最常用的构件,由两个锥形管构成,如图1所示,其中一个为收缩管,另一个为扩张管。拉瓦尔喷管是推力室的重要组成部分。喷管的前半部是由大变小向中间收缩至喷管喉部。喉部之后又由小变大向外扩张。燃烧室中的气体受高压流入喷嘴的前半部,穿过喉部后由后半部逸出。这一架构可使气流的速度因喷截面积的变化而变化,使气流从亚音速到音速,直至加速至超音速。所以,人们把这种喷管叫跨音速喷管。瑞典工程师De Laval 在1883年首先将它用于高速汽轮机,现在这种喷管广泛应用于喷气发动机和火箭发动机。 图1 拉伐尔喷管结构图 2.拉伐尔喷管的几何条件 2.1变截面一维定常等熵流动 在变截面一维定常流动中只考虑截面积变化这一种驱动势,忽略摩擦、传热、重力等其他驱动势,因此流动是绝热无摩擦的,即等熵流动,变截面定常等熵流动模型如图2所示。 变截面一维定常等熵流动的控制方程组为: Const m VA ρ== (1) 0dp VdV ρ+= (2) 2102d h V ? ?+= ?? ? (3) 2.2截面积变化对流动特性的影响 管道的形状变化可以用截面积变化dA 来表示。 (a) 截面积变化对流速的影响 图2 变截面一维定常等熵流动模型
数学分析中求极限的方法总结
数学分析中求极限的方法 总结 This model paper was revised by the Standardization Office on December 10, 2020
数学分析中求极限的方法总结 1 利用极限的四则运算法则和简单技巧 极限的四则运算法则叙述如下: 定理:如果0 x x lim f x =,lim g x =x x →→A B ()() (1)[]0 lim ()()lim ()lim ()x x x x x x f x g x f x g x →→→±=±=A ±B (2)[]0 x x lim f x g x =lim f x)lim ()x x x x g x →→→??=A?B ()()( (3)若B ≠0 (4)0 x lim c ()lim ()x x x f x c f x c →→?=?=A (5)[]00lim ()lim ()n n n x x x x f x f x →→??==A ????(n 为自然数) 上述性质对于,,x x x →∞→+∞→-∞也同样成立i 由上述的性质和公式我们可以看书函数的和、差、积、商的极限等于函数极限的和、差、积、商。 例1. 求225 lim 3x x x →+-的极限 解:由定理中的第三式可以知道 例2. 求3 x →的极限
式子经过化简后就能得到一个只有分母含有未知数的分式,直接求极限即可 例3. 已知 ()1111223 1n x n n = +++ ??-?,求lim n n x →∞ 解: 观察 11=112 2-? 111=2323- ?因此得到 ()1111223 1n x n n = +++ ??-? 所以 1lim lim 11n n n x n →∞→∞ ?? =-= ??? 2 利用导数的定义求极限 导数的定义:函数f(x)在0x 附近有定义,χ??,则 如果 存在, 则此极限值就称函数f(x)在点0x 的导数记为 () 0'f x 。 即 在这种方法的运用过程中,首先要选好f(x)。然后把所求极限都表示成f(x)在定点 x 的导数。
数学分析求极限的方法
求极限的方法 具体方法 ⒈利用函数极限的四则运算法则来求极限 定理1①:若极限)(lim 0 x f x x →和)(lim x g x x →都存在,则函数)(x f ±)(x g ,)()(x g x f ? 当0x x →时也存在且 ①[])()()()(lim lim lim 0 .00 x g x f x g x f x x x x x →→→± = ± ②[])()()()(lim lim lim 0 x g x f x g x f x x x x x x →→→?= ? 又若0)(lim 0 ≠→x g x x ,则 ) ()(x g x f 在0x x →时也存在,且有 ) ()() ()(lim lim lim x g x f x g x f x x x x x x →→→= 利用极限的四则运算法则求极限,条件是每项或每个因子极限存在,一般所给的变量都不满足这个条件,如 ∞ ∞、 0等情况,都不能直接用四则运算法则, 必须要对变量进行变形,设法消去分子、分母中的零因子,在变形时,要熟练掌握饮因式分解、有理化运算等恒等变形。 例1:求2 42 2 lim --- →x x x 解:原式=()() ()022 22lim lim 2 2 =+= -+-- - →→x x x x x x ⒉用两个重要的极限来求函数的极限 ①利用1sin lim =→x x x 来求极限 1sin lim =→x x x 的扩展形为: 令()0→x g ,当0x x →或∞→x 时,则有 ()() 1sin lim =→x g x g x x 或()() 1sin lim =∞ →x g x g x
数学分析中求极限方法总结
数学分析中求极限的方法总结 1 利用极限的四则运算法则和简单技巧 极限的四则运算法则叙述如下: 定理1.1 (1 (2(3)若B ≠ (4(5)[] 0lim ()lim ()n n n x x x x f x f x →→??==A ???? (n 为自然数) i 由上述的性质和公式我们可以看书函数的和、差、积、商的极限等于函数极限的和、差、积、商。 例1. 求225 lim 3 x x x →+-的极限 解:由定理中的第三式可以知道 ()()222 22 lim 55lim 3lim 3x x x x x x x →→→++=-- 22 2 2 2 lim lim5 lim lim3x x x x x x →→→→+= + 2259 23+ ==-- 例2. 求3 x →
33 22 x x →→ = 3 x→ = 1 4 = 式子经过化简后就能得到一个只有分母含有未知数的分式,直接求极限即可例3. 已知() 111 1223 1 n x n n =+++ ??-? 解:观察 11 =1 122 - ? 111 = 2323 - ? 因此得到() 111 12231 n x n n =+++ ??-? 1111111 1 3311 n n n =-+-+-+- -- 所以 1 lim lim 11 n n n x n →∞→∞ ?? =-= ? ?? 2 利用导数的定义求极限 导数的定义:函数f(x) 如果 ()() 00 lim lim x x f x x f x y x x ?→?→ +?- ? = ?? 存在, 则此极限值就称函数f(x) () 'f x。 即
极限分析法
临界、极值问题—极限分析法 某种物理现象变化为另一种物理现象的转折状态叫做临界状态。临界状态也可理解为“恰好出现”或“恰恰不出现”某种现象的状态。平衡物体的临界状态是指物体所处的状态将要被破坏而尚未破坏的状态。涉及临界状态的问题叫做临界问题,解答临界问题的基本思维方法是假设推理法。 一:从相对静止到相对运动 1.跨过定滑轮的轻绳两端,分别系着物体A 和B ,物体A 放在倾 角为θ的斜面上,如图。已知物体A 的质量为m ,物体A 与斜面 间的动摩擦因数为μ (μ<tan θ),滑轮的摩擦不计,要使物 体A 静止在斜面上,求物体B 的质量取值范围。 二:绳子从张紧到断裂 2.如图,不计重力的细绳AB 与竖直墙夹角为60o,轻杆BC 与竖直墙夹角为30o,杆可绕C 自由转动,若细绳承受的最大拉力为200N ,轻杆能承受的最大压力为300N ,则在B 点最多能挂多重的物体? 三:从接触到分离 3.如图,半径为R 的光滑球,重为G ,光滑木块厚为h ,重为G 1,用至少 多大的水平力F 推木块才能使球离开地面? 4.如图,物体重10牛,物体与竖直墙的摩擦系数为0.5,用一个与水平成450角的力F 作用在物体上,要使物体静止与墙上,则力F 的取值范围是? 5.如图,把重为20牛的物体放在倾角为300的粗糙斜面上,并静止,物体右端与固定在斜面上的轻弹簧相连,若物体与斜面的最大静摩擦力为12牛,则弹簧的弹力取值范围是? 6如图,已知木块m 1=1千克,m 2=4千克,叠放在光滑的水平面上,两木块间的摩擦系数μ=0.4,现用水平力F 拉m 1,欲使m 1,m 2保持相对静止,求力F 的取值范围? 7.把长方体切成质量分别为m 和M 的两部分,切面与底面的夹角为θ,长方体置于光滑的水平地面,切面亦光滑,问至少用多大的力推m ,m 才相对于M 滑动。 8.将质量为1千克的小球挂在倾角为300的光滑斜面上,斜面体 的质量为2千克,地面光滑,现用力F 向右拉斜面体,欲使小 球与斜面体保持相对静止,求力F 最大不能超过多少? 现用力F 向左堆斜面体,欲使小球与斜面体保持相对静止,求 力F 最大不能超过多少? 9.如图,小车上放有由轻质弹簧连接的质量为M a =1千克,M b =0.5 千克的A,B 两物体,两物体与小车间的摩擦系数分别为μa =0.4, μb =0.2,弹簧的劲度系数K=0.2牛/厘米,为使两物体随小车一 起向右加速运动,弹簧的最大伸长是多少厘米? 10.质量m=1千克的物体放在倾角370的斜面上,斜面体质量M=2 千克,斜面与物体的摩擦系数μ=0.2,地面光滑,现对斜面体施 加一水平推力F ,要使物体m 相对斜面M 静止,力F 应为多大?
数学分析中求极限的方法汇总
数学分析中求极限的方法汇总
作者:日期:
数学分析中求极限的方法总结 1 利用极限的四则运算法则和简单技巧极限的四则运算法则叙述如 下:定理 1.1 :如果lim f(x)= ,lim g(x)= x x 0 x x0 1lim f (x) g (x) lim f x) lim g(x) x x0 x x0 x x0 2 ) lim f(x)g ( x)= lim f ( x) lim g(x) x x x x x x 3 ) 若B ≠0 则: f (x) lim lim f (x) x x 0 g(x) lim x x0 4lim c f (x) c lim f(x) c x x0 x x0 lim f(x) n x lim x f (x) n 5x x0 x x0 (n 为自然 上述性质对于x ,x ,x 也同样成立i 由上述的性质和公式我们可以看书函数的和、差、积、商的极限等于函数极限的和、差、积、商。 lim x 2 5 例 1. 求x 2 x 3 的极限 解:由定理中的第三式可以知道 x12 lim 例 2. 求x 3 x 3 的极限 解:分子分母同时乘以x 1 2 2 2 5 23
x 1 2 x 1 2 lim x 3 x 3 x 1 2 li m x 3 x 3 x 3 x 1 2 1 4 式子经过化简后就能得到一个只有分母含有未知数的分式,直接求极限即可 2 利用导数的定义求极限 导数的定义:函数 f(x) 在 x 0 附近有定义, , 则 y f x 0 x f x 0 如果 存在, x12 x3 例 3. 1 1 1 已知 x n 11 2 21 3 n 11 n 观察 1 2=1 2 11 因此得到 x n 11 2 1 12 1 1 2 1 2 1 1 n 所以 ,求 lim x n 1 n n-1 3 n 1n 13 13 lim x n lim 1 1 n n n n 1 1 1 n 1n 1 n li x m 0 x y li x m 0 f x 0 x f x x
数学分析中极限的求法总结
数学分析中极限的求法总结 1.1 利用极限的定义求极限 用定义法证明极限,必须有一先决条件,即事先得知道极限的猜测值A ,这种情况一般较困难推测出,只能对一些比较简单的数列或函数推测分析出极限值,然后再去用定义法去证明,在这个过程中,放缩法和含绝对值的不等式总是密切相连的。 例:()0 lim x x f x A →=的ε-δ 定义是指:?ε>0, ?δ=δ(0x ,ε)>0,0<|x-0x | <δ?|f(x)-A|<ε 为了求δ 可先对0x 的邻域半径适当限制, 如然后适当放大|f(x)-A |≤φ(x) (必然保证φ(x)为无穷小),此时往往要用含绝对值的不等式: |x+a |=|(x-0x )+(0x +a)|≤|x-0x |+|0x +a|<|0x +a |+δ1 域|x+a|=|(x-0x )+(0x +a)|≥|0x +a|-|x-0x |>|0x +a|-δ1 从φ(x)<δ2,求出δ2后, 取δ=min(δ1,δ2),当0<|x-0x |<δ 时,就有|f(x)-A|<ε. 例:设lim n n x a →∞=则有12 ...lim n n x x x a n →∞++=. 证明:因为lim n n x a →∞=,对110()N N εε?>?=,,当1n N >时, -2 n x a ε ∣∣<于是当1n N >时, 1212......n n x x x x x x na a n n +++∣+++-∣∣-∣= 0ε<<1 其中112N A x a x a x =∣-∣+∣-∣+∣-α∣是一个定数,再由 2 A n ε <,解得2A n ε> ,故取12max ,A N N ε?? ??=???????? 12...+=22n x x x n N n εεε+++>-α<当时,。 1.2 利用极限的四则运算性质求极限 定理[1]:若极限0 lim ()x x f x →和0 lim ()x x g x →都存在,则函数)(x f ±)(x g ,)()(x g x f ?当 0x x →时也存在且 ①[]0 lim ()()lim ()lim ()x x x x x x f x g x f x g x →→→±=± ②[]0 lim ()()lim ()lim ()x x x x x x f x g x f x g x →→→?=?
拉瓦尔喷管FLUENT模拟
一收缩-扩张喷管实例1.1问题描述 本节内容主要依托收缩-扩张喷管内的流动计算展开。喷管外形如图1-1所示,A 为沿轴圆形截面面积,喷管的外形尺寸满足如下条件(单位:m): 21.0x A +=5 .05.0<<-x 计算求解时可以将模型琪简化为二维轴对称问题,边界条件为:入口压力P m =101325Pa,入口总温T i0=300K,出口静压P 0=3738.9Pa。 图1-1喷管几何示意图 1.2创建几何模型 (1)设定工作目录 File→Change Working Dir,选择文件存储路径。 (2)创建Point,如图1-2所示。 Step 1通过输入坐标的方法创建P_1、P_2。选择Geometry 标签栏中的,单击,选择Create 1point(创建一个点),输入P_1的坐标,单击Apply 按钮确定,如图1-3所示。P_2创建方法与之相似,坐标为(0.5,0,0)。 Step 2创建点集3。因为横截面积为21.0x A +=,因此沿X 轴方向半径的函数为:5.02]/)1.0[()( x x R +=。单击,在Explicit Locations 下拉菜单中选择Create Multiple points,按照如图1-4所示输入数据,单击Apply 按钮确定。单击Apply 按钮确定。
图1-3创建P_1图1-4创建点集3 (3)创建Curve,如图1-5所示。 图1-5创建Curve结果图 Step1选择Geometry标签栏,单击创建Curve。如图1-6所示,单击,再单击,依次选择点集3中的各点连成曲线,创建C_4。 Step2采用Step1的方法创建其余三条Curve。 (4)定义Part。 ICEM中定义Part的名称将会是导出网格后边界的名称,可以简化在求解器
二维喷管曲面网格划分及数值计算
流动与传热数值计算二维喷管曲面网格划分及数值计算 学生姓名范健学 学号17106051 班级热能10-4班
二维喷管曲面网格划分及数值计算 中国矿业大学(徐州)221116 范健学 【摘要】:采用ANSYS14.5软件对二维喷管进行非结构面网格划分,设定一定的边界条件,通过FLUENT14.5,生成速度标量,静温云图,压力云图,流线图,用以分析一定边界条件下的相关参数的分布。可用于对其他的二维喷管模型的分析。 [Abstract]: The ANSYS14.5 software for two-dimensional nozzle unstructured surface meshing, setting certain boundary conditions, through FLUENT14.5, generate speed scalar, static temperature contours, pressure contours, flow chart, with the under certain boundary conditions in order to analyze the distribution of the relevant parameters. Can be used for other models of the two-dimensional nozzle. 关键词:边界层,数值仿真,缩放喷管,FLUENT数值模拟 1.引言 拉瓦尔喷管是火箭发动机和航空发动机最常用的构件,由两个锥形管构成,如图一所示,其中一个为收缩管,另一个为扩张管。拉瓦尔喷管是推力室的重要组成部分。喷管的前半部是由大变小向中间收缩至一个窄喉。窄喉之后又由小变大向外扩张至箭底。箭体中的气体受高压流入喷嘴的前半部,穿过窄喉后由后半部逸出。这一架构可使气流的速度因喷截面积的变化而变化,使气流从亚音速到音速,直至加速至跨音速。所以,人们把这种喇叭形喷管叫跨音速喷管。 2.
数学分析中极限的求法综述
数学分析中极限的求法综述 摘要:本文主要归纳了数学分析中求极限的十四种方法, 1:利用两个准则 求极限, 2:利用极限的四则运算性质求极限, 3:利用两个重要极限公式求极限, 4:利用单侧极限求极限,5:利用函数的连续性求极限, 6:利用无穷小量的性质求极限, 7:利用等价无穷小量代换求极限, 8:利用导数的定义求极限, 9:利用中值定理求极限, 10:利用洛必达法则求极限, 11:利用定积分求和式的极限,12:利用级数收敛的必要条件求极限, 13:利用泰勒展开式求极限, 14:利用换元法求极限。 关键词: 夹逼准则, 单调有界准则, 无穷小量的性质, 洛必达法则, 中 值定理, 定积分, 泰勒展开式, 级数收敛的必要条件. 极限是数学分析的基础,数学分析中的基本概念来表述,都可以用极限来描述。如函数y =f(x)在0x x =处导数的定义,定积分的定义,偏导数的定义,二重积分,三重积分的定义,无穷级数收敛的定义,都是用极限来定义的。极限是研究数学分析的基本公具。极限是贯穿数学分析的一条主线。学好极限是从以下两方面着手。1:是考察所给函数是否存在极限。2:若函数否存在极限,则考虑如何计算此极限。本文主要是对第二个问题即在极限存在的条件下,如何去求极限进行综述。 1:利用两个准则求极限。 (1)夹逼准则:若一正整数 N,当n>N 时,有n x ≤n y ≤n z 且lim lim ,n n x x x z a →∞→∞==则有 lim n x y a →∞= . 利用夹逼准则求极限关键在于从n x 的表达式中,通常通过放大或缩小的方法找出两个有相同极限值的数列{}n y 和 {}n z ,使得n n n y x z ≤≤。 例[1] n x = + 求n x 的极限
高等数学常用极限求法1
求函数极限的方法和技巧 摘要: 本文就关于求函数极限的方法和技巧作了一个比较全面的概括、综合。 关键词:函数极限 引言 在数学分析与微积分学中,极限的概念占有主要的地位并以各种形式出现而贯穿全部容,因此掌握好极限的求解方法是学习数学分析和微积分的关键一环。本文就关于求函数极限的方法和技巧作一个比较全面的概括、综合,力图在方法的正确灵活运用方面,对读者有所助益。 主要容 一、求函数极限的方法 1、运用极限的定义 例: 用极限定义证明: 12 23lim 22=-+-→x x x x 证: 由2 4 4122322-+-=--+-x x x x x x ()2 2 22 -=--= x x x 0>?ε 取εδ= 则当δ<-<20x 时,就有 ε<--+-12 2 32x x x 由函数极限δε-定义有:
12 23lim 22=-+-→x x x x 2、利用极限的四则运算性质 若 A x f x x =→)(lim 0 B x g x x =→)(lim 0 (I)[]=±→)()(lim 0 x g x f x x )(lim 0 x f x x →±B A x g x x ±=→)(lim 0 (II)[]B A x g x f x g x f x x x x x x ?=?=?→→→)(lim )(lim )()(lim 0 (III)若 B ≠0 则: B A x g x f x g x f x x x x x x ==→→→)(lim ) (lim )()(lim 0 00 (IV )cA x f c x f c x x x x =?=?→→)(lim )(lim 0 (c 为常数) 上述性质对于时也同样成立-∞→+∞→∞→x x x ,, 例:求 4 53lim 22+++→x x x x 解: 453lim 22+++→x x x x = 2 5 4252322=++?+ 3、约去零因式(此法适用于型时0 ,0x x →) 例: 求12 16720 16lim 23232+++----→x x x x x x x 解:原式=() () ) 12102(65) 2062(103lim 2 23223 2 +++++--+---→x x x x x x x x x x x =) 65)(2() 103)(2(lim 222+++--+-→x x x x x x x
极限思维法、特殊值法、量纲法、等解高中物理选择题
高中物理“超纲”选择题解题方法 1.有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断。例如从解的物理量的单位,解随某些已知量变化的趋势,解在一定特殊条件下的结果等方面进行分析,并与预期结果、实验结论等进行比较,从而判断解的合理性或正确性。 举例如下:如图所示,质量为M 、倾角为θ的滑块A 放于水平地面上。把质量为m 的滑块B 放在A 的斜面上。忽略一切摩擦,有人求得B 相对地面的加速度a = M +m M +msin 2θ gsinθ,式中 g 为重力加速度。 对于上述解,某同学首先分析了等号右侧量的单位,没发现问题。他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”。但是,其中有一项是错误..的。请你指出该项。( ) A .当θ=0?时,该解给出a =0,这符合常识,说明该解可能是对的 B .当θ=90?时,该解给出a =g ,这符合实验结论,说明该解可能是对的 C .当M ≥m 时,该解给出a =gsinθ,这符合预期的结果,说明该解可能是对的 D .当m ≥M 时,该解给出a = sin g θ ,这符合预期的结果,说明该解可能是对的 2.某个由导电介质制成的电阻截面如图所示。导电介质的电阻率为ρ、制成内、外半径分别为a 和b 的半球壳层形状(图中阴影部分),半径为a 、电阻不计的球形电极被嵌入导电介质的球心为一个引出电极,在导电介质的外层球壳上镀上一层电阻不计的金属膜成为另外一个电极。设该电阻的阻值为R 。下面给出R 的四个表达式中只有一个是合理的,你可能不会求解R ,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断。根据你的判断,R 的合理表达式应为 ( ) A .R=ab a b πρ2) (+ B .R=ab a b πρ2) (- C .R= ) (2a b ab -πρ D .R= ) (2a b ab +πρ 3.图示为一个半径为R 的均匀带电圆环,其单位长度带电量为η。取环面中心O 为原点,以垂直于环面的轴线为x 轴。设轴上任意点P 到O 点的距离为x ,以无限远处为零电势,P 点电势的大小为Φ。下面给出Φ的四个表达式(式中k 为静电力常量),其中只有一个是合理的。你可
(完整word版)数学分析中求极限的方法总结
精心整理 数学分析中求极限的方法总结 1利用极限的四则运算法则和简单技巧 极限的四则运算法则叙述如下: 定理1.1 (1 (2 (3 (4(5 例1.例2.例3.已知()1111223 1n x n n =+++??-?L L 解:观察 11=1122-?1 1=232-?因此得到()11112231n x n n = +++??-?L L
所以1lim lim 11 n n n x n →∞→∞?? =-= ??? 2利用导数的定义求极限 导数的定义:函数f(x) 如果 存在, 则此极限值就称函数f(x) ()0'f x 。 即 的导数。 例 3(2 例5:x x x x 10 ) 1() 21( lim +-→ 解:为了利用极限e x x x =+→10 )1(lim 故把原式括号内式子拆成两项,使得第一项为1,第二项和括号外 的指数互为倒数进行配平。
x x x x 1 0) 1()21(lim +-→=x x x x 1 0131(lim +-+→ =313 310]131[(lim -+--+→=+-+ e x x x x x x 例6:20cos 1lim x x x -→ 解:将分母变形后再化成“0/0”型所以 2 x 例7:求 4例8:x 解:数值.因此 例8:求x x sin ln lim 2 π → 解:复合函数x sin ln 在2 π = x 处是连续的,所以在这点的极限值就等于该点处的函数值 即有2sin ln sin ln lim 2 π π =→ x x
=1 ln 2 sin lim =π =0 5利用两个准则求极限。 (1)函数极限的迫敛性:若一正整数N,当n>N 时,有n n n x y z ≤≤且lim lim ,n n x x x z a →∞→∞==则有lim n x y a →∞=。 利用夹逼准则求极限关键在于从n x 的表达式中,通常通过放大或缩小的方法找出两个有相同极限值的数列{}n y 和{}n z ,使得n n n y x z ≤≤。 例9(2)例12解:由1x 即数列{令A x n n =∞ →lim 对n n x x +=+61两边取极限, 有A 2 60A -A -=解得A=3,或2A =-。 因为...)2,1(0 =>n x n ,所以0A ≥,舍去2A =-,故lim 3n n x →∞ = 6利用洛必达法则求未定式的极限 定义6.1:若当x a →(或x →∞)时,函数()f x 和()F x 都趋于零(或无穷大),则极限
极限求法总结
极限的求法 1、利用极限的定义求极限 2、直接代入法求极限 3、利用函数的连续性求极限 4、利用单调有界原理求极限 5、利用极限的四则运算性质求极限 6. 利用无穷小的性质求极限 7、无穷小量分出法求极限 8、消去零因子法求极限 9、 利用拆项法技巧求极限 10、换元法求极限 11、利用夹逼准则求极限[3] 12、利用中值定理求极限 13、 利用罗必塔法则求极限 14、利用定积分求和式的极限 15、利用泰勒展开式求极限 1 6、分段函数的极限 1、利用极限的定义求极限 用定义法证明极限,必须有一先决条件,即事先得知道极限的猜测值A ,这种情况一般较困难推测出,只能对一些比较简单的数列或函数推测分析出极限值,然后再去用定义法去证明,在这个过程中,放缩法和含绝对值的不等式总是密切相连的。 例:()0 lim x x f x A →=的ε-δ 定义是指:?ε>0, ?δ=δ(0x ,ε)>0,0<|x-0x | <δ?|f(x)-A|<ε 为了求δ 可先对0x 的邻域半径适当限制, 如然后适当放大|f(x)-A |≤φ(x) (必然保证φ(x)为无穷小),此时往往要用含绝对值的不等式: |x+a |=|(x-0x )+(0x +a)|≤|x-0x |+|0x +a|<|0x +a |+δ1 域|x+a|=|(x-0x )+(0x +a)|≥|0x +a|-|x-0x |>|0x +a|-δ1 从φ(x)<δ2,求出δ2后, 取δ=min(δ1,δ2),当0<|x-0x |<δ 时,就有|f(x)-A|<ε.
例:设lim n n x a →∞ =则有12 (i) n n x x x a n →∞++=. 证明:因为lim n n x a →∞ =,对110()N N εε?>?=,,当1n N >时, -2 n x a ε ∣∣<于是当 1n N >时, 1212......n n x x x x x x na a n n +++∣+++-∣ ∣-∣= 0ε<<1 其中112N A x a x a x =∣-∣+∣-∣+∣-α∣是一个定数,再由 2 A n ε <,解得2A n ε> ,故取12max ,A N N ε?? ??=???????? 12...+=22n x x x n N n εεε+++>-α<当时,。 2、 直接代入法求极限 适用于分子、分母的极限不同时为零或不同时为 例 1. 求 . 分析 由于 , 所以采用直接代入法. 解 原式= 3、利用函数的连续性求极限 定理[2]:一切连续函数在其定义区间内的点处都连续,即如果0x 是函数)(x f 的定义区间内的一点,则有)()(lim 00 x f x f x x =→。 一切初等函数在其定义域内都是连续的,如果()f x 是初等函数,0x 是其定义域内一点,则求极限0 lim ()x x f x →时,可把0x 代入()f x 中计算出函数值,即 lim ()x x f x →=0()f x 。
