2015电子科技大学_图论期末考试复习题

2015电子科技大学 图论考试复习题
关于图论中的图,以下叙述不正确的是
A .图中点表示研究对象,边或有向边表示研究对象之间的特定关系。
B .图论中的图,画边时长短曲直无所谓。
C .图中的边表示研究对象,点表示研究对象之间的特定关系。
D .图论中的图,可以改变点与点的相互位置,只要不改变点与点的连接关系。
一个图中最长的边一定不包含在最优生成树内。
下面哪个图形不与完全二分图K 3,3同构? A . B . C . D .
有10条边的5顶单图必与K 5同构。
完全二分图K m ,n 的边数是 A .m B .n C .m +n D .mn
无向完全图K n 的边数为 A .n B .n 2 C .n (n -1) D .n (n -1)/2
若一个无向图有5个顶点,如果它的补图是连通图,那么这个无向图最多有 条边。
对于两个图,如果顶点数目相等,边数相等,次数相等的顶点数目也相等,则这两个图同构。
有15个顶的单图的边数最多是 A .105 B .210 C .21 D .45
图G 如右,则dacbeb
A .是G 中的一条道路
B .是G 中的一条道路但不是行迹
C .是G 中的一条行迹但不是轨道
D .不是G 的一条道路
图G 如右,则befcdef A .是G 的一个圈 B .是G 的一条道路但不是行迹
C .是G 的一条行迹但不是轨道
D .是G 的一条轨道但不是圈
v1
36
7
图G如右图所示,则ω (G)=
A.1 B.2
C.7 D.8
下列图形中与其补图同构的是
A.B.C.D.
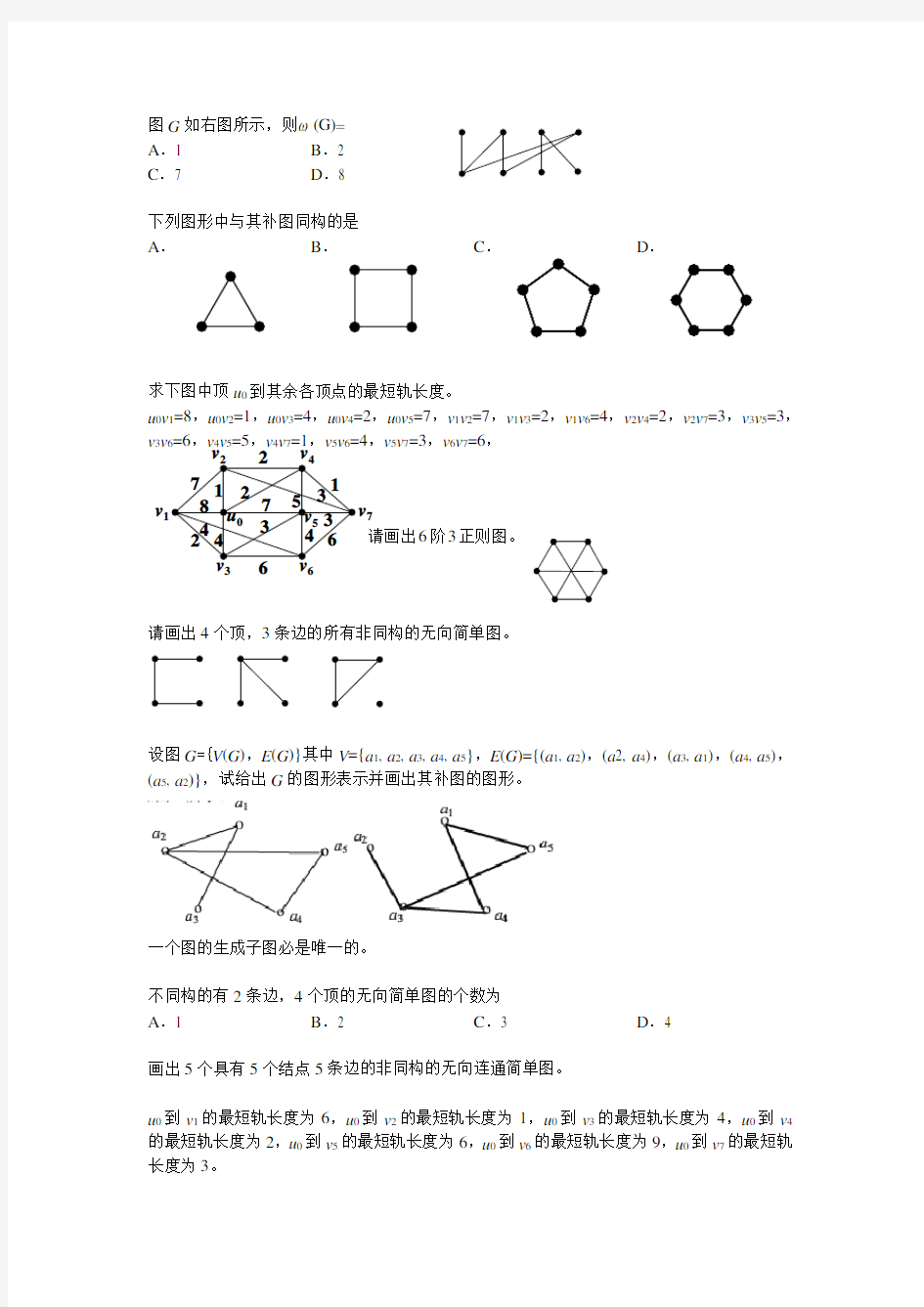
求下图中顶u0到其余各顶点的最短轨长度。
u0v1=8,u0v2=1,u0v3=4,u0v4=2,u0v5=7,v1v2=7,v1v3=2,v1v6=4,v2v4=2,v2v7=3,v3v5=3,v3v6=6,v4v5=5,v4v7=1,
v5v
6
=4,v
5
v7=3,v6v7=6,
请画出6阶3正则图。
请画出4个顶,3条边的所有非同构的无向简单图。
设图G={V(G),E(G)}其中V
={
a1, a2, a3, a4, a5},E(G)={(a1, a2),(a2, a4),(a3, a1),(a4, a5),(a5, a2)},试给出G的图形表示并画出其补图的图形。
一个图的生成子图必是唯一的。
不同构的有2条边,4个顶的无向简单图的个数为
A.1 B.2 C.3 D.4
画出5个具有5个结点5条边的非同构的无向连通简单图。
u0到v1的最短轨长度为6,u0到v2的最短轨长度为1,u0
到v3的最短轨长度为4,u0到v4的最短轨长度为2,u0到v5的最短轨长度为6
,u0到v6的最短轨长度为9,u0到v7的最短轨长度为3。
v 11
1074用Dijkstra 算法求下图中从v 1点到其他任意一点的最短路。
v 1v 3
v 1v 2
v 1v 2v 5 v 1v 3v 4 v 1v 2v 5v 6 v 1v 2v 5v 6v 7
设有城市v 1,v 2,v 3,v 4,v 5,v 6,各城市之间的距离如下表。使用Dijkstra 算法求城市v 1到其他各城市的最短路径以及最短距离。要求说明求解过程(提示:应将城市之间的道路图
解:下面的表格给出了求解v
到其他各顶点之间的最短距离的Dijkstra 算法执行过程:
最后得到v 1到其他各城市的最短路径及最短距离为:
v 1到v 2的最短路径是:v 1v 2 长度为1 v 1到v 3的最短路径是:v 1v 2v 3 长度为3 v 1到v 4的最短路径是:v 1v 2v 3v 5v 4 长度为7 v 1到v 5的最短路径是:v 1v 2v 3v 5 长度为4 v 1到v 6的最短路径是:v 1v 2v 3v 5v 4v 6 长度为9
求下图中顶v 1到v 11的最短轨及最短距离。
L
100个顶点的星的最大顶点次数是 。
做一个图G ,使其顶的次序列为(5,5,4,4,3,3,2,2,2)。
v 6
7
下列哪个序列不可能构成一个图的顶点次数序列?
A.(2,2,2,2,2) B.(3,3,3,3) C.(1,2,3,4,5) D.(2,2,3,4,5)
已知图G中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G的边数是.
任取n个人组成的人群,n≥2,证明至少有两位,他们在人群中的朋友一样多。
证明:把n个人看做n个点,如果两个人是朋友,则在这两个点之间连一条边,这样可以得到一个含n个顶的单图。
显然顶的最大次数为n-1,如果这n个顶的次数不一样,则它们必为0,1,2,…,n-1,而次为0的顶与各顶都不相邻,因此不可能有顶的次为n-1,出现矛盾。因此n个顶的次数必至少有两个是相等的。
所以至少有两位,他们在人群中的朋友一样多。
设G是一个含n个顶点的无向简单图,n是大于等于2的奇数.证明图G与它的补图G C中的奇数次顶点个数相等。
E(G C)是由完全图K n的边删去E(G)所得到的.所以对于任意结点u∈V(G),u在G和G C中的次数之和等于u在K n中的次数.由于n是大于等于2的奇数,从而K n的每个顶点都是偶数度的(n?1≥(2)度),于是若u∈V(G)在G中是奇数次顶点,则它在G C中也是奇数次顶点.故图G与它的补图G C的奇数次顶点个数相等。
具有m条边的树有几个顶点?
A .m
B .1m -
C .m 1
D .
2
m 完全二分图K m,n 的边数是: A .m B .n C .m+n D .mn
有n 个顶的图中,圈的长度最大值为 A .2n B .n C .n+1 D .n ?1
含5个顶、3条边的不同构的无向图有 A .2个 B .3个 C .4个 D .5个
图G 如右所示,与G 同构的图是 A . B .
C .
D .
v 1,v 2,v 3,v 4,v 5,v 6是6个城市,下面矩阵的(i ,j )号元素是v i 到v j 的机票票价,试为一个旅行者制作一张由v 1到各城去旅游的最便宜的航行路线图。 050
4025105001520251501020402010010252520100551025
25
55
轾¥犏犏¥犏犏ゥ犏犏犏犏¥犏犏¥
犏臌
完全图K 4的生成树的数目为 。
一棵树有2个2度顶点,1 个3度顶点,3个4度顶点,则其1度顶点的个数是 A .5 B .7 C .8 D .9
有6个顶的不同构的树共有 棵。
设图G 是有6个顶点的连通图,顶点的总度数为18,则可从G 中删去 条边后使之变成树。 4
已知一棵无向树T 中有8个顶点,4度、3度、2度的顶点各一个,T 的树叶数为 。
有n(n>1)个顶的树T,下面说法不正确的是
A.T是二分图B.T是可平面图
C.T中存在完美匹配D.T中任意两点间有唯一轨道相连接
设G是有n个结点,m条边的连通图,为了得到G的一棵生成树,必须从G中删去的边数是
A.m?n+1 B.m?n C.m+n+1 D.n?m+1
无向简单图G是棵树,当且仅当
A.G连通且边数比顶点数少1 B.G连通且顶点数比边数少1
C.G的边数比顶点数少1 D.G中没有圈
下面给出的集合中,哪一个是前缀码
A.{0,10,110,101111} B.{01,001,000,1}
C.{b,c,aa,ab,aba} D.{1,11,101,001,0011}
给定一个序列集合{1,01,10,11,001,000},若去掉其中的元素,则该序列集合构成前缀码。
若一棵典型有序二元树有2n-1个顶点,则它的树叶数是
A.n B.2n C.n-1 D.2
下面那种描述的单图不一定是树。
A.无回路的连通图B.有n个顶点,n-1条边的图
C.每对顶点都有通路的图D.连通但删去一条边则不连通的图
下列无向图一定是树的是
A.连通图B.无圈但添加一条边后有圈的图
C.每对顶点间都有路的图D.连通且E(G)=V(G)-1
求生成树个数时,将一个树对应一个Prufer序列,如果树T的对应Prufer序列为(2,3,2,3),则标号为2的顶点的次数是
A.1 B.2 C.3 D.4
右图是二分图。
一个有13个顶的简单图G中有3个顶的次数是4,4个顶的次数是3,6个顶的次数是1,则图G一定是树。
设树T中有2个3度顶点和3个4度顶点,其余的顶点都是树叶,则T中有片树叶。
10
若T 是图G 的生成树,则 A .T 必唯一 B .G 不一定是连通图 C .T 中必不含圈 D .G 中不含圈
若G 是一个含p 个顶点,q 条边的图,若q ≥p ,则G 中必有圈。
有4个连通片组成的17个顶的森林的边数为 A .16 B .15 C .14 D .13
设G 是一个满足|E (G )|≥|V (G )|的图,则G 中必有圈。
在下图中,用Kruskal 算法构造最小生成树,写出边添加到生成树的边序列,并画出生成树。
答:
求下图的最优树T (不要求中间过程,只要求画出最小生成树, 并给出T 的权和)。
答:
权和为17。
求下图的最小生成树,并给出权值(只给结果,不要过程)
a
答:
权和为28。
求下图的最小生成树,并给出权值。
权和为16。
假设用于通信的电文仅由8个字母 {a , b , c , d , e , f , g , h } 构成,它们在电文中出现的概率分别为{ 0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10},试为这8个字母设计哈夫曼编码。 解:a , 1100;b , 00;c , 11110;d , 1110;e ,10;f , 11111;g , 01;h ,1101
画出带权0,2,0.17,0.13,0.1,0.1,0.08,0.06,0.06,
0.07,0.03的Huffman 树。
画出带权0.1,0.1,0.1,0.1,0.15,0.2,0.25
的Huffman 树。
0.020.03
0.060.050.070.100.40.60.170.280.190.320.110.211.00
1.000.100.100.130.130.200.200.34
0.260.60
0.400.17
0.080.170.090.060.070.030.06
v 3
65
v 365
假定通信中出现的字母为a , b , c , d , e , f , g , h ,其出现的频率如下表。试画出这组字母(权)的
设T 是树叶权为1,2,3,4,5的Huffman 树,那么树T 的带权路径长为 。33
有99个顶点的典型有序二元树的叶子数是 。
一个出城汽车队行驶时不得超车,但每车都可以进入路过的一个胡同里去加油,再在某时刻退出胡同插队继续开行,共有5辆不同的汽车。则开出城的不同车队种数是 。
行餐后姊妹去洗碗,洗前已把5个不同花色的碗摞成一摞。妹妹把姐姐洗过的碗每次拿一个放入消毒柜,也摞成一摞。由于小妹贪玩,碗被放入消毒柜可能不及时,姐姐则把洗过的碗摞在旁边,则小妹摞起的碗摞可能的种数是 。 答:42
对一个括号序列进行检测,从左向右数到第99个括号时,记录了右括号 个,因此得出结论为坏括号序列。 50
对一个好括号序列进行检测,从左向右至少数到第 个括号时,会记录下50个右括号。 100
画出所有不同构的5顶点树。
1.000.6
0.2
0.40.350.250.150.20.20.1
0.1
0.10.1g h 0.250.1e f 0.450.3
0.15d a c 1b 0.55
以下说法错误的是
A. 同构的图具有相同的顶点数和边数
B. 同胚的图边数相同,但顶点数不同
C. 如果一个图是可平面的,那么与它同构的图也是可平面的
D. 如果一个图是可平面的,那么与它同胚的图也是可平面的
如果一个3-正则简单平面图的每个面都有3条边,则这个图的边数是
A.3 B.4 C.5 D.6
图H是下面平面图G的一个平面嵌入,则图H的面数是
A.5 B.6 C.7 D.8
如果平面图G有v个顶点,e条边和f个平面,则
A.v-e+f=2 B.e-v+f=2 C.v+e-f=2 D.e+v-f=2
具有6 个顶点,12条边的连通简单平面图中,每个面的边数是
A.2 B.3 C.4 D.5
设G为一个连通的平面图,G有5个顶点和9条边,则G有个面。6
n(n≥3)阶极大平面图的面数等于。
2n-4
n(n≥3)阶极大平面图的边数等于。
3n-6
100个顶点的极大连通平面图中最多有个面。196
100个面的极大连通平面图中最多有个顶点。52
画出面数最多的5顶点连通平面图的平面嵌入,并指出它有几个面。
6个面。
如果单图G是平面图,那么它一定有一个次数不超过5的顶。
不妨设G是连通的,否则考虑它的每一个连通分支。
设G有n个顶,m条边,f个面。因为G是单图,每个面至少有三条边,所以3f≤2m。如果每个顶的次数都不小于6,那么有6n≤2m。
由欧拉公式得2=n-m+f≤m/3-m+2m/3=0,矛盾。
所以至少一个顶次数不超过5。
证明不存在7条棱的多面体。
若有7条棱的多面体,因为每个面上至少三条边,所以2ε (G) ≥3φ (G),φ (G)≤14/3,所以φ (G)=4。代入Euler公式得ν (G)=5,但φ (G)=4的多面体是惟一的,它有四个顶,与ν (G)=5矛盾。故无七棱多面体。
若简单平面图G的顶数不少于11个,则G C不是平面图。
画出面数最多的6顶点连通二分平面图的平面嵌入,并指出它有几个面。
4个面
完全图K2n能够分解为_______个边不相交的1因子之并。
n-1
完全图K2n+1能够分解为_______个边不相交的2因子之并。
n
下列图中可1因子分解的是
A.B.C.D.
给5位同学各写好一封信的信笺,又写好了给这5位同学的信封,把信笺都插错了信封的方法数为
A.48 B.44 C.36 D.24
有n把钥匙和n把锁混在一起,确定知道每把锁都能有一把钥匙打开,锁匠想把它们一对对的分开,那么有多少种分法是每对中的钥匙都无法打开锁的。(1)给出求解上述问题的递归公式,并证明之;(2)算出n=6时问题的解。
(1)设第i把钥匙为x i,第i把锁为y i,X={x1,x2, …,x n},Y={y1,y2, …,y n}。把x i和y i视为顶点,当且仅当i≠j时,x i和y j相邻,得到二分图G。图G是n-1次正则的二分图,G有完备匹配。问题转化为求G的完备匹配个数b(n)。
如果钥匙x1错配给锁y2时,
(1)x2错配给y1,则可能的G中的完备匹配之个数为b(n-2)。
(2)x2不错配给y1,则可能的G中的完备匹配之个数为b(n-1)。
而x1错配的可能有n-1种。所以b(n)=(n-1)[b(n-1)+b(n-2)]。
(2)显然,b(1)=0,b(2)=1,
所以b(3)=2,b(4)=9,b(5)=44,b(6)=265。
给n位同学各写好一封信的信笺,又写好了给这5位同学的信封,把信笺都插错了信封的方法数设为b(n),则b(n)
A.b(n-1)+b(n-2) B.(n-1)[b(n-1)+b(n-2)]
C.n[b(n-1)+b(n-2)] D.2(n-1)[b(n-1)+b(n-2)]
给6位同学各写好一封信的信笺,又写好了给这6位同学的信封,把信笺都插错了信封的方法数为
A.120 B.240 C.265 D.288
下列哪个图无完备匹配
A.k次正则2分图B.Petersen图(单星妖怪)
C.K2n D.K2,4
r=5,当s= 时,完全二部图K r,s才可能存在完美匹配。5
K10,10有种完美匹配。10
右图G的覆盖数β (G)=
A.2 B.3
C.4 D.5
K3,5的覆盖数β (K3,5)=
A.2 B.3 C.4 D.5
某公司有5名工作人员x1,x2,x3,x4,x5,他们每人承担y1,y2,y3,y4,y5这5项工作中的一项,
每人对每项工作创造的价值用下边的矩阵表示,公司领导根据每个人的特长如何合理分工,使得这5个工作人员对公司创造的总价值最大?
答:最佳匹配是{x1y4,x2y1,x3y3,x4y2,x5y5} 用匈牙利算法求下图的最大匹配。
{x1y1,x2y2,x3y5,x4y3,x5y4}
用匈牙利算法求下图的最大匹配。
12345 1
2
3
4
5
35541
22022
24410
01100
12133
y y y y y x
x
x
x
x
轾
犏
犏
犏
犏
犏
犏
犏
犏
犏
臌
12345
12
345
{x 1y 2,x 2y 1,x 3y 3,x 5y 5}
今有赵、钱、孙、李、周五位教师,要承担语文、数学、物理、化学、英语五门课程。已知赵熟悉数学、物理、化学三门课程,钱熟悉语文、数学、物理、英语四门课程,孙、李、周都只熟悉数学、物理两门课程。问能否安排他们都只上他们熟悉的一门课程,使得每门课程都有人教(用图论方法求解)。
解:用x 1,x 2,x 3,x 4,x 5表示赵、钱、孙、李、周五位教师,用y 1,y 2,y 3,y 4,y 5表示语文、数学、物理、化学、英语五门课程。某位教师熟悉某门课程,则在两点之间连一条边,因此得到下面的二分图。
取S ={x 3,x 4,x 5},则N (S )={y 1,y 2},故|N (S )|<|S |。
由Hall 定理知,不存在把x 1,x 2,x 3,x 4,x 5皆许配的匹配,
因此不能安排他们都只上他们熟悉的一门课程,使得每门课程都有人
教。
对于下面的二分图,图中虚线给出了初始匹配M ={x 1y 1,x 2y 4,x 3y 2,x 4y 3,x 6y 5},从该初始匹配开始,利用匈牙利算法求其最大匹配。要求写出求解过程。(提示:虚线和实线都是该二分图的边)
解:由不饱和点x 5出发构造增广路径P :x 5y 2x 3y 1x 1y 3x 4y 6,构造新的匹配:
M ’={x 5y 2,x 3y 1,x 1y 3,x 4y 6,x 2y 4,x 6y 5},M ’是一个最大匹配,如下图虚线所示。
从下图中给定的M ={x 1y 1,x 3y 5,x 5y 3}开始,用匈牙利算法求下图中
的完备匹配。
取未被M 许配的顶x 2,由x 2出发得可增广轨x 2y 3x 5y 5x 3y 2, 构造新的匹配:M ’={x 1y 1,x 2y 3,x 5y 5,x 3y 2}。
再取未被M ’许配的顶x 4,由x 4出发得可增广轨x 4y 3x 2y 2x 3y 5x 5y 4,构
造新的匹配:M ’’={x 1y 1,x 4y 3,x 2y 2,x 3y 5,x 5y 4}。
分派甲、乙、丙、丁、戊五人去完成五项工作,每人完成一项工作,每人完成各项任务时间
1234
5
123456
1234
56
5
4321
用x 1,x 2,x 3,x 4,x 5表示甲、乙、丙、丁、戊五个人,y 1,y 2,y 3,y 4,y 5表示A 、B 、C 、D 、E 五项工作,对应的权取20 工作时间,得权矩阵为
取正常初始顶标l (y i )=0,l (x 1)=13,l (x 2)=14,l (x 3)=13,l (x 4)=14,l (x 5)=16,构作G 1如图, 用匈牙利算法求得最大匹配M ={x 1y 2,x 2y 4,x 3y 5,x 4y 3,x 5y 1},这是个完备匹配,因此即为最佳匹配。
因此甲完成B 工作,乙完成D 工作,丙完成E 工作,丁完成C 工作,戊完成A 工作,总花费时间最少为7+6+7+6+4=30。
平面图的对偶图是连通图。
下图G 是平面图。
设连通平面图G 有6个面,8个顶点,则G 条边。 12
关于平面图G 和其几何对偶图G *的关系,下列说法中不正确的是 A .平面图G 的面数等于其对偶图的顶点数 B .平面图G 的边数等于其对偶图的边数
C .平面图(G *)*≌G ,其中G *表示G 的对偶图
D .平面图的对偶图是连通平面图。
下列哪个图是极大平面图
A .顶为7,边数为15的单图
B .K 5
C .K 3,3
D .正方体
把平面分为α个区域,使任两个区域相邻,则α的最大值为 A .5
B .4
C .3
D .2
下列哪个图不是极大平面图
1234512345 813111311
1211141414
1338611561414101610131011y y y y y x x x x x 轾犏犏犏犏犏犏犏犏犏臌
5
4321
A.正四面体B.正六面体C.正八面体D.正二十面体
下面哪个图是平面图
A.K5B.K2,3C.K6D.K3,3
Kuratowsky认为可作为判定图的可平面性依据的基本不可平面图之一是
A.K3A.K4A.K5A.K6
以下说法错误的是
A.同构的图具有相同的顶点数和边数
B.同胚的图边数相同,但顶点数不同
C.如果一个图是可平面的,那么与它同构的图也是可平面的
D.如果一个图是可平面的,那么与它同胚的图也是可平面的
下列图中哪个的对偶图是自身?
A.K3B.K4C.K5D.K6
15阶圈C15的顶色数是
A.2 B.3 C.6 D.15
设G为n顶m条边的无向连通单图,下列命题为假的是
A.G一定有生成树B.m一定大于n
C.G的边色数χ'(G)≥Δ(G) D.G的最大度Δ(G)≤n-1
完全图K15的顶色数是
A.2 B.3 C.6 D.15
完全图G的色多项式P(G,t)是
A.t(t-1)2B.t(t-1)(t-2) C.t3D.t(t-1)(t+1)
图G的色多项式P(G,t)是t4-4t3+6t2-3t,则图G的边数是
A.3 B.4 C.5 D.6
图G的色多项式P(G,t)是t4-4t3+6t2-3t,则图G的顶数是
A.3 B.4 C.5 D.6
完全图K15的边色数是
A.2 B.3 C.6 D.15
15阶圈C15的边色数是
A.2 B.3 C.6 D.15
完全图K8的边色数是
A.2 B.3 C.7 D.8
求下图G的色多项式P(G,k)
答:P(G,k)=k(k-1)(k-2)(k-3)(k-4)+3k(k-1)(k-2)(k-3)+k(k-1)(k-2) =k5-7k4+18k3-20k2+8k
求下图G的色多项式P(G,k)
答:P(G,k)=k(k-1)(k-2)(k-3)(k-4)+3k(k-1)(k-2)(k-3)+2k(k-1)(k-2) =k5-7k4+20k3-26k2+10k
求下图G的色多项式P(G,k)
答:P(G,k)=k(k-1)(k-2)(k-3)(k-4)+2k(k-1)(k-2)(k-3)+k(k-1)(k-2) =k5-8k4+24k3-31k2+14k
求下图G的色多项式P(G,k)
答:P(G,k)=k(k-1)(k-2)(k-3)(k-4)+2k(k-1)(k-2)(k-3)
=k5-8k4+23k3-28k2+12k
K3,4的边色数为。
Petersen图(单星妖怪)的边色数为。
下图的点色数为_______;边色数为_______
有8个顶的轮,其顶色数是。
有8个顶的轮,其顶色数是。
顶大于2的树T的顶色数是。
右图G 的独立数α (G )= A .1 B .2 C .3 D .4
右图G 的支配数γ (G )= A .1 B .2 C .3 D .4
右图G 的独立数α (G )= A .1 B .2 C .3 D .4
右图G 的支配数γ (G )= A .1 B .2 C .3 D .4
任意一个p 阶图,总有K 3子图或4个点的独立集,则p 的最小值为 A .6 B .7 C .8 D .9
一群人中,总有3个人互相认识或者彼此不认识,则这群人的人数至少是 A .5 B .6 C .7 D .8
任意一个p 阶图,总有K 3子图或3个点的独立集,则p 的最小值为( ) A .4 B .5 C .6 D .7
有8种化学品a ,b ,c ,d ,e ,f ,g ,h 要放进贮藏室保管。出于安全原因,下列各组药品不能贮在同一个室内:a-f ,a-c ,a-h ,e-f ,e-g ,g-h ,b-h ,b-d ,c-d ,f-g ,b-f ,d-e ,c-g ,d-g ,问贮藏这8种药品至少需要多少个房间? 以8种药品作为顶点,若两种药品不能贮在同一个室内,则它们之间有一条边,这样得右图,转化为图的正常顶着色问题。
(1)对各顶点按次数的递减顺序排列为gfdechab ;
(2)对g 及不与之相邻点a 、b 着1色;
(3)对f 及不与之相邻点d 、h 着2色; (4)对e 和c 着3色。 故χ(G )≤3;又因为e ,f ,g 为K 3子图,故着色数χ(G )≥3,从而χ(G )=3。
因此贮藏这8种药品至少需要3个房间。贮藏方式之一为gab ,dfh ,
ce 。
以下说法错误的是
A .欧拉回路必经过图中所有的边 B. 欧拉回路必经过图中所有的顶点 C. 哈密顿回路必经过图中所有的边 D. 哈密顿回路必经过图中所有的顶点
无向图G 存在欧拉行迹,当且仅当 A .G 中所有结点的度数全为偶数 B .G 中至多有两个奇数度结点
f
C .G 连通且所有结点的度数全为偶数
D .G 连通且至多有两个奇数度结点
以下必为欧拉图的是
A .顶点度数全为偶数的连通图
B .奇数顶点只有2个的图 C
.存在欧拉迹的图 D .没有回路的连通图。
下图中是Euler 图的是
A .
B .
C .
D .
下列图中为欧拉图的是
A .
B .
C .
D .
下图中既是欧拉图又是哈密顿图的是 A .K 9 B .K 10 C .K 2,3 D .K 3,3
设G 为完全二部图K 2,3,下面命题中为真的是 A .G 为Euler 图 B .G 为Hamilton 图 C .G 为平面图 D .G 为正则图
在Petersen 图(单星妖怪)中至少添加 条边才能构成欧拉图。5
有4个顶的无向连通图G 是欧拉图,
A .1,2,3,4
B .2,4,6,8
C .1,2,4,6
D .5,2,3,4
设m ≥1,n ≥3,下面命题中,为真的是 A .完全图K n 都是Euler 图 B .完全二分图K n ,m 都是Euler 图 C .完全图K n 都是Hamilton 图 D .完全二分图K n ,m 都是Hamilton 图
构造Euler 图,其顶点数p 和边数q 满足p ,q 的奇偶性相反。
有四个村庄的地下各有一个防空洞甲、乙、丙、丁,相邻两个防空洞之间有地道相通,且每个防空洞各有一条地道与地面相通,如下图所示(图中◎表示地道)。问能否从某一个防空洞开始,每个地道走一次且仅走一次后回到该防空洞。要求有一定的分析过程。
丁丙
乙甲
求下图的中国邮路问题,设v i为邮局。(1)写出“倍边”的过程;(2)列出最后所得的从v1出发的中国邮路。
v3
(1)图中,奇次顶集为{v1,v2,v4,v3}。计算出每对顶的距离:
d(v1,v2)=4,d(v1,v3)=5,d(v1,v4)=7,d(v2,v3)=2,d(v2,v4)=5,d(v3,v4)=3,
求出{v1,v2,v4,v3}构成的完全加权图的最佳匹配M={v1v2,v3v4},
P(v1,v2)=v1v7v2,P(v3,v4)=v3v4,在G中沿P(v1,v2)与P(v3,v4)变成同权“倍边”。
(2)v1v7v2v3v4v5v1v6v2v7v3v4v7v1。
一个连通的无向图G,如果它的所有顶点的度数都是偶数,那么它具有一条A.Hamilton回路B.Euler回路C.Hamilton轨D.含所有顶的圈
设完全图K n有n个顶点(n≥2),m条边,K n中存在欧拉回路的条件是
A.m为奇数B.n为偶数C.n为奇数D.m为偶数
K7中两两无公共边的Hamilton圈有
A.2B.3 C.4 D.7
下面哪个图不是Hamilton图
Petersen图(单星妖怪)是Hamilton图。
若G是一个Hamilton图,则G一定是( ).
A.平面图B.自对偶图C.欧拉图D.连通图
若G是一个Euler图,则G一定是( ).
A.平面图B.Hamilton图C.连通图D.自对偶图
Petersen 图(单星妖怪)是 A .Hamilton 图 B .Euler 图 C .平面图 D .非平面图
K 11中有 条边不重的Hamilton 回路。5
若图G 的任一对顶u ,v 皆有d (u )+d (v )≥V (G ),则G 是Hamilton 图。
若G 是Hamilton 图,则对于V (G )的任意子集S 都有ω (G -S )≤|S |。
在下列图中,既是Euler 图又是Hamilton 图的是
A .
B .
C .
D .
设G 是n (n ≥3)阶单图,则其顶的最小次数δ≥n /2是G 为哈密尔顿图的 A .必要条件 B .充分条件 C .充分必要条件 D .既不充分也不必要条件
设G 是有10个顶点的无向图,对于G 中任意两个不邻接的顶点u 和v ,均有d (u )+d (v )≥9,则G 是Hamilton 图。
作一个图,使其是Euler 图但非Hamilton 图。
画出两个具有8条边、6个顶的无向简单图,并使其是Euler 图。 画出两个具有7条边、6个顶的无向简单图,并使其是Euler 图。
下列图中,v 2可达v 4的是 A . B . C . D .
下列有向图中是强连通图的是
A .
B .
C .
D .
对具有m 条边的单图定向能得到______个不同的有向图。2m
4v v
34v
343
4v 2v
3
电子科技大学研究生试题《图论及其应用》(参考答案)
电子科技大学研究生试题 《图论及其应用》(参考答案) 考试时间:120分钟 一.填空题(每题3分,共18分) 1.4个顶点的不同构的简单图共有__11___个; 2.设无向图G 中有12条边,已知G 中3度顶点有6个,其余顶点的度数均小于3。则G 中顶点数至少有__9___个; 3.设n 阶无向图是由k(k ?2)棵树构成的森林,则图G 的边数m= _n-k____; 4.下图G 是否是平面图?答__是___; 是否可1-因子分解?答__是_. 5.下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。 图G 二.单项选择(每题3分,共21分) 1.下面给出的序列中,是某简单图的度序列的是( A ) (A) (11123); (B) (233445); (C) (23445); (D) (1333). 2.已知图G 如图所示,则它的同构图是( D ) 3. 下列图中,是欧拉图的是( D ) 4. 下列图中,不是哈密尔顿图的是(B ) 5. 下列图中,是可平面图的图的是(B ) A C D A B C D
6.下列图中,不是偶图的是( B ) 7.下列图中,存在完美匹配的图是(B ) 三.作图(6分) 1.画出一个有欧拉闭迹和哈密尔顿圈的图; 2.画出一个有欧拉闭迹但没有哈密尔顿圈的图; 3.画出一个没有欧拉闭迹但有哈密尔顿圈的图; 解: 四.(10分)求下图的最小生成树,并求其最小生成树的权值之和。 解:由克鲁斯克尔算法的其一最小生成树如下图: 权和为:20. 五.(8分)求下图G 的色多项式P k (G). 解:用公式 (G P k -G 的色多项式: )3)(3)()(45-++=k k k G P k 。 六.(10分) 22,n 3个顶点的度数为3,…,n k 个顶点的度数为k ,而其余顶点的度数为1,求1度顶点的个数。 解:设该树有n 1个1度顶点,树的边数为m. 一方面:2m=n 1+2n 2+…+kn k 另一方面:m= n 1+n 2+…+n k -1 v v 1 3 图G
图论期末考试整理复习资料
目录 第一章图的基本概念 (2) 二路和连通性 (4) 第二章树 (4) 第三章图的连通度 (6) 第四章欧拉图与哈密尔顿图 (8) 一,欧拉图 (8) 二.哈密尔顿图 (10) 第五章匹配与因子分解 (14) 一.匹配 (14) 二.偶图的覆盖于匹配 (15) 三.因子分解 (16) 第六章平面图 (20) 二.对偶图 (24) 三.平面图的判定 (25) 四.平面性算法 (28) 第七章图的着色 (34) 一.边着色 (34) 二.顶点着色 (35)
第九章 有向图 (40) 二 有向树 (41) 第一章 图的基本概念 1. 点集与边集均为有限集合的图称为有限图。 2. 只有一个顶点而无边的图称为平凡图。 3. 边集为空的图称为空图。 4. 既没有环也没有重边的图称为简单图。 5. 其他所有的图都称为复合图。 6. 具有二分类(X, Y )的偶图(或二部图):是指该图的点集可以分解为两个(非空)子 集 X 和 Y ,使得每条边的一个端点在 X 中,另一个端点在Y 中。 7. 完全偶图:是指具有二分类(X, Y )的简单偶图,其中 X 的每个顶点与 Y 的每个顶点 相连,若 |X|=m ,|Y|=n ,则这样的偶图记为 Km,n 8. 定理1 若n 阶图G 是自补的(即 ),则 n = 0, 1(mod 4) 9. 图G 的顶点的最小度。 10. 图G 的顶点的最大度。 11. k-正则图: 每个点的度均为 k 的简单图。 例如,完全图和完全偶图Kn,n 均是正则图。 12. 推论1 任意图中,奇点的个数为偶数。 ()G δ()G ?
13. 14.频序列:定理4 一个简单图G的n个点的度数不能互不相同。 15.定理5 一个n阶图G相和它的补图有相同的频序列。 16. 17. 18.对称差:G1△G2 = (G1∪G2) - (G1∩G2) = (G1-G2)∪(G2-G1) 19.定义:联图在不相交的G1和G2的并图G1+G2中,把G1的每个顶点和G2的每个 顶点连接起来所得到的图称为G1和G2的联图,记为G1∨G2 20.积图:积图设G1= (V1, E1),G2 = (V2, E2),对点集V = V1×V2中的任意两个点u = (u1,u2)和v = (v1,v2),当(u1 = v1和u2 adj v2) 或(u2 = v2 和u1 adj v1) 时就把u 和v 连接起来所得到的图G称为G1和G2积图。记为G = G1×G2 设G1= (V1, E1),G2 = (V2, E2),对点集V = V1×V2中的任意两个点u = (u1,u2)和v = (v1,v2),当(u1 adj v1) 或(u1= v1 和u2 adj v2) 时就把u 和v 连接起来所得到的图G称为G1和G2的合成图。记为G=G1[G2]。
2004图论复习题答案
图论复习题答案 一、判断题,对打,错打 1.无向完全图是正则图。 () 2.零图是平凡图。() 3.连通图的补图是连通图.() 4.非连通图的补图是非连通图。() 5.若连通无向简单图G中无圈,则每条边都是割边。() 6.若无向简单图G是(n,m)图,并且m=n-1,则G是树。() 7.任何树都至少有2片树叶。() 8.任何无向图G都至少有一个生成树。() 9.非平凡树是二分图。() 10.所有树叶的级均相同的二元树是完全二元树。() 11.任何一个位置二元树的树叶都对应唯一一个前缀码。() 12. K是欧拉图也是哈密顿图。() 3,3 13.二分图的对偶图是欧拉图。() 14.平面图的对偶图是连通图。() 页脚内容1
15.设G*是平面图G的对偶图,则G*的面数等于G的顶点数。() 二、填空题 1.无向完全图K6有15条边。 2.有三个顶点的所有互不同构的简单无向图有4个。 3.设树T中有2个3度顶点和3个4度顶点,其余的顶点都是树叶,则T中有10片树叶。 4.若连通无向图G是(n,m)图,T是G的生成树,则基本割集有n-1个,基本圈有m-n+1个。 5.设连通无向图G有k个奇顶点,要使G变成欧拉图,在G中至少要加k/2条边。 6.连通无向图G是(n,m)图,若G是平面图,则G有m-n+2个面。 三、解答题 1.有向图D如图1所示,利用D的邻接矩阵及其幂运算 求解下列问题: (1)D中长度等于3的通路和回路各有多少条。 (2)求D的可达性矩阵。 (3)求D的强分图。 解:(1) a b c d e 图1 页脚内容2
页脚内容3 M=????????????????000101000000001 010*******M 2=?? ? ? ??????? ?????010******* 000101000001000 M 3=????????????????10000 01000010000001010000M 4=??? ???? ? ??? ?????00010 01000 100000100000010 由M 3可知,D 中长度等于3的通路有5条,长度等于3的回路有3条。 (2) I+M+M 2+M 3+M 4=????????????? ???100000100000100 0001000001 +??????????? ?? ???000101000000001 010******* +??????????? ?? ???010000001000010 1000001000 +??? ???? ? ??? ?? ???100000100001000 0001010000 + ????????????????00010 01000100000100000010 =??? ???? ???? ?? ???21020 1301011111 020******* D 的可达性矩阵为 R=B (I+M+M 2+M 3+M 4)=??? ???? ? ????? ???110101********* 1101011011 b c d e 图1
集合论与图论 试题A
本试卷满分90分 (06级计算机、信息安全专业、实验学院) 一、判断对错(本题满分10分,每小题各1分) ( 正确画“√”,错误画“×”) 1.对每个集合A ,A A 2}{∈。 (×) 2.对集合Q P ,,若?==Q P Q Q P ,,则P =?。 (√) 3.设,,:X A Y X f ?→若)()(A f x f ∈,则A x ∈。 (×) 4.设,,:Y B Y X f ?→则有B B f f ?-))((1。 (×) 5.若R 是集合X 上的等价关系,则2R 也是集合X 上的等价关系。 (√) 6.若:f X Y →且f 是满射,则只要X 是可数的,那么Y 至多可数的。(√) 7.设G 是有10个顶点的无向图,对于G 中任意两个不邻接的顶点u 和v, 均有9deg deg ≥+v u ,则G 是哈密顿图。 (×) 8.设)(ij a A =是 p 个顶点的无向图G 的邻接矩阵,则对于G 的顶点i v , 有∑==p j ij i a v 1deg 成立。 (√) 9. 设G 是一个),(q p 图,若1-≥p q ,则]/2[)(q p G ≤χ。 (×) 10.图G 和1G 同构当且仅当G 和1G 的顶点和边分别存在一一对应关系。(×)
二.填空(本题40分,每空各2分) 1.设}},{,{φφ=S 则=S 2 }}}{,{}},{{},{,{φφφφφ 。 2.设B A ,是任意集合,若B B A =\,则A 与B 关系为 φ==B A 。 3.设1)(,0)()(,:};3,2{},1,0{},,,{===→===c f b f a f Y X f Z Y c b a X , 3)1(,2)0(,:==→g g Z Y g ,则)()(c f g a f g ,分别为 2,3 。 4.设X 和Y 是集合且X m =,Y n =,若n m ≤,则从X 到Y 的单射的 个数为 !m C m n 。 5.设}2,1{},,,2,1{==B n X ,则从X 到Y 的满射的个数为 22-n 。 6.设)}2,4(),1,3(),3,2{()},4,3(),2,2(),2,1{(},4,3,2,1{===S R X ,则 =)(R S R )}2,3(),4,2(),4,1{( 。 7. 设???? ??=???? ??=5123454321,415235432121σσ,则???? ??=235411234521σσ 。 8. 设)},(),,(),,{(},,,,{a c c b b a R d c b a X ==,则 )},(),,(),,(),,(),,(),,(),,(),,(),,{(b c a c a b c b c a b a c c b b a a R =+ 。 9. 设X 为集合且X n =,则X 上不同的自反或对称的二元关系的个数 为 22222222n n n n n n +--+- 。 10.设}}{},{},,{{},,,,{d c b a A d c b a X ==是X 的一个划分,则由A 确定的 X 上的等价关系为 )},(),,(),,(),,(),,(),,{(d d c c a b b a b b a a 。 11.}10,,2,1{ =S ,在偏序关系“整除”下的极大元为 6,7,8,9,10 。 12.给出一个初等函数)(x f ,使得它是从)1,0(到实数集合R 的一一对应, 这个函数为 x ctg π或-x ctg π或)2/(ππ-x tg 。 13. 设G 是),(p p 连通图,则G 的生成树的个数至多为 p 。
图论复习题
(二)图论复习题 一、选择题 1.设图G =
是简单回路的边不重复。 6.设G 是简单有向图,可达矩阵P(G)刻划下列关系中的是( C ) A 、点与边 B 、边与点 C 、点与点 D 、边与边 7.下列哪一种图不一定是树(C )。 A.无简单回路的连通图 B. 有n 个顶点n-1条边的连通图 C. 每对顶点间都有通路的图 D. 连通但删去一条边便不连通的图 8.在有n 个结点的连通图中,其边数(B ) A.最多有n-1条 B.至少有n-1条 C.最多有n 条 D.至少有n 条 9.下列图为树的是(C )。 A 、>><><><=<},,,,,{},,,,{1d c b a a a d c b a G B 、>><><><=<},,,,,{},,,,{2d c d b b a d c b a G C 、>><><><=<},,,,,{},,,,{3a c d a b a d c b a G D 、>><><><=<},,,,,{},,,,{4d d c a b a d c b a G 10、下面的图7-22是(C )。 A.完全图; B.平面图; C.哈密顿图; D. 欧拉图。 二、填空题 1.无向完全图K 6有 15 条边。[6×(6-1)]/2=15 2.设连通无向图G 有k 个奇顶点,要使G 变成欧拉图,在G 中至少要 加 k/2 条边。 解:∵任何图中的奇点的个数为偶数
图论试题浙师大
思考练习 第一章 1对任意图,证明。 证:,故。 2 在一次聚会有个人参加,其中任意6个人中必有3个人互相认识或有3个人互不认识。举例说明,将6个人改成5个人,结论不一定成立。 证:构图如下:图的顶点代表这6个人,两个顶点相邻当且仅当对应的两个人 互相认识。则对于图中任意一个点或。 不妨设及它的3个邻点为。若中有任意两个点,不妨设为 ,相邻,则对应的3个人互相认识;否则,中任意两个点不邻, 即它们对应的3个人互不认识。 若这5个人构成的图是5圈时,就没有3个人互相认识或有3个人互不认识。 3 给定图 画出下列几个子图: (a) ; (b); (c)
解:(a) (b) (c) 第二章 1设是一个简单图,。证明:中存在长度至少是的路。 证:选取的一条最长路,则的所有邻点都在中,所以
,即中存在长度至少是的路。 2证明:阶简单图中每一对不相邻的顶点度数之和至少是,则是连通图。 证:假设不连通,令、是的连通分支,对,有 ,与题设矛盾。故连通。 3设是连通图的一个回路,,证明仍连通。 证:,中存在路, 1、若,则是中的路; 2、若,则是中的途径,从而中存在 路。 故连通。 4图的一条边称为是割边,若。证明的一条边是割边当且仅当不含在的任何回路上。 证:不妨设连通,否则只要考虑中含的连通分支即可。 必要性:假设在的某一回路上,则由习题2.13有连通,,与是割边矛盾。故不在回路中。 充分性:假设不是割边,则仍连通,存在路,则就是含的一个回路,与不在回路中矛盾。故是割边。 5证明:若是连通图,则。 证:若是连通图,则。
第三章 1 证明:简单图是树当且仅当中存在一个顶点到中其余每个顶点有且只有一条路。 证:必要性:由定理3.1.1立即可得。 充分性:首先可见连通。否则,设有两个连通分支、,且, 则到中的顶点没有路,与题设矛盾。 其次,中无回路。否则,若有回路。由于连通,到上的点有路, 且设与的第一个交点为,则到上除外其余点都至少有两条路,又与题设矛盾。 故是树。 2 设图有个连通分支,。证明含有回路。 证:假设中不含回路。设的个连通分支为,则每个连通无回路,是树。从而 , 与题设矛盾,故无回路。 3是连通简单图的一条边。证明在的每个生成树中当且仅当是的割边。 证:必要性:假设不是的割边,即连通,有生成树,与在的每个生成树矛盾。故不是的割边。 充分性:假设存在一棵生成树,使得不在中,从而连通,与是的割边矛盾。故在的每个生成树中。 4设是至少有3个顶点的连通图,证明中存在两个顶点,使得仍
运筹学期末试题
《运筹学》试题样卷(一) 一、判断题(共计10分,每小题1分,对的打√,错的打X ) 1. 无孤立点的图一定是连通图。 2. 对于线性规划的原问题和其对偶问题,若其中一个有最优解, 另一个也一定有最优解。 3. 如果一个线性规划问题有可行解,那么它必有最优解。 4.对偶问题的对偶问题一定是原问题。 5.用单纯形法求解标准形式(求最小值)的线性规划问题时,与0 >j σ对应的变量 都可以被选作换入变量。 6.若线性规划的原问题有无穷多个最优解时,其对偶问题也有无穷 多个最优解。 7. 度为0的点称为悬挂点。 8. 表上作业法实质上就是求解运输问题的单纯形法。 9. 一个图G 是树的充分必要条件是边数最少的无孤立点的图。 二、建立下面问题的线性规划模型(8分) 某农场有100公顷土地及15000元资金可用于发展生产。农场劳动力情况为秋冬季3500人日;春夏季4000人日。如劳动力本身用不了时可外出打工,春秋季收入为25元 / 人日,秋冬季收入为20元 / 人日。该农场种植三种作物:大豆、玉米、小麦,并饲养奶牛和鸡。种作物时不需要专门投资,而饲养每头奶牛需投资800元,每只鸡投资3元。养奶牛时每头需拨出1.5公顷土地种饲料,并占用人工秋冬季为100人日,春夏季为50人日,年净收入900元 / 每头奶牛。养鸡时不占用土地,需人工为每只鸡秋冬季0.6人日,春夏季为0.3人日,年净收入2元 / 每只鸡。农场现有鸡舍允许最多养1500只鸡,牛栏允许最多养200头。三种作物每年需要的人工及收入情况如下表所示: 试决定该农场的经营方案,使年净收入为最大。
三、已知下表为求解某目标函数为极大化线性规划问题的最终单纯形表,表中54,x x 为 (1)写出原线性规划问题;(4分) (2)写出原问题的对偶问题;(3分) (3)直接由上表写出对偶问题的最优解。(1分) 四、用单纯形法解下列线性规划问题(16分) 3212max x x x Z +-= s. t. 3 x 1 + x 2 + x 3 ≤ 60 x 1- x 2 +2 x 3 ≤ 10 x 1+ x 2- x 3 ≤ 20 x 1 , x 2 , x 3 ≥0 五、求解下面运输问题。 (18分) 某公司从三个产地A 1、A 2、A 3 将物品运往四个销地B 1、B 2、B 3、B 4,各产地的产量、各销地的销量和各产地运往各销地每件物品的运费如表所示: 问:应如何调运,可使得总运输费最小? 六、灵敏度分析(共8分) 线性规划max z = 10x 1 + 6x 2 + 4x 3 s.t. x 1 + x 2 + x 3 ≤ 100 10x 1 +4 x 2 + 5 x 3 ≤ 600 2x 1 +2 x 2 + 6 x 3 ≤ 300 x 1 , x 2 , x 3 ≥ 0
离散数学图论部分经典试题及答案
离散数学图论部分综合练习 一、单项选择题 1.设图G 的邻接矩阵为 ??? ???? ? ????? ???0101 010******* 11100100110 则G 的边数为( ). A .6 B .5 C .4 D .3 2.已知图G 的邻接矩阵为 , 则G 有( ). A .5点,8边 B .6点,7边 C .6点,8边 D .5点,7边 3.设图G =
图三 7.设有向图(a )、(b )、(c )与(d )如图四所示,则下列结论成立的是 ( ) . 图四 A .(a )是强连通的 B .(b )是强连通的 C .(c )是强连通的 D .(d )是强连通的 应该填写:D 8.设完全图K n 有n 个结点(n ≥2),m 条边,当( )时,K n 中存在欧拉回路. A .m 为奇数 B .n 为偶数 C .n 为奇数 D .m 为偶数 9.设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ). A .e -v +2 B .v +e -2 C .e -v -2 D .e +v +2 10.无向图G 存在欧拉通路,当且仅当( ). A .G 中所有结点的度数全为偶数 B .G 中至多有两个奇数度结点 C .G 连通且所有结点的度数全为偶数 D .G 连通且至多有两个奇数度结点 11.设G 是有n 个结点,m 条边的连通图,必须删去G 的( )条边,才能确定G 的一棵生成树. A .1m n -+ B .m n - C .1m n ++ D .1n m -+ 12.无向简单图G 是棵树,当且仅当( ). A .G 连通且边数比结点数少1 B .G 连通且结点数比边数少1 C .G 的边数比结点数少1 D .G 中没有回路. 二、填空题 1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结 点,则G 的边数是 . 2.设给定图G (如图四所示),则图G 的点割 ο ο ο ο c a b f
图论考试
图论考试
————————————————————————————————作者:————————————————————————————————日期: 2
3 电子科技大学研究生试卷 (考试时间:至,共__2_小时) 课程名称图论及其应用教师学时60 学分 教学方式讲授考核日期_2012__年___月____日成绩 考核方式:(学生填写) 一、填空题(填表题每空1分,其余每题2分,共30分) 1.n 阶k 正则图G 的边数()m G =___ ___2 nk ; 2.3个顶点的不同构的简单图共有___4___个; 3.边数为m 的简单图G 的不同生成子图的个数有__2___m 个; 4. 图111(,)G n m =与图222(,)G n m =的积图12G G ?的边数为1221____n m n m +; 5. 在下图1G 中,点a 到点b 的最短路长度为__13__; 6. 设简单图G 的邻接矩阵为A ,且2311201 21111 13022102001202A ?? ? ? ?= ? ? ?? ? ,则图G 的边数 为 __6__; 学号姓名学院 ……………………密……………封……………线……………以…………… 4 5 6 6 4 1 1 2 7 2 4 3 a b G 1
4 7. 设G 是n 阶简单图,且不含完全子图3K ,则其边数一定不会超过 2___4n ?? ???? ; 8.3K 的生成树的棵数为__3__; 9. 任意图G 的点连通度()k G 、边连通度()G λ、最小度()G δ之间的关系为 __()()()____k G G G λδ≤≤; 10. 对下列图,试填下表(是??类图的打〝√ 〞,否则打〝?〞)。 ① ② ③ 能一笔画的图 Hamilton 图 偶图 可平面图 ① ? √ ? √ ② ? ? ? √ ③ ? √ √ √ 二、单项选择(每题2分,共10分) 1.下面命题正确的是(B ) 对于序列(7,5,4,3,3,2),下列说法正确的是: (A) 是简单图的度序列; (B) 是非简单图的度序列; (C) 不是任意图的度序列; (D)是图的唯一度序列. 2.对于有向图,下列说法不正确的是(D) (A) 有向图D 中任意一顶点v 只能处于D 的某一个强连通分支中; (B) 有向图D 中顶点v 可能处于D 的不同的单向分支中; (C) 强连通图中的所有顶点必然处于强连通图的某一有向回路中; (D)有向连通图中顶点间的单向连通关系是等价关系。 3.下列无向图可能不是偶图的是( D )
图论与组合数学期末复习题含答案
组合数学部分 第1章 排列与组合 例1: 1)、求小于10000的含1的正整数的个数; 2、)求小于10000的含0的正整数的个数; 解:1)、小于10000的不含1的正整数可看做4位数,但0000除外.故有9×9×9×9-1=6560个.含1的有:9999-6560=3439个 2)、“含0”和“含1”不可直接套用。0019含1但不含0。在组合的习题中有许多类似的隐含的规定,要特别留神。不含0的1位数有19个,2位数有29个,3位数有39个,4位数有49个 不含0小于10000的正整数有() ()73801919999954321=--=+++个含0小于10000的正整数9999-7380=2619个。 例2: 从[1,300]中取3个不同的数,使这3个数的和能被3整除,有多少种方案? 解:将[1,300]分成3类: A={i|i ≡1(mod 3)}={1,4,7,…,298}, B={i|i ≡2(mod 3)}={2,5,8,…,299}, C={i|i ≡0(mod 3)}={3,6,9,…,300}. 要满足条件,有四种解法: 1)、3个数同属于A; 2)、3个数同属于B ; 3)、3个数同属于C; 4)、A,B,C 各取一数;故共有3C(100,3)+1003=485100+1000000=1485100。 例3:(Cayley 定理:过n 个有标志顶点的数的数目等于2-n n ) 1)、写出右图所对应的序列; 2)、写出序列22314所对应的序列; 解: 1)、按照叶子节点从小到大的顺序依次去掉节点(包含与此叶子 节点相连接的线),而与这个去掉的叶子节点相邻的另外一个点值则记入序列。如上图所示,先去掉最小的叶子节点②,与其相邻的点为⑤,然后去掉叶子节点③,与其相邻的点为①,直到只剩下两个节点相邻为止,则最终序列为51155.。 2)、首先依据给定序列写出(序列长度+2)个递增序列,即1234567,再将给出序列按从小到大顺序依次排列并插入递增序列得到:7。我们再将给出序列22314写在第一行,插入后的递增序列写在第二行。如下图第一行所示: ??→????? ??--②⑤67112223344522314??→???? ? ??--②⑥11223344672314 ??→????? ??--③②11233447314??→???? ? ??--①③11344714
图论模拟题
浙江师范大学《图论》考试卷 (2007-2008学年第一学期) 考试类别 闭卷 使用学生 行知数学 051.052. 考试时间 150 分钟 出卷时间 2008年1月4日 说明:考生应将全部答案都写在答题纸上,否则作无效处理。 一、填空题 (25%) 1、给定图G 11 (1)给出图G 的一条最长路_______; (2)给出图G 的二个参数值λ(G)= ,κ(G)= ; (3)给出图G 的一个最大独立集 ; (4)作出子图G[u 2,u 5,u 7,u 9,u 11,u 12]________,G-{u 8,u 9,u 12}____________, G-{u 1u 3,u 1u 4,u 1u 7,u 1u 10}_________ _______; 2、图G 是二分图的充分必要条件是 ; 3、G=(X,Y,E)是二分图,无孤立点,则β1(G) 与α0(G)的关系是 ; 4、Ramsey 数r(k,t)、r(k-1,t) 和r(k,t-1) 的关系是 ; 5、G 是含有56个顶点的无回路图,且对G中任两个不相邻的顶点v u ,,G+uv 有唯一的回路,则G的边数为____________; 6、图G 有Euler 环游的充要条件是____; 二、设七个字母在通迅中出现频率分别为a;25%,b;22%,c;20%,d;12%,e;10%,f;6%,g;5%。编一个最优前缀码,并画出相应的最优二元树。 (15%) 三、 证明:非平凡连通图G 至少有二个非割点。 (10%) 四、 G 是点色数χ(G)=2的k —正则简单图。证明G 有k 个边不交的完美对集M 1,M 2, ┄, M k , 使 E(G)= M 1∪M 2∪┄∪M k 。 (13%) 五、 给出平面图G 的顶点数p(G)、边数q(G)、面数 )(G ?和连通分支数ω(G)的一个关系式, 并给予证明。 (15%) 六、 G 是p 个顶点的简单图,对G 中每一对不相邻的顶点u 、v,均有d G (u)+d G (v)≥p-1。 (1) 证明G 有Hamilton 路;(2) G 是二连通图吗?为什么?。 (12%) 七、设G是连通图,若对每个真子集V 0?V(G) ,只要∣V 0∣≤k-1,G- V 0仍连通.证明q(G)≥ kp(G)/2 。 (10%)
电子科技大学2017年图论期末试卷
1 2017年图论课程练习题 一.填空题 1.图1中顶点a 到顶点b 的距离d (a ,b )= 。 a b 9 图1 1 2.已知图G 的邻接矩阵0 11011 01001 1010001011001 0A = ,则G 中长度为2的途径总条数为 。 3.图2中最小生成树T 的权值W (T )= 。 4.图3的最优欧拉环游的权值为 。 12 图 2
2 图3 5.树叶带权分别为1,2,4,5,6,8的最优二元树权值为 。 二.单项选择 1.关于图的度序列,下列说法正确的是( ) (A) 对任意一个非负整数序列来说,它都是某图的度序列; (B) 若非负整数序列12(,,,)n d d d π= 满足1n i i d =∑为偶数,则它一定是图序 列; (C) 若图G 度弱于图H ,则图G 的边数小于等于图H 的边数; (D) 如果图G 的顶点总度数大于或等于图H 的顶点总度数,则图G 度优 于图H 。 2.关于图的割点与割边,下列说法正确的是( ) (A) 有割边的图一定有割点; (B) 有割点的图一定有割边; (C) 有割边的简单图一定有割点; (D) 割边不在图的任一圈中。 3.设()k G ,()G λ,()G δ分别表示图G 的点连通度,边连通度和最小度。下面说法错误的是( )
3 (A) 存在图G ,使得()k G =()G δ=()G λ; (B) 存在图G ,使得()()()k G G G λδ<<; (C) 设G 是n 阶简单图,若()2n G δ ≥ ,则G 连通,且()()G G λδ=; (D) 图G 是k 连通的,则G 的连通度为k 。 4.关于哈密尔顿图,下列命题错误的是( ) (A) 彼得森图是非哈密尔顿图; (B) 若图G 的闭包是哈密尔顿图,则其闭包一定是完全图; (C) 若图G 的阶数至少为3且闭包是完全图,则图G 是哈密尔顿图; (D) 设G 是三阶以上简单图,若G 中任意两个不邻接点u 与v ,满足 ()()d u d v n +≥,则G 是哈密尔顿图。 5.下列说法错误的是( ) (A) 有完美匹配的三正则图一定没有割边; (B) 没有割边的三正则图一定存在完美匹配; (C) 任意一个具有哈密尔顿圈的三正则图可以1因子分解; (D) 完全图21n K +是n 个哈密尔顿圈的和。 三、 设无向图G 有10条边,3度与4度顶点各2个,其余顶点度数均小于3,问G 中至少有几个顶点?在最少顶点数的情况下,写出G 的度序列,该度序列是一个图序列吗?。
图论复习题
一、选择题 1设图G=
[PPT 40] :哈密尔顿回路要求走遍所有的点,即是基本回路的点不重复,也可以是简单回路的边不重复。 6. 设G是简单有向图,可达矩阵P(G)刻划下列关系中的是(C ) A、点与边 B、边与点 C、点与点 D、边与边 7. 下列哪一种图不一定是树(C)。 A.无简单回路的连通图 B. 有n个顶点n-1条边的连通图 C. 每对顶点间都有通路的图 D. 连通但删去一条边便不连通的图 8. 在有n 个结点的连通图中,其边数(B) A. 最多有n-1 条 B. 至少有n-1 条 C. 最多有n 条 D. 至少有n 9. 下列图为树的是 ( C)。 A 、G 1 {a,b,c,d},{a,a ,a,b ,c,d B 、G 2 {a,b,c,d},{a,b ,b,d, c,d C 、 G3 {a,b,c,d}, {a,b ,a,d, c,a D 、G4{a,b,c,d},{a,b ,a,c ,d,d } } } } 10、面的图7-22 是(C)。
12年图论试题
电子科技大学研究生试卷 (测试时间:至,共__2_小时) 课程名称图论及其使用教师学时60 学分 教学方式讲授考核日期_2012__年___月____日成绩 考核方式:(学生填写) 一、填空题(填表题每空1分,其余每题2分,共30分) 1.n 阶k 正则图G 的边数()m G =___ ___2 nk ; 2.3个顶点的不同构的简单图共有___4___个; 3.边数为m 的简单图G 的不同生成子图的个数有__2___m 个; 4. 图111(,)G n m =和图222(,)G n m =的积图12G G ?的边数为1221____n m n m +; 5. 在下图1G 中,点a 到点b 的最短路长度为__13__; 6. 设简单图G 的邻接矩阵为A ,且 23 112012********* 102001202A ?? ? ? ?= ? ? ??? ,则图G 的边数为 __6__; 7. 设G 是n 阶简单图,且不含完全子图3K ,则其边数一定不会超过2___4n ?? ????; 8.3K 的生成树的棵数为__3__; 9. 任意图G 的点连通度()k G 、边连通度()G λ、最小度()G δ之间的关系为 __()()()____k G G G λδ≤≤; 10. 对下列图,试填下表(是??类图的打〝√ 〞,否则打〝?〞)。 ① ② ③ 学号姓名学院 ……………………密……………封……………线……………以……………内……………答……………题……………无……………效…………………… 4 5 6 6 4 1 1 2 7 2 4 3 a b G 1
能一笔画的图 Hamilton 图 偶图 可平面图 ① ? √ ? √ ② ? ? ? √ ③ ? √ √ √ 二、单项选择(每题2分,共10分) 1.下面命题正确的是(B ) 对于序列(7,5,4,3,3,2),下列说法正确的是: (A) 是简单图的度序列; (B) 是非简单图的度序列; (C) 不是任意图的度序列; (D)是图的唯一度序列. 2.对于有向图,下列说法不正确的是(D) (A) 有向图D 中任意一顶点v 只能处于D 的某一个强连通分支中; (B) 有向图D 中顶点v 可能处于D 的不同的单向分支中; (C) 强连通图中的所有顶点必然处于强连通图的某一有向回路中; (D)有向连通图中顶点间的单向连通关系是等价关系。 3.下列无向图可能不是偶图的是( D ) (A) 非平凡的树; (B)无奇圈的非平凡图; (C) n (1)n ≥方体; (D) 平面图。 4.下列说法中正确的是( C ) (A)连通3正则图必存在完美匹配; (B)有割边的连通3正则图一定不存在完美匹配; (C)存在哈密尔顿圈的3正则图必能1因子分解; (D)所有完全图都能作2因子分解。 5. 关于平面图,下列说法错误的是( B ) (A) 简单连通平面图中至少有一个度数不超过5的顶点; (B)极大外平面图的内部面是三角形,外部面也是三角形; (C) 存在一种方法,总可以把平面图的任意一个内部面转化为外部面; (D) 平面图的对偶图也是平面图。 三、 (10分)设G 和其补图G 的边数分别为12,m m ,求G 的阶数。 解:设G 的阶数为n 。 因12(1) 2n n m m -+=…………………………………4分 所以:212220n n m m ---=……………………..2分
运筹学期末试题
一、判断题(共计10分,每小题1分,对的打√,错的打X) 1.无孤立点的图一定是连通图。 2.对于线性规划的原问题和其对偶问题,若其中一个有最优解, 另一个也一定有最优解。 3.如果一个线性规划问题有可行解,那么它必有最优解。 4.对偶问题的对偶问题一定是原问题。 5.用单纯形法求解标准形式(求最小值)的线性规划问题时,与 > j σ 对应的变量都可以被选作换入变量。 6.若线性规划的原问题有无穷多个最优解时,其对偶问题也有无穷 多个最优解。 7. 度为0的点称为悬挂点。 8. 表上作业法实质上就是求解运输问题的单纯形法。 9. 一个图G 是树的充分必要条件是边数最少的无孤立点的图。 二、建立下面问题的线性规划模型(8分) 某农场有100公顷土地及15000元资金可用于发展生产。农场劳动力情况为秋冬季3500人日;春夏季4000人日。如劳动力本身用不了时可外出打工,春秋季收入为25元/ 人日,秋冬季收入为20元/ 人日。该农场种植三种作物:大豆、玉米、小麦,并饲养奶牛和鸡。种作物时不需要专门投资,而饲养每头奶牛需投资800元,每只鸡投资3元。 养奶牛时每头需拨出1.5公顷土地种饲料,并占用人工秋冬季为100人日,春夏季为50人日,年净收入900元 / 每头奶牛。养鸡时不占用土地,需人工为每只鸡秋冬季0.6人日,春夏季为0.3人日,年净收入2元 / 每只鸡。农场现有鸡舍允许最多养1500只 三、已知下表为求解某目标函数为极大化线性规划问题的最终单纯形表,表中5 4 ,x x 为松弛变量,问题的约束为?形式(共8分)
(1)写出原线性规划问题;(4分) (2)写出原问题的对偶问题;(3分) (3)直接由上表写出对偶问题的最优解。(1分) 四、用单纯形法解下列线性规划问题(16分) 3212max x x x Z +-= s. t. 3 x 1 + x 2 + x 3 ≤ 60 x 1- x 2 +2 x 3 ≤ 10 x 1+ x 2- x 3 ≤ 20 x 1, x 2 , x 3 ≥0 五、求解下面运输问题。 (18分) 某公司从三个产地A 1、A 2、A 3 将物品运往四个销地B 1、B 2、B 3、B 4,各产地的产量、各销地的销量和各产地运往各销地每件物品的运费如表所示: 六、灵敏度分析(共8分) 线性规划max z = 10x 1 + 6x 2 + 4x 3 s.t. x 1 + x 2 + x 3 ≤ 100 10x 1 +4 x 2 + 5 x 3 ≤ 600 2x 1 +2 x 2 + 6 x 3 ≤ 300 x 1 , x 2 , x 3 ≥ 0 的最优单纯形表如下:
图论复习题(中文)
1、设G是一个哈密尔顿图,则G一定是( )。 (1) 欧拉图 (2) 树(3) 平面图 (4) 连通图 答:(4)(考察图的定义) 2、一个图的哈密尔顿路是一条通过图中( )的路。 答:所有结点一次且恰好一次 3、在有向图中,结点v的出度deg+(v)表示( ),入度deg-(v)表示( )。答:以v为起点的边的条数,以v为终点的边的条数 4、设G是一棵树,则G 的生成树有( )棵。 (1) 0 (2) 1 (3) 2 (4) 不能确定 答:1 5、n阶无向完全图K n 的边数是( ),每个结点的度数是( )。 答: 2)1 ( n n , n-1 6、一棵无向树的顶点数n与边数m关系是( )。 答:m=n-1 7、一个图的欧拉回路是一条通过图中( )的回路。 答:所有边一次且恰好一次 8、有n个结点的树,其结点度数之和是( )。 答:2n-2(结点度数的定义) 9、n个结点的有向完全图边数是( ),每个结点的度数是( )。 答:n(n-1),2n-2 10、一个无向图有生成树的充分必要条件是( )。 答:它是连通图 11、设G是一棵树,n,m分别表示顶点数和边数,则 (1) n=m (2) m=n+1 (3) n=m+1 (4) 不能确定。 答:(3) 12、设T=〈V,E〉是一棵树,若|V|>1,则T中至少存在( )片树叶。 答:2 13、任何连通无向图G至少有( )棵生成树,当且仅当G 是( ),G的生成树只有一棵。 答:1,树
14、设G是有n个结点m条边的连通平面图,且有k个面,则k等于: (1) m-n+2 (2) n-m-2 (3) n+m-2 (4) m+n+2。 答:(1) 15、设T是一棵树,则T是一个连通且( )图。 答:无简单回路 16、设无向图G有16条边且每个顶点的度数都是2,则图G有( )个顶点。 (1) 10 (2) 4 (3) 8 (4) 16 答:(4) 17、设无向图G有18条边且每个顶点的度数都是3,则图G有( )个顶点。 (1) 10 (2) 4 (3) 8 (4) 12 答:(4) 18、设图G=
