6.5函数的曲线的凹向与拐点

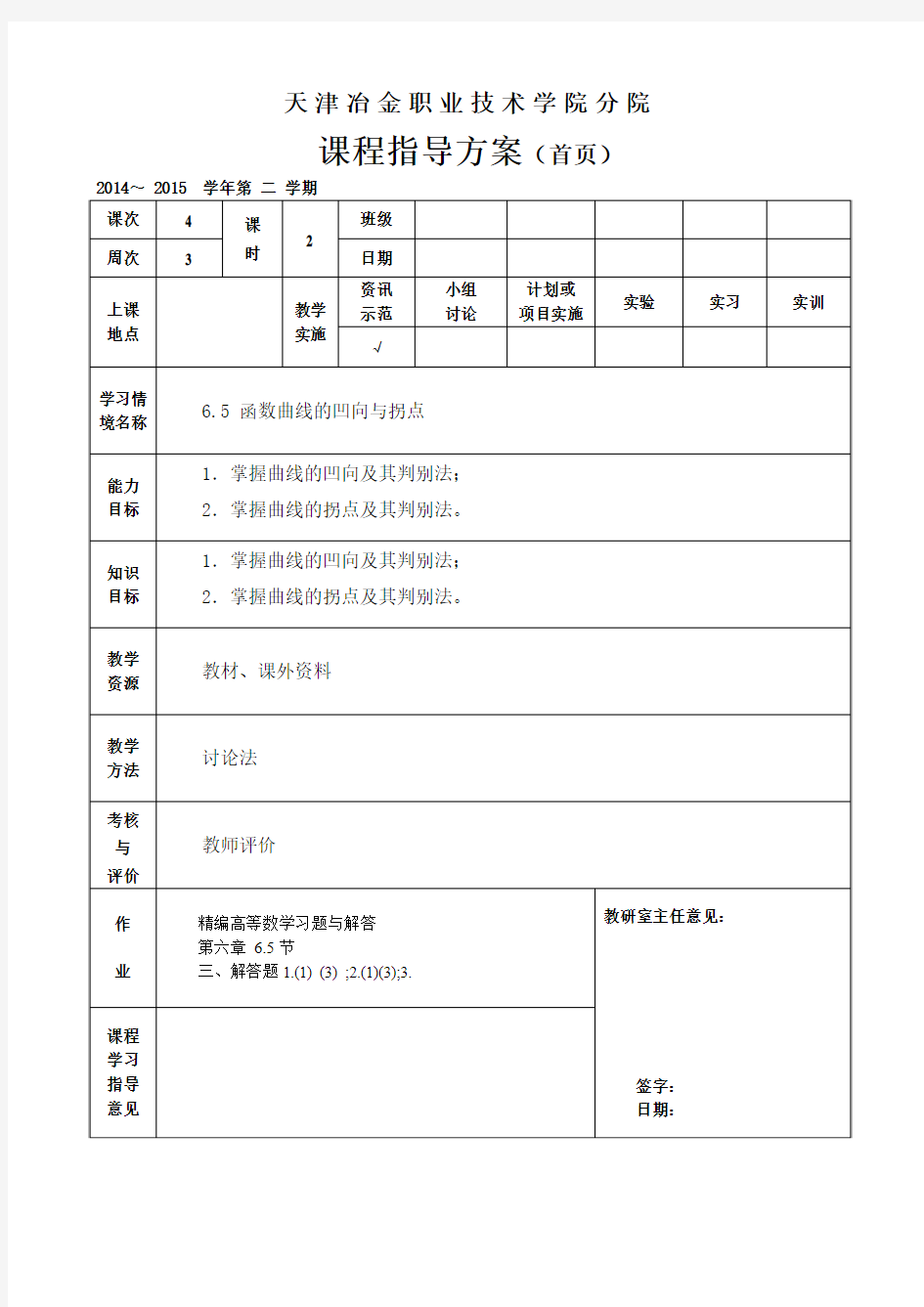
天津冶金职业技术学院分院课程指导方案（首页）

天津冶金职业技术学院分院教师授课教案

天津冶金职业技术学院教师授课教案

二阶导数的应用---曲线的凹凸性与拐点

二阶导数的应用---曲线的凹凸性与拐点教学目标与要求通过学习，使学生掌握利用二阶导数的符号判定函数在某一区间上凹凸性的方法，为更好地描绘函数图形打好基础，同时，理解拐点的定义和意义。教学重点与难点教学重点：利用函数的二阶导数判断曲线的凹凸性与拐点。教学难点：理解拐点的定义和意义。教学方法与建议证明曲线凹凸性判定定理时，除了利用“拉格朗日中值定理”证明外，还可用“泰勒定理”来证明；如果利用“拉格朗日中值定理”证明，则要配合函数图形来分析讲解如何想到需要两次使用“拉格朗日中值定理”的思路，切忌脱离图形，机械证明，让学生领悟不到思想，摸不着头脑。在讲函数的凹凸性和曲线拐点的定义时，要强调凹凸性并不是曲线的固有性质，而是函数的性质，与所选的坐标系有关；而拐点是曲线的固有性质，与所选的坐标系无关。教学过程设计 1. 问题提出与定义函数的单调性对于描绘函数图形有很大作用，但仅仅由单调性还不能准确描绘出函数的图形。比如，如果在区间上，，则我们知道在区间上单调增，但作图（参见图1）的时候，我们不能判断它增加的方式（是弧，还是弧），即不能判断曲线的凹凸性，所以研究曲线的凹凸性对于把握函数的性态、作图等是很有必要的！在图1中，对于上凸的曲线弧，取其上任意两点，不妨取作割线，我们总会发现不论两点的位置，割线段总位于弧段的下方，这种位置关系可以用不等式

来描述。同理，对于上凹的曲线弧，总可用不等式来描述。由此，我们想到对曲线的凹凸性做如下定义：凹凸性定义设在区间I上连续，如果对I 上任意两点，，恒有则称在I上的图形是（向上）凹的，简称为凹弧；如果恒有则称在I上的图形是（向上）凸的，或简称为凸弧。如果沿曲线从左向右走，则图形是（向上）凸的曲线的几何意义相当于右转弯，图形是（向上）凹的曲线相当于左转弯，而有切线的凹凸弧的分界点正是曲线转向的点，我们把这样的点称为拐点。 2. 凹凸性判定定理的引入 y O y f x =() x y O y f x =() 曲线凹凸性的定义自然能判别曲线的凹凸性，但实际使用起来需要取两个点，且两个不等式对于一些表达式较复杂的函数来说判断起来也不容易。因此，我们就想能否用其它方法来判定曲线的凹凸性。函数的单调性能由的符号确定，而对于凹凸性它束手无策，所以我们猜想凹凸性是否和有关经过分析，并利用泰勒公式，可证实我们的猜想是正确的，函数图形的凹凸性的确和的符号有关,于是得到了判断曲线凹凸性的定理。定理设在上连续, 在内具有二阶连续导数,那么：（1）若在内>0，则在上的图形是凹的；（2）若在内<0，则在上的图形是凸的。 3. 判别凹凸性和拐点举例例1判断曲线y x3的凹凸性

函数的凹凸性与拐点

第16 次理论课教学安排

图1 2.4导数的应用----曲线的凹凸与拐点课题：曲线的凹凸与拐点目的要求：理解曲线凹凸性的概念、掌握判断函数图形的凹凸性、求函数图形的拐点等方法。重、难点：判断函数图形的凹凸性、求函数图形的拐点教学方法：讲练结合教学时数：1课时教学进程：函数的单调性可用函数的一阶到函数来判定，对于同样的递增函数有着不同的增法，如向上凸的增或凹的增，那么对于这两种不同的增法我们如何刻画那？一、曲线的凹凸与拐点 1．曲线的凹凸定义和判定法从图1可以看出曲线弧ABC 在区间()c a ,内是向下凹入的，此时曲线弧ABC 位于该弧上任一点切线的上方；曲线弧CDE 在区间()b c ,内是向上凸起的，此时曲线弧CDE 位于该弧上任一点切线的下方．关于曲线的弯曲方向，我们给出下面的定义：定义1 如果在某区间内的曲线弧位于其任一点切线的上方，那么此曲线弧叫做在该区间内是凹的；如果在某区间内的曲线弧位于其任一点切线的下方，那么此曲线弧叫做在该区间内是凸的．例如，图1中曲线弧ABC 在区间()c a ,内是凹的，曲线弧CDE 在区间()b c ,内是凸的．由图1还可以看出，对于凹的曲线弧，切线的斜率随x 的增大而增大；对于凸 x y o () y f x =A B x y o () y f x =A B

的曲线弧，切线的斜率随x 的增大而减小．由于切线的斜率就是函数()x f y =的导数，因此凹的曲线弧，导数是单调增加的，而凸的曲线弧，导数是单调减少的．由此可见，曲线()x f y =的凹凸性可以用导数()x f '的单调性来判定．而()x f '的单调性又可以用它的导数，即()x f y =的二阶导数()x f ''的符号来判定，故曲线 ()x f y =的凹凸性与()x f ''的符号有关．由此提出了函数曲线的凹凸性判定定理：定理1 设函数()x f y =在()b a ,内具有二阶导数．（1）如果在()b a ,内，()x f ''＞0，那么曲线在()b a ,内是凹的；（2）如果在()b a ,内，()x f ''＜0，那么曲线在()b a ,内是凸的．例１判定曲线3 x y =的凹凸性． 2．拐点的定义和求法定义2 连续曲线上凹的曲线弧和凸的曲线弧的分界点叫做曲线的拐点．定理2(拐点存在的必要条件) 若函数()x f 在0x 处的二阶导数存在,且点 ()()00,x f x 为曲线()x f y =的拐点,则().00=''x f 我们知道由()x f ''的符号可以判定曲线的凹凸．如果()x f ''连续，那么当()x f ''的符号由正变负或由负变正时，必定有一点0x 使()0x f ''＝0．这样，点()()00,x f x 就是曲线的一个拐点．因此，如果()x f y =在区间()b a ,内具有二阶导数，我们就可以按下面的步骤来判定曲线()x f y =的拐点: (1) 确定函数()x f y =的定义域； (2) 求()x f y ''=''；令()x f ''＝0，解出这个方程在区间()b a ,内的实根； (3) 对解出的每一个实根0x ，考察()x f ''在0x 的左右两侧邻近的符号．如果()x f ''在0x 的左右两侧邻近的符号相反，那么点()()00,x f x 就是一个拐点，如果()x f ''在0x 的左右两侧邻近的符号相同，那么点()()00,x f x 就不是拐点．例２求曲线2 3 3x x y -=的凹凸区间和拐点．解（1）函数的定义域为()+∞∞-,；（2）()1666,632 -=-=''-='x x y x x y ；令0=''y ，得1=x ；（3）列表考察y ''的符号（表中“”表示曲线是凹的，“” 表示曲线是凸的）： x ()1,∞- 1 ()+∞,1 y '' - 0 + 曲线y 拐点 ()2,1-

曲线的凹凸性与拐点

·复习函数的单调性的定义，函数的极值。 ·引入由函数的单调性我们可知道曲线上升与下降的情况，还应知道它的弯曲方向以及不同弯曲方向的分界点，这就是曲线的凹向与拐点。 ·讲解新课曲线的凹凸性与拐点 1 曲线的凹凸定义及判定法定义1 如果曲线位于其每一点切线的上方，那么称曲线弧是凹的（如图（1）所示），如果曲线位于其每一点切线的下方，那么称曲线弧是凸的（如图（2））． y O x x y O y f x =() （2）是描述一阶导数的单调性的。从上图可以看出，如果曲线是凹的，切线的倾斜角随x 的增大而增大，由导数的几何意义知()f x '随x 的增大而增大，即函数的一阶导数是单调增加的，所以()0f x ''>；同样，如果曲线是凸的，切线的倾斜角随x 的增加而减少，就是()f x '随x 的增大而减少，即函数的一阶导数是单调减少的，所以()0f x ''<。反之结论是否成立呢？下面给出曲线凹凸性的判定定理。定理1 设函数)(x f y =在[,]a b 内连续，在),(b a 内具有一阶和二阶导数，那么（1）若在),(b a 内，0)(>''x f ，则曲线曲线)(x f y =在[,]a b 上是凹的. （2）

若在),(b a 内，0)(<''x f ，则曲线曲线)(x f y =在[,]a b 上是凸的．例1 判定曲线x y ln =的凹凸性．解：函数x y ln =的定义域为),0(+∞，且21 )(,1)(x x f x x f -=''='．因为在),0(+∞上)(x f ''恒为负，所以曲线x y ln =在其定义域内是凸的．例2 判定曲线x y 1 =的凹凸性．解：函数x y 1 = 的定义域为),0()0,(+∞-∞ ，且322 ,1x y x y =''-='．因为当0x 时0>''y ，所以曲线在)0,(-∞内是凸的，在),0(+∞内是凹的， 2 曲线的拐点及其求法定义2 把连续曲线凹凸部分的分界点叫做曲线的拐点．定理2 （拐点的必要条件）若函数)(x f y =在0x 处的二阶导数0()f x ''存在，且点00(,())x f x 为曲线)(x f y =的拐点，则0()0f x ''=。如何来求曲线的拐点呢？由于拐点是曲线的凹凸部分的分界点，所以拐点左右两侧近旁的()f x ''必然异号，因此，曲线拐点横坐标x 0只可能是使()f x ''=0的点。如3x y =中，点（0，0）就是曲线3x y =的拐点，但在x y 1 = 中，虽然点0=x 的左右近旁)(x f ''异号，但由于在点0=x 处曲线不连续，故不能说点（0，0）是曲线x y 1 =的拐点。函数二阶导数不存在的点，在曲线上相应的点也可能是拐点．如函数 3x y =的二阶导数在0=x 处不存在，但点（0，0）却是曲线的拐点．

曲线的凹凸性与拐点

曲线的凹凸性与拐点为了进一步研究函数的特性并正确地作出函数的图形，需要研究曲线的弯曲方向.在几何上，曲线的弯曲方向是用曲线的“凹凸性”来描述的. 一、曲线的凹凸性从图3-12（a ），（b ）可以观察到. 定义1 如果在某区间内的连续且光滑曲线弧总是位于其任一点切线的上方，则称此曲线弧在该区间内是凹的；如果在某区间内的曲线弧总是位于其任一点切线的下方，则称此曲线弧在该区间内是凸的，相应的区间分别称为凹区间与凸区间. 从图3-12还可以看到如下事实：对于凹的曲线弧，其切线的斜率()f x '随着x 的增大而增大，即() f x '单调增加；对于凸的曲线弧，其切线的斜率 ()f x '随着x 的增大而减少，即()f x '单调减少.而函数()f x '的单调性又可用它的导数，即()f x 的二阶导数()f x ''的符号来判定，故曲线()y f x =的凹凸性与()f x ''的符号有关. 定理1 设函数()f x 在区间(,)a b 上具有二阶导数. （1）如果在区间(,)a b 上，有()f x ''>0，那么曲线在(,)a b 上是凹的；（2）如果在区间(,)a b 上，有()f x ''<0，那么曲线在(,)a b 上是凸的. 例1 判定曲线ln y x =的凹凸性. 解函数的定义域为(0,)+∞，而 211 ,y y x x '''==- 因此曲线ln y x =在(0,)+∞内是凸的. 例2 讨论曲线3y x =的凹凸区间. 解函数的定义域为(,)-∞+∞， 2 3,6y x y x '''== 显然，当0x >时，0y ''<；当0x <时，0y ''>.因此(,0)-∞为曲线的凸区间，(0,)+∞为曲线的凹区间. 二、曲线的拐点在例2 中，点(0,0)为凸的曲线弧与凹的曲线弧的连接点，对这种点有如下定义. 定义2 在连续曲线上，凹凸曲线弧的分界点，称为曲线的拐点. 下面来讨论曲线()y f x =拐点的求法. 由于拐点是曲线凹凸弧的连接点，如果()f x ''存在且连续，则在拐点的左右近旁()f x ''

二阶导数的应用---曲线的凹凸性与拐点

二阶导数的应用 ---曲线的凹凸性与拐点教学目标与要求通过学习，使学生掌握利用二阶导数的符号判定函数在某一区间上凹凸性的方法，为更好地描绘函数图形打好基础，同时，理解拐点的定义和意义。教学重点与难点教学重点：利用函数的二阶导数判断曲线的凹凸性与拐点。教学难点：理解拐点的定义和意义。教学方法与建议证明曲线凹凸性判定定理时，除了利用"拉格朗日中值定理”证明外，还可用"泰勒定理”来证明；如果利用“拉格朗日中值定理”证明，则要配合函数图形来分析讲解如何想到需要两次使用“拉格朗日中值定理”的思路，切忌脱离图形，机械证明，让学生领悟不到思想，摸不着头脑。在讲函数的凹凸性和曲线拐点的定义时，要强调凹凸性并不是曲线的固有性质，而是函数的性质，与所选的坐标系有关；而拐点是曲线的固有性质，与所选的坐标系无关。教学过程设计 1?问题提出与定义函数的单调性对于描绘函数图形有很大作用，但仅仅由单调性还不能准确描绘出函数的图形。比如，如果在区间L r上，丿' ■，则我们知道丿，在区间-'?〔上单调增，但作图（参见图1）的时候，我们不能判断它增加的方式（是弧V匸U，还是弧二注），即不能判断曲线的凹凸性，所以研究曲线的凹凸性对于把握函数的性态、作图等是很有必要的！在图1中，对于上凸的曲线弧A~-'~，取其上任意两点，不妨取：1作割线，我们总会发现不论两点的位置，割线段总位于弧段的下方，这种位置关系可以用不等式来描述。同理，对于上凹的曲线弧上：匸，总可用不等式 1 2 来描述。由此，我们想到对曲线的凹凸性做如下定义：凹凸性定义设在区间I上连续，如果对i上任意两点"，勺，恒有 1 2

考研数学：曲线凹凸性及拐点典型题型分析

考研数学：曲线凹凸性及拐点典型题型分析来源：文都教育在考研数学中，高等数学导数的应用部分有多个考点，其中之一是曲线的凹凸性和拐点。凹凸性和拐点是函数图形的一种特性，从几何意义上讲，凹凸性反映的是曲线的弯曲方向，而拐点则是指曲线的弯曲方向发生改变的点，从代数意义上讲，凹函数或凸函数就是指二阶导数不变号的函数，当然，这里说的不变号一般是相对于某一个区间而言的。下面文都考研蔡老师对曲线的凹凸性及拐点的判断方法和典型题型做些分析总结，供考研的同学复习时参考。一、凹凸性和拐点的判断方法 1. 凹凸性判断方法：设()f x 在[,]a b 上连续，在(,)a b 内二阶可导，则当()0f x ''>时，()f x 在[,]a b 上的图形是凹的；当()0f x ''<时，则()f x 在[,]a b 上的图形是凸的。 2、拐点判断方法：先求出()0f x ''=的点和二阶导数不存在的点0x ，若函数()f x 在点0x 的左、右邻域内的二阶导数存在并且符号相反，则00(,())x f x 是曲线的拐点。二、典型题型分析例1. 设函数()y y x =由参数方程33113311 33x t t y t t =++=-+??????? 确定，求()y y x =的极值和曲线 ()y y x =的凹凸区间及拐点。解：由0dy dx =，得1t =±，22234(1)d y t dx t =+，222211110,022 t t d y d y dx dx =-==-<=>，极大值为(1)1y -=，极小值为5 1()33 y =-；令2210,03d y t x dx ===得，；当2200d y t dx <<时，，得凸区间为1(,)3 -∞，当

曲线的凹凸性及拐点

一、曲线的凹凸性及拐点引导学生观察下列图象 1.定义1 设函数()y f x =在区间(),a b 内可导，（1）若曲线()y f x =位于其每点切线的下方（割线位于曲线的下方），则称曲线()y f x =在区间(),a b 内是凸的，区间(),a b 称为函数()f x 的凸区间. （2）若曲线()y f x =位于其每点切线的上方（割线位于曲线的上方），则称曲线()y f x =在区间(),a b 内是凹的，区间(),a b 称为函数()f x 的凹区间. 2.定义2 曲线上凹弧和凸弧的分界点称为曲线的拐点. 3.定理1 设函数()f x 在闭区间[],a b 上连续，在开区间(),a b 内具有二阶导数，（1）若在(),a b 内，()0f x ''<，则曲线()y f x =在区间(),a b 内是凸的. （2）若在(),a b 内，()0f x ''>，则曲线()y f x =在区间(),a b 内是凹的. 4.求曲线凹凸区间和拐点的步骤如下：（1）求出函数的一阶导数()f x '，再求二阶导数()f x ''；（2）求出二阶导数()0f x ''=的点，以及()f x ''不存在的点；（3）考察每个点处的左、右二阶导数是否异号，从而确定哪些点处取得拐点；（4）求出每个二阶导数变号点处的函数值，从而得到曲线的全部拐点. 例1、讨论曲线32395y x x x =--+的凹凸性，并求其拐点. x a b 凹弧凸弧

例2、讨论曲线4321y x x =-+的凹凸性，并求其拐点. 二、函数曲线的曲率曲线的下凸和上凸说的是曲线的弯曲方向，而曲线的曲率说的是曲线的弯曲程度。直线段没有弯曲，所以认为它的曲率为0. 一般情形下，如图1，弧 AB 的全曲率规定为起点A 处切线方向与终点B 处切线方向的偏差θ?. 可是，弧 CD 的全曲率与弧 AB 的全曲率相同，但前者显然比后者弯曲得更厉害一些。这就是说，弧的弯曲程度与弧本身的长度有关。因此，就像测量物理量或几何量时先确定一个单位那样，把单位长度弧的全曲率取作测量弧时曲率的单位，而把长度为s ?的弧的全曲率θ?同弧长s ?的比值/s θ??，称为该弧的平均曲率。它有点像质点运动的平均速度。像定义质点运动的瞬时速度那样，把极限定义为弧 AB 在点A 处的曲率 (其中θ?为弧 AB 的全曲率, s ?为弧 AB 的长度)。对于半径为R 的圆周来说 (图2)，由于θ?=?R s ，所以圆周上任一点处的曲率都相等，且曲率为 R s s K s 1d d lim 0==??=→?θθ (半径的倒数) 对于一般的弧来说，虽然弧上各点处的曲率可能不尽相同，但是当弧上点A 处的曲率0A K ≠时，我们可以设想在弧的凹方一侧有一个圆周，它与弧在点A 相切 (即有公切线)且半径1/A A R K =. 这样的圆周就称为弧上点A 处的曲率圆；而它的圆心称为弧上点A 处的曲率中心。如图3中那个抛物线在原点O 或点(1,) A a 的曲率圆。请注意，因为曲率有可能是负数(在实际应用中，有时把绝对值A K 称为曲率)，而曲率半径要与曲率保持相同的正负号，所以曲率半径也有可能是负数。保留曲率或曲率半径的正负号，以便说明曲线的弯曲方向。 A B A 0d lim lim d s K s s s θθθ→?→??===? ?

函数的凹凸性与拐点

第16 次理论课教学安排课程名称高等数学课程类型必修课√选修课授课专业授课内容 2.4导数的应用（三）授课学时 2 授课类型理论课√上机课□讨论□习题课□其它□ 教学目的与要求1、理解曲线凹凸性的概念 2、掌握曲线凹凸性的判别方法 3、掌握拐点的求法教学重点、难点重点：曲线的凹凸性与拐点难点：曲线的凹凸性与拐点教学方法以讲授为主，讲练结合教学过程一、问题引入二、讲授新课三、总结及作业布置参考资料（1）《高等数学》夏国斌主编省规划教材、安徽大学出版社（2）《高等数学》程伟主编、孙祖康主审中国科技大学出版社（3）《高等数学》，夏国斌主编，电子科技大学出版社（4）《高等数学学习指导》，吴方庭主编，电子科技大学出版社