补充知识

1.普朗克公式推导

普朗克把黑体看作是由带电的谐振子所组成的, 并假设这些谐振子的能量不能连续变化, 而只能取一些分立的能量值, 它是最小能量0ε的整数倍: 0000,2,3,,,n εεεε , 这些分立的能量值称之为谐振子的能级. 显然, 这样的假设是与经典理论相抵触的, 因为根据经典理论, 振子可能具有的能量不应受任何限制; 而普朗克正是在经典理论中引进这样一个假设后, 才得出了黑体幅射的正确公式. 由经典理论, 振子能量为0n E n ε=的几率与()0exp n kT ε-成比例, 所以振子的平均能量是

0000

0000

exp exp exp exp n n n n n n n E n kT kT E n n kT kT εεεεε∞

∞

==∞

∞

==??

??

-- ?

???

?

?

=

=

????

--

?

?????∑

∑∑∑ (1)

利用公式

20

11,11n

n

n x x x x

x x

∞

==++++=

<-∑

令()0exp x kT ε=-, 把(1)式的分母写成()10[1exp ]kT ε---, 再利用公式

()

2

1

11y ny

ny

y

y

n n d d e

ne

e

dy

dy e

e -∞

∞

----===-

=-

=

--∑∑

令0y kT

ε=

, 把(1)式的分子写成

()

00

2

1kT

kT

e

e εε-

-

-, 所以

()

()000

00

000

2

111

1kT

kT

kT

kT

kT kT

e

e

E e e

e e εεεεεεεεε-

-

-

-

-

=

=

=

---- (2)

再将这个平均能量乘上空腔单位体积内频率ν到d νν+之间的振动数目2

38d c

πνν, 得到黑体辐射

公式

2

381

h kT d d c

e νν

επνρνν=

- (3)

此式与维恩由热力学得出的普遍公式(1)比较, 可以看出0ε必须与振子的固有频率ν成比例.

0h εν=, (4)

比例常数h 称之为普朗克常数, 它的数值由实验得出. 将(4)代入(3)式中, 则普朗克辐射公式写成

3

3

811

h kT h d d c

e νν

πνρνν=

- (5)

公式(5)与实验符合的非常好.

当辐射频率很高, 使得1h kT ν 时, (5)式分母中的1可以略去, 于是得到

3

3

8h kT

h d e d c

ννπνρνν-=

,

这就是维恩公式.

当辐射频率很低, 使得1h kT ν 时, (5)式分母中的指数可以按h kT ν展开,

1h kT h e kT

ν

ν=+

+

,

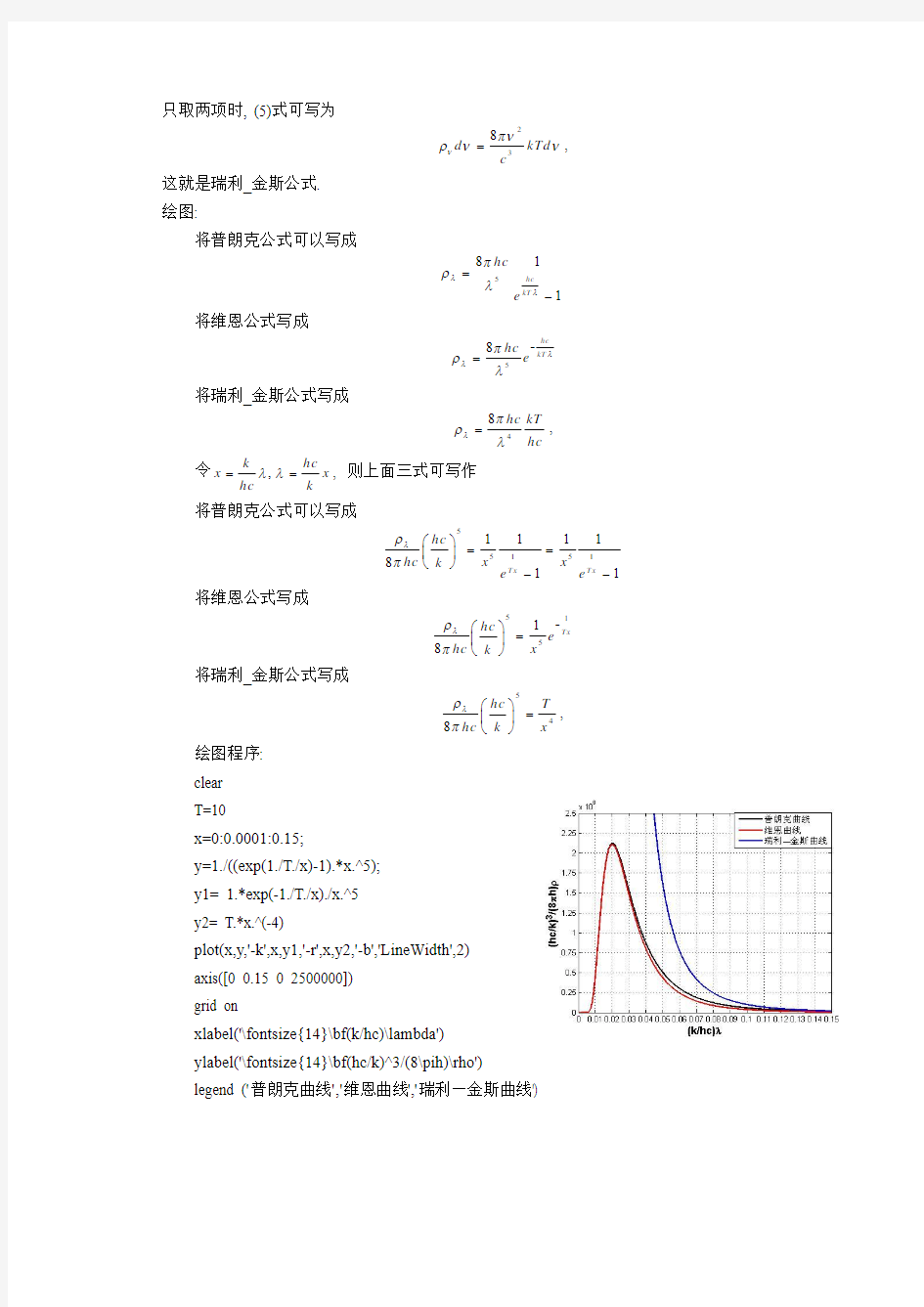
只取两项时, (5)式可写为

2

38d kTd c

νπνρνν=

,

这就是瑞利_金斯公式. 绘图:

将普朗克公式可以写成

5

81

1

hc

kT hc

e λλπρλ

=

-

将维恩公式写成

5

8hc kT hc

e

λ

λπρλ

-

=

将瑞利_金斯公式写成

4

8hc kT

hc

λπρλ

=

,

令,k hc x x

hc

k

λλ=

=

, 则上面三式可写作

将普朗克公式可以写成

5

1

1

5

5

1

1

1181

1

Tx Tx hc hc x

x

k e e λρπ??==

???--

将维恩公式写成

5

1

518Tx

hc e

hc x

k λρπ-??= ??? 将瑞利_金斯公式写成

5

48T

hc hc x

k λρπ??= ???, 绘图程序: clear T=10

x=0:0.0001:0.15;

y=1./((exp(1./T./x)-1).*x.^5); y1= 1.*exp(-1./T./x)./x.^5 y2= T.*x.^(-4)

plot(x,y,'-k',x,y1,'-r',x,y2,'-b','LineWidth',2) axis([0 0.15 0 2500000]) grid on

xlabel('\fontsize{14}\bf(k/hc)\lambda') ylabel('\fontsize{14}\bf(hc/k)^3/(8\pih)\rho') legend ('普朗克曲线','维恩曲线','瑞利—金斯曲线')

clear T=1

x=0:0.001:1.5;

y=1./((exp(1./T./x)-1).*x.^5); y1= 1.*exp(-1./T./x)./x.^5 y2= T.*x.^(-4)

plot(x,y,'-k',x,y1,'-r',x,y2,'-b','LineWidth',2) axis([0 1.5 0 25]) grid on

xlabel('\fontsize{14}\bf(k/hc)\lambda') ylabel('\fontsize{14}\bf(hc/k)^3/(8\pih)\rho') legend ('普朗克曲线','维恩曲线','瑞利—金斯曲线')

2. 康普顿公式推导

以ω 和ω ￠光子在碰揰前和碰揰后的能量，0μ表示粒子的静止质量. 如图2.2所示，设碰揰前光子沿OA 方向运动，动量ωc ；碰揰后沿OB 方向运动,动量为ωc ￠. 碰揰前电子静止于O 点，动量为零；碰揰后电子沿OC 以速度v 运动.根据相对论，电子碰揰后动能为

22

0μc μc

动量为

μv

由于碰揰前后能量守恒，因而有

2

01ωωμc 轾￠=+ (1)

式中βv =，以θ表示OB 与OA 的夹角(散射角)，θ￠表示OC 与OA 夹角，那么动量守恒沿OA

方向和垂直于OA 方向的表示式为

cos μv ωωθθc c

￠￠=+

(2)

0sin ωθθc

￠￠=

-

(3)

由(3)式取平方得出2cos θ￠

()222222222

2

2

2

2

2

0000222

2

2

222

22

2

2

2

002

2

2sin sin 1cos cos 1111cos sin 11μv

μv

μv

μv

ωθθθ

θc

β

β

β

β

μv

μv

ωθθ

β

β

c

￠ⅱ

=

=

-

=

-

----￠￠=

---

ωc

A

图2.2康普顿散射

将(2)式平方之后得

2

22

202cos cos 1μv ωωθθc c β

骣￠÷?￠-=÷?÷÷?桫- 将前式代入得:

222

2

22

2

22

2

2

02222

2

2

22222

2

2

2

2

2

02

222

2

2

2

22

22

2

02

2

2

2

2cos cos sin 12cos sin cos 12cos 1μv

ωωωωωθθθc

c

c β

c

μv

ωωωωωθθθc

c

c

c

β

μv

ωωωωθc

c

c

β

ⅱ +

-=

-

-ⅱ +

+

-=

-ⅱ+

-

=

-

222

22222

02

2cos 1μv c ωωωωθβ

ⅱ+-=

-

2

2

2

2

422222

24

0002

2

2

42

2

2

2

2

2

4002

2cos 112cos 1μv c μc

ωωωωθμc

β

β

μc

ωωωωθμc β

ⅱ+-=

=

---ⅱ+-+=

-

再把 (1)式取平方

(

)

()2

02

2

2

2

0242

2

222

2

2

4

000

2

1

221ωωμc μc ωωμc

μc

ωωωωμc

ωωμc β

轾

￠=+骣÷￠-+=ⅱ +-+-

+=

-

将上面得到的结果联立求解:

()242222222400022422222240022212cos 1μc ωωωωμc ωωμc βμc ωωωωθμc β ì??ⅱ +-+-+=??-?

í??ⅱ?+-+=????

两式相减得:

()2

2

2

0021cos sin

2

ωωθωωθωωμc

μc

￠ⅱ-=

-=

把角频率和波长的关系式22,πc πc ωωλ

λ￠=

=

￠

代入后，

2

2

02

2

022222sin

2

11

212sin

2

πc πc πc πc θλλμc

λλ

πc θλλμc λλ

-=

ⅱ

-

=ⅱ

我们得到波长的变化是

2

04Δsin

2

πθλλλμc

￠=-=

(4)

这公式由康普顿首先得出，由康普顿和吴有训用实验证实.

3.玻尔理论

当电子由参量为m E 的定态跃迁到能量为n E 的定态时, 所吸收或发射的辐射频率ν满足下述关系

()

,n m

E E n m h

ν-=

> (1)

为了确定电子可能运动的轨道, 玻尔提出下面的轨道量子化条件; 设q 是电子的一个广义坐标,

p

是对应的广义动量, 则

pdq nh =? (2)

回路积分是沿轨道积一圈, n 是正整数, 称为量子数.

由玻尔的这些假设很容易求得氢原子的能级. 设电子绕原子核作圆周运动,以a 表示电子的可能运动轨道的半径, 取角位移θ为广义坐标, 则广义动量是2d p a dt

θθμ=. 因为电子在辏力

场中运动, p θ等于常数, 由(2)式得

22

2d p d a

nh dt

π

θθθπμ==?

(3)

根据经典力学, 电子的运动方程是

2

2

2

e d a a dt θμ??= ???

2

22

2

d a

e dt a a θμ

??

????

?????

=???

?

(4) 由(3)和(4)两式消去

d dt

θ, 得到

2

222

22

2

4n h

n a e

e

πμμ=

=

(5)

1n =时, 圆周轨道的半径是

202

a e

μ=

(6)

0a 称为第一玻尔半径. 电子的动能是

2

2

2

1

122e d T a a dt θμ??

== ?

??

, 势能是2

e

U a

=-

, 所以电子的能量为

()2

42

2

1.

1,2,3,22e

e

E T U n a

n μ=+=-

=-

=

电子由量子数为n 的状态跃迁到量子数为()m m n <的状态时, 所发射的辐射频率, 由(1)知是

4

4

22222

21111124e e h n m m n μμνπ????

==-+- ? ?????

这正是巴尔末公式, 里德伯常数42

4e

R μπ=

.

3.固体比热

用普朗克假设也可以解释固体比热. 如果把固体中的原子看作是谐振子, 则由((2)和(4)式, 原子的平均能量为

1

h kT h E e ν

ν

=

-

因而有

()()

2

2

2

1

h kT

h kT

E e h T

kT

e

ν

νν?=

?-

由这式子可以看出每一个原子对比热的贡献

E T

??在温度高时1h kT ν

??

???

为k , 而在温度很低时1h kT ν??

???

趋近于零.