最直观的奇异值分解意义_作用_SVD分解意义

最直观形象的SVD分解
SVD分解(奇异值分解),本应是本科生就掌握的方法,然而却经常被忽视。实际上,SVD分解不但很直观,而且极其有用。SVD分解提供了一种方法将一个矩阵拆分成简单的,并且有意义的几块。它的几何解释可以看做将一个空间进行旋转,尺度拉伸,再旋转三步过程。
首先来看一个对角矩阵,
几何上, 我们将一个矩阵理解为对于点(x, y)从一个平面到另一个平面的映:
射
下图显示了这个映射的效果: 平面被横向拉伸了3倍,纵向没有变化。
对于另一个矩阵
它的效果是
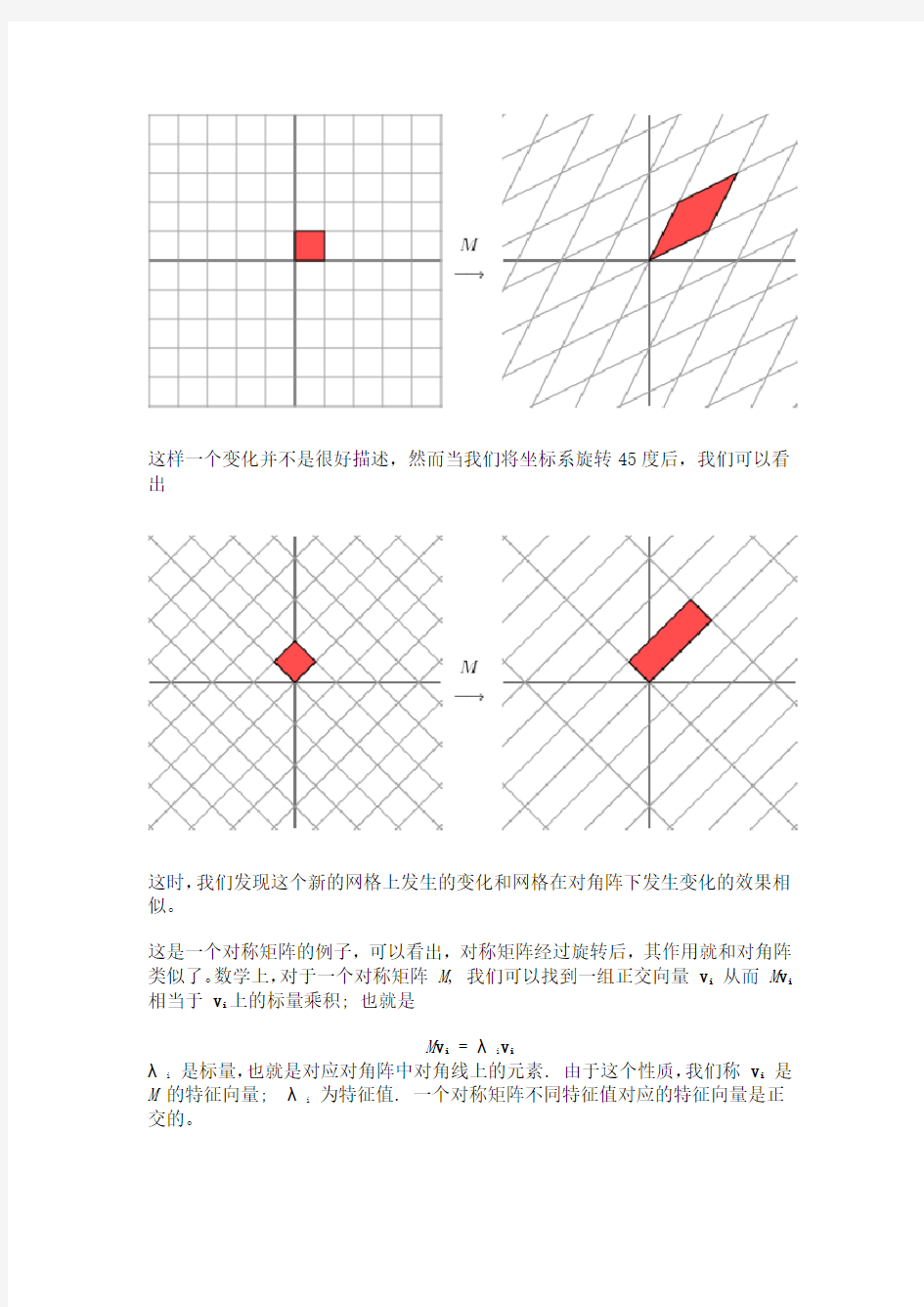
这样一个变化并不是很好描述,然而当我们将坐标系旋转45度后,我们可以看出
这时,我们发现这个新的网格上发生的变化和网格在对角阵下发生变化的效果相似。
这是一个对称矩阵的例子,可以看出,对称矩阵经过旋转后,其作用就和对角阵类似了。数学上,对于一个对称矩阵M, 我们可以找到一组正交向量v i从而M v i 相当于v
i
上的标量乘积; 也就是
M v
i = λ
i
v
i
λi是标量,也就是对应对角阵中对角线上的元素. 由于这个性质,我们称v i是M的特征向量; λ
i
为特征值. 一个对称矩阵不同特征值对应的特征向量是正交的。
对于更广泛的情况,我们看看是否能从一个正交网格转换到另一个正交网格. 考:
虑一个非对称矩阵
这个矩阵的效果形象的称为剃刀(shear)。
这个矩阵将网格在水平方向拉伸了,而垂直方向没有变化。如果我们将网格旋转大约58度,这两个网格就又会都变为正交的了。
奇异值分解:
考虑一个 2 *2 矩阵, 我们可以找到两组网格的对应关系。用向量表示,那就是
当我们选择合适的单位正交向量v
1和v
2
, M v1和M v2也是正交的
.
我们使用u
1
和u
2
代表M v1和M v2的方向. M v1和M v2的长度表示为σ1和σ2,也就是网格在每个方向的拉伸. 这两个拉伸值叫做M的奇异值(sigular value)
和前面类似,我们可以有
M v
1
= σ
1
u
1
M v
2
= σ
2
u
2
我们一直讨论的v
1和v
2
是一对正交向量,对于一般的向量x,我们有这样的
投影关系
x = (v
1x) v
1
+ (v
2
x) v
2
也就是说
M x = (v
1
x) M v1 + (v2x) M v2
M x = (v
1x) σ
1
u
1
+ (v
2
x) σ
2
u
即
M x = u
1σ
1
v
1
T x + u
2
σ
2
v
2
T x ---> M = u
1
σ
1
v
1
T + u
2
σ
2
v
2
T
这个关系可以写成矩阵形式
M = UΣV T
U的列是u
1和u
2
, Σσ
1
和σ
2
构成的对角阵, V的列是v1和v2. 即V
描述了域中的一组正交基,U描述了相关域的另一组正交基,Σ表述了U中的向量与V中向量的拉伸关系。
寻找奇异值分解
奇异值分解可以应用于任何矩阵,对于前面的例子,如果我们加上一个圆,那它会映射成一个椭圆,椭圆的长轴和短轴定义了新的域中的正交网格,可以被表示为M v1 and M v2。
换句话说,单位圆上的函数 |M x| 在v1取得最大值,在v2取得最小值. 这将单位圆上的函数优化问题简化了。可以证明,这个函数的极值点就出现在M T M的特征向量上,这个矩阵一定是对称的,所以不同特征值对应的特征向量v
i
是正交的.
σi = |M v i|就是奇异值, u i是M v i方向的单位向量.
M v
i = σ
i
u
i
M v
j = σ
j
u
j
.
M v
i M v
j
= v
i
T M T M v
j
= v
i
M T M v
j
= λ
j
v
i
v
j
= 0.
也就是
M v
i M v
j
= σ
i
σ
j
u
i
u
j
= 0
因此, u
i 和u
j
也是正交的。所以我们就把一组正交基v
i
变换到了另一组正交
基u
i
.
另一个例子
我们来看一个奇异矩阵(秩为1,或只有一个非零奇异值)
它的效果如下
在这个例子中,第二个奇异值为0,所以 M = u
1σ
1
v
1
T. 也就是说,如果有奇异
值为0,那么这个矩阵就有降维的效果。因为0奇异值对应的维度就不会出现在右边。这对于计算机科学中的数据压缩极其有用。例如我们想压缩下面的15 25 像素的黑白图像
我们可以看出这个图像中只有三种列,即
把图像表示成一个15 25 的矩阵,总共有 375 个元素.
然而当我们做了奇异值分解,会发现非零奇异值仅有3个,
σ1 = 14.72,σ2 = 5.22,σ3 = 3.31
因此,这个矩阵就可以被表示为 M=u1σ1v1T + u2σ2v2T + u3σ3v3T
也就是说我们用三个长度为15的向量v
i ,三个长度为25的向量u
i
,以及三个奇
异值,总共123个数字表示了这个375个元素组成的矩阵。奇异值分解找到了矩阵中的冗余信息实现了降维。
可以看出,奇异值分解捕获了图像中的主要信息。因此,又假设上一个例子里引入了噪声,
当我们用同样的方法做奇异值分解,我们得到如下非零奇异值
σ1= 14.15,σ2= 4.67,σ3= 3.00,σ4= 0.21,σ5= 0.19,...,σ15= 0.05 显然,前三个奇异值比其他的大很多,说明其中包括了绝大部分信息。如果我们只要前三个,
M u
1σ
1
v
1
T + u
2
σ
2
v
2
T + u
3
σ
3
v
3
T
我们就实现了图像的降噪。
Noisy image Improved image
图片和实例来源于https://www.360docs.net/doc/963661273.html,
特征值分解与奇异值分解
特征值:一矩阵A作用与一向量a,结果只相当与该向量乘以一常数λ。即A*a=λa,则a 为该矩阵A的特征向量,λ为该矩阵A的特征值。 奇异值:设A为m*n阶矩阵,A H A的n个特征值的非负平方根叫作A的奇异值。记 (A) 为σ i 上一次写了关于PCA与LDA的文章,PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。在上篇文章中便是基于特征值分解的一种解释。特征值和奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。 在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing) 另外在这里抱怨一下,之前在百度里面搜索过SVD,出来的结果都是俄罗斯的一种狙击枪(AK47同时代的),是因为穿越火线这个游戏里面有一把狙击枪叫做 SVD,而在Google上面搜索的时候,出来的都是奇异值分解(英文资料为主)。想玩玩战争游戏,玩玩COD不是非常好吗,玩山寨的CS有神马意思啊。国内的网页中的话语权也被这些没有太多营养的帖子所占据。真心希望国内的气氛能够更浓一点,搞游戏的人真正是喜欢制作游戏,搞Data Mining的人是真正喜欢挖数据的,都不是仅仅为了混口饭吃,这样谈超越别人才有意义,中文文章中,能踏踏实实谈谈技术的太少了,改变这个状况,从我自己做起吧。 前面说了这么多,本文主要关注奇异值的一些特性,另外还会稍稍提及奇异值的计算,不过本文不准备在如何计算奇异值上展开太多。另外,本文里面有部分不算太深的线性代数的知识,如果完全忘记了线性代数,看本文可能会有些困难。 一、奇异值与特征值基础知识: 特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系,我在接下来会谈到,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧:
奇异值分解的一些特性以及应用小案例
第一部分:预备知识 1.1 矩阵的F-范数与矩阵迹的关系 引理:设m n A R ?∈,令()ij m n A a ?=,则2211 ||||||()()m n T T F ij i j A a tr AA tr A A === ==∑∑;其中,()tr ?定义如下: 令方阵11 12121 22212r r r r rr m m m m m m M m m m ?? ??? ?=???? ?? ,则11221 ()r rr ii i tr M m m m m ==+++=∑ ,即矩阵M 的迹。注意,()tr ?只能作用于方阵。 那么,下面来看下为什么有2211 ||||||()()m n T T F ij i j A a tr AA tr A A === ==∑∑? 首先,22 11 ||||||m n F ij i j A a === ∑∑这个等式是矩阵F-范数的定义,即一个矩阵的F-范数等于矩阵中每个元素的平方和。 其次,因11121212221 2 ()n n ij m n m m mn a a a a a a A a a a a ???????==?? ???? ,则11 2111222212m m T n n mn a a a a a a A a a a ?? ????=?? ? ? ?? ,易得2211 ()()||||||m n T T ij F i j tr AA tr A A a A ==== =∑∑。(T AA 或T A A 的第r 个对角元素等于第r 行或列元素的平方和,所有对角元素之和就是矩阵每个元素的平方和,即有上式成立。)此过程如图1和图2所示。
主成份(PCA)与奇异值分解(SVD)的通俗解释
主成份(PCA)与奇异值分解(SVD)的通俗解释 主成分分析 1.问题描述 在许多领域的研究与应用中,往往需要对反映事物的多个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息,但也在一定程度上增加了数据采集的工作量,更重要的是在大多数情况下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性,同时对分析带来不便。如果分别对每个指标进行分析,分析往往是孤立的,而不是综合的。盲目减少指标会损失很多信息,容易产生错误的结论。 2.过程 主成分分析法是一种数据转换的技术,当我们对一个物体进行衡量时,我们将其特征用向量(a1,a2,a3,...an)进行表示,每一维都有其对应的variance(表示在其均值附近离散的程度);其所有维的variance之和,我们叫做总的variance;我们对物体进行衡量时,往往其特征值之间是correlated的,比如我们测量飞行员时,有两个指标一个是飞行技术(x1),另一个是对飞行的喜好程度(x2),这两者之间是有关联的,即correlated的。我们进行PCA(主成分分析时),我们并
没有改变维数,但是我们却做了如下变换,设新的特征为(x1,x2,x3...,xn); 其中 1)x1的variance占总的variance比重最大; 2)除去x1,x2的variance占剩下的variance比重最大;.... 依次类推; 最后,我们转换之后得到的(x1,x2,...xn)之间都是incorrelated,我们做PCA时,仅取(x1,x2,....xk),来表示我们测量的物体,其中,k要小于n。主成分的贡献率就是某主成分的方差在全部方差中的比值。这个值越大,表明该主成分综合X1,X2,…,XP信息的能力越强。如果前k 个主成分的贡献率达到85%,表明取前k个主成分基本包含了全部测量指标所具有的信息,这样既减少了变量的个数又方便于对实际问题的分析和研究。 注意,当(a1,a2,a3,...an)之间都是incorrelated时,我们就没有做PCA的必要了 数据点在上图所示的方向上进行投影后,数据仍然有着很大的variance,但在下图所示的方向上,投影后的数据的variance就很小。
矩阵分解及其简单应用
矩阵分解是指将一个矩阵表示为结构简单或具有特殊性质若干矩阵之积或之和,大体分为三角分解、分解、满秩分解和奇异值分解.矩阵地分解是很重要地一部分内容,在线性代数中时常用来解决各种复杂地问题,在各个不同地专业领域也有重要地作用.秩亏网平差是测量数据处理中地一个难点,不仅表现在原理方面,更表现在计算方面,而应用矩阵分解来得到未知数地估计数大大简化了求解过程和难度. 矩阵地三角分解 如果方阵可表示为一个下三角矩阵和一个上三角矩阵之积,即,则称可作三角分解.矩阵三角分解是以消去法为根据导出地,因此矩阵可以进行三角分解地条件也与之相同,即矩阵地前个顺序主子式都不为,即.所以在对矩阵进行三角分解地着手地第一步应该是判断是否满足这个前提条件,否则怎么分解都没有意义.矩阵地三角分解不是唯一地,但是在一定地前提下,地分解可以是唯一地,其中是对角矩阵.矩阵还有其他不同地三角分解,比如分解和分解,它们用待定系数法来解求地三角分解,当矩阵阶数较大地时候有其各自地优点,使算法更加简单方便.资料个人收集整理,勿做商业用途 矩阵地三角分解可以用来解线性方程组.由于,所以可以变换成,即有如下方程组:资料个人收集整理,勿做商业用途 先由依次递推求得,,……,,再由方程依次递推求得,,……,. 资料个人收集整理,勿做商业用途 必须指出地是,当可逆矩阵不满足时,应该用置换矩阵左乘以便使地个顺序主子式全不为零,此时有:资料个人收集整理,勿做商业用途 这样,应用矩阵地三角分解,线性方程组地解求就可以简单很多了. 矩阵地分解 矩阵地分解是指,如果实非奇异矩阵可以表示为,其中为正交矩阵,为实非奇异上三角矩阵.分解地实际算法各种各样,有正交方法、方法和方法,而且各有优点和不足.资料个人收集整理,勿做商业用途 .正交方法地分解 正交方法解求分解原理很简单,容易理解.步骤主要有:)把写成个列向量(,,……,),并进行正交化得(,,……,);) 单位化,并令(,,……,),(,,……,),其中;). 这种方法来进行分解,过程相对较为复杂,尤其是计算量大,尤其是阶数逐渐变大时,就显得更加不方便.资料个人收集整理,勿做商业用途 .方法地分解 方法求分解是利用旋转初等矩阵,即矩阵()来得到地,()是正交矩阵,并且(()).()地第行第列 和第行第列为,第行第列和第行第列分别为和,其他地都为.任何阶实非奇异矩阵可通过左连乘()矩阵(乘积为)化为上三角矩阵,另,就有.该方法最主要地是在把矩阵化为列向量地基础上找出和,然后由此把矩阵地一步步向上三角矩阵靠近.方法相对正交方法明显地原理要复杂得多,但是却计算量小得多,矩阵()固有地性质很特别可以使其在很多方面地应用更加灵活.资料个人收集整理,勿做商业用途 .方法地分解 方法分解矩阵是利用反射矩阵,即矩阵,其中是单位列向量,是正交矩阵,.可以证明,两个矩阵地乘积就是矩阵,并且任何实非奇异矩阵可通过连乘矩阵(乘积为)化为上三角矩阵,则.这种方法首要地就是寻找合适地单位列向量去构成矩阵,
SVD奇异值分解
有关SVD奇异值分解的研究 ZDP 有关SVD奇异值分解,主要看了两个方面的内容:1.关于矩阵的SVD分解。 2.SVD所代表的最小二乘问题。主要是为了用SVD求取最小二乘解。 1. 关于矩阵的SVD分解:相当于主成分分析,找出哪些特征比较重要。奇异值的大小代表了左奇异向量和右奇异向量的重要程度。舍弃一些小奇异值对应的向量相当于消除一些没有太大影响的特征,从而提取出矩阵的主要特征。可以用于压缩从而减少内存的使用,以及滤波去噪。 2.关于最小二乘主要参考了网上的一份资料,SVD(奇异值分解)算法及其评估,在附件中可以找到。 这里主要说一下看资料时遇到的问题以及一些注意事项。矩阵的乘法本质上就是进行坐标的变换,由一种坐标系转变为另一种坐标系的过程。由行空间的一组正交基经由A矩阵变换为列空间一组正交基的过程。A?V=U?Σ。A=U?Σ?V T这里U为A的列空间正交基,Σ为奇异值,V为行空间正交基。V中所谓的行空间正交基,是[V1,V2,??,V n],也是列向量的形式。 针对方程组:A?X=b可以理解成X向量经由矩阵A变换成了b向量。同时可以表示成U?Σ?V T?X=b这里要注意是X向量的变换为从右向左的。V T?X为第一次变换,?Σ为第二次变换,?U为第三次变换。 从另一个角度看坐标变换的问题,A?V=U?Σ这个式子可以理解为一组正交基经矩阵A变换成了另一组正交基,这里Σ为缩放因子。 方程组的解X=V?Σ+?U T?b这里由于矩阵A不一定为方阵,引入广义逆的概念将SVD的应用范围进行了推广。 进行SVD的具体数值解法在文章中都有具体的介绍,这里介绍两个比较有意思的公式:A T A=V?ΣTΣ?V T;AA T=U?ΣΣT?U T。其中A T A为对称正定阵,V为A T A的特征向量,U为AA T的特征向量,ΣTΣ=ΣΣT为特征值。 https://www.360docs.net/doc/963661273.html,/s/blog_b1b831150101ey41.html
2019机器学习中的数学 5 强大的矩阵奇异值分解 SVD.doc
机器学习中的数学 5 强大的矩阵奇异 值分解SVD 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 版权声明: 本文由LeftNotEasy发布于本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@https://www.360docs.net/doc/963661273.html, 前言: 上一次写了关于PCA与LDA的文章,PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。在上篇文章中便是基于特征值分解的一种解释。特征值和奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。 在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing) 另外在这里抱怨一下,之前在百度里面搜索过SVD,出来的结果都是俄罗斯的一种狙击枪(AK47同时代的),是因为穿越火线这个游戏里面有一把狙击枪叫做SVD,而在Google上面搜索的时候,出来的都是奇异值分解(英文资料为主)。想玩玩战争游戏,玩玩COD不是非常好吗,玩山寨的CS有神马意思啊。
奇异值分解及其应用
奇异值分解及其应用 This model paper was revised by the Standardization Office on December 10, 2020
PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。特征值和奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。 在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing) 奇异值与特征值基础知识 特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系,我在接下来会谈到,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧: 如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式: 这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式: 其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。我这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵: 它其实对应的线性变换是下面的形式:
奇异值分解
奇异值分解(SVD) --- 几何意义 奇异值分解( The singular value decomposition ) 该部分是从几何层面上去理解二维的SVD:对于任意的 2 x 2 矩阵,通过SVD可以将一个相互垂直的网格(orthogonal grid)变换到另外一个相互垂直的网格。 我们可以通过向量的方式来描述这个事实: 首先,选择两个相互正交的单位向 量v1 和v2, 向量M v1和M v2正交。 u1和u2分别表示M v1和M v2的单位向量, σ1* u1= M v1和σ2* u2= M v2。σ1和σ2分别表示这不同方向向量上的模,也称作为矩阵M的奇异值。
这样我们就有了如下关系式 M v1= σ1u1 M v2= σ2u2 我们现在可以简单描述下经过M线性变换后的向量x 的表达形式。由于向量 v1和v2是正交的单位向量,我们可以得到如下式子: x = (v1x) v1 + (v2x) v2 这就意味着: M x = (v1x) M v1 + (v2x) M v2 M x = (v1x) σ1u1 + (v2x) σ2u2 向量内积可以用向量的转置来表示,如下所示 v x = v T x 最终的式子为 M x = u1σ1v1T x + u2σ2v2T x M = u1σ1v1T + u2σ2v2T 上述的式子经常表示成 M = UΣV T u 矩阵的列向量分别是u1,u2 ,Σ是一个对角矩阵,对角元素分别是对应的σ1和σ2,V 矩阵的列向量分别是v1,v2。上角标T表示矩阵V 的转置。 这就表明任意的矩阵M是可以分解成三个矩阵。V 表示了原始域的标准正交基,u 表示经过M 变换后的co-domain的标准正交基,Σ表示了V 中的向量与u 中相对应向量之间的关系。(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.) 如何获得奇异值分解?( How do we find the singular decomposition? ) 事实上我们可以找到任何矩阵的奇异值分解,那么我们是如何做到的呢?假设在 原始域中有一个单位圆,如下图所示。经过M 矩阵变换以后在co-domain中单位圆会变成一个椭圆,它的长轴(M v1)和短轴(M v2)分别对应转换后的两个标准正交向量,也是在椭圆范围内最长和最短的两个向量。
SVD分解
数学之美之SVD分解2012-07-03 10:48:59 分类:C/C++ 所谓SVD,就是要把矩阵进行如下转换:A = USV T the columns of U are the eigenvectors of the AA T matrix and the columns of V are the eigenvectors of the A T A matrix. V T is the transpose of V and S is a diagonal matrix. By definition the nondiagonal elements of diagonal matrices are zero. The diagonal elements of S are a special kind of values of the original matrix. These are termed the singular values of A. 1 The Frobenius Norm 一个矩阵所有元素的平方和再开方称为这个矩阵的Frobenius Norm。特殊情况下,行矩阵的Frobenius Norm 为该向量的长度 2 计算A转置 A*At At*A
3 计算S 在SVD中,将AAt的特征值从大到小排列,并开方,得到的就是奇异值。 比如上图中,特征值为40,10.因此奇异值为6.32,3.16。矩阵的奇异值有如下特性: a 矩阵的奇异值乘积等于矩阵行列式的值 6.32*3.16 = 20 = |A| b 矩阵A的 Frobenius Norm等于奇异值的平方和的开方 总结一下计算S的步骤:1 计算A T和A T A;2 计算A T A的特征值,排序并开方。 由此可以得到S,下面来看如何计算 U,V T 4 计算V和V T 利用A T A的特征值来计算特征向量
矩阵分解——SVD分解
定义:设A 是m*n 矩阵,A H A 的特征值为0..........121===≥≥≥≥+n r r λλλλλ,则称 )....3,2,1......(r i i i ==λσ为矩阵A 的奇异值, r 为A 的秩。存在m 阶酉矩阵U 和N 阶酉矩阵V ,使得V U A r N r M r r M r N r ???? ?? ??=-?-?--?∑ )()()() (000,其中????? ?????? ?=∑r σσσ.... 2 1 。 在matlab 中的实现为: (1)S=svd(A) -----仅返回A 的奇异值S (2)[U,S,V]=svd(A) ------返回完全的形式 ????? ??????? 128 4 11731062951 构造矩阵 >> A=reshape(1:12,4,3) A = 1 5 9 2 6 10 3 7 11 4 8 12 求矩阵的奇异值 >> S=svd(A) S = 25.4368 1.7226 0.0000 矩阵的分解 >> [U,S,V]=svd(A) U = -0.4036 0.7329 0.4120 0.3609 -0.4647 0.2898 -0.8184 -0.1741 -0.5259 -0.1532 0.4006 -0.7345 -0.5870 -0.5962 0.0057 0.5477 S = 25.4368 0 0 0 1.7226 0 0 0 0.0000 0 0 0 V = -0.2067 -0.8892 0.4082
-0.8298 0.3804 0.4082 在这里我们知道, U*S*V ans = 1.4682 8.8076 -5.2222 2.1852 10.3842 -5.2338 2.9021 11.9609 -5.2455 3.6191 13.5375 -5.2572 其并不为原始的A. 应用:很多情况下,线性方程组Ax=b 没有解,因此我们计算其最小二乘解,即使得||Ax-b||2最小的x ,设A 的SVD 分解为V U A r N r M r r M r N r ???? ?? ?? =-?-?--?∑ )()()() (000, 由于2-范数具有酉不便性,因此||Ax-b||2=b Vx U r N r M r r M r N r -?????? ? ? -?-?--?∑ )()()() (000=b U Vx H r N r M r r M r N r -???? ?? ??-?-?--?∑ )()()() (000,由 此Ax=b 的最小二乘解即是b U Vx H r N r M r r M r N r =???? ?? ?? -?-?--?∑ )()()() (000的最小二乘解。 令Vx y =,b U c H =,c y r N r M r r M r N r =???? ?? ?? -?-?--?∑ )()()() (000的最小二乘解为 ]0....,0,0,,..... ,[ 2 2 11 r r c c c y σσσ=,所以原方程组的最小二乘解为:y V x H =。 示例:求线性方程组?? ?? ? ?????=???????? ??3214232 21 x 构造矩阵 >> A=[1 2;2 3;2 4]; >> b=[1 2 3]'; 判断有无解 >> rank(A) ans = 2 >> rank([A,b]) ans = 3 由于rank(A)!= rank([A,b]),所以方程无解。 求解U,S,V >> [U,S,V]=svd(A) U =
最直观的奇异值分解意义_作用_SVD分解意义
最直观形象的SVD分解 SVD分解(奇异值分解),本应是本科生就掌握的方法,然而却经常被忽视。实际上,SVD分解不但很直观,而且极其有用。SVD分解提供了一种方法将一个矩阵拆分成简单的,并且有意义的几块。它的几何解释可以看做将一个空间进行旋转,尺度拉伸,再旋转三步过程。 首先来看一个对角矩阵, 几何上, 我们将一个矩阵理解为对于点(x, y)从一个平面到另一个平面的映: 射 下图显示了这个映射的效果: 平面被横向拉伸了3倍,纵向没有变化。 对于另一个矩阵 它的效果是
这样一个变化并不是很好描述,然而当我们将坐标系旋转45度后,我们可以看出 这时,我们发现这个新的网格上发生的变化和网格在对角阵下发生变化的效果相似。 这是一个对称矩阵的例子,可以看出,对称矩阵经过旋转后,其作用就和对角阵类似了。数学上,对于一个对称矩阵M, 我们可以找到一组正交向量v i从而M v i 相当于v i 上的标量乘积; 也就是 M v i = λ i v i λi是标量,也就是对应对角阵中对角线上的元素. 由于这个性质,我们称v i是M的特征向量; λ i 为特征值. 一个对称矩阵不同特征值对应的特征向量是正交的。
对于更广泛的情况,我们看看是否能从一个正交网格转换到另一个正交网格. 考: 虑一个非对称矩阵 这个矩阵的效果形象的称为剃刀(shear)。 这个矩阵将网格在水平方向拉伸了,而垂直方向没有变化。如果我们将网格旋转大约58度,这两个网格就又会都变为正交的了。 奇异值分解:
考虑一个 2 *2 矩阵, 我们可以找到两组网格的对应关系。用向量表示,那就是 当我们选择合适的单位正交向量v 1和v 2 , M v1和M v2也是正交的 . 我们使用u 1 和u 2 代表M v1和M v2的方向. M v1和M v2的长度表示为σ1和σ2,也就是网格在每个方向的拉伸. 这两个拉伸值叫做M的奇异值(sigular value) 和前面类似,我们可以有 M v 1 = σ 1 u 1 M v 2 = σ 2 u 2
奇异值分解及其应用
PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。特征值和奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。 在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing) 奇异值与特征值基础知识 特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系,我在接下来会谈到,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧: 特征值
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式: 这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式: 其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。我这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵: 它其实对应的线性变换是下面的形式: 因为这个矩阵M乘以一个向量(x,y)的结果是:
特征值分解及奇异值分解在数字图像中的应用
特征值分解及奇异值分解在数字图像中的应用 摘要:目前,随着科学技术的高速发展,现实生活中有大量的信息用数字进行存储、处理和传送。而传输带宽、速度和存储器容量等往往有限制,因此数据压缩就显得十分必要。数据压缩技术已经是多媒体发展的关键和核心技术。图像文件的容量一般都比较大,所以它的存储、处理和传送会受到较大限制,图像压缩就显得极其重要。当前对图像压缩的算法有很多,特点各异,类似JPEG 等许多标准都已经得到了广泛的应用。本文在简单阐述了矩阵特征值的数值求解理论之后,介绍了几种常用的求解矩阵特征值的方法,并最终将特征值计算应用到图像压缩中。以及奇异值分解(Singular Value Decomposition ,SVD) 。奇异值分解是一种基于特征向量的矩阵变换方法,在信号处理、模式识别、数字水印技术等方面都得到了应用。由于图像具有矩阵结构,有文献提出将奇异值分解应用于图像压缩[2],并取得了成功,被视为一种有效的图像压缩方法。本文在奇异值分解的基础上进行图像压缩。 关键词:特征值数值算法;奇异值分解;矩阵压缩;图像处理 引言 矩阵的特征值计算虽然有比较可靠的理论方法,但是,理论方法只适合于矩阵规模很小或者只是在理论证明中起作用,而实际问题的数据规模都比较大,不太可能采用常规的理论解法。计算机擅长处理大量的数值计算,所以通过适当的数值计算理论,写成程序,让计算机处理,是一种处理大规模矩阵的方法,而且是一种好的方法。常用的特征值数值方法包括幂法、反幂法、雅克比方法、QR 分解法等。其中,幂法适用于求解矩阵绝对值最大的特征值,反幂法适合求解矩阵的逆矩阵的特征值,雅克比方法适合求解对称矩阵的特征值,QR分解法主要使用于求中小型矩阵以及对称矩阵的全部特征值。矩阵乘以一个向量的结果仍是同维数的一个向量。因此,矩阵乘法对应了一个变换,把一个向量变成同维数的另一个向量,变换的效果当然与方阵的构造有密切关系。图像压缩处理就是通过矩阵理论减少表示数字图像时需要的数据量,从而达到有效压缩。数字图像的质量很大程度上取决于取样和量化的取样数和灰度级。取样和量化的结果是一个实际的矩阵。图像压缩是数据压缩技术在数字图像上的应用,它的目的是减少图像数据中的冗余信息从而用更加高效的格式存储和传输数据。图像数据之所以能被压缩,就是因为数据中存在着冗余。图像数据的冗余主要表现为:图像中相邻像素间的相关性引起的空冗余;图像序列中不同帧之间存在相关性引起的时间冗
主成份(PCA)与奇异值分解(SVD)的通俗解释
主成份(PCA)与奇异值分解(SVD)的通俗解释 主成分分析 1.问题描述在许多领域的研究与应用中,往往需要对反映事物的多个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息,但也在一定程度上增加了数据采集的工作量,更重要的是在大多数情况下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性,同时对分析带来不便。如果分别对每个指标进行分析,分析往往是孤立的,而不是综合的。盲目减少指标会损失很多信息,容易产生错误的结论。 2.过程主成分分析法是一种数据转换的技术,当我们对一个物体进行衡量时,我们将其特征用向量(a1,a2,a3,...an )进行表示,每一维都有其对应的variance (表示在其均值附近离散的程度);其所有维的variance 之和,我们叫做总的variance ;我们对物体进行衡量时,往往其特征值之间是correlated 的,比如我们测量飞行员时,有两个指标一个是飞行技术(x1 )另一个是对飞行的喜好程度(x2 ),这两者之间是有关联的,即correlated 的。我们进行PCA (主成分分析时),我们并
没有改变维数,但是我们却做了如下变换,设新的特征为 (x1,x2,x3...,xn ) ; 其中 1)x1 的variance 占总的variance 比重最大; 2)除去x1,x2 的variance 占剩下的variance 比重最大;依次类推; 最后,我们转换之后得到的(x1,x2,...xn) 之间都是incorrelated ,我们做PCA 时,仅取( x1,x2, xk ) ,来表 示我们测量的物体,其中,k要小于n。主成分的贡献率就 是某主成分的方差在全部方差中的比值。这个值越大,表明该主成分综合X1 , X2,…,XP信息的能力越强。如果前k 个主成分的贡献率达到85% ,表明取前k 个主成分基本包含了全部测量指标所具有的信息,这样既减少了变量的个数又方便于对实际问题的分析和研究。 注意,当( a1,a2,a3,...an )之间都是incorrelated 时,我们就没有做PCA 的必要了 数据点在上图所示的方向上进行投影后,数据仍然有着很大的 variance, 但在下图所示的方向上,投影后的数据的variance 就很小。
我所理解的奇异值分解
我所理解的奇异值分解SVD 1、 奇异值与奇异值分解定理 奇异值定理: 设m n A C ?∈,r=rank(A),则一定存在m 阶酉矩阵U 和n 阶酉矩阵V 和对角矩阵1212(,, ,)(1,2,,)r r i diag i r σσσσσσσ∑=≥≥≥=,且,而 ,使得H A U V =∑,称为A 的奇异值分解。 复数域内的奇异值: 设(0)m n H r A C r A A ?∈>,的特征值为1210r r n λλλλλ+≥≥ ≥>=== 则称1,2, ,)i i n σ==为A 的正奇异值;当A 为零矩阵时,它的奇异值都是零。易见,矩阵A 的奇异值的个数等于A 的列数,A 的非零奇异值的个数等于rank(A)。 2、 奇异值分解的理解 奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r 大的奇异值来近似描述矩阵。 r r r T r r r T v u v u v u V U V U A σσσ+++=∑=∑= 222111即A 可表示为r 个秩为一的举证的和,这是A 得奇异值分解的紧凑格式。 3、 奇异值分解特征 奇异值分解的第一个特征是可以降维。A 表示 n 个 m 维向量 ,通过奇异值分解可表示成 m + n 个 r 维向量 ,若A 的秩 r 远远小于 m 和 n ,则通过奇异值分解可以大大降低 A 的维数。可以计算出 ,当 r SVD分解 SVD分解(奇异值分解),本应是本科生就掌握的方法,然而却经常被忽视。实际上,SVD分解不但很直观,而且极其有用。SVD分解提供了一种方法将一个矩阵拆分成简单的,并且有意义的几块。它的几何解释可以看做将一个空间进行旋转,尺度拉伸,再旋转三步过程。 首先来看一个对角矩阵, 几何上, 我们将一个矩阵理解为对于点(x, y)从一个平面到另一个平面的映: 射 下图显示了这个映射的效果: 平面被横向拉伸了3倍,纵向没有变化。 对于另一个矩阵 它的效果是 这样一个变化并不是很好描述,然而当我们将坐标系旋转45度后,我们可以看出 这时,我们发现这个新的网格上发生的变化和网格在对角阵下发生变化的效果相似。 这是一个对称矩阵的例子,可以看出,对称矩阵经过旋转后,其作用就和对角阵类似了。数学上,对于一个对称矩阵M, 我们可以找到一组正交向量v i从而M v i 相当于v i 上的标量乘积; 也就是 M v i = λ i v i λi是标量,也就是对应对角阵中对角线上的元素. 由于这个性质,我们称v i是M的特征向量; λ i 为特征值. 一个对称矩阵不同特征值对应的特征向量是正交的。 对于更广泛的情况,我们看看是否能从一个正交网格转换到另一个正交网格. 考: 虑一个非对称矩阵 这个矩阵的效果形象的称为剃刀(shear)。 这个矩阵将网格在水平方向拉伸了,而垂直方向没有变化。如果我们将网格旋转大约58度,这两个网格就又会都变为正交的了。 奇异值分解: 考虑一个 2 *2 矩阵, 我们可以找到两组网格的对应关系。用向量表示,那就是 当我们选择合适的单位正交向量v 1和v 2 , M v1和M v2也是正交的 . 我们使用u 1 和u 2 代表M v1和M v2的方向. M v1和M v2的长度表示为σ1和σ2,也就是网格在每个方向的拉伸. 这两个拉伸值叫做M的奇异值(sigular value) 和前面类似,我们可以有 M v 1 = σ 1 u 1 M v 2 = σ 2 u 2 SVD分解 SVD分解是LSA的数学基础,本文是我的LSA学习笔记的一部分,之所以单独拿出来,是因为SVD可以说是LSA的基础,要理解LSA必须了解SVD,因此将LSA笔记的SVD一节单独作为一篇文章。本节讨论SVD分解相关数学问题,一个分为 3个部分,第一部分讨论线性代数中的一些基础知识,第二部分讨论SVD矩阵分解,第三部分讨论低阶近似。本节讨论 的矩阵都是实数矩阵。 基础知识 1. 矩阵的秩:矩阵的秩是矩阵中线性无关的行或列的个数 2. 对角矩阵:对角矩阵是除对角线外所有元素都为零的方阵 3. 单位矩阵:如果对角矩阵中所有对角线上的元素都为1,该矩阵称为单位矩阵 4. 特征值:对一个M x M矩阵C和向量X,如果存在λ使得下式成立 则称λ为矩阵C的特征值,X称为矩阵的特征向量。非零特征值的个数小于等于矩阵的秩。 5. 特征值和矩阵的关系:考虑以下矩阵 该矩阵特征值λ 1 = 30,λ2 = 20,λ3 = 1。对应的特征向量 假设V T=(2,4,6) 计算S x V T 有上面计算结果可以看出,矩阵与向量相乘的结果与特征值,特征向量有关。观察三个特征值λ 1 = 30,λ2 = 20,λ 3 = 1,λ3值最小,对计算结果的影响也最小,如果忽略λ3,那么运算结果就相当于从(60,80,6)转变为(60,80,0),这 两个向量十分相近。这也表示了数值小的特征值对矩阵-向量相乘的结果贡献小,影响小。这也是后面谈到的低阶近似 的数学基础。 矩阵分解 1. 方阵的分解 1) 设S是M x M方阵,则存在以下矩阵分解 其中U 的列为S的特征向量,为对角矩阵,其中对角线上的值为S的特征值,按从大到小排列: 2) 设S是M x M 方阵,并且是对称矩阵,有M个特征向量。则存在以下分解 其中Q的列为矩阵S的单位正交特征向量,仍表示对角矩阵,其中对角线上的值为S的特征值,按从大到小排列。最后,Q T=Q-1,因为正交矩阵的逆等于其转置。 2. 奇异值分解 上面讨论了方阵的分解,但是在LSA中,我们是要对Term-Document矩阵进行分解,很显然这个矩阵不是方阵。这时需要奇异值分解对Term-Document进行分解。奇异值分解的推理使用到了上面所讲的方阵的分解。 假设C是M x N矩阵,U是M x M矩阵,其中U的列为CC T的正交特征向量,V为N x N矩阵,其中V的列为C T C的正交特征向量,再假设r为C矩阵的秩,则存在奇异值分解: 其中CC T和C T C的特征值相同,为 Σ为M X N,其中,其余位置数值为0,的值按大小降序排列。以下是Σ的完整数学定义: σi称为矩阵C的奇异值。 用C乘以其转置矩阵C T得: 上式正是在上节中讨论过的对称矩阵的分解。 奇异值分解的图形表示:奇异值分解意义 作用 SVD分解意义
SVD分解
