微积分公式总结

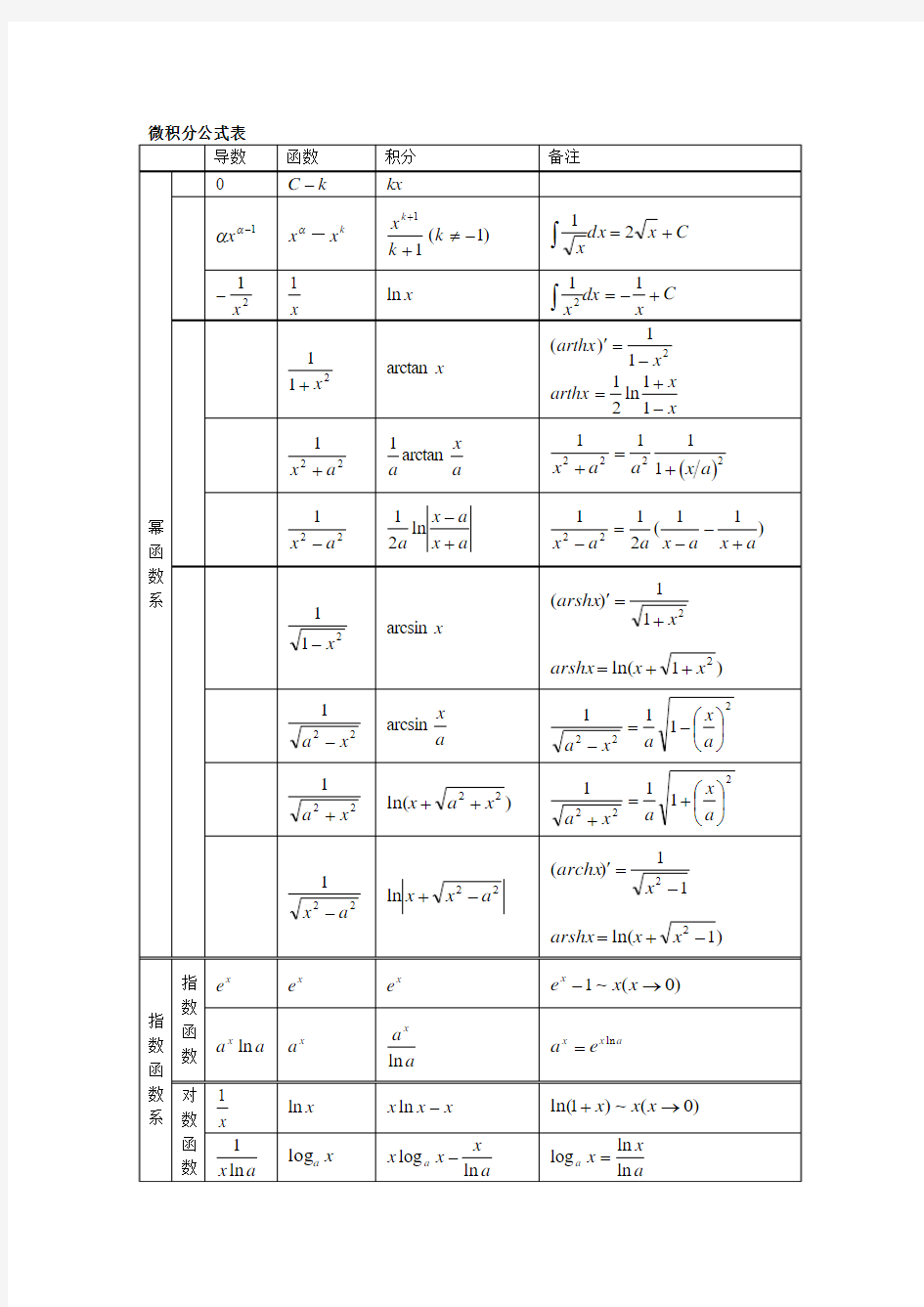
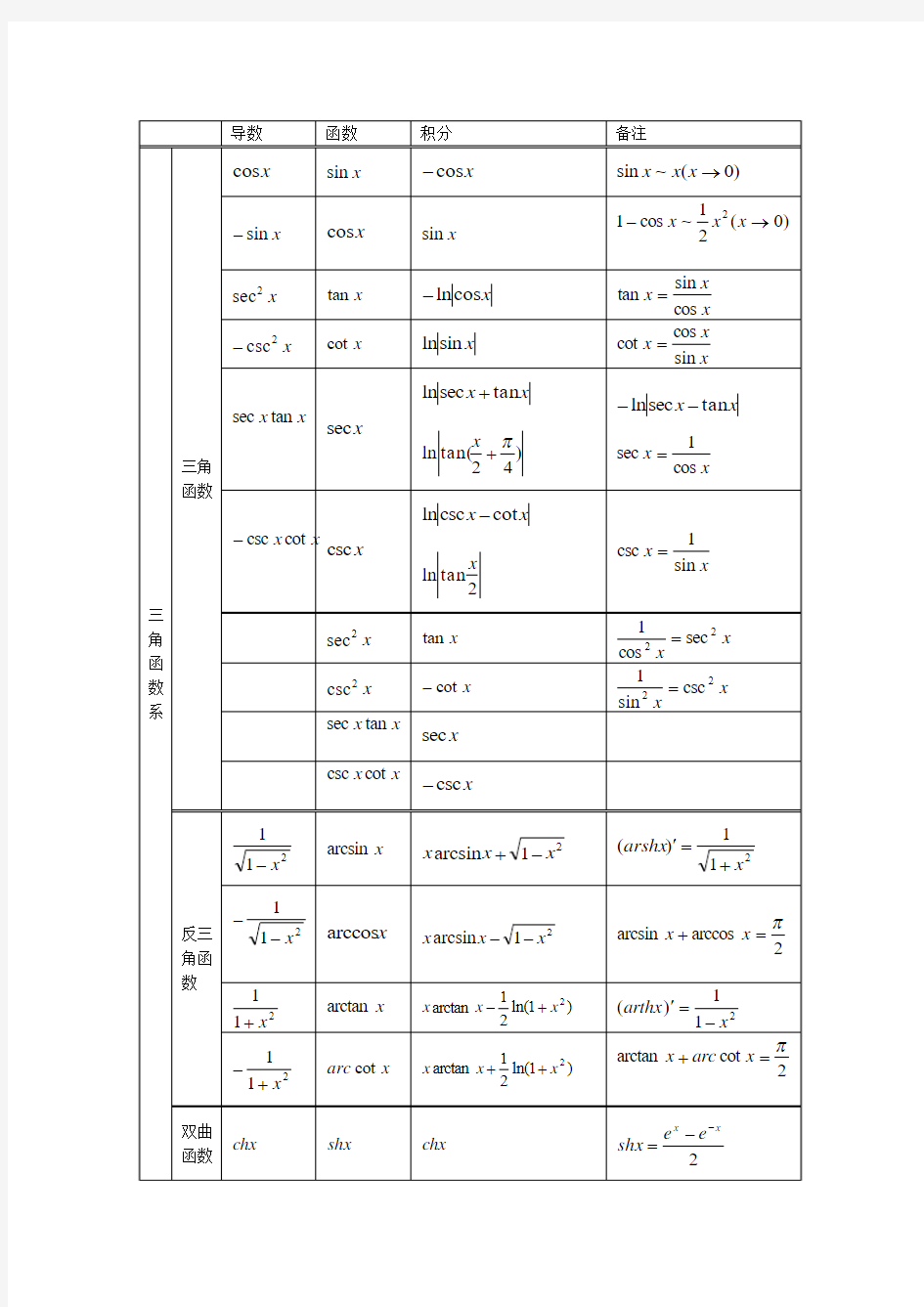
微积分公式表

sin -1(-x) = -sin -1

x cos -1(-x) = π - cos -1

x tan -1(-x) = -tan -1

x cot -1(-x) = π - cot -1

x sec -1(-x) = π - sec -1

x csc -1(-x) = - csc -1

·和差角公式： ·和差化积公式：

·倍角公式：

·半角公式：

αααααααααααα

ααα

cos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 12

cos 12cos 2cos 12

sin -=

+=-+±=+=-=+-±

=+±=-±=ctg tg

·正弦定理：R C

B b A a 2sin sin sin === ·余弦定理：

C ab b a c cos 2222-+=

sin

2sin 2cos cos 2cos

2cos 2cos cos 2sin

2cos 2sin sin 2cos

2sin

2sin sin β

αβαβαβ

αβ

αβα-+=--+=+-+=--+=+α

ββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±?=

±?±=

±=±±=±1

)(1)(sin sin cos cos )cos(sin cos cos sin )sin( α

ααααααααα23333133cos 3cos 43cos sin 4sin 33sin tg tg tg tg --=

-=-=α

αααααααααα

αα22222212221

2sin cos sin 211cos 22cos cos sin 22sin tg tg tg ctg ctg ctg -=

-=-=-==

·反三角函数性质：arcctgx arctgx x x -=

arccos 2

arcsin π

高阶导数公式——莱布尼兹（Leibniz ）公式：

)

()

()()2()1()(0

)

()()

)1()1(!2)1()

(n k k n n n n n

k k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+

'+==---=-∑

中值定理与导数应用：

拉格朗日中值定理。

时，柯西中值定理就是当柯西中值定理：拉格朗日中值定理：x x F f a F b F a f b f a b f a f b f =''=

---'=-)(F )

()

()()()()())(()()(ξξξ

曲率：

;0.)

1(lim M s M M :.,13202a

K a K y y ds d s K M M s

K tg y dx y ds s =='+''==??='?'???=

=''+=→?的圆：半径为直线：点的曲率：弧长。：化量；点，切线斜率的倾角变点到从平均曲率：其中弧微分公式：α

ααα

定积分的近似计算：

???----+++++++++-≈

++++-≈

+++-≈

n n n b

n n b

a n y y y y y y y y n

b x f y y y y n a b x f y y y n

b x f )](4)(2)[(3)(])(2

[)()()(1312420110110 抛物线法：梯形法：矩形法：

级数审敛法：

1.函数定义域的求法：

≠0 , (-∞,0) U (0,+∞)

≥0, [0, +∞ ] ﹥0, (0, +∞) ≠k π+π/2 , k ∈Z y=cotx, D:x ≠k π , k ∈Z y=arcsin(或arccosx) , D: |x|≤1, [-1, 1]

2.常见的偶函数：……

常见的奇函数：……

3.常见的函数周期：sinx , cosx , 其周期T=2π；

tanx , cotx , |sinx| , |cosx| , 其周期 T=π.

4.三个恒等式：π/2 ; arctanx + arccotx = π/2

5.常用的等价形式：当x →0 ㏑(1+ x) ~ x –1 ~ x , 1-cosx ~ (1/2)x ~ (1/n)x

由慢到快由慢到快

7.积分中值定理：若f(x)在[a,b]上连续，则在[a,b]上至少存在一个点ξ使 ∫

f(x)dx=f(ξ)(b-a)

8.微分中值定理：若函数f(x)满足条件：函数f(x)内恒有

f(x)≤f(x)≥在 f ′9.洛尔定理：设函数[a,b]f(a)=f(b)，

则

在(a,b)内至少存在一个ξ，使f ′(ξ)=0

10.拉格朗日中值定理：设函数f(x)满足条件：在闭区间[a,b](a,b)内可

导；f(a)=f(b)，则在(a,b)内至少存在一个ξ， ′(ξ)

散。

存在，则收敛；否则发、定义法：

时，不确定

时，级数发散

时，级数收敛

，则设：、比值审敛法：

时，不确定时，级数发散

时，级数收敛

，则设：别法）：—根植审敛法（柯西判—、正项级数的审敛法n n n n n n n n n n s u u u s U U u ∞

→+∞→∞

→+++=??

??=><=???

??=><=lim ;3111lim 2111lim 1211 ρρρρρρρρ

。的绝对值其余项，那么级数收敛且其和

如果交错级数满足—莱布尼兹定理：—的审敛法或交错级数1113214321,0lim )0,(+∞

→+≤≤?????=≥>+-+-+-+-n n n n n n n n u r r u s u u u u u u u u u u u

绝对收敛与条件收敛：

∑∑∑∑>≤-+++++++++时收敛

１时发散ｐ级数：收敛；

级数：收敛；

发散，而调和级数：为条件收敛级数。收敛，则称发散，而如果收敛级数；肯定收敛，且称为绝对收敛，则如果为任意实数；，其中11

)1(1)1()1()2()1()2()2()1(232121p n p n n n u u u u u u u u p n n n n

希臘字母 (Greek Alphabets)

幂级数：

0)3(lim

)3(111

1111

221032=+∞=+∞

===

≠==><+++++≥-<++++++++∞→R R R a a a a R R x R x R x R x a x a x a a x x x x x x x n n n

n n n n n 时，时，时，的系数，则是，，其中求收敛半径的方法：设称为收敛半径。

，其中时不定

时发散时收敛

，使在数轴上都收敛，则必存收敛，也不是在全

，如果它不是仅在原点　对于级数时，发散

时，收敛于

ρρρ

ρρ

函数展开成幂级数：

+++''+'+===-+=+-++-''+-=∞→++n

n n n n n n n n x n f x f x f f x f x R x f x x n f R x x n x f x x x f x x x f x f !

)0(!2)0()0()0()(00

lim )(,)()!1()

()(!

)()(!2)())(()()(2010)1(00)(2

0000时即为麦克劳林公式：充要条件是：可以展开成泰勒级数的余项：函数展开成泰勒级数：ξ

欧拉公式：

???

????-=+=+=--2sin 2cos sin cos ix ix ix ix ix e e x e e x x i x e 或 e x

=1+x+!22x +!33x +…+!

n x n

+ …

sin x = x-!33x +!55x -!77x +…+)!12()1(1

2+-+n x n n + … cos x = 1-!22x +!44x -!66x +…+)!

2()1(2n x n

n -+ …

ln (1+x) = x-22x +33x -44x +…+)!

1()1(1

+-+n x n n + … tan -1

x = x-33x +55x -77x +…+)

12()1(1

2+-+n x n n + … (1+x)r

=1+r x+!2)1(-r r x 2+!

3)2)(1(--r r r x 3

+… -1

Γ(x) = ?

∞

x-1e -t

d t = 2?

∞

0t 2x-12

t e -d t = ?∞

(ln t

x-1 d t

倒數關係: sin ζcsc ζ=1; tan ζcot ζ=1; cos ζsec ζ=1 商數關係: tan ζ=

θθcos sin ; cot ζ= θ

sin cos 平方關係: cos 2

ζ+ sin 2

ζ=1; tan 2

ζ+ 1= sec 2

ζ; 1+ cot 2

ζ= csc 2

微积分上重要知识点总结

1、常用无穷小量替换 2、关于邻域:邻域的定义、表示(区间表示、数轴表示、简单表示);左右邻域、空心邻域、有界集。 3、初等函数:正割函数sec就是余弦函数cos的倒数;余割函数就是正弦函数的倒数;反三角函数:定义域、值域 4、收敛与发散、常数A为数列的极限的定义、函数极限的定义及表示方法、函数极限的几何意义、左右极限、极限为A的充要条件、极限的证明。 5、无穷小量与无穷大量:无穷小量的定义、运算性质、定理(无穷小量与极限的替换)、比较、高阶无穷小与同阶无穷小的表示、等价无穷小、无穷大量于无穷小量的关系。 6、极限的性质:局部有界性、唯一性、局部保号性、不等式性质(保序性)。 7、极限的四则运算法则。 8、夹逼定理(适当放缩)、单调有界定理(单调有界数列必有极限)。 9、两个重要极限及其变形 10、等价无穷小量替换定理 11、函数的连续性:定义(增量定义法、极限定义法)、左右连续 12、函数的间断点:第一类间断点与第二类间断点,左、右极限都存在的就是第一类间断点,第一类间断点有跳跃间断点与可去间断点。左右极限至少有一个不存在的间断点就是第二类间断点。 13、连续函数的四则运算 14、反函数、复合函数、初等函数的连续性 15、闭区间上连续函数的性质:最值定理、有界性定理、零值定理、介值定理。 16、导数的定义、左右导数、单侧导数、左右导数的表示、可导则连续。 17、求导法则与求导公式:函数线性组合的求导法则、函数积与商的求导法则、反函数的求导法则、复合函数求导法则、对数求导法、基本导数公式 18、隐函数的导数。 19、高阶导数的求法及表示。 20、微分的定义及几何意义、可微的充要条件就是可导。 21、A微分的基本公式与运算法则dy=f’(x0)Δx、

高数积分公式大全

常用积分公式（一）含有ax b +的积分(0a ≠) 1． d x ax b +?＝1 ln ax b C a ++ 2．()d ax b x μ +? ＝ 11 ()(1) ax b C a μμ++++（1μ≠-） 3． d x x ax b +?＝21 (ln )ax b b ax b C a +-++ 4．2d x x ax b +? ＝22311()2()ln 2ax b b ax b b ax b C a ?? +-++++???? 5． d ()x x ax b +?＝1ln ax b C b x +-+ 6． 2d () x x ax b +? ＝ 21ln a ax b C bx b x +-++ 7． 2 d ()x x ax b +?＝21(ln )b ax b C a ax b ++++ 8．22d ()x x ax b +? ＝2 31(2ln )b ax b b ax b C a ax b +-+-++ 9． 2 d () x x ax b +? ＝211ln ()ax b C b ax b b x +-++ 的积分 10． x C + 11．x ?＝2 2 (3215ax b C a - 12．x x ?＝2223 2(15128105a x abx b C a -+ 13． x ? ＝22 (23ax b C a -

14 ． 2x ? ＝222 3 2(34815a x abx b C a -+ 15 ．? (0) (0) C b C b ?+>< 16 ． ? 2a b - 17． d x x ? ＝b ?18 ． x ? ＝2a x -+ （三）含有2 2 x a ±的积分 19． 22d x x a +?=1arctan x C a a + 20． 22d ()n x x a +?=2221222123d 2(1)()2(1)()n n x n x n a x a n a x a ---+-+-+? 21． 22d x x a -?=1ln 2x a C a x a -++ （四）含有2 (0)ax b a +>的积分 22．2d x ax b +? ＝(0) (0) C b C b ?+>+< 23． 2d x x ax b +?＝2 1ln 2ax b C a ++

微积分2方法总结

第七章矢量代数与空间解析几何 ★类型（一）向量的运算解题策略 1. a a a ?=，2.},,{321a a a a = ， .||232221a a a a ++= 3. 利用点积、叉积、混合积的性质及几何意义. ★类型（二）求直线方程解题策略首先考虑直线方程的点向式与一般式，否则再用其它形式. 类型（三）直线点向式与参数式转化类型（四）异面直线 ★类型（五）点到直线的距离、两直线的夹角 ★类型（六）求平面方程解题策略平面方程的点法式、一般式、平面束. 类型（七）直线与平面的位置类型（八）求曲线与曲面方程解题对策一般用定义求曲线与曲面方程疑难问题点拨一般参数方程?? ???===Γ)()()(:t h z t g y t f x 绕Oz 轴旋转所成旋转曲面∑的方程 .)]}([{)]}([{212122z h g z h f y x --+=+ 证如图4-7，设),,(z y x M 是曲面上任意一点，而M 是由曲线Γ上某点),,(1111z y x M （对应的参数为t 1）绕Oz 轴旋转所得到。因此有).(),(),(111111t h z t g y t f x === ,1z z =,2 12122y x y x +=+),()(111z h t t h z -=?=? )]([)],([1111z h g y z h f x --==，故所求旋转曲面方程为.)]}([{)]}([{212122z h g z h f y x --+=+ 特别地，若Γ绕Oz 轴旋转时，且Γ参数方程表示为???==). (),(z g y z f x 则 ).()(2222z g z f y x +=+ 事实上，由前面的证明过程可知),(),(1111z g y z f x ==1z z =，212122y x y x +=+ ),(),(11z g y z f x ==? 故).()(2222z g z f y x +=+ 图4-7

积分公式表,常用积分公式表

积分公式表 1、基本积分公式： (1) (2) (3) (4) (5) (6) (7) (8) (8) (10) (11) 2、积分定理：（1）()()x f dt t f x a ='??????? （2）()()()()[]()()[]()x a x a f x b x b f dt t f x b x a '-'='??????? （3）若F （x ）是f （x ）的一个原函数，则)()()()(a F b F x F dx x f b a b a -==? 3、积分方法 ()()b ax x f +=1；设：t b ax =+

()()222x a x f -=；设：t a x sin = ()22a x x f -=；设：t a x s e c = ()22x a x f +=；设：t a x t a n = ()3分部积分法：??-=vdu uv udv 附：理解与记忆对这些公式应正确熟记.可根据它们的特点分类来记. 公式（1）为常量函数0的积分，等于积分常数. 公式（2）、（3）为幂函数的积分，应分为与 . 当时，，积分后的函数仍是幂函数，而且幂次升高一次. 特别当时，有 . 当时，公式（4）、（5）为指数函数的积分，积分后仍是指数函数，因为，故（，）式右边的是在分母，不在分子，应记清. 当时，有 . 是一个较特殊的函数，其导数与积分均不变.

应注意区分幂函数与指数函数的形式，幂函数是底为变量，幂为常数；指数函数是底为常数，幂为变量.要加以区别，不要混淆.它们的不定积分所采用的公式不同. 公式（6）、（7）、（8）、（9）为关于三角函数的积分，通过后面的学习还会增加其他三角函数公式. 公式（10）是一个关于无理函数的积分公式（11）是一个关于有理函数的积分下面结合恒等变化及不定积分线性运算性质，举例说明如何利用基本积分公式求不定积分. 例1 求不定积分. 分析：该不定积分应利用幂函数的积分公式. 解：（为任意常数）例2 求不定积分. 分析：先利用恒等变换“加一减一”，将被积函数化为可利用基本积分公式求积分的形式.

微积分知识点归纳

知识点归纳 1. 求极限 2.1函数极限的性质P35 唯一性、局部有界性、保号性 P34 A x f x x =→)(lim 0 的充分必要条件是：A x f x f x f x f x x x x == +==-+-→→)()0()()0(lim lim 0 000 2.2 利用无穷小的性质P37：定理1有限个无穷小的代数和仍是无穷小。 0)sin 2(30 lim =+→x x x 定理2有界函数与无穷小的乘积是无穷小。 0)1 sin (20 lim =→x x x 定理3无穷大的倒数是无穷小。反之，无穷小的倒数是无穷大。例如：lim ∞→x 12132335-++-x x x x ∞= , lim ∞→x 131 23523+--+x x x x 0= 2.3利用极限运算法则P41 2.4利用复合函数的极限运算法则P45 2.4利用极限存在准则与两个重要极限P47 夹逼准则与单调有界准则，

lim 0→x x x tan 1=，lim 0→x x x arctan 1=，lim 0→x x x arcsin 1=， lim )(∞→x ?)())(11(x x ??+e =，lim 0 )(→x ?) (1 ))(1(x x ??+e = 2.6利用等价无穷小P55 当0→x 时， x x ~sin ，x x ~tan ， x x ~arcsin ，x x ~arctan ，x x ~)1ln(+， x e x ~，221 ~cos 1x x -，x x αα++1~)1(，≠α0 为常数 2.7利用连续函数的算术运算性质及初等函数的连续性P64 如何求幂指函数)()(x v x u 的极限？P66 )(ln )()()(x u x v x v e x u =，)(ln )()(lim )(lim x u x v x v a x a x e x u →=→ 2.8洛必达法则P120 lim a x →)() (x g x f )() (lim x g x f a x ''=→ 基本未定式：00，∞∞ ，其它未定式 ∞?0，∞-∞，00，∞1，0∞（后三个皆为幂指函数） 2. 求导数的方法 2.1导数的定义P77： lim 00|)(→?==='='x x x dx dy x f y x x f x x f x y x ?-?+ =??→?) ()(000lim h x f h x f h ) ()(000lim -+=→

高数微积分公式大全总结的比较好

高数微积分公式大全总结的比较好 Last revised by LE LE in 2021

高等数学微积分公式大全一、基本导数公式 ⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=? ⑻()csc csc cot x x x '=-? ⑼()x x e e '= ⑽()ln x x a a a '= ⑾()1 ln x x '= ⑿()1 log ln x a x a '= ⒀( )arcsin x '= ⒁( )arccos x '= ⒂()21arctan 1x x '= + ⒃()2 1arccot 1x x '=-+⒄()1x '= ⒅ ' = 二、导数的四则运算法则三、高阶导数的运算法则（1）()()() () () ()() n n n u x v x u x v x ±=±???? （2）()() ()()n n cu x cu x =???? （3）()()() ()n n n u ax b a u ax b +=+???? （4）()()() () ()()()0 n n n k k k n k u x v x c u x v x -=?=???? ∑ 四、基本初等函数的n 阶导数公式（1）() () !n n x n = （2）() () n ax b n ax b e a e ++=? (3)() () ln n x x n a a a = (4)()() sin sin 2n n ax b a ax b n π??+=++??? ??? ?? (5) ()()cos cos 2n n ax b a ax b n π??+=++??? ????? (6)() () () 1 1! 1n n n n a n ax b ax b +??? =- ? +?? + (7) ()() () ()() 1 1! ln 1n n n n a n ax b ax b -?-+=-???? + 五、微分公式与微分运算法则 ⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx = ⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =- ⑺()sec sec tan d x x xdx =? ⑻()csc csc cot d x x xdx =-? ⑼()x x d e e dx = ⑽()ln x x d a a adx = ⑾()1 ln d x dx x =

微积分心得范文

微积分心得范文微积分学习心得学号11120472 姓名吴心怡班级七班学号11120471 姓名吴亚男班级七班时间，如同轨道上疾驰的列车，匆匆行驶，不留一点痕迹的我们的寒假就这样over掉了了。恍惚之间，我们就要开始正式上课了。我们依稀还记得，放假前，老师们说让好好复习，来学校不久便是冬季学期的期末考试了，可是，嘿嘿~~自己却不得不承认有很大一部分的时间是被荒废了的。但早早来学校，我们好好静下心来思考了一下学习的经验和方法。突然有了要好好学习的冲动，可能以前真的是我们对学习不够上心的缘故吧。对于学习方面，以前我总觉得数学一直处于主心骨的位置，它是我从小的梦想、我的骄傲。可是自从大学以来的第一个学期，微积分却着实让我们倍受打击。成绩的不再拔尖，沉痛的打击了我的自信心。但是，通过和老师交流，与同学讨论，让我明白强中自有强中手，而自己，并不是笨，只是有些方面自己做的不够，只要深切去思考自己的学习方法，自己依旧有很大的进步空间。首先我们觉得大学里的学习课后巩固很重要，光靠一周两次大课的学习，远远不够。并且，课上老师可能会因为进度问题而降得很快，很多时候我们会跟不上老师的速度，这时，如果课后不再看老师局的

例题，课上的疑问会永远得不到解答。在此情况下谈想进步是不可能的。然而课后的巩固应该从两方面着手，一方面是教学大纲上要求必须掌握的内容，这些是考试必考内容，或许看似很简单的内容，确实解题目的最基本的基础。秋季学期的期末考正是由于自己对基本知识忽略，在一些很简单的题目丢了分，惨痛的教训给了哦我们深刻的教训，夯实基础知识，才能维纳最重要的考试打下良好的基础。另一方面。是自己认为在内容掌握上的盲点和误区，这些事最容易忘记的，也是应用熟练程度最差的。而考试不会因为这是自己认为的难点就会不考，所以认真钻研这些题目便可为自己在分数上的突破起决定性作用。同时，复习一定要有耐心，要持之以恒。学习上最大的忌讳便是三天打鱼两天晒网，这样的学习不会有任何收获。知识既然学习了，我们就要好好消化，不能让它成为大脑中的脂肪。周期性的复习才不会使大脑一片空白，一周一次或两周一次，可以根据自己的记忆力而定，以适合自己的为基准便可以。

(完整版)高等数学常用公式大全

高数常用公式平方立方： 22222222 332233223223332233222(1)()()(2)2()(3)2()(4)()()(5)()()(6)33()(7)33()(8)222(a b a b a b a ab b a b a ab b a b a b a b a ab b a b a b a ab b a a b ab b a b a a b ab b a b a b c ab bc ca -=+-++=+-+=-+=+-+-=-+++++=+-+-=-+++++= 21221)(9)()(),(2) n n n n n n a b c a b a b a a b ab b n ----++-=-++++≥L 三角函数公式大全两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1 -cotAcotB + cot(A-B) =cotA cotB 1 cotAcotB -+ 倍角公式 tan2A =A tan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3 π -a) 半角公式 sin( 2 A )=2cos 1A - cos( 2 A )=2cos 1A + tan( 2 A )=A A cos 1cos 1+- cot(2 A )=A A cos 1cos 1-+ tan( 2 A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2 b a -

微积分基础知识总结以及泰勒公式

§3.3 泰勒公式常用近似公式，将复杂函数用简单的一次多项式函数近似地表示，这是一个进步。当然这种近似表示式还较粗糙（尤其当较大时），从下图可看出。上述近似表达式至少可在下述两个方面进行改进： 1、提高近似程度，其可能的途径是提高多项式的次数。 2、任何一种近似，应告诉它的误差，否则，使用者“ 心中不安”。将上述两个想法作进一步地数学化：对复杂函数，想找多项式来近似表示它。自然地，我们希望尽可能多地反映出函数所具有的性态 —— 如：在某点处的值与导数值；我们还关心的形式如何确定；近似所产生的误差。【问题一】设在含的开区间内具有直到阶的导数，能否找出一个关于的次多项式近似 ? e x x x x x ≈+≈1,sin ()充分小 x f x ()p x n ()p x n () f x ()p x n () p x n () f x ()R x f x p x n n ()()() =-f x ()x 0n +1() x x -0n ) ,,1,0()()() 1()()()()(0)(0) (0202010n k x f x p x x a x x a x x a a x p k k n n n n ==-++-+-+=且f x ()

【问题二】若问题一的解存在，其误差的表达式是什么? 一、【求解问题一】问题一的求解就是确定多项式的系数。 …………… 上述工整且有规律的求系数过程，不难归纳出： R x f x p x n n ()()() =-a a a n 01,,, p x a a x x a x x a x x n n n ()()()()=+-+-++-0102020 ∴=a p x n 00() '=+-+-++--p x a a x x a x x na x x n n n ()()()()1203020123 ∴ ='a p x n 10() ''=??+???-+???-++?-??--p x a a x x a x x n n a x x n n n ()()()()()213243123040202 ∴ ??=''2120a p x n () '''=???+????-+????-++?-?-??--p x a a x x a x x n n n a x x n n n ()()()()()()3214325431234050203 ∴???='''32130a p x n ()

高等数学积分公式大全

创作编号： GB8878185555334563BT9125XW 创作者：凤呜大王* 常用积分公式（一）含有ax b +的积分(0a ≠) 1． d x ax b +?＝1 ln ax b C a ++ 2．()d ax b x μ +? ＝ 11 ()(1) ax b C a μμ++++（1μ≠-） 3． d x x ax b +?＝21 (ln )ax b b ax b C a +-++ 4．2d x x ax b +? ＝22311()2()ln 2ax b b ax b b ax b C a ?? +-++++???? 5． d ()x x ax b +?＝1ln ax b C b x +-+ 6． 2 d () x x ax b +? ＝21ln a ax b C bx b x +-++ 7． 2 d ()x x ax b +?＝21(ln )b ax b C a ax b ++++ 8．22 d ()x x ax b +?＝2 31(2ln )b ax b b ax b C a ax b +-+-++

9． 2 d () x x ax b +? ＝211ln ()ax b C b ax b b x +-++ 的积分 10 ． x ? C + 11 ．x ? ＝2 2 (3215ax b C a - 12 ．x x ? ＝2223 2(15128105a x abx b C a -++ 13 ． x ? ＝22 (23ax b C a - 14 ． 2x ? ＝222 3 2(34815a x abx b C a -++ 15 ．? (0) (0) C b C b ?+>< 16 ． ? ＝2a bx b -- 17 ． x ? ＝b ?18． 2d x x ? ＝2a + （三）含有2 2 x a ±的积分 19． 22d x x a +?=1arctan x C a a +

积分公式大全

2 常用积分公式（一）含有ax b +的积分(0a ≠) 1．d x ax b +?＝1 ln ax b C a ++ 2．()d ax b x μ +?＝1 1() (1)ax b C a μμ++++（1μ≠-） 3．d x x ax b +?＝2 1(ln )ax b b ax b C a +-++ 4 5 6．2 d () x x ax b +?＝2 1ln a ax b C bx b x +-++ 7．2 d ()x x ax b +?＝2 1(ln )b ax b C a ax b ++++ 8． 2 2d ()x x ax b +?＝ 2 31(2ln )b ax b b ax b C a ax b +-+-++ 9．2 d () x x ax b +?＝2 11ln ()ax b C b ax b b x +-++ 的积分 10 ．x ?＝ C 11 ．x ?＝2 2(3215ax b C a -

4 22 23．2 d x x ax b +?＝2 1ln 2ax b C a ++ 24． 2 2d x x ax b +?＝2 d x b x a a ax b -+? 25．2d () x x ax b +? ＝ 2 21ln 2x C b ax b ++ 26．2 2 d ()x x ax b +?＝2 1d a x bx b ax b --+? 27．32d () x x ax b +? ＝ 2222 1ln 22ax b a C b x bx +-+ 28．2 2 d ()x ax b +?＝2 2 1d 2()2x x b ax b b ax b +++? （五）含有2 ax bx c + +(0) a >的积分 29．2 d x ax bx c ++?＝ 22(4) (4) C b ac C b ac +<+> 30．2 d x x ax bx c ++? ＝2 21d ln 22b x ax bx c a a ax bx c ++- ++? (0) a >的积分 31．＝1 arsh x C a +＝ln(x C +

大学微积分1方法总结

第一章函数、极限、连续注 “★”表示方法常用重要. 一、求函数极限的方法 ★1.极限的四则运算；★2.等价量替换；★3.变量代换；★4.洛比达法则；★5.重要极限；★6.初等函数的连续性；7.导数的定义；8. 利用带有佩亚诺余项的麦克劳林公式；9.夹逼定理；10利用带有拉格朗日余项的泰勒公式；11.拉格朗日定理；★12. 无穷小量乘以有界量仍是无穷小量等. ★二、已知函数极限且函数表达式中含有字母常数，确定字母常数数值的方法运用无穷小量阶的比较、洛必达法则或带有佩亚诺余项的麦克劳林公式去分析问题，解决问题。三、无穷小量阶的比较的方法利用等价无穷小量替换或利用洛必达法则，无穷小量的等价代换或利用带有皮亚诺余项的佩亚诺余项公式展开四、函数的连续与间断点的讨论的方法如果是)(x f 初等函数，若)(x f 在0x x =处没有定义，但在0x 一侧或两侧有定义，则0x x =是间断点，再根据在0x x =处左右极限来确定是第几类间断点。如果)(x f 是分段函数，分界点是间断点的怀疑点和所给范围表达式没有定义的点是间断点。

五、求数列极限的方法 ★1.极限的四则运算；★2. 夹逼定理；★3. 单调有界定理； 4. )()(lim )()(lim ∞=?∞=∞ →+∞→A n f A x f n x ；5. 数列的重要极限；6.用定积分的定义求数列极限；7. 利用若∑∞ =1n n a 收敛，则0lim =∞→n n a ；8. 无穷小量乘以有界量仍是无穷小量；9.等价量替换等. 【评注】1. 数列的项有多项相加或相乘式或∞→n 时，有无穷项相加或相乘，且不能化简，不能利用极限的四则运算， 2.如果数列的项用递推关系式给出的数列的收敛性或证明数列极限存在，并求极限.用单调有界定理 3.对数列极限的未定式不能用洛比达法则。因为数列作为函数不连续，更不可导，故对数列极限不能用洛比达法则. 4.由数列{}n a 中的通项是n 的表达式，即).(n f a n =而)(lim )(lim x f n f x n ∞ →∞→与是特殊与一般的关系，由归结原则知 ★5. 有lim 1011()()n n i i f f x dx n n →∞ ==?∑或1lim 1001()()n n i i f f x dx n n -→∞==?∑ 第二章一元函数微分学 ★一、求一点导数或给处在一点可导推导某个结论的方法：利用导数定义，经常用第三种形式二、研究导函数的连续性的方法：

5.2 微积分基本公式-习题

1．设函数0 cos x y tdt = ?，求'(0)y ，'()4 y π。【解】由题设得'()cos y x x =，于是得 '(0)cos01y ==，'()cos 4 4 2 y ππ == 。 2．计算下列各导数： ⑴20x d dx ?；【解】20x d dx ?2)x =2= ⑵ 1t d dt dx ；【解】1t d dt dx 1 ()t d dt dx =-=-=。 ⑶ cos 2 sin cos()x x d t dt dx π?；【解】cos 2sin cos()x x d t dt dx π?0cos 2 2sin 0[cos()cos()]x x d t dt t dt dx ππ=+?? 》 0cos 22 sin 0cos()cos()x x d d t dt t dt dx dx ππ= +?? sin cos 2200 [cos()]cos()x x d d t dt t dt dx dx ππ=-+?? 22cos(sin )(sin )cos(cos )(cos )d d x x x x dx dx ππ=-+ 22cos(sin )cos cos[(1sin )](sin )x x x x ππ=-+-- 22cos(sin )cos cos(sin )sin x x x x πππ=--- 22cos(sin )cos cos(sin )sin x x x x ππ=-+ 2cos(sin )(sin cos )x x x π=-。 ⑷2ln 1 x x d dt dx t ?。【解】 2ln 1x x d dt dx t ?21ln 11 1[]x x d dt dt dx t t =+?? 21ln 111x x d d dt dt dx t dx t =+?? …

微积分公式与定积分计算练习大全

微积分公式与定积分计算练习（附加三角函数公式）一、基本导数公式 ⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=? ⑻()csc csc cot x x x '=-? ⑼ ()x x e e '= ⑽ ()ln x x a a a '= ⑾ ()1 ln x x '= ⑿ () 1log ln x a x a '= ⒀ ( )arcsin x '= ⒁( )arccos x '= ⒂ ()21arctan 1x x '=+ ⒃() 21arccot 1x x '=-+⒄()1 x '= ⒅ '= 二、导数的四则运算法则 ()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v ''' -??= ??? 三、高阶导数的运算法则（1）()()() () () () () n n n u x v x u x v x ±=±??? ? （2）()() ( ) ()n n cu x cu x =??? ? （3）()() () ()n n n u ax b a u ax b +=+??? ? （4） ()()() ( ) ()() ()0 n n n k k k n k u x v x c u x v x -=?=???? ∑ 四、基本初等函数的n 阶导数公式（1） ()() ! n n x n = （2） ()() n ax b n ax b e a e ++=? (3) ()() ln n x x n a a a = (4) ()() sin sin 2n n ax b a ax b n π??+=++??? ??? ??(5) ()()cos cos 2n n ax b a ax b n π??+=++??? ???? ? (6) () () () 1 1! 1n n n n a n ax b ax b +???=- ?+?? + (7) ()() () ()() 1 1! ln 1n n n n a n ax b ax b -?-+=-???? + 五、微分公式与微分运算法则

常用微积分公式大全

常用微积分公式大全 Company number：【0089WT-8898YT-W8CCB-BUUT-202108】

常用微积分公式基本积分公式均直接由基本导数公式表得到，因此，导数运算的基础好坏直接影响积分的能力，应熟记一些常用的积分公式. 因为求不定积分是求导数的逆运算,所以由基本导数公式对应可以得到基本积分公式.。 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11)

对这些公式应正确熟记.可根据它们的特点分类来记. 公式（1）为常量函数0的积分，等于积分常数. 公式（2）、（3）为幂函数的积分，应分为与. 当时，，积分后的函数仍是幂函数，而且幂次升高一次. 特别当时，有. 当时，公式（4）、（5）为指数函数的积分，积分后仍是指数函数，因为，故（，）式右边的是在分母，不在分子，应记清. 当时，有. 是一个较特殊的函数，其导数与积分均不变. 应注意区分幂函数与指数函数的形式，幂函数是底为变量，幂为常数；指数函数是底为常数，幂为变量.要加以区别，不要混淆.它们的不定积分所采用的公式不同. 公式（6）、（7）、（8）、（9）为关于三角函数的积分，通过后面的学习还会增加其他三角函数公式.

公式（10）是一个关于无理函数的积分公式（11）是一个关于有理函数的积分下面结合恒等变化及不定积分线性运算性质，举例说明如何利用基本积分公式求不定积分. 例1 求不定积分. 分析：该不定积分应利用幂函数的积分公式. 解：（为任意常数）例2 求不定积分. 分析：先利用恒等变换“加一减一”，将被积函数化为可利用基本积分公式求积分的形式. 解：由于，所以（为任意常数）例3 求不定积分.

微积分知识点小结

第一章函数一、本章提要基本概念函数，定义域，单调性，奇偶性，有界性，周期性，分段函数，反函数，复合函数，基本初等函数，初等函数第二章极限与连续一、本章提要 1.基本概念函数的极限，左极限，右极限，数列的极限，无穷小量，无穷大量，等价无穷小，在一点连续，连续函数，间断点，第一类间断点（可去间断点，跳跃间断点），第二类间断点. 2.基本公式 (1) 1sin lim =→口口口， (2) e ) 11(lim 0 =+ →口口口 (口代表同一变量). 3.基本方法 ⑴ 利用函数的连续性求极限； ⑵ 利用四则运算法则求极限； ⑶ 利用两个重要极限求极限； ⑷ 利用无穷小替换定理求极限； ⑸ 利用分子、分母消去共同的非零公因子求 0形式的极限； ⑹ 利用分子，分母同除以自变量的最高次幂求∞ ∞形式的极限； ⑺ 利用连续函数的函数符号与极限符号可交换次序的特性求极限； ⑻ 利用“无穷小与有界函数之积仍为无穷小量”求极限. 4.定理左右极限与极限的关系，单调有界原理，夹逼准则，极限的惟一性，极限的保号性，极限的四则运算法则，极限与无穷小的关系，无穷小的运算性质，无穷小的替换定理，无穷小与无穷大的关系，初等函数的连续性，闭区间上连续函数的性质. 第三章导数与微分一、本章提要 1. 基本概念

瞬时速度，切线，导数，变化率，加速度，高阶导数，线性主部，微分． 2.基本公式基本导数表，求导法则，微分公式，微分法则，微分近似公式． 3.基本方法 ⑴利用导数定义求导数； ⑵利用导数公式与求导法则求导数； ⑶利用复合函数求导法则求导数； ⑷隐含数微分法； ⑸参数方程微分法； ⑹对数求导法； ⑺利用微分运算法则求微分或导数．第四章微分学的应用一、本章提要 1. 基本概念未定型,极值点,驻点,尖点,可能极值点,极值,最值,曲率,上凹,下凹,拐点,渐近线,水平渐近线,铅直渐近线． 2.基本方法 ⑴用洛必达法则求未定型的极限； ⑵函数单调性的判定； ⑶单调区间的求法； ⑷可能极值点的求法与极大值（或极小值）的求法； ⑸连续函数在闭区间上的最大值及最小值的求法； ⑹求实际问题的最大（或最小）值的方法； ⑺曲线的凹向及拐点的求法； ⑻曲线的渐近线的求法； ⑼一元函数图像的描绘方法． 3. 定理柯西中值定理,拉格朗日中值定理,罗尔中值定理, 洛必达法则,函数单调性的判定定理,极值的必要条件,极值的第一充分条件,极值的第二充分条件,曲线凹向的判别法则．第五章不定积分一、本章提要 1. 基本概念原函数，不定积分． 2.基本公式

高等数学一微积分考试必过归纳总结要点重点

高等数学(一)微积分一元函数微分学( 第三章、第四章) 一元函数积分学（第五章）第一章函数及其图形第二章极限和连续多元函数微积分（第六章）高数一串讲教材所讲主要内容如下：全书内容可粗分为以下三大部分：第一部分函数极限与连续（包括级数）第二部分导数及其应用（包括多元函数）第三部分积分计算及其应用（包括二重积分和方程）第一部分函数极限与连续一、关于函数概念及特性的常见考试题型： 1、求函数的自然定义域。 2、判断函数的有界性、周期性、单调性、奇偶性。 3、求反函数。 4、求复合函数的表达式。二、极限与连续常见考试题型： 1、求函数或数列的极限。 2、考察分段函数在分段点处极限是否存在，函数是否连续。

3、函数的连续与间断。 4、求函数的渐进线。 5、级数的性质及等比级数。 6、零点定理。每年必有的考点第三部分导数微分及其应用常见考试题型： 1、导数的几何意义； 2、讨论分段函数分段点的连续性与可导性。 3、求函数的导数：复合函数求导，隐含数求导，参数方程求导； 4、讨论函数的单调性和凹凸性，求曲线的拐点； 5、求闭区间上连续函数的最值； 6、实际问题求最值。每年必有的考点第四部分积分计算及应用考试常见题型 1、不定积分的概念与计算； 2、定积分的计算； 3、定积分计算平面图形的面积； 4、定积分计算旋转体的体积； 5、无穷限反常积分 6、二重积分 7、微分方程最近几年考题中，积分计算的题目较多，而且也有一定的难度。第一部分函数极限与连续一、关于函数概念及特性的常见考试题型： 1、求函数的自然定义域。 2、判断函数的有界性、周期性、单调性、奇偶性。 3、求反函数。 4、求复合函数的表达式。 log log x的定义域是___________. 2007.7 例1..函数y= 23 知识点：定义域

微积分总结下册

微积分(B II)总结 chapteｒ8 多元函数微分学８、1 多元函数的极限先瞧极限就是否存在(一个方向组(ｙ=kx)或两个方向趋近于极限点(给定方向必须当x满足极限过程时,ｙ也满足极限过程))。如果存在,能先求的先求,能用等价无穷小替换的就替换,最后考虑夹逼准则。 8、２偏导数点导数定义(多用于分段函数的分界点) f x (x,y)=lim D x?0 f(x +D x,y )-f(x ,y ) D x f xx (x ,y )=lim D x?0 f x (x +D x,y )-f x (x ,y ) D x 例:求f(x,y)=f x (0,0) ,就就是求分段函数的点偏导数 f(x,y)在(x 0,y )连续,但偏导数不一定存在(如:锥) 8.３全微分函数可微,则偏导数必存在(逆否命题可证明函数不可微,证明时,把右边前两项移到左边,瞧它就是不就是r的高阶无穷小) D z=?z ?x D x+ ?z ?y D y+o(r) dz=?z ?x dx+ ?z ?y dy

例: 对于某一点处的全微分,也可能要用到点导数。 8、４多元复合函数求导 8、4、1链式求导法则 z(x,y)=f(u(x,y),v(x,y)) ?z ?x = ?f ?u ?u ?x + ?f ?v ?v ?x

链式求导法则要求函数对每个中间变量求偏导,乘以中间变量对自变量求偏导。而所谓函数对第一中间变量求偏导就就是说另外把两个中间变量瞧做不变。小心:中间变量要带入,例: (在计算z对u的偏导时,相当于把v,t瞧做不变) 这里的u,ｖ要带入(第三行),并且z就是具体的函数,所以在对中间变量求偏导数时,偏导数可以求出来 8、4.２隐函数求偏导全微分性质的不变性例: ①用全微分形式的不变性两边同时取全微分,相当于(-xy)为中间变量,求出全微分后,直接出偏导

常用积分公式

常用积分公式（一）含有ax b +的积分(0a ≠) 1．d x ax b +?＝1 ln ax b C a ++ 2．()d ax b x μ +?＝1 1()(1)ax b C a μμ++++（1μ≠-） 3．d x x ax b +?＝21 (ln )ax b b ax b C a +-++ 4．2d x x ax b +?＝22 311()2()ln 2ax b b ax b b ax b C a ??+-++++???? 5．d ()x x ax b +?＝1ln ax b C b x +-+ 6．2d ()x x ax b +?＝2 1ln a ax b C bx b x +-++ 7．2d ()x x ax b +?＝2 1(ln )b ax b C a ax b ++++ 8．22d ()x x ax b +?＝231(2ln )b ax b b ax b C a ax b +-+-++ 9．2d ()x x ax b +?＝2 11ln ()ax b C b ax b b x +-++

的积分 10 ．x ? C 11 ．x ? ＝2 2 (3215ax b C a -+ 12 ．x x ? ＝2223 2(15128105a x abx b C a -+ 13 ． x ＝2 2(23ax b C a - 14 ． 2x ＝22232(34815a x abx b C a -++ 15 ．＝(0) (0) C b C b ? +>< 16 ． ? 2a b - 17 ． x ＝b 18 ． x ＝ 2a + （三）含有22 x a ±的积分

微积分基本公式

微积分公式

tan -1 x = x-33x +55x -7 7 x +…+)12()1(12+-+n x n n + … (1+x)r =1+r x+!2)1(-r r x 2+! 3)2)(1(--r r r x 3 +… -1