截长补短法填辅助线拔高练习
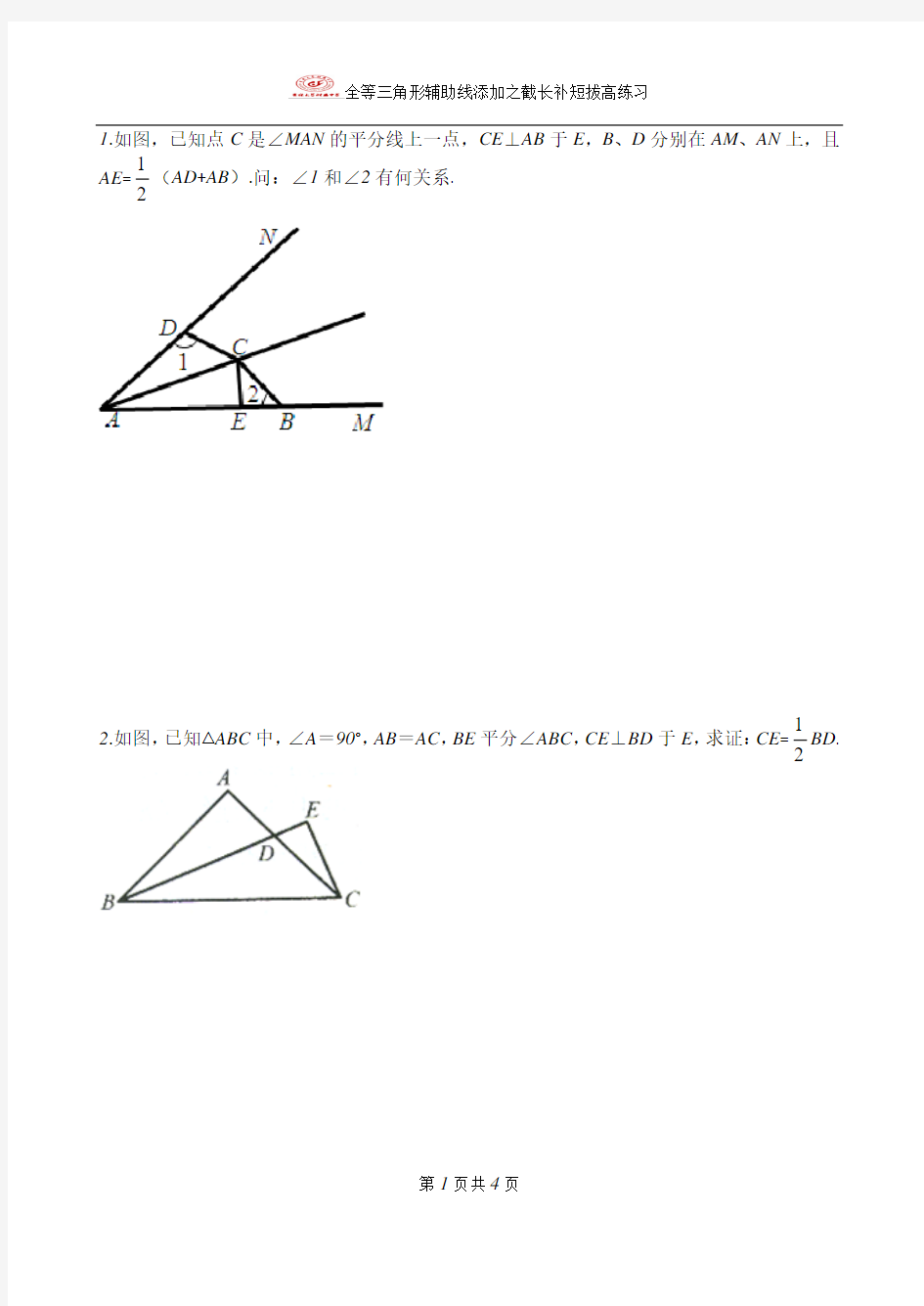

1.如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且
AE=1
2
(AD+AB).问:∠1和∠2有何关系.
2.如图,已知△ABC中,∠A=90°,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE=1
2 BD.
3. 如图,已知正方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE =DF.
4.如图,已知四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE恰好平分∠ABC,判断AB的长与AD+BC的大小关系并证明.
5.如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,判断AC的长与AE+CD 的大小关系并证明.
6.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,且EG∥AB交CB于G,判断CF与GB的大小关系并证明。
7.△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.
【精品】几何必会模型:截长补短辅助线模型带答案
【精品文档,百度专属】 本文为word版资料,可以任意编辑修 本文为word版资料,可以任意编辑修 截长补短辅助线模型 模型:截长补短 如图①,若证明线段AB、CD、EF之间存在EF=AB +CD,可以考虑截长补短法. 截长法:如图②,在EF上截取EG=AB,再证明GF =CD即可. 补短法:如图③,延长AB至H点,使BH=CD,再证 明AH=EF即可. 模型分析 截长补短的方法适用于求证线段的和差倍分关系. 截长,指在长线端中截取一段等于已知的线段;补短,指将一条短线端延长,延长部分等于已知线段. 该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程. 模型实例 例1:如图,已知在△ABC中,∠C=2∠B,∠1=∠2 .求证:AB=AC+CD . 证法一,截长法: 如图①,在AB上取一点E,使AE=AC,连接DE. ∵AE=AC,∠1=∠2,AD=AD, ∴△ACD≌△AED , ∴CD=DE,∠C=∠3 . ∵∠C=2∠B, ∴∠3=2∠B=∠4+∠B , ∴∠4=∠B , ∴DE=BE , ∴CD=BE. ∵AB=AE+BE, ∴AB=AC+CD .
证法二,补短法: 如图②,延长AC到点E,使CE=CD,连接DE . ∵CE=CD,∴∠4=∠E . ∵∠3=∠4+∠E,∴∠3=2∠E . ∵∠3=2∠B,∴∠E=∠B . ∵∠1=∠2,AD=AD, ∴△EAD≌△BAD,∴AE=AB. 又∵AE=AC+CE, ∴∴AB=AC+CD . 例2:如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD . 求证:AO+BO=2CO . 证明:在线段AO上取一点E,使CE=AC,连接DE . ∵CD=CD,DC⊥OA, ∴△ACD≌△ECD, ∴∠A=∠CED . ∵∠A=∠GBD , ∴∠CED=∠GBD , ∴1800-∠CED=1800-∠GBD , ∴∠OED=∠OBD . ∵OD平分∠AOB, ∴∠AOD=∠BOD . ∵OD=OD, ∴△OED≌△OBD , ∴OB=OE, ∴AO+BO=AO+OE=OE+2CE+OE=OE+CE+OE+CE=2(CE+OE)=2CO .
全等三角形辅助线系列之三截长补短类辅助线作法大全
全等三角形辅助线系列之三 与截长补短有关的辅助线作法大全 一、截长补短法构造全等三角形 截长补短法,是初中数学几何题中一种辅助线的添加方法,也是把几何题化难为易的一种思想.所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段等于已知的两条较短线段中的一条,然后证明其中的另一段与已知的另一条线段相等;所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等,然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后,使之构成某种特定的三角形进行求解. 截长补短法作辅助线,适合于证明线段的和、差、倍、分等类的题目. 典型例题精讲 【例1】 如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度 数. 【解析】法一:如图所示,延长AB 至E 使BE BD =,连接ED 、EC . 由AC AB BD =+知AE AC =, 而60BAC ∠=?,则AEC ?为等边三角形. 注意到EAD CAD ∠=∠,AD AD =,AE AC =, 故AED ACD ??≌. 从而有DE DC =,DEC DCE ∠=∠, 故2BED BDE DCE DEC DEC ∠=∠=∠+∠=∠. 所以20DEC DCE ∠=∠=?,602080ABC BEC BCE ∠=∠+∠=?+?=?. 法二:在AC 上取点E ,使得AE AB =,则由题意可知CE BD =. 在ABD ?和AED ?中,AB AE =,BAD EAD ∠=∠,AD AD =, 则ABD AED ??≌,从而BD DE =, 进而有DE CE =,ECD EDC ∠=∠, AED ECD EDC ∠=∠+∠=2ECD ∠. 注意到ABD AED ∠=∠,则: 13 18012022 ABC ACB ABC ABC ABC BAC ∠+∠=∠+∠=∠=?-∠=?, 故80ABC ∠=?. 【答案】见解析.
常见辅助线作法
正确熟练地掌握辅助线的作法和规律,也是迅速解题的关键,如何准确地作出需要的辅助线,简单介绍几种方法: 方法一:从已知出发作出辅助线: 例1.已知:在△ABC 中,AD 是BC 边的中线,E 是AD 的中点,F 是BE 延长线与 AC 的交点,求证:AF=FC 2 1 分析:题设中含有D 是BC 中点,E 是AD 中点,由此可以联想到三角形中与边中点有密 切联系的中位线,所以,可有如下2种辅助线作法: (1)过D 点作DN ∥CA ,交BF 于N ,可得N 为BF 中点,由中位线定理得 DN=FC 21,再证△AEF ≌△DEN ,则有AF=DN ,进而有AF=FC 2 1 (2)过D 点作DM ∥BF ,交AC 于M ,可得FM=CM ,FM=AF ,则有AF=FC 2 1 方法二:分析结论,作出辅助线 例2:如图,AD 是△ABC 的高,AE 是△ABC 的外接圆直径, 求证:AB ·AC=AE ·AD 分析:要证AB ·AC=AE ·AD ,需证 AC AE AD AB = (或AC AD AE AB =),需证△ABE ∽△ADC (或△ABD ∽△AEC ), 这就需要连结BE (或CE ),形成所需要的三角形,同时得 ∠ABE=∠ADC=900 (或∠ADB=∠ACE=900 )又∠E=∠C (或∠B=∠E 因而得证。 方法三:“两头凑”(即同时分析已知和结论)作出辅助线 例3:过△ABC 的顶点C 任作一直线,与边AB 及中线AD 分别交于点F 和E ; 求证:AE ∶ED=2AF ∶FB 分析:已知D 是BC 中点,那么在 三角形中可过中点作平行线得中位线; 若要出现结论中的AE ∶ED ,则应有一条与EF D 点作DM ∥EF 交AB 于M ,可得 FM AF FM AF ED AE 22==证BF=2FM
初中几何常见辅助线作法口诀及习题大全
人说几何很困难,难点就在辅助线。辅助线,如何添?把握定理和概念。还要刻苦加钻研,找出规律凭经验。三角形 图中有角平分线,可向两边作垂线。也可将图对折看,对称以后关系现。角平分线平行线,等腰三角形来添。角平分线加垂线,三线合一试试看。线段垂直平分线,常向两端把线连。要证线段倍与半,延长缩短可试验。三角形中两中点,连接则成中位线。三角形中有中线,延长中线等中线。四边形 平行四边形出现,对称中心等分点。梯形里面作高线,平移一腰试试看。平行移动对角线,补成三角形常见。证相似,比线段,添线平行成习惯。等积式子比例换,寻找线段很关键。直接证明有困难,等量代换少麻烦。斜边上面作高线,比例中项一大片。
作辅助线的方法一:中点、中位线,延线,平行线。如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的。二:垂线、分角线,翻转全等连。如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生。其对称轴往往是垂线或角的平分线。三:边边若相等,旋转做实验。如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生。其对称中心,因题而异,有时没有中心。故可分“有心”和“无心”旋转两种。四:造角、平、相似,和、差、积、商见。如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关。在制造两个三角形相似时,一般地,有两种方法:第一,造一个辅助角等于已知角;第二,是把三角形中的某一线段进行平移。故作歌诀:“造角、平、相似,和差积商见。”托列米定理和梅叶劳定理的证明辅助线分别是造角和平移的代表)五:两圆若相交,连心公共弦。如果条件中出现两圆相交,那么辅助线往往是连心线或公共弦。六:两圆相切、离,连心,公切线。如条件中出现两圆相切(外切,切),或相离(含、外离),那么,辅助线往往是连心线或外公切线。七:切线连直径,直角与半圆。如果条件中出现圆的切线,那么辅助线是过切点的直径或半径使出现直角;相反,条件中是圆的直径,半径,那么辅助线是过直径(或半径)端点的切线。即切线与直径互为辅助线。如果条件中有直角三角形,那么作辅助线往往是斜边为直径作辅助圆,或半圆;相反,条件中有半圆,那么在直径上找圆周角——直角为辅助线。即直角与半圆互为辅助线。八:弧、弦、弦心距;平行、等距、弦。如遇弧,则弧上的弦是辅助线;如遇弦,则弦心距为辅助线。如遇平行线,则平行线间的距离相等,距离为辅助线;反之,亦成立。如遇平行弦,则平行线间的距离相等,所夹的弦亦相等,距离和所夹的弦都可视为辅助线,反之,亦成立。有时,圆周角,弦切角,圆心角,圆角和圆外角也存在因果关系互相联想作辅助线。九:面积找底高,多边变三边。如遇求面积,(在条件和结论中出现线段的平方、乘积,仍可视为求面积),往往作底或高为辅助线,而两三角形的等底或等高是思考的关键。如遇多边形,想法割补成三角形;反之,亦成立。另外,我国明清数学家用面积证明勾股定理,其辅助线的做法,即“割补”有二百多种,大多数为“面积找底高,多边变三边”。
全等三角形作辅助线专题一重点截长补短法可
D C B A E D F C B A 全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转”. 3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________. 2:如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小. 3:如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE. E D C B A 中考应用: 以ABC ?的两边AB、AC为腰分别向外作等腰Rt ABD ?和等腰Rt ACE ?,90, BAD CAE ∠=∠=? 连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC ?为直角三角形时,AM与DE的位置关系是,线段AM与DE的数量关系是; (2)将图①中的等腰Rt ABD ?绕点A沿逆时针方向旋转?θ(0<θ<90)后,如图②所示,(1)
初中几何常见辅助线作法口诀
初中几何常见辅助线作法口诀 人说几何很困难,难点就在辅助线。辅助线,如何添?把握定理和概念。还要刻苦加钻研,找出规律凭经验。 三角形 图中有角平分线,可向两边作垂线。也可将图对折看,对称以后关系现。角平分线平行线,等腰三角形来添。角平分线加垂线,三线合一试试看。线段垂直平分线,常向两端把线连。要证线段倍与半,延长缩短可试验。三角形中两中点,连接则成中位线。三角形中有中线,延长中线等中线。四边形 平行四边形出现,对称中心等分点。梯形里面作高线,平移一腰试试看。平行移动对角线,补成三角形常见。证相似,比线段,添线平行成习惯。等积式子比例换,寻找线段很关键。直接证明有困难,等量代换少麻烦。斜边上面作高线,比例中项一大片。 圆 半径与弦长计算,弦心距来中间站。圆上若有一切线,切点圆心半径连。切线长度的计算,勾股定理最方便。要想证明是切线,半径垂线仔细辨。是直径,成半圆,想成直角径连弦。弧有中点圆心连,垂径定理要记全。圆周角边两条弦,直径和弦端点连。弦切角边切线弦,同弧对角等找完。要想作个外接圆,各边作出中垂线。还要作个内接圆,内角平分线梦圆如果遇到相交圆,不要忘作公共弦。内外相切的两圆,经过切点公切线。若是添上连心线,切点肯定在上面。要作等角添个圆,证明题目少困难。辅助线,是虚线,画图注意勿改变。假如图形较分散,对称旋转去实验。基本作图很关键,平时掌握要熟练。解题还要多心眼,经常总结方法显。切勿盲目乱添线,方法灵活应多变。分析综合方法选,困难再多也会减。虚心勤学加苦练,成绩上升成直线。
作辅助线的常用方法
在利用三角形三边关系证明线段不等关系时,如直接证不出 来,可连接两点或廷长某边构成三角形,使结论中出现的线段在一个或几个三角形中,再运用三角形三边的不等关系证明,如: 例1、 已知如图1-1:D 、E 为△ABC 内两点, 求证:AB+AC>BD+DE+CE. 证明:(法一) 将DE 两边延长分别交AB 、AC 于M 、N , 在△AMN 中,AM+AN > MD+DE+NE;(1) 在△BDM 中,MB+MD>BD ; (2) 在△CEN 中,CN+NE>CE ; (3) 由(1)+(2)+(3)得: AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE ∴AB+AC>BD+DE+EC (法二:图1-2) 延长BD 交 AC 于F ,廷长CE 交BF 于G , 在△ABF 和△GFC 和△GDE 中有: AB+AF> BD+DG+GF (三角形两边之和大于第三边)…(1) GF+FC>GE+CE (同上)………………………………..(2) DG+GE>DE (同上)…………………………………….(3) 由(1)+(2)+(3)得: AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE ∴AB+AC>BD+DE+EC 。 一、 在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时,可连接两 点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理: 例如:如图2-1:已知D 为△ABC 内的任一点,求证:∠BDC>∠BAC 。 因为∠BDC 与∠BAC 不在同个三角形中,没有直接的联系,可适当添加辅助线构造新的三角形,使∠BDC 处于在外角的位置,∠BAC 处于 在内角的位置; 证法一:延长BD 交AC 于点E ,这时∠BDC 是△EDC 的外角, A B C D E N M 1 1-图A B C D E F G 2 1-图A B C D E F G 1 2-图
截长补短模型(几何解题模型)
初中几何典型解题模型 中考看数学,数学看几何.在中考科目中,数学最能体现差距;在数学中,几何是拉开数学的重中之重。《初中几何典型解题模型》希望帮助同学们解决“几何”这一痛点难点.学习几何,如果采用题海战术,忽视技巧和方法总结,往往事倍功半,收效甚微.本书在分析海量中考几何试题的基础上,总结解题方法与技巧,整理出中考中最高频的十二类几何模型,为每个模型打造“模型分析+典型例题+练习巩固”三部分内容: 模型分析——认识经典模型、识别模型,给出经典模型对应的结论,提供解析与证明. 典型例题——精选经典例题,匹配经典模型,利用模型进行实战应用 练习——依托题库大数据,经典模型高度匹配练习,每一道练习都是经典题,是模型实例黄金搭档. 本书定位于成绩中等及偏上学生,在高度、深度和难度上都接近中考,帮助同学们解决中考常见难点,有效提高做题效率。
目录 第一章8字模型与飞标模型 【模型2:角的飞镖模型】 【模型3:边的8字模型】 【模型4:边的飞镖模型】 第二章角平分线四大模型 【模型1:角平分线上的点向两边做垂线】【模型2:截取构造对称全等】 【模型3:角平分线+垂线构造等腰三角形】【模型4:角平分线+平行线构造等腰三角形】第三章截长补短模型 【模型:截长补短模型】 第四章手拉手模型 【模型:手拉手模型】 第五章三垂直全等模型 【模型:三垂直全等模型】 第六章将军饮马模型 【模型1:定直线与两定点】 【模型2:角与定点】 【模型3:两定点一定长】 第七章蚂蚁行程模型 【模型:角的飞镖模型】
第八章中点四大模型 【模型1:倍长中线或与中线有关的线段构造全等三角形】【模型2:等腰三角形底边中点与顶角连接用“三线合一”】【模型3:倍长中线或与中线有关的线段构造全等三角形】【模型4:已知直角三角形斜边中点,考虑构造斜边中线】第九章半角模型 【模型:半角模型】 第十章相似模型 【模型1:A、8模型】 【模型2:共边共角型】 【模型3:一线三等模型】 【模型4:倒数型】 【模型5:与圆有关的简单相似】 【模型6:相似与旋转】 第十一章圆中的辅助线 【模型1:连半径构造等腰三角形】 【模型2:构造直角三角形】 【模型3:与圆的切线有关的辅助线】 第十二章辅助圆 【模型1:共端点、等线段模型】 【模型2:直角三角形共斜边模型】 附:巩固练习解析
几何证明中常用辅助线——中线倍长法及截长补短
来源:网络转载 几何证明中常用辅助线 (一)中线倍长法: 例1、求证:三角形一边上的中线小于其他两边和的一半。 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE. 3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF (二)截长补短法 教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补 D A B C M T E A B C D 图1-1
短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .求证:∠BAD + ∠BCD =180°. 分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺 ? ? ?==BP BP PD PE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD . N 图3-1 P 1 2 N A B C D E 图3-2
∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE . 在Rt △APE 与Rt △CPD 中, ?? ? ??=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180° 例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2. 求证:AB =AC +CD . (三)其它几种常见的形式: 1、有角平分线时,通常在角的两边截取相等的线段,构造全等三角形。 例1、如图1:已知AD 为△ABC 的中线,且∠1=∠2,∠3=∠4,求证:BE +CF >EF. 2、有以线段中点为端点的线段时,常延长加倍此线段,构造全等三角形。 A B C D E F N 1 图123 4 C A 12
(完整版)相似三角形中几种常见的辅助线作法(有辅助线)
相似三角形中几种常见的辅助线作法 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种: 一、添加平行线构造“A ”“X ”型 例1:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,求:BE :EF 的值. 解法一:过点D 作CA 的平行线交BF 于点P ,则 ∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE :EF=5:1. 解法二:过点D 作BF 的平行线交AC 于点Q , ∴BE :EF=5:1. 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T , ∵BD=2DC ∴ ∴BE :EF=5:1. 变式:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点, 连结BE 并延 长交AC 于F, 求AF :CF 的值. 解法一:过点D 作CA 的平行线交BF 于点P , 解法二:过点D 作BF 的平行线交AC 于点Q , 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T , , 1==AE DE FE PE ,2==DC BD PF BP ,则2==EA DA EF DQ ,3==DC BC DQ BF , EF EF EF EF DQ EF BF BE 563=-=-=-=,则DC CT DT 2 1 ==;TC BT EF BE =, DC BT 2 5=
例2:如图,在△ABC的AB边和AC边上各取一点D和E,且使AD=AE, DE延长线与BC延长线相交于F ,求证: (证明:过点C作CG//FD交AB于G) 例3:如图,△ABC中,AB 2.截长补短 1.已知ACB ?,B ACB ∠=∠,D ,E 分别是AB 及AC 延长线上的一点,且BD CE =,连接DE 交底BC 于G ,求证GD GE =. 答案:见解析 解析: 解法1: 过E 作EF AB ∥,交BC 的延长线于F ,则=B F ∠∠ ∵3=4∠∠,3=B ∠∠,4B ∴∠=∠ ∴4=F ∠∠,∴CE =CF , 在GEF ?与GDB ?中, 12DB CE EF B F ∠=∠?? ==??∠=∠? ∴GFE GBD ??≌AAS () G E D C B A 1 2 43 F K C G E D B A ∴G DG =E 解法2: 过D 点作DK AC ∥交BC 于K , 过D 点作DF BC ∥交AC 于F , ∴四边形DKCF 是平行四边形, ∴DK =FC ,1ACB ∠=∠, ∵B ACB ∠=∠,∴1B ∠=∠, ∴DB =DK =CE =CF , ∴C 是EF 中点,又∵BC DF ∥, ∴G 是DE 中点,∴DG =EG 2.如图所示,在ABC △中,100A ∠=?,40ABC ∠=?,BD 是ABC ∠的平分线,延长 BD 至E ,使DE AD =.求证:BC AB CE =+ 答案:见解析 1F K C G E D B A E D C A 解析: 在BC 上取一点F ,使得BF BA =,连接DF , ∵BD 是ABC ∠的平分线,∴ABD FBD ∠=∠, 在ADB △与FDB △中, ABD FB BF BA BD BD D =?=∠=∠? ??? ∴ADB FDB △≌△(SAS), ∴DF AD =, 又∵DA DE =, ∴DF DE = ∵100A ∠=?,AB AC = ∴40ABC ∠=? ∵BD 是ABC ∠的平分线, ∴20ABD ∠=? ∴60ADB FDB ∠=∠=?, ∵60CDE ADB ∠=∠=?, ∴60FDC EDC ∠=∠=?, 在DCF △与DCE △中, F E D C A 五种辅助线助你证全等 姚全刚 在证明三角形全等时有时需添加辅助线,对学习几何证明不久的学生而言往往是难点?下面介绍证明全等时常见的五种辅助线,供同学们学习时参考. 一、截长补短 一般地,当所证结论为线段的和、差关系,且这两条线段不在同一直线上时,通常可以考虑用 截长补短的办法:或在长线段上截取一部分使之与短线段相等;或将短线段延长使其与长线段相等. 例1.如图1,在△ ABC 中,/ ABC=60 ° , AD、CE 分别平分/ BAC、/ ACB .求证: AC=AE+CD . 分析:要证AC=AE+CD , AE、CD不在同一直线上.故在AC上截取AF=AE,则只要证明 CF=CD . 证明:在AC上截取AF=AE,连接OF. ?/ AD、CE 分别平分/ BAC、/ ACB,/ ABC=60 ° ???/ 1 + Z 2=60 ° ,A Z 4=Z 6= / 1 + Z 2=60 ° . 显然,△ AEO ◎△ AFO,?/ 5= / 4=60 ° ,?/ 7=180° — (/ 4+ / 5) =60 ° 在厶DOC 与厶FOC 中,/ 6= / 7=60°,/ 2= / 3, OC=OC ???△ DOC ◎△ FOC, CF=CD ? AC=AF+CF=AE+CD 截长法与补短法,具体作法是在某条线段上截取一条线段与特定线段相等, 或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。这种作 法,适合于证明线段的和、差、倍、分等类的题目。 例2:如图甲,AD// BC 点E在线段AB上,/ ADE=/CDE / DC=Z ECB 求证: CD=AD F BC 思路分析: 1)题意分析:本题考查全等三角形常见辅助线的知识:截长法或补短法。 2)解题思路:结论是CDAC+BC,可考虑用“截长补短法”中的“截长”,即在CD上截取CF=CE,只要再证DF=DA即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的。 解答过程: 证明:在CD上截取CF=BC如图乙 6 = CS CE= CE ???△ FCE^A BCE(SAS, ???/ 2=Z 1。 又??? AD// BC ???/ ADG-Z BCD:180°, ???/ DC+Z CD=90°, 截长补短类辅助线作法 ? “截长”就是将三条线段中最长的那条线段一分为二,使其中的一条线段等于已知的两条较短线段中的一条,然后证明其中的另一段与已知的另一条线段的数量关系; “补短”就是将三条线段中一条已知的较短的线段延长至与另一条已知的较短的长度相等,然后证明延长后的线段与最长的已知线段的数量关系. ? 注:1、截长补短类辅助线解决的一般是三条线段之间的数量关系问题,特别要注意线段前系数不是“1”的时候,一般会涉及到含特殊角的直角三角形 2、具体在利用截长或者补短构造辅助线时要结合题目条件选择恰当的方法,并 不是所有题目截长和补短都可以 例题精讲 1、如图所示,是边长为的正三角形,是顶角为的等腰三角形, 以为顶点作一个的,点、分别在、上,求的周长. 2、已知:如图,△ABC中,,BD平分∠ABC,BC上有动点P. (1)DP⊥BC时(如图1),求证:; (2)DP平分∠BDC时(如图2),BD、CD、CP三者有何数量关系? 3、已知中,,、分别平分和,、交于点,试判断、、的数量关系,并加以证明. 4、(2014初二上期末昌平区)如图,AD是△ABC的角平分线,点F,E分别在边AC,AB上,且. (1)求证:; (2)如果,探究线段AE,AF,FD之间满足的等量关系,并证明. 5、如图所示,是边长为的正三角形,是顶角为的等腰三角形,以为顶点作一个的,点、分别在、上,求的周长. 6、如图所示,已知正方形ABCD中,M为CD的中点,E为MC上一点,且 .求证:. 7、五边形ABCDE中,,,,求证:AD 平分∠CDE. 8、如图,在△ABC中,,D是三角形外一点,且,.求证: 9、(2012初二上期中中关村中学)如图1所示:,AE、DE分别平分 和,并交于E点.过点E的直线分别交AM、DN于B、C.(1)如图2,当点B、C分别位于点AD的同侧时,猜想AD、AB、CD之间的存在的数量关系:____ _____. (2)试证明你的猜想. (3)若点B、C分别位于点AD的两侧时,试写出AD、AB、CD之间的关系,并选择一个写出证明过程. 10、(2012初二上期中北达资源中学)(1)如图,四边形ABPC中,, 初中数学常用辅助线 一.添辅助线有二种情况: 1按定义添辅助线: 如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。 2按基本图形添辅助线: 每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形, 添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”!这样可防止乱添线,添辅助线也有规律 可循。举例如下: (1)平行线是个基本图形: 当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等 第三条直线 (2)等腰三角形是个简单的基本图形: 当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三 角形。 (3)等腰三角形中的重要线段是个重要的基本图形: 出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线 组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。 (4)直角三角形斜边上中线基本图形 出现直角三角形斜边上的中点往往添斜边上的中线。出现线段倍半关 系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三 角形斜边上中线基本图形。 (5)三角形中位线基本图形 几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。 (6)全等三角形: 全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形:或添对称轴,或将三角形沿对称轴翻转。当几何问题中出现一组或两组相等线段位于一组对顶角两边且成一直线时可添加中心对称形全等三角形加以证明,添加方法是将四个端点两两连结或过二端点添平行线 *(7)相似三角形: 相似三角形有平行线型(带平行线的相似三角形),相交线型,旋转型;当出现相比线段重叠在一直线上时(中点可看成比为1)可添加平行线得平行线型相似三角形。若平行线过端点添则可以分点或另一端点的线段为平行方向,这类题目中往往有多种浅线方法。 (8)特殊角直角三角形 当出现30,45,60,135,150度特殊角时可添加特殊角直角三角形,利用45角直角三角形三边比为1:1:√2;30度角直角三角形三边比为1:2:√3进行证明 (9)半圆上的圆周角 截长补短专题 知识导航 “截长补短”是几何证明题中十分重要的方法,通常用来证明几条线段的数量关系,即若题目条件或结论中含有“c b a =+”的条件,需要添加辅助线时可以考虑“截长补短”的方法。 截长法: 在较长的线段上截取一条线段等于较短线段,再设法证明较长线段的剩余线段等于另外的较短线段。 补短法: ①延长较短线段中的一条,使延长出来的线段等于另外的较短线段,然后证明两线段之和等于较长线段。即延长a ,得到b ,证:c b a =+。 ②延长较短线段中的一条,使延长后的线段等于较长线段,然后证明延长出来的部分等于另一条较短线段。即延长a ,得到c ,证:a c b -=。 【核心考点1】角平分线相关截长补短 1. 如图,BP 平分ABC ∠,D 为BP 上一点,E ,F 分别在BA ,BC 上,且满足DE DF =, 若140BED ∠=?,则BFD ∠的度数是( ) A .40? B .50? C .60? D .70? 【分析】 作DG AB ⊥于G ,DH BC ⊥于H ,根据角平分线的性质得到DH DG =,证明 Rt DEG Rt DFH ???,得到DEG DFH ∠=∠,根据互为邻补角的性质得到答案. 【解答】 解:作DG AB ⊥于G ,DH BC ⊥于H , D 是ABC ∠平分线上一点,DG AB ⊥,DH BC ⊥, DH DG ∴=, 在Rt DEG ?和Rt DFH ?中, DG DH DE DF =?? =?, ()Rt DEG Rt DFH HL ∴???, DEG DFH ∴∠=∠,又180DEG BED ∠+∠=?, 180BFD BED ∴∠+∠=?, BFD ∴∠的度数18014040=?-?=?, 故选:A . 初中数学证明题常见辅助线作法规律 初中数学证明题常见辅助线作法记忆歌诀;及几何规律汇编;人们从来就是用自己的聪明才智创造条件解决问题的,;初中几何常见辅助线作法歌诀;人说几何很困难,难点就在辅助线;辅助线,如何添?把握定理和概念;还要刻苦加钻研,找出规律凭经验;三角形;图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试 初中数学证明题常见辅助线作法记忆歌诀 及几何规律汇编 人们从来就是用自己的聪明才智创造条件解决问题的,当问题的条件不够时,添加辅助线构成新图形,形成新关系,使分散的条件集中,建立已知与未知的桥梁,把问题转化为自己能解决的问题,这是解决问题常用的策略。 初中几何常见辅助线作法歌诀 人说几何很困难,难点就在辅助线。 辅助线,如何添?把握定理和概念。 还要刻苦加钻研,找出规律凭经验。 三角形 图中有角平分线,可向两边作垂线。也可将图对折看,对称以后关系现。角平分线平行线,等腰三角形来添。角平分线加垂线,三线合一试试看。线段垂直平分线,常向两端把线连。要证线段倍与半,延长缩短可试验。三角形中两中点,连接则成中位线。三角形中有中线,延长中线等中线。四边形 平行四边形出现,对称中心等分点。梯形里面作高线,平移一腰试试看。平行移动对角线,补成三角形常见。证相似,比线段,添线平行成习惯。等积式子比例换,寻找线段很关键。直接证明有困难,等量代换少麻烦。斜边上面作高线,比例中项一大片。圆 半径与弦长计算,弦心距来中间站。圆上若有一切线,切点圆心半径连。切线长度的计算,勾股定理最方便。要想证明是切线,半径垂线仔细辨。是直径,成半圆,想成直角径连弦。弧有中点圆心连,垂径定理要记全。圆周角边两条弦,直径和弦端点连。弦切角边切线弦,同弧对角等找完。要想作个外接圆,各边作出中垂线。还要作个内接圆,内角平分线梦圆。如果遇到相交圆,不要忘作公共弦。内外相切的两圆,经过切点公切线。若是添上连心线,切点肯定在上面。要作等角添个圆,证明题目少困难。辅助线,是虚线,画图注意勿改变。假如图形较分散,对称旋转去实验。基本作图很关键,平时掌握要熟练。 截长补短类辅助线作法 “截长”就就是将三条线段中最长得那条线段一分为二,使其中得一条线段等于已知得两条较短线段中得一条,然后证明其中得另一段与已知得另一条线段得数量关系; “补短”就就是将三条线段中一条已知得较短得线段延长至与另一条已知得较短得长度相等,然后证明延长后得线段与最长得已知线段得数量关系。注:1、截长补短类辅助线解决得一般就是三条线段之间得数量关系问题,特别要注意线段前系数不就是“1”得时候,一般会涉及到含特殊角得直角三角形2、具体在利用截长或者补短构造辅助线时要结合题目条件选择恰当得方法,并不就是所有题目截长与补短都可以 例题精讲 1、如图所示,就是边长为得正三角形,就是顶角为得等腰三角形,以为顶点作一个得,点、分别在、上,求得周长. 2、已知:如图,△ABC中,,BD平分∠ABC,BC上有动点P. (1)DP⊥BC时(如图1),求证:; (2)DP平分∠BDC时(如图2),BD、CD、CP三者有何数量关系? 3、已知中,,、分别平分与,、交于点,试判断、、得数量关系,并加以证明. 4、(2014初二上期末昌平区)如图,AD就是△ABC得角平分线,点F,E分别在边AC,AB上,且. (1)求证:; (2)如果,探究线段AE,AF,FD之间满足得等量关系,并证明。 5、如图所示,就是边长为得正三角形,就是顶角为得等腰三角形,以为顶点作一个得,点、分别在、上,求得周长. 6、如图所示,已知正方形ABCD中,M为CD得中点,E为MC上一点,且。求证:。 7、五边形ABCDE中,,,,求证:AD平分∠CDE。 8、如图,在△ABC中,,D就是三角形外一点,且,.求证: 9、(2012初二上期中中关村中学)如图1所示:,AE、DE分别平分与,并交于E点、过点E得直线分别交AM、DN于B、C、?(1)如图2,当点B、C分别位于点AD得同侧时,猜想AD、AB、CD之间得存在得数量关系:_________、 (2)试证明您得猜想、 (3)若点B、C分别位于点AD得两侧时,试写出AD、AB、CD之间得关系,并选择一个写出证明过程、 10、(2012初二上期中北达资源中学)(1)如图,四边形ABPC中,,,,求证:. 第七章截长补短 模型:截长补短 如图①,若证明线段AB、CD、EF之间存在EF=AB+CD,可以考虑截长补短 法. 截长法:如图②,在EF上截取EG=AB,再证明GF=CD即可. 补短法:如图③,延长AB至H点,使BH=CD,再证明AH=EF 即可. 模型分析 截长补短的方法适用于求证线段的和差倍分关系. 截长,指在长线端中截取一段等于已知的线段;补短,指将一条短线端延长,延长部分等于已知线段. 该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程. 模型实例 例1 如图,已知在△ABC中,∠C=2∠B,∠1=∠2 .求证:AB=AC+CD . 例2 如图,∠ABC+∠BCD=1800,BE、CE分别平分∠ABC、∠DCB .求证:AB+CD=BC . 基础题: 1.如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD . 求证:AO+BO=2CO . 2.如图,在△ABC中,∠BAC=600,AD是∠BAC的平分线,且AC=AB+BD .求∠ABC的度数 . 3.如图,在△ABC中,∠ABC=600,AD、CE分别平分∠BAC、∠ACB .求证:AC=AE+CD . 4. 如图,五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=1800.求证:AD平分∠CDE . 5.如图,已知△ABC中,AH⊥BC于H,∠C=35°,且AB+BH=HC,求∠B度数. 6.已知,如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF.求证:∠EAF=∠BAD. 7.已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:(1)MN=DN﹣BM;(2)AH=AB. 全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折” ? 2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转” ? 3) 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4) 过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5) 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明?这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ ABC中,AB=5,AC=3,则中线AD的取值范围是 _______________ . 2 :如图,△ ABC中,E、F分别在AB、AC 上, DE丄DF,D是中点,试比较BE+CF 与EF的大小. 3 :如图,△ ABC中,BD=DC=AC ,E是DC的中点,求证:AD平分/ BAE. 中考应用: ABC的两边AB、AC为腰分别向外作等腰Rt ABD和等腰Rt ACE BAD CAE 90,连接DE,M、N分别是BC、DE的中点?探究:AM与DE的位 置关系及数量关系. (1 )如图① 当ABC为直角三角形时,AM与DE的位置关系 是________________ ,线段AM与DE的数量关系是________________ ; (2 )将图①中的等腰Rt ABD绕点A沿逆时针方向旋转(0< <90)后,如图②所示,(1 ) 初中常见辅助线作法 任何几何题目都需分析题目条件和结论找到解题思路,本讲从常见的条件和结论出发说明50种辅助线作法,分三角形部分、四边形部分、解直角三角形部分、圆。每种辅助线作法均配备了例题和练习。 三角形部分 1.在利用三角形三边关系证明线段不等关系时,如果直接证不出来,可连结两点或延长某 边构造三角形,使结论中出现的线段在一个或几个三角形中,再利用三边关系定理及不等式性质证题. 例:如图,已知D 、E 为△ABC 内两点,求证:AB +AC >BD +DE +CE . 证法(一):将DE 向两边延长,分别交AB 、AC 于M 、N 在△AMN 中, AM + AN >MD +DE +NE ① 在△BDM 中,MB +MD >BD ② 在△CEN 中,CN +NE >CE ③ ①+②+③得 AM +AN +MB +MD +CN +NE >MD +DE +NE +BD +CE ∴AB +AC >BD +DE +CE 证法(二)延长BD 交AC 于F ,延长CE 交BF 于G , 在△ABF 和△GFC 和△GDE 中有, ①AB +AF >BD +DG +GF ②GF +FC >GE +CE ③DG +GE >DE ∴①+②+③有 AB +AF +GF +FC +DG +GE >BD +DG +GF +GE +CE +DE ∴AB +AC >BD +DE +CE 注意:利用三角形三边关系定理及推论证题时,常通过引辅助线,把求证的量(或与求证 有关的量)移到同一个或几个三角形中去然后再证题. 练习:已知:如图P 为△ABC 内任一点, 求证: 1 2 (AB +BC +AC )<P A +PB +PC <AB +BC +AC 2.在利用三角形的外角大于任何和它不相邻的内角证明角的不等关系时,如果直接证不出来, 可连结两点或延长某边,构造三角形,使求证的大角在某个三角形外角的位置上,小角处在内角的位置上,再利用外角定理证题. 例:已知D 为△ABC 内任一点,求证:∠BDC >∠BAC 证法(一):延长BD 交AC 于E , F G N M E D C B A中考数学专题复习-常用辅助线截长补短
全等三角形常用辅助线做法
截长补短类辅助线作法
初中数学常见辅助线做法
几何辅助线之截长补短 总结+例题
初中数学证明题常见辅助线作法规律
截长补短类辅助线作法
几何辅助线——截长补短
全等三角形作辅助线专题一(重点_截长补短法)可打印版
初中几何常见辅助线作法50种
