指数函数与对数函数

网络课程内部讲义
指数函数与对数函数教师:司马红丽
https://www.360docs.net/doc/b16574706.html, “在线名师”→ 资料室 免费资料任你下载
指数函数与对数函数
【知识要点归纳】
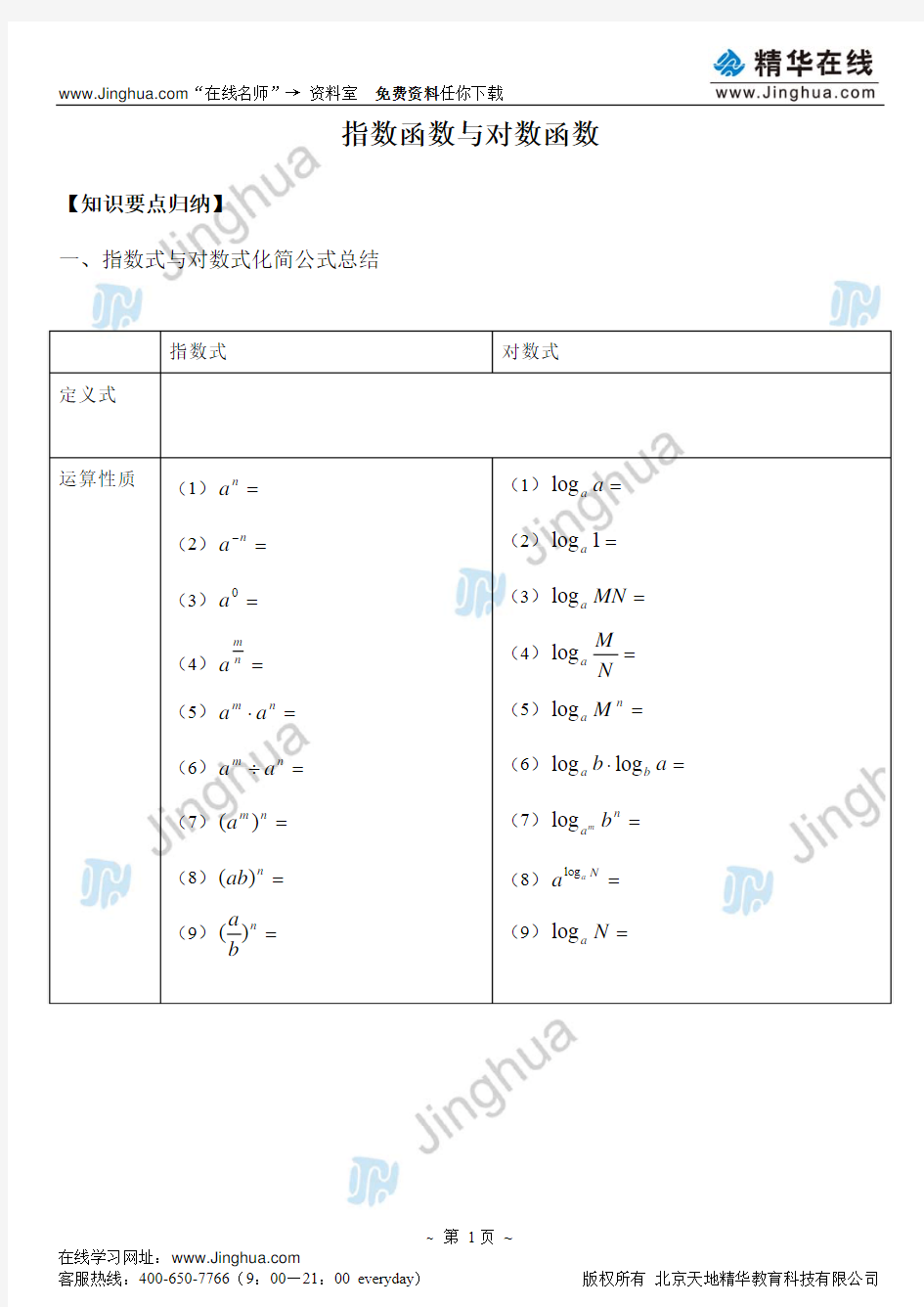
一、指数式与对数式化简公式总结 (2)=a
(3)=0
a (4)=n
m a
(5)=?n
m
a a (6)=÷n
m
a a (7)=n m a )( (8)=n a
b )( (9)=n
b
a )(
(2)=1log a (3)=MN a log (4)=N
M a
log (5)=n
a M
log
(6)=?a b b a log log (7)=n
a b m log (8)=N
a a
log
(9)=N a log
https://www.360docs.net/doc/b16574706.html, “在线名师”→ 答疑室 随时随地提问互动
二、指数函数和对数函数的图像和性质总结
指数函数
对数函数
定义式
图象
定义域 值域 单调性 定点
a 的大小与
图象的关系
抽象性质
【经典例题】
例1:化简 (1)若1
2
a <=
(2)23
12
log 4(8)+?= .
https://www.360docs.net/doc/b16574706.html, “在线名师”→ 资料室 免费资料任你下载
(3)2log (2)log log a a a M N M N ?=+,则
N
M
的值为( ) A .4
1
B .4
C .1
D .4或1
(4)已知2
2
1,0,0x y x y +=>>,且1
log (1),log ,log 1y a a
a x m n x
+==?则等于( )。 A .m n + B .m n ? C .()12m n + D .()1
2
m n ?
例2:设f (x )=4x
4x +2
,若0 < a < 1,试求:
(1)f (a )+f (1-a )的值;
(2)f (11 001)+f (21 001)+f (31 001)+…+f (1 000
1 001)的值.
例3:已知f (x ) = a x , g (x ) = log a x (a > 0且a ≠ 1),若f (3) g (3) < 0, 则f (x )与g (x )在同一坐标系内的图
象可能是( )
https://www.360docs.net/doc/b16574706.html, “在线名师”→ 答疑室 随时随地提问互动
例4:若x 0是方程2x =
x 1
的解,则x 0∈( ) A .(0,0.5)
B .(0.5,1)
C .(1, 1.5)
D .(1.5, 2)
例5:比较下列各组数中两个值的大小: (1)3.2log 1.1与2.2log 2.1; (2)7.0log 3.0与9.2log 1.2; (3)b a log 与)10(log 1< 。 例6:求下列函数的定义域。 (1)0.5log (43)y x =? (2)) 34(log 1 )(2 2?+?=x x x f https://www.360docs.net/doc/b16574706.html, “在线名师”→ 资料室 免费资料任你下载 例7:若函数4 1 )1([log 2 2+ ?+=x a ax y 的定义域为R ,求实数a 的取值范围。 例8:已知函数f (x ) = log a (2-ax )在[0,1]上为减函数,则a 的取值范围是( ) A .(0,1) B .(1,2) C .(0,2) D .[2,+∞) 例9:已知函数1010()1010x x x x f x ???=+,判断()f x 的奇偶性和单调性。 例10:已知函数2 2 2(3)lg 6 x f x x ?=?, (1)求()f x 的定义域; (2)判断()f x 的奇偶性。 https://www.360docs.net/doc/b16574706.html, “在线名师”→ 答疑室 随时随地提问互动 【课堂练习】 1.设P = {y | y = x 2, x ∈ R }, Q = {y | y = 2x , x ∈ R },则( ) A .Q = P B .Q P C .P ∩Q = {2,4} D .P ∩Q = {(2,4)} 2.函数y = |log 2x |的图象是( ) 3.已知函数f (x )= lg x x +?11,若f (a )= b ,则f (-a )等于( ) A .b B .-b C .b 1 D .-b 1 4.已知函数f (x ) = ???≤>) 0( 3)0( log 2x x x x 时f [f (41 )]的值是( ) A.9 B. 91 C.-9 D.-9 1 5.下列说法正确的是( ) A .8lg 6lg > B .48.09.084> C .0 2.5 2.50.5< D .4log 6log 5.05.0> 6.下列各式,化简后其值不等于1的是 ( ) A .22log 6log 3? B .lg 2lg 5+ C .log log a b b a ? D .82log 9log 3÷ 7.若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍,则a =( ) A . 4 2 B . 2 2 C . 4 1 D . 2 1 8.(2009辽宁)函数()f x 满足:x ≥ 4,则()f x =0.5x ;当x < 4时()f x = (1)f x +, 则2(2log 3)f += A .1/24 B .1/12 C .1/8 D .3/8 9.函数) 2()lg 1f x x x =+?是 (奇、偶)函数。 10.函数f (x ) = a x (a > 0且a ≠ 1)在区间[1,2]上的最大值比最小值大 2 a ,则a 的值为______. https://www.360docs.net/doc/b16574706.html, “在线名师”→ 资料室 免费资料任你下载 【课堂练习】参考答案 1、B ,P =[0,+∞),Q =(0,+∞)。 2、D 3、B 4、B 5、B 6、D 7、A 8、A 9、奇 )(),()1lg(11lg )1lg()(222x f x f x x x x x x x f R x ∴?=?+?=?+=++=?∈且∵为奇函数。 10、 21或23,当a >1时,f (x )为增函数,a 2-a =2a ,得a =2 3 当0 3 C 咨询电话:4006-211-001 WWW r haOfangfa COm 1 指数函数和对数函数 重点、难点: 重点:指数函数和对数函数的概念、图象和性质。 难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数 a . 1及O ::: a ::: 1两种不同情况。 1、指数函数: 定义:函数y =a x a . 0且a --1叫指数函数。 定义域为R 底数是常数,指数是自变量。 认识。 图象特征 函数性质 (1)图象都位于X 轴上方; (1)X 取任何实数值时,都有 a X A0 ; (2)图象都经过点(0, 1); (2)无论a 取任何正数,X = 0时,y = 1 ; (3) y — 2 , y — 10在第一象限内的纵坐 \ > 0 ,贝U a X A 1 (3)当 a > 1 时,{ →, X 标都大于1,在第二象限内的纵坐标都小于 1, < < 0 ,贝U a <1 X A 0 ,贝U a x V 1 y = — [的图象正好相反; 当 0 ca c1 时,< X £ 0 ,贝U a x A 1 k (4) y =2X , y=10X 的图象自左到右逐渐 (4)当a >1时,y =a x 是增函数, 当0cac1时,y=a x 是减函数。 为什么要求函数 y = a 中的a 必须a . 0且a = 1。 X 因为若a ::;0 时, X 1、对三个指数函数 a = 0 , y = 0 a =1 时,y = 1 =1x 的反函数不存在, y =a x ,y =Iog a X 在 上升,y = f l]的图象逐渐下降。 k2 J ①所有指数函数的图象交叉相交于点(0,1),如y=2x和y=10x相交于(0,1), 的图象在y =2x的图象的上方,当X :::0 ,刚好相反,故有1 0 2. 22及10 ^ ::: 2 ^。 步认识无限个函数的图象。 2、对数: 定义:如果a tl = N(a . 0且a ■■ 1),那么数b就叫做以a为底的对数,记作b = Iog a N (a是底数,N是 真数,log a N是对数式。) 由于N ^a b . 0故log a N中N必须大于0。 当N为零的负数时对数不存在。 (1)对数式与指数式的互化。 由于对数是新学的,常常把不熟悉的对数式转化为指数式解决问题,如: 分析:对于初学者来说,对上述问题一般是束手无策,若将它写成 比较好办。 解:设Iog 0.32 X ■? 0 时,y = 10 % ②y =2x与y X 的图象关于y轴对称。 ③通过y = 2 X X 三个函数图象,可以画出任意一个函数y = a 示意图,如y =3x的图象,一定位于y =2x和y =IO x两个图象的中间,且过点(0, 1),从而y = X 也由关于y轴的对称性,可得的示意图,即通过有限个函数的图象进 再改写为指数式就 第二章 函数 三 指数函数与对数函数 【考点阐述】指数概念的扩充.有理指数幂的运算性质.指数函数.对数.对数的运算性质.对数函数. 【考试要求】(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质.(5)理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图像和性质.(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题. 【考题分类】 (一)选择题(共15题) 1.(安徽卷文7)设 232555 322555a b c ===(),(),() ,则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a 【答案】A 【解析】2 5 y x =在0x >时是增函数,所以a c >,2()5x y =在0x >时是减函数,所以c b >。 【方法总结】根据幂函数与指数函数的单调性直接可以判断出来. 2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b a x (ab ≠0,| a |≠| b |)在同一直角坐标系 中的图像可能是 【答案】D 【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-11矛盾,选D 。 3.(辽宁卷文10)设525b m ==,且112a b +=,则m = (A (B )10 (C )20 (D )100 【答案】 D 解析:选A.211 log 2log 5log 102,10, m m m m a b +=+==∴= 又0,m m >∴= 4.(全国Ⅰ卷理8文10)设a= 3 log 2,b=In2,c=1 2 5 - ,则 A. a 指数函数和对数函数 知能目标 1. 理解分数指数幂的概念, 掌握有理指数幂的运算性质. 掌握指数函数的概念、图象和性质. 2. 理解对数的概念, 掌握对数的运算性质. 掌握对数函数的概念、图象和性质. 3. 能够运用指数函数和对数函数的性质解决某些简单的实际问题. 综合脉络 1. 以指数函数、对数函数为中心的综合网络 2. 指数式与对数式有如下关系(指数式化为对数式或对数式化为指数式的重要依据): 0a (N log b N a a b >=?=且)1a ≠ 指数函数与对数函数互为反函数, 它们的图象关于直线x y =对称, 指数函数与对数函数 的性质见下表: 3. 指数函数,对数函数是高考重点之一 指数函数,对数函数是两类重要的基本初等函数, 高考中既考查双基, 又考查对蕴含其中的函 数思想、等价转化、分类讨论等思想方法的理解与运用. 因此应做到能熟练掌握它们的图象与性 质并能进行一定的综合运用. (一) 典型例题讲解: 例1.设a >0, f (x)= x x e a a e -是R 上的奇函数. (1) 求a 的值; (2) 试判断f (x )的反函数f - 1 (x)的奇偶性与单调性. 例2. 是否存在实数a, 使函数f (x )=)x ax (log 2 a -在区间]4 ,2[上是增函数? 如果存在, 说明a 可以取哪些值; 如果不存在, 请说明理由. 例3. 已知x 满足≤+6x 2a a 4x 2x a a +++)1a ,0a ( ≠>, 函数y =)ax (log x a 1 log 2 a 12 a ? 的值域为]0 ,8 1[-, 求a 的值. (二) 专题测试与练习: 幂函数、指数函数和对数函数·对数及其运算法则·教案 如果a(a>0,a≠1)的b次幂等于N,就是ab=N,那么数b就叫做以a为底N的对数,记作 logaN=b, 其中a叫做底数,N叫做真数,式子logaN叫做对数式. 练习1 把下列指数式写成对数形式: 练习2 把下列对数形式写成指数形式: 练习3 求下列各式的值: 因为22=4,所以以2为底4的对数等于2. 因为53=125,所以以5为底125的对数等于3. 师:由定义,我们还应注意到对数式logaN=b中字母的取值范围是什么? 生:a>0且a≠1;b∈R;N∈R. 师:N∈R?(这是学生最易出错的地方,应一开始让学生牢牢记住真数大于零.) 生:由于在实数范围内,正数的任何次幂都是正数,因而ab=N中N总是正数. 师:要特别强调的是:零和负数没有对数. 师:定义中为什么规定a>0,a≠1? 生:因为若a<0,则N取某些值时,b可能不存在,如b=log(-2)8不存在;若a=0,则当N不为0时,b不存在,如log02不存在;当N为0时,b可以为任何正数,是不唯一的,即log00有无数个值;若a=1,N 不为1时,b不存在,如log13不存在,N为1时,b可以为任何数,是不唯一的,即log11有无数多个值.因此,我们规定:a>0,a≠1. 师:(板书)对数logaN(a>0且a≠1)在底数a=10时,叫做常用对数,简记lgN;底数a=e时,叫做自然对数,记作lnN,其中e是个无理数,即e≈2.718 28……. 练习4 计算下列对数: lg10000,lg0.01,2log24,3log327,10lg105,5log51125. 师:请同学说出结果,并发现规律,大胆猜想. 生:2log24=4.这是因为log24=2,而22=4. 生:3log327=27.这是因为log327=3,而33=27. 生:10lg105=105. 生:我猜想alogaN=N,所以5log51125=1125. alogaN=N(a>0,a≠1,N>0).(用红笔在字母取值范围下画上曲线) 证明:设指数等式ab=N,则相应的对数等式为logaN=b,所以ab=alogaN=N. 师:你是根据什么证明对数恒等式的? 生:根据对数定义. 师:(分析小结)证明的关键是设指数等式ab=N.因为要证明这个对数恒等式,而现在我们有关对数的知 第七讲: 指数函数和对数函数 知能目标 1. 理解分数指数幂的概念, 掌握有理指数幂的运算性质. 掌握指数函数的概念、图象和性质. 2. 理解对数的概念, 掌握对数的运算性质. 掌握对数函数的概念、图象和性质. 3. 能够运用指数函数和对数函数的性质解决某些简单的实际问题. 综合脉络 1. 以指数函数、对数函数为中心的综合网络 2. 指数式与对数式有如下关系(指数式化为对数式或对数式化为指数式的重要依据): 0a (N log b N a a b >=?=且)1a ≠ 指数函数与对数函数互为反函数, 它们的图象关于直线x y =对称, 指数函数与对数函数 的性质见下表: 3. 指数函数,对数函数是高考重点之一 指数函数,对数函数是两类重要的基本初等函数, 高考中既考查双基, 又考查对蕴含其中的函 数思想、等价转化、分类讨论等思想方法的理解与运用. 因此应做到能熟练掌握它们的图象与性 质并能进行一定的综合运用. (一) 典型例题讲解: 例1.设a >0, f (x)= x x e a a e - 是R 上的奇函数. (1) 求a 的值; (2) 试判断f (x )的反函数f -1 (x)的奇偶性与单调性. 例2. 是否存在实数a, 使函数f (x )=)x ax (log 2 a -在区间]4 ,2[上是增函数? 如果存在, 说明a 可以取哪些值; 如果不存在, 请说明理由. 例3. 已知x 满足≤+6x 2a a 4x 2x a a +++)1a ,0a ( ≠>, 函数y =)ax (log x a 1 log 2 a 12 a ? 的值域为]0 ,8 1[- , 求a 的值. (二) 专题测试与练习: 一. 选择题 1. 设0x >且) (0,b a, ,1b a x x ∞+∈<<, 则a 、b 的大小关系是 ( ) A. 1a b << B. 1b a << C. a b 1<< D. b a 1<< 2. 如果1a 0<<, 那么下列不等式中正确的是 ( ) A. 21 31 )a 1()a 1(->- B. )a 1(log ) a 1(+- C. 2 3)a 1()a 1(+>- D. 1)a 1()a 1(>-+ 3. 已知x 1是方程3x lg x =+的一个根, 2x 是方程310x x =+的一个根, 那么21x x +的值 是 ( ) A. 6 B. 3 C. 2 D. 1 4. ,0z log log log y log log log x log log log 324243432===则z y x ++的值为 ( ) A. 50 B. 58 C. 89 D. 111 5. 当1a >时, 在同一坐标系中, 函数x a y -=与=y x log a 的图象是图中的 ( ) 6. 若函数)x (f 与=)x (g x ) 2 1 (的图象关于直线x y =对称, 则)x 4(f 2 -的单调递增区间是( ) A. ]2 ,2(- B. ) ,0[∞+ C. )2 ,0[ D. ]0 ,(-∞ 二. 填空题 7. 已知522x x =+-, 则=+-x x 88 . 8. 若函数=y 2x log 2+的反函数定义域为),3(∞+ , 则此函数的定义域为 . 9. 已知=y )ax 3(log a -在]2 ,0[上是x 的减函数, 则a 的取值范围是 . 10.函数=)x (f )1a ,0a (a x ≠>在]2 ,1[上的最大值比最小值大2 a , 则a 的值为 . 三. 解答题 11. 设 1x 0 <<, 试比较|)x 1(log a -|与|)x 1(log a +|的大小. 【教学设计中学数学】 区县雁塔区 学校西安市航天中学 姓名贾红云 联系方式 邮编710100 《指数函数、幂函数、对数函数增长的比较》教学设计 一、设计理念 《普通高中数学课程标准》明确指出:“学生的数学学习活动,不应该只限于接受、记忆、模仿和练习,高中数学课程还应该倡导自主探索、动手实践、合作交流、阅读自学等信息数学的方式;课程内容的呈现,应注意反映数学发展的规律以及学生的认知规律,体现从具体到抽象,特殊到一般的原则;教学应注意创设情境,从具体实例出发,展现数学知识的发生、发展过程,使学生能够从中发现问题、提出问题,经历数学的发现和创造过程,了解知识的来龙去脉等”。本节课是北师大版高中数学必修Ⅰ第三章第6节内容,本节专门研究指数函数、幂函数、对数函数的增长的比较,目的是探讨不同类型的函数模型,在描述实际增长问题时的不同变化趋势,通过本节课的学习,可以引导学生积极地开展观察、思考和探究活动,利用几何画板这种信息技术工具,可以让学生从动态的角度直观观察指数函数、幂函数、对数函数增长情况的差异,使学生有机会接触一些过去难以接触到的数学知识和数学思想,并为学生提供了学数学、用数学的机会,体现了发展数学应用意识、提高实践能力的新课程理念。 二、教学目标 1.结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数模型的意义,理解它们增长的差异性; 2.能借助信息技术,利用函数图像和表格,对几种常见增长类型的函数增长的情况进行比较,体会它们增长的差异; 3.体验指数函数、幂函数、对数函数与现实世界的密切联系及其在刻画实际问题中的作用,体会数学的价值. 三、教学重难点 教学重点:认识指数函数、幂函数、对数函数增长的差异,体会直线上升、指数爆炸、对数增长的含 义。 教学难点:比较指数函数、幂函数、对数函数增长的差异 四、教学准备 ⒈提醒学生带计算器; ⒉制作教学用幻灯片; ⒊安装软件:几何画板 ,准备多媒体演示设备 五、教学过程 ㈠基本环节 ⒈创设情景,引起悬念 杰米和韦伯的故事 一个叫杰米的百万富翁,一天,碰上一件奇怪的事,一个叫韦伯的人对他说,我想和你定个合同,我将在整整一个月中每天给你 10万元,而你第一天只需给我一分钱,而后每一天给我的钱是前一天的两倍。杰米说:“真的?!你说话算数?” 合同开始生效了,杰米欣喜若狂。第一天杰米支出一分钱,收入10万元;第二天,杰米支出2分钱,收入10万元;第三天,杰米支出4分钱,收入10万元;第四天,杰米支出8分钱,收入10万元…..到了第二十天,杰米共得到200万元,而韦伯才得到1048575分,共10000元多点。杰米想:要是合同定两个月、三个月多好! 你愿意自己是杰米还是韦伯? 【设计意图】创设情景,构造问题悬念,激发兴趣,明确学习目标 ⒉复习旧知,提出问题 图1-1 图1-2 图1-3 ⑴ 如图1-1,当a 时,指数函数x y a =是单调 函数,并且对于0x >,当底数a 越大时,其 函数值的增长就越 ; ⑵ 如图1-2当a 时,对数函数log a y x =是单调 函数,并且对1x >时,当底数a 越 时 其函数值的增长就越快; ⑶ 如图1-3当0x >,0n >时,幂函数n y x =是增函数,并且对于1x >,当n 越 时,其函数值 指数函数和对数函数知识点总结及练习题 一.指数函数 (一)指数及指数幂的运算 n m n m a a = s r s r a a a +=? rs s r a a =)( r r r b a ab =)( (二)指数函数及其性质 1.指数函数的概念:一般地,形如x a y =(0>a 且1≠a )叫做指数函数。 2.指数函数的图象和性质 10<a 6 54321 -1 -4-2 2460 1 6 5 4 3 2 1 -1 -4-2 246 1 定义域 R 定义域 R 值域y >0 值域y >0 在R 上单调递减 在R 上单调递增 非奇非偶函数 非奇非偶函数 定点(0,1) 定点(0,1) 二.对数函数 (一)对数 1.对数的概念:一般地,如果N a x =(0>a 且1≠a ),那么x 叫做以a 为底N 的对数,记作N x a log =,其中a 叫做底数,N 叫做真数,N a log 叫做对数式。 2.指数式与对数式的互化 幂值 真数 x N N a a x =?=log 底数 指数 对数 3.两个重要对数 (1)常用对数:以10为底的对数N lg (2)自然对数:以无理数 71828.2=e 为底的对数N ln (二)对数的运算性质(0>a 且1≠a ,0,0>>N M ) ①MN N M a a a log log log =+ ②N M N M a a a log log log =- ③M n M a n a log log = ④换底公式:a b b c c a log log log =(0>c 且1≠c ) 关于换底公式的重要结论:①b m n b a n a m log log = ②1log log =?a b b a (三)对数函数 1.对数函数的概念:形如x y a log =(0>a 且1≠a )叫做对数函数,其中x 是自变量。 2对数函数的图象及性质 0 一、指数的性质 (一)整数指数幂 1.整数指数幂概念: a n n a a a a 个???= )(* ∈N n ()010a a =≠ ()1 0,n n a a n N a -*= ≠∈ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2)()(),n m mn a a m n Z =∈ (3)()()n n n ab a b n Z =?∈ 其中m n m n m n a a a a a --÷=?=, ()1n n n n n n a a a b a b b b --??=?=?= ??? . 3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a ( )* ∈>N n n ,1,那么这个数叫做a 的n 次方根, 即: 若a x n =,则x 叫做a 的n 次方根, ()* ∈>N n n ,1 例如:27的3次方根3273=, 27-的3次方根3273-=-, 32的5次方根2325=, 32-的5次方根2325-=-. 说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 ⑤式子n a 叫根式,n 叫根指数,a 叫被开方数。 ∴ n a =. . 4.a 的n 次方根的性质 一般地,若n 是奇数,则a a n n =; 若n 是偶数,则?? ?<-≥==0 0a a a a a a n n . 5.例题分析: 例1.求下列各式的值: (1)() 338- (2) ()210- (3)()44 3π- (4) ()()b a b a >-2解:略。 例2.已知,0<N n n ,1, 化简:()()n n n n b a b a ++-. 解:当n 是奇数时,原式a b a b a 2)()(=++-= 当n 是偶数时,原式a b a a b b a b a 2)()(||||-=--+-=++-= 所以,()()n n n n b a b a ++-22a n a n ?=? -?为奇数 为偶数 . 例3.计算:407407-++ 解:407407-++52)25()25(22=-++= 例4.求值: 54 925-+. 解:549 25-+4 25254 5 49252 )(-+=-+= 452622525+=-+= 2 1 54152 += +=)( (二)分数指数幂 1.分数指数幂: ()10 2 5 0a a a ==> ()124 3 0a a a ==> 即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式; 如果幂的运算性质(2)() n k kn a a =对分数指数幂也适用, 例如:若0a >,则3 223233a a a ???== ??? ,4 554544a a a ???== ???, 23a = 4 5 a =. 即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。 规定:(1)正数的正分数指数幂的意义是)0,,,1m n a a m n N n *=>∈>; (2)正数的负分数指数幂的意义是)10,,,1m n m n a a m n N n a -* == >∈>. 2.分数指数幂的运算性质:整数指数幂的运算性质对于分数指数幂也同样适用 指数函数与对数函数知识点总结 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次 方根,其中n >1,且n ∈N * . 当n 是奇数时, a a n n =,当n 是偶数时, ?? ?<≥-==) 0() 0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: ) 1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1*>∈>= = - n N n m a a a a n m n m n m 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3)s r r a a ab =)( ),,0(R s r a ∈>. (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自变量,函数的定义域为R . 二、对数函数 (一)对数 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数, 记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln . 指数式与对数式的互化 幂值 真数 (二)对数的运算性质 如果0>a ,且1≠a ,0>M ,0>N ,那么: ○ 1 M a (log ·=)N M a log +N a log ; ○ 2 =N M a log M a log -N a log ; ○ 3 n a M log n =M a log )(R n ∈. 注意:换底公式 a b b c c a log log log = (0>a ,且1≠a ;0>c ,且1≠c ; 0>b ). 利用换底公式推导下面的结论 (1)b m n b a n a m log log =; (2)a b b a log 1log =. (二)对数函数 指数函数和对数函数 重点、难点: 重点:指数函数和对数函数的概念、图象和性质。 难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数 y a y x x a ==,log 在a >1及01<≠01且叫指数函数。 定义域为R ,底数是常数,指数是自变量。 为什么要求函数y a x =中的a 必须a a >≠01且。 因为若a <0时,()y x =-4,当x =1 4 时,函数值不存在。 a =0,y x =0,当x ≤0,函数值不存在。 a =1时,y x =1对一切x 虽有意义,函数值恒为1, 但y x =1的反函数不存在,因为要求函数y a x =中的a a >≠01且。 1、对三个指数函数y y y x x x ==?? ? ? ?=21210,,的图 象的认识。 对图象的进一步认识,(通过三个函数相互关系的比较): ①所有指数函数的图象交叉相交于点(0,1),如y x =2和y x =10相交于()01,,当x >0 时,y x =10的图象在y x =2的图象的上方,当x <0,刚好相反,故有10222>及 10222--<。 ②y x =2与y x =?? ?? ?12的图象关于y 轴对称。 ③通过y x =2,y x =10,y x =?? ?? ?12三个函数图象,可以画出任意一个函数y a x =(a a >≠01且)的示意图,如y x =3的图象,一定位于y x =2和y x =10两个图象的中 间,且过点()01,,从而y x =?? ???13也由关于y 轴的对称性,可得y x =?? ? ? ?13的示意图,即 通过有限个函数的图象进一步认识无限个函数的图象。 2、对数: 定义:如果a N a a b =>≠()01且,那么数b 就叫做以a 为底的对数,记作b N a =log (a 是底数,N 是真数,log a N 是对数式。) 由于N a b =>0故log a N 中N 必须大于0。 当N 为零的负数时对数不存在。 (1)对数式与指数式的互化。 (2)对数恒等式: 由a N b N b a ==()log ()12 将(2)代入(1)得a N a N log = 运用对数恒等式时要注意此式的特点,不能乱用,特别是注意转化时必须幂的底数和对数的底数相同。 计算: () 313 2 -log 解:原式==?? ?? ?-=3 131 2 222 13 1 3 log log 。 (3)对数的性质: ①负数和零没有对数; ②1的对数是零; ③底数的对数等于1。 (4)对数的运算法则: ①()()log log log a a a MN M N M N R =+∈+ , ②()log log log a a a M N M N M N R =-∈+ , ③()()log log a n a N n N N R =∈+ ④()log log a n a N n N N R =∈+ 1 例1.设a >0, f (x)=x x e a a e -是R 上的奇函数. (1) 求a 的值; (2) 试判断f (x )的反函数f - 1 (x)的奇偶性与单调性. 解:(1) 因为)x (f 在R 上是奇函数, 所以)0a (1a 0a a 1 0) 0(f >=?=-? =, (2) =-?∈++=--)x (f )R x (2 4 x x ln )x (f 121 -=++-24x x ln 2=++2 4x x ln 2)x (f 1--, ∴)x (f 1-为奇函数. 用定义法可证)x (f 1 -为单调增函数. 例2. 是否存在实数a, 使函数f (x )=)x ax (log 2 a -在区间]4 ,2[上是增函数? 如果存在, 说明a 可以取哪些值; 如果不存在, 请说明理由. 解:设x ax ) x (u 2-=, 对称轴a 21x = . (1) 当1a >时, 1a 0 )2(u 2 a 21>??????>≤; (2) 当1a 0<<时, 81a 00)4(u 4 a 21 ≤≥. 综上所述: 1a > 1.(安徽卷文7)设 232 555 322555a b c ===(),(),() ,则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a 【答案】A 【解析】2 5 y x =在0x >时是增函数,所以a c >,2 ()5x y =在0x >时是减函数,所以c b >。 2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b a x (ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可 能是【答案】D 【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1 指数函数和对数函数 重点、难点: 重点:指数函数和对数函数的概念、图象和性质。 难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数y a y x x a ==,l o g 在a >1及01<≠01且叫指数函数。 定义域为R ,底数是常数,指数是自变量。 为什么要求函数y a x =中的a 必须a a >≠01且。 因为若a <0时,()y x =-4,当x = 14 时,函数值不存在。 a =0,y x =0,当x ≤0,函数值不存在。 a =1时,y x =1对一切x 虽有意义,函数值恒为1,但 y x =1的反函数不存在, 因为要求函数y a x =中的 a a >≠01且。 1、对三个指数函数y y y x x x ==?? ?? ?=21210,,的图象的 认识。 图象特征与函数性质: 对图象的进一步认识,(通过三个函数相互关系的比较): ①所有指数函数的图象交叉相交于点(0,1),如y x =2和y x =10相交于()01,,当x >0时,y x =10的图象在y x =2的图象的上方,当x <0,刚好相反,故有10222>及10222--<。 ②y x =2与y x =?? ? ? ?12的图象关于y 轴对称。 ③通过y x =2,y x =10,y x =?? ? ? ?12三个函数图象,可以画出任意一个函数y a x =(a a >≠01且)的 示意图,如y x =3的图象,一定位于y x =2和y x =10两个图象的中间,且过点()01,,从而y x =?? ? ? ? 13也由 关于y 轴的对称性,可得y x =?? ? ? ?13的示意图,即通过有限个函数的图象进一步认识无限个函数的图象。 2、对数: 定义:如果a N a a b =>≠()01且,那么数b 就叫做以a 为底的对数,记作b N a =l o g (a 是底数,N 是真数,log a N 是对数式。) 由于N a b =>0 故log a N 中N 必须大于0。 当N 为零的负数时对数不存在。 (1)对数式与指数式的互化。 由于对数是新学的,常常把不熟悉的对数式转化为指数式解决问题,如: 求lo g .032524?? ? ? ? 分析:对于初学者来说,对上述问题一般是束手无策,若将它写成log .032524?? ? ? ?=x ,再改写为指数式就比较好办。 解:设log .032524?? ? ? ?=x 一、幂函数 1、幂的有关概念 正整数指数幂: ...() n n a a a a n N =∈ g123 零指数幂: 01(0) a a =≠ 负整数指数幂: 1 (0,) p p a a p N a -=≠∈ 分数指数幂:正分数指数幂的意义是: (0,,,1) m n m n a a a m n N n =>∈> 且 负分数指数幂的意义是: 1 (0,,,1) m n m n m n a a m n N n a a - ==>∈> 且 2、幂函数的定义 一般地,函数 a y x =叫做幂函数,其中x是自变量,a是常数(我们只讨论a是有理数的情况). 3、幂函数的图象 幂函数a y x = 当 11 ,,1,2,3 32 a= 时的图象见左图;当 1 2,1, 2 a=--- 时的图象见上图: 由图象可知,对于幂函数而言,它们都具有下列性质: a y x =有下列性质: (1)0a >时: ①图象都通过点(0,0),(1,1); ②在第一象限内,函数值随x 的增大而增大,即在(0,)+∞上是增函数. (2)0a <时: ①图象都通过点(1,1); ②在第一象限内,函数值随x 的增大而减小,即在(0,)+∞上是减函数; ③在第一象限内,图象向上与y 轴无限地接近,向右与x 轴无限地接近. (3)任何幂函数的图象与坐标轴至多只有一个交点; (4)任何幂函数图象都不经过第四象限; (5)任何两个幂函数的图象最多有三个交点. 二、指数函数 ①定义:函数)1,0(≠>=a a a y x 且称指数函数, 1)函数的定义域为R ; 2)函数的值域为),0(+∞; 3)当10<a 时函数为增函数. 4)有两个特殊点:零点(0,1),不变点(1,)a . 5)抽象性质: ()()(),()()/()f x y f x f y f x y f x f y +=?-= 三、对数函数 如果b a N =(0a >,1a ≠),那么b 叫做以a 为底N 的对数,记作log a N b = log b a a N N b =?=(0a >,1a ≠,0N >). 1.对数的性质 ()log log log a a a MN M N =+. log log log a a a M M N N =-. 指数函数对数函数计算题30-1 1、计算:lg 5·lg 8000+06.0lg 6 1lg )2 (lg 23++. 2、解方程:lg 2(x +10)-lg(x +10)3=4. 3、解方程:23log 1log 66-=x . 4、解方程:9-x -2×31-x =27. 5、解方程:x )8 1(=128. 6、解方程:5x+1=12 3-x . 7、计算:10log 5log )5(lg )2(lg 2233+ +·.10 log 18 8、计算:(1)lg 25+lg2·lg50; (2)(log 43+log 83)(log 32+log 92). 9、求函数121log 8.0--= x x y 的定义域. 10、已知log 1227=a,求log 616. 11、已知f(x)=1322+-x x a ,g(x)=522 -+x x a (a >0且a ≠1),确定x 的取值范围,使得f(x)>g(x). 12、已知函数f(x)=321121x x ?? ? ??+-. (1)求函数的定义域;(2)讨论f(x)的奇偶性;(3)求证f(x)>0. 13、求关于x 的方程a x +1=-x 2+2x +2a(a >0且a ≠1)的实数解的个数. 14、求log 927的值. 15、设3a =4b =36,求a 2+b 1的值. 16、解对数方程:log 2(x -1)+log 2x=1 17、解指数方程:4x +4-x -2x+2-2-x+2+6=0 18、解指数方程:24x+1-17×4x +8=0 19、解指数方程:22)223()223( =-++-x x ±2 20、解指数方程:014332 14111=+?------x x 21、解指数方程:042342222=-?--+-+x x x x 指数函数和对数函数 重点、难点: 重点:指数函数和对数函数的概念、图象和性质。 难点:指数函数和对数函数的相互关系及性质的应用,以及逻辑划分思想讨论函数 y a x ,y log a x 在 a 1及 0 a 1两种不同情况。 1、指数函数: y x 且a 叫指数函数。 定义:函数 aa 0 1 定义域为 R ,底数是常数,指数是自变量。 为什么要求函数 y a x 中的 a 必须 a 0且a 1 。 因为若 a 0时, y 4 x ,当 x 1 时,函数值不存在。 4 a 0 , y 0x ,当 x 0 ,函数值不存在。 a 时, y 1 x x 虽有意义,函数值恒为 1,但 1 对一切 y 1x 的反函数不存在, 因 为 要 求 函 数 y a x 中 的 a 0且 a 1 。 x 1、对三个指数函数 y 2 x , y 1 ,y 10x 的图象的 2 认识。 图象特征与函数性质: 图象特征 函数性质 ( 1)图象都位于 x 轴上方; ( 1) x 取任何实数值时,都有 a x 0 ; 2 0 1 ); ( 2)无论 a 取任何正数, x 0 时, y 1 ; ( )图象都经过点( , ( 3) y 2x , y 10 x 在第一象限内的纵坐 ( 3)当 a x 0,则 a x 1 1 时, 0,则 a x 1 标都大于 1,在第二象限内的纵坐标都小于 1, x 1 y 2 x x 0,则 a x 1 当 0 的图象正好相反; a 1时, 0,则 a x 1 x ( 4) y 2x , y 10 x 的图象自左到右逐渐 ( 4)当 a 1 时, y a x 是增函数, 一、指数的性质 (一)整数指数幂 1.整数指数幂概念: 43 421Λa n n a a a a 个???= )(*∈N n ()0 10a a =≠ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2) ()(),n m mn a a m n Z =∈ (3)()()n n n ab a b n Z =?∈ 其中m n m n m n a a a a a --÷=?=, ()1n n n n n n a a a b a b b b --??=?=?= ??? . 3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a ( )* ∈>N n n ,1,那么这个数叫做a 的n 次方根, 即: 若a x n =,则x 叫做a 的n 次方根, ()* ∈>N n n ,1 例如:27的3次方根3273=, 27-的3次方根3273-=-, 32的5次方根2325=, 32-的5次方根2325-=-. 说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 指数函数和对数函数 知识点总结 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方根,其中n >1,且n ∈N * . 负数没有偶次方根;0的任何次方根都是0,记作00=n 。 当n 是奇数时,a a n n =,当n 是偶数时,?? ?<≥-==) 0() 0(||a a a a a a n n 2.正数的分数指数幂,规定: 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质),,0(R s r a ∈> (1)r a ·s r r a a += ;(2)rs s r a a =)( ;(3) s r r a a ab =)( (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自 变量,函数的定义域为R . 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 做以.a 为底..N 的对数,记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 说明: ○1 注意底数的限制0>a ,且a x N a =?log ;③注意对数的书 写格式. N a log 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数Λ71828.2=e 为底的对数的对数N ln . 2、对数的运算性质:如果0>a ,且1≠a ,0>M ,0>N ,那么: ○1 M a (log ·=)N M a log +N a log ; ○ 2 =N M a log M a log -N a log ;③n a M log n =M a log )(R n ∈. 注意:换底公式a b b c c a log log log =(0>a ,且1≠a ;0>c ,且 1≠c ;0>b ) . 利用换底公式推导下面的结论 (1)b m n b a n a m log log = ; (2)a b b a log 1log =. 3、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对数函数,其中x 是自变量,对数指数函数公式全集
指数函数与对数函数高考题
指数函数和对数函数
幂函数、指数函数和对数函数_对数及其运算法则_教案
指数函数和对数函数
指数函数对数函数幂函数增长速度的比较教学设计
指数函数和对数函数知识点总结
《指数函数和对数函数》知识点汇总及习题详解)
指数函数与对数函数知识点总结
指数、对数函数公式
高考指数函数与对数函数专题复习
对数指数函数公式全集
指数函数、对数函数和幂函数知识点归纳
指数函数对数函数计算题30-1
指数函数和对数函数公式(全)
指数函数和对数函数复习有详细知识点和习题详解
指数函数和对数函数 知识点总结
