泰勒公式

常用泰勒公式

简介 在数学上, 一个定义在开区间(a-r, a+r)上的无穷可微的实变函数或复变函数f的泰勒级数是如下的幂级数 这里，n!表示n的阶乘而f(n)(a) 表示函数f在点a处的n阶导数。如果泰勒级数对于区间(a-r, a+r)中的所有x都收敛并且级数的和等于f(x)，那么我们就称函数f(x)为解析的。当且仅当一个函数可以表示成为幂级数的形式时，它才是解析的。为了检查级数是否收敛于f(x)，我们通常采用泰勒定理估计级数的余项。上面给出的幂级数展开式中的系数正好是泰勒级数中的系数。 如果a = 0, 那么这个级数也可以被称为麦克劳伦级数。 泰勒级数的重要性体现在以下三个方面：首先，幂级数的求导和积分可以逐项进行，因此求和函数相对比较容易。第二，一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数，并使得复分析这种手法可行。第三，泰勒级数可以用来近似计算函数的值。 对于一些无穷可微函数f(x) 虽然它们的展开式收敛，但是并不等于f(x)。例如，分段函数f(x) = exp(?1/x2) 当x≠ 0 且f(0) = 0 ，则当x = 0所有的导数都为零，所以这个f(x)的泰勒级数为零，且其收敛半径为无穷大，虽然这个函数f仅在x = 0 处为零。而这个问题在复变函数内并不成立，因为当z沿虚轴趋于零时 exp(?1/z2) 并不趋于零。 一些函数无法被展开为泰勒级数因为那里存在一些奇点。但是如果变量x是负指数幂的话，我们仍然可以将其展开为一个级数。例如，f(x) = exp(?1/x2) 就可以被展开为一个洛朗级数。 Parker-Sockacki theorem是最近发现的一种用泰勒级数来求解微分方程的定理。这个定理是对Picard iterati on一个推广。 [编辑]

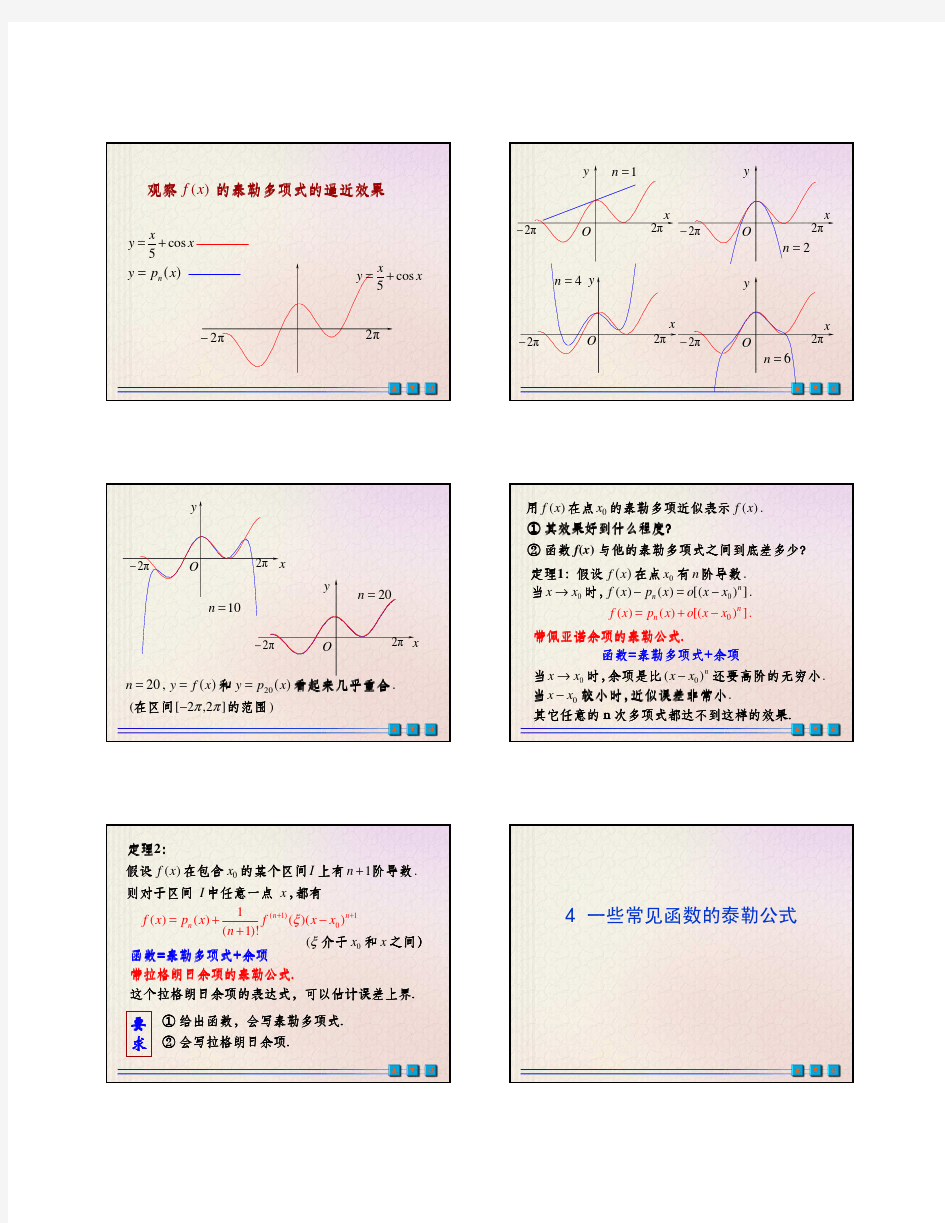
些常用函数及其泰勒展开式的图像

图 1 )exp(x y =及其 Taylor 展开式 其中， 。 ! 4!3!21)(; ! 3!21)(; ! 21)(; 1)(;)exp(4 32443 23322211x x x x x P y x x x x P y x x x P y x x P y e x y x ++++==+++==++==+==== -3 -2-1 0123 -50 5 10 15 20 25 Figure 1 y=exp(x) and its Taylor expansion equation X Y

图 2 )sin(x y =及其 Taylor 展开式 其中， 。 ! 7!5!3)(; !5!3)(; ! 3)(; )();sin(7 53775 35533311x x x x x P y x x x x P y x x x P y x x P y x y -+-==+-==-===== -4 -3-2-1 01234 -8-6-4-202468Figure 2 y=sin(x) and its Taylor expansion equation X Y

图 3 )cos(x y =及其 Taylor 展开式 其中， 。 ! 8!6!4!21)(; !6!4!21)(; ! 4!21)(; !21)(); cos(8 642886 42664 2442 22x x x x x P y x x x x P y x x x P y x x P y x y +-+-==-+-==+-==-=== -4 -3-2-1 01234 -8-6 -4 -2 2 4 Figure 3 y=cos(x) and its Taylor expansion equation X Y

泰勒公式及其在解题中的应用

本科生毕业设计（论文） （ 2014届） 设计（论文）题目泰勒公式及其在解题中应用 作者周立泉 分院理工分院用数学1001班 指导教师（职称）徐华（讲师） 专业班级数学与应用数学） 论文字数 8000 论文完成时间 2014年4月3日 杭州师范大学钱江学院教学部制

泰勒公式及其在解题中应用 数学与应用数学1001班周立泉指导教师徐华 摘要：泰勒公式是数学分析中的一个重要公式，它的基础思想是运用多项式来逼近一个已知函数，而该多项式的系数由给定的函数的各阶导数决定．本文主要归纳了其在证明不等式、等式，求极限，求近似值等各方面的应用． 关键词：泰勒公式;数学分析;导数 Taylor Formula and Its Application in Solving Problem Mathematics and Applied Mathematics class 1001 ZhouLiQuan Instructor: XuHua Abstract：Taylor's formula is an important equation of mathematical analysis, it is the basic idea is to use polynomial approximation to a known function, and the polynomial coefficients given by the derivatives of the function determined. This paper describes the method to prove the Taylor formula,summarized in inequalities, find the limit,the approximate value and the other applications. Keyword:Taylor's formula;Mathematical analysis; derivative.

一些常用函数及其泰勒(Taylor)展开式的图像

其中， 。 ! 4!3!21)(; ! 3!21)(; ! 21)(; 1)(;)exp(4 32443 23322211x x x x x P y x x x x P y x x x P y x x P y e x y x ++++==+++==++==+==== -3 -2-1 0123 -50 5 10 15 20 25 Figure 1 y=exp(x) and its Taylor expansion equation X Y

其中， 。 ! 7!5!3)(; !5!3)(; ! 3)(; )();sin(7 53775 35533311x x x x x P y x x x x P y x x x P y x x P y x y -+-==+-==-===== -4 -3-2-1 01234 -8-6-4-202468Figure 2 y=sin(x) and its Taylor expansion equation X Y

其中， 。 ! 8!6!4!21)(; !6!4!21)(; ! 4!21)(; !21)(); cos(8 642886 42664 2442 22x x x x x P y x x x x P y x x x P y x x P y x y +-+-==-+-==+-==-=== -4 -3-2-1 01234 -8-6 -4 -2 2 4 Figure 3 y=cos(x) and its Taylor expansion equation X Y

其中， 。 4 32)(; 3 2)(; 2 )(; )();1ln(4 32443 23322211x x x x x P y x x x x P y x x x P y x x P y x y -+-==+-==-====+= -1 -0.50 0.51 1.52 -3-2 -1 1 2 3 Figure 4 y=ln(x) and its Taylor expansion equation X Y

北大版高等数学第四章微分中值定理与泰勒公式答案习题

习题4.5 x (,3 2 )3 2 (3 2 ,0) 0(0, 3 2 ) 3 2 (3 2 ,+) f0+00+ f拐点拐 点 拐 点x(,0) -∞0(0,1)1(1,2)2(2,) +∞y'0++0 y''++ y 极小值拐点极大值 ()() ()() 2 22222 22 222 32 1.() ()212,()12(2)4 3 642320,0,. 2 x x x x x x x x f x xe f x e x e e x f x e x x xe e x x xe x x - ------- = ''' -=-=--- =-+=-+==± 求函数 的凸凹性区间及拐点. 解= 23 2 1 ,(,). 3 2(2)0,0,2. 220, 1. y x x x y x x x x x y x x =-∈-∞∞ '=-=-== ''=-== 作下列函数的图形： 2.

222223.,(,).2(2)(2)0,0,2;(2)(22)(42)0,2 2. x x x x x x x x y x e x y xe x e e x x e x x x y e x x e x e x x x --------'=∈-∞+∞=-=-=-==''=--+-=-+==± x (,0)-∞ (0,22)- 22- (22,2)- 2 (2,22)+ 22+ (22,)++∞ y ' - + + - - y '' + + - - 0 + y ? 极小值 ? 拐点 ? 极大值 ? 拐点 ? 22231 4.,0. 11 10, 2 1;. y x x x x y x x x y x =+≠-'=-==''=±=

北大版高等数学第四章 微分中值定理与泰勒公式答案 习题4.1

习题 4.1 3 2 12121.()32[0,1][1,2]R o lle 0,(0)(1)(2)0,()[0,1][1,2]R o lle 620,6 3 (0,1),(1,2),()()0. 332.f x x x x f f f f f x x x x x x f x f x =-+==='-+== = ''====2 验证函数在区间及上满足定理的条件并分别求出导数为的点. 处处可导故在区间及上满足定理的条件.f (x )=3x 讨论下列 解11 1 1 ()[1,1]R o lle ,,(1,1),()0. (1)()(1)(1),,;(2)()1(1)()(1)(1)(1)(1) (1)(1)()0,(1,1),()0. 1 (2)(m n m n m n m n f x c f c f x x x m n f x f x m x x n x x m n x x m m x n n x c f c m f x -----∈-'==+-=- '=+--+--'=+----== ∈-=+'函数在区间上是否满足定理的条件若满足求使为正整数解1/3 2),(0). 33.()ln [1,],?11(),()(1)ln ln 11(1), 1. 4.L ag ran g e (1)|sin sin |||; (2)|tan tan |||,,(/2,/2);(3) ln x f f x x e c f x f e f e e c e x c y x x y x y y x x y b a b b b a ππ-'=- =='= -=-== -=--≤--≥-∈--<<不存在写出函数在区间上的微分中值公式并求出其中的应用中值定理,证明下列不等式:解2 2 2 (0). (1)|sin sin ||(sin )|()||co s |||||.(2)|tan tan ||(tan )|()|sec ||||.(3) ln ln ln (ln )|()((,)). 5.()(1)(4)x c x c x c a a b a x y x x y c x y x y y x x y x c y x y x b a b b a b a b a x b a c a b a a c a P x x x ===-<<'-=-=-≤-'-=-=-≥----'<=-=-= ∈< =--证明多项式的导函数的证1,212,. ()1,2,R o lle ,,,()(2,1),(1,1),(1,2). 6.,,,:()co s co s 2co s (0,). n n P x P x c c c f x c x c x c n x π±±---=+++ 三个根都是实根并指出它们的范围有四个实根根根据定理它的导函数有三个实根又作为四次多项式的导函数是三次多项式,最多三个实根,故的导函数的三个根都是实根,分别在区间设为任意实数证明函数在内必有根证

证明泰勒公式

泰勒中值定理：若函数f(x)在开区间（a，b）有直到n+1阶的导数，则当函数在此区间内时，可以展开为一个关于（x-x.)多项式和一个余项的和： f(x)=f(x.)+f'(x.)(x-x.)+f''(x.)/2!?(x-x.)^2,+f'''(x.)/3!?(x-x.)^3+……+f(n) (x.)/n!?(x-x.)^n+Rn 其中Rn=f(n+1)(ξ)/(n+1)!?(x-x.)^(n+1),这里ξ在x和x.之间，该余项称为拉格朗日型的余项。 （注：f(n)(x.)是f(x.)的n阶导数，不是f(n)与x.的相乘。） 证明：我们知道f(x)=f(x.)+f'(x.)(x-x.)+α（根据拉格朗日中值定理导出的有限增量定理有limΔx→0 f(x.+Δx)-f(x.)=f'(x.)Δx），其中误差α是在limΔx→0 即limx→x.的前提下才趋向于0，所以在近似计算中往往不够精确；于是我们需要一个能够足够精确的且能估计出误差的多项式： P(x)=A0+A1(x-x.)+A2(x-x.)^2+……+An(x-x.)^n 来近似地表示函数f(x)且要写出其误差f(x)-P(x)的具体表达式。设函数P(x)满足P(x.)=f(x.),P'(x.)=f'(x.),P''(x.)=f''(x.),……,P(n)(x.)=f(n)(x.),于是可以依次求出A0、A1、A2、……、An。显然，P(x.)=A0,所以 A0=f(x.)；P'(x.)=A1,A1=f'(x.)；P''(x.)=2!A2,A2=f''(x.)/2!……P(n) (x.)=n!An,An=f(n)(x.)/n!。至此，多项的各项系数都已求出，得： P(x)=f(x.)+f'(x.)(x-x.)+f''(x.)/2!?(x-x.)^2+……+f(n)(x.)/n!?(x-x.)^n. 接下来就要求误差的具体表达式了。设Rn(x)=f(x)-P(x),于是有 Rn(x.)=f(x.)-P(x.)=0。所以可以得出Rn(x.)=Rn'(x.)=Rn''(x.)=……=Rn(n) (x.)=0。根据柯西中值定理可得Rn(x)/(x-x.)^(n+1)=Rn(x)-Rn(x.)/(x-x.)^(n+1)-0=Rn'(ξ1)/(n+1)(ξ1-x.)^n(注：(x.-x.)^(n+1)=0),这里ξ1在x和x.之间；继续使用柯西中值定理得Rn'(ξ1)-Rn'(x.)/(n+1)(ξ1-x.)^n- 0=Rn''(ξ2)/n(n+1)(ξ2-x.)^(n-1)这里ξ2在ξ1与x.之间；连续使用n+1次后得出Rn(x)/(x-x.)^(n+1)=Rn(n+1)(ξ)/(n+1)!，这里ξ在x.和x之间。但 Rn(n+1)(x)=f(n+1)(x)-P(n+1)(x),由于P(n)(x)=n!An,n!An是一个常数，故P(n+1)(x)=0，于是得Rn(n+1)(x)=f(n+1)(x)。综上可得，余项 Rn(x)=f(n+1)(ξ)/(n+1)!?(x-x.)^(n+1)。一般来说展开函数时都是为了计算的需要，故x往往要取一个定值，此时也可把Rn(x)写为Rn。 麦克劳林展开式：若函数f(x)在开区间（a，b）有直到n+1阶的导数，则当函数在此区间内时，可以展开为一个关于x多项式和一个余项的和： f(x)=f(0)+f'(0)x+f''(0)/2!?x^2,+f'''(0)/3!?x^3+……+f(n)(0)/n!?x^n+Rn 其中Rn=f(n+1)(θx)/(n+1)!?x^(n+1),这里0<θ<1。 证明：如果我们要用一个多项式P(x)=A0+A1x+A2x^2+……+Anx^n来近似表示函数f(x)且要获得其误差的具体表达式，就可以把泰勒公式改写为比较简单的形式即当x.=0时的特殊形式： f(x)=f(0)+f'(0)x+f''(0)/2!?x^2,+f'''(0)/3!?x^3+……+f(n)(0)/n!?x^n+f(n+1)

常见泰勒公式展开式

泰勒公式 泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。 泰勒公式得名于英国数学家布鲁克·泰勒，他在1712年的一封信里首次叙述了这个公式。泰勒公式是为了研究复杂函数性质时经常使用的近似方法之一，也是函数微分学的一项重要应用内容历史发展 泰勒公式是高等数学中的一个非常重要的内容，它将一些复杂的函数逼近近似地表示为简单的多项式函数，泰勒公式这种化繁为简的功能，使得它成为分析和研究许多数学问题的有力工具。 18世纪早期英国牛顿学派最优秀的代表人物之一的数学家泰勒( Brook T aylor)，其主要著作是1715年出版的《正的和反的增量方法》，书中陈述了他于1712年7月给他老师梅钦信中提出的著名定理——泰勒定理。1717年,泰勒用泰勒定理求解了数值方程。泰勒公式是从格雷戈里——牛顿差值公式发展而来，它是一个用函数在某点的信息描述其附近取值的公式。如果函数足够光滑,在已知函数某一点各阶导数的前提下,泰勒公式可以利用这些导数值作为系数构建一个多项式来近似该函数在这一点的邻域中的值。1772年，拉格朗日强调了泰勒公式的重要性，称其为微分学基本定理，但是泰勒定理的证明中并没有考虑级数的收敛性，这个工作直到19世纪20年代，才由柯西完成。泰勒定理开创了有限差分理论，使任何单变量函数都

可以展开成幂级数，因此，人们称泰勒为有限差分理论的奠基者。 泰勒公式是数学分析中重要的内容，也是研究函数极限和估计误差等方面不可或缺的数学工具，泰勒公式集中体现了微积分“逼近法”的精髓，在近似计算上有独特的优势。利用泰勒公式可以将非线性问题化为线性问题，且具有很高的精确度，因此其在微积分的各个方面都有重要的应用。泰勒公式可以应用于求极限、判断函数极值、求高阶导数在某点的数值、判断广义积分收敛性、近似计算、不等式证明等方面。

常用的泰勒公式

常用的泰勒公式 e^x = 1+x+x^2/2!+x^3/3!+……+x^n/n!+…… ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1) sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞

泰勒公式及其应用典型例题

泰勒公式及其应用 常用近似公式，将复杂函数用简单的一次多项式函数近似地表示，这是一个进步。当然这种近似表示式还较粗糙（尤其当较大时），从下图可看出。 上述近似表达式至少可在下述两个方面进行改进： 1、提高近似程度，其可能的途径是提高多项式的次数。 2、任何一种近似，应告诉它的误差，否则，使用者“心中不安”。 将上述两个想法作进一步地数学化： 对复杂函数，想找多项式来近似表示它。自然地，我们希望尽可能多地反映出函数所具有的性态——如：在某点处的值与导数值；我们还关心的形式如何确定；近似所产生的误差。 【问题一】 设在含的开区间内具有直到阶的导数，能否找出一个关于的次多项式

近似? 【问题二】 若问题一的解存在，其误差的表达式是什么? 一、【求解问题一】 问题一的求解就是确定多项式的系数。 …………… 上述工整且有规律的求系数过程，不难归纳出：

于是，所求的多项式为： (2) 二、【解决问题二】 泰勒(Tayler)中值定理 若函数在含有的某个开区间内具有直到阶导数，则当时，可以表示成 这里是与之间的某个值。 先用倒推分析法探索证明泰勒中值定理的思路：

这表明： 只要对函数及在与之间反复使用次柯西中值定理就有可能完成该定理的证明工作。 【证明】 以与为端点的区间或记为，。 函数在上具有直至阶的导数， 且 函数在上有直至阶的非零导数， 且 于是，对函数及在上反复使用次柯西中值定理，有

三、几个概念 1、 此式称为函数按的幂次展开到阶的泰勒公式； 或者称之为函数在点处的阶泰勒展开式。 当时，泰勒公式变为 这正是拉格朗日中值定理的形式。因此，我们也称泰勒公式中的余项。 为拉格朗日余项。 2、对固定的，若 有

常用十个泰勒展开公式

常用bai泰勒展开公式如下： 1、due^x = 1+x+x^2/2!+x^3/3!+……zhi+x^n/n!+…… 2、daoln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1) 3、sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞

9、cosh x = 1+x^2/2!+x^4/4!+……+(-1)k*(x^2k)/(2k)!+……(-∞

常用的泰勒公式

常用的泰勒公式 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】

常用的泰勒公式 e^x = 1+x+x^2/2!+x^3/3!+……+x^n/n!+…… ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1) sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k- 1)!+……。(-∞

泰勒公式的理解及泰勒公式

对泰勒公式的理解及泰勒公式的应用 1 函数展开与向量空间 泰勒公式是函数展开的一种工具,也就是说,利用泰勒公式将函数展成幂级数是函数展开的一种方法,当然,函数的展开方法有多种,例如：用泰勒公式展开、三角级数的展开等。为更好地理解函数展开的意义以及泰勒公式的应用，文章先对函数的展开进行论述,然后,用例题对其应用做进一步的说明。 在高等数学中,函数展开有许多不同的形式,最常用的有如下两种类型的函数级数展开。 1.1 函数的泰勒展开（幂级数展开） 若函数f(x)在区间｛x｜｜x-x 0｜＜R｝内无穷可微,且它的Lagrange余项r n(x)当n→∞ 时,收敛于零,则在这区间内有： 1 2 函数的三角级数展开 若函数f(x)在区间［-π,π］上连续且逐段光滑,则在这区间内有： 从函数展开式(1)和(2)两边的项来看,左边的函数f(x)作为一个整体,它只有有限的一项,而右边却包含着无限多项,说明在一定条件下,有限形式的函数可以用无限形式的级数来表示, 关于这一点,可以从另一个视角来看，若把展开式(1)和(2)中的函数系： ｛1,(x-x0),(x-x 0)2,(x-x0)3,…,(x-x0)n,…｝ {1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…} 分别看成无限维函数空间的两个坐标系, 其中的函数就是相应的坐标向量,则f(x)就可以看作这个空间的一个点（或一个向量）,则两级数的系数组成的两个数列: ｛a0,a1,a2,…,a n｝与｛a0,a1,b1,a2,b2，…，n,b n,…｝ 就是f(x)分别在这两个坐标系中的坐标,于是从形式来看，f(x)作为这无限维空间中的一个点（一个向量）,但从数来看，f(x)在这个空间中却要用无限个坐标来决定.在高等数学中, 根据问题的需要,进行有限与无限形式的相互变换,在解决数学问题中是常有的。可见,换个角度看函数的展开,会给人加深印象,能在原有的基础上根深蒂固。 谈到有限与无限,在高等数学中,根据问题的需要,进行有限与无限形式的相互变换,在解决数学问题中是常常会用到的,这就是泰勒公式的魅力所在.比如说：函数的分解与求和,函数关系的证明等,就要用这种有限与无限之间的变换方法。

最新北大版高等数学第四章微分中值定理与泰勒公式答案第四章总练习题

北大版高等数学第四章微分中值定理与泰勒公式答案第四章总 练习题

第四章总练习题 000000001..()()[()()]. ()(),[0,].()()(),(0)0. Lagrange ,(0,1)()(0)(),f x h f x h f x h f x h h f x x f x x x h g g x f x x f x x g g h g g h h θθθθθθ''+--=++-+--∈'''=++-=∈'-=00设y=f(x)在[x -h,x +h](h>0)内可导证明存在,0<<1使得令g(x)=(x)在[0,h]内可导,根据公式存在使得 证00000 ()()[()()].2.:0,()1/4()1/2lim ()1/4,lim ()1/2.4(())211()(124x x f x h f x h f x h f x h h x x x x x x x x x x θθθθθθθθ→→+∞ ''+--=++-≥= ≤≤=== = =+=++=+即证明当时中的满足且 00). 11()(12), 441 11()(12)(1(1)2). 442 11 lim ()lim (12).44 1 lim ()lim (12)4 1 lim 4x x x x x x x x x x x x x x x x θθθθ→→→+∞→+∞≥+=-=+≤+++-==+==+=由算术几何平均不等式得 2 2 111lim lim .442 3,012 3.()()[0,2]1, 1,01 (2)(0)1().12 0, 1x x x x f x f x x x x x f f f x x x = ===?-≤≤??=??<<+∞??-≤≤?-? '==?--<<+∞??设求在闭区间上的微分中值定理的中间值. 解2/23/21. 221111,;,()[0,2]222x x x f x x -=--=-=-=-=1 在闭区间上的微分中值定理的中间值为2

泰勒展开式

函数的幂级数展开式 通过前面的学习我们看到，幂级数不仅形式简单，而且有一些与多项式类似的性质。而且我们还发现有一些可以表示成幂级数。为此我们有了下面两个问题： 问题1：函数f(x)在什么条件下可以表示成幂级数 ； 问题2：如果f(x)能表示成如上形式的幂级数，那末系数c n(n=0,1,2,3,…)怎样确定？ 下面我们就来学习这两个问题。 泰勒级数我们先来讨论第二个问题.假定f(x)在a的邻区内能表示成 这种形式的幂级数，其中a是事先给定某一常数，我们来看看系数c n与f(x)应有怎样的关系。 由于f(x)可以表示成幂级数，我们可根据幂级数的性质，在x=a的邻区内f(x)可任意阶可导.对其幂级数两端逐次求导。得： ， ， ……………………………………………… ， ……………………………………………… 在f(x)幂级数式及其各阶导数中，令x=a分别得： 把这些所求的系数代入得： 该式的右端的幂级数称为f(x)在x+a处的泰勒级数. 关于泰勒级数的问题 上式是在f(x)可以展成形如的幂级数的假定下得出的.实际上，只要f(x)在x=a处任意阶可导，我们就可以写出函数的泰勒级数。

问题：函数写成泰勒级数后是否收敛？是否收敛于f(x)？ 函数写成泰勒级数是否收敛将取决于f(x)与它的泰勒级数的部分和之差 是否随n→＋∞而趋向于零.如果在某一区间I中有那末f(x)在x=a处的泰勒级数将在区间I中收敛于f(x)。此时，我们把这个泰勒级数称为函数f(x)在区间I中的泰勒展开式. 泰勒定理 设函数f(x)在x=a的邻区内n+1阶可导，则对于位于此邻区内的任一x，至少存在一点c,c 在a与x之间，使得： 此公式也被称为泰勒公式。(在此不加以证明） 在泰勒公式中，取a=0，此时泰勒公式变成： 其中c在0与x之间, 此式子被称为麦克劳林公式。 函数f(x)在x=0的泰勒级数称为麦克劳林级数.当麦克劳林公式中的余项趋于零时，我们称相应的泰勒展开式为麦克劳林展开式. 即： 几种初等函数的麦克劳林的展开式 1.指数函数e x 2.正弦函数的展开式

一些常用的泰勒公式

一些常用的泰勒公式 作者：余世明 单位：星茂装饰有限公司 摘要：一些常用的泰勒公式 关键字：泰勒公式 前切点泰勒公式 后切点泰勒公式 中间切点泰勒公式 城市：上海 邮政编码：200011 中图分类号:O17 title: Some common Taylor formulas author: Yu Shiming company: Xinmao Decoration company city: Shanghai postcode: 200011 digest: Some common Taylor formulas 正文： 很容易推导下面的公式： K --+---=?3)2(2)1()(!3)()(!2)())(()(c x x f c x x f c x x f dx x f 1 由此可以通过牛顿莱布尼兹公式得到一下公式： Λ----+ -------=?])(!3)()(!3)([])(!2)()(!2)([)])(())(([)(3)2(3)2(2)1(2)1(c a a f c b b f c a a f c b b f c a a f c b b f dx x f b a 2 当 c=a 公式 2 为： Λ--+---=? 3)2(2)1()(!3)()(!2)())(()(a b b f a b b f a b b f dx x f b a 3 当 c=b 公式 2 为： Λ+-+-+-=?3)2(2)1()(! 3)()(!2)())(()(a b a f a b a f a b a f dx x f b a 4 当 c=0 公式 2 为： Λ--+---=?]!3)(!3)([]!2)(!2)([])()([)(3)2(3)2(2)1(2)1(a a f b b f a a f b b f a a f b b f dx x f b a 5 还可以利用以下公式，前半部分用公式4，后半部分用公式3： ???+=c a b c b a dx x f dx x f dx x f )()()( 6 或者可以利用以下公式进行积分： Λ+-+-+-+=3!3)(2!2)()1()()())(()()()3()2(c x c x c x c f c f x f c f c f 积分得到公式如下： Λ+-+-+-+=?????dx c x dx c x dx c x c f dx c f dx x f b a c f b a c f b a b a b a 3!3) (2!2)()1()()()()()()()3()2(

常用的泰勒公式

常用的泰勒公式 Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】

常用的泰勒公式 e^x = 1+x+x^2/2!+x^3/3!+……+x^n/n!+…… ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|<1) sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞

泰勒公式的深刻理解

泰勒公式的深刻理解 1 学生对泰勒公式的疑惑及其根源分析 泰勒公式这一节的教学目标是要求学生理解泰勒公式,并了解它的一些应用。然而,在完成教学任务后仍有相当多的学生心存疑惑,不能不说这是教学上的一个失败。平时和学生聊起数学的学习,谈到泰勒公式, 很多学生都说不理解;讲课中要用到泰勒公式时,学生也会叫喳喳的,表现出畏难的情绪。和同事们谈起这事,上过这门课的教师都有同感。学生在什么地方卡住了呢？在与学生沟通中发现学生通常会这样来描述他们的疑惑:不知道它是什么意思,不知道它有什么用。是什么原因导致了学生的不理解？通过进一步与学生沟通和不断地思考,我们做出如下分析: (1)教科书中泰勒公式的表达方式与学生的思维方式不一致。 我们采用的教材是同济大学应用数学系编写的《高等数学》,教材中的泰勒公式以定理的形式给出: 泰勒中值定理如果函数f (x)在含有x0的某个开区间(a,b)内具有直到(n+1)阶的导数,则对任一 ,(1) 其中 (2) 这里x 为x与x0之间的某个值x。 公式(1)称为n阶泰勒公式。 刚从中学步入大学,大部分学生还没有完全适应大学的思维方式。公式(1)的右端由两部分构成:x-x0的多项式和余项R n(x),复杂的多项式加上一个需要附加说明的余项和学生心中公式(在中学中认识的公式)的表达方式不一致,由于学生的抽象思维没有达到一定的程度,他们还无法接受这么一个有着附加说明(而且说明也很抽象)的公式,用学生的话说就是不知道它讲的是什么。 (2)泰勒公式证明过程的抽象性加深了学生的疑惑。 泰勒公式是通过重复应用柯西中值定理来证明的,过程比较抽象, 由于学生没有理解泰勒公式的表达式,也就是说没有完全弄清楚定理的条件和结论,在这种学生还没有做好准备的情况下,公式证明过程的抽象性只能加深学生的疑惑。 (3)例题的讲解没有给学生的理解带来预期的帮助。 由于没有分重视学生思维方式上的差异,教师通常认为给出泰勒公式后,针对一些常见的函数写出相应的泰勒公式,再简单地提一提近似 94 中国科教创新导刊 China Education Innovation Herald 计算就可以达到目标了。的确,学生也能模仿例题完成作业,但是学生仍表示不知道这个公式有什么用。也就是说学生并没有理解例题的作用,没有将例题和泰勒公式的理解联系在一起,认为例题也就是套着公式(1)写出相应的式子罢了。在没有理解泰勒公式的前提下,写出常见函数的泰勒公式对学生来说只是一种机械行为,没有任何意义。 2 教学设计 通常的教学过程都是以泰勒公式的证明、常见函数的泰勒公式为重点和难点,基于以上的分析,我们在教学设计时改换思路,教学中对以下三方面进行了尝试,取得了较好的教学效果: (1)把重点放在问题的提出和泰勒公式的引入上。通常情况下教师在这里花的时间并不多,在大部分学生还理不清头绪的时候老师就已经给出抽象的泰勒中值定理了。根据学生的具体情况,我们认为这部分内容对于我们的学生理解泰勒公式有很大的帮助,讲好了有事半功倍的作用,因此我们把重点放在这里。 (2)尝试用另外一种形式来描述泰勒公式,以促进学生的理解。 (3)改变例题的讲解方式。将第一个例题的重点由写出泰勒公式改为近似计算,以加强学生对泰勒公式的理解并了解它的一些应用。 具体设计思路如下: (1)问题的提出。 微分的近似计算公式的缺点:在实际应用中有可能不满足精度要求。问题:如何才能提高精度？ (2)提出猜想。 微分的近似计算公式实质上就是用一次多项式P1(x)=a0+a1(x-x0) 来拟合函数,那么能否用n次多项式P n(x)=a0+a1(x-x0)+a2(x-x0)2+a n(xx0)n来拟合函数呢？ (3)拟合系数的选取。 问题:如果要用多项式来拟合函数:,系数a i(i=1,?n)该如何选取？ 从微 分的近似 计算公式出发,研究一次多项式P1(x)的系数与函数f (x)的关系: 1 函数f (x)之间的关系: 。 将上述关系作为拟合条件进行推广:如果要用多项式来拟合函数, 即有,那么可以猜想拟合多项式P n(x)与函数f (x)之间应该有下列关系: , 由 此可得到拟合系数与函数的之间的关系:于是可选取多项式 ,有 ,由此推出拟合多项式P(x)与

常用等价无穷小 _泰勒公式_三角函数

x →0 （1） sinx ～x （2） arcsinx ～x （3） tanx ～x （4） arctanx ～x （5） 1?cos x ～x 22 （6） ?x ?1~x （7） a x ?1~xlna （8） ln(1+x)～x （9） log a (1+x )= x ln a （10） (1+x )u ?1~ux （11） √n ?1~x n （12） √?1~x 2 （13） x ?sin x ~arc sin x ?x~ x 36 （14） tan x ?x~x ?arctan π~ x 33 （15） tan x ?sin x ~x 32 （16） ln (1+x )?x~?x 22 x →1 （1） ln x =ln [1+(x ?1)]~x ?1 （2） x x ?1~?x ln x ?1~x ln x 泰勒公式 ?x =1+x +x 2+?+x n

sin x=x?x3 + x5 ??+(?1)n?1 x2n?1 () cosx=1?x2 + x4 ??+(?1)n x2n () ln(x+1)=x?x2 2 + x3 3 ??+(?1)n?1 x n n 1 1+x =1?x+x2??+(?1)n x n 1 =1+x+x2+?+x n √x+1=1+x ? x2 1√1+x =1? x 2 + 3 8 x2 tan x=x+x3 3 + 2 15 x5 三角函数公式 1+tan2x=s?c2x s?c2x?1=tan2x 1+cot2x=csc2x csc2x?1=cot2x sin2x=1 2(1?cos2x)sin2x 2 =1 2 (1?cos x) cos2x=1 2(1+cos2x)cos2x 2 =1 2 (1+cos x) cos2x=cos2x?sin2x sin2x=2sin x?cos x 常用积分公式 ∫ 1 √x ?x=2√x+C