树状数组
树状数组:它能够高效地获取数组中连续n个数的和. 数组{a}中的元素可能不断地被修改,怎样才能快速地获取连续几个数的和?
2、树状数组基本操作传统数组(共n个元素)的元素修改和连续元素求和的复杂度分别为O(1)和O(n)。树状数组通过将线性结构转换成伪树状结构(线性结构只能逐个扫描元素,而树状结构可以实现跳跃式扫描),使得修改和求和复杂度均为O(lgn),大大提高了整体效率。给定序列(数列)A,我们设一个数组C满足C[i] = A[i–2^k+ 1] + … + A[i]其中,k为i在二进制下末尾0的个数,i从1开始算!则我们称C为树状数组。下面的问题是,给定i,如何求2^k? 答案很简单:2^k=i&(i^(i-1)) ,也就是i&(-i) 下面进行解释:
以i=6为例(注意:a_x表示数字a是x进制表示形式):(i)_10 = (0110)_2 (i-1)_10=(0101)_2 i xor (i-1) =(0011)_2 i and (i xor (i-1)) =(0010)_2 2^k = 2
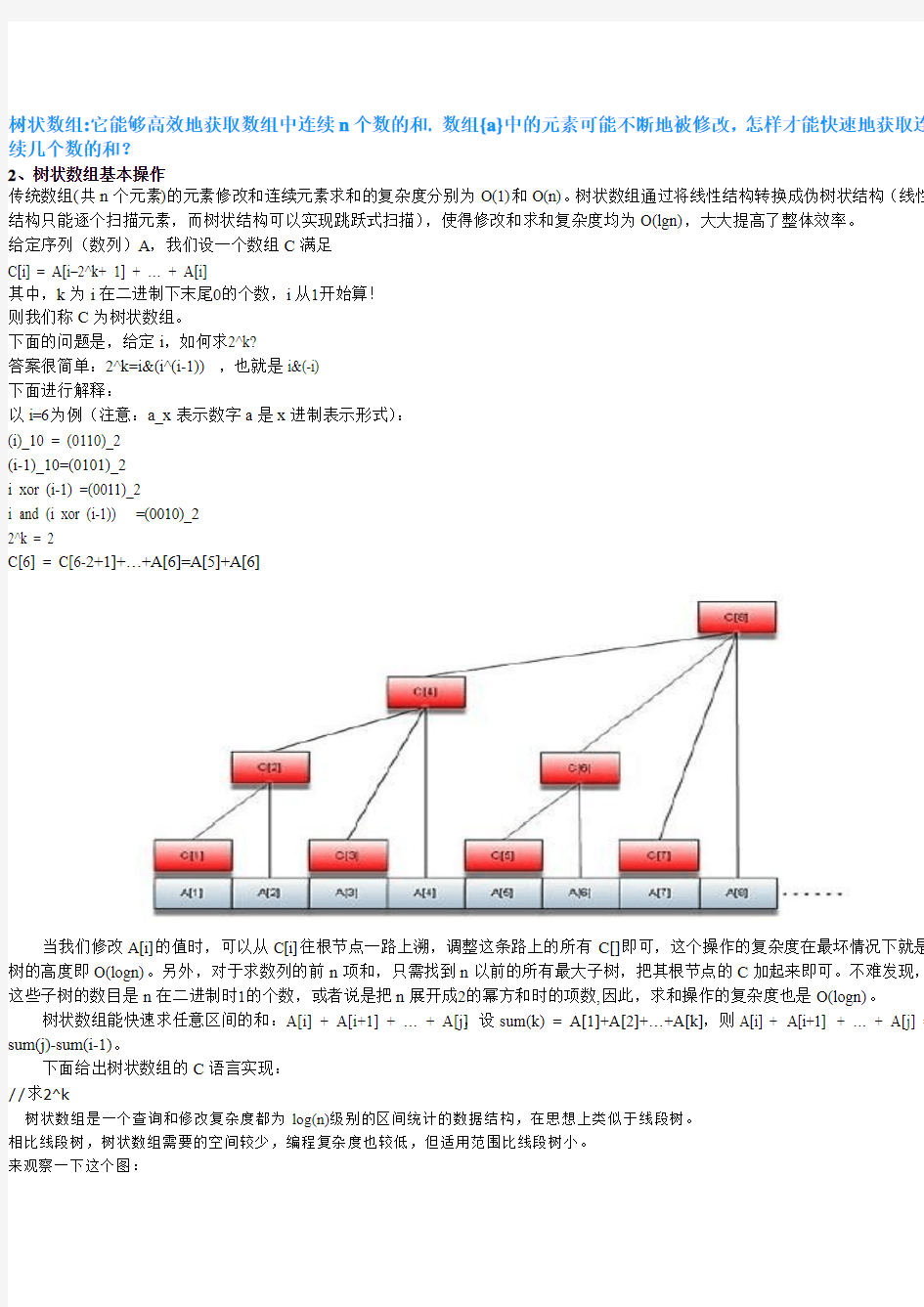
C[6] = C[6-2+1]+…+A[6]=A[5]+A[6]
当我们修改A[i]的值时,可以从C[i]往根节点一路上溯,调整这条路上的所有C[]即可,这个操作的复杂度在最坏情况下就是树的高度即O(logn)。另外,对于求数列的前n项和,只需找到n以前的所有最大子树,把其根节点的C加起来即可。不难发现,这些子树的数目是n在二进制时1的个数,或者说是把n展开成2的幂方和时的项数,因此,求和操作的复杂度也是O(logn)。
树状数组能快速求任意区间的和:A[i] + A[i+1] + … + A[j],设sum(k) = A[1]+A[2]+…+A[k],则A[i] + A[i+1] + … + A[j] = sum(j)-sum(i-1)。
下面给出树状数组的C语言实现://求2^k
树状数组是一个查询和修改复杂度都为log(n)级别的区间统计的数据结构,在思想上类似于线段树。相比线段树,树状数组需要的空间较少,编程复杂度也较低,但适用范围比线段树小。来观察一下这个图:
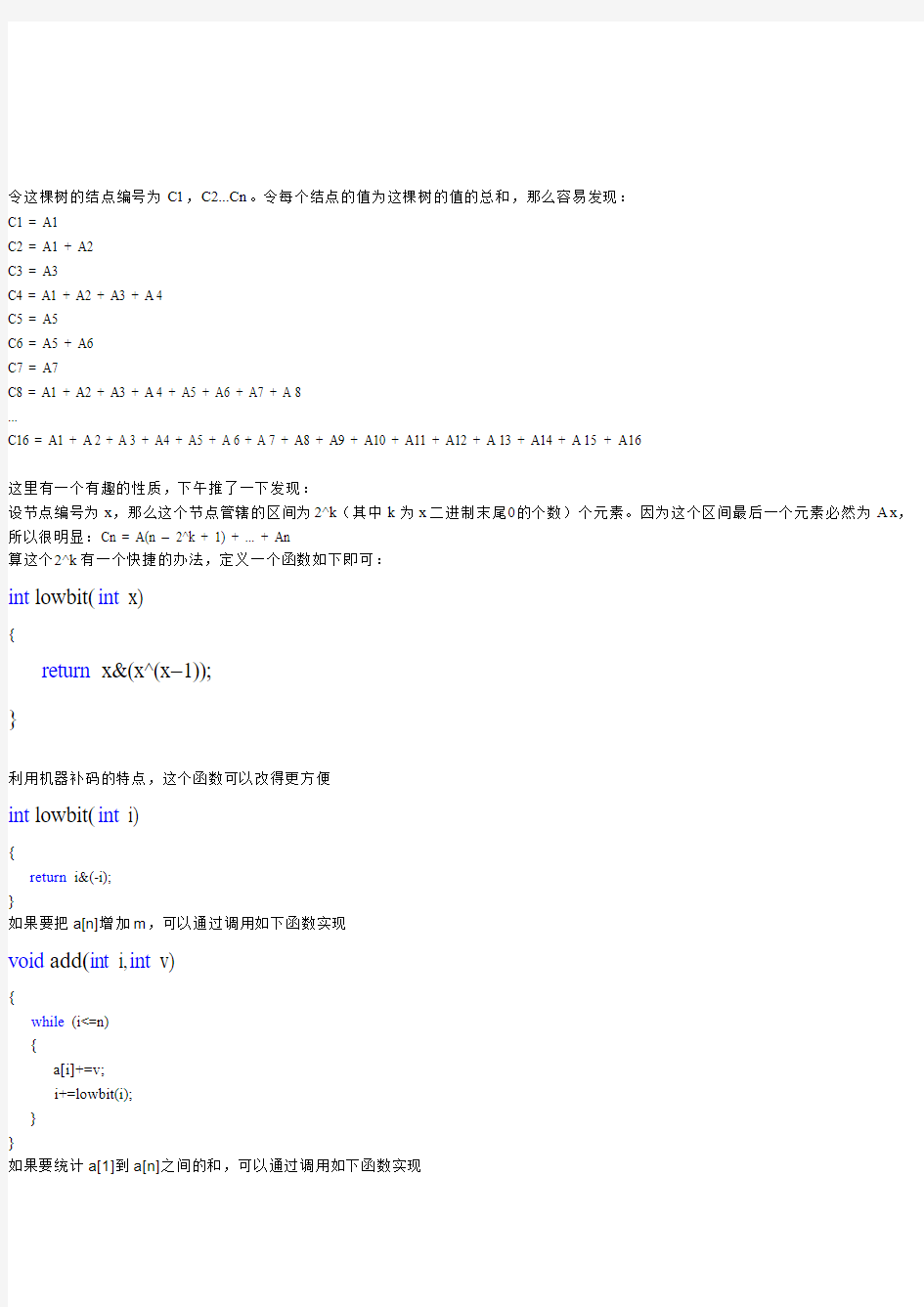
令这棵树的结点编号为C1,https://www.360docs.net/doc/cb17287813.html,。令每个结点的值为这棵树的值的总和,那么容易发现:C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
这里有一个有趣的性质,下午推了一下发现:
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为A x,所以很明显:Cn = A(n – 2^k + 1) + ... + An
算这个2^k有一个快捷的办法,定义一个函数如下即可:
int lowbit(int x)
{
return x&(x^(x–1));
}
利用机器补码的特点,这个函数可以改得更方便
int lowbit(int i)
{
return i&(-i);
}
如果要把a[n]增加m,可以通过调用如下函数实现
void add(int i,int v)
{
while (i<=n)
{
a[i]+=v;
i+=lowbit(i);
}
}
如果要统计a[1]到a[n]之间的和,可以通过调用如下函数实现
int sum(int i)
{
int s=0;
while (i>0)
{
s+=a[i];
i-=lowbit(i);
}
return s;
}
1、概述
树状数组(binary indexed tree),是一种设计新颖的数组结构,它能够高效地获取数组中连续n个数的和。概括说,树状数组通常用于解决以下问题:数组{a}中的元素可能不断地被修改,怎样才能快速地获取连续几个数的和?
2、树状数组基本操作
传统数组(共n个元素)的元素修改和连续元素求和的复杂度分别为O(1)和O(n)。树状数组通过将线性结构转换成伪树状结构(线性结构只能逐个扫描元素,而树状结构可以实现跳跃式扫描),使得修改和求和复杂度均为O(lgn),大大提高了整体效率。给定序列(数列)A,我们设一个数组C满足C[i] = A[i–2^k+ 1] + … + A[i]
其中,k为i在二进制下末尾0的个数,i从1开始算!则我们称C为树状数组。
下面的问题是,给定i,如何求2^k? 答案很简单:2^k=i&(i^(i-1)) ,也就是i&(-i) 下面进行解释:
以i=6为例(注意:a_x表示数字a是x进制表示形式):(i)_10 = (0110)_2
(i-1)_10=(0101)_2
i xor (i-1) =(0011)_2
i and (i xor (i-1)) =(0010)_2
2^k = 2
C[6] = C[6-2+1]+…+A[6]=A[5]+A[6]数组C的具体含义如下图所示:
当我们修改A[i]的值时,可以从C[i]往根节点一路上溯,调整这条路上的所有C[]即可,这个操作的复杂度在最坏情况下就是树的高度即O(logn)。另外,对于求数列的前n项和,只需找到n以前的所有最大子树,把其根节点的C加起来即可。不难发现,这些子树的数目是n在二进制时1的个数,或者说是把n展开成2的幂方和时的项数,因此,求和操作的复杂度也是O(logn)。树状数组能快速求任意区间的和:A[i] + A[i+1] + … + A[j],设sum(k) = A[1]+A[2]+…+A[k],则A[i] + A[i+1] + … + A[j] = sum(j)-sum(i-1)。
下面给出树状数组的C语言实现:
1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 //求2^k
intlowbit(intt)
{
returnt & ( t ^ ( t - 1 ) );
}
//求前n项和
intsum(intend)
{
intsum = 0;
while(end > 0)
{
sum += in[end];
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
end -= lowbit(end); }
returnsum;
}
//增加某个元素的大小voidplus(intpos,intnum) {
while(pos <= n)
{
in[pos] += num;
pos += lowbit(pos); }
}
3、扩展——二维树状数组一维树状数组很容易扩展到二维,二维树状数组如下所示:C[x][y] = sum(A[i][j])
其中,x-lowbit[x]+1 <= i<=x且y-lowbit[y]+1 <= j <=y [poj 2155 Matrix]
【题意】01序列,用^操作修改某个区间的值,求修改后某个点的值。【做法】如果要修改[a,b]区间的值=》修改[a,1]+[b,1]的值即可,如何快速修改是难点,我们用树状数组能够快速的记录某个区间[x,1]的值,即利用了x&(-x)
修改的每个关键点(用x&(-x) 计算的点)点只是记录了这段区间被修改过一次,这样就能用树状的性质
用logn的时间快速修改值了。那么查找的x点值时候只要看在x-n的树的路径中总共被修改了奇偶次数即可比如修改[8,6] 转为修改[8,1] [5,1] [8,1]修改后就改变了8节点的值(+1)[5,1]修改了(5,4节点的值) 此时每个节点的值为:
1 2 3 4 5 6 7 8 0 0 0 1 1 0 0 1如果再次修改[6,5] =》[6 1] [4 1] [6,1]分别修改了(6,4) [4,1]修改了(4) 此时每个节点的值为:1 2 3 4 5 6 7 8 0 0 0 3 1 1 0 1 Q4 的结果为4->8 = 4 Q1 的结果为1->2->4->8 =4 Q5 ………… 5->6->8 = 3 [总结]树状数组用updata操作来更新点的值。用sumup来统计某一区间的值。void Update(int x, int c) {
int i;
for (i = x; i < maxn; i += Lowbit(i)) {
tree[i] += c;
} } int sumup(int x) {
int i;
int temp(0);
for (i = x; i >= 1; i -= Lowbit(i)) {
temp += tree[i];
} return temp; }如果用updata里面的操作来修改某个区间的值,用sumup里面的操作得到某个点的值void Update(int x, int c) {
int i;
for (i = x; i >0; i -= Lowbit(i)) {
tree[i] += c;
} } int Sumup(int x) {
int i;
int temp(0);
for (i = x; i { temp += tree[i]; } return temp; } poj 1195 Mobile phones(二维树状数组) (2011-07-23 10:44:04) 标签:it分类:ACM Mobile phones Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 8810 Accepted: 3906 Description Suppose that the fourth generation mobile phone base stations in the Tampere area operate as follows. The area is divided into squares. The squares form an S * S matrix with the rows and columns numbered from 0 to S-1. Each square contains a base station. The number of active mobile phones inside a square can change because a phone is moved from a square to another or a phone is switched on or off. At times, each base station reports the change in the number of active phones to the main base station along with the row and the column of the matrix. Write a program, which receives these reports and answers queries about the current total number of active mobile phones in any rectangle-shaped area. Input The input is read from standard input as integers and the answers to the queries are written to standard output as integers. The input is encoded as follows. Each input comes on a separate line, and consists of one instruction integer and a number of parameter integers according to the following table. The values will always be in range, so there is no need to check them. In particular, if A is negative, it can be assumed that it will not reduce the square value below zero. The indexing starts at 0, e.g. for a table of size 4 * 4, we have 0 <= X <= 3 and 0 <= Y <= 3. Table size: 1 * 1 <= S * S <= 1024 * 1024 Cell value V at any time: 0 <= V <= 32767 Update amount: -32768 <= A <= 32767 No of instructions in input: 3 <= U <= 60002 Maximum number of phones in the whole table: M= 2^30 Output Your program should not answer anything to lines with an instruction other than 2. If the instruction is 2, then your program is expected to answer the query by writing the answer as a single line containing a single integer to standard output. Sample Input 0 4 1 1 2 3 2 0 0 2 2 1 1 1 2 1 1 2 -1 2 1 1 2 3 3 Sample Output 3 4 Source code: #include #include #include #define le 1025 int pic[le][le]; int n; int lowbit(int p){ return p&(-p); } void add(int x,int y,int d){ int i=y; while(x<=n){ y=i; while(y<=n){ pic[x][y]+=d; y+=lowbit(y); } x+=lowbit(x); } } int sum(int x,int y){ int i=y,s=0; while(x>0){ y=i; while(y>0){ s+=pic[x][y]; y-=lowbit(y); x-=lowbit(x); } return s; } void init(){ int i,j; for(i=0;i<=n;i++) for(j=0;j<=n;j++) pic[i][j]=0; } int input(){ int i,X,Y,A,L,B,R,T,num; while(scanf("%d",&i)==1){ if(i==3) return1; else if(i==0){ scanf("%d",&n); init(); } else if(i==1){ scanf("%d%d%d",&X,&Y,&A); add(X+1,Y+1,A); } else{ scanf("%d%d%d%d",&L,&B,&R,&T); num=sum(R+1,T+1); num+=sum(L,B); num-=sum(L,T+1); num-=sum(R+1,B); printf("%d\n",num); } } return0; } int main(void){ return0; } POJ 2182 lost cows 2011-09-27 20:30:07| 分类:数据结构|字号大中小订阅 有编号1到N,打乱次序。现给出一个序列,序列中每一个数代表这个位置的之前编号比它小的数的个数,找出当前位置的初始编号。算法:从后向前扫描,遇到数字a,说明它是剩余序列中第a+1个数,找到该编号后删去,重复上述操作。找的过程要借助于线段树,看一个区间内未被删除的数字个数能否满足使当前要找的数成为第a+1个,能则递归左子树,否则递归右子树,直至到叶子节点,那么叶子节点的值就是其初始编号。==================================================================================================== = #include seg[num].rest--; if ( seg[num].left == seg[num].right ) return seg[num].left; else if ( seg[num*2].rest >= n ) return query(num*2,n); else return query(num*2+1,n-seg[num*2].rest); } //*********************************************** int main() { int i; //freopen("2182.txt","r",stdin); scanf("%d",&N); for (i=2; i<=N; i++) scanf("%d",&range[i]); range[1] = 0; build(1,1,N); for (i=N; i>=1; i--) ans[i] = query(1,range[i]+1); for (i=1; i<=N; i++) printf("%d\n",ans[i]); return 0; } 题意:给定n个区间,问每个区间所覆盖的区间的个数。思路:第三道树状数组,终于有感觉了,要不就傻X了,对区间排序,然后树状数组查询,思路和Stars那道差不多,不过还要处理重合区间的情况,只需排序后O(N)扫描一遍就好了。 /*Cows 2481 * 树状数组第三题,对牛排序即可,注意要* 排除体型相等的牛. */ #include #include #include #include #include #include #include #include using namespace std; const int BORDER = (1<<20)-1; const int MAXSIZE = 37; const int MAXN = 100200; const int INF = 1000000000; #define CLR(x,y) memset(x,y,sizeof(x)) #define ADD(x) x=((x+1)&BORDER) #define IN(x) scanf("%d",&x) #define OUT(x) printf("%d\n",x) #define MIN(m,v) (m)<(v)?(m):(v) #define MAX(m,v) (m)>(v)?(m):(v) #define ABS(x) ((x)>0?(x):-(x)) typedef struct{ int s,e; int id; }Node; Node node[MAXN]; int tre[MAXN],n_tre; int n; int ans[MAXN],same[MAXN]; int lowbit(int x) { return x&(-x); } void modify(int ind,int delta) { while( ind <= n_tre) { tre[ind] += delta; ind += lowbit(ind); } } int get_sum(int ind) { int sum = 0; while(ind > 0) { sum += tre[ind]; ind -= lowbit(ind); } return sum; } bool cmp(const Node& a,const Node& b) if(a.e == b.e) return a.s < b.s; return a.e > b.e; } int init() { n_tre = 100400; CLR(same,0); CLR(tre,0); CLR(ans,0); return0; } int input() { for(int i = 0; i < n; ++i) { scanf("%d%d",&node[i].s,&node[i].e); ++node[i].s; ++node[i].e; node[i].id = i; } return0; } int _find_same() { int i,j,tmp; for(i = 1; i < n; ++i) { tmp = 0; if(node[i-1].s == node[i].s && node[i-1].e == node[i].e) same[i] = same[i-1] + 1; } return0; } int work() { int i,j,s,e,tmp; sort(node,node+n,cmp); _find_same(); for(i = 0; i < n; ++i) { ans[node[i].id] = get_sum(node[i].s)-same[i]; modify(node[i].s,1); printf("%d",ans[0]); for(i = 1; i < n; ++i) printf("%d",ans[i]); printf("\n"); return0; } int main() { while(IN(n)) { if(!n) break; init(); input(); work(); } return0; } C++算法基础复习NOIP2014 1.二分法 通过每次把答案所在小区间收缩一半的方法,使区间的两个端点逐步迫近答案,以求得答案(近似值),这种方法叫做二分法。 一般来说,能够应用二分法的题目必须满足以下条件:答案存在单调性,通常用于对于二分所得到的答案进行验证,或者对数组进行查找。时间复杂度:O(n*log n) ①对一个数组进行查找,要求返回查找元素在数组中的位置,若不存在,则返回-1(查找数据) int search(int* a, int len, int goal) { int low = 0; int high = len - 1; while(low <= high) //边界条件 { int middle = (low + high)/2; //定义中间数据 if(a[middle] == goal) return middle; //若找到答案,返回答案位置 else if(a[middle] > goal) high = middle - 1; //大于答案,向右查找 else low = middle + 1; //小于答案,向左查找 } return -1; //未找到答案,返回-1 } ②对答案的二分查找 double find() { double l,r,mid; const double e=0.0001; //浮点数精度设置 while(r-l>e) { mid=(l+r)/2; if(f(mid)) l=mid; //f(x)为条件函数,用来验证答案是否符合要求 else r=mid; } return r; } 2.动态规划 把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。 动态规划适用于与前文有关,并且与后面的数据无关的题目。动态规划可以求解多种类型的问题,比如上升序列,下降序列,最大连续子串等。由于动态规划算法的多样性,时间复杂度各有千秋。 ①线性查找:上升序列,下降序列,最大连续子串等。时间复杂度O(n2)/O(n) : (1)导弹拦截: for(int i=0;i 树状数组及其应用 ( Binary Indexed Trees ) 一、什么是树状数组 【引例】 假设有一列数{A i}(1<=i<=n),支持如下两种操作: 1.将A k的值加D。(k,D是输入的数) 2.输出A s+A s+1+…+A t(s,t都是输入的数,s<=t) 分析一:线段树 建立一颗线段树(线段长度1~n)。一开始所有结点的count值等于0。 对于操作1,如果把A k的值加D,则把所有覆盖了A k的线段的count值加D。只有log2n 条线段会受到影响,因此时间复杂度是O(log2n)。 每条线段[x..y]的count值实际上就是A x+A x+1+…+A y的值。 对于操作2,实际上就是把[s..t]这条线段分解成为线段树中的结点线段,然后把所有的结点线段的count值相加。该操作(ADD操作)在上一讲线段树中已介绍。时间复杂度为O (log2n)。 分析二:树状数组 树状数组是一种特殊的数据结构,这种数据结构的时空复杂度和线段树相似,但是它的系数要小得多。 增加数组C,其中C[i]=a[i-2^k+1]+……+a[i](k为i在二进制形式下末尾0的个数)。由c数组的定义可以得出: 为了对树状数组有个形象的认识,我们先看下面这张图。 如图所示,红色矩形表示的数组C[]就是树状数组。我们也不难发现,这个k就是该节点在树中的高度,因而这个树的高度不会超过logn。 【操作1】修改A[i]的值。可以从C[i]往根节点一路上溯,调整这条路上的所有C[]即可,这个操作的复杂度在最坏情况下就是树的高度即O(logn)。 定理1:若a[k]所牵动的序列为C[p1],C[p2]……C[p m],则p1=k,而p i+1=p i+2li (l i为p i在二进制中末尾0的个数)。 例如a[1]……a[8]中,a[3] 添加x; p1=k=3 p2=3+20=4 p3=4+22=8 p4=8+23=16>8 由此得出,c[3]、c[4]、c[8]亦应该添加x。 定理的证明如下: 【引理】 若a[k]所牵动的序列为C[p1],C[p2] ……C[p m],且p1 转载自South_wind的专栏 常见的数据结构运用总结 考虑到Obsidian三个成员的擅长领域,这段时间都在做杂题,算是学习各种算法吧,趁现在休息的时间,而且大家马上要备战今年的比赛了,写写自己专攻方面的一些心得吧 扯开线段树、平衡树这些中高级的东西,先说说基础的数据结构 栈 算是代码量最小的数据结构?出栈进栈都只有一句话而已 常见用途: 消去一个序列中的相同元素(做法大家应该都知道了吧,见过很多次了) 维护一个单调的序列(所谓的单调栈,dp的决策单调?) 表达式求值(经典的栈运用,如果使用的很熟悉的话,可以处理一元、二元运算,不过最近没见过类似的题目了) 用于辅助其他算法(计算几何中的求凸包) 队列 队列应该还是很常见的数据结构了,如果专攻图论的话,spfa应该是写烂了的 这里说到的队列,是狭义的普通的队列和循环队列,不包括后面讲的一些变形 注意循环队列的写法,尽量不要使用取模运算,不然的话,遇到不厚道的出题者,可以把取模的循环队列卡到死 常见用途: 主要用于辅助其他算法,比如说spfa,bfs等(建议习惯用stl的孩子手写queue,毕竟就几行代码而已,偷懒会付出代价的。。。) 双端队列 如果写dp写的多的话,这个东西应该还是算是比较基础的东西了,双端队列多用于维护一个满足单调性的队列 还是建议手写,stl的deque使用块状链表写的,那东西的复杂度是O(Nsqrt(N))的,不要被迷惑了。 常见用途: dp的单调性优化,包括单调队列优化和斜率优化,都要用到这个结构 计算几何中的算法优化,比如半平面交 树的分治问题中利用单调队列减少转移复杂度 链表Dancing Links 写图论的不要告诉我不会写这货,链表可以写单双向,循环非循环的,高级点儿的可以考虑十字链表,麻花链表 不过链表可以说是树形结构的基础,如果这个掌握的不好,那么树形结构写起来就会很纠结 链表的优势在于可以O(1)的插入删除,如果要求插入的位置只是在序列的两端的话,这个数据结构是最方便的了(无视双端队列) hash表就是用链表实现的,熟悉hash的同学可以试试看怎么使你的hash效率提高 树状数组 武钢三中 吴豪【引言】 在解题过程中,我们有时需要维护一个数组的前缀和S[i]=A[1]+A[2]+...+A[i]。但是不难发现,如果我们修改了任意一个A[i],S[i]、S[i+1]...S[n]都会发生变化。可以说,每次修改A[i]后,调整前缀和S[]在最坏情况下会需要O(n)的时间。当n非常大时,程序会运行得非常缓慢。因此,这里我们引入“树状数组”,它的修改与求和都是O(logn)的,效率非常高。 【理论】 为了对树状数组有个形 象的认识,我们先看下面这张图。 如图所示,红色矩形表示的数组C[]就是树状数组。 这里,C[i]表示A[i-2^k+1]到A[i]的和,而k则是i在二进制时末尾0的个数,或者说是i用 2的幂方和表示时的最小指数。( 当然,利用位运算,我们可以直接计算出2^k=i&(i^(i-1)) )同时,我们也不难发现,这个k就是该节点在树中的高度,因而这个树的高度不会超过logn。所以,当我们修 改A[i]的值时,可以从C[i]往根节点一路上溯,调整这条路上的所有C[]即可,这个操作的复杂度在最坏情况下就是树的高度即O(logn)。另外,对于求数列的前n项和,只需找到n以前的所有最大子树,把其根节点的C加起来即可。不难发现,这些子树的数目是n在二进制时1的个数,或者说是把n展开 成2的幂方和时的项数,因此,求和操作的复杂度也是O(logn)。 接着,我们考察这两种操作下标变化的规律: 首先看修改操作: 已知下标i,求其父节点的下标。我们可以考虑对树从逻辑上转化: 如图,我们将子树向右对称翻折,虚拟出一些空白结点(图中白色),将原树转化成完全二叉树。 有图可知,对于节点i,其父节点的下标与翻折出的空白节点下标相同。 因而父节点下标 p=i+2^k (2^k是i用2的幂方和展开式中的最小幂,即i为根节点子树的规模)即 p = i + i&(i^(i-1)) 。 接着对于求和操作: 因为每棵子树覆盖的范围都是2的幂,所以我们要求子树i的前一棵树,只需让i减去2的最小幂即可。即 p = i - i&(i^(i-1)) 。 至此,我们已经比较详细的分析了树状数组的复杂度和原理。 在最后,我们将给出一些树状数组的实现代码,希望读者能够仔细体会其中的细节。 【代码】 求最小幂2^k: in t L o wb i t(in t t) { retur n t & ( t ^ ( t - 1 ) ); } 求前n项和: in t S um(in t e n d) { in t sum = 0; wh il e(e n d> 0) { 【树状数组】数星星(POJ2352 star) Time Limit:1000MS Memory Limit:65536K Total Submit:23 Accepted:16 Description 天文学家经常观察星象图。星象图中用平面上的点来表示一颗星星,每一颗星星都有一个笛卡尔坐标。设定星星的等级为其左下角星星的总数。天文学家们想知道星星等级的分布情况。 比如上图,5号星星的等级为3(其左下角有编号为1、2、4的星星共三颗)。2号星星和4号星星的等级为1。在上图中只有一颗星星等级为0,两颗星星等级为1,一颗星星等级为2,一颗星星等级为3。 给定一个星象图,请你写一个程序计算各个等级的星星数目。 Input 输入的第一行包含星星的总数N (1<=N<=15000)。接下来N行,描述星星的坐标(X,Y)(X和Y用空格分开,0<=X,Y<=32000)。星象图中的每个点处最多只有一颗星星。所有星星按Y坐标升序排列。Y坐标相等的星星按X坐标升序排列。 Output 输出包含N行,每行一个整数。第一行包含等级0的星星数目,第二行包含等级1的星星数目,依此类推,最后一行包含等级为N-1的星星数目。 Sample Input 5 1 1 5 1 7 1 3 3 5 5 Sample Output 1 2 1 1 ?const maxn=60000; ?var i,n,x,y,k:longint; ?a:array[0..15000] of longint; ?c,stars:array[0..60000] of longint; ?procedure add(p,d:longint); ?begin ? while p<=maxn do begin ? c[p]:=c[p]+d; ? p:=p+p and (-p); ? end; ?end; ?function sum(p:longint):longint; ?var res:longint; ?begin ? res:=0; ? while p>0 do begin ? res:=res+c[p]; p:=p-p and (-p); ? end; ? exit(res); ?end; ?begin ?readln(n); ?for i:=1 to n do begin ? readln(x,y); ? add(x+1,1); ? k:=sum(x+1)-1; ? stars[k]:=stars[k]+1; ?end; ?for i:=0 to n-1 do writeln(stars[i]); ?end. 高一入学测试说明 一、命题指导思想 符合选拔性测试的规律和要求,反映各测试科目初中课程标准的整体要求,部分内容可 超出初中各科教学大纲,以有利于选拔具有学习潜能和创新精神的合格新生。 试题以能力测试为主导,在考查考生对基础知识、基本技能和方法掌握程度的同时,注 重能力和科学素养的考查,注重考查运用所学知识分析、解决具体问题的能力;强调知识之间的内在联系;注重理论联系实际。全面落实对“知识与技能”、“过程与方法”、“情感态度与 价值观”三维目标的考查。 二、测试范围内容和测试能力要求 语文测试说明 主题内容 测试范围 依据初中、高中课程标准,根据广东奥林匹克学校对高一奥班新生 文化素质的要求,结合奥校初中、高中语文教学实际,确定语文科测 试内容。 考查内容主要分为“语言文字运用”、“古代诗文阅读”、“现代 文阅读”和“写作”四大板块。 一、语言文字运用 正确、熟练、有效地运用语言文字。 1.识记 (1)识记现代汉语普通话常用字的字音 (2)识记并正确书写现代常用规范汉字 2.表达应用 (1) 正确使用词语(包括熟语) (2) 辨析并修改病句 (3) 扩展语句,压缩语段 (4) 正确运用常见的修辞手法 (5) 语言表达简明、连贯、得体、准确 二、古代诗文阅读 阅读浅易的古代诗文。 1.识记常见的名句名篇。 2.理解 (1)理解常见的文言实词和虚词 (2)翻译文中的句子 3.分析综合 (1)筛选文中的信息 (2)归纳内容要点,概括中心意思 三、现代文阅读 (一)文学类文本阅读 阅读鉴赏中外文学作品。 2 / 7 1、整体把握文学作品的内容、情感、形象 2、理清作者思路和作品线索 3、揣摩作品中的精彩细节 4、品味语言,领悟内涵 5、鉴赏作品的写作技巧和艺术特色 6、探索作品蕴涵的民族心理和人文精神 (二)实用类文本阅读 1、整体把握实用类文本的主要内容 2、阅读科技、社科、新闻作品,筛选信息,概括要点 3、运用文中知识对相关实际问题进行分析推断 4、阅读论述类文章,理解观点与材料之间的联系 5、联系实际,对文中的观点作出自己的判断 6、体会和分析实用类文本的语言特点 四、写作 能熟练写作记叙文,会写简单的论述类、实用类等文章。 能力要求考查考生识记、理解、分析综合、鉴赏评价、表达应用和探究六种能力,其中阅读理解、分析归纳和写作能力是考查的重点。 测试题型1.选择题约25% 2.非选择题约75% 数学I 测试说明 主题内容 测试范围 命题范围为国家教育部2001 年颁布的《全日制义务教育数学课程标 准(实验稿)》、《义务教育课程标准实验教科书——数学(七、八、 九年级)》(人民教育出版社)所规定的内容。主要包括: (1)实数及其运算 (2)整式、分式、二次根式的概念与运算 (3)一元一次方程、一元二次方程、方程组 (4)一元一次不等式、一元一次不等式组 (5)一次函数、反比例函数、二次函数的性质及其图象 (6)三角形、四边形、多边形、圆及相应图形的性质 (7)平移、对称、旋转、相似等图形变换的性质 (8)概率、统计中的概念与运算 3 / 7 (9)以上内容在实际问题中的应用 能力要求 主要考查五种数学能力和四种思想方法,即: (1)空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数 据处理能力 (2)等价转换思想、函数与方程思想、数形结合思想、分类讨论思想 测试题型 (1)选择题,共6 道 (2)填空题,共6 道 (3)解答题,共4 道 树状数组求区间和的一些常见模型 树状数组在区间求和问题上有大用,其三种复杂度都比线段树要低很多……有关区间求和的问题主要有以下三个模型(以下设A[1..N]为一个长为N的序列,初始值为全0): (1)“改点求段”型,即对于序列A有以下操作: 【1】修改操作:将A[x]的值加上c; 【2】求和操作:求此时A[l..r]的和。 这是最容易的模型,不需要任何辅助数组。树状数组中从x开始不断减lowbit(x)(即x&(-x))可以得到整个[1..x]的和,而从x开始不断加lowbit(x)则可以得到x 的所有前趋。代码: void ADD(int x, int c) { for (int i=x; i<=n; i+=i&(-i)) a[i] += c; } int SUM(int x) { int s = 0; for (int i=x; i>0; i-=i&(-i)) s += a[i]; return s; } 操作【1】:ADD(x, c); 操作【2】:SUM(r)-SUM(l-1)。 (2)“改段求点”型,即对于序列A有以下操作: 【1】修改操作:将A[l..r]之间的全部元素值加上c; 【2】求和操作:求此时A[x]的值。 这个模型中需要设置一个辅助数组B:B[i]表示A[1..i]到目前为止共被整体加了多少(或者可以说成,到目前为止的所有ADD(i, c)操作中c的总和)。 则可以发现,对于之前的所有ADD(x, c)操作,当且仅当x>=i时,该操作会对A[i] 的值造成影响(将A[i]加上c),又由于初始A[i]=0,所以有A[i] = B[i..N]之和!而ADD(i, c)(将A[1..i]整体加上c),将B[i]加上c即可——只要对B数组进行操作就行了。 这样就把该模型转化成了“改点求段”型,只是有一点不同的是,SUM(x)不是求B[1..x]的和而是求B[x..N]的和,此时只需把ADD和SUM中的增减次序对调即可(模型1中是ADD加SUM减,这里是ADD减SUM加)。代码: void ADD(int x, int c) { for (int i=x; i>0; i-=i&(-i)) b[i] += c; } int SUM(int x) { int s = 0; for (int i=x; i<=n; i+=i&(-i)) s += b[i]; return s; } 操作【1】:ADD(l-1, -c); ADD(r, c); 操作【2】:SUM(x)。 (3)“改段求段”型,即对于序列A有以下操作: 【1】修改操作:将A[l..r]之间的全部元素值加上c; 【2】求和操作:求此时A[l..r]的和。 这是最复杂的模型,需要两个辅助数组:B[i]表示A[1..i]到目前为止共被整体加了多少(和模型2中的一样),C[i]表示A[1..i]到目前为止共被整体加了多少的总和(或者说,C[i]=B[i]*i)。 对于ADD(x, c),只要将B[x]加上c,同时C[x]加上c*x即可(根据C[x]和B[x]间的关系可得); 而ADD(x, c)操作是这样影响A[1..i]的和的:若x 《信息学奥林匹克教程(数据结构篇) 奥赛经典高级教程系列(奥赛经典高级教程系列)》 内容简介 为了进一步推广、普及计算机技术,提高竞赛水平,在原来编写的一套《信息学奥林匹克教程》(基础篇·提高篇·语言篇)的基础了,我们又编写了这本《数据结构篇》。 《数据结构篇》主要帮助学生全面地掌握数据结构知识与应用技巧,相对于其他数据结构书不同之处就在于增加了一些针对性的例题和习题,着眼点是提高数据结构的应用方法与技巧,是一本具有实战意义的教材。 从逻辑角度看,数据可归结为三种基本结构:线性结构、树结构和图结构;从存储角度看,数据可归结为四种基本结构:顺序结构、链接结构、索引结构和散列结构。每一种逻辑结构可根据不同需要采用不同的存储结构,或者不同的存储结构的组合。数据的逻辑结构和存储结构确定后,再结合指定运算的算法,就容易利用一种程序设计语言编写出程序。通过数据结构的学习,能够大大提高程序设计能力和水平。 《数据结构篇》是为广大信息学爱好者学习数据结构而精心编著的一本教材。本书内容比较全面,着重于实用与实战,在算法分析上简明扼要,细致清晰,便于自学。全书共分十章:第一章为概论,它为学习以后的各章做准备;第二章至第五章为线性结构;第六章和第七章分别为树结构和图结构,分别讨论了每一种逻辑结构所对应的存储结构和相应的算法;第八章和第九章分别为查找与排序,它包含了数据处理中主要使用的几种查找和内排序方法;最后一章为读者提供了检测知识的模拟试题及解答。 作者简介 向期中,长郡中学特级教师,湖南省计算机学会理事,国际金牌教练,国家教育部计算机课程咨询委员会委员。对中小学计算机教育事业有一种执着的追求,参加工作20年来,一直以“当一流教师,办一流教育,出一流人才”为自己的工作目标,对中小学计算机教学和青少年信息学奥林匹克竞赛的辅导倾注了全部热情和心血。在信息学奥林匹克竞赛培训中把“先做人,后成才”的育人理念贯穿到整个奥赛培训的始终,学生在愉快的学习中取得了一个个辉煌的成绩:在近几年的信息学奥林匹克竞赛中,辅导的学生有100多人获湖南省一等奖,11人次进入国家集训队,3人进入国家代表队,3人获国际金牌。撰写了《信息学(计算机)国际奥林匹克Turbo Pas—cal 6.0》等十多部信息学专著。多次荣获园丁奖和全国优秀辅导员称号,还先后获得全国中小学计算机教育先进工作者、湖南省优秀教师和全国信息学奥林匹克竞赛高级指导教师等荣誉称号。 线段树 目录 定义 基本结构 实现代码 树状数组 编辑本段定义 区间在[1,5]内的线段树 线段树又称区间树,是一种对动态集合进行维护的二叉搜索树,该集合中的每个元素 x 都包含一个区间 Interval [ x ]。 线段树支持下列操作: Insert(t,x):将包含区间 int 的元素 x 插入到树中; Delete(t,x):从线段树 t 中删除元素 x; Search(t,i):返回一个指向树 t 中元素 x 的指针。 编辑本段基本结构 线段树是建立在线段的基础上,每个结点都代表了一条线段[a , b]。长度为1的线段称为元线段。非元线段都有两个子结点,左结点代表的线段为[a , (a + b ) / 2],右结点代表的线段为[( a + b ) / 2 , b]。 右图就是一棵长度范围为[1 , 5]的线段树。 长度范围为[1 , L] 的一棵线段树的深度为log ( L - 1 ) + 1。这个显然,而且存储一棵线段树的空间复杂度为O(L)。 线段树支持最基本的操作为插入和删除一条线段。下面以插入为例,详细叙述,删除类似。 将一条线段[a , b] 插入到代表线段[l , r]的结点p中,如果p不是元线段,那么令mid=(l+r)/2。如果b 插入(删除)操作的时间复杂度为O (Log N)。 上面的都是些基本的线段树结构,但只有这些并不能做什么,就好比一个程序有输入没输出,根本没有任何用处。 最简单的应用就是记录线段有否被覆盖,并随时查询当前被覆盖线段的总长度。那么此时可以在结点结构中加入一个变量int count;代表当前结点代表的子树中被覆盖的线段长度和。这样就要在插入(删除)当中维护这个count值,于是当前的覆盖总值就是根节点的count值了。 另外也可以将count换成bool cover;支持查找一个结点或线段是否被覆盖。[1] 相信对算法设计或者数据结构有一定了解的人对线段树都不会太陌生。它是能够在log(MaxLen)时间内完成线段的添加、删除、查询等操作。但一般的实现都有点复杂而线段树应用中有一种是专门针对点的。(点树?)它的实现却非常简单。 这种数据结构有什么用?我们先来考虑一下下面的需求(全部要求在LogN 时间内完成):如何知道一个点在一个点集里的大小“排名”?很简单,开一个点数组,排个序,再二分查找就行了;如何在一个点集内动态增删点?也很简单,弄个平衡树就行了(本来平衡树比线段树复杂得多,但自从世界上有了STL set 这么个好东东,就……^_^)那如果我既要动态增删点,也要随时查询到一个点的排名呢?那对不起,可能就要出动到我们的“点树”了。 其实现原理很简单:每当增加(或删除)一个大小为X的点时,就在树上添加(或删除)一条(X,MaxLen)的线段(不含端点),当要查询一个点的排名时,只要看看其上有多少条线段就可以了。针对这一需求,这里有个非常简单的实现(见以下代码,十多行,够短了吧?)其中clear()用于清空点集;add()用于添加一个点;cntLs()返回小于n的点的个数,也就是n的升序排名,类似地cntGt 是降序排名。 这个点树有什么用呢?其中一个应用时在O(NlogN)时间内求出一个排列的逆序数(https://www.360docs.net/doc/cb17287813.html,/show_problem.php?pid=1484,你有更好的算法吗?欢迎交流)方法是每读到一个数x,就让逆序数+=cntGt(x);然后再 add(x)。 这个实现还可以进行一些扩展。比如删除del(int n),只要把add(int n)中的++size换成--size,把a[i/2]++改成a[i/2]--即可。另外还可以通过二分查找功能在O(logN)时间内查到排名第n的点的大小。应该也可以三四行内搞定。 补充:杨弋同学在2008年信息学奥赛冬令营上新发明了一种线段树的省空间堆式存储法,具体方法可以见08年冬令营课件. 编辑本段实现代码 template < int N > // 表示可用区间为[0,N),其中N必须是2的幂数; class PointTree { int a[ 2 * N]; int size; void clear() { memset( this , 0 , sizeof ( * this ));} void add( int n) { Vijos 1448校门外的树 校门外有很多树,有苹果树,香蕉树,有会扔石头的,有可以吃掉补充体力的…… 如今学校决定在某个时刻在某一段种上一种树,保证任一时刻不会出现两段相同种类的树,现有两个操作: K=1,读入l,r表示在l~r之间种上的一种树 K=2,读入l,r表示询问l~r之间能见到多少种树 (l,r>0) 输入第一行n,m表示道路总长为n,共有m个操作 接下来m行为m个操作 输出对于每个k=2输出一个答案 样例输入 5 4 1 1 3 2 2 5 1 2 4 2 3 5 样例输出 1 2 括号序列+树状数组 什么是括号序列下面简单介绍一下(感谢tiger教会我) 假设有一个长度是20的数轴,现在我们要在2 15之间种上一种树,那么我们可以在2处添加一个‘(’,在15的地方添加一个‘)’,这就是简单的括号序列。 如果要统计某个区间树的种类,例如3 10,我们只需要统计10之前(包括10)有多少个‘(’,统计3之前有多少个‘)’,(不包括3)。 这样光说可能很难理解,下面给一个实例。 左括号和右括号表示的是在这些区间内种上了树。(日,感觉有点像在画大便) 假设这时候需要统计的是 5 10之间有多少种树,那么,只要在10之前种的树都是有效的(这时候先不管5的限制),也就是统计左括号的个数,一共是6个,下面加上5个限制,也就是说,在5之前,我们统计一下有多少右括号,也就是能与左括号匹配掉的括号有多少个?换句话说,就是有多少种树被限制了(自己意会下把,实在是用文字说不出来); 把程序也拿出来晒晒把(脑残的vijos,用writeln6个点超时,用write过了,还9ms) program vijos; var c1,c2:array[0..50000]of longint; n,m:longint; function lowbit(x:longint):longint; begin lowbit:=x and (x xor (x-1)); end; procedure addl(i:longint); begin while i<=n do begin inc(c1[i]); inc(i,lowbit(i)); end; end; procedure addr(i:longint); begin while i<=n do begin inc(c2[i]); inc(i,lowbit(i)); end; end; function findl(i:longint):longint; begin findl:=0; while i>0 do 从《Cash》谈一类分治算法的应用 分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同.求出子问题的解,就可得到原问题的解.分治算法非常基础,但是分治的思想却非常重要,本文将从今年NOI 的一道动态规划问题Cash开始谈如何利用分治思想来解决一类与维护决策有关的问题: 例一.货币兑换(Cash)1 问题描述 小Y最近在一家金券交易所工作.该金券交易所只发行交易两种金券:A .每个持有金券的顾 纪念券(以下简称A券)和B纪念券(以下简称B券) 客都有一个自己的帐户.金券的数目可以是一个实数. 每天随着市场的起伏波动,两种金券都有自己当时的价值,即每一单位金 券当天可以兑换的人民币数目.我们记录第K天中A券和B券的价值 分别为A K 和B K(元/单位金券). 为了方便顾客,金券交易所提供了一种非常方便的交易方式:比例交易法.比例交易法分为两个方面: A) 卖出金券:顾客提供一个[0,100]内的实数OP 作为卖出比例,其意义为:将OP%的A券和OP%的B券以当时的价值兑换为人民币; B) 买入金券:顾客支付IP 元人民币,交易所将会兑换给用户总价值为IP 的金券,并且,满足提供给顾客的A券和B券的比例在第K天恰好为Rate K; 例如,假定接下来 3 天内的A 假定在第一天时,用户手中有100 元人民币但是没有任何金 券.用户可以执行以下的操作: 1NOI 2007,货币兑换 注意到,同一天内可以进行多次操作. 小Y 是一个很有经济头脑的员工,通过较长时间的运作和行情测算, 他已经知道了未来N天内的A券和B券的价值以及Rate.他还希望 能够计算出来,如果开始时拥有S元钱,那么N天后最多能够获得多少元钱. 算法分析 不难确立动态规划的方程: 设f [i]表示第i天将所有的钱全部兑换成A, B券,最多可以得到多少A券.很容易可以得到一个O(n2)的算法: f [1]←S * Rate[1] / (A[1] * Rate[1] + B[1]) Ans←S For i← 2 to n For j← 1 to i-1 x←f [j] * A[i] + f [j] / Rate[j] * B[i] If x > Ans Then Ans←x End For f [i] ←Ans * Rate[i] / (A[i] * Rate[i] + B[i]) End For Print(Ans) O(n2)的算法显然无法胜任题目的数据规模.我们来分析对于i的两个决策j 和k,决策j比决策k优当且仅当: (f [j] –f [k]) * A[i] + (f [j] / Rate[j] –f [k] / Rate[k]) * B[i] > 0. 不妨设f [j] < f [k],g[j] = f [j] / Rate[j],那么 (g[j] –g[k]) / (f[j] –f[k]) < -a[i] / b[i]. 这样我们就可以用平衡树以f [j]为关键字来维护一个凸线,平衡树维护一个点 SASLP ├─01.基础(base) │├─01.高精度(bignum) │├─02.排序(sort) ││├─01.选择排序(select sort) ││├─02.冒泡排序(bubble sort) ││├─03.希尔排序(shell sort) ││├─04.快速排序(quick sort) ││├─05.归并排序(merge sort) ││├─06.堆排序(heap sort) ││└─07.桶排序(bucket sort) │├─03.分治法(dichotomy) │├─04.动态规划(dynamic programming) ││├─01.单调队列(humdrum queue) ││├─02.四边形不等式() ││└─03.决策单调性() │├─05.贪心(greedy) │└─06.搜索(search) │├─01.深度优先搜索(depth first search) │├─02.宽度优先搜索(breadth first search) │└─03.迭代加深搜索(iterative deepening) ├─02.数学(maths) │├─01.高斯消元(gauss elimination) │├─02.同余(modular arithmetic) │├─03.进位制() │├─04.开方(evolution) │└─x.01.群论(group theory) ├─03.数据结构(data structure) │├─01.线性表(linear table) ││├─01.栈(stack) ││├─02.队列(queue) ││├─03.哈希表(hash array) ││└─04.链表(linked list) │├─02.优先队列(priority queue) ││├─01.堆(heap) ││└─02.单调队列(humdrum queue) │├─03.线段树(interval tree) │├─04.树状数组(tree array) │├─05.二叉查找树&平衡树(binary search tree & balanced search tree) ││├─01.二叉查找树(binary search tree) ││├─02.伸展树(splay) ││├─03.Treap(treap) ││├─04.SBT(size balanced tree) 1SHAOLIN N个数,第一个是1000000000,后面的数都小于这个数。每次添加一个数时,找到与该数差最小的。 查找问题,用map或set即可。 Map.find或set.find,复杂度O(logN)。 然后iter++和iter—得到相邻点 Iterator只支持++,--操作。可能得多定义几个变量 Set,直接*iter得到值 Map,iter->first得到key,iter->second得到value 2丑数 一个数,如果其因数只有2、3、5、7,则称该数为丑数。 第一个丑数是1 给定一个整数N,N<10000,求第n小的丑数 3有序表第k小和 A、B均为升序数组 求任意组合a[i]+b[j]中值为第k小的值,并求对应i,j(若有并列输出i最小的,再相等输出j最小的) 4线段树1 有一个数组,每次可以执行 1将数列中的某个数加上某个数 2询问一个区间的和 操作个数Q<=100000,数组长度n<=100000 5线段树2 例题:有一个数组,每次可以执行 1将数列中的某个区间加上某个数 2询问一个区间的和 6线段树3 例题:有一个数组,每次可以执行 1将数列中的某个区间加上某个数 2将数列中的某个区间全部修改为某个数 3询问一个区间的和 线段树多类信息的维护 7线段树4 例题:有一个数组,每次可以执行 1将数列中的某个区间加上某个数 2将数列中的某个区间乘以某个数 3将数列中的某个区间改成某个数 4查询区间和,平方和,立方和 8树状数组例题 给定一个n*n的矩阵,其中元素为0或1.初始A[i][[j]=0 现给定两种操作 操作1给定两对数据x1,y1,x2,y2,将左上角为x1,y1,右下角为x2,y2的矩形中的所有元素进行not运算。C x1 y1 x2 y2 操作2为查询一个坐标内的值。Q x y N<=1000,T<=50000,T表示操作个数 9GROUP多校4 给定n个数分别为1~n(无序),给定一个区间[L,R],求区间内的数可以分成多少个组,要求组间的数是连续的。 10比赛 有n个人进行比赛,每个人有一个能力值。 N个人排成一列。分别为a1~an,仅满足 i POJ上一些题目在 http://162.105.81.202/course/problemSolving/ 可以找到解题报告。 《算法艺术与信息学竞赛》的习题提示在网上可搜到 一.动态规划 参考资料: 刘汝佳《算法艺术与信息学竞赛》 《算法导论》 推荐题目: https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1141 简单 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=2288 中等,经典TSP问题 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=2411 中等,状态压缩DP https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1112 中等 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1848 中等,树形DP。 可参考《算法艺术与信息学竞赛》动态规划一节的树状模型 https://www.360docs.net/doc/cb17287813.html,/show_problem.php?pid=1234 中等,《算法艺术与信息学竞赛》中的习题 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1947 中等,《算法艺术与信息学竞赛》中的习题 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1946 中等,《算法艺术与信息学竞赛》中的习题 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1737 中等,递推 https://www.360docs.net/doc/cb17287813.html,/JudgeOnline/problem?id=1821 中等,需要减少冗余计算 https://www.360docs.net/doc/cb17287813.html,/show_problem.php?pid=2561 中等,四边形不等式的简单应用 ·AVL树·红黑树·伸展树·树堆·节点大小平衡树 ·B+树·B*树·B x树·UB树·2-3树·2-3-4·(a,b)-树·Dancing tree ·H树 ·基数树 ·八叉树·k-d树·vp-树·R树·R*树·R+树·X ·线段树·希尔伯特R树·优先R树 并且左右两个子树都是一棵平衡二叉树。构造与调整方法平衡二叉树的常用算法有红黑树、AVL、Treap、伸展树等。 堆(二叉堆) ---------------------------------------------------------------------------------------------------------- ----- 堆是一种完全二叉树,效率很高,常用的排序算法、Dijkstra算法、Prim算法等都要用堆(优先级队列)优化。一般的二叉堆不能进行有效查找和堆之间的合并。 (插入,获得及删除最小值) 可并堆 可以在O(logN)时间内完成两个堆的合并操作的二叉堆。如左偏堆,二项堆,斐波那契堆。 最优二叉树(哈夫曼树) ---------------------------------------------------------------------------------------------------------- ------- 给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree)。 字典树 ---------------------------------------------------------------------------------------------------------- ------ 又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来节约存储空间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。 AVL树 ---------------------------------------------------------------------------------------------------------- --------- 是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个儿子子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。 伸展树 昨天学了一下树状数组,随笔都写了一大半,结果一个不小心就把他给删了,哎。。。。。。今天就当是复习吧!再写一次。 如果给定一个数组,要你求里面所有数的和,一般都会想到累加。但是当那个数组很大的时候,累加就显得太耗时了,时间复杂度为O(n),并且采用累加的方法还有一个局限,那就是,当修改掉数组中的元素后,仍然要你求数组中某段元素的和,就显得麻烦了。所以我们就要用到树状数组,他的时间复杂度为O(lgn),相比之下就快得多。下面就讲一下什么是树状数组: 一般讲到树状数组都会少不了下面这个图: 下面来分析一下上面那个图看能得出什么规律: 据图可知:c1=a1,c2=a1+a2,c3=a3,c4=a1+a2+a3+a4,c5=a5,c6=a5+a6,c7=a7,c8=a1+a2+a3+a4+a5+a6+a7+a8,c9=a9,c10=a9+a10, c11=a11........c16=a1+a2+a3+a4+a5+.......+a16。 分析上面的几组式子可知,当i 为奇数时,ci=ai ;当i 为偶数时,就要看i 的因子中最多有二的多少次幂,例如,6 的因子中有2 的一次幂,等于 2 ,所以c6=a5+a6(由六向前数两个数的和),4 的因子中有 2 的两次幂,等于4 ,所以c4=a1+a2+a3+a4(由四向前数四个数的和)。 (一)有公式:cn=a(n-a^k+1)+.........+an(其中k 为n 的二进制表示中从右往左数的0 的个数)。 那么,如何求a^k 呢?求法如下: lowbit()的返回值就是2^k 次方的值。 求出来2^k 之后,数组c 的值就都出来了,接下来我们要求数组中所有元素的和。 (二)求数组的和的算法如下: (1)首先,令sum=0,转向第二步; (2)接下来判断,如果n>0 的话,就令sum=sum+cn转向第三步,否则的话,终止算法,返回sum 的值; (3)n=n - lowbit(n)(将n的二进制表示的最后一个零删掉),回第二步。 代码实现: (三)当数组中的元素有变更时,树状数组就发挥它的优势了,算法如下(修改为给某个节点i 加上x ): (1)当i<=n 时,执行下一步;否则的话,算法结束; (2)ci=ci+x ,i=i+lowbit(i)(在i 的二进制表示的最后加零),返回第一步。 代码实现:C++基础复习
树状数组及其应用
数据结构总结
树状数组
1701 【树状数组】数星星(POJ2352 star) 1702 【树状数组】矩阵(POJ 2155)
华附高一入学测试说明
树状数组求区间和的一些常见模型
信息学奥林匹克教程(数据结构篇)
线段树
Vijos 1448校门外的树(树状数组与线段树)
从《Cash》谈一类分治算法的应用
信息学奥赛知识结构图
经典算法练习题
POJ分类
计算机科学中的树
一维与二维树状数组
