高一数学必修4三角函数的性质练习题

必修四
高一数学三角函数练习题(一)
一、选择题
1、若 –π/2<α<0,则点)cos ,(tan αα位于( ) A .第一象限 B .第二象限
C .第三象限
D .第四象限
2.若5
4
cos =α,),0(πα∈则αcot 的值是( ) A .
3
4 B .43 C . 34± D .4
3
±
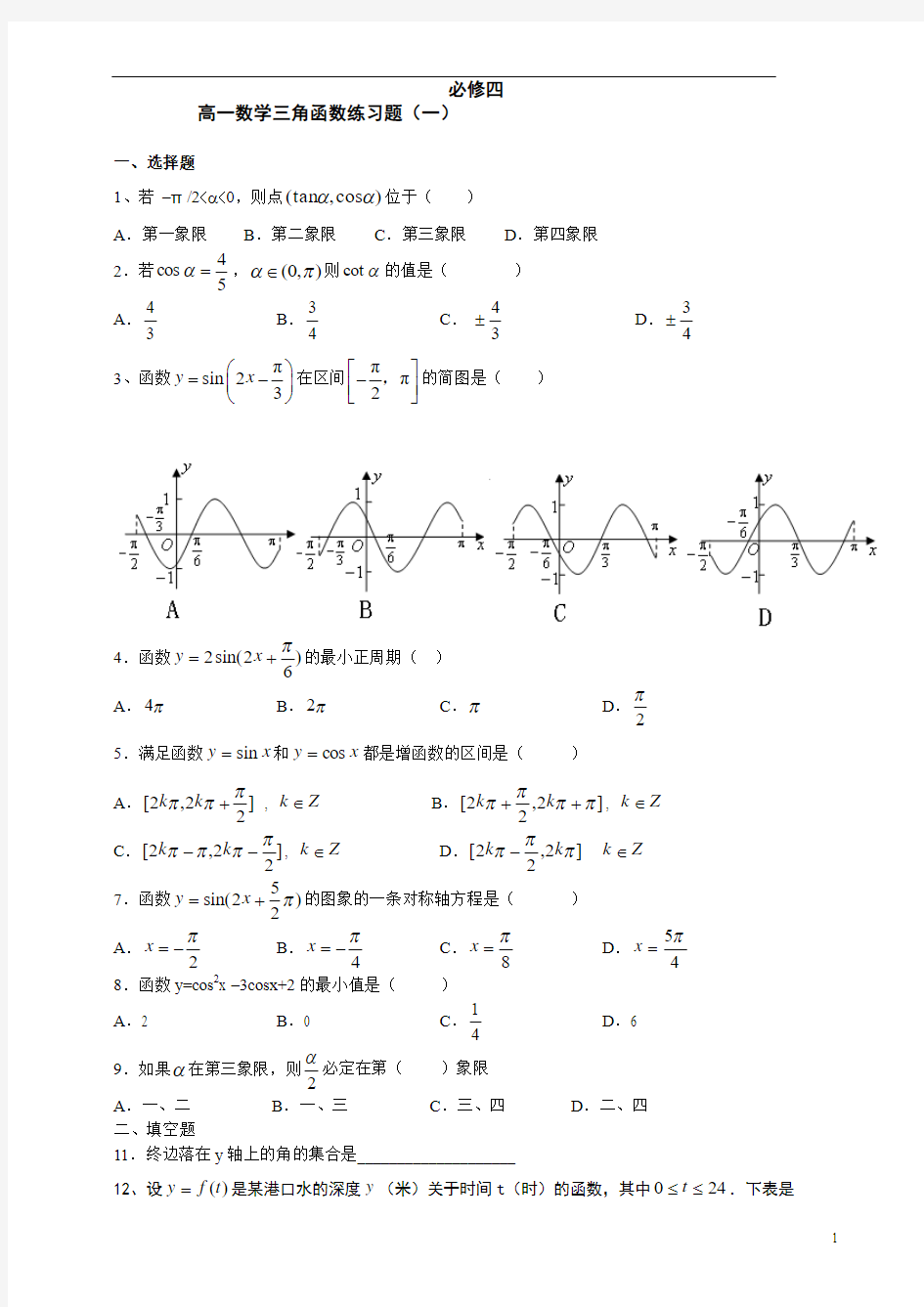
3、函数πsin 23y x ?
?=-
??
?在区间ππ2??-????
,的简图是( )
4.函数)6
2sin(2π
+=x y 的最小正周期( )
A .π4
B .π2
C .π
D .
2
π
5.满足函数x y sin =和x y cos =都是增函数的区间是( )
A .]2
2,2[π
ππ+
k k , Z k ∈ B .]2,2
2[πππ
π++k k , Z k ∈ C .]22,2[π
πππ-
-k k , Z k ∈
D .]2,22[ππ
πk k -
Z k ∈
7.函数)2
5
2sin(π+=x y 的图象的一条对称轴方程是(
)
A .2
π
-
=x
B .4
π
-
=x
C .8
π
=x
D .4
5π=
x 8.函数y=cos 2x –3cosx+2的最小值是( )
A .2
B .0
C .
4
1 D .6
9.如果α在第三象限,则
2
α
必定在第( )象限
A .一、二
B .一、三
C .三、四
D .二、四 二、填空题
11.终边落在y 轴上的角的集合是____________________
12、设)(t f y =是某港口水的深度y (米)关于时间t (时)的函数,其中240≤≤t .下表是
该港口某一天从0时至24时记录的时间t 与水深y 的关系: X 0 3
6
9 12
15
18
21
24 Y
12
15.1 12.1
9.1
11.9 14.9 11.9 8.9
12.1
经长期观察,函数)(t f y =的图象可以近似地看成函数)sin(?ω++=t A k y 的图象.下面的函数中,最能近似表示表中数据间对应关系的函数有(填序号)________ (1).]24,0[,6sin 312∈+=t t y π
(2).]24,0[),6sin(312∈++=t t y ππ
(3).]24,0[,12
sin
312∈+=t t y π
(4).]24,0[),2
12
sin(
312t t y π
π
+
+=
13.函数x x f cos 21)(-=的定义域是___________________________ 14.已知a
a x --=
43
2cos ,且x 是第二、三象限角,则a 的取值范围是________ 15、函数π()3sin 23f x x ??
=-
??
?
的图象为C ,则如下结论中正确的序号是 _____ ①、图象C 关于
直线11π12x =
对称; ②、图象C 关于点2π03?? ???,对称; ③、函数()f x 在区间π5π1212??- ???
,内是增函数; ④、由3sin 2y x =的图角向右平移π
3
个单位长度可以得到图象C . 三、解答题:
16.设)4,3(t t P --是角α终边上不同于原点O 的某一点,请求出角α的正弦、余弦、和正切的三角函数之值
.。
17、 已知函数f(x)=Asin(ωx+?)的图象如图所示,试依图指出:
(1)、f(x)的最小正周期; (2、)使f(x)=0的x 的取值集合; (3)、使f(x)<0的x 的取值集合; (4)、f(x)的单调递增区间和递减区间;(5)、求使f(x)取最小值的x 的集合; (6)、图象的对称轴方程;(7)、图象的对称中心.
18、化简
)4sin()2
3sin()
8cos()2
cos()5sin(πθπ
θθπθπ
πθ---
---
-
19、已知cos3(0)y a b x b =->的最大值为
32,最小值为1
2
-。求函数4sin(3)y a bx =-的周期、最值,并求取得最值时的x 之值;并判断其奇偶性。
20、如图,某大风车的半径为2m ,每12s 旋转一周,它的最低点O 离地面0.5m 。风车圆周上一点A 从最低点O 开始,运动()t s 后与地面的距离为()h m 。
⑴求函数()h f t =的关系式; ⑵画出函数()h f t =的图象。
21、如图所示,函数π
2cos()(00)2
y x x >ωθωθ=+∈R ,,≤
≤的图象与y 轴相交于点M (03),,且该函数的最小正周期为π.
(1)求θ和ω的值; (2)已知点π02
A ?? ???
,,点P 是该函数图象上一点,
点00()Q x y ,是PA 的中点,当032y =
,0ππ2x ??
∈????
,时,求0x 的值
总复习参考答案:
1 2 3 4 5 6 7 8 9 10 B A
A
C
D
A
A
B
D
C
11.
},
2
|{Z
k k ∈+
=π
παα 12
、 (1).]24,0[,6
sin
312∈+=t t y π
13. Z k k k ∈++],3
5
2,32[ππππ 14. )23,1(- 15、
①②③
17题、
O 1
O
A
18题、原式=-sin θ 19题、a=12;b=1 20题、y=2.5-2cos π
6 t (t≥0)
21题、解:(1)将0x =,3y =代入函数2cos()y x ωθ=+中得3
cos 2
θ=, 因为π02θ≤≤
,所以π6θ=.由已知πT =,且0ω>,得2π2π
2T π
ω=
==. (2)因为点π
02
A ?? ???
,,00()Q x y ,是PA 的中点,032y =
.所以点P 的坐标为0π232x ??- ???
,. 又因为点P 在π2cos 26y x ?
?=+
??
?的图象上,且0ππ2x ≤≤,所以05π3cos 462x ??-= ??
?, 07π5π19π4666x -≤≤,从而得05π11π466x -=或05π13π
466x -=,
三角函数练习题(二)
A 组
一、选择题:共6小题
1.(易 函数最大最小值)用A 和B 分别表示函数1
sin 13y x =-的最大值和最小值,则A B +等于( )
A.
23
B.2
3
-
C.4
3
-
D.2-
2.(易 函数单调性)下列函数,在[,2
ππ]上是增函数的是( ) A.cos2y x =
B.cos y x =
C.sin 2y x =
D.sin y x =
3.(易 函数单调区间)下列区间中,函数3sin()6
y x π
=+的递减区间是( ) A.[,]22ππ-
B.2[,]33ππ
C.22[,]33
ππ- D.[,0]-π 4. (中 三角函数的奇偶性及周期)下列函数中是奇函数,且最小正周期是π的函数是( ) A.tan 2y x =
B.sin y x =
C.πsin 22y x ??
=+
???
D.3πcos 22y x ??
=-
???
5.(中,三角函数的对称性)若函数cos()3y x ωπ=+(0)ω>的图象相邻两条对称轴间距离为2
π
,则ω等于( )
A.
12
B.12
C.2
D.4
6.(中,函数的值域)sin sin y x x =-的值域是( )
A.[2,0]-
B.[0,1]
C.[1,1]-
D.[1,0]- 二、填空题:共3小题
7.(易 正切函数的周期)已知函数1sin y x =、2tan y x =的最小正周期分别为1T 、2T 则12T T += .
8.(易 函数的奇偶性)若)(x f 为奇函数,且0>x 时,x x x f sin )(2-=,则0 ①对任意的?,f (x )都是非奇非偶函数; ②不存在?,使f (x )既是奇函数,又是偶函数; ③存在?,使f (x )是奇函数; ④对任意的?,f (x )都不是偶函数. 其中一个假命题的序号是_____.因为当?=_____时,该命题的结论不成立. 三、解答题:共2小题 10.(中,函数的值域)设全集[1,1]U =-,函数21 ()()sin 1 f x x x =∈+R 的值域为 A,sin ()()sin 2 x g x x x =∈+R 的值域为B,求()()U U A B 痧. 11.(中,正切函数的性质)求函数()tan 2 3f x x ??=+ ???π π的定义域、周期和单调递增区间. B 组 一、填空题:共6小题 1.(易 三角函数的图像性质)下列叙述中正确的个数为( ) ①tan y x =在R 上是增函数; ②sin ,[0,2y x x =∈π]的图像关于点(,)P π0成中心对称图形; ③cos ,[0,2y x x =∈π]的图像关于直线x =π成轴对称图形; ④正弦、余弦函数sin y x =、cos y x =的图像不超出两直线1y =-、1y =所夹的范围. A.1个 B.2个 C.3个 D.4个 2.(中 三角函数最值)已知函数f(x)=2sin ωx(ω>0)在区间[3π-,4 π ]上的最小值是-2,则ω的最小值等于( ) A. 32 B.2 3 C.2 D.3 3.(中 三角函数单调性)使函数x y sin =递减且函数x y cos =递增的区间是( ) A.( ,223ππ) B.(2,22 k k k π π-π)(∈)Z C.(2,22k k k ππ+π+π)(∈)Z D.(2,22 k k k 3π π+ππ+ )(∈)Z 4.(中 三角函数定义域)如果[0,2]x ∈π,则函数x x y cos sin -+=的定义域为( ) A.[0,]π B.[, ]22π3π C.[,2 π π] D.[,223ππ] 5.(中 函数对称性)已知函数f (x )=a sin2x +cos2x (a ∈R )图象的一条对称轴方程为x =π 12 ,则a 的值为 ( ) A. 33 B.21 C.2 3 D.32 6.(中 三角函数最值)若函数()(13tan )cos f x x x =+,02 x π ≤< ,则()f x 的最大值为( ) A.1 B.2 C.31+ D.32+ 二、填空题:共3小题 7.(易 )设3 ()sin 1f x ax b x =++,(,a b 为常数),且(5)7f =,则(5)f -= . 8.(中 三角函数的对称性周期性) 设f (x )=A sin(ωx +φ)(A >0,ω>0)的图象关于直线x =π 3 对称,它 的最小正周期是π,则f (x )图象上的一个对称中心是________(写出一个即可). 9.(难 函数图像)函数[]()sin 2|sin |,0,2f x x x x =+∈π的图象与直线k y =有且仅有两个不同的交点,则k 的取值范围是__________. 三、解答题:共2小题 10. (中 三角函数的奇偶性)判断函数f (x )=lg(sin x +x 2sin 1+)的奇偶性. 11. (中 三角函数对称性最大最小值)设函数()sin(2) (0),()f x x y f x ??=+-π<<=图像的一条对称轴是直线8 x π=. (1)求?; (2)若函数2(),(y f x a a a =+∈为常数R )在113[,]244 x ππ ∈上的最大值和最小值之和为1, 求a 的值. C 组 解答题:共2小题 1.(难 三角函数单调性最大最小值)已知函数2 ()2sin 1f x x x θ=+-,31[,]22 x ∈- (1)当6 θπ = 时,求()f x 的最大值和最小值; (2)若()f x 在31 [,]22 x ∈-上是单调函数,且[0,2)θ∈π,求θ的取值范围 2.(较难 三角函数周期性)设)0(cos sin )(>+=ωωωx b x a x f 的周期T =π,最大值为()412 f π =, (1)求ω、a 、b 的值; (2)若α、β为方程()0f x =的两根,且α、β的终边不共线,求tan()αβ+的值. 参考答案 A 组 一、选择题:共6小题 1.D 当1sin =x 时1sin 13y x =-有最大值32-,当1sin -=x 时1 sin 13y x =-有最小值3 4-,所以A+B=- 2. 2.A x y cos =在[0,2]π的增区间为[,2]ππ,x y 2cos =的增区间为ππ2?? ????, 3.B x y sin =的递减区间为3( 2,2)22k k ππ+π+π,所以3s i n ()6 y x π =+的递减区间为4(2,2)33k k ππ+π+π,其中2[,]33ππ4[2,2]33 k k ππ?+π+π,故选B. 4.D 四个选项中为奇函数的是A 和D,其中x y 2t a n =的最小正周期为2 π .而 3cos(2)cos(2)cos(2)sin 2222 y x x x x πππ =-=π+-=--=-,最小正周期为π,故选D. 5. C x y cos =的图象相邻两条对称轴距离为π,要使cos()3 y x ωπ =+的图像相邻两条对称轴的距离 为2 π ,则其周期缩小为原来的一半,所以2=ω. 6.A 当0sin >x 时,0sin sin sin sin =-=-=x x x x y ;当0sin 2 π 1212,2T T T T =π=π?+=π 8.x x sin 2 -- 设0 2+=---=-,又因为)(x f 为奇函 数,则x x x f x f sin )()(2+=-=-,所以x x x f sin )(2--=. 9.①,k π(k ∈Z );或者①, 2π+k π(k ∈Z );或者④,2 π +k π(k ∈Z ) 当?=2k π,k ∈Z 时,f (x )=sin x 是奇函数.当?=2(k +1)π,k ∈Z 时f (x )=-sin x 仍是奇函数.当 ?=2k π+2 π ,k ∈Z 时,f (x )=c os x ,或当?=2k π-2 π ,k ∈Z 时,f (x )=-c os x ,f (x )都是偶函数.所以②和 ③都是正确的.无论?为何值都不能使f (x )恒等于零.所以f (x )不能既是奇函数又是偶函数.①和④都是假命题. 三、解答题:共2小题 10.解:∵2 0sin 1x ≤≤,∴2 1sin 12x ≤+≤, ∴1 12 y ≤≤, ∴1[,1]2A =,而[1,1]U =-,∴1[1,)2 U A =-e; 由sin ()sin 2x g x x = +,得sin sin 2x y x =+,于是2sin 1y x y =-, ∴1sin 1x -≤≤,∴2111 y y -≤ ≤-,解得113y -≤≤, ∴1{|1}3B y y =-≤≤.而[1,1]U =-,∴1 (,1]3U B =e; ∴11 ()()(,)32 U U A B = 痧. 11.解:由232x k +≠+ππππ,得1 23 x k ≠+(k ∈Z ). ∴函数()f x 的定义域是1|2,3 x x k k ? ?≠+∈??? ? Z ; 由于()()()tan tan tan 2223232 3f x x x x f x ??????=+=++=++=+ ? ?????????πππππ ππ, 因此函数()f x 的最小正周期为2. 由2232k x k - +<+<+ππππππ,k ∈Z ,解得51 2233 k x k -+<<+,k ∈Z . 因此,函数的单调递增区间是512,23 3 k k ??-++ ??? ,k ∈Z . B 组 一、填空题:共6小题 1. C ①错,其余正确. 2. B 由22x ωππ- ≤≤得到一个单调递增区间是[,]22ωωππ-,依题意3,322 ωωππ-≤-∴≥ 3.D 在区间3( ,2)2ππ上x y sin =单调递增,不合要求.在区间3(2,2)2 k k π π+ππ+上x y sin =递减,x y cos =为递减函数,故选D. 4.C 依题意得???≤≥0cos 0sin x x ,即0322 x x ≤≤π?? ?ππ ≤≤??,[,]2x π∴∈π,故选C 5.A ∵x =π12是对称轴,∴f (0)=f (π6),即cos0=a sin π3+cos π3,∴a =3 3. 6.B 因为()(13tan )cos f x x x =+=cos 3sin x x +=2cos()3 x π - 当3 x π = 是,函数取得最大值为2.故选B 二、填空题:共3小题 7.5- 715sin 5)5(3=++=b a f ,则65sin 53 =+b a , 又51615sin 5)5(3-=+-=+--=-b a f 8.(π12,0) ∵T =2πω=π,∴ω=2,又∵函数的图象关于直线x =π 3 对称, 所以有sin(2×π3+φ)=±1,∴φ=k 1π-π 6(k 1∈Z ), 由sin(2x +k 1π-π6)=0得2x +k 1π-π 6 =k 2π(k 2∈Z ), ∴x =π12+(k 2-k 1)π2,当k 1=k 2时,x =π12 , ∴f (x )图象的一个对称中心为(π 12,0). 9.(1,3) 3sin ,[0,) ()sin 2sin sin ,[,2]x x f x x x x x ∈π?=+=? -∈ππ? ,由其图像可知当直线k y =,)3,1(∈k 时与 []()sin 2|sin |,0,2 f x x x x =+∈π的图像与直线k y =有且仅有两个不同的交点. 三、解答题:共2小题 10.分析:判断奇偶性首先应看定义域是否关于原点对称,然后再看f (x )与f (-x )的关系. 解析:定义域为R ,又f (x )+f (-x )=lg1=0, 即f (-x )=-f (x ),∴f (x )为奇函数. 11.(1)∵2x π= 是它的一条对称轴,∴282k ?ππ?+=π+. ∴,4k ?π=π+又0?-π<<,得4 ?3π =-; (2)由(1)得3 ()sin(2)4 f x x =-π ∴32sin(2)4y x a =-π+,又332644 x ππ ≤-π≤, ∴max min 2,1,y a y a =+=+∴231,a +=∴ 1.a =- 解答题:共2小题 C 组 1. 解:(1)当6θπ= 时,4 5)21(1)(22 -+=-+=x x x x f )(x f ∴在]2 1 ,23[-- 上单调递减,在]21,21[-上单调递增. ∴当21-=x 时,函数)(x f 有最小值45 - 当21=x 时,函数)(x f 有最小值4 1- (2)要使()f x 在31[,]22 x ∈- 上是单调函数,则3 sin 2θ-≤- 或1sin 2θ-≥, 即2 3 sin ≥ θ或21sin -≤θ,又[0,2θ∈π), 解得[, ][,]3366 θπ2π7π11π ∈ . 2.解析:(1))sin()(22?ω++= x b a x f ,∴T =π,∴2ω=, 又()f x 的最大值为( )412 f π =. ∴224a b =+ ① ,且12 2cos b 122sin a 4π+π=②, 由①、②解出a =2 , b =3. (2)()2sin 223cos24sin(2)3 f x x x x π =+=+,∴()()0f f αβ==, ∴4sin(2)4sin(2)33αβππ+ =+, ∴22233k απβππ+=++,或22(2)33 k αβππ +=π+π-+, 即k αβ=π+ (βα、 共线,故舍去) ,或6 k αβπ +=π+, ∴3 tan()tan()63 k αβπ+=π+= ()k ∈Z 三角函数图像及性质练习题 1.已知4k <-,则函数cos 2(cos 1)y x k x =+-的最小值是( ) A.1 B.1- C.21k + D.21k -+ 2.已知f (x )的图象关于y 轴对称,且它在[0,+∞)上是减函数,若f (lg x )>f (1),则x 的取值范围是( ) A.( 10 1 ,1) B.(0, 101)∪(1,+∞) C.( 10 1,10) D.(0,1)∪(10,+∞) 3.定义在R 上的函数f (x )既是偶函数又是周期函数.若f (x )的最小正周期是π,且当x ∈[0,2π ] 时,f (x )=sin x ,则f ( 3 π 5)的值为( ) A.- 21 B.2 1 C.-23 D.23 4.定义在R 上的函数f (x )满足f (x )=f (x +2),当x ∈[3,5]时,f (x )=2-|x -4|,则( ) A.f (sin 6π)<f (cos 6π ) B.f (sin1)>f (cos1) C.f (cos 3π2)<f (sin 3 π2) D.f (cos2)>f (sin2) 5.关于函数f (x )=sin 2x -( 32)|x |+21 ,有下面四个结论,其中正确结论的个数为 ( ) . ①()f x 是奇函数 ②当x >2003时,1 ()2 f x > 恒成立 ③()f x 的最大值是23 ④f (x )的最小值是12- A.1 B.2 C.3 D.4 6.使)tan lg(cos θθ?有意义的角θ是( ) A.第一象限的角 B.第二象限的角 C.第一、二象限的角 D.第一、二象限或y 轴的非负半轴上的角 7 函数lg(2cos y x =的单调递增区间为 ( ) . A .(2,22)()k k k Z ππππ++∈ B .11 (2,2)()6 k k k Z ππππ++ ∈ C .(2,2)()6 k k k Z π ππ- ∈ D .(2,2)()6 k k k Z π ππ+∈ 8.已知函数()sin()(0,)f x x x R ωφω=+>∈,对定义域内任意的x ,都满足条件(6)()f x f x +=,若 sin(3),sin(3)A x B x ωφωωφω=++=+-,则有 ( ) . A. A>B B. A=B C.A 任意角的三角函数 一、教学目标 1、知识目标:借助单位圆理解任意角的三角函数(正弦、余弦、正切) 的定义,根据定义探讨出三角函数值在各个象限的符号,掌握同一个角的不同三角函数之间的关系。 2、能力目标:能应用任意角的三角函数定义求任意角的三角函数值。 3、情感目标:培养数形结合的思想。 二、教材分析 1、教学重点:理解任意角三角函数(正弦、余弦、正切)的定义。 2、教学难点:从函数角度理解三角函数。 3、教学关键:利用数形结合的思想。 三、教学形式:讲练结合法 四、课时计划:2节课 五、教具:圆规、尺子 六、教学过程 (一)引入 我们已经学过锐角三角函数,知道他们都是以锐角为自变量,以比值 为函数值的函数,你能用直角坐标系中的终边上点的坐标来表示锐角 三角函数吗? 设锐角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,那么它 的终边在第一象限,在α的终边上任取一点P (a,b ),它与原点的距离 r=22b a +>0.根据初中学过的三角函数定义,我们有αsin =r b , r a αcos = a b αtan =,取r=1,则a b tan αa,cos αb,αsin ===,引入单位圆概念。 (二)新课 1、设α是以任意角,它的终边与单位圆交于P (x,y ),那么: (1) y 叫做α的正弦,记作αsin , 即y αsin =; (2) x 叫做α的余弦,记作αcos ,即x αcos =; (3) x y 叫做α的正切,记作αtan ,即x y αtan =)0(≠x . 注:用单位圆定义的好处就在于r=1,点的横坐标表示余弦值,纵坐标 表示正弦值。 2、根据任意角的三角函数定义,得到三种函数值在各象限的符号。 通过观察发现:第一象限全为正,第二象限只有正弦为正,第三象限只有正切为正,第四象限只有余弦为正。总结出一条法则:一全正,二正弦,三正切,四余弦。 注:这有利于培养学生观察和思考的能力,以方便记忆。 3、利用勾股定理可以推出:1cos sin 22=+αα,根据三角函数定义,当)(2z k k ∈+≠π πα时,有αα αtan cos sin =。这就是说同一个角α的正弦、余弦的平方和等于1,商等于角α的正切。 4、例题 例1求 3 5π的正弦、余弦和正切值。 解:在直角坐标系中,作3π5=∠AOB ,易知AOB ∠的终边与单位圆的交点 坐标为)2 3,21 (-,所以 高一数学必修4 第一章三角函数测试卷 一、选择题(每小题5分,共50分) 1.下列各组角中,终边相同的角是 ( ) A . π2k 与)(2 Z k k ∈+ππ B .)(3 k 3Z k k ∈± ππ π与 C .ππ)14()12(±+k k 与)(Z k ∈ D .)(6 6 Z k k k ∈± + π ππ π与 2.已知角α的终边过点()m m P 34, -,()0≠m ,则ααcos sin 2+的值是( ) A .1或-1 B . 52或 52- C .1或5 2 - D .-1或52 3.一个半径为R 的扇形,它的周长为4R ,则这个扇形所含弓形的面积为 ( ) A . 2)1cos 1sin 2(2 1 R ?- B . 1cos 1sin 2 12 ?R C . 2 2 1R D .221cos 1sin R R ??- 4.已知αα αα αtan ,5cos 5sin 3cos 2sin 那么-=+-的值为 ( ) A .-2 B .2 C .16 23 D .- 16 23 5.1sin 、1cos 、1tan 的大小关系为 ( ) A .1tan 1cos 1sin >> B .1cos 1tan 1sin >> C .1cos 1sin 1tan >> D .1sin 1cos 1tan >> 6.为得到函数)3 2sin(π -=x y 的图象,只需将函数)6 2sin(π + =x y 的图像( ) A .向左平移 4π个单位长度 B .向右平移4π 个单位长度 C .向左平移2π个单位长度 D .向右平移2π 个单位长度 7.函数sin(2)3 y x π =+图像的对称轴方程可能是( ) A .6x π=- B .12 x π =- C .6x π=D .12x π=8.已知函数1tan sin )(++=x b x a x f ,满足.7)5(=f 则)5(-f 的值为 ( ) A .5 B .-5 C .6 D .-6 9.函数)4 sin(π +=x y 在下列哪个闭区间上为增函数 ( ) A .]4 , 4 3 [π π- B .]0,[π- C .]4 3 ,4[ππ- D .]2 ,2[π π- 三角函数公式 (一)同角三角函数的基本关系式 (1)平方形式:sin 2α+cos 2α=1 (2)倒数形式:sinα/cosα=tanα (二)诱导公式 (1)sin (2k π+α)=sin α cos (2k π+α)=cos α tan (2k π+α)=tan α (其中k ∈Z) (2)sin (2k π-α)=-sin α cos (2k π-α)=cos α tan (2k π-α)=-tan α (其中k ∈Z) (3)sin (-α)=-sin α cos (-α)=cosα tan (-α)=-tan α (4)sin (π-α)=sin α cos (π-α)=-cosα tan (π-α)=-tan α (5)sin (π+α)=-sin α cos (π+α)=-cos α tan (π+α)=tan α (6)sin (π/2-α)=cos α cos (π/2-α)=sin α (7)sin (π/2+α)=cos α cos (π/2+α)=-sin α (8)sin (3π/2+α)=-cos α cos (3π/2+α)=sin α (9)sin (3π/2-α)=-cos α cos (3π/2-α)=-sin α (三) 两角和与差的三角函数公式 (1)sin (α+β)=sin αcosβ+cos αsinβ (2)sin (α-β)=sin αcosβ-cos αsinβ (3)cos (α+β)=cos αcosβ-sin αsinβ (4)cos (α-β)=cos αcosβ+sin αsinβ (5)tan (α+β)= tanα+tanβ1-tanαtanβ (6) tan (α-β)=tanα-tanβ1+tanαtanβ (四)二倍角的正弦、余弦和正切公式 (1)sin2α=2sin αcos α (2)cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α (3)tan2α= 2tan α/(1-tan 2α) (五)三角函数的降幂公式 (六)半角的正弦、余弦和正切公式 (七)(辅助角的三角函数的公式) (八)正、余弦定理公式及其变形 ● a sinA =b sinB =c sinC =2R (R 为△ABC 的外接圆的半径) ● a 2=b 2+c 2-2bccosA ● b 2= a 2+ c 2-2accosB ● c 2= b 2+ a 2-2abcosC (ⅰ) sinA=a 2R ,sinB=b 2R ,sinC=c 2R (ⅱ)a=2RsinA b=2RsinB c=2RsinC (ⅲ)a:b:c=sinA: sinB: sinC (ⅳ)asinB=bsinA bsinC=csinB asinC=csinA (九)常用的三角形面积公式 (ⅰ) S=12 absinC=12 acsinB=12 bcsinA (ⅱ)S =12 (a+b+c)r (r 为△ABC 的内切圆的半径) (ⅲ)S=abc 4R (R 为△ABC 的外接圆的半径) (十)利用余弦定理判断三角形的形状 (ⅰ)在△ABC 中,若a 2﹤b 2+c 2,则0°﹤A ﹤90°;反之,若0°﹤A ﹤90°,则a 2﹤b 2+c 2。 (ⅱ)在△ABC 中,若a 2=b 2+c 2,则A=90°;反之,若A=90°,则a 2=b 2+c 2。 (ⅲ)在△ABC 中,若a 2﹥b 2+c 2,则90°﹤A ﹤180°;反之,若90°﹤A ﹤180°,则a 2﹥b 2+c 2。 高一数学同步测试(1)—角的概念·弧度制 一、选择题(每小题5分,共60分,请将所选答案填在括号内) 1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A 、B 、C 关系是( ) A .B=A ∩C B .B ∪C=C C .A ?C D .A=B=C 2.下列各组角中,终边相同的角是 ( ) A . π2 k 与)(2Z k k ∈+ π π B .)(3k 3Z k k ∈± ππ π与 C .ππ)14()12(±+k k 与 )(Z k ∈ D .)(6 6Z k k k ∈± + π πππ与 3.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是 ( ) A .2 B . 1 sin 2 C .1sin 2 D .2sin 4.设α角的终边上一点P 的坐标是)5 sin ,5(cos π π ,则α等于 ( ) A . 5 π B .5 cot π C .)(10 32Z k k ∈+ππ D .)(5 92Z k k ∈- ππ 5.将分针拨慢10分钟,则分钟转过的弧度数是 ( ) A . 3 π B .- 3 π C . 6 π D .-6 π 6.设角α和β的终边关于y 轴对称,则有 ( ) A .)(2 Z k ∈-= βπ α B .)()2 1 2(Z k k ∈-+ =βπα C .)(2Z k ∈-=βπα D .)()12(Z k k ∈-+=βπα 7.集合A={}, 32 2|{},2|Z n n Z n n ∈±=?∈= ππααπαα, B={}, 2 1 |{},3 2|Z n n Z n n ∈+=?∈=ππββπ ββ, 则A 、B 之间关系为 ( ) A .A B ? B .B A ? C .B ?A D .A ?B 8.某扇形的面积为12 cm ,它的周长为4cm ,那么该扇形圆心角的度数为 ( ) A .2° B .2 C .4° D .4 9.下列说法正确的是 ( ) A .1弧度角的大小与圆的半径无关 B .大圆中1弧度角比小圆中1弧度角大 ≠ ≠ ≠ 人教版数学必修四三角函数 复习讲义 本页仅作为文档页封面,使用时可以删除 This document is for reference only-rar21year.March 第一讲 任意角与三角函数诱导公式 1. 知识要点 角的概念的推广: 平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。 象限角的概念: 在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 终边相同的角的表示: α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k k αθπ=+∈Z 。 注意:相等的角的终边一定相同,终边相同的角不一定相等. α终边在x 轴上的角可表示为:,k k Z απ=∈; α终边在y 轴上的角可表示为:,2 k k Z π απ=+∈; α终边在坐标轴上的角可表示为:,2 k k Z π α= ∈. 角度与弧度的互换关系:360°=2π 180°=π 1°=0.01745 1=57.30°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零. α与2 α的终边关系: 任意角的三角函数的定义: 设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点), 它与原点的距离是0r =>,那么sin ,cos y x r r αα==, ()tan ,0y x x α= ≠,cot x y α=(0)y ≠,sec r x α=()0x ≠,()csc 0r y y α=≠。 三角函数值只与角的大小有关,而与终边上点P 的位置无关。 三角函数线的特征:正弦线MP“站在x 轴上(起点在x 轴上)”、余弦线 OM“躺在x 轴上(起点是原点)”、正切线AT“站在点(1,0)A 处(起点是A )” 同角三角函数的基本关系式: 1. 平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= 2. 倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, 3. 商数关系:sin cos tan ,cot cos sin αα αααα = = 注意:1.角α的任意性。 2.同角才可使用。 3.熟悉公式的变形形 式。 三角函数诱导公式:“ (2 k πα+)”记忆口诀: “奇变偶不变,符号看象限” 典型例题 例1.求下列三角函数值: (1)cos210o; (2)sin 4 5π 例2.求下列各式的值: (1)sin(-3 4π ); (2)cos(-60o)-sin(-210o) 例3.化简 ) 180sin()180cos() 1080cos()1440sin(?--?-?-?-?+?αααα 例4.已知cos(π+α)=-2 1,2 3π<α<2π,则sin(2π-α)的值是( ). 必修4三角函数综合测试题及答案详解 一、选择题 1.下列说法中,正确的是( ) A .第二象限的角是钝角 B .第三象限的角必大于第二象限的角 C .-831°是第二象限角 D .-95°20′,984°40′,264°40′是终边相同的角 2.若点(a,9)在函数y =3x 的图象上,则tan a π 6的值为( ) A .0 B.3 3 C .1 D. 3 3.若|cos θ|=cos θ,|tan θ|=-tan θ,则θ 2的终边在( ) A .第一、三象限 B .第二、四象限 C .第一、三象限或x 轴上 D .第二、四象限或x 轴上 4.如果函数f (x )=sin(πx +θ)(0<θ<2π)的最小正周期是T ,且当x =2时取得最大值,那么( ) A .T =2,θ=π 2 B .T =1,θ=π C .T =2,θ=π D .T =1,θ=π 2 5.若sin ? ???? π2-x =-32,且π 7.将函数y =sin x 的图象向左平移φ(0≤φ<2π)个单位长度后,得到y =sin ? ?? ?? x -π6的图象,则φ=( ) A.π6 B.5π6 C.7π6 D.11π6 8.若tan θ=2,则2sin θ-cos θ sin θ+2cos θ的值为( ) A .0 B .1 C.34 D.54 9.函数f (x )=tan x 1+cos x 的奇偶性是( ) A .奇函数 B .偶函数 C .既是奇函数又是偶函数 D .既不是奇函数也不是偶函数 10.函数f (x )=x -cos x 在(0,+∞)内( ) A .没有零点 B .有且仅有一个零点 C .有且仅有两个零点 D .有无穷多个零点 三角函数 公式大全 姓名: 1、两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) = tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1 -cotAcotB + cot(A-B) =cotA cotB 1 cotAcotB -+ 2、倍角公式 tan2A = A tan 12tanA 2 - Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 3、三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan( 3π+a)·tan(3 π-a) 4、半角公式 sin( 2A )=2cos 1A - cos( 2A )=2 cos 1A + tan( 2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan( 2 A )=A A sin cos 1-=A A cos 1sin + 5、和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cos b = 2cos 2b a +cos 2 b a - cosa-cosb = -2sin 2b a +sin 2 b a - tana+tanb=b a b a cos cos ) sin(+ 6、积化和差 sinasinb = -21 [cos(a+b)-cos(a-b)] cosacosb = 21 [cos(a+b)+cos(a-b)] sinacosb = 2 1 [sin(a+b)+sin(a-b)] cosasinb = 2 1 [sin(a+b)-sin(a-b)] 必修四第一章三角函数测试题 班别 姓名 分数 一、选择题 1.已知cos α=1 2 ,α∈(370°,520°),则α等于 ( ) A .390° B .420° C .450° D .480° 2.若sin x ·tan x <0,则角x 的终边位于 ( ) A .第一、二象限 B .第二、三象限 C .第二、四象限 D .第三、四象限 3.函数y =tan x 2 是 ( ) A .周期为2π的奇函数 B .周期为π 2的奇函数C .周期为π的偶函数D .周期为2π的偶函数 4.已知函数y =2sin(ωx +φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于 ( ) A .1 B .2 C.12 D.13 5.函数f (x )=cos(3x +φ)的图象关于原点成中心对称,则φ等于 ( ) A .-π2 B .2k π-π 2 (k ∈Z ) C .k π(k ∈Z ) D .k π+π 2(k ∈Z ) 6.若sin θ+cos θsin θ-cos θ =2,则sin θcos θ的值是 ( ) A .-310 B.310 C .±310 D.34 7.将函数y =sin x 的图象上所有的点向右平行移动π 10 个单位长度,再把所得各点的横坐标伸 长到原来的2倍(纵坐标不变),所得图象的函数解析式是 ( ) A .y =sin ? ???2x -π10 B .y =sin ????2x -π5 C .y =sin ????12x -π10 D .y =sin ??? ?12x -π 20 8.在同一平面直角坐标系中,函数y =cos ????x 2+3π2(x ∈[0,2π])的图象和直线y =1 2的交点个数是 ( ) A .0 B .1 C .2 D .4 9.已知集合M =???? ??x |x =k π2+π4,k ∈Z ,N ={x |x =k π4+π 2,k ∈Z }.则 ( ) A .M =N B .M N C .N M D .M ∩N =? 1.4—1.5 三角函数的图象与性质 一、正弦函数的图象与性质 1、利用描点法作函数图象 (列表、描点、连线) 自变量x 2π- 32π- π- 2 π- 0 2π π 32 π 2π 函数值sin x 0 1 0 1- 0 1 1- 0 注意:(1)由于sin(2k π+α)=sin α,因此作正弦函数图象时,我们经常采用 “五点法”:......(0..,.0)..,.(.2 π ,.1)..,.(.π,.0)..,.(.23π ,-..1)..,.(2..π,.0)..;. 再通过向左、右平移(每次2π个单位),即可得正弦函数图象;(2)正弦函数自变量一般采用弧度制。 二、余弦函数的图象 1、余弦函数的图象:y =cosx =sin(x + 2π)可将正弦函数y =sinx 向左平移2 π 个单位得到。 2、“五点作图法”: (0..,.1.).,. (.2 π ,.0.).,. (.π,-..1.).,. (.23π ,.0.).,. (2..π,.1.). – – π 2 π 2 π - 2π 5π π- 2π- 5π- O x y 1 1- 三、正、余弦函数的性质 f(x)=sinx h(x)=cosx f(x)=sinx h(x)=cosx 定义域 R R 值域 [-1,1] 当x =2k π+ 2π 时,f(x)max =1 当x =2k π-2π 时,f(x)min =-1 [-1,1] 当x =2k π时,f(x)max =1 当x =2k π+π时,f(x)min =-1 单调区间 [2 k π-2π,2 k π+2 π ] 单增 [2 k π+2 π ,2 k π+23π] 单减 [2 k π,2 k π+π] 单减 [2 k π+π,2 k π+2π] 单增 对称轴 x =k π+2 π x =k π 对称中心 (k π,0) (k π+ 2 π ,0) 周期性 sin(2 k π+α)=sin α cos(2 k π+α)=cos α 最小正周期为2π 奇偶性 sin(-α)=-sin α 奇函数 cos(-α)=cos α 例1:求下列函数的定义域。 (1)f(x)=x sin (2)f(x)=2 1cos -x 高中数学必修四三角函数重要公式 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与-α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα (以上k∈Z) 诱导公式记忆口诀 ※规律总结※ 上面这些诱导公式可以概括为: 对于k·π/2±α(k∈Z)的个三角函数值, ①当k是偶数时,得到α的同名函数值,即函数名不改变; ②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan. (奇变偶不变) 然后在前面加上把α看成锐角时原函数值的符号。 (符号看象限) 例如: sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。 当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。 所以sin(2π-α)=-sinα y x 1 1 2 3 O (人教版)高二数学必修4第一章三角函数单元测试题(含答案) 一、选择题:本大题共12个小题,每小题5分,共 60分.在每小题给出的四个选项中,只有一个是符合题目要求的. 1 . A B . C D 2.下列函数中,最小正周期为 的是 A . B . C . D . 3.已知 , ,则 A B C D . 4.函数 是周期为的偶函数,且当 A B C . D .2 5 A B 个单位 C 个单位 D .向右平 移 6 .函数的零点个数为 A .5 B .7 C .3 D .9 7 .函数 可取的一组值为 A B C D 8 .已知函数 的值可能是 A B C D . 9 ,则 这个多边形为 A .正六边形 B .梯形 C .矩形 D .正五边 形 10 .函数有3个零点,则 的值为 A .0 B .4 C .2 D .0,或2 11 .对于函数的一组值计 ,所得的结果可能是 A .0与1 B .1 C .101 D .与 12.给出下列3个命题: ①函数; ②函数 ③ A.0 B.1 C.2 D.3 二、填空题:本大题共4个小题,每小题5分,共20分.把正确答案填在题中横线上.13.角的终边过点,且,则的值为▲. 14.设,若函数在上单调递增,则的取值范围是▲. 15.已知,则▲. 16.函数个单位,所的函数为偶函数; 的最大值为▲. 三、解答题:本大题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分) 已知扇形的周长为4,那么当扇形的半径为何值时,它的面积最大,并求出最大面积,以及相应的圆心角. 18.(本小题满分12分) 已知函数时,取得最小值 (Ⅰ)求函数的最小正周期; (Ⅱ)求函数的解析式. 19.(本小题满分12分) 若,为第四象限角,求 20.(本小题满分12分) 求下列函数的值域 (Ⅰ) (Ⅱ). 21.(本小题满分12分) 已知函数.求的 (Ⅰ)定义域; (Ⅱ)单调递增区间; (Ⅲ)值域. 22.(本小题满分12分) 《三角函数》【知识网络】 一、任意角的概念与弧度制 1、将沿x轴正向的射线,围绕原点旋转所形成的图形称作角. 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角 2、同终边的角可表示为 {}()360k k Z ααβ? =+∈ x 轴上角:{}()180k k Z αα=∈ y 轴上角:{}()90180k k Z αα=+∈ 3、第一象限角:{}()0360 90360k k k Z αα? ?+<<+∈ 第二象限角:{}()90360180360k k k Z αα??+<<+∈ 第三象限角:{}()180360270360k k k Z αα? ?+<<+∈ 第四象限角: {}()270 360360360k k k Z αα??+<<+∈ 4、区分第一象限角、锐角以及小于90的角 第一象限角:{}()0360 90360k k k Z αα? ?+<<+∈ 锐角: {}090αα<< 小于90的角:{}90αα< 5、若α为第二象限角,那么 2 α 为第几象限角? ππαππ k k 222 +≤≤+ ππ α ππ k k +≤ ≤ +2 2 4 ,24,0παπ≤≤=k ,2345,1παπ≤≤=k 所以2 α 在第一、三象限 6、弧度制:弧长等于半径时,所对的圆心角为1弧度的圆心角,记作1rad . 7、角度与弧度的转化:01745.0180 1≈=?π 815730.571801'?=?≈? = π 8、角度与弧度对应表: 9、弧长与面积计算公式 弧长:l R α=?;面积:211 22 S l R R α=?=?,注意:这里的α均为弧度制. 二、任意角的三角函数 1、正弦:sin y r α=;余弦cos x r α=;正切tan y x α= 其中(),x y 为角α 终边上任意点坐标,r = 2、三角函数值对应表: 3、三角函数在各象限中的符号 口诀:一全正,二正弦,三正切,四余弦.(简记为“全s t c ”) 三角函数 一、选择题 1.已知 α 为第三象限角,则 2 α 所在的象限是( ). A .第一或第二象限 B .第二或第三象限 C .第一或第三象限 D .第二或第四象限 2.若sin θcos θ>0,则θ在( ). A .第一、二象限 B .第一、三象限 C .第一、四象限 D .第二、四象限 3.sin 3π4cos 6π5tan ?? ? ??3π4-=( ). A .- 4 3 3 B . 4 3 3 C .- 4 3 D . 4 3 4.已知tan θ+θ tan 1 =2,则sin θ+cos θ等于( ). A .2 B .2 C .-2 D .±2 5.已知sin x +cos x =5 1(0≤x <π),则tan x 的值等于( ). A .-4 3 B .-3 4 C .4 3 D .3 4 6.已知sin α >sin β,那么下列命题成立的是( ). A .若α,β 是第一象限角,则cos α >cos β B .若α,β 是第二象限角,则tan α >tan β C .若α,β 是第三象限角,则cos α >cos β D .若α,β 是第四象限角,则tan α >tan β 7.已知集合A ={α|α=2k π±3π2,k ∈Z },B ={β|β=4k π±3 π 2,k ∈Z },C = {γ|γ=k π± 3 π 2,k ∈Z },则这三个集合之间的关系为( ). A .A ?B ?C B .B ?A ?C C .C ?A ?B D .B ?C ?A 8.已知cos (α+β)=1,sin α=3 1,则sin β 的值是( ). A .3 1 B .-3 1 C . 3 2 2 D .- 3 2 2 9.在(0,2π)内,使sin x >cos x 成立的x 取值范围为( ). A .??? ??2π , 4π∪??? ??4π5 ,π B .?? ? ??π , 4 π C .?? ? ??4π5 ,4π D .??? ??π , 4 π∪?? ? ??23π ,4π5 10.把函数y =sin x (x ∈R )的图象上所有点向左平行移动3 π 个单位长度,再把所得图象上所有点的横坐标缩短到原来的2 1 倍(纵坐标不变),得到的图象所表示的函数是( ). A .y =sin ?? ? ? ?3π - 2x ,x ∈R B .y =sin ??? ??6π + 2x ,x ∈R C .y =sin ??? ? ?3π + 2x ,x ∈R D .y =sin ??? ? ? 32π + 2x ,x ∈R 二、填空题 11.函数f (x )=sin 2 x +3tan x 在区间??? ???3π 4π ,上的最大值是 . 12.已知sin α= 552,2 π ≤α≤π,则tan α= . 13.若sin ??? ??α + 2π=53,则sin ?? ? ??α - 2π= . 14.若将函数y =tan ??? ? ? 4π + x ω(ω>0)的图象向右平移6π个单位长度后,与函 数y =tan ?? ? ??6π + x ω的图象重合,则ω的最小值为 . 15.已知函数f (x )=21(sin x +cos x )-2 1 |sin x -cos x |,则f (x )的值域是 . 16.关于函数f (x )=4sin ?? ? ? ?3π + 2x ,x ∈R ,有下列命题: ①函数 y = f (x )的表达式可改写为y = 4cos ?? ? ? ?6π - 2x ; ②函数 y = f (x )是以2π为最小正周期的周期函数; ③函数y =f (x )的图象关于点(- 6 π ,0)对称; 数学必修四三角函数公式盘点与归纳 1、诱导公式: sin(2kπ+α)=sinα, cos(2kπ+α)=cosα sin(-α)=-sinα, cos(-α)=cosα sin(2π-α)=-sinα, cos(2π-α)=cosα sin(π-α)=sinα, cos(π-α)=-cosα sin(π+α)=-sinα, cos(π+α)=-cosα sin(+α)=cosα, cos(+α)=-sinα sin(-α)=cosα, cos(-α)=sinα 2、同角三角函数基本关系: sin2α+cos2α=1, =tanα, tanα×cotα=1, 1+tan2α=, 1+cot2α= cosα=, sinα= 3、两角和与差的三角函数: cos(α+β)=cosαcosβ-sinαsinβ, cos(α-β)=cosαcosβ+sinαsinβ, sin(α+β)=sinαcosβ+cosαsinβ, sin(α-β)=sinαcosβ-cosαsinβ tan(α+β)=, tan(α-β)=, 4、二倍角的三角函数: sin2α=2sinαcosα, cos2α=cos2α-sin2α =1-2sin2α =2cos2α-1, tan2α=, sin=, cos=, tan= = = 5、万能公式: sin2α=, cos2α= 6、合一变式: asinα+bcosα =sin(α+γ)(tanγ=)7、其他公式: sinαcosβ=[sin(α+β)+sin(α-β)], cosαsinβ=[sin(α+β)-sin(α-β)], cosαcosβ=[cos(α+β)+cos(α-β)],sinαsinβ=[cos(α+β)-cos(α-β)],sinα+sinβ=2sin cos, sinα-sinβ=2cos sin, cosα+cosβ=2cos cos, cosα-cosβ=2sin cos 第一讲 任意角与三角函数诱导公式 1. 知识要点 角的概念的推广: 平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。 象限角的概念: 在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 终边相同的角的表示: α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k k αθπ=+∈Z 。 注意:相等的角的终边一定相同,终边相同的角不一定相等. α终边在x 轴上的角可表示为:,k k Z απ=∈; α终边在y 轴上的角可表示为:,2 k k Z π απ=+∈; α终边在坐标轴上的角可表示为:,2 k k Z π α= ∈. 角度与弧度的互换关系:360°=2π 180°=π 1°= 1=°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零. α与2 α的终边关系: 任意角的三角函数的定义: 设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点), 它与原点的距离是0r =>,那么sin ,cos y x r r αα==, ()tan ,0y x x α= ≠,cot x y α=(0)y ≠,sec r x α=()0x ≠,()csc 0r y y α=≠。 三角函数值只与角的大小有关,而与终边上点P 的位置无关。 三角函数线的特征:正弦线MP“站在x 轴上(起点在x 轴上)”、余弦线OM“躺在x 轴上(起点是原点)”、正切线AT“站在点(1,0)A 处(起点是A )” 同角三角函数的基本关系式: 1. 平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= 2. 倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, 3. 商数关系:sin cos tan ,cot cos sin αα αααα = = 注意:1.角α的任意性。 2.同角才可使用。 3.熟悉公式的变 形形式。 三角函数诱导公式:“ (2 k πα+)”记忆口诀: “奇变偶不变,符号看象限” 典型例题 例1.求下列三角函数值: (1)cos210o; (2)sin 4 5π 例2.求下列各式的值: (1)sin(-3 4π ); (2)cos(-60o)-sin(-210o) 例3.化简 ) 180sin()180cos() 1080cos()1440sin(?--?-?-?-?+?αααα 三角函数 单元测试 一、选择题 1.sin 210=o ( ) A . B . C .12 D .12 - 2.下列各组角中,终边相同的角是 ( ) A .π2k 或()2k k Z π π+∈ B . (21)k π+或(41)k π± )(Z k ∈ C .3 k π π± 或k ()3 k Z π ∈ D .6 k π π+ 或()6 k k Z π π± ∈ 3.已知cos tan 0θθ?<,那么角θ是( ) A .第一或第二象限角 B .第二或第三象限角 C .第三或第四象限角 D .第一或第四象限角 4.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是 ( ) A .2 B . 1sin 2 C .1sin 2 D .2sin 5.为了得到函数2sin(),36 x y x R π =+∈的图像,只需把函数2sin ,y x x R =∈的图 像上所有的点( ) A .向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的3 1 倍(纵坐标不变) B .向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的3 1 倍(纵坐标不变) C .向左平移6 π 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) D .向右平移6 π 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) 6.设函数()sin ()3f x x x π? ?=+∈ ?? ?R ,则()f x ( ) A .在区间2736ππ?? ? ??? ,上是增函数 B .在区间2π? ? -π-??? ?,上是减函数 C .在区间84ππ?? ????,上是增函数 D .在区间536ππ?? ???? ,上是减函数 7.函数sin()(0,,)2 y A x x R π ω?ω?=+>< ∈的部分图象如图所示, 则函数表达( ) A .)48sin(4π+π-=x y B .)48sin(4π -π=x y C .)48sin(4π-π-=x y D .)4 8sin(4π +π=x y 8. 函数sin(3)4 y x π =-的图象是中心对称图形,其中它的一个对称中心是 ( ) A .,012π??- ??? B . 7,012π??- ??? C . 7,012π?? ??? D . 11,012π?? ??? 9.已知()21cos cos f x x +=,则 ()f x 的图象是下图的 ( ) A B C D 10.定义在R 上的偶函数()f x 满足()()2f x f x =+,当[]3,4x ∈时,()2f x x =-,则 ( ) A .11sin cos 22f f ??? ?< ? ???? ? B . sin cos 33f f ππ??? ?> ? ???? ? C .()()sin1cos1f f < D .33sin cos 22f f ??? ?> ? ???? ? 二、填空题 11.若2cos 3 α=,α是第四象限角,则sin(2)sin(3)cos(3)απαπαπ-+---=___ 12.若tan 2α=,则22sin 2sin cos 3cos αααα++=___________ 13.已知3sin 4πα??+= ???,则3sin 4πα?? - ??? 值为 14.设()f x 是定义域为R ,最小正周期为 32 π 的周期函数,若必修4三角函数的图像和性质专题练习
高中数学必修4三角函数教案
高一数学_必修4_三角函数测试卷(含答案)
高一数学必修一和必修四的三角函数公式
高中数学必修4三角函数测试题
人教版数学必修四三角函数复习讲义
高中数学必修4三角函数综合测试题
必修4三角函数公式大全(经典)
必修四第一章三角函数测试题(含答案)
必修四三角函数的图象与性质讲义
高中数学必修四三角函数重要公式
(人教版)高二数学必修4第一章三角函数单元测试题(含答案)
必修4三角函数所有知识点归纳归纳
高中数学必修4三角函数测试题答案详解1
数学必修四三角函数公式总结与归纳
人教版数学必修四三角函数复习讲义
必修4三角函数单元测试题(含答案)
