自由落体法测重力加速度的智能系统

第8卷 第4期2009年12月 太原师范学院学报(自然科学版)J OU RNAL OF TA IYUAN NORMAL UN IV ERSIT Y (Natural Science Edition )
Vol.8No.4 Dec.2009自由落体法测重力加速度的智能系统
袁树青1 范学东2 乔纪平1 冯亚强1
(1.太原理工大学,山西太原030024;2.国家广电总局725台,山西灵石031308)
〔摘要〕 开发了一套自由落体测重力加速度的智能系统,该系统包括下位机硬件部分,主要是利用A T89S52单片机对通过两个光电门的时间进行处理,通过串口通信将数据发送至PC 机;还包括上位机软件的编制,这部分利用LabV IEW 编程软件开发了一个数据处理显示平台.系统极大地改善了实验环境、丰富了实验内容以及提高了实验效率.
〔关键词〕 重力加速度;光电门;串口通信;虚拟仪器
〔文章编号〕 167222027(2009)0420081204 〔中图分类号〕 O4239 〔文献标识码〕 A
0 引言
重力加速度的测量是高校普通物理实验课中的必做实验,而自由落体测定仪(如图1所示)则是常用的测量仪器.它由支柱、真空吸嘴和两个光电门组成.金属小球下落时分别对两个光电门挡光,控制光电计时仪开始或停止计时[1].
图1 自由落体测定仪Fig.1 Acceleration of gravity measuring
instruments using f ree 2fall method 光电门Ⅰ放在A 处不动,光电门Ⅱ放在B 处,金属小球从O
点自由落体运动,先测量A 、B 之间的距离S 1和小球从A 到B 所
用的时间t 1,接着将光电门Ⅱ移到C 处再一次让小球自由下落,测
量A 、C 之间的距离S 2和小球从A 到C 得时间t 2,则有
S 1=v A t 1+
12gt 21(1)S 2=v A t 2+12gt 22(2)
式中,v A 是小球是小球经过A 点处的速度.联立上式可得重力加
速度
g =2(S 2/t 2-S 1/t 1)(t 2-t 1)
-1(3) 传统自由落体测定仪由毫秒计时器显示物体经过两个光电门的时间,最后经过繁琐的手工计算求得重力加速度,其主要缺点是
实验效率较低.本文开发了一种在微机辅助的智能处理系统,包括基于单片机A T89S52的数据采集系统和基于PC 的虚拟处理系统,可以完成时间数据的采集、存储与显示以及重力加速度的计算,并且进行误差分析.该系统可有效提高实验效率,突出了学生对物理现象和概念的关注及理解,增强了其对物理实验的兴趣.1 系统下位机硬件电路及程序
1.1 硬件电路
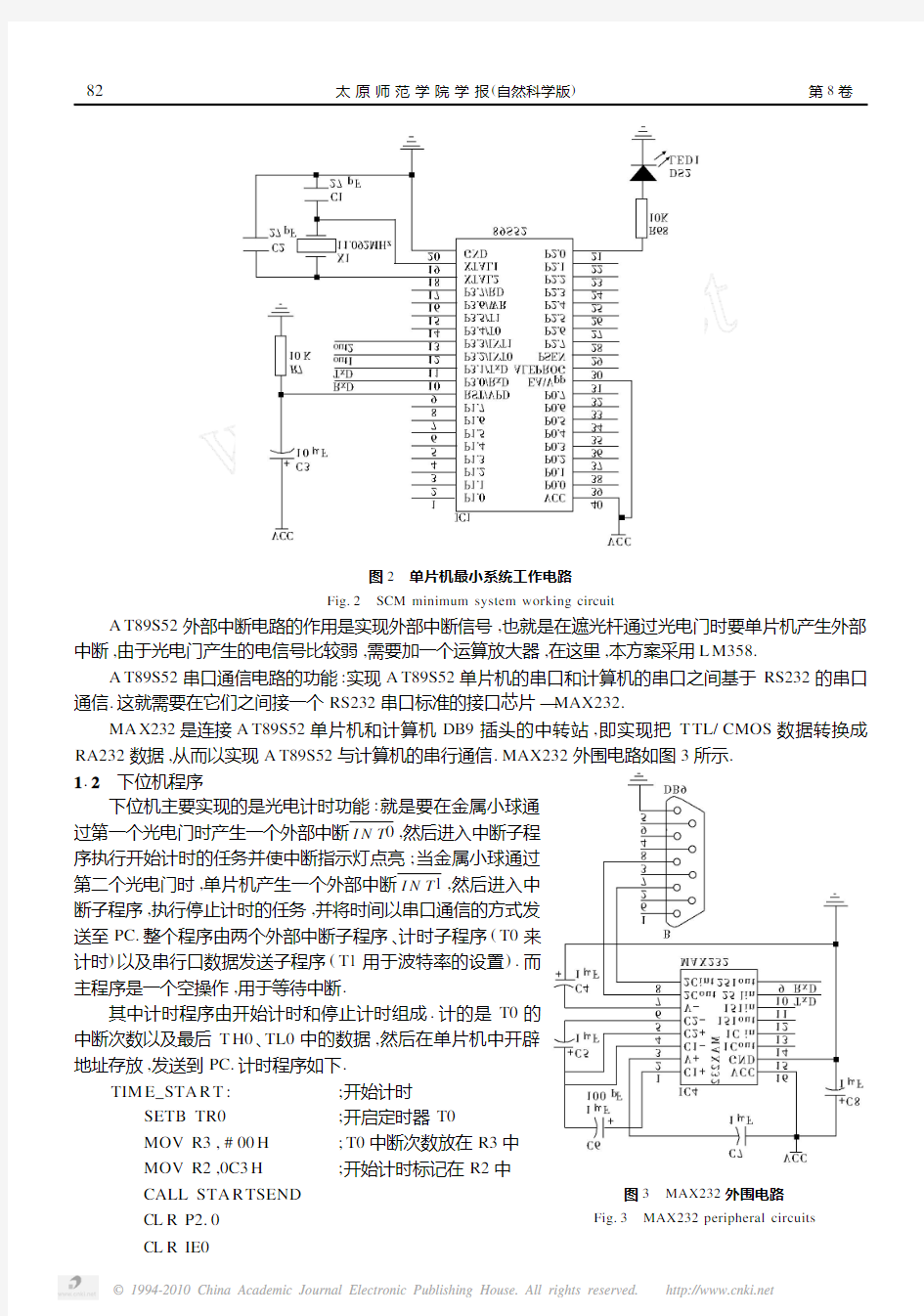
本系统采用A T89S52芯片,完成从光电门接收数据,并把接收到的数据发送到PC 机,而其他外围设备或芯片都起到辅助作用.
A T89S52的最小系统电路图如图2所示,它由三部分组成:复位电路、时钟电路、中断指示电路[2].复位电路和时钟电路都是使单片机正常工作所必须的电路,而对于指示灯电路是为了说明有外部中断信号.
3收稿日期:2009209227
作者简介:袁树青(19812),女,河北唐山人,硕士,太原理工大学理学院物理系助理工程师,主要从事物理实验教学和研究工作.
图2 单片机最小系统工作电路
Fig.2 SCM minimum system working circuit
A T89S52外部中断电路的作用是实现外部中断信号,也就是在遮光杆通过光电门时要单片机产生外部中断,由于光电门产生的电信号比较弱,需要加一个运算放大器,在这里,本方案采用L M358.
A T89S52串口通信电路的功能:实现A T89S52单片机的串口和计算机的串口之间基于RS232的串口通信.这就需要在它们之间接一个RS232串口标准的接口芯片—MAX232.
MA X232是连接A T89S52单片机和计算机DB9插头的中转站,即实现把T TL/CMOS 数据转换成RA232数据,从而以实现A T89S52与计算机的串行通信.MAX232外围电路如图3所示
.
图3 MAX232外围电路Fig.3 MAX232peripheral circuits
1.2 下位机程序
下位机主要实现的是光电计时功能:就是要在金属小球通
过第一个光电门时产生一个外部中断I N T 0,然后进入中断子程
序执行开始计时的任务并使中断指示灯点亮;当金属小球通过
第二个光电门时,单片机产生一个外部中断I N T 1,然后进入中
断子程序,执行停止计时的任务,并将时间以串口通信的方式发
送至PC.整个程序由两个外部中断子程序、计时子程序(T0来
计时)以及串行口数据发送子程序(T1用于波特率的设置).而
主程序是一个空操作,用于等待中断.
其中计时程序由开始计时和停止计时组成.计的是T0的
中断次数以及最后T H0、TL0中的数据,然后在单片机中开辟
地址存放,发送到PC.计时程序如下.
TIM E_STA R T : ;开始计时
SETB TR0
;开启定时器T0 MOV R3,#00H
;T0中断次数放在R3中 MOV R2,0C3H
;开始计时标记在R2中 CALL STA R TSEND
CL R P2.0
CL R IE0
28太原师范学院学报(自然科学版) 第8卷
CL R IE1
SETB EX0
SETB EX1
RETI
TIM E_STO P :
CL R TR0
CALL STOPSEND
MOV TL0,#TL0STAR T
MOV T H0,#T H0STA R T
SETB P2.0
CL R IE0
CL R IE1
SETB EX0
SETB EX1
MOV R2,#3C H
RETI
2 上位机LabV IEW 程序设计
系统的前面板包括:实验参数输入、测量步骤选择和显示三部分[3].
通过实验参数输入部分可以对小球的质量和两个光电门的位置进行自由设置,例如S 1取30cm ,S 2取130cm.测量步骤选择下拉列表中包括本实验的三个实验步骤,即测量t 1,测量t 2和数据处理,依次选择这三个步骤,可以对t 1,t 2重复测量5次,计算重力加速度以及误差,并表示出测量结果.显示部分用于显示测量次数,测得的时间量值及两个光电门的位置、实验结果和相对误差.
3 系统运行结果及分析
按测量步骤运行每一步,完成各步骤后,结果显示如图
4.
图4 运行结果
Fig.4 Running results
经过运行可知,误差在允许的范围内,说明该系统设计正确,测试准确,运行可靠.
4 结论
本文设计了一种基于LabV IEW 仿真软件的智能重力加速度测定仪,完成了对时间数据采集、数据存3
8 第4期 袁树青等:自由落体法测重力加速度的智能系统
48太原师范学院学报(自然科学版) 第8卷
储、数据处理和结果显示的全部过程.只要在软件上稍加改动,就可将其应用到其他有关需要计时的实验中去,有力地促进了大学物理实验的教学.
参考文献:
[1] 王云才.大学物理实验教程[M].第3版.北京:科学出版社,2008:1602161
[2] 张俊藻.单片机中级教程[M].第2版.北京:北京航空航天出版社,2006:25237
[3] 陈锡辉,张银鸿.LabV IEW8.20程序设计从入门到精通[M].北京:清华大学出版社,2007:17228
Intelligent System of Acceleration of G ravity
Measuring Instruments Using Free2fall Method
Yuan Shuqing1 F an Xuedong2 Q iao Jiping1 Feng Yaqiang1
(1.Taiyuan University of Technology,Taiyuan030024;
2.The State Administration of Radio Film and Television725Station,Lingshi031308,China)
〔Abstract〕 The article has developed an intelligent system measuring acceleration of gravity using f ree2fall met hod.The system includes t he hardware component s,mainly using A T89S52mi2 crocontroller p rocessing time data getting f rom t he two optical gates,and sending t he data to t he PC t hrough t he serial port.The software system part,using LabV IEW is also included.It has de2 veloped a data p rocessing and display platform.This system greatly improved t he experimental environment,Enriched t he experimental content and imp roved t he efficiency of t he experiment.
〔K ey w ords〕 acceleration of gravity;p hotoelectric gate;serial communication;LabV IEW
【责任编辑:王映苗】
(上接第47页)
参考文献:
[1] 孙家广,杨长贵.计算机图形学(新版)[M].北京:清华大学出版社,1995
[2] John Walkenbach.中文版Excel2007高级VBA编程宝典[M].冯 飞,焦瑜净,译.北京:清华大学出版社,2009
[3] Peter Rakos.Microsoft Excel:Revolutionary3D Game Engine?[EB/OL]https://www.360docs.net/doc/f09704593.html,/view/feat ure/3563/
microsoft_excel_revolutionary_3d_.php,2008203206
Application of Microsoft Excel in Experiments of R aster G raphics
Yang Xuhua
(College of Mathematics and Information Science,Huanggang Normal University,Huanggang438000,China)
〔Abstract〕 U sing Excel on experiment s of raster grap hics,we can make experimental design more convenient,experimental operation flexible,experimental result s int uitive,achieve better ex2 perimental result s.
〔K ey w ords〕 Excel;raster grap hics;experiment s;Bresenham circle algorit hms
【责任编辑:王映苗】
用凯特摆测量重力加速度实验报告
用凯特摆测量重力加速度 实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。 实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期: 刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复 摆绕通过重心G的转轴的转动惯量为I G 。 当G轴与O轴平行时,有I=I G+mh2 ∴ ∴复摆的等效摆长l=( I G+mh2 )/mh 2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O′,可使 该摆以O为悬点的摆动周期T?与以O′为悬点的摆动周期T?相同, 可证得|OO′|=l,可精确求得l。 3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆 锤得位置使正、倒悬挂时得摆动周期T?≈T?。 ∴4π2/g=(T?2+T?2)/2l + (T?2-T?2)/2(2h?-l) = a + b 实验仪器:凯特摆、光电探头、米尺、数字测试仪。 实验内容:1、仪器调节 选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本 对称,并相互平行,用米尺测出l的值,粗略估算T值。 将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借 助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。 将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自 动记录一个周期的时间。 2、测量摆动周期T?和T? 调整四个摆锤的位置,使T?和T?逐渐靠近,差值小于,测量正、 倒摆动10个周期的时间10T?和10T?各测5次取平均值。 3、计算重力加速度g及其标准误差σg 。 将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。 测出|GO|即h?,代入公式计算g。 推导误差传递公式计算σg 。 实验数据处理:1、l的值 l=?(l?+l?+l?)= σ=,u A =σ/=, ∴ΔA =t P ?u A =*= u B=ΔB /C=3= ∴u L == T e == 2、T?和T?的值 T?= σ=*10ˉ?s,u A =σ/=*10ˉ?s ∴ΔA =t P ?u A =*=*10ˉ?s u B=ΔB /C=3=*10ˉ?s ∴u T1 ==*10ˉ?s T?= σ=*10ˉ?s,u A =σ/=*10ˉ?s ∴ΔA =t P ?u A =*=*10ˉ?s u B=ΔB /C=3=*10ˉ?s
实验2自由落体法测定重力加速度(详写)
《实验2 自由落体法测定重力加速度》 实验报告 一、实验目的和要求 1、学会用自由落体法测定重力加速度; 2、用误差分析的方法,学会选择最有利的测量条件减少测量误差。 二、实验描述 重力加速度是很重要的物理参数,本实验通过竖直安放的光电门测量自由落体时间来求重力加速度,如何提高测量精度以及正确使用光电计时器是 实验的重要环节。 三、实验器材 MUJ-5C型计时计数测速仪(精度),自由落体装置(刻度精度),小钢球,接 球的小桶,铅垂线。 四、实验原理 实验装置如图1。 在重力实验装作用下,物体的下落运动是匀加速直线运动, 其运动方程为 s=v0t+1/2g t2 该式中,s是物体在t时间内下落的距离;v0是物体运动的初 速度;g是重力加速度;若测得s, v0,t,即求出g值。 若使v0=0,即物体(小球)从静止释放,自由落体,则可 避免测量v0的麻烦,而使测量公式简化。但是,实际测量S 时总是存在一些困难。本实验装置中,光电转换架的通光孔总 有一定的大小,当小铁球挡光到一定程度时,计时-计数-计频 仪才开始工作,因此,不容易确定小铁球经光电转换架时的挡 光位置。为了解决这个问题,采用如下方法: 让小球从O点处开始下落,设它到A处速度为v0,再经过 t1时间到达B处,令AB间距离为s1,则 gt12 s1=v0t1?1 2 同样,经过时间t2后,小球由A处到达B’处,令AB’间 的距离为s2,则有 s2=v0t2+1/2g t22 化简上述两式,得: 图1 实验装置图g=2(s2t1-s1t2)/ t1t22-t2t12=2(s2/t2-s1/t1)/ t2-t1 --------------------------------------------(1)上述方法中,s2, s1由立柱上标尺读出,巧妙避免了测量距离的困难。(注:B,B’为同一光电门,只是距离A的远近不同)
自由落体运动的规律及经典例题及答案
自由落体运动的规律 【知识讲解】 自由落体运动 一、定义 物体只在重力作用下从静止开始下落的运动,叫自由落体运动。在没有空气阻力时,物体下落的快慢跟物体的重力无关。 1971年美国宇航员斯科特在月球上让一把锤子和一根羽毛同时下落,观察到它们同时落到月球表面。此实验说明:①在月球上无大气层。②自由落体运动的快慢与物体的质量无关。 自由落体运动在地球大气层里是一种理想运动,但掌握了这种理想运动的规律,也就为研究实际运动打下了基础。当空气阻力不太大,与重力相比较可以忽略时,实际的落体运动可以近似地当作自由落体运动。 对自由落体运动的再研究: 为了纪念伽利略的伟大贡献,1993年4月8日来自世界各地的一些科学家,用精密自动投卸仪把不同材料制成的木球、铝球、塑料球等许多小球从比萨斜塔上44米高处同时投下,用精密电子仪器和摄像机记录,结果发现所有小球同时以同一速度落地。 所以,一般情况下,物体在空气中下落,可以忽略空气的影响,近似地认为是自由落体运动。 二、自由落体运动的条件 1、从静止开始下落,初速为零。 2、只受重力,或其它力可忽略不计。(这是一种近似,忽略了次要因素,抓住了主要因素,这是一种理想化研究方法) 三、自由落体运动的性质 伽利略不但巧妙地揭示了亚里士多德观点的内部矛盾,还对自由落体运动的性质做了许多研究。他的研究方法是提出假设——数学推理——实验验证――合理外推。 伽利略所处的年代还没有钟表,计时仪器也较差,自由落体运动又很快,伽利略为了研究落体运动,利用当时的实验条件做了在斜面上从静止开始下滑的直线运动(目的是为了“冲淡重力),证明了在阻力很小的情况下小球在斜面上的运动是匀变速直线运动,用逻辑推理外推到斜面倾角增大到90°的情况,小球将自由下落,成为自由落体,他认为这时小球仍然会保持匀变速直线运动的性质,多么巧妙啊! 正确与否需要用实验来验证,如图是处理课本中的自由落体纸带运动轨迹。 猜想:自由落体是匀变速直线运动
测量重力加速度实验Acceleration due to gravity
Acceleration due to gravity 1. Aim: To measure ‘g’, the acceleration due to gravity using a simple pendulum. 2. Theory: A simple pendulum consists of a particle of mass m, attached to a frictionless pivot P by a cable of length L and negligible mass. When the particle is pulled away from its equilibrium position by an angle θand released, it swings back and forth as Figure 1 shows. By attaching a pen to the bottom of the swinging particle and moving a strip of paper beneath it at a steady rate, we can record the position of the particle as time passes. The graphical record reveals a pattern that is similar (but not identical) to the sinusoidal pattern for simple harmonic motion. Figure 1 A simple pendulum swinging back and forth about the pivot P. If the angle θis small, the swinging is approximately simple harmonic motion. Gravity causes the back-and-forth rotation about the axis at P. The rotation speeds up as the particle approaches the lowest point and slows down on the upward part of the swing. Eventually the angular speed is reduced to zero, and the particle swings back. If the angle of oscillation is large, the pendulum does not exhibit simple harmonic motion. The motion of a simple pendulum is nearly simple harmonic. The periodic time T is related to the length L of the pendulum and the local acceleration due to gravity g. 2 T=or 2 2 4 T L g π ?? = ? ?? If we measure the periodic time T for different lengths L, and plot T2 versus L,
实验一自由落体重力加速度的测定
实验一自由落体重力加速度的测定 一、实验目的 1. 通过测定重力加速度,加深对匀加速运动规律的理解: 2. 学习用光电法计时; 3. 学习用落体法测定重力加速度. 二、仪器组成 YJ-LG-3自由落体重力加速度测定仪、YJ-LG-3自由落体重力加速度测定仪专用毫秒计、钢球、卷尺等 三、仪器结构 1. YJ-LG-3自由落体重力加速度测定仪专用毫秒 计面板如图l所示 2. 自由落体测定仪如图2所示 四、实验原理 在重力作用下,物体的下落运动是匀加速直线运 动.可用下列方程来描述: 式中s是在时间t内物体下落的距离.g是重力加速度.如果物体下落的初速度为0,即Vo=0时, 可见若能测得物体在最初t秒内通过的距离S,就可以 估算出g的值,在实验中要严格保证初速度为零有一定 的困难.,故常采用下列方法:实验时,让物体从静止开 始自由下落.如图3所示,设它到达A点的速度为V0. 从A点开始,经过时间t1到达B点,令A、B两点的距 离为S1., 则 若保持上述的初始条件不变,则从A点起,经过时
间t2后.物体到达C点.令A、C两点的距离为S2.则 由式3和式4得: 以上两式相减,得: 那么就有 这里不再出现初速度值,式中的各值均可用自由落体测定仪测量得到. 五、实验步骤 1.调节自由落体仪垂直.将重锤装置安装好,调整底座上的调节螺旋,使重锤悬线与 落体仪两立柱平行. 2.将第一光电门放在立柱A处.如离顶端20cm处,调第二光电门于B处.如两光电门相距90cm处,将实验装置上的激光器、接收器与YJ-LG-3自由落体重力加速度测定仪专 用毫秒计连接,打开电源,可看见激光器发出红光. 3.调节上、下两个激光器。使激光束平行地对准重锤线后,取下重锤装置. 4.保持上、下两个激光器位置不变,调节上、下两个接收器分别与对应的激光器对准(使激光束垂直射入接收器入射孔),直至用手指通过上、下两光电门时,专用毫秒计能正常计 时. 5.按动YJ-LG-3自由落体重力加速度测定仪专用毫秒计功能键(使用方法见附录),选择计时精度为0.0001s,(测完一组数据后,按动复位键归零). 6.用手指托住钢球至落球定位孔,迅速松开手指,记录钢球自由下落通过上、下两光 电门的时间t1。 7.用卷尺置于两光电门之间,测出两激光束之间的距离S1。 8. 重复以上步骤,测量八组数据,求平均值. 9.重复以上步骤,改变两光电门距离,用卷尺置于两光电门之间,测出两激光束之间 的距离S2,测量八组t2数据,求平均值. 10.将实验数据填入下表.并按式(8)计算重力加速度g.求其误差.
气垫导轨测重力加速度 大学物理实验
气垫导轨测重力加速度 【试验目的】: 1.研究测重力加速度的方法; 2.测量本地区的重力加速度。 【实验原理】: 当气轨水平放置时,自由漂浮的滑块所受的合外力为零,因此,滑块在气轨上可以静止,或以一定的速度作匀速直线运动。在滑块上装一与滑块运动方向严格平行、宽度为的挡光板,当滑块经过设在某位置上的光电门时,挡光板将遮住照在光敏管上的光束,因为挡光板宽度一定,遮光时间的长短与滑块通过光电门的速度成反比,测出挡光板的宽度L和遮光时间t,则滑块通过光电门的平均速度为: V=L/t (1-1) 若挡板很小,则在挡光范围内滑块的速度变化也很小,故可以把平均速度看成是滑块经过光电门的瞬时速度。挡板越小,则平均速度越准确地反映该位置上滑块的瞬时速度,显然,如果滑块作匀速直线运动,则滑块通过设在气轨任何位置的光电门时瞬时速度都相等,毫秒计上显示的时间相同,在此情形下,滑块速度的测量值与挡板的大小无关。 若滑块在水平方向受一恒力作用,滑块将作匀加速直线运动,分别测出滑块通过相距S的2个光电门的始末速度和V1和V2则滑块的加速度: 2as=v12–v22 (1-2) 将式(1-1)代入(1-2)中 得: 2as=L2(1/t22-1/t12) (1-3) 其原理如图1. 气垫导轨与水平面的夹角为α 则 a=g*ginα. (1-4) 【待测物理量】: V〈物体运动速度〉、a〈物体运动加速度〉、g〈本地区的加速度〉、α〈气垫导轨与水平面的夹角〉、Δt〈物体在两光电门之间的运动时间〉. 【实验仪器及其使用介绍】: 气垫导轨、数字毫秒计、滑块、游标卡尺、垫块。 一、气垫导轨 气垫导轨是一种现代化的力学实验仪器。实物如下图所示:
浅谈自由落体法测重力加速度
自由落体法测量重力加速度 实验仪器 自由落体装置(如图) ,数字毫秒计,光电门(两个) ,铁球。 实验原理 设光电门 A 、B 间的距离为 s ,球下落到 A 门时的速度为 0v ,通过 A 、 B 间的时间为 t ,则成立: 2/s 20gt t v += (1) 两边除以 t ,得: 2//s 0gt v t += (2) 设 x=t , y =t /s ,则: 2/y 0gx v += (3) 这是一直线方程,当测出若干不同 s 的 t 值,用 x = t 和 y = s / t 进行直线拟合,设所得斜率为 b ,则由 b = g / 2 可求出 g , g = 2b (4) 实验步骤 (1)调节实验装置的支架,使立柱为铅直,再使落球能通过 A 门 B 门的中点。 (2)测量 A 、B 两光电门之间的距离 s 。 (3)测量时间 t 。
(4)计算各组的 x , y 值,用最小二乘法做直线拟合,求出斜率 b 及其标准 偏差 b s 、 ()b u (注意:在取 b 的时,由于立柱调整不完善,落球中心 未通过光电门的中点,立柱上米尺的误差均给 s 值引入误差,也是 b 的不确定度来源,一般此项不确定度(B 类评定)较小,可略去不计,所以 ()b u = b s )。 (5)计算 g 及其标准不确定度 ()g u 。 实验要点 1.仪器连接 用专用导线将自由落体仪的上、下光控门分别与SSM-5C 计时-计数-计频仪的光电输入插座A 、B 相连接,用导线将电磁铁与SSM-5C 计时-计数-计频仪后面电压输出相连。 2.仪器调整与调试 ⑴自由落体仪的调整:接通电磁铁开关,使它吸住铅锤线。调节三脚座螺钉使铅锤线通过两光控门的中心,以保证小钢球下落时准确地通过光控门。 ⑵SSM-5C 计时-计数-计频仪的调试:接通电源,将功能选择开关调至计时, 输入信号分配开关SN 指向2,将后面电压输出调至 6V ,检查两光控门的光源是否对正光敏管,用手遮一下上光控门,计时开始,再遮一下下光控门,计时停止,即为正常。 注意事项 (1)利用铅垂线和立柱的调节螺丝,确保离住处与铅直。保证小球下落时, 两个光电门遮光位置均相同。 (2)测量时一定要保证支架稳定、不晃动。路程 s 的准确测量对实验结果影响很大。
单摆测重力加速度实验报告
一、实验目的 1.学会秒表、米尺的正确使用。 2.理解单摆法测定重力加速的原理。 3.研究单摆振动的周期与摆长、摆角的关系。 4.学习系统误差的修正及在实验中减小不确定度的方法。 二、实验仪器 单摆装置,停表(精度为0.01s ),钢卷尺(精度为0.05cm ),游标卡尺(精度为0.02mm )。 三、实验原理 单摆的振动周期决定于重力加速度g 和摆长L ,只需要量出摆长L 并测定摆动周期,就能够得到g 。 如图:当θ<5?时,圆弧可近似的看成直线,f 也可 近似的看成沿着这条直线,则有sin θ=x L ,f=Fsin θ= -mg x L =-m g L x 由牛顿第二定律得:a=f m 则有 a=-g L x 令ω=g L x 最终得单摆的运动方程为 X=A cos(ωt +2π+φ) 其中T=2π ω =2π√ g =4π2 L T 考虑到摆 球是有大小的,故g =4π2 L+ d 2T 摆长L 用米尺测量,摆球直径d 用游 标卡尺测量,周期T 用停表测量。 四、实验步骤 1.测量摆长L 。用米尺测量摆线支点与摆球顶点的距离l 。用游标卡尺测量小球的直径d ,则摆长L=l+d 2 。 2.测量摆动周期T 。用手把摆球拉直偏离平衡位置5度左右,让其在
一个垂直面内自由摆动,小球越过平衡位置瞬间开始计时,连续默数 。 100次全振动时间t,T=t 100 3.为了减小误差,重复测量5次将数据记录于下表中。 五、数据记录与处理
六、结果与讨论 兰州的重力加速度g=9.973±0.005m/s2,结果有偏差,原因有以下几点; 1、测量单摆周期时的反应时间。 2、在测量摆线长度时对最后一位数字的估读。 3、环境方面,温度、湿度、空气阻力的变化都会影响实验结果。 4、悬线质量的影响。 5、摆角角度的影响。 七、试验问题 1、直接测量单摆往返一次的时间会受到人的反应时间的影响,通过多次测量求平均值的方法可以减小误差。 2、1 11.4 3、受空气阻力影响摆幅越来越小,但其周期不变;用木球代替铜球时,因木球密度较小,受空气阻力的影响会变大。
大学物理实验报告单摆测重力加速度
——利用单摆测重力加速度 班级: 姓名: 学号: 西安交通大学模拟仿真实验实验报告 实验日期:2014年6月1日 老师签字:_____ 同组者:无 审批日期:_____ 实验名称:利用单摆测量重力加速度仿真实验 一、实验简介 单摆实验是个经典实验,许多著名的物理学家都对单摆实验进行过细致的研究。本实验的目的是学习进行简单设计性实验的基本方法,根据已知条件和测量精度的要求,学会应用误差均分原则选用适当的仪器和测量方法,学习累积放大法的原理和应用,分析基本误差的来源及进行修正的方法。 二、实验原理 用一根绝对挠性且长度不变、质量可忽略不计的线悬挂一个质点,在重力作用下在铅垂平面内作周期运动,就成为单摆。单摆在摆角小于5°(现在一般认为是小于10°)的条件下振动时,可近似认为是简谐运动。而在实际情况下,一根不可伸长的细线,下端悬挂一个小球。当细线质量比小球的质量小很多,而且小球的直径又比细线的长度小很多时,此种装置近似为单摆。单摆带动是满足下列公式: 进而可以推出: 式中L 为单摆长度(单摆长度是指上端悬挂点到球重心之间的距离);g 为重力加速度。如果测量得出周期T 、单摆长度L ,利用上面式子可计算出当地的重力加速度g 。 西安交通大学物理仿真实验报告
三、实验内容 1. 用误差均分原理设计单摆装置,测量重力加速度g. 设计要求: (1)根据误差均分原理,自行设计试验方案,合理选择测量仪器和方法. (2)写出详细的推导过程,试验步骤. (3)用自制的单摆装置测量重力加速度g,测量精度要求△g/g < 1%. 可提供的器材及参数: 游标卡尺,米尺,千分尺,电子秒表,支架,细线(尼龙线),钢球,摆幅测量标尺(提供硬白纸板自制),天平(公用). 假设摆长l≈70.00cm;摆球直径D≈2.00cm;摆动周期T≈1.700s; 米尺精度△ 米≈0.05cm;卡尺精度△ 卡 ≈0.002cm;千分尺精度△ 千 ≈0.001cm; 秒表精度△ 秒 ≈0.01s;根据统计分析,实验人员开或停秒表反应时间为0.1s 左右,所以实验人员开,停秒表总的反应时间近似为△ 人 ≈0.2s. 2. 对重力加速度g的测量结果进行误差分析和数据处理,检验实验结果是否 达到设计要求. 3. 研究单摆周期与摆长,摆角,悬线的质量和弹性系数,空气阻力等因素的关 系,试分析各项误差的大小. 四、实验仪器 单摆仪,摆幅测量标尺,钢球,游标卡尺(图1-图4)
重力加速度测量设计性试验
重力加速度测量(设计性实验) 【实验目的】 (1)推导单摆测量重力加速度的公式。 (2)掌握单摆测量重力加速度实验的实验设计方法及验证方法。 (3)掌握间接测量量不确定度的计算方法。 (4)了解单摆测量重力加速度实验的主要误差来源。 (5)估算实验仪器的选取参数并设计实验数据记录表格。 【设计实验】 设计性实验的设计过程主要有以下几步: (1)根据待测的物理量确定出实验方法(理论依据),推导出测量的数学公式;判定方法误差给测量结果带来的影响。 (2)根据实验方法及误差设计要求,分析误差来源,确定所需要采用的测量仪器(包括量程、精度等)以及测量环境应达到的要求(如空气、电磁、振动、温度、海拔高度等)。 (3)确定实验步骤、需要测量的物理量、测量的重复次数等。 (4)设计实验数据表格及要计算的物理量。 (5)实验验证。要用测得的实验数据,采用误差理论来验证实验结果。若不符合测量要求,则需对上述步骤中的有关参数做出适当调整并重做实验,据测得的实验数据进行实验验证,以此类推直到符合要求为止。 设计实验的原则应在满足设计要求的前提下,尽可能选用简单、精度低的仪器,并能降低对测量环境的要求,尽量减少实验测量次数。 【设计要求】 (1)测定本地区的重力加速度,要求重力加速度的相对不确度小于0.5%,即 g 0.5u g ≤%。确 定所需仪器的量程和精度,以及测量参数(摆长和摆动次数)。 (2)本实验是测量重力加速度的设计性实验,但考虑到设计难度、仪器资源的限制等因素,规定其实验方法采用单摆法。 (3)可用仪器有:钢卷尺(1 mm/2 m ,表示最小分度值为1 mm ,量程为2 m ,下同)、钢直尺(1 mm/1 m )、游标卡尺(0.02 mm/20 cm )、普通直尺(1 mm/20 cm )、电子秒表(0.01 s )、单摆实验仪(含摆线、摆球等)。 【实验内容】 (1)原理分析。写出单摆法测量公式完整的推导过程及近似要求,并画出原理图(查阅相关书籍及网站)。 (2)误差分析。分析实验过程中的主要误差来源并估算。 (3)不确定度的推导与计算。 (4)估算实验参数(摆长和摆动次数)。 (5)设计实验步骤与数据表格。 (6)实验与验证。 【设计提示】
实验二重力加速度的测定(精)
实验二重力加速度的测定 一、单摆法 实验内容 1.学习使用秒表、米尺。 2.用单摆法测量重力加速度。 教学要求 1.理解单摆法测量重力加速度的原理。 2.研究单摆振动的周期与摆长、摆角的关系。 3.学习在实验中减小不确定度的方法。 实验器材 单摆装置(自由落体测定仪),秒表,钢卷尺 重力加速度是物理学中一个重要参量。地球上各个地区重力加速度的数值,随该地区的地理纬度和相对海平面的高度而稍有差异。一般说,在赤道附近重力加速度值最小,越靠近南北两极,重力加速度的值越大,最大值与最小值之差约为1/300。研究重力加速度的分布情况,在地球物理学中具有重要意义。利用专门仪器,仔细测绘各地区重力加速度的分布情况,还可以对地下资源进行探测。 伽利略在比萨大教堂内观察一个圣灯的缓慢摆动,用他的脉搏跳动作为计时器计算圣灯摆动的时间,他发现连续摆动的圣灯,其每次摆动的时间间隔是相等的,与圣灯摆动的幅度无关,并进一步用实验证实了观察的结果,为单摆作为计时装置奠定了基础。这就是单摆的等时性原理。 应用单摆来测量重力加速度简单方便,因为单摆的振动周期是决定于振动系统本身的性质,即决定于重力加速度g和摆长L,只需要量出摆长,并测定摆动的周期,就可以算出g值。 实验原理 单摆是由一根不能伸长的轻质细线和悬在此线下端体积很小的重球所构成。在摆长远大于球的直径,摆球质量远大于线的质量的条件下,将悬挂的小球自平衡位置拉至一边(很小距离,摆角小于5°),然后释放,摆球即在平衡位置左右作周期性的往返摆动,如图2-1所示。 θ 图2-1 单摆原理图
摆球所受的力f 是重力和绳子张力的合力,f 指向平衡位置。当摆角很小时(θ<5°),圆弧可近似地看成直线,f 也可近似地看作沿着这一直线。设摆长为L ,小球位移为x ,质量为m ,则 sin θ= L x f=psin θ=-mg L x =-m L g x (2-1) 由f=ma ,可知a=- L g x 式中负号表示f 与位移x 方向相反。 单摆在摆角很小时的运动,可近似为简谐振动,比较谐振动公式:a =m f =-ω2 x 可得ω= l g 于是得单摆运动周期为: T =2π/ω=2π g L (2-2) T 2 =g 2 4πL (2-3) 或 g=4π22T L (2-4) 利用单摆实验测重力加速度时,一般采用某一个固定摆长L ,在多次精密地测量出单摆的周期T 后,代入(2-4)式,即可求得当地的重力加速度g 。 由式(2-3)可知,T 2 和L 之间具有线性关系,g 2 4π为其斜率,如对于各种不同的 摆长测出各自对应的周期,则可利用T 2—L 图线的斜率求出重力加速度g 。 上述单摆测量g 的方法依据的公式是(2-2)式,这个公式的成立是有条件的,否则将使测量产生如下系统误差: 1. 单摆的摆动周期与摆角的关系,可通过测量θ<5°时两次不同摆角θ1、θ2的周期值进行比较。在本实验的测量精度范围内,验证出单摆的T 与θ无关。 实际上,单摆的周期T 随摆角θ增加而增加。根据振动理论,周期不仅与摆长L 有关,而且与摆动的角振幅有关,其公式为: T=T 0[1+( 21)2sin 22θ+(4231??)2sin 22 θ+……] 式中T 0为θ接近于0o 时的周期,即T 0=2πg L 2.悬线质量m 0应远小于摆球的质量m ,摆球的半径r 应远小于摆长L ,实际上任何一个单摆都不是理想的,由理论可以证明,此时考虑上述因素的影响,其摆动周期为:
(完整版)重力加速度的测定实验报告
重力加速度的测定 一,实验目的 1,学习秒表、米尺的正确使用 2,理解单摆法和落球法测量重力加速度的原理。 3,研究单摆振动的周期与摆长、摆角的关系。 4,学习系统误差的修正及在实验中减小不确定度的方法。 二,实验器材 单摆装置,停表(精度为0.01s),钢卷尺(精度为1mm),游标卡尺(精度为0.02mm) 三,实验原理 单摆是由一根不能伸长的轻质细线和悬在此线下端体积很小的重球所构成。在摆长远大于球的直径,摆球质量远大于线的质量的条件下,将悬挂的小球自平衡位置拉至一边(很小距离,摆角小于5°),然后释放,摆球即在平衡位置左右作周期性的往返摆动,如图2-1所示。 f =F sinθf θ T=F cosθ F= mg L 单摆原理图
摆球所受的力f 是重力和绳子张力的合力,f 指向平衡位置。当摆角很小时(θ<5°),圆弧可近似地看成直线,f 也可近似地看作沿着这一直线。设摆长为L ,小球位移为x ,质量为m ,则 L x = θsin f=θsin F =-L x mg - =-m L g x 由f=ma ,可知a=- L g x 式中负号表示f 与位移x 方向相反。 单摆在摆角很小时的运动,可近似为简谐振动,比较谐振动公式:a = m f =-ω2 x 可得ω=l g ,即02 22=+x dt x d ω,解得)cos(0?ω+=t A x ,0A 为振幅,?为初相。 应有[])2cos())((cos )cos(000?πω?ω?ω++=++=+=t A T t A t A x 于是得单摆运动周期为:T =ωπ 2=2πg L 即 T 2=g 2 4πL 或 g=4π22 T L 又由于细线不是完全没有质量,他在外力作用下也不可能完成伸长,所以,单摆的重力加速度公式修正为 22 21 4T d L g +=π 四,实验步骤 1,数据采集 (1)测量摆长L 用米尺测量摆球支点和摆球顶点或最低点的间距l ,用游标卡尺测量小球的直径d,则摆长 d l L 2 1+= (2)测量摆动周期 用手把摆球拉至偏离平衡位置约? 5放开,让其在一个铅直面内自由摆动,当小球通过平衡位置的瞬间,开始计时,连续默数100次全振动时间为t ,再除以100,得到周期T 。 (3)将所测数据列于下表中,并计算出摆长、周期及重力加速度。
高一物理自由落体运动公式
高一物理自由落体运动公式 1.初速度Vo=0 2.末速度Vt=gt 3.下落高度h=gt2/2(从Vo位置向下计算) 4.推论Vt2=2gh 注: (1)自由落体运动是初速度为零的匀加速直线运动,遵循匀变速 直线运动规律; (2)a=g=9.8m/s2≈10m/s2(重力加速度在赤道附近较小,在高山处比平地小,方向竖直向下)。 (3)竖直上抛运动 1.位移s=Vot-gt2/2 2.末速度Vt=Vo-gt(g=9.8m/s2≈10m/s2) 3.有用推论Vt2-Vo2=-2gs 4.上升最大高度Hm=Vo2/2g(抛出点算起) 5.往返时间t=2Vo/g(从抛出落回原位置的时间) 注: (1)全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值; (2)分段处理:向上为匀减速直线运动,向下为自由落体运动, 具有对称性; (3)上升与下落过程具有对称性,如在同点速度等值反向等。 一、自由落体运动。 1、什么是自由落体运动。 物体只在重力作用下,从静止开始下落的运动叫做自由落体运动。 2、自由落体运动的特点。
从自由落体运动的定义出发,显然自由落体运动是初速度为零的直线运动;因为下落物体只受重力的作用,而对于每一个物体它所受 的重力在地面附近是恒定不变的,因此它在下落过程中的加速度也 是保持恒定的。而且,对不同的物体在同一个地点下落时的加速度 也是相同的。关于这一点各种实验都可以证明,如课本上介绍的 “牛顿管实验”以及同学们会做的打点计时器的实验等。综上所述,自由落体运动是初速度为零的竖直向下的匀加速直线运动。 二、自由落体加速度。 1、在同一地点,一切物体在自由落体运动中加速度都相同。这 个加速度叫自由落体加速度。因为这个加速度是在重力作用下产生的,所以自由落体加速度也叫做重力加速度。通常不用“a”表示, 而用符号“g”来表示自由落体加速度。 2、重力加速度的大小和方向。 同学们可以参看课本或其他读物就会发现在不同的地点自由落体加速度一般是不一样的。 如:广州的自由落体加速度是9.788m/s2,杭州是9.793m/s2, 上海是9.794m/s2,华盛顿是9.801m/s2,北京是9.80122m/s2,巴 黎是9.809m/s2,莫斯科是9.816m/s2。即使在同一位置在不同的高 度加速度的值也是不一样的。如在北京海拔4km时自由落体加速度 是9.789m/s2,海拔8km时是9.777m/s2,海拔12km时是 9.765m/s2,海拔16km时是9.752m/s2,海拔20km时是9.740m/s2。 尽管在地球上不同的地点和不同的高度自由落体加速度的值一般都不相同,但从以上数据不难看出在精度要求不高的情况下可以近 似地认为在地面附近(不管什么地点和有限的高度内)的自由落体加 速度的值为:g=9.765m/s2。 在粗略的计算中有时也可以认为重力加速度g=10m/s2。重力加 速度的方向总是竖直向下的。看过"高一物理自由落体运动公式"的 还看了:
重力加速度的精确测量与研究
重力加速度的精确测量与研究 指导教师:孙爱民学生姓名:张禹 2006级物理学(3)班学号:200672010361 摘要:本文在总结传统测量重力加速度方法的基础上,通过搭建新的实验装置,探究一种新的测量重力加速度的方法。该方法具有操作方便、简单的优点,并且提高了实验数据精确度,符合探究式学习的教育理念。 关键词:自由落体;重力加速度;光电门;瞬时速度 Accurate measurement of gravitational acceleration and Research Zhang Yu,Sun Ai-min Abstract:This thesis explores a new approach to the accurate measurement of acceleration of gravity on account of a summary of existed approaches .the novel approach applies new experiment devices which improve much in the accuracy of experiment data. The presented approach is easy to operate and accords whit the education notion of exploratory study. Keywords :Free Fall;Acceleration of gravity;Optical gate;Instantaneous velocity 引言 重力加速度g是物理学中的一个重要参量,在实际工作中,常常需要知道重力加速度的大小。重力加速度g的测定是个传统的实验,其实验方法通常有落体法测量重力加速度、用摆测量重力加速度和用液体测量重力加速度[1]。其中落体法测量重力加速度又可分为自由落体法、气垫导轨法、斜槽法等[2]。每种方法都有各自的优缺点,测量结果的精确度也不尽相同,但总体来说所测出的实验数据精确度普遍较低。传统的用光电门测量重力加速度g时,通常存在多次测量时小球高度不固定、挡光部分不相同等缺点,并且用小球作重物时经过光电门因偏心引起的会引起误差[3]。为了提高测量结果的精确度,本文采用自己搭建的实
高中物理:《自由落体加速度》
高中物理:自由落体加速度 [探究导入] 利用如图甲所示的实验装置测定重力加速度.用手捏住纸带上端把纸带拉成竖直状态,并使重物停在靠近打点计时器处.先接通电源,再松开纸带让重物自由下落,打点计时器在纸带上打下一系列的点. (1)如何根据打上点的纸带(如图乙)求出重物的重力加速度? 提示:可用下列两种方法求出重力加速度: ①由v n =x n +x n +12T 求出各点的瞬时速度,作出v -t 图像,v -t 图像是一条过原点的倾斜直线,斜率表示加速度. ②由位移差公式Δx =aT 2计算加速度. (2)重力加速度的方向如何? 提示:方向竖直向下. 1.自由落体加速度的方向:总是竖直向下的. 2.自由落体加速度的大小:在同一地点,一切物体的重力加速度都相同.在不同地理位置处的重力加速度一般不同,赤道上物体的重力加速度最小;南(北)极处重力加速度最大;物体所处地理位置的纬度越大,重力加速度越大.一般的计算中,可以取g =9.8 m /s 2或g =10 m/s 2. [易错提醒] 物体在其他星球上也可以做自由落体运动,但同一物体在不同的星球上所受重力一般不同,所以下落时的加速度一般不同. [典例2] 关于自由落体运动的加速度g ,下列说法中正确的是( ) A .重的物体的g 值大 B .同一地点,轻重物体的g 值一样大
C.g值在地球上任何地方都一样大 D.g值在赤道处大于在北极处 [解析]自由落体加速度又叫作重力加速度.在同一地点,所有物体的重力加速度都是相等的,与物体的质量、运动状态均无关,A错误,B正确;在不同地点,重力加速度是不同的,两极处大于赤道处,C、D错误. [答案] B 2.关于重力加速度的说法正确的是() A.在比萨斜塔同时由静止释放一大一小两个金属球,二者同时着地,说明二者运动的加速度相同,这个加速度就是当地的重力加速度 B.地球上各处的重力加速度g值都相同 C.北京的重力加速度为9.8 m/s2,说明在北京做下落运动的物体,每经过1 s速度增加9.8 m/s D.成都和苏州的重力加速度都竖直向下,两者的方向相同 解析:在比萨斜塔释放的金属球,受到的空气阻力远远小于球的重力,可以认为金属球做自由落体运动,故球运动的加速度为当地重力加速度,因下落的高度和运动时间相同,所以二者的加速度相同,A正确;地球上各处的重力加速度的大小一般不同,方向虽然均竖直向下,但因地球是球形的,在不同地区方向并不相同,故B、D错误;在北京下落的物体不一定做自由落体运动,其加速度也不一定等于重力加速度,故C错误. 答案:A
自由落体重力加速度测量仪
自由落体重力加速度测量仪/重力加速度测量仪型号:HAD-LG-2 利用自由落体(条形物体)测定重力加速度,比球体测量准确.方便.配有数字毫秒计,五位半数显. 自由落体实验仪 1 自由落体重力加速度测量仪概述 自由落体实验仪是基础力学教学实验的必备仪器,利用自由落体实验仪可进行定性观测和定量研究物体在自由落体状态下的运动规律。从而达到教学演示实验的目的。 HAD-LG-2型为:主体高度1.6m,铸铁腿三脚支架,底座稳固,抗震动好,利于实验室摆放操作。 从教学使用出发,HAD-LG-1型为:主体高度1.2m,便携式三脚支架,底座轻巧,便于移动,利于课堂演示教学。 以上两种自由落体实验仪均可与J0201-G-2型计时器, J0201-CC存贮式计时器,J0201-CHJ存贮式数字毫秒计,J0416-2型多用大屏幕数字显示测试仪配合使用,适用于中学进行物理教学的演示实验或分组实验。 本仪器还可以与J02015-2型简易频闪光源和照相机同步配合使用,用频闪照像法研究自由落体运动的规律。 2 重力加速度测量仪技术性能 2.1 仪器总高: HAD-LG-1型≥1.2m ;HAD-LG-2型≥1.6m 2.2 实验有效高度: HAD-LG-1型≥1.0m ;xe77FT-LG-2型≥1.4m 2.3 电磁铁电源: DC6V 2.4 钢球直径: 18mm 2.5 g值实验相对误差:≤ 2% 3 结构与特点 3.1 见图一。仪器由带有标尺的铝合金型材为主体,顶端装有电磁铁吸球器,中间装有两个可任意移动的光电门光电传感器,下端装有接球架网,立柱下端固定在可调节的三脚支架上。 3.2 钢球的起始位置由电磁铁的固定支架端板的下端“ ”形的下边沿作为位置指针,能方便地调节确定钢球自由下落的起始刻度基准。 3.3 立柱上端装有电磁铁吸球器,当电磁铁线圈接通直流6V电源时,电磁铁吸住钢球,切断电源时,钢球下落作自由落体运动。电磁铁的支架上还装有两个接线柱,可以与频闪光源的同步输入开关及学生实验电源直流6V相连接用于频闪照相实验用。(注:原接电缆的接线端子可卸下不用) 3.4 两个光电门由小型聚光电珠和光敏接收管组成。两个光电门可以上下任意移动,在立柱上的位置由光电门支架的凹型槽底边所对标尺的刻度决定。
测重力加速度
设计性实验 重力加速度的测量 重力加速度g 是一个反映地球引力强弱的地球物理常数,它与地球上各个地区的经纬度、海拔高度及地下资源的分布有关,一般说来,两极的g 最大,赤道附近的g 最小,两者相差约1/300。重力加速度的测定在理论、生产和科学研究中都具有重要意义。 实验研究课题 1、测定本地区重力加速度g 值,测量结果至少有4 位有效数字,并要求百分误差小于1%。 2、试比较各种实验测量方法的优缺点。讨论各种实验测量方法中,哪些量可测得精确?哪些量不易测准?并说明如何减小或消除影响精确测量的各种因素等。 可选择的仪器 单摆、三线摆、复摆、圆球、重锤、米尺、游标卡尺、光电门、数字毫秒计(手机秒表代替)、杨氏模量测量仪等。 设计方案举例: 测量重力加速度的方法很多,有单摆、复摆、开特摆、三线摆、气垫导轨法和自由落体仪法等等,它们各有特点。 下面例举几种比较典型的方案。 方案一、单摆法 一、实验目的: 1、掌握实验原理及方法,进一步熟悉根据什么以及如何选择实验仪器和测量工具; 2、利用单摆测定重力加速度g 值; 3、分析受力情况,讨论误差原因,评价测量结果。 二、实验原理 单摆是用重量可忽视的细线吊起一质量为m 的小重锤,使其左右摆动,当摆角为θ时,重锤所受合外力大小sin =?f mg θ(图1),其中g 为当地的重力 加速度,这时锤的线加速度为sin ?g θ。设单摆长为 L ,则摆的角加速度 sin /=?g L αθ。当摆角很小时(小于 5°),可认为 ,这时sin ≈θθ,即振动的角加速度和角位移成比例,式中的负号表示角加速度和角位移的方向总是相反。此时单摆的振动是简谐振动。从理论分析得知,其振动周期 T 和上述比例系数的关系是
自由落体加速度实验报告
竭诚为您提供优质文档/双击可除自由落体加速度实验报告 篇一:实验2自由落体法测定重力加速度(详写) 《实验2自由落体法测定重力加速度》 实验报告 一、实验目的和要求 1、学会用自由落体法测定重力加速度; 2、用误差分析的方法,学会选择最有利的测量条件减少测量误差。 二、实验描述 重力加速度是很重要的物理参数,本实验通过竖直安放的光电门测量自由落体时间来求重力加速度,如何提高测量精度以及正确使用光电计时器是实验的重要环节。三、实验器材 muJ-5c型计时计数测速仪(精度0.1ms),自由落体装置(刻度精度0.1cm),小钢球,接球的小桶,铅垂线。四、实验原理 实验装置如图1。
在重力实验装作用下,物体的下落运动是匀加速直线运动,其运动方程为 s=??0t+1/2g??2 该式中,s是物体在t时间内下落的距离;??0是物体运动的初速度;g是重力加速度;若测得s,??0,t,即求出g 值。 若使??0=0,即物体(小球)从静止释放,自由落体,则可避免测量??0的麻烦,而使测量公式简化。但是,实际测量s时总是存在一些困难。本实验装置中,光电转换架的通光孔总有一定的大小,当小铁球挡光到一定程度时,计时-计数-计频仪才开始工作,因此,不容易确定小铁球经光电转换架时的挡光位置。为了解决这个问题,采用如下方法:让小球从o点处开始下落,设它到A处速度为??0,再经过??1时间到达b处,令Ab间距离为??1,则 2 ??1=??0??1?????1 21 同样,经过时间??2后,小球由A处到达b’处,令Ab’间 的距离为??2,则有 2 s2=??0t2+1/2g??2
化简上述两式,得: 22 g=2 (??2??1-??1??2)/??1??2-t2??1=2(??2/??2-??1/??1)/?? 2-??1 图1实验装置图 --------------------------------------------(1)上述方法中,??2,??1由立柱上标尺读出,巧妙避免了 测量距离的困难。(注:b,b’为同一光电门,只是距离A的远近不同) g的不确定度与光电转换架的位置有关。根据不确定度 的绝对值合成公式,采用求标值的方法来选择最有利的条件,求出最佳操作范围。经实际推导,得: 2?s+??0???114???t?g=++??????(2) 211221 式中,取???1=???2=???,???1=???2=???2 要使?g较小,则: ①?t,?s,要多次测量后求出; ②??0要尽量小; ③b的位置要尽量靠近顶端,b’的位置要尽量靠近底端。 五、重点和难点 1、重力加速度测量方法; 2、保持支架铅直; 3、光电
