第四章扩散方程的数值求解

扩散方程稳态扩散与非稳态扩散

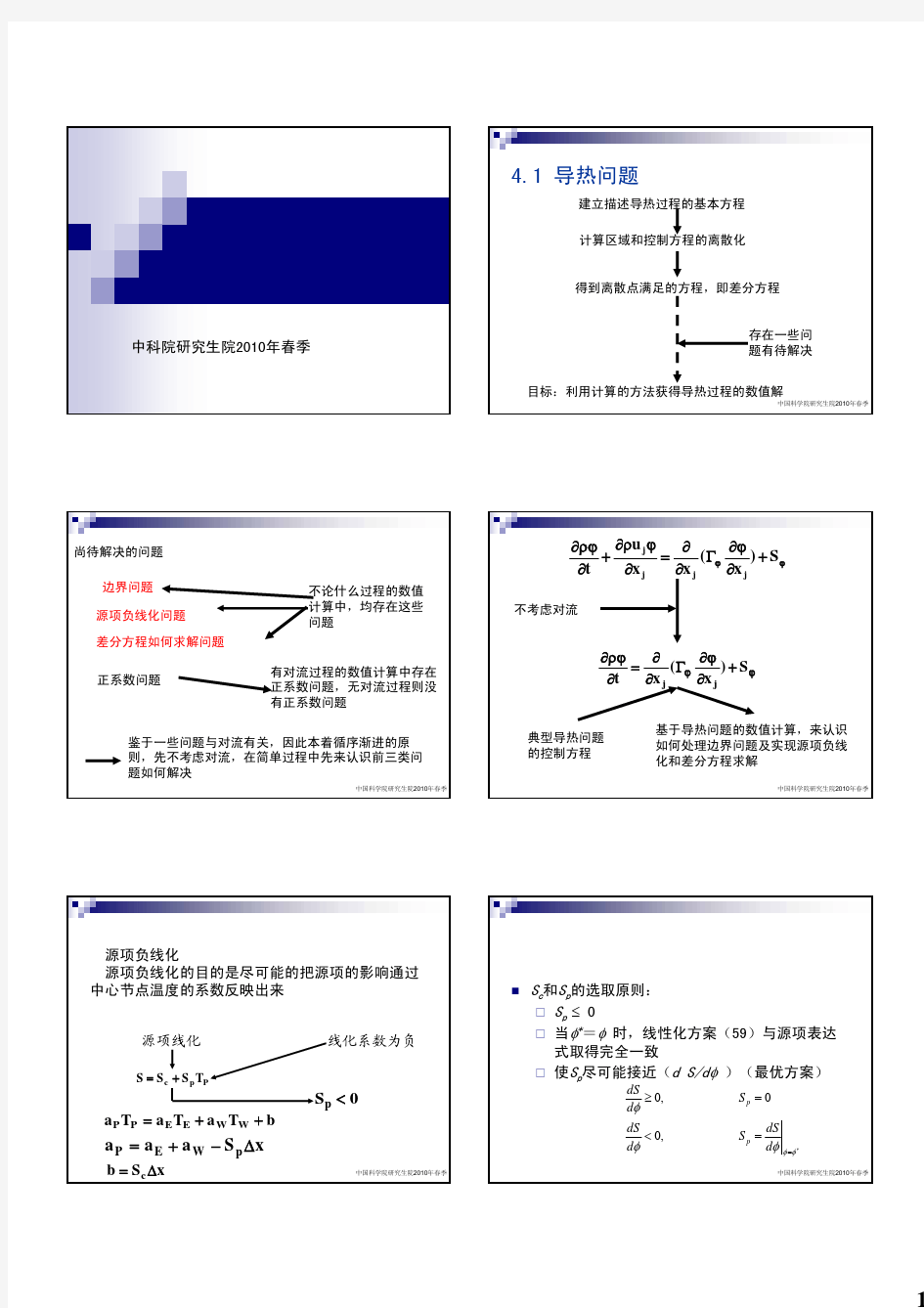
扩散方程稳态扩散与非稳态扩散 1．稳态扩散下的菲克第一定律（一定时间内，浓度不随时间变化dc/dt=0） 单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量（扩散通量）与该面积处的浓度梯度成正比 即J=－D（dc/dx） 其中D：扩散系数，cm2/s，J：扩散通量，g/cm2〃s ，式中负号表明扩散通量的方向与浓度梯度方向相反。 可见，只要存在浓度梯度，就会引起原子的扩散。 x轴上两单位面积1和2，间距dx，面上原子浓度为C1、C2 则平面1到平面2上原子数n1=C1dx ，平面2到平面1上原子数n2=C2dx 若原子平均跳动频率f, dt时间内跳离平面1的原子数为 n1f〃dt 跳离平面2的原子数为n2fdt，但沿一个方向只有1/2的几率，则单位时间内两者的差值即扩散原子净流量。 令，则上式 2．扩散系数的测定：

其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒，心部通渗碳气氛，外部为脱碳气氛，在一定温度 下经过一定时间后，碳原子从内壁渗入，外壁渗出达到平衡，则为稳态扩散单位时单位面积中碳流量： A：圆筒总面积，r及L：园筒半径及长度，q：通过圆筒的碳量 则： 即： 则： q可通过炉内脱碳气体的增碳求得，再通过剥层法测出不同r处的碳含量，作出C-lnr曲线可求得D。 第一定律可用来处理扩散中浓度不因时间变化的问 3．菲克第二定律：解决溶质浓度随时间变化的情况，即dc/dt≠0

两个相距dx垂直x轴的平面组成的微体积，J1、J2为进入、流出两平面间的扩散通量，扩散中浓度变化为，则单元体积中溶质积累速率为 （Fick第一定律） （Fick第一定律） （即第二个面的扩散通量为第一个面注入的溶质与在这一段距离内溶质浓度变化引起的扩散通量之和） 若D不随浓度变化，则 故： 4．Fick第二定律的解：很复杂，只给出两个较简单但常见问题的解 a. 无限大物体中的扩散

第三章 一维扩散方程

第三章 一维扩散方程 本章讨论一维扩散方程。首先，从随机过程中的一维扩散方程的讨论可直接得到扩散方程的解。然后对非齐次和各类边值问题相应的扩散方程作了讨论。讨论的方程类型 （1）直线上的齐次和非齐次扩散方程： 2,,0 (,0)() t xx u c u x t u x x ??=-∞<<∞>? =?；（利用随机过程的理论得到结论，再直接验证） (,),,0 (,0)() t xx u ku f x t x t u x x ?-=-∞<<∞>?? =?；（算子方法，与常微分方程类比） （2）半直线上的扩散方程0,0,0(,0)(),(0,)0t xx u ku x t u x x u t ?-=<<∞>?? =??=? ；（其它非齐次边界等） 对扩散方程理论方面的探讨：最大（最小）值原理。由此证明方程解的唯一性和稳定性。 §3.1全直线上的扩散方程 首先讨论随机过程中的扩散过程。设想粒子在一维直线上作连续随机游动（Brown 运动），满足性质：在t ?时间内位移转移概率为均值为0，方差为2 t σ?的正态分布。在时刻t 处于x 的概率密度记为(,)Pr(())u x t dx X t x dx ==。则 2 ()2(,)(,)x y t u x t t u y t dy σ-∞ -?-∞+?=?， 或 2 2 (,)(,)y u x t t u x y t dy ∞ -+?= +? 2222 1 [(,)(,)(,)()]2 y x xx u x t u x t y u x t ty o t dy σ∞ - = ++?+?? 21 (,)(,)()2 xx u x t u x t t o t σ=+?+? 因此， 2 2 t xx u u σ= 。 可见：一维Brown 运动的状态概率密度满足扩散方程。 从随机过程的角度，可直接写出状态概率密度： 22()2(,)(,0)y x t u x t e u y dy σ-∞ - = ?。 所以，有如下定理。 定理 扩散方程2,,0 (,0)() t xx u c u x t u x x ??=-∞<<∞>?=?的解为

抛物形扩散方程的有限差分法及数值实例

偏微分方程数值解 所在学院：数学与统计学院 课题名称：抛物形扩散方程的有限差分法及数值实例学生姓名：向聘

抛物形扩散方程的有限差分法及数值实例 1.1抛物型扩散方程 抛物型偏微分方程是一类重要的偏微分方程。考虑一维热传导方程： 22(),0u u a f x t T t x ??=+<≤?? (1.1.1) 其中a 是常数，()f x 是给定的连续函数。按照初边值条件的不同给法，可将(1.1.1)的定解分为两类： 第一，初值问题（Cauchy 问题）：求足够光滑的函数()t x u ,，满足方程(1.1.1)和初始条件： ()()x x u ?=0,, ∞<<∞-x (1.1.2) 第二，初边值问题（也称混合问题）：求足够光滑的函数()t x u ,，满足方程(1.1.1)和初始条件： ()()x x u ?=0,, 0x l << (1.1.3) 及边值条件 ()()0,,0==t l u t u ， T t ≤≤0 (1.1.4) 假定()x f 和()x ?在相应的区域光滑，并且于()0,0，()0,l 两点满足相容条件,则上述问题有唯一的充分光滑的解。 1.2抛物线扩散方程的求解 下面考虑如下热传导方程 22()(0.)(,)0(,0)()u u a f x t x u t u L t u x x ????=+????? ==??=??? (1.2.1) 其中，0x l <<，T t ≤≤0,a (常数)是扩散系数。 取N l h = 为空间步长，M T =τ为时间步长，其中N ，M 是自然数，用两族

平行直线jh x x j ==, ()N j ,,1,0 =和k t t k τ ==, ()M k ,,1,0 =将矩形域 G {}T t l x ≤≤≤≤=0;0分割成矩形网格。其中 (),j k x t 表示网格节点；h G 表示 网格内点（位于开矩形G 中的网格节点）的集合；h G 表示位于闭矩形G 中的网格节点的集合；h Γ表示h G -h G 网格边界点的集合。 k j u 表示定义在网点(),j k x t 处的待求近似解，N j ≤≤0，M k ≤≤0。 现在对方程进行差分近似： (一) 向前差分格式 =-+τ k j k j u u 111 2 2(())k k k j j j j j j u u u a f f f x h +--++= (1.2.2) ()j j j x u ??==0， k u 0=k N u =0 (1.2.3) 计算后得： 111(12)k k k k j j j j j u ru r u ru f τ++-=+-++ (1.2.4) 其中，2 a r h τ = ，1,,1,0-=N j ，1,,1,0-=M k 。 显然，这是一个四点显示格式，每一层各个节点上的值是通过一个方程组求解到的。方程组如下： 1000 121011000 232121000 3432310001121(12)(12)(12)(12)N N N N N u ru r u ru f u ru r u ru f u ru r u ru f u ru r u ru f ττττ----?=+-++?=+-++??=+-++? ???=+-++? (1.2.5) 若记 () T k N k k k u u u 1 21,,,-= u ，()()()()T N x x x 121,,,-=???? ，()()()()T N x f x f x f 121,,,-=τττ f 则显格式(1.2.4)可写成向量形式 10 ,0,1,,1 k k k M φ +?=+=-?=? u Au f u (1.2.6) 其中

扩散方程的差分解法

扩散方程的差分解法 在研究热传导过程、扩散过程、边界层现象时，我们常常遇到抛物型方程，这类方程中最典型、最简单的就是热传导方程。热传导方程中的自变量中包括时间t ，它是描述一种随时间变化的物理过程，即所谓不定常现象。这类问题的基本定解问题应是初值问题，即在初始时刻（t=0）时给定定解条件，求解t>0时的解。 本文主要运用有限差分法对一维扩散方程进行求解，并对差分解的适定性、相容性、收敛性及稳定性进行分析，同时与解析解进行对比。 1.扩散方程 一维扩散方程为： 22u u t x α??=?? （1） 式中，u 为因知量，α为扩散系数，x 为坐标，t 为时间。 其定解条件如下： 初始条件： (,0)() 0x u x f x L =≤≤ （2） 边界条件： 12(0,)() , (,)()u t f t u L t f t == （3） 一般假定函数()f x ，1()f t ，2()f t 满足连接条件，即1(0)(0) f f =，2()(0) f L f =。 2.有限差分法 有限差分法是数值计算解微分方程古老的方法之一，也是系统化地、数值地求解数学物理方法的方程。其控制方程中的导数用离散点上函数值的差商代替。 差分格式可以分为显格式和隐格式。所谓显格式是指在任一结点上因变量在新是时间层上的值可以通过之前的时间层上相邻结点变量的值显式解出来。由于这些层的变量值是已知的，当时间向前推进时，空间点上的新的变量值就只需逐点计算就行了，因此显格式计算起来比较省事。隐格式则是指任一结点上变量在新的时间层的值，不能通过之前的时间层上相邻结点的值显式解出来，它不仅与之前的时间层上的已知值有关，而且也与新时间层的相邻结点的变量值有关。因而一个差分方程常常包括几个相邻结点上的未知数，未知数的个数取决于格式的构成形式。为了解出这些未知数需要联立新的方程，而每引进一个新的方程往往又同时引进了新的未知数。因此，隐格式总是伴随着求解巨大的代数方程组。隐格式的主要缺点是计算工作量大，因而不如显格式计算得快，但这只是就时间步长一样的情况而言的。隐格式的主要优点是时间步长可以比显格式能够采用的最大步长大很多。显格式的时间步长受到稳定性条件的限制，而隐格式则几乎不受限制。 3.方程的离散 3.1 显格式 采用时间前差及第n 时间层的空间中心差，得一维扩散方程的显格式解： 111 2 2()n n n n n j j j j j u u u u u t x α ++---+=?? （4） 即 111(2) n n n n n j j j j j u u r u u u ++-=+-+ （5）

微分方程数值解法

《微分方程数值解法》 【摘要】自然界与工程技术中的很多现象，可以归结为微分方程定解问题。其中，常微分方程求解是微分方程的重要基础内容。但是，对于许多的微分方程，往往很难得到甚至不存在精确的解析表达式，这时候，数值解提供了一个很好的解决思路。，针对于此，本文对常微分方程数值解法进行了简单研究，主要讨论了一些常用的数值解法，如欧拉法、改进的欧拉法、Runge —Kutta 方法、Adams 预估校正法以及勒让德谱方法等，通过具体的算例，结合MA TLAB 求解画图，初步给出了一般常微分方程数值解法的求解过程。同时，通过对各种方法的误差分析，让大家对各种方法的特点和适用范围有一个直观的感受。 【关键词】 常微分方程 数值解法 MA TLAB 误差分析 引言 在我国高校，《微分方程数值解法》作为对数学基础知识要求较高且应用非常广泛的一门课程，不仅 在数学专业，其他的理工科专业的本科及研究生教育中开设这门课程．近四十年来，《微分方程数值解法》不论在理论上还是在方法上都获得了很大的发展．同时，由于微分方程是描述物理、化学和生物现象的数学模型基础，且它的一些最新应用已经扩展到经济、金融预测、图像处理及其他领域 在实际应用中，通过相应的微分方程模型解决具体问题，采用数值方法求得方程的近似解，使具体问题迎刃而解。 2 欧拉法和改进的欧拉法 2.1 欧拉法 2.1.1 欧拉法介绍 首先，我们考虑如下的一阶常微分方程初值问题 ???==0 0)() ,('y x y y x f y （2--1） 事实上，对于更复杂的常微分方程组或者高阶常微分方程，只需要将x 看做向量，（2--1）就成了一个一阶常微分方程组，而高阶常微分方程也可以通过降阶化成一个一阶常微分方程组。 欧拉方法是解常微分方程初值问题最简单最古老的一种数值方法，其基本思路就是把（2--1）中的导数项'y 用差商逼近，从而将一个微分方程转化为一个代数方程，以便求解。 设在[]b a ,中取等距节点h ，因为在节点n x 点上，由（2--1）可得：

一维扩散方程的差分法matlab

一维扩散方程的差分法 m a t l a b Company number【1089WT-1898YT-1W8CB-9UUT-92108】

一维扩散方程的有限差分法 ——计算物理实验作业七 陈万 题目： 编程求解一维扩散方程的解 取1.0,1.0,1.0,10,0.1,0,1,1,0,1,1max 0222111======-=====τh D t a c b a c b a 。输出t=1,2,...,10时刻的x 和u(x),并与解析解u=exp(x+0.1t)作比较。 主程序： % 一维扩散方程的有限差分法 clear,clc; %定义初始常量 a1 = 1; b1 = 1; c1 = 0; a2 = 1;b2 = -1; c2 = 0; a0 = 1.0; t_max = 10; D = 0.1; h = 0.1; tao = 0.1; %调用扩散方程子函数求解 u = diffuse_equation(a0,t_max,h,tao,D,a1,b1,c1,a2,b2,c2); 子程序1： function output = diffuse_equation(a0,t_max,h,tao,D,a1,b1,c1,a2,b2,c2) % 一维扩散方程的有限差分法，采用隐式六点差分格式(Crank-Nicolson) % a0: x 的最大值 % t:_max: t 的最大值

% h: 空间步长 % tao: 时间步长 % D：扩散系数 % a1,b1,c1是（x=0）边界条件的系数；a2,b2,c2是（x=a0）边界条件的系数 x = 0:h:a0; n = length(x); t = 0:tao:t_max; k = length(t); P = tao * D/h^2; P1 = 1/P + 1; P2 = 1/P - 1; u = zeros(k,n); %初始条件 u(1,:) = exp(x); %求A矩阵的对角元素d d = zeros(1,n); d(1,1) = b1*P1+h*a1; d(2:(n-1),1) = 2*P1; d(n,1) = b2*P1+h*a2; %求A矩阵的对角元素下面一行元素e e = -ones(1,n-1);

偏微分方程数值解法答案

1. 课本2p 有证明 2. 课本812,p p 有说明 3. 课本1520,p p 有说明 4. Rit2法，设n u 是u 的n 维子空间，12,...n ???是n u 的一组基底，n u 中的任一元素n u 可 表为1n n i i i u c ?==∑ ，则,11 11()(,)(,)(,)(,)22j n n n n n n i j i j j i j j J u a u u f u a c c c f ???=== -=-∑∑是12,...n c c c 的二次函数，(,)(,)i j j i a a ????=，令 () 0n j J u c ?=?，从而得到12,...n c c c 满足1 (,)(,),1,2...n i j i j i a c f j n ???===∑，通过解线性方程组，求的i c ，代入1 n n i i i u c ?==∑， 从而得到近似解n u 的过程称为Rit2法 简而言之，Rit2法：为得到偏微分方程的有穷维解，构造了一个近似解，1 n n i i i u c ?== ∑， 利用,11 11()(,)(,)(,)(,)22j n n n n n n i j i j j i j j J u a u u f u a c c c f ???===-=-∑∑确定i c ，求得近似解n u 的过程 Galerkin 法：为求得1 n n i i i u c ? == ∑形式的近似解，在系数i c 使n u 关于n V u ∈，满足(,)(,) n a u V f V =，对任 意 n V u ∈或（取 ,1j V j n ?=≤≤） 1 (,)(,),1,2...n i j i j i a c f j n ???===∑的情况下确定i c ，从而得到近似解1 n n i i i u c ?==∑的过程称 Galerkin 法为 Rit2-Galerkin 法方程： 1 (,)(,)n i j i j i a c f ???==∑ 5. 有限元法：将偏微分方程转化为变分形式，选定单元的形状，对求解域作剖分，进而构 造基函数或单元形状函数，形成有限元空间，将偏微分方程转化成了有限元方程，利用 有效的有限元方程的解法，给出偏微分方程近似解的过程称为有限元法。 6. 解：对求解区间进行网格剖分，节点01......i n a x x x x b =<<<<=得到相邻节点1,i i x x -

一类反应扩散方程解的长时间行为

I 一类反应扩散方程解的长时间行为 摘 要 本文主要在一个有界光滑区域中讨论了一类带有齐次Dirichlet 边值条件的反应扩散方程解的长时间行为，其方程的形式如下： 其中 偏微分算子是一致抛物的， ，满足一定条件。 对于以上方程，我们首先定义了该方程的弱解，之后我们在有限维空间中构造了一系列该方程的近似解，并证明了在维数趋于无穷时，存在子列收敛于该方程的弱解。最后，我们利用先验估计得到了该方程弱解的存在唯一性。 在获得方程弱解的存在唯一性后，我们便能定义伴随方程的解半群，并由此研究伴随方程解半群的全局吸引子。 为了证明解半群在 中存在全局吸引子，我们证明 了伴随方程的解半群在 与中有界吸收集的存在性，并利用Sobolev 紧嵌入定理得到了全局吸引子的存在性。 关 键 词：反应扩散方程；Galerkin 方法；全局吸引子；弱解

II ABSTRACT In this thesis, we mainly consider the long-time behavior of solutions for the following reaction-diffusion equation with homogeneous Dirichlet boundary condition in a bounded smooth domain : where The partial differential operator is uniformly parabolic, and satisfies some additional assumptions. First of all, we give the definition of weak solutions, and then, we construct a sequence of approximate solution in a n dimension subspace and show that there exists a subsequence will convergent to a weak solution of this problem when n goes to infinite. Finally, we establish the existence and uniqueness of weak solution by some aprior estimates. With the help of the existence and the uniqueness of weak solutions, we define the solution semigroup associate with the problem and investigate the existence of a global attractor for the semigroup. To prove the existence of a global attractor, we show that there exist bounded absorbing sets in and and obtain existence of a global attractor in by using the Sobolev compactness embedding theorem. KEY WORDS: Reaction-diffusion equation; Galerkin’s method ; Global attractor; Weak solution

一维对流扩散方程的数值解法

一维对流扩散方程的数值解法 对流-扩散方程是守恒定律控制方程的一种模型方程，它既是能量方程的表示形式，同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。因此，以对流-扩散方程为例，来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。 1 数学模型 本作业从最简单的模型方程，即一维、稳态、无源项的对流扩散方程出发，方程如下： 22, 02f f f U D x t x x ???+=≤≤??? (1) 初始条件 (),0sin(2)f x t A kx π== (2) 解析解 ()()()224,sin 2Dk t f x t e A k x Ut ππ-=- (3) 式中，1,0.05,0.5,1U D A k ==== 函数(3)描述的是一个衰减波的图像，如图1所示 t=0 t=0.5 t=1 图1 函数()()()224,sin 2Dk t f x t e k x Ut ππ-=- 的图像（U=1，D=0.05，k=1） 2 数值解法 2.1 数值误差分析 在网格点(),i n 上差分方程的数值解n i f 偏离该点上相应的偏微分方程的精确解 (),f i n 的值，称为网格节点上的数值误差。 当取定网格节点数21N =时，观察差分方程的解与微分方程的解在不同时间步长下的趋近程度，其中时间步长分别取值0.05,0.025,0.0125,0.0005t ?=。

（a ）21,0.05N t =?= （b ）21,0.025N t =?= （c ）21,0.0125N t =?= （d ）201,0.0005N t =?= 图2 数值误差随步长的变化情况 从图2的(a)~(d)可以定性的看出，数值误差与步长的大小有关。在满足稳定性条件的前提下，数值误差随着时间步长的减小而减小，同时，图（d ）表示增大网格的分辨率也有助于减小网格误差。 为了对数值误差有一个定量的认识，接下来取定时间步长为0.0005t ?=，分别算出 11,21,41,61,81,101,121,161N =时，指标E =1所示。 表1 不同网格节点数下指标E 的值

基于Peclet数判别法的一维对流扩散方程分类研究

基于Peclet 数判别法的一维对流扩散方程分类研究 摘要：采用Peclet 数的绝对值大小来判别一维对流扩散方程为对流占优型或是扩散占优型方程，运用三种隐式差分格式—中心隐式格式、对流C-N 型格式和扩散C-N 格式，对不同Peclet 数的算例进行离散和求解。然后，将计算区域中所有节点的解析解与数值解表示成矩阵形式，并求解出它们的矩阵2范数之后作比较，两者越接近则代表差分格式精度越高。通过比较得出了当方程Peclet 数的绝对值小于等于0.5时，方程为扩散占优型方程。在离散方法选取方面，针对扩散项的离散可以采用更高精度的差分格式，如扩散C-N 格式；当Peclet 数的绝对值大于等于20时，方程为对流占优型方程。此时，针对对流项可以采用更高精度的差分格式，如对流C-N 格式；当Peclet 数的绝对值介于0.5与20之间时，无法用Peclet 数判断方程类型,不过可以选择折衷的离散格式减小误差，如中心隐式格式。 关键字：一维对流扩散方程 Peclet 数判别法 有限差分方法 数值模拟 MR(2010)主题分类号：39A14；65M06 中图分类号：O242.2 文献标识码： A 1.引言 一维对流扩散方程是描述流体流动和传热问题的一类线性化模型方程。土壤、大气等多孔介质中水、盐分、温度以及污染物质的对流扩散问题都会遇到此类方程。在一维对流扩散方程的求解过程中，反映流体对流和扩散两种物理作用的分别是对流项和扩散项。所以，根据方程中对流项还是扩散项占主导作用，通常可将方程分为对流占优型和扩散占优型两类方程。然而，要想得到精确度较高的数值结果，这两种类型方程的离散方法不能采用相同的离散格式。因此，需要有一种判别方法来判断方程的类型，关于对流占优型和扩散占优型方程的判别方法一直是近年来研究的热点问题。这对研究不同类型的方程使用合适的差分格式进行离散具有实际的意义。由于Peclet 数的绝对值表示了对流作用相对扩散作用的大小，即绝 大，扩散所起的作用就可以忽略。反之，当Peclet 数为零时，方程就为纯扩散方程。本文选用一维定解非稳态对流扩散方程为例，通过考察Peclet 数的绝对值大小来对方程进行分类，方程一般形式如下： 2(,),,0 122(1)(,0)()(,)(),(,)()12(,) u u u a f x t x x x t t x x u x g x u x t t u x t t u u x t υ?φ???? ?? ?? ????+=+≤≤≥???==== 其中a 和υ分别代表对流项系数和扩散项系数。假定求解区间长度为s ， Peclet 数的绝对值

微分方程的分类及其数值解法

微分方程的分类及其数值解法 微分方程的分类： 含有未知函数的导数，如dy/dx=2x 、ds/dt=0.4都是微分方程。 一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。微分方程有时也简称方程。 一、常微分方程的数值解法： 1、Euler 法： 00d (,), (1.1)d (), (1.2) y f x y x y x y ?=???=? 001 (),(,),0,1,,1n n n n y y x y y hf x y n N +=??=+=-? (1.4) 其中0,n b a x x nh h N -=+=. 用(1.4)求解(1.1)的方法称为Euler 方法。 后退Euler 公式???+==+++),,(),(111 00n n n n y x hf y y x y y 梯形方法公式 )].,(),([2 111+++++=n n n n n n y x f y x f h y y 改进的Euler 方法11(,),(,),1().2p n n n c n n p n p c y y hf x y y y hf x y y y y ++?=+??=+???=+??? 2、Runge-Kutta 方法： p 阶方法 ： 1()O h -=?总体截断误差局部截断误差 二阶Runge-Kutta 方法 ??? ????++==++=+),,(),,(,2212 1211hk y h x f k y x f k k h k h y y n n n n n n

一维对流扩散方程的稳定性条件推导

一维稳态对流扩散方程稳定性条件的推导 姓名： 班级：硕5015 学号： 2015/12/15

证明： 一维稳态对流扩散方程： 22u x x φφρ??=Γ?? 采用控制容积积分法，对上图P 控制的容积作积分，取分段线性型线，对均分网格可得下列离散方程： ()()()()()()()()11112222e w e w P E W e w e w w w e e u u u u x x x x φρρφρφρδδδδ??????ΓΓΓΓ+-+=-++????????????????记：()()()()1122e w P e w w e a u u x x ρρδδΓΓ=+-+ ()()12 e E e e a u x ρδΓ=- ()()12w W w w a u x ρδΓ= + 定义通过界面的流量u ρ记为F ,界面上单位面积扩散阻力的倒数x δΓ记为D ,则原式简化为： P P E E W W a a a φφφ=+ 12 E e e a D F =- 12 W w w a D F =+ ()P E W e w a a a F F =++- 令 u x F Pe D ρδ==Γ 则 1111222 E W P Pe Pe φφφ????-++ ? ?????=

当Pe 大于2以后，数值解出现了异常；P φ小于其左右邻点之值，在无源项情 况下是不可能的。因为当2Pe >时系数12 E e e a D F =-小于零，即右边点的通过对流及扩散作用对中间点所产生的影响是负的，这会导致物理上产生不真实的解，所以2u x Pe ρδ=≤Γ 证毕。

一维扩散方程的差分法matlab

一维扩散方程的有限差分法 ——计算物理实验作业七 陈万 题目： 编程求解一维扩散方程的解 取1.0,1.0,1.0,10,0.1,0,1,1,0,1,1max 0222111======-=====τh D t a c b a c b a 。输出t=1,2,...,10时刻的x 和u(x),并与解析解u=exp(x+0.1t)作比较。 主程序： % 一维扩散方程的有限差分法 clear,clc; %定义初始常量 a1 = 1; b1 = 1; c1 = 0; a2 = 1;b2 = -1; c2 = 0; a0 = 1.0; t_max = 10; D = 0.1; h = 0.1; tao = 0.1; %调用扩散方程子函数求解 u = diffuse_equation(a0,t_max,h,tao,D,a1,b1,c1,a2,b2,c2); 子程序1：

function output = diffuse_equation(a0,t_max,h,tao,D,a1,b1,c1,a2,b2,c2) % 一维扩散方程的有限差分法，采用隐式六点差分格式 (Crank-Nicolson) % a0: x的最大值 % t:_max: t的最大值 % h: 空间步长 % tao: 时间步长 % D：扩散系数 % a1,b1,c1是（x=0）边界条件的系数；a2,b2,c2是（x=a0）边界条件的系数 x = 0:h:a0; n = length(x); t = 0:tao:t_max; k = length(t); P = tao * D/h^2; P1 = 1/P + 1; P2 = 1/P - 1;

常微分方程数值解法

i.常微分方程初值问题数值解法 常微分方程初值问题的真解可以看成是从给定初始点出发的一条连续曲线。差分法是常微分方程初值问题的主要数值解法，其目的是得到若干个离散点来逼近这条解曲线。有两个基本途径。一个是用离散点上的差商近似替代微商。另一个是先对微分方程积分得到积分方程，再利用离散点作数值积分。 i.1 常微分方程差分法 考虑常微分方程初值问题：求函数()u t 满足 (,), 0du f t u t T dt =<≤ （i.1a ） 0(0)u u = (i.1b) 其中(,)f t u 是定义在区域G : 0t T ≤≤, u <∞上的连续函数，0u 和T 是给定的常数。我们假设(,)f t u 对u 满足Lipschitz 条件，即存在常数L 使得 121212(,)(,), [0,]; ,(,)f t u f t u L u u t T u u -≤-?∈∈-∞∞ （i.2） 这一条件保证了（i.1）的解是适定的，即存在，唯一，而且连续依赖于初值0u 。 通常情况下，（i.1）的精确解不可能用简单的解析表达式给出，只能求近似解。本章讨论常微分方程最常用的近似数值解法-差分方法。先来讨论最简单的Euler 法。为此，首先将求解区域[0,]T 离散化为若干个离散点： 0110N N t t t t T -=<< <<= （i.3） 其中n t hn =，0h >称为步长。 在微积分课程中我们熟知，微商（即导数）是差商的极限。反过来，差商就是微商的近似。在0t t =处，在（i.1a ）中用向前差商 10()()u t u t h -代替微商du dt ，便得 10000()()(,())u t u t hf t u t ε=++ 如果忽略误差项0ε，再换个记号，用i u 代替()i u t 便得到 1000(,)u u hf t u -= 一般地，我们有 1Euler (,), 0,1, ,1n n n n u u hf t u n N +=+=-方法： （i.4） 从(i.1b) 给出的初始值0u 出发，由上式可以依次算出1,,N t t 上的差分解1,,N u u 。

物理分析课程设计---一维扩散方程求解

课程设计报告 课程名称：核反应堆物理分析题目：一维扩散方程求解院系：核科学与工程学院班级： 学号： 姓名： 指导教师： 成绩： 教师签名： 日期：2011 年6月日

目录 摘要 (1) 课程设计的目的与要求 (1) 设计正文 (1) 课程设计总结或结论 (3) 参考文献 (4)

摘要和关键词 摘要 这个设计用微分方程的差分数值求解方法，运用MATLAB编程计算出一维扩散方程中子通量密度的离散解。 关键词：一维扩散方程 一．课程设计的目的与要求 学习使用微分方程的数值解法（差分方法）来近似求解一维扩散方程，掌握差分方法的核心思想，熟练使用matlab数据处理，origin绘图软件。通过给定的微分方程及边界条件，计算平板型，圆柱形，球形反应堆中子通量密度分布。 二．设计正文 通过查找有关资料，根据二阶线性微分方程 ○1 转换为差分方程的一般公式 其中 ○2 h为给定步长, 我们把原方程化简为○3

对比方程○1和○3得出 ○4 把○4代入○2 等式右端向量 差分方程其实就是一个线性方程组，此线性方程组的系数矩阵为： 则有 这是一个三对角阵，故可用追赶法解式○3。 下面通过matlab程序来计算变换后的差分方程的解。 所编程序如下： clear; N=input('请输入参数：'); alpha=input('请输入alpha值：'); if alpha==0 rmax=input('请输入平板的厚度：'); f0=input('请输入平板中心的中子通量密度：'); elseif alpha==1 rmax=input('请输入堆芯半径：'); f0=input('请输入圆柱中心的中子通量密度：'); elseif alpha==2 rmax=input('请输入堆芯半径：'); f0=input('请输入球形中心的中子通量密度：'); end

微分方程数值解法答案

包括基本概念，差分格式的构造、截断误差和稳定性，这些内容是贯穿整个教材的主线。解答问题关键在过程，能够显示出你已经掌握了书上的内容，知道了解题方法。这次考试题目的类型：20分的选择题，主要是基本概念的理解，后面有五个大题，包括差分格式的构造、截断误差和稳定性。 习题一 1． 略 2． y y x f -=),(，梯形公式：n n n n n n y h h y y y h y y )121(),(2111+-+=+- =+++，所以0122)1(01])121[()121()121(y h h y h h y h h y h h n h h n n n +--+--+-+=+-+==+-+= ，当0→h 时， x n e y -→。 同理可以证明预报-校正法收敛到微分方程的解. 3． 局部截断误差的推导同欧拉公式; 整体截断误差: ? ++++++-++≤1 ),())(,(11111n n x x n n n n n n n dx y x f x y x f R εε 11)(++-++≤n n n y x y Lh R ε，这里R R n ≤ 而111)(+++-=n n n y x y ε，所以 R Lh n n += -+εε1)1(，不妨设1

微分方程数值解――

微分方程数值解―― 第二章 习题 1． 设)('x f 为)(x f 的一阶广义导数，试用类似办法定义)(x f 的k 阶广义导数) () (x f k （ ,2,1=k ）。 解：对一维情形，函数的广义导数是通过分部积分来定义的。 我们知，)(x f 的一阶广义导数位)(x g ，如果满足 dx x x f dx x x g b a b a )()()()('?? -=?? 类似的，)(x f 的k 阶广义导数为)()() (x f x g k =，如果有 dx x x f dx x x g b a k k b a )()()1()()()(?? -=?? 2． 试建立与边值问题 ?????====<<=+=) 2.1(0)()(,0)()() 1.1(,''44b u b u a u a u b x a f u dx u d Lu 等价的变分问题。 证明： 设}0)()(,0)()(),(|{' '2====∈=b v a v b v a v I H v v V 对方程)1.1(两边同乘以v ，再关于x 在),(b a 上积分)(V v ∈，得 ??=+b a b a fvdx vdx u dx u d )(44 其中 dx dx dv dx u d dx dx dv dx u d dx u d v dx u d d v vdx dx u d b a b a b a b a b a ???? -=-==33 33333344|)( dx dx v d dx u d dx dv dx u d dx u d d dx dv b a b a b a ??+-=-=22222222|)( dx dx v d dx u d b a ? = 2 222 (*) 记dx uv dx v d dx u d v u a b a ?+=)(),(2 222，?=b a fvdx v f ),(。于是我们得到以下等价变分问题的提法：

偏微分方程的数值解法

《偏微分方程数值解法》试题 （专业：凝聚态物理学号：60 姓名：鄢建军）1.考虑定解问题 （1）用迎风格式（）求解 1,0 (,0) 0,0 t x u u x u x x += ? ? ≤ ? ? =? ?> ? ? 。 利用迎风格式编写Fortran程序语言，运行结果如下： Fig 1.迎风格式求解结果 （2）用Beam-Warming 格式（）求解。 利用Beam—Warming格式编写Fortran程序语言，运行结果如下：

Fig 2. Beam —Warming 格式求解结果 （3） 比较两种方法结果的异同。 将两种格式运行的结果绘制在一起，要求时间步长和空间步长在两种格式中都相同，运行结果如下图所示： Fig 3. 迎风格式和Beam-Warming 格式求解结果比较 从两种格式的运行结果来看，都存在边缘的误差现象，相比而言，Beam-Warming 格式的运行结果差一些。但是理论上分析，迎风格式的截断误差为()h οτ+，而Beam-Warming 格式的截断误差为22()h h οττ++。稳定性上来分析，迎风格式的稳定性较好，要求1(/)a h λλτ≤=，Beam-Warming 格式的稳定性条件为2(/)a h λλτ≤=。 2. 考虑定解问题2121110,04(,0)sin ,0(0,)(,)0u u a x l t t u x x x l l u t u l t π???-=<

实际计算时，取下列参数：a=1；1l =2.计算进行到合适的时刻为止。要求： （1） 用加权隐式格式（）求解该问题，研究不同θ值对解的影响。 用加权隐式格式求解该问题，研究不同θ值对解的影响。采用的差分格式为 12212[(1)]0n n j j n n x j x j u u a u u h θδθδτ++---+=， 其截断误差为：2221(),21(),2o h o h τθτθ?+≠????+=??，稳定性条件为：112,(0),1221,(1).2 a λθθθ?≤≤

一维抛物线方程混合边界问题matlab求解(一维扩散方程)

在差分方法中分为前差、后差、中心差以及显式、隐式、中心式。这些概念分别对应着对空间和时间的离散。 针对以上抛物线方程的求解方法，分别采用向前、向后、对称六点和三行式进行计算。 一维抛物线的一般方程为 此题为混合边界问题 1、前差的一般格式为 将τ 成为网比，记做r，则差分格式可以写成 ?2

将上标为k+1的放在一边，k的放在一边，这样就可以写成矩阵形式。 根据已知条件便可以求解。（下面是前差的matlab代码） r=10; x=0:0.1:1; t=0:0.1:1; U=[]; U(:,1)=0; U(:,11)=0; U(1,:)=sin(pi.*x); for i=2:11 %%行 for j=2:10 %% 列 U(i,j)=r*U(i-1,j-1)+(1-2*r)*U(i-1,j)+r*U(i-1,j+1); end end figure; surf(x,t,U); 例题中并没有给出t的具体值，这里取了1，如同正方形laplace方程一样，纯粹为了好求。上面两个for循环代替了矩阵的作用。如果想改成矩阵，很简单，自行解决。

2、后差的一般格式为 这里请注意前差后差的不同点在于右式中上标的变化。 附上matlab代码： h=0.1; k=0.1; N=1/h; M=1/0.1; r=k/h^2; for i=1:N-1 B(i)=sin(i/N*pi); end U(:,1)=B; A=diag(ones(1,N-1)*(1+2*r))-diag(ones(1,N-2)*r,1)-diag(ones(1,N-2)*r, -1); for i=2:M+1 U(:,i)=A\U(:,i-1); end Z=[zeros(11,1),U',zeros(11,1)]; [X,Y]=meshgrid(linspace(1,0,11),linspace(1,0,11)); surf(X,Y,Z);