Ab initio investigation of the intermetallics in the Nb Sn binary system

Ab initio investigation of the intermetallics in the Nb–Sn binary system

I.Papadimitriou,C.Utton and P.Tsakiropoulos

?

Department of Materials Science and Engineering,The University of She?eld,Sir Robert Had?eld Building,Mappin Street,

She?eld S13JD,UK

Received 3August 2014;revised 8December 2014;accepted 10December 2014

Abstract—The elastic and thermodynamic properties of the stable intermetallics in the Nb–Sn system were studied by the ?rst-principles pseudo-potential plane-wave method based on density functional theory.The elastic constants,Debye temperatures,bulk,shear and Young’s moduli and Poisson’s ratios were calculated for all the phases.Nb 3Sn has the highest bulk,shear and elastic moduli of the Nb–Sn intermetallics.The elastic properties at 0K and the Debye temperatures of the Nb 6Sn 5and NbSn 2phases are reported for the ?rst time.The enthalpies of formation were calculated for all the intermetallics.The ?nite-temperature elastic properties of the Nb and Nb 3Sn were calculated using the quasi-static approxima-tion.The thermal expansion coe?cients of Nb and Nb 3Sn were also obtained.ó2014Acta Materialia Inc.Published by Elsevier Ltd.All rights reserved.

Keywords:Ab initio calculations;Elastic constants;Enthalpy of formation;Intermetallic phases

1.Introduction

High-temperature structural materials with operating temperature capability that exceeds that of modern Ni-based superalloys ($1423K)are currently being developed to meet environmental and performance targets for future gas turbines.Creep and oxidation property goals have been proposed for the next generation of ultrahigh-temperature alloys [1,2].These are forecast to require coatings,like the Ni-based superalloys that they will replace.

Alloys based on refractory metal intermetallics have been studied as candidate materials due to their potential to o?er a balance of mechanical and environmental proper-ties combined with low density [1,2].Among the alloys studied,developmental Nb-silicide-based alloys have exceeded the proposed creep goal and have room-tempera-ture fracture toughness above 20MPa m 1/2[1].Alloying has signi?cantly improved the intrinsically poor oxidation of binary Nb–Si alloys [1–4],eliminating pest oxidation [5],and has closed the gap with the target property [1].Tin is one of the elements that has been shown to bene?t the oxidation of Nb-silicide-based alloys [1,6]when present at low concentrations and in synergy with speci?c alloying additions.Tin suppresses Nb 3Si [7],whereas in synergy with Ti and with Ti,Fe and Cr encourages,respectively,the transformation of b Nb 5Si 3to a Nb 5Si 3[7]and the for-mation of metastable Nb 3Si [8],while improvement in

oxidation is linked with the formation of Sn-rich interme-tallic below the scale [5,6].Whether or not spallation of the scale occurs seems to depend on the type of Nb–Sn intermetallic(s)stabilized at the scale–alloy interface and on their properties.

In order to understand alloy behavior in ternary and higher-order systems,knowledge of thermal and physical properties of the intermetallic compounds that are key to the development of the new alloys is critical.Phase equilib-ria data in Nb–Si-based systems with Sn are limited.Advancing our understanding of how alloying with Sn a?ects the microstructure and properties of Nb-silicide-based alloys and improving alloy design require a better understanding of the properties of the phases in the Nb–Sn binary system.

In the Nb–Sn system there are three stable intermetallics [9].Nb 3Sn has the A15structure,which is a close-packed structure whose stability is largely governed by size [10],has a primitive cell of 8atoms and belongs to the space group Pm 3n ;its Pearson symbol is cP 8and is of the Cr 3Si type;its melting temperature is 2647K.Nb 6Sn 5has a D2H-25orthorhombic structure with a primitive cell of 22atoms and belongs to the Immm space group with oI 45Pearson symbol and is of the a Ti 6Sn 5type;its melting temperature is $1180K.NbSn 2has the D2H-24orthorhombic struc-ture,Pearson symbol oI 48,space group Fddd and is of the CuMg 2type with its primitive cell containing 12atoms;its melting temperature is $1100K.Nb 3Sn has attracted interest due to its superconducting properties [11],with a transition temperature of 18.9K,and its high melting tem-perature.The other two intermetallics are also regarded as

https://www.360docs.net/doc/f818373465.html,/10.1016/j.actamat.2014.12.017

1359-6462/ó2014Acta Materialia Inc.Published by Elsevier Ltd.All rights reserved.

?Corresponding

author.Fax:+44(0)1142225943;e-mail:p.tsakir-opoulos@she?https://www.360docs.net/doc/f818373465.html,

Available online at https://www.360docs.net/doc/f818373465.html,

ScienceDirect

Acta Materialia 86(2015)

23–33

https://www.360docs.net/doc/f818373465.html,/locate/actamat

superconductors,with transition temperatures of 2.68and 2.07K for NbSn 2and Nb 6Sn 5,respectively [12].

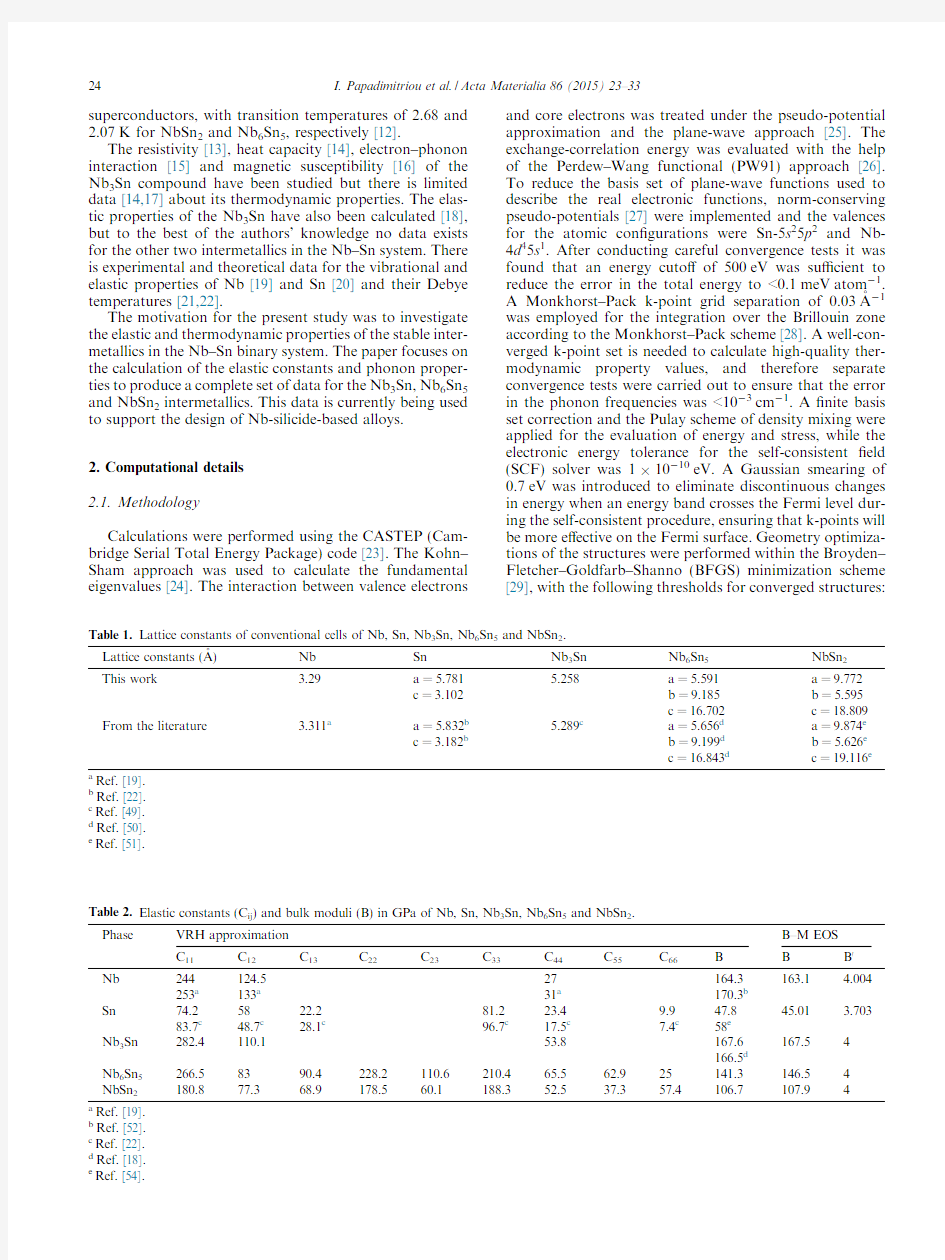
The resistivity [13],heat capacity [14],electron–phonon interaction [15]and magnetic susceptibility [16]of the Nb 3Sn compound have been studied but there is limited data [14,17]about its thermodynamic properties.The elas-tic properties of the Nb 3Sn have also been calculated [18],but to the best of the authors’knowledge no data exists for the other two intermetallics in the Nb–Sn system.There is experimental and theoretical data for the vibrational and elastic properties of Nb [19]and Sn [20]and their Debye temperatures [21,22].

The motivation for the present study was to investigate the elastic and thermodynamic properties of the stable inter-metallics in the Nb–Sn binary system.The paper focuses on the calculation of the elastic constants and phonon proper-ties to produce a complete set of data for the Nb 3Sn,Nb 6Sn 5and NbSn 2intermetallics.This data is currently being used to support the design of Nb-silicide-based https://www.360docs.net/doc/f818373465.html,putational details 2.1.Methodology

Calculations were performed using the CASTEP (Cam-bridge Serial Total Energy Package)code [23].The Kohn–Sham approach was used to calculate the fundamental eigenvalues [24].The interaction between valence electrons and core electrons was treated under the pseudo-potential approximation and the plane-wave approach [25].The exchange-correlation energy was evaluated with the help of the Perdew–Wang functional (PW91)approach [26].To reduce the basis set of plane-wave functions used to describe the real electronic functions,norm-conserving pseudo-potentials [27]were implemented and the valences for the atomic con?gurations were Sn-5s 25p 2and Nb-4d 45s 1.After conducting careful convergence tests it was found that an energy cuto?of 500eV was su?cient to reduce the error in the total energy to <0.1meV atom à1.

A Monkhorst–Pack k-point grid separation of 0.03A

?à1was employed for the integration over the Brillouin zone according to the Monkhorst–Pack scheme [28].A well-con-verged k-point set is needed to calculate high-quality ther-modynamic property values,and therefore separate convergence tests were carried out to ensure that the error in the phonon frequencies was <10à3cm à1.A ?nite basis set correction and the Pulay scheme of density mixing were applied for the evaluation of energy and stress,while the electronic energy tolerance for the self-consistent ?eld (SCF)solver was 1?10à10eV.A Gaussian smearing of 0.7eV was introduced to eliminate discontinuous changes in energy when an energy band crosses the Fermi level dur-ing the self-consistent procedure,ensuring that k-points will be more e?ective on the Fermi surface.Geometry optimiza-tions of the structures were performed within the Broyden–Fletcher–Goldfarb–Shanno (BFGS)minimization scheme [29],with the following thresholds for converged structures:

Table 2.Elastic constants (C ij )and bulk moduli (B)in GPa of Nb,Sn,Nb 3Sn,Nb 6Sn 5and NbSn 2.Phase VRH approximation B–M EOS C 11C 12C 13

C 22

C 23

C 33

C 44C 55

C 66

B B B 0Nb 244124.527164.3163.1 4.004253a 133a 31a 170.3b Sn 74.25822.281.223.49.947.845.01 3.70383.7c 48.7c 28.1c 96.7c 17.5c 7.4c

58e Nb 3Sn 282.4110.153.8167.6167.54166.5d Nb 6Sn 5266.58390.4228.2110.6210.465.562.925141.3146.54NbSn 2

180.8

77.3

68.9178.560.1188.352.5

37.357.4

106.7

107.9

4

a

Ref.[19].b

Ref.[52].c

Ref.[22].d

Ref.[18].e

Ref.[54].

Table https://www.360docs.net/doc/f818373465.html,ttice constants of conventional cells of Nb,Sn,Nb 3Sn,Nb 6Sn 5and NbSn 2.

Lattice constants (A ?)Nb Sn Nb 3Sn Nb 6Sn 5NbSn 2This work

3.29

a =5.781

c =3.102 5.258

a =5.591

b =9.185

c =16.702a =9.772b =5.595c =18.809From the literature

3.311a a =5.832b c =3.182b

5.289c

a =5.656d

b =9.199d

c =16.843d

a =9.874e

b =5.626e

c =19.116e

a

Ref.[19].b

Ref.[22].c

Ref.[49].d

Ref.[50].e

Ref.[51].

24I.Papadimitriou et al./Acta Materialia 86(2015)23–33

energy change per atom,maximum residual force,maxi-mum atomic displacement and maximum stress less than

1?10à7eV,1?10à4eV A

?à1,1?10à4A ?and 0.001GPa,respectively.2.2.Elastic properties

The elastic constants of a material describe its response to an applied stress,or the stress required to maintain a dis-tortion.The method to determine elastic constants con-sisted of applying a given strain and calculating the stress.The unit cell was kept ?xed at each deformation and the internal coordinates were optimized.Both stress and strain have three tensile and three shear components,giving six in total.The linear elastic constants form a 6?6matrix such that r i =C ij e j for small stress r and strain e .This matrix can be reduced as the strain patterns (sets of distortions)are based on the crystal structure of each phase by taking advantage of the linear combinations of the second-order elastic constants.Thus,the maximum number of patterns required for an orthorhombic structure is three,two for tetragonal and one for cubic cells.Six strain steps (varying from à0.003to 0.003)were used for each pattern to obtain a reliable linear ?t of the stress–strain relationship.

For the orthorhombic Nb 6Sn 5and NbSn 2phases a ser-ies of 18geometry optimizations were conducted in order to evaluate the nine independent elastic constants C 11,C 12,C 13,C 22,C 23,C 33,C 44,C 55and C 66.After acquiring the elastic constants matrix and con?rming that the mechanical stability criteria [30]are satis?ed,the bulk (B),Young’s (E)and shear (G)moduli and Poisson’s ratio (v)were obtained by using the Voigt–Reuss–Hill approxi-mation (VRH)[31,32].The Debye temperature at low tem-peratures was determined from elastic constants using the equations in Ref.[33],since at low temperatures the vibra-tional excitations arise solely from acoustic modes,i.e.when the Debye temperature is associated with lattice vibrations.In order to con?rm the values of the bulk mod-uli,a ?t of the energies vs.the volumes of the strained struc-tures in the third-order Birch–Murnaghan equation of state (B–M EOS)[34]was carried out.2.3.Linear response method

The entropic contributions play a predominant role in the structural stability of intermetallic phases.In the case of strongly ordered compounds the main contribution comes from the vibrational entropy,as the electronic and con?gurationally entropies are considered to be relatively small [35].Density functional perturbation theory (DFPT),or linear response,which is one of the most popular meth-ods of lattice dynamics [36,37],was used in order to obtain the vibrational density of states.When ionic positions are perturbed,the dynamic matrix and phonon frequencies can be obtained.It was ?rst ensured that every system was in the ground state,i.e.the geometry optimization was fully converged as any underconverged structure could yield imaginary phonon frequency eigenvalues,which is indicative of mechanical instability.After directly comput-ing the phonon frequencies on a Monkhorst–Pack q-vector

grid with 0.05A

?à1separation,the results were interpolated onto a very dense q-point set,and thus the phonon density of states (DOS)was obtained for each phase under investi-gation.By using the phonon DOS and the data in Ref.[36],

T a b l e 3.C a l c u l a t e d s h e a r m o d u l u s (G ),e l a s t i c m o d u l u s (E )i n G P a ,P o i s s o n ’s r a t i o (v ),C a u c h y p r e s s u r e s (C 12–C 44f o r c u b i c ,C 13–C 44a n d C 12–C 66f o r t e t r a g o n a l a n d h e x a g o n a l a n d C 12–C 66,C 13–C 55a n d C 23–C 44f o r o r t h o r h o m b i c )i n G P a ,G /B r a t i o a n d D e b y e t e m p e r a t u r e (H D )f r o m e l a s t i c c o n s t a n t s f o r N b ,S n ,N b 6S n 5,N b S n 2a n d N b 3S n .

P h a s e

G E

v

C 12–C 44C 13–C 44C 12–C 66C 13–C 55C 23–C 44G /B

H D (K )V R H

V R H

P h o n o n D O S

E l a s t i c c o n s t a n t s N b 37.437.5a

104.3101.9a

0.39497.5

0.228277268275b

267c

S n 17.318f

46.250f

0.339à1.248.10.362181170202e

N b 3S n 6574.9d

172.7195.3d

0.32856.30.388291336308b

282d N b 6S n 5

54143.70.3315827.545.10.382201218N b S n 251.4

132.9

0.292

19.9

31.67.6

0.482239256

a

R e f .[52].b R e f .[21].c R e f .[53].d R e f [18].e R e f .[22].f R e f .[54].

I.Papadimitriou et al./Acta Materialia 86(2015)23–33

25

Fig.1.Phonon density of states of Nb,Sn,Nb3Sn,Nb6Sn5and NbSn2.

Phonon contribution to free energies calculated by the linear response method for all intermetallics and single elements.The Nb,Nb3Sn(numbered3,4and5,respectively)are very close to each other.The NbSn2curve is denoted as1and the curve of Sn diagram as(a),for a smaller range of temperatures(1200–1700K),showing the curves of Nb6Sn5,Nb,Nb3Sn.

are extracted from the volume dependencies of the pho-non density of states calculated at 0K.The procedure consists of three main steps.The ?rst is to express the

0K elastic constants as a function of volume,using the stress–strain approach described in Section 2.2.The sec-ond step is to calculate the equilibrium volume V(T,P)at every given temperature using the quasi-harmonic approximation (see Section 2.3)by minimizing the total free energy with respect to volume,thus ?nding the equi-librium volume at each temperature.In the present study the investigated structures were obtained by varying the ratio V/V 0(V 0being the equilibrium volume)from 0.991to 1.006in increments of 0.003.In all the structures the internal freedoms within the unit cell were fully relaxed before proceeding to the phonon calculations.In the third step the computed elastic constants from the ?rst step at the volume V(T,P)were approximated as the correspond-ing values at ?nite temperatures.In order for the evalua-tion of the elastic constants as a function of temperature to be as accurate as possible,high-precision geometry optimization calculations for di?erent volumes and

robust

contributions to the enthalpy of formation and (b)calculated total enthalpy of formation vs.temperature for Table 4.Calculated enthalpies of formation of Nb 6Sn 5,NbSn 2and Nb 3Sn.

Temperature (K)Enthalpy of formation (kJ mol à1)Nb 3Sn Nb 6Sn 5NbSn 20à16.542à25.755à18.434298à15.628à24.829

à17.583

298à16.57c 298à16.19c 298à16.4b 298à16a

à22a à16a

a

Ref.[42].b Ref.[43].c

Ref.[44].

phonon calculations are needed to obtain accurate pho-non DOS at di?erent https://www.360docs.net/doc/f818373465.html,ing the approximation described above,resource-intensive free energy vs.strain calculations are avoided.Furthermore,application of inhomogeneous strain is not required as this method con-siders volume rather than strain,which is much cheaper in calculation cost terms as the symmetry of the crystal is retained.

In the above procedure the assumption was made that any change in the elastic constants was solely due to the thermal expansion,which is in accordance with reports [40]for cubic symmetry.Furthermore,the thermal expan-sion of cubic systems can be regarded as isotropic.Hence,in this study the quasi-static approximation was imple-mented only for the cubic Nb and Nb3Sn phases.

3.Results and discussion

3.1.Elastic properties at0K

The calculated lattice constants of Nb,Sn,Nb3Sn, Nb6Sn5and NbSn2are given in Table1.The values obtained in the present work are in good agreement with those reported in the literature.The highest deviation ($2.5%)is for the c lattice parameter of Sn.Table2

gives Fig.4.Temperature dependence of the volume of(a)Nb and(b)Nb3Sn.

the results for the independent elastic constants (C ij ),bulk moduli (B)calculated from elastic constants according to the VRH approximation,and the bulk moduli and ?rst pressure derivatives of bulk moduli (B 0)from the B–M EOS for all compounds and elements at 0K.The mechan-ical stability criteria [30]were satis?ed for all phases.The elastic constants and bulk moduli were in good agreement with experimental data for the pure elements [19,22]and with a previous theoretical study [18]of Nb 3Sn.Further-more,the bulk moduli obtained by the B–M EOS ?tting were in very good agreement with those calculated

using

Fig.5.The C 11(1),C 12(2)and C 44(3)elastic constants of (a)Nb and (b)Nb 3Sn vs.temperature.

Table 5.Calculated elastic constants and bulk and shear moduli in GPa of Nb and Nb 3Sn at 300K compared with available experimental results.Phase C 11C 12C 44B G Nb 233.7119.325.2157.435.2235a 121a 28.2a 159a 37.5a Nb 3Sn

265.4104.851.3158.361.4253.8b

112.4b

39.6b

159.5b

50.1b

a Ref.[47].

b

Ref.[48](single crystal).

the VRH approximation,with the biggest deviation ($3.5%)for Nb6Sn5.Nb3Sn had the highest bulk modulus (166.5GPa).The bulk modulus decreased to141.3GPa for Nb6Sn5and to106.7GPa for NbSn2.Thus,among the three intermetallics the Nb3Sn phase is the most resistant to uniform compression.

The calculated values of the shear(G)and Young’s(E) moduli are given in Table3.Nb3Sn has the highest shear modulus,and this decreases in the same sequence as the bulk modulus,which means that Nb3Sn is the most resis-tant compound of the three to plastic deformation.The same is true for the ranking of the intermetallics in terms of their sti?ness with the elastic modulus(E)values being 172.7GPa for Nb3Sn,143.7GPa for Nb6Sn5and 132.9GPa for NbSn2.

The values of the Cauchy pressures(C12–C44for cubic, C13–C44and C12–C66for tetragonal and hexagonal,and C12–C66,C13–C55and C23–C44for orthorhombic)are also listed in Table3.According to Ref.[41],for metallic bond-ing a positive value of Cauchy pressure means a more duc-tile material.Pugh’s index of ductility[55](the shear modulus over bulk modulus ratio(G/B))and the

Poisson’s Fig.6.Bulk(1),shear(2)and Young’s(3)moduli of(a)Nb and(b)Nb3Sn vs.temperature.

ratio(v)are the parameters that also indicate ductility.A compound is considered brittle if the G/B ratio is>0.57 or v is<0.26.Thus,the data in Table3indicates that the least ductile stable intermetallic in the Nb–Sn binary system is NbSn2.

3.2.Enthalpies of formation

The vibrational DOS for the compounds and elemental phases is shown in Fig.1.All the eigenfrequencies were found to be real,hence it is con?rmed that the compounds under investigation are mechanically stable.After obtain-ing the computed phonon DOS,the vibrational contribu-tion to the free energy per atom(F phon(T))was calculated and is presented for the compounds and elemen-tal phases in Fig.2.The F phonon(T)of the intermetallics decreases in the following order:Nb3Sn–Nb6Sn5–NbSn2 with the?rst two almost coinciding and the latter decreas-ing much faster.After taking F phonon(T)into account,the phonon contribution to the enthalpy of formation(D H f phon (T))was evaluated(Fig.3a).The D H f phon(T)rises faster in the following order:NbSn2–Nb6Sn5–Nb3Sn.In Fig.3b the enthalpy of formation vs.temperature of all the stable intermetallic compounds of the Nb–Sn system is

shown. Fig.7.The Poisson’s ratios of(a)Nb and(b)Nb3Sn vs.temperature.

In Table4the enthalpies of formation of the intermetallics of the present study are compared with the available litera-ture[42–44]and it can be seen that there is good agreement.

3.3.Temperature dependence of elastic properties

In order to investigate the temperature dependence of the elastic properties of the cubic phases in the present study(Nb and Nb3Sn),the quasi-static approximation was implemented.First the temperature dependence of the volume was calculated,as discussed in Section 2.4. The volume vs.temperature curves of Nb and Nb3Sn are shown in Fig.4.The linear thermal expansion coe?cients at293K of Nb and Nb3Sn were calculated using this data and were respectively$7.9?10à6and$6.4?10à6Kà1,in good agreement with the literature[45,46].In Fig.5the elastic constants vs.temperature of the cubic phases are https://www.360docs.net/doc/f818373465.html,paring the results for Nb with the literature [47]it can be seen that overall the agreement is very good (Table5).The C44constant of Nb becomes negative at 2750K,which coincides with its melting point.Moreover C44decreased slower than the other independent constants, and C11decreased the fastest.The results for Nb3Sn were also in good agreement with the experimental data[48]. The curves of the C12and C44constants had similar slopes, with the latter decreasing slightly slower than the former, while the curve of C11showed the steepest descent of all three independent elastic constants.The largest discrepancy at300K was noticed for the C44coe?cient with the results of the current study and the literature being$51and $40GPa,respectively.

After obtaining the elastic constants of both phases,the bulk,shear and elastic moduli were computed with the VRH approximation(Fig.6).All the moduli decreased with increasing temperature.The bulk and elastic moduli of the Nb and Nb3Sn exhibited similar gradients and the shear modulus decreased more slowly.The bulk modulus curve of the Nb3Sn crosses the Young’s modulus curve at 2600K where the former becomes higher.Furthermore, owing to the above behavior of the bulk and shear moduli of both phases,the Poisson’s ratio showed an increasing slope(Fig.7).In the case of Nb,v increased to$0.47close to the melting point,starting from$0.39(see Table3)at 0K.For Nb3Sn,onthe other hand,the total increase was smaller,from$0.328at0K(Table3)to$0.335at the compound’s melting point.In addition,it must be noted that the curve increases more slowly until$2200K,above which it rises signi?cantly.

3.4.Debye temperatures

The phonon DOS was used to calculate the Debye tem-peratures.It should be noted that it is considered more dif-?cult to obtain accurate values using phonon DOS rather than the elastic constants(see Section3.3),because as a low-temperature property the Debye temperature is deter-mined by low-energy phonons,i.e.the acoustic phonons. The lower the temperature,the smaller the part that the Brillouin zone contributes to thermodynamics.The values calculated using the phonon DOS(Table3)were in very good agreement with Refs.[18,21]and those calculated from the elastic constant values.For the elemental and intermetallic phases,both the results for the Debye temper-atures calculated from the phonon DOS and the elastic constants were in excellent agreement with the available data in the literature(Table3).

4.Conclusions

First-principles calculations were carried out for the intermetallic compounds Nb3Sn,Nb6Sn5and NbSn2and for the elements Nb and Sn.The elastic constants,bulk, shear and Young’s moduli,Poisson’s ratio and Debye tem-peratures were calculated for all the phases and were in good agreement with the available data in the literature. It is concluded that of all the Nb–Sn intermetallic com-pounds,Nb6Sn5is the least brittle.The elastic properties and Debye temperature of the Nb6Sn5and NbSn2interme-tallics were reported for the?rst time.Furthermore,the enthalpies of formation vs.temperature were calculated for all the intermetallic https://www.360docs.net/doc/f818373465.html,bining the quasi-harmonic with the quasi-static approximation,the temper-ature dependence of the bulk,shear and elastic moduli and Poisson’s ratios of Nb and Nb3Sn were calculated and were in good agreement with the available data in the literature. The thermal expansion coe?cients of Nb and Nb3Sn were also obtained.

Acknowledgements

The support of this work by the FP-7Accelerated Metallurgy project and the EPSRC–Rolls Royce research partnership,and useful discussion with Dr A.Scott,are gratefully acknowledged. References

[1]B.P.Bewlay,M.R.Jackson,M.F.X.Gigliotti,in:R.L.

Fleischer,J.H.Westbrook(Eds.),Intermetallic Compounds: Principles and Practice,vol.3,John Wiley,New York,2001, p.541.

[2]P.Tsakiropoulos,Beyond nickel based superalloys,in:R.

Blockley,W.Shyy(Eds.),Encyclopedia of Aerospace Engi-neering,John Wiley,New York,2010,p.2345.

[3]J.Geng,P.Tsakiropoulos,G.Shao,Mater.Sci.Eng.A441

(2006)26.

[4]K.Zelenitsas,P.Tsakiropoulos,Mater.Sci.Eng.A416

(2006)269.

[5]J.Geng,P.Tsakiropoulos,G.Shao,Intermetallics15(2007)

69.

[6]J.Geng,P.Tsakiropoulos,G.Shao,Intermetallics15(2007)

270.

[7]N.Vellios,P.Tsakiropoulos,Intermetallics15(2007)1518.

[8]N.Vellios,P.Tsakiropoulos,Intermetallics18(2010)1729.

[9]C.To?olon,C.Servant,J.C.Gachon,B.Sundman,J.Phase

Equil.23(2002)134.

[10]A.K.Sinha,Prog.Mater.Sci.15(1972)79.

[11]D.Dew-Hughes,Cryogenics15(1975)435.

[12]J.P.Charlesworth,Phys.Lett.21(1966)501.

[13]Z.Fisk,G.W.Webb,Phys.Rev.Lett.36(1976)1084.

[14]G.W.Webb,Z.Fisk,J.J.Engelhardt,S.D.Bader,Phys.Rev.

B15(1977)2624.

[15]B.M.Klein,L.L.Boyer,D.A.Papaconstantopoulos,Phys.

Rev.Lett.42(1979)530.

[16]W.Rehwald,M.Rayl,R.W.Cohen,G.D.Cody,Phys.Rev.

B6(1972)363.

[17]G.S.Knapp,S.D.Bader,Z.Fisk,Phys.Rev.B13(1976)

3783.

[18]M.Sundareswari,S.Ramasubramanian,M.Rajagopalan,

Solid State Commun.150(2010)2057.

32I.Papadimitriou et al./Acta Materialia86(2015)23–33

[19]P.Soderlind,O.Eriksson,J.M.Wills,A.M.Boring,Phys.

Rev.B48(1993)5844.

[20]J.Moon,K.Cho,M.Cho,Int.J.Precis.Eng.Manuf.13

(2012)1191.

[21]C.Kittel,Introduction to Solid State Physics,eigth ed.,John

Wiley,New York,2005,p.116.

[22]J.A.Rayne,B.S.Chandrasekhar,Phys.Rev.120(1960)1658.

[23]S.J.Clark,M.D.Segall, C.J.Pickard,P.J.Hasnip,M.J.

Probert,K.Refson,M.C.Payne,Z.Kristall.220(2005)567.

[24]W.Kohn,L.J.Sham,Phys.Rev.140(1965)A1133.

[25]M.C.Payne,M.P.Teter, D.C.Allan,T.A.Arias,J.D.

Joannopoulos,Rev.Mod.Phys.64(1992)1045.

[26]J.P.Perdew,J.A.Chevary,S.H.Vosko,K.A.Jackson,M.R.

Pederson,D.J.Singh,C.Fiolhais,Phys.Rev.B46(1992) 6671.

[27]J.S.Lin,A.Qteish,M.C.Payne,V.Heine,Phys.Rev.B47

(1993)4174.

[28]H.J.Monkhorst,J.D.Pack,Phys.Rev.B13(1976)5188.

[29]B.G.Pfrommer,M.Cote,S.G.Louie,M.L.Cohen,J.

Comput.Phys.131(1997)233.

[30]M.Born,J.Phys.Chem.Solids7(1939)591.

[31]R.Hill,Proc.Phys.Soc.Lond.Sect.A65(1952)349.

[32]A.Z.Reuss,Angew.Math.Mech.9(1929)49.

[33]O.L.Anderson,J.Phys.Chem.Solids24(1963)909.

[34]F.Birch,Phys.Rev.71(1947)809.

[35]Y.Wang,C.Woodward,S.H.Zhou,Z.K.Liu,L.Q.Chen,

Scr.Mater.52(2005)17.

[36]S.Baroni,S.de Gironcoli,A.Dal Corso,P.Giannozzi,Rev.

Mod.Phys.73(2001)515.

[37]S.De Gironcoli,Phys.Rev.B51(1995)6773.[38]S.L.Shang,H.Zhang,Y.Wang,Z.K.Liu,J.Phys.Condens.

Matter.22(2010)375403.

[39]Y.Wang,J.J.Wang,H.Zhang,V.R.Manga,S.L.Shang,

L.Q.Chen,Z.K.Liu,J.Phys.Condens.Matter.22(2010) 225404.

[40]O.Gulseren,R.E.Cohen,Phys.Rev.B65(2002)064103.

[41]D.G.Pettifor,Mater.Sci.Technol.8(1992)345.

[42]F.deBoer,R.Boom,W.C.Mattens, A.R.Miedema,

A.K.Niessen,Cohesion in Metals,Transition Metal Alloys.

Amsterdam:North Holland,1988.

[43]A.R.Miedema,P.F.Dechatel,F.R.Deboer,Phys.B&C100

(1980)1.

[44]R.A.Schi?man,D.M.Bailey,High Temp.Sci.15(1982)165.

[45]R.Grill,A.Gnadenberger,Int.J.Refract.Metal Hard Mater.

24(2006)275.

[46]D.P.Boso,M.Le?k,B.A.Schre?er,Cryogenics46(2006)

569.

[47]R.J.Wasilewski,J.Phys.Chem.Solids26(1965)1643.

[48]K.R.Keller,J.J.Hanak,Phys.Lett.21(1966)263.

[49]C.Paduani,Braz.J.Phys.37(2007)1073.

[50]J.R.Ogren,T.G.Ellis,J.F.Smith,Acta Crystallogr.A18

(1965)968.

[51]T.Wo¨lpl,W.Jeitschko,J.Alloy Compd.210(1994)185.

[52]C.J.Smithells,Metal References Book,?fth ed.,Butterworth,

London,1976,p.975.

[53]F.Chu,M.Lei,S.A.Maloy,J.J.Petrovic,T.E.Mitchell,Acta

Mater.44(1996)3035.

[54]A.M.James,M.P.Lord,Macmillan’s Chemical and Physical

Data,Macmillan,London,1992.

[55]S.F.Pugh,Phil.Mag.45(1954)823.

I.Papadimitriou et al./Acta Materialia86(2015)23–3333