第2章拉压作业参考解答
材料力学习题册答案-第2章-拉压

一、 选择题
1.图 1 所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将(
A.平动
B.转动
C.不动
D.平动加转动
D)
2.轴向拉伸细长杆件如图 2 所示,则正确的说法是 ( C )
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布,2-2 面上应力均匀分布 D.1-1 面上应力均匀分布,2-2 面上应力非均匀分布
30KN 1
300mm
l1 解:(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
(2)
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示,试作图表示节点 C 的垂直位移,设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段:σ3= =
Pa=25MPa
2.图为变截面圆钢杆 ABCD,已知 =20KN, = =35KN, = =300mm, =400mm,
D
3
C
P3
2
,绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解:
-
50KN
l2 15KN
l1
20KN
+
AB 段:σ1=
=
=176.9MPa
BC 段:σ2=
反力均匀分布,圆柱承受轴向压力 P,则基座剪切面的剪力
。ห้องสมุดไป่ตู้
第02章拉压题解
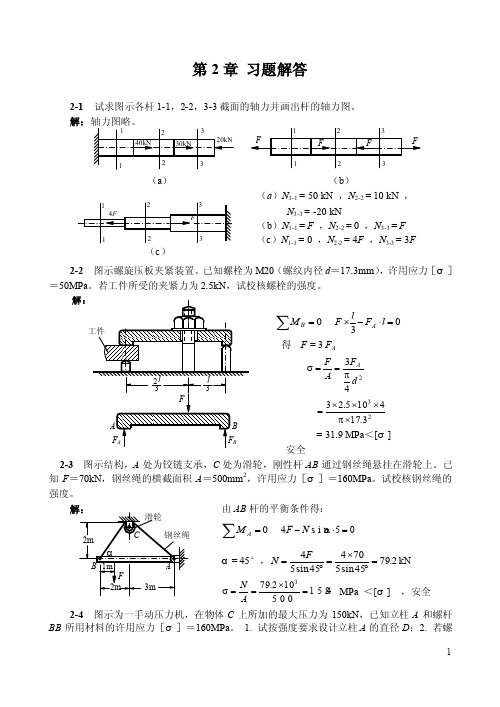
第2章 习题解答2-1 试求图示各杆1-1,2-2,3-3截面的轴力并画出杆的轴力图。
解:(a )N 1-1 = 50 kN ,N 2-2 = 10 kN ,N 3-3 = -20 kN(b )N 1-1 = F ,N 2-2 = 0 ,N 3-3 = F(c )N 1-1 = 0 ,N 2-2 = 4F ,N 3-3 = 3F2-2 图示螺旋压板夹紧装置。
已知螺栓为M20(螺纹内径d =17.3mm ),许用应力[ζ]=50MPa 。
若工件所受的夹紧力为2.5kN ,试校核螺栓的强度。
∑=0BM03=⋅-⨯l F lF A得F = 3 F A243dF A F Aπ==σ233.174105.23⨯π⨯⨯⨯== 31.9 MPa <[ζ]安全2-3 图示结构,A 处为铰链支承,C 处为滑轮,刚性杆AB 通过钢丝绳悬挂在滑轮上。
已知F =70kN ,钢丝绳的横截面积A =500mm 2,许用应力[ζ]=160MPa 。
试校核钢丝绳的强度。
由AB 杆的平衡条件得:∑=0A M 05s i n 4=⋅α-N F α= 45°,2.7945sin 570445sin 54=︒⨯=︒=F N kN4.158500102.793=⨯==σA N MPa <[ζ] ,安全 2-4 图示为一手动压力机,在物体C 上所加的最大压力为150kN ,已知立柱A 和螺杆BB 所用材料的许用应力[ζ]=160MPa 。
1. 试按强度要求设计立柱A 的直径D ;2. 若螺(a )(b )杆BB 的内径d =40mm ,试校核其强度。
解:由平衡条件得 752150==A N kN 1. 由立柱的强度条件 24DN A N AA A π==σ≤[ζ] 得 D ≥4.2416010754][43=⨯π⨯⨯=πζA N mm2. 螺杆的应力1194010150423=⨯π⨯⨯==σBB BB A N MPa <[ζ] 螺杆强度足够。
[拉压、扭转作业解答

材料力学习题详解第二章拉伸、压缩与剪切题图(a)所示结构中,若钢拉杆BC的横截面直径为10mm,试求拉杆内应力。
设BC连接的1和2两部分均为刚体。
解:首先根据刚体系的平衡条件,求出BC杆的内力。
刚体1受力图如题图(b)所示,平衡条件为DM=∑, 1.5 4.530N AF F F⨯+⨯-⨯=①刚体2受力图如题图(c)所示,平衡条件为EM=∑, 1.50.750A NF F⨯-⨯=②解①、②式得BC杆的内力为6NF kN=故拉杆BC杆内的应力为()32361076.410104NFPa MPaAσπ-⨯===⨯⨯题图(a)所示结构中,1、2两杆的横截面直径分别为10mm和20mm。
试求两杆内的应力。
设两根横梁皆为刚体。
解:先求1、2杆的轴向内力,选取AB 杆为受力体,其受力图如题图(b)所示,由平衡条件有0yF=∑, 10NA NC F F += ①0AM=∑, 10210NC F ⨯-⨯= ②解①、②式,得 10NA F kN =, 20NC F kN = 故1、2杆内的应力分别为()3123101012710104Pa MPa σπ-⨯==⨯⨯()3223201063.720104Pa MPa σπ-⨯==⨯⨯如题图所示,直径为10mm 的圆杆,在拉应力F =10kN 的作用下,试求最大切应力,并求与木杆的横截面夹角为30α=︒的斜截面上正应力及切应力。
解:受轴向载荷杆,斜截面上的应力公式为2cos N F A ασα=, sin 22N FAατα=当45α=︒时,杆内切应力达到最大值,所以3max21010sin 2sin 9063.72220.014N F F Pa MPa A A ταπ⨯==︒==⨯在与木杆的横截面夹角为30︒的斜截面上,正应力及切应力分别为3230210103cos3095.50.0144FPa MPaAσπ︒⎛⎫⨯=︒=⨯=⎪⨯⎝⎭()330210103sin23055.120.014FPa MPaAτπ︒⎛⎫⨯=⨯︒=⨯=⎪⎪⨯⎝⎭题图(a)所示的双杠杆夹紧机构,需产生一对20kN的夹紧力,试求水平连杆AB 及二斜连杆BC和BD的横截面直径。
第2章拉压作业参考解答

aEADj + 4.5aEADj = 2aF , Dj = 2F 5.5EA
4. 再由 Hooke 定律:
FN1
=
EADj
=
2F 5.5
=
0.3636F
FN 2
= 1.5EADj
=
1.5´ 2F 5.5
2
(1)图(a)为开槽拉杆,两端受力 F=14kN,b=20mm,b0=10mm,δ=4mm。 (2)图(b)为阶梯形杆,AB 段杆横截面面积为 80mm2,BC 段杆横截面面积为 20mm2, CD 段杆横截面面积为 120mm2。 (3)图(c)为变截面拉杆,上段 AB 的横截面面积为 40mm2,下段 BC 的横截面面积为
DG
=
Dl2
-
2 3
Dl1
-
1 3
Dl3=6.89 ´10-4
m
5
2-15 求附图示圆锥形杆在轴向力 F 作用下的伸长量。弹性模量为 E。
解答 对于截面缓变的圆锥形杆可假设横截面上正应力均匀分布。横截面面积为
A(x)
=
1 4
p [d1l
-
(d1
-
d2 )x]2
/l2
ò ò ò Dl =
l
edx =
FN1
FN3
FN2
D
(2)
(b) 整体分析,示力图见附图(3)。
å M Ai = 0 : FN1 ´1 + 3´ 3´1.5 = 0
FN1 = -13.5kN
FAx A
FAy FN1
B
s1
=
FN 1 A1
=
-13.5 ´103 850 ´10-6
=
-15.88MPa
第二章拉压(1)
B
x
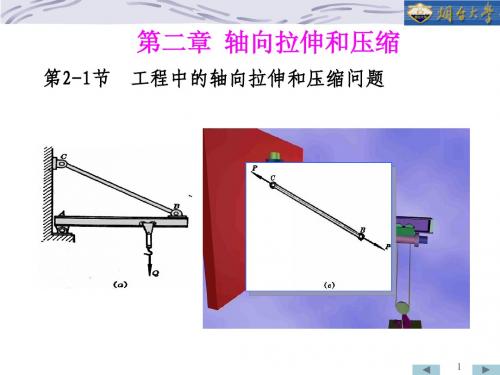
李禄昌 例2-2 求图示杆各截面上的轴力
解:
N 1 = 10 kN
A
B
C
D
N 2 = 10 − 15 = −5kN
N 3 = −20 kN
N 注意确定控制面。 注意确定控制面。
10KN ㈩
x
5KN ㈠ 20KN
8
李禄昌
5、绘制轴力图的方法与步骤如下: 、绘制轴力图的方法与步骤如下: ⑴、确定作用在杆件上的外载荷与约束力; 确定作用在杆件上的外载荷与约束力; ⑵、根据杆件上作用的载荷以及约束力,确定控制 根据杆件上作用的载荷以及约束力,确定控制 确定轴力图的分段点: 轴力图的分段点 面,确定轴力图的分段点:在有集中力作用处即为 轴力图的分段点; 轴力图的分段点; 应用截面法, 用假想截面从控制面之间 从控制面之间将杆 ⑶ 、 应用截面法 , 用假想截面 从控制面之间 将杆 件截开, 在截开的截面上, 画出未知轴力, 并假设 件截开 , 在截开的截面上 , 画出未知轴力, 为正方向; 对截开的部分杆件建立平衡方程, 为正方向 ; 对截开的部分杆件建立平衡方程 , 确定 轴力的大小与正负 ; 坐标系, ⑷、建立FN-x坐标系,将所求得的轴力值标在坐 标系中,画出轴力图。 标系中,画出轴力图。
问题:直杆上作用有 个载荷 而且AB段与 个载荷, 段与BC段杆横截面面积 问题:直杆上作用有4个载荷,而且 段与 段杆横截面面积 不相等,材料不同。各段杆的横截面上的轴力如何分布?哪个横 不相等,材料不同。各段杆的横截面上的轴力如何分布? 截面上的正应力最大?哪个横截面上承载能力最差、最危险? 截面上的正应力最大?哪个横截面上承载能力最差、最危险?
6
李禄昌 设一杆轴线同时受力P 的作用, 例2-1 设一杆轴线同时受力 1 , P2 , P3 的作用,其作用点分别为 A、C、B , 求杆的轴力画轴力图。 求杆的轴力画轴力图。 P2=3kN 只计算内力时, 只计算内力时,不 P1=2kN P3=1kN 设正法与绘内力图 考虑面积影响, 实际集中力并非 考虑面积影响,故 A B 有机结合起来。 有机结合起来。 C 集中在一点处。 用等直杆件。 集中在一点处 用等直杆件。 。
材料力学第二章 轴 向拉压习题及答案

第二章轴向拉压一、选择题1.图1所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将( D)A.平动B.转动C.不动D.平动加转动2.轴向拉伸细长杆件如图2所示,其中1-1面靠近集中力作用的左端面,则正确的说法应是( C)A.1-1、2-2面上应力皆均匀分布B.1-1、2-2面上应力皆非均匀分布C.1-1面上应力非均匀分布,2-2面上应力均匀分布D.1-1面上应力均匀分布,2-2面上应力非均匀分布(图1)(图2)3.有A、B、C三种材料,其拉伸应力—应变实验曲线如图3所示,曲线( B)材料的弹性模量E大,曲线( A )材料的强度高,曲线( C)材料的塑性好。
4.材料经过冷作硬化后,其( D)。
A.弹性模量提高,塑性降低B.弹性模量降低,塑性提高C.比例极限提高,塑性提高D.比例极限提高,塑性降低5.现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图4所示结构中两种合理选择方案是( A)。
A.1杆为钢,2杆为铸铁B.1杆为铸铁,2杆为钢C.2杆均为钢D.2杆均为铸铁(图3)(图4)(图5)6.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的是(B)。
A. 弹性阶段;B.屈服阶段;C.强化阶段;D.局部变形阶段。
7.铸铁试件压缩破坏(B)。
A. 断口与轴线垂直;B. 断口为与轴线大致呈450~550倾角的斜面;C. 断口呈螺旋面;D. 以上皆有可能。
8.为使材料有一定的强度储备,安全系数取值应( A )。
A .大于1; B. 等于1; C.小于1; D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向,过截面形心C 方向相对,作用线与杆轴线重合D 方向相对,沿同一直线作用10. 图6所示一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N 1,N 2和N 3,三者的关系为( B )。
《材料力学》第2章轴向拉(压)变形习题解答

其方向。 解:斜截面上的正应力与切应力的公式为:
ασσα20cos = αστα2sin 2 = 式中,MPa mm N A N 1001001000020===σ,把α的数值代入以上二式得:
[习题 2-7] 一根等直杆受力如图所示。已知杆的横截面面积 A 和材料的弹性模量 E 。试作轴力图,并求杆端点 D 的位移。 解: (1)作轴力图
[习题 2-9] 一根直径 mm d 16=、长 m l 3=的圆截面杆,承受轴 向拉力 kN F 30=,其伸长为 mm l 2.2=?。试求杆横截面上的应 力与材料的弹性模量 E 。 解:(1)求杆件横截面上的应力 MPa mm N A N 3.1491614.34 110302 23=???==σ (2)求弹性模量 因为:EA Nl l = ?, 所以:GPa MPa l l l A l N E 6.203)(9.2035902 .23000 3.149==?=??=???=σ。 [习题 2-10] (1)试证明受轴向拉伸(压缩)的圆截面杆横截 面沿圆周方向的线应变 s ε等于直径方向的线应变 d ε。 (2)一根直径为 mm d 10=的圆截面杆,在轴向力 F 作用下,直 径减小了 0.0025mm 。如材料 的弹性模量 GPa E 210=,泊松比 3.0=ν,试求该轴向拉力 F 。 (3)空心圆截面杆,外直径 mm D 120=,内直径 mm d 60=,材 料的泊松比 3.0=ν。当其轴向拉伸时,已知纵向线应变 001.0=, 试求其变形后的壁厚。 解:(1)证明 d s εε= 在圆形截面上取一点 A ,连结圆心 O 与 A 点,则 OA 即代表直 径方向。过 A 点作一条直线 AC 垂直于 OA ,则 AC 方向代表圆周方向。νεεε-==AC s(泊
《材料力学》第2章 轴向拉压变形 习题解

第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a )解:(1)求指定截面上的轴力 FN =-11FF F N -=+-=-222(2)作轴力图轴力图如图所示。
(b )解:(1)求指定截面上的轴力 FN 211=-2222=+-=-F F N (2)作轴力图FF F F N =+-=-2233 轴力图如图所示。
(c )解:(1)求指定截面上的轴力 FN 211=-FF F N =+-=-222(2)作轴力图FF F F N 32233=+-=- 轴力图如图所示。
(d )解:(1)求指定截面上的轴力 FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-(2)作轴力图 中间段的轴力方程为: x aFF x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
2400mm A =解:(1)求指定截面上的轴力kNN 2011-=- )(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力MPa mm N A N 504001*********-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
21200mm A =22300mm A =23400mm A =解:(1)求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章作业参考解答2-1 试绘出附图中各杆的轴力图。
习题2-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)、(e)、(f)。
2-2 附图a,b 为拉压杆的轴力图,试分别作出各杆的受力图。
习题2-2附图解答 各杆受力见解答附图(a)、(b)。
(a) F N /kN2F/3 F/3(b) F N(c) F N(d) F N(e) F N2FF (f) F N(a)(b)40kNF N210kN/mF Cx F CyC (1) D2-3 求附图所示结构中指定杆内的应力。
已知(a )图中杆的横截面面积A 1=A 2=1150mm 2,(b )图中杆的横截面面积A 1=850mm 2,A 2=600mm 2,A 3=500mm 2。
习题2-3附图解答 (a )根据对称性可知支座的约束反力为40kN ,取附图(1)脱离体。
021044402.2 :02=´´+´-=åN CiF M解得kN F N 36.362=。
MPa A F N 62.311011501036.3663222=´´==-s取铰D 分析,示力图见附图(2)。
å=0ix F :012/22212=+´-N N F FkN F F N N 65.402/521=´=MPa A F N 3.351011501065.4063111=´´==-s (b ) 整体分析,示力图见附图(3)。
05.1331 :01=´´+´=åN Ai F MkN F N 5.131-=MPa A F N 88.1510850105.1363111-=´´-==-s 分析铰B ,示力图见附图(4)。
02/ :013=-=åN N ixF F F,kN F N 09.193-=MPa A F N 18.38105001009.1963333-=´´-==-skN F F F FN N N iy5.13 ,02/ :0232==+=åMPa A F N 5.2210600105.1363122=´´==-s2-4 求附图所示各杆内的最大正应力。
F (2)AB F N1F AxF Ay(3)(4)(1)图(a )为开槽拉杆,两端受力F =14kN ,b =20mm ,b 0=10mm ,δ=4mm 。
(2)图(b )为阶梯形杆,AB 段杆横截面面积为80mm 2,BC 段杆横截面面积为20mm 2,CD 段杆横截面面积为120mm 2。
(3)图(c )为变截面拉杆,上段AB 的横截面面积为40mm 2,下段BC 的横截面面积为30mm 2,杆材料重度g r =78kN/m 3。
习题2-4附图解答 (1)最大正应力出现在杆件的开槽段。
MPa A F N 0.350104)1020(101463=´´-´==-s (2)分段计算正应力,最后确定最大正应力。
MPa AB0.100108010863=´´=-s ,MPa BC 0.9501020101963=´´=-s MPa CD67.161012010263=´´=-s ,故最大正应力为950.0MPa. (3)首先计算最大轴力。
BC 段最大轴力kN F N 00117.127810305.0126max 1=´´´+=-AB 段最大轴力在A 处,kN F AN 00273.127810)405.0305.0(126=´´´+´+=-MPa BC 04.40010301000117.1263max=´´=-s ,MPa AB 07.30010401000273.1263max =´´=--s 可得杆件最大正应力为400.04MPa ,发生在B 截面。
F RE(1)习题2-6附图F RE习题2-10附图2-6 求附图所示铰接构架中,直径为20mm 的圆拉杆CD 中的正应力。
解答 首先整体分析求E 处约束力。
055354 :0=´-´-=åRE Ai F M解得kN F RE 10=。
分析BE ,示力图见附图(1)。
038.04 :0=´-=åDC RE BiF F M解得kN F DC 667.16= MPa DC 05.53102014.310667.1662413=´´´´=-s2-7 一直径为15mm ,标距为200mm 的圆合金钢杆,在比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加到58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,试确定材料的弹性模量E 、泊松比ν和比例极限σp 。
解答 MPa A F N P 48.3301015104.5862413=´´´==-p s 3105.42009.0-´==D =l l e ,MPa E 3361044.73105.41048.330´=´´==-e s 310467.115022.0-´-=-=D =¢l l e ,326.0105.410467.1||33=´´=¢=--e e u2-10 附图所示短柱由两种材料制成,上段为钢材,长200mm ,截面尺寸为100mm×100mm ;下段为铝材,长300mm ,截面尺寸为200mm×200mm ,当柱顶受力F 作用时,柱子总长度减少了0.4mm ,试求F 值。
已知E 钢=200GPa ,E 铝=70GPa 。
解答 柱中的轴力均为F ,总的变形(缩短)为213.02.0A E FA E F l 铝钢+=D ,即 kN AE A E lF 0.19312.02.010703.01.01.0102002.0104.03.02.099321=´´´+´´´´=úûùêëé+D =-铝钢2-11 附图示等直杆AC ,材料的重度为g r ,弹性模量为E ,横截面面积为A 。
求直杆B 截面的位移ΔB 。
解答 AB 段内轴力为gAx F F N r --=1 BC 段内轴力为gAx F F N r --=22 B 点位移为杆BC 的变形量: EAgAl Fl EA dx gAx F llB 225.12)2(r r D +-=+-=ò2-12 附图所示受力结构中,ABC 杆可视为刚性杆,BD 杆的横截面面积A =400mm 2,材料弹性模量E =2.0×105MPa 。
求C 点的竖直位移ΔCy 。
解答 求BD 杆的轴力,示力图见附图。
:0=åAiM02145sin 0=-´D FkN F D 22= BD 杆的伸长量m l 56113100.510400100.221022--´=´´´´´=D C 点的竖直位移为m l B C y y 410414.1222-´=D =D =D2-14 附图示结构中,AB 可视为刚性杆。
AD 为钢杆,横截面面积A 1=500mm 2,弹性模量E 1=200GPa ;CG 为铜杆,横截面面积A 2=1500mm 2,弹性模量E 2=100GPa ;BE 为木杆,横截面面积A 3=3000mm 2,弹性模量E 3=10GPa 。
当G 点处作用有F =60kN 时,求该点的竖直位移ΔG 。
解答 1.求各杆轴力,由平衡方程可以求出kNF F kNF F kN F F NCG NBE NAD 6020,4012==-==-==2.求各杆的变形(缩短)m A E l F l AD NAD 4693111104105001020011040--´-=´´´´´-==D (伸长)m A E l F l CG NCG 4693222102101500101005.01060--´=´´´´´==D (缩短)m A E l F l BE NBE 46933331067.6103000101011020--´-=´´´´´-==D 3.由几何关系求G 点竖直位移ΔGm l l l G 43121089.63132-´D -D -D =D =习题2-11附图习题2-12附图F DF yC 习题2-14附图2-15 求附图示圆锥形杆在轴向力F 作用下的伸长量。
弹性模量为E 。
解答 对于截面缓变的圆锥形杆可假设横截面上正应力均匀分布。
横截面面积为 2221141/])([)(l x d d l d x A --=p212120221120044 ])([4)(d d E Fl l d d E Fl x d d l d dxE Fl x EA Fdx dx l lllp p pe ==--===D òòò2-16 附图示水塔结构,水和塔共重W =400kN ,同时还受侧向水平风力F =100kN 作用。
若支杆①、②和③的容许压应力[σc ]=100MPa ,容许拉应力[σt ]=140MPa ,试求每根支杆所需要的面积。
解答 分析水箱,示力图见附图(1).:0å=ixF kN F N 4.14121002-=-=:0å=AiMkN F N 250)100400(213-=+-=:0å=iyFkN F N 501002504001-=++-=由强度条件设计截面 236311105.0101001050|][|m F A c N -´=´´=³s 23632210414.110100104.141|][|m F A c N -´=´´=³s 236333105.21010010250|][|m F A c N -´=´´=³s 2-18 附图所示结构中的CD 杆为刚性杆。
