C++实现PID控制算法-b46fc4db50e2524de5187e77
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现(完整版) 在现代工业生产中,为了实现对生产过程的精确控制,我们需要采用一种能够根据实际需求自动调整参数的控制算法。
PID(Proportional-Integral-Derivative)控制算法就是这样一种广泛应用于工业控制系统的算法。
本文将详细介绍PID控制算法的C语言实现,包括算法的基本原理、实现方法以及注意事项。
我们来了解一下PID控制算法的基本原理。
PID控制器由三个部分组成:比例(P)、积分(I)和微分(D)。
这三个部分分别对误差信号进行处理,然后将处理后的信号相加得到控制输出。
具体来说,比例部分根据误差信号的大小产生相应的控制作用;积分部分对误差信号进行累积,以消除系统的静差;微分部分对误差信号的变化趋势进行预测,以便及时调整控制策略。
通过这三个部分的综合作用,PID控制器能够实现对生产过程的精确控制。
接下来,我们来看一下如何用C语言实现PID控制算法。
我们需要定义一些变量来存储所需的参数和状态信息。
例如,我们需要定义比例系数Kp、积分系数Ki、微分系数Kd以及误差信号e等。
我们还需要定义一些变量来存储上一次的误差信号和积分项等。
这些变量的定义如下:```cdouble Kp, Ki, Kd; // 比例、积分、微分系数double e; // 当前误差信号double de; // 当前误差信号的导数double last_e; // 上一次的误差信号double integral; // 积分项有了这些变量之后,我们就可以开始实现PID控制器的计算过程了。
PID控制器的计算过程主要包括以下几个步骤:1. 计算误差信号:当前误差信号等于期望值与实际值之差。
2. 计算比例项:比例项等于当前误差信号乘以比例系数Kp;3. 计算积分项:积分项等于当前误差信号乘以积分系数Ki加上累积误差信号乘以积分系数Ki;4. 计算微分项:微分项等于当前误差信号的导数乘以微分系数Kd;5. 计算控制输出:控制输出等于比例项、积分项和微分项之和。
C语言实现PID算法

C语言实现PID算法#include <stdio.h>struct _pid {int pv; /*integer that contains the process value*/int sp; /*integer that contains the set point*/float integral;float pgain;float igain;float dgain;int deadband;int last_error;};struct _pid warm,*pid;int process_point, set_point,dead_band;float p_gain, i_gain, d_gain, integral_val,new_integ;;/*------------------------------------------------------------------------pid_initDESCRIPTION This function initializes the pointers in the _pid structure to the process variable and the setpoint. *pv and *sp areinteger pointers.------------------------------------------------------------------------*/void pid_init(struct _pid *warm, int process_point, int set_point){struct _pid *pid;pid = warm;pid->pv = process_point;pid->sp = set_point;}/*------------------------------------------------------------------------pid_tuneDESCRIPTION Sets the proportional gain (p_gain), integral gain (i_gain), derivitive gain (d_gain), and the dead band (dead_band) ofa pid control structure _pid.------------------------------------------------------------------------*/void pid_tune(struct _pid *pid, float p_gain, float i_gain, float d_gain, int dead_band) {pid->pgain = p_gain;pid->igain = i_gain;pid->dgain = d_gain;pid->deadband = dead_band;pid->integral= integral_val;pid->last_error=0;}/*------------------------------------------------------------------------pid_setintegDESCRIPTION Set a new value for the integral term of the pid equation.This is useful for setting the initial output of thepid controller at start up.------------------------------------------------------------------------*/void pid_setinteg(struct _pid *pid,float new_integ){pid->integral = new_integ;pid->last_error = 0;}/*------------------------------------------------------------------------pid_bumplessDESCRIPTION Bumpless transfer algorithim. When suddenly changing setpoints, or when restarting the PID equation after anextended pause, the derivative of the equation can causea bump in the controller output. This function will helpsmooth out that bump. The process value in *pv shouldbe the updated just before this function is used.------------------------------------------------------------------------*/void pid_bumpless(struct _pid *pid){pid->last_error = (pid->sp)-(pid->pv);}/*------------------------------------------------------------------------pid_calcDESCRIPTION Performs PID calculations for the _pid structure *a. This function uses the positio nal form of the pid equation, and incorporates an integral windup prevention algorithim. Rectangu lar integration is used, so this function must be repeated on a consistent time basis for accurate con trol.RETURN V ALUE The new output value for the pid loop.USAGE #include "control.h"*/float pid_calc(struct _pid *pid){int err;float pterm, dterm, result, ferror;err = (pid->sp) - (pid->pv);if (abs(err) > pid->deadband){ferror = (float) err; /*do integer to float conversion only once*/pterm = pid->pgain * ferror;if (pterm > 100 || pterm < -100){pid->integral = 0.0;}else{pid->integral += pid->igain * ferror;if (pid->integral > 100.0){pid->integral = 100.0;}else if (pid->integral < 0.0) pid->integral = 0.0;}dterm = ((float)(err - pid->last_error)) * pid->dgain;result = pterm + pid->integral + dterm;}else result = pid->integral;pid->last_error = err;return (result);}void main(void)float display_value;int count=0;pid = &warm;// printf("Enter the values of Process point, Set point, P gain, I gain, D gain \n");// scanf("%d%d%f%f%f", &process_point, &set_point, &p_gain, &i_gain, &d_gain);process_point = 30;set_point = 40;p_gain = (float)(5.2);i_gain = (float)(0.77);d_gain = (float)(0.18);dead_band = 2;integral_val =(float)(0.01);printf("The values of Process point, Set point, P gain, I gain, D gain \n");printf(" %6d %6d %4f %4f %4f\n", process_point, set_point, p_gain, i_gain, d_gain); printf("Enter the values of Process point\n");while(count<=20){scanf("%d",&process_point);pid_init(&warm, process_point, set_point);pid_tune(&warm, p_gain,i_gain,d_gain,dead_band);pid_setinteg(&warm,0.0); //pid_setinteg(&warm,30.0);//Get input value for process pointpid_bumpless(&warm);// how to display outputdisplay_value = pid_calc(&warm);printf("%f\n", display_value);//printf("\n%f%f%f%f",warm.pv,warm.sp,warm.igain,warm.dgain);count++;}}PID算法/******************************************************************** *********************************** PID控制算法 PID Control Algorithm* 在仿真和实验中,航向预估控制方法和与之对比的常规控制方法的控制器均采用增量PID算法,* 且两者的比例、积分和微分系数一样.增量PID算法如式(7)所示:* ΔU = U(k)-U(k-1) =Kp*[e(k)-e(k-1)]+Ki*e(k)+Kd*[e(k)-2*e(k-1)+e(k-2)]* 其中:Kp、Ki、Kd分别为比例、积分和微分放大系数,u(k)表示第k个采样时刻的控制量,e(k)表示第k个采样时刻的航向输入偏差.********************************************************************* **********************************/void PID_Calc(int PID_EK){long deltaU,tmp;deltaU = (long)u_dbPIDKp.IntData*(PID_EK-PID_EK_1); // 增量计算deltaU +=(long)u_dbPIDKi.IntData*PID_EK;tmp = (long)PID_EK-(2*PID_EK_1)+PID_EK_2;deltaU +=tmp* u_dbPIDKd.IntData;PID_UK = PID_UK_1+deltaU; // 结果if(PID_UK>4095000) PID_UK = 4095000;else if(PID_UK<0) PID_UK=0;PID_UK_1 = PID_UK; // 保存新的K-1次输出值PID_EK_2 = PID_EK_1; // 保存新的K-1次输入值PID_EK_1 = PID_EK;}PID是比例,积分,微分的缩写,Uo(N)=P*E(N)+I*[E(N)+E(N-1)+...+E(0)]+D*[E(N)-E(N-1)]E-误差P--改变P 可提高响应速度,减小静态误差,但太大会增大超调量和稳定时间。
PID算法程序—位置式PID控制算法

PID算法程序—位置式PID控制算法位置式PID控制算法是一种经典的控制算法,用来实现对于被控对象位置的精确控制。
本文将介绍位置式PID控制算法的原理和实现方式。
位置式PID控制算法的原理是基于被控对象的位置反馈信号,通过比较设定值和实际值之间的差异,进行控制动作的调整。
PID控制算法分为三个部分,即比例(Proportional)、积分(Integral)和微分(Derivative)控制。
比例控制通过比较设定值和实际值的差异,按照一个比例系数进行控制。
比例控制的作用是根据误差的大小来产生一个合适的控制量,使得误差越大,则控制量越大。
比例控制的数学公式为:P=Kp*e,其中P为控制量,Kp为比例系数,e为误差。
积分控制通过对误差进行累计,按照一个积分系数进行控制。
积分控制的作用是根据误差的累积量来产生一个较长期的平均控制量,以消除一些系统方面的偏差。
积分控制的数学公式为:I = Ki * ∫e dt,其中I为控制量,Ki为积分系数,∫e dt为误差的累积量。
微分控制通过对误差的变化率进行控制,按照一个微分系数进行控制。
微分控制的作用是根据误差的变化趋势来产生一个瞬时控制量,以抑制控制过程中的震荡和超调现象。
微分控制的数学公式为:D = Kd * de/dt,其中D为控制量,Kd为微分系数,de/dt为误差的变化率。
位置式PID控制算法的输出为PID控制量,即PID=P+I+D。
PID控制量经过执行机构(如电机)的作用,使被控对象达到设定值。
PID控制算法是一个迭代过程,通过不断调整PID系数,使控制系统的稳态误差趋于零,且响应时间和稳定性都符合要求。
在实际应用中,需要根据被控对象的特性和控制要求,调整PID控制算法的参数。
比例系数Kp决定了响应的敏感度,积分系数Ki决定了控制的稳定性,微分系数Kd决定了控制的平滑性。
通过合理调整这些参数,可以实现对被控对象位置的精确控制。
PID控制算法的实现可以通过编程语言来实现。
温度控制的PID算法 及C程序实现
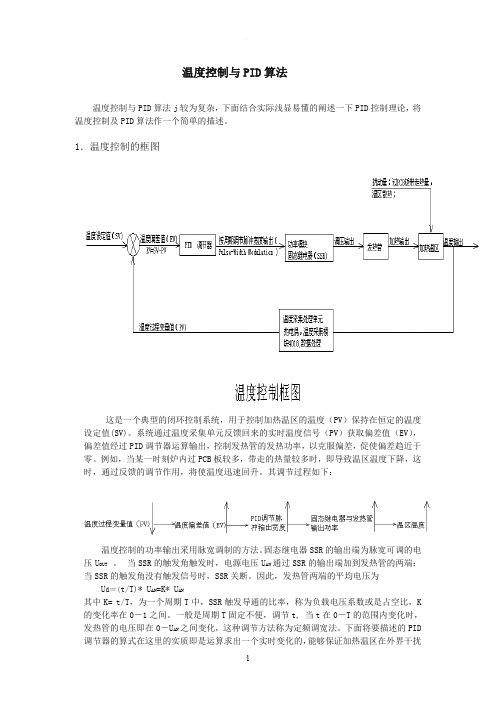
温度控制与PID算法温度控制与PID算法j较为复杂,下面结合实际浅显易懂的阐述一下PID控制理论,将温度控制及PID算法作一个简单的描述。
1.温度控制的框图这是一个典型的闭环控制系统,用于控制加热温区的温度(PV)保持在恒定的温度设定值(SV)。
系统通过温度采集单元反馈回来的实时温度信号(PV)获取偏差值(EV),偏差值经过PID调节器运算输出,控制发热管的发热功率,以克服偏差,促使偏差趋近于零。
例如,当某一时刻炉内过PCB板较多,带走的热量较多时,即导致温区温度下降,这时,通过反馈的调节作用,将使温度迅速回升。
其调节过程如下:温度控制的功率输出采用脉宽调制的方法。
固态继电器SSR的输出端为脉宽可调的电压U OUT 。
当SSR的触发角触发时,电源电压U AN通过SSR的输出端加到发热管的两端;当SSR的触发角没有触发信号时,SSR关断。
因此,发热管两端的平均电压为U d=(t/T)* U AN=K* U AN其中K=t/T,为一个周期T中,SSR触发导通的比率,称为负载电压系数或是占空比,K 的变化率在0-1之间。
一般是周期T固定不便,调节t, 当t在0-T的范围内变化时,发热管的电压即在0-U AN之间变化,这种调节方法称为定频调宽法。
下面将要描述的PID 调节器的算式在这里的实质即是运算求出一个实时变化的,能够保证加热温区在外界干扰的情况下仍能保持温度在一个较小的范围内变化的合理的负载电压系数K。
2.温度控制的两个阶段温度控制系统是一个惯性较大的系统,也就是说,当给温区开始加热之后,并不能立即观察得到温区温度的明显上升;同样的,当关闭加热之后,温区的温度仍然有一定程度的上升。
另外,热电偶对温度的检测,与实际的温区温度相比较,也存在一定的滞后效应。
这给温度的控制带来了困难。
因此,如果在温度检测值(PV)到达设定值时才关断输出,可能因温度的滞后效应而长时间超出设定值,需要较长时间才能回到设定值;如果在温度检测值(PV)未到设定值时即关断输出,则可能因关断较早而导致温度难以达到设定值。
基于C语言的数字PID控制算法及实现

参考文献
[1] 曹 书 生 , 等 . 网 络 业 务 流 模 型 综 述 [J]. 江 苏 通 信 技 术 ,2003,(05) [2] 刘 建 辉 , 等 . 基 于 离 散 MMDP 信 源 模 型 的 ATM 网 络 排 队 性 能 仿 真 [J]. 计 算 机 仿 真 . [3] 杨 敏 维 .ATM 突 发 模 型 MMDP 的 信 元 丢 失 率 估 计 [J]. 湖 南 大 学 学 报 ,1999,(02). [4] 陈 文 云 , 等 . 基 于 ON/OFF 信 源 模 型 的 信 元 丢 失 分 析 [J]. 数 字 通 信 ,2 000, (01 ). [5] 程 伟 明 . 基 于 ATM 网 络 的 多 媒 体 通 信 [J]. 现 代 电 信 科 技 ,1998, (07 ). [6] 过 莉 .ATM 网 络 实 时 通 信 系 统 的 响 应 时 间 分 析 [J]. 电 机 电 器 技 术 , 2 00 3 , ( 06 ) . [7] 张 如 娟 . 基 于 ATM 技 术 的 多 协 议 信 息 传 送 及 应 用 [J]. 甘肃科技 , 2001,(03). [8] A bdelnaser Adas.Traffic Models in Broadband Networks[J]. IEEE communications Magazine. Ju期 , 一 般 为 200ms, e ( k ) 为 系 统 第 k 次 采 样 时 刻 的 偏 差 值 , e ( k -l) 为 系 统 第 ( k -l) 次 采 样 时 刻 的 偏 差 值 , i 为 采 样 序 号 , i =0,1,2, … 。 将 上 面 的 (3) 式 和 (4) 式 代 入 (1) 式 , 则 可 以 得 到 离 散 的 PID 表 达 式 i T e( j ) + TD [ e ( k )- e ( k -1)]} u ( i )= K p { e ( i )+ T (5) T 1 j =0 如 果 采 样 周 期 T 足 够 小 (200ms), 该 算 式 可 以 很 好 的 逼 近 模 拟 PID 算式 , 因 而 使 被 控 过 程 与 连 续 控 制 过 程 十 分 接 近 。 通 常 把 (5) 式 称 为 PID 的 位 置 式 控 制 算 法 。 若 把 (5) 式 进 行 转 化 , 则 : 0.2 td u ( i )= k * e +k* e +k* (p v x -p v 1 ) (6 ) 0 .2 i ti i 式 (6) 即 为 数 字 PID 控 制 算 法 的 编 程 表 达 式 ,p vx 为 第 ( i -1) 次 测 量 值 ,p v1 为 第 i 次 测 量 值 。 其 程 序 流 程 图 如 图 1所 示 。 其 中 给 定 转 换 s v1 /25+1 是 要 把 设 定 值 数 模 转 化 , 比 如 要 求 给 定 液 位 100CM, 则 通 过 转 换 100/25+1=5, 代 表 的 是 最 高 液 位 所 测 量 的 电 压 为 5V 。 而 对 于 数 模 转 化 (O P1 +25)/ 6 .2 5 是 要 把 输 出 转 化 为 电 流 大 小 , 假 如 输 出 O P1 为 1 0 0% , 那 么 (100+25)/6.25=20, 代 表 输 出 为 最 大 电 流 20MA 。 对 于 输 入 输 出 量 ,要 注 意 内 部 的 数 模 /模 数 转 换 关 系 :经 过 变 送 器 输 出 (1 ~ 5v) 模 拟 量 , 送 入 A/D 模 块 转 化 为 (0 ~ 250) 数 字 量 , 数 字 量 要 与 给 定 量 进 行 比 较 , 就 必 须 要 数 模 转 化 , 把 0 ~ 250 十 进 制 数 转 换 为 1.00 ~ 5.00V, 数 据 处 理 公 式 参 考 下 面 程 序 。 反 之 ,同 样 可 把 (4 ~ 20mA) 进 行 模 数 转 化 , 得 出 0 ~ 250 十 进 制 数 , 再 经 过 D/A 模 块 , 把模拟量送给执行元件。 ( 图 1)
pid控制算法c语言

pid控制算法c语言PID控制算法是一种常用的控制算法,它可以通过对系统的反馈信号进行处理,实现对系统的控制。
在工业自动化、机器人控制、航空航天等领域都有广泛的应用。
本文将介绍PID控制算法的基本原理和C 语言实现方法。
一、PID控制算法的基本原理PID控制算法是由比例控制、积分控制和微分控制三个部分组成的。
其中,比例控制部分根据系统的误差信号进行控制,积分控制部分根据误差信号的积分值进行控制,微分控制部分根据误差信号的微分值进行控制。
三个部分的输出信号相加,得到最终的控制信号。
比例控制部分的输出信号为:P(t) = Kp * e(t)其中,Kp为比例系数,e(t)为误差信号。
积分控制部分的输出信号为:I(t) = Ki * ∫e(t)dt其中,Ki为积分系数,∫e(t)dt为误差信号的积分值。
微分控制部分的输出信号为:D(t) = Kd * de(t)/dt其中,Kd为微分系数,de(t)/dt为误差信号的微分值。
最终的控制信号为:U(t) = P(t) + I(t) + D(t)二、C语言实现方法PID控制算法的C语言实现方法如下:1. 定义PID控制器的结构体typedef struct{float Kp; //比例系数float Ki; //积分系数float Kd; //微分系数float e; //误差信号float e_last; //上一次误差信号float integral; //误差信号的积分值}PID;2. 初始化PID控制器void PID_Init(PID *pid, float Kp, float Ki, float Kd){pid->Kp = Kp;pid->Ki = Ki;pid->Kd = Kd;pid->e = 0;pid->e_last = 0;pid->integral = 0;}3. 计算PID控制器的输出信号float PID_Calculate(PID *pid, float target, float feedback) {float output;pid->e = target - feedback; //计算误差信号pid->integral += pid->e; //计算误差信号的积分值output = pid->Kp * pid->e + pid->Ki * pid->integral + pid->Kd * (pid->e - pid->e_last); //计算控制信号pid->e_last = pid->e; //保存上一次误差信号return output;}4. 调用PID控制器int main(){PID pid;float target = 50; //目标值float feedback = 0; //反馈值float output;PID_Init(&pid, 0.1, 0.01, 0.01); //初始化PID控制器while(1){feedback = get_feedback(); //获取反馈值output = PID_Calculate(&pid, target, feedback); //计算控制信号set_output(output); //设置输出信号}return 0;}以上是PID控制算法的C语言实现方法,可以根据实际情况进行调整和优化。
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现(完整版) 嘿,伙计们!今天我们要聊聊一个非常实用的技能——PID控制算法。
PID是英文Proportional-Integral-Derivative的缩写,翻译过来就是“比例积分微分”。
这个算法在我们的日常生活中随处可见,比如空调、洗衣机等家电的温度调节,还有汽车的速度控制等等。
那么,这个看似高深莫测的算法到底是怎么实现的呢?别急,让我们一起揭开它的神秘面纱吧!我们来了解一下PID控制算法的基本概念。
PID控制算法主要包括三个部分:比例(P)、积分(I)和微分(D)。
这三个部分分别对误差进行处理,然后将处理后的结果相加,得到控制输出。
具体来说,比例部分主要负责消除误差的瞬时成分;积分部分主要负责消除误差的稳态成分;微分部分则负责预测误差的未来变化趋势。
通过这三个部分的综合作用,我们可以实现对系统的精确控制。
接下来,我们来看一下PID控制算法的具体实现。
我们需要定义一些变量和参数,比如比例系数Kp、积分系数Ki、微分系数Kd以及采样时间Ts等。
这些参数的选择对于算法的效果至关重要,需要根据实际应用场景进行调整。
然后,我们需要不断地对系统进行采样,计算出当前的状态值和期望值之间的误差e(t)。
误差e(t)可以通过以下公式计算得到:e(t) = 期望值实际值有了误差e(t),我们就可以开始计算PID控制器的输出了。
根据之前的介绍,PID控制器的输出由比例、积分和微分三个部分组成。
具体计算过程如下:1. 比例部分:计算比例系数Kp乘以误差e(t),得到比例输出u(t);2. 积分部分:计算积分系数Ki乘以误差e(t)的时间积分,得到积分输出u(t);3. 微分部分:计算微分系数Kd乘以误差e(t)的时间微分,得到微分输出u(t)。
将比例、积分和微分三个部分的输出相加,得到最终的控制输出u(t)。
这样,我们就完成了一次PID控制算法的计算过程。
这只是理论上的实现方法,实际上还需要考虑一些其他因素,比如控制器的稳定性、响应速度等。
C++实现PID控制算法

C++实现PID控制算法|C++/VC/MFC/PID算法2008-06-10 18:50第一步:控制系统的结构仿真我们要用C++实现对这个单输入单输出系统的PID控制算法,就需要先进行结构仿真,系统结构和对象的数学模型如上图所示,我们取定参数:K=2、T1=1、T2=2.5,tao=0.6(tao 代表上面那个延时参数)。
系统性能指标要求:超调<=10%,调节时间Ts<=10秒,绘制出系统的单位阶跃响应。
控制器采用PID控制器,控制器参数包括:kp、ki、kd、T(采样时间)。
对被控对象采用Z变换进行离散化,离散化后的离散化对象为:yout(k)=-den(2)yout(k-1)-den(3)yout(k-2)+num(2)u(k-1)+num(3)u(k-2) tao=0yout(k)=-den(2)yout(k-1)-den(3)yout(k-2)+num(2)u(k-1-n)+num(3)u(k-2-n) tao/T=n,n>1为整数den、num参数的获取参看“C++实现PID控制算法理论分析|C++/VC/MFC/PID算法”2、参数声明在算法中要用到很多参数,为了方便我们定义一个结构体。
typedef struct tagPid{double tao; //系统纯延时参数,一般为采样时间的整数倍double ts; //采样时间int n; //n=tao/tsdouble rin,yout,u; //系统输入、系统输出、PID控制器输出double kp,ki,kd; //PID控制器参数double error_1,error_2; //,前1、2次的误差,在增量PID算法中需要error_2double error,perror,ierror,derror; //用于计算PID输出u的参数double den_1,den_2,den_3; //Z传函分母的系数double num_1,num_2,num_3; //Z传函的分子系数double yout_[2]; //系统输出过去时刻的值CArray<double,double> u_; //控制器过去时刻的输出值,就是上面公式中的u(k-2-n) 等 int size_Y out;//Y out的大小,算法循环次数,每次的输出值计入数组Y out,用来绘制输出曲线CArray<double,double> Y out; //输出数据数组double maxY out,minY out; //输出值的最大值和最小值}Pid;定义控制对象参数:double m_t1,m_t2,m_k,m_tao; //控制对象参数3、初始化参数void CICDoc::PidInit(Pid* pid){m_t1=1;m_t2=2.5;m_k=2;pid->ts=0.1;pid->tao=0.6;pid->n=(int)(pid->tao/pid->ts+0.5);pid->rin=1;pid->yout=0.0;pid->u=0.0;pid->kp=0.70;pid->ki=0.15;pid->kd=0.90;pid->error_1=0.0;pid->error_2=0.0;pid->error=0.0;pid->perror=0.0;pid->ierror=0.0;pid->derror=0.0;double z1,z2,b,c;if (m_t1==m_t2){z1=exp(-(pid->ts/m_t1)); //e(-T/T1) z2=z1pid->num_1=0;pid->num_2=m_k*(1-z1-pid->ts*z1/m_t1);pid->num_3=m_k*(z1*z1-z1+pid->ts*z1/m_t1);pid->den_1=1;pid->den_2=-2*z1;pid->den_3=z1*z1;}else{z1=exp(-(pid->ts/m_t1)); //e(-T/T1)z2=exp(-(pid->ts/m_t2)); //e(-T/T2)b=m_t1/(m_t2-m_t1);c=m_t2/(m_t1-m_t2);pid->num_1=0;pid->num_2=m_k*(1+b*z1+c*z2);pid->num_3=m_k*(z1*z2+b*z2+c*z1);pid->den_1=1;pid->den_2=-(z1+z2);pid->den_3=z1*z2;}pid->yout_[0]=0.0;pid->yout_[1]=0.0;pid->u_.SetSize(pid->n+2,0);for (int i=0;i<pid->n+2;i++){pid->u_[i]=0.0;}pid->size_Y out=500;pid->Y out.SetSize(pid->size_Y out);for (int i=0;i<pid->size_Y out-1;i++){pid->Y out[i]=0.0;}//最大值和最小值初始化为第一个值pid->maxY out=pid->Y out[0];pid->minY out=pid->Y out[0];}4、PID控制算法for (int k=0;k<pid.size_Y out;k++){pid.rin=1; //阶跃信号pid.u=pid.kp*pid.perror+pid.ki*pid.ierror+pid.kd*pid.derror;////输出限幅if (pid.u>10){pid.u=10;}if (pid.u<-10){pid.u=-10;}pid.yout=(pid.den_2)*(pid.yout_[0])+(pid.den_3)*(pid.yout_[1])+(pid.num_2)*(pid.u_[pid. n])+(pid.num_3)*(pid.u_[pid.n+1]);pid.error=(pid.rin)-(pid.yout);pid.perror=pid.error;pid.ierror=pid.ierror+pid.error*pid.ts;pid.derror=(pid.error-pid.error_1)/pid.ts;pid.error_2=pid.error_1;pid.error_1=pid.error;pid.yout_[1]=pid.yout_[0];pid.yout_[0]=pid.yout;for (int j=pid.n+1;j>0;j--){pid.u_[j]=pid.u_[j-1];}pid.u_[0]=pid.u;pid.Y out[k]=pid.yout;//得到最大输出值if (pid.Y out[k]>pid.maxY out) {pid.maxY out=pid.Y out[k];}//得到最小输出值if (pid.Y out[k]<pid.minY out) {pid.minY out=pid.Y out[k];}}。
