人教版数学八年级上册11.2与三角形有关的角能力培优训练含答案
部编版人教初中数学八年级上册《11.2 与三角形有关的角 同步练习题及答案》最新精品优秀测试题

前言:该同步练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点,精心编辑而成。
以高质量的同步练习题助力考生查漏补缺,在原有基础上更进一步。
(最新精品同步练习题)11.2 与三角形有关的角基础巩固1.(题型三角度a)如图11-2-1,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为()图11-2-1A.80°B.50°C.30°D.20°2.(题型一)如图11-2-2,在△ABC中,∠A=80°,∠B=40°,D,E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是()图11-2-2A.40°B.60°C.80°D.120°3.(题型一)若三角形的一个内角等于另外两个内角之差,则这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定4.(题型一)如图11-2-3,一根直尺EF压在三角形30°的角∠BAC上,与两边AC,AB分别交于点M,N,那么∠CME+∠BNF=()图11-2-3A.135°B.150°C.180°D.不能确定5.(题型一)如图11-2-4,在△ABC中,∠ABD=∠DBE=∠EBC,∠ACD=∠DCE=∠ECB,若∠BEC=145°,则∠BDC=()图11-2-4A.100°B.105°C.110°D.115°6.(题型三角度a)将一副直角三角板,按图11-2-5叠放在一起,则图中α的度数是 .图11-2-57.(题型一)如图11-2-6,EF∥BC,AC平分∠BAF,∠B=80°,则∠C的度数是.图11-2-68.(知识点2)如图11-2-7,在Rt△ACB中,∠ACB=90°,CD⊥AB,则图中互余的角有对.图11-2-79.(知识点3)如图11-2-8,已知在△ABC中,∠A=40°,剪去∠A后成四边形,∠1+∠2=°.。
八年级上册数学11.2与三角形有关的角练习题(含答案)

11.2与三角形有关的角练习题姓名:_______________班级:_______________考号:______________一、选择题1、在中,,则的度数为(???)A.?????B.??????C.??????D.2、如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=(??)A.70°?????B.80°??????C.90°?????D.100°3、如图8,AB=BC=CD,且∠A=15°,则∠ECD=(????)A.30°??????B.45°??????C.60°???????D.75°4、如图,在ΔABC中,AC=DC=DB,∠ACD=100°,则∠B等于(??)A.50°??????B.40°??????C.25°????D.20°第4题第5题5、如图,△ABC中,,点D、E分别在AB、AC上,则的大小为(????)??A、??????B、??????C、?????D、第6题第7题第9题6、如图,已知,∠1=130o,∠2=30o,则∠C=??????.7、如下图所示,已知:∠AEC的度数为110°,则∠A+∠B+∠C+∠D的度数为(??)A.110°?????B.130°?????C.220°???D.180°8、已知等腰三角形的一个角为75°,则其顶角为(?)A.30°???B.75°???C.105°????D.30°或75°9、如图,已知,若,,则C等于(???)A.20°????B.35°??????C.45°????D.55°10、如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()第10题第11题第12题11、如图,已知△ABC的两条高BE、CF相交于点O,,则的度数为(??)A.95o???B.130o??????C.140o???D.150o12、如图,已知与相交于点,,如果,,则的大小为(???)A.??????B.?????C.???????D.13、如图,在△ABC中,∠C=90o,∠B=40o,AD是角平分线,则∠ADC等于A.25o?????B.50o???????C.65o??????D.70o第13题第14题14、如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为()A.?20°????B.40°??????C.30°????D.25°15、如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是(????)A.45°?????B.54°?????C.40°?????D.50°第15题第16题第18题16、如图7-7,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA 的度数为(?????).?A.50°??B.60°??C.70°??D.80°17、适合条件的三角形ABC是(????)A.锐角三角形??B.直角三角形C.钝角三角形?D.等边三角形???????????18、如图1,若∠1=110°,∠2=135°,则∠3等于A.55°????B.65°????C.75°????D.85°19、如图,在△AB C中,∠A=60°,∠ABC=50°,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是(?)①∠ACB=70°;??????②∠BFC=115°;③∠BDF=130°;?④∠CFE=40°;A.①②?????B.③④?????C.①③????D.①②③第19题第20题20、如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠DBE=∠DCE.其中正确结论的个数为( )A.0??????B.1??????C.2??????D.3二、填空题21、如图,∠l=20°,∠2=25°,∠A=35°,则∠BDC=???????????.第21题第22题第23题22、如下图,?∠A=27°,?∠CBE=96°,?∠C=30°,?则∠ADE的度数是________度.?23、如图,∠1,∠2,∠3的大小关系是??????.24、如图,∠A=50°,∠ACD=38°,∠ABE=32°,则∠BFC= _________ .第24题第25题第26题25、如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=50°,则∠ACD的度数为.26、如图,已知△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=42°,∠C=70°,则∠DAE=????°.27、△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC是??????三角形.28、如图,⊿ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=????????度。
八年级上册数学11.2与三角形有关的角练习题(含答案)

八年级上册数学11.2与三角形有关的角练习题(含答案)八年级上册数学11.2与三角形有关的角练习题(含答案)题1:已知三角形ABC,∠B=60°,BM⊥AC于M,且AM=2,MC=4,请计算AC的长度。
解:由于∠B=60°,且三角形ABC为直角三角形,可以计算出BM 的长度。
根据勾股定理,可得AB=√(AM^2+BM^2)=√(2^2+4^2)=√(4+16)=√20=2√5。
由此可知BC=2AB=2*2√5=4√5。
因此,AC=√(AM^2+MC^2)=√(2^2+4^2)=√(4+16)=√20=2√5。
题2:在三角形ABC中,∠B=90°,BD是BC的中线,且∠ADB=30°,请计算∠ACD的度数。
解:由于∠B=90°,且BD是BC的中线,可以得知∠DBC=90°/2=45°。
又∠ADB=30°,因此∠BDC=∠ADB+∠DBC=30°+45°=75°。
根据三角形内角和定理,得知∠ACD=180°-∠BDC=180°-75°=105°。
题3:已知∠A=60°,在三角形ABC中,以下哪两条边相等?A. AB=BCB. BC=ACC. AB=ACD. 无法确定解:由于∠A=60°,根据等角对应定理可得∠B=60°。
根据等角定理可知,∠A=∠B,故可以得出结论AB=BC。
题4:已知三角形ABC,∠A=45°,∠B=30°,请计算∠C的度数。
解:∠A=45°,∠B=30°,可计算出∠C的度数。
根据三角形内角和定理,得知∠C=180°-∠A-∠B=180°-45°-30°=105°。
题5:已知三角形ABC,AC=10,BC=6,且∠A=60°,求三角形ABC的面积。
人教版八年级数学第11章第2节 与三角形有关的角双基培优 基础练习(含答案)

人教版八年级数学第11章第1节与三角形有关的角双基培优基础练习一、选择题(12×3=36分)1.将一副三角板按图中方式叠放,则∠α等于( B )A. 90°B. 75°C. 60°D. 45°2. 若∆ABC三个内角的关系为∠A3=∠B4=∠C5,则三角形的形状为( A )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形3. 如图,在△ABC中,∠ACB=100°,∠A=20°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( B )A. 20°B. 40°C. 55°D. 304. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( C )A.40°B.45°C.50°D.55°5. 如图,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为(B)A.65°B.35°C.55°D.45°6. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30,∠2=20°,则∠B=(D)A. 20°B. 30°C. 40°D. 50°7. 在△ABC中,若AB=9,BC=6,则第三边CA的长度可以是(B)A. 3B. 9C. 15D. 168.如图,AD,CE为△ABC的角平分线且交于O点,∠DAC=30°,∠ECA=35°,则∠ABO等于(A)A. 25°B. 30°C. 35°D. 40°9.如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2=(B).A. 100°B. 101°C.103°D. 105°10.如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,则∠BMN的度数是( C)A. 80°B. 90°C.100°D. 105°11. 如图,∠B=60°,∠C=40°,∠ADC=3∠A,则∠A的度数为( C)A. 80°B. 30°C. 50°D. 无法确定12.如图,AE平分△ABC外角∠CAD,且AE∥BC,给出下列结论:①∠DAE=∠CAE;②∠DAE=∠B;③∠CAE=∠C;④∠B=∠C;⑤∠C+∠BAE=180°,其中正确的个数有( A )A. 5个B. 4个C. 3个D. 2个二、填空题(5×3=15分)13. 在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理___三角形的内角和是180°__.14.如图,在∠ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= 66.5°.15.若等腰三角形的两边长是2和5,则此等腰三角形的周长是___12____.16.如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为__56_度.17.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B=__30°__.三、解答题(8+9+10+10+10+10+12)18. 如图,在△ABC中,∠A=55°,∠ABD=32°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.解:在△ABC中,∵∠A=55°,∠ACB=70°,∴∠ABC=55°,∵∠ABD=32°,∴∠CBD=∠ABC–∠ABD=23°,∵CE平分∠ACB,∴∠BCE=1∠ACB=35°,2∴在△BCE中,∠DEC=∠CBD+∠BCE=58°.19. 如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?试说明你找出的规律的正确性.解:2∠A =∠1+∠2,理由是:延长BD 和CE 交于A ′,∵把△ABC 沿DE 折叠,当点A 落在四边形BCDE 内部,∴∠ADE =∠A ′DE ,∠AED =∠A ′ED ,∴2∠ADE =180°-∠1,2∠AED =180°-∠2,∴∠ADE =90°-12∠1,∠AED =90°-12∠2,∵在△ADE 中,∠A =180°-(∠AED +∠ADE ),∴∠A =12∠1+12∠2, 即2∠A =∠1+∠2.20. 如图,在△ABC 中,CH 是外角∠ACD 的平分线,BH 是∠ABC 的平分线,∠A =58°,求∠H 的度数.解:∵∠A=58°,∴∠ABC+∠ACB=180°−∠A=180°−58°=122°…①∵BH 是∠ABC 的平分线,∴∠HBC=12∠ABC ,∵∠ACD 是△ABC 的外角,CH 是外角∠ACD 的角平分线,∴∠ACH=12 (∠A+∠ABC),∴∠BCH=∠ACB+∠ACH=∠ACB+12 (∠A+∠ABC),∵∠H+∠HBC+∠ACB+∠ACH=180°,∴∠H+12∠ABC+∠ACB+12 (∠A+∠ABC)=180°,即∠H+(∠ABC+∠ACB)+ 12∠A=180°…②,把①代入②得,∠H+122°+12×58°=180°,∴∠H=29°.21. (1)如图①所示,∠1+∠2与∠B +∠C 有什么关系?为什么?(2)如图②若把△ABC 纸片沿DE 点折叠当点A 落在四边形BCED 内部时,则∠A 与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.【答案】(1)∠1+∠2=∠B +∠C;(2)规律:α+β=2∠A .理由见解析解:(1)∠1+∠2=∠B+∠C ,理由如下:∵如图1,在△AED 和△ACB 中,∠1+∠2+∠A=∠A+∠B+∠C=180°(三角形内角和等于180°),∴∠1+∠2=∠B+∠C (等量代换);(2)规律:α+β=2∠A ,理由如下:∵在△ADE 中,∠1+∠2=180°﹣∠A (三角形内角和等于180°),在四边形BCED 中,∠BDE+∠DEC+∠B+∠C=360°(四边形内角和等于360°),又∵根据题(1)得∠1+∠2=∠B+∠C (已证),∴2(∠1+∠2)+α+β=360°(等量代换),∴2(180°﹣∠A )+α+β=360°(等量代换),∴α+β=2∠A .22. 如图,在△ABC 中,BD ⊥AC 于D .若∠A :∠ABC :∠ACB=3:4:5,E 为线段BD 上任一点. (1)试求∠ABD 的度数;(2)求证:∠BEC >∠A .解:(1)∵∠A+∠ABC+∠ACB=180°,∠A :∠ABC :∠ACB=3:4:5,∴∠A=45°,∠B=60°,∠C=75°,∵BD ⊥AC ,∴∠ADB=90°,∴∠ABD=90°-∠A=45°;(2)∵∠BEC 是△CDE 的外角,∴∠BEC >∠BDC ,∵∠BDC 是△ABD 的外角,∴∠BDC >∠A ,∴∠BEC >∠A .23. 如图,△ABC 中,∠A =100∘,⑴BI 、CI 分别平分∠ABC ,∠ACB ,求∠BIC 的度数?⑵若BM 、CM 分别平分∠ABC ,∠ACB 的外角平分线,求∠M 的度数?解:⑴∵∠A =100°.∵∠ABC +∠ACB =180°﹣100°=80°.∵BI 、CI 分别平分∠ABC ,∠ACB ,∴∠IBC =12∠ABC ,∠ICB =12∠ACB , ∴∠IBC +∠ICB =12∠ABC +12∠ACB =12(∠ABC +∠ACB )=12×80°=40°,∴∠I =180°﹣(∠IBC +∠ICB )=180°﹣40°=140°;⑵∵∠ABC +∠ACB =80°,∴∠DBC +∠ECB =180°﹣∠ABC +180°﹣∠ACB=360°﹣(∠ABC +∠ACB )=360°﹣80°=280°.∵BM 、CM 分别平分∠ABC ,∠ACB 的外角平分线,∴∠1=12∠DBC ,∠2=12ECB ,∴∠1+∠2=12×280°=140°,∴∠M =180°﹣∠1﹣∠2=40°.24. 如图,在△ABC 中,AD 平分∠BAC 交BC 于点D ,AE ⊥BC ,垂足为E ,且CF ∥AD .(1)如图1,若△ABC 是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度; (2)若图1中的∠B=x ,∠ACB=y ,则∠CFE= ;(用含x 、y 的代数式表示)(3)如图2,若△ABC 是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.【答案】(1)20;(2)12y ﹣12x ;(3)(2)中的结论成立.解:(1)∵∠B=30°,∠ACB=70°,∴∠BAC=180°﹣∠B ﹣∠ACB=80°,∵AD 平分∠BAC ,∴∠BAD=40°,∵AE ⊥BC ,∴∠AEB=90°∴∠BAE=60°∴∠DAE=∠BAE ﹣∠BAD=60°﹣40°=20°,∵CF ∥AD ,∴∠CFE=∠DAE=20°;故答案为20;(2)∵∠BAE=90°﹣∠B ,∠BAD=12∠BAC=12(180°﹣∠B ﹣∠BCA ),∴∠CFE=∠DAE=∠BAE ﹣∠BAD=90°﹣∠B ﹣12(180°﹣∠B ﹣∠BCA )=12(∠BCA ﹣∠B )=12y ﹣12x .故答案为12 y ﹣12x ;(3)(2)中的结论成立.∵∠B=x ,∠ACB=y ,∴∠BAC=180°﹣x ﹣y ,∵AD 平分∠BAC ,∴∠DAC=12∠BAC=90°﹣12x ﹣12y ,∵CF ∥AD ,∴∠ACF=∠DAC=90°﹣12x ﹣12y ,∴∠BCF=y+90°﹣12x ﹣12y=90°﹣12x+12y ,∴∠ECF=180°﹣∠BCF=90°+12x ﹣12y ,∵AE ⊥BC ,∴∠FEC=90°,∴∠CFE=90°﹣∠ECF=12y ﹣12x .。
初中数学人教版八年级上册第十一章《三角形》练习册(含答案)11.2 与三角形有关的角
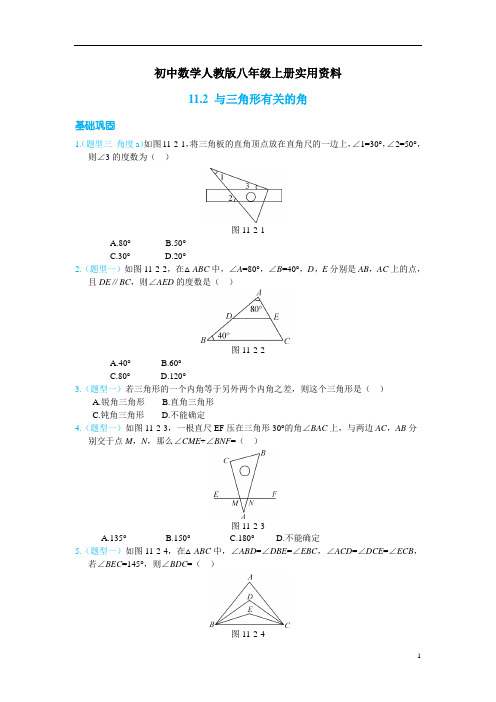
初中数学人教版八年级上册实用资料11.2 与三角形有关的角基础巩固1.(题型三角度a)如图11-2-1,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为()图11-2-1A.80°B.50°C.30°D.20°2.(题型一)如图11-2-2,在△ABC中,∠A=80°,∠B=40°,D,E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是()图11-2-2A.40°B.60°C.80°D.120°3.(题型一)若三角形的一个内角等于另外两个内角之差,则这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定4.(题型一)如图11-2-3,一根直尺EF压在三角形30°的角∠BAC上,与两边AC,AB分别交于点M,N,那么∠CME+∠BNF=()图11-2-3A.135°B.150°C.180°D.不能确定5.(题型一)如图11-2-4,在△ABC中,∠ABD=∠DBE=∠EBC,∠ACD=∠DCE=∠ECB,若∠BEC=145°,则∠BDC=()图11-2-4A.100°B.105°C.110°D.115°6.(题型三角度a)将一副直角三角板,按图11-2-5叠放在一起,则图中α的度数是.图11-2-57.(题型一)如图11-2-6,EF∥BC,AC平分∠BAF,∠B=80°,则∠C的度数是.图11-2-68.(知识点2)如图11-2-7,在Rt△ACB中,∠ACB=90°,CD⊥AB,则图中互余的角有对.图11-2-79.(知识点3)如图11-2-8,已知在△ABC中,∠A=40°,剪去∠A后成四边形,∠1+∠2= °.图11-2-810.(知识点2)如图11-2-9,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°.求∠DAE的度数.图11-2-911.(题型二角度b)如图11-2-10,∠1,∠2,∠3的大小关系是.图11-2-1012.(题型一)(1)如图11-2-11(1),有一块直角三角板XYZ放置在△ABC下,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C.在△ABC中,∠A=30°,则∠ABC+∠ACB=度,∠XBC+∠XCB=度.(2)如图11-2-11(2),改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.(1)(2)图11-2-1113.(题型一、二)(1)如图11-2-12,在△ABC中,AD⊥BC于点D,AE平分∠BAC,且∠C大于∠B.求证:∠EAD=12(∠C-∠B).(2)若把问题(1)中的“AD⊥BC于点D”改为“点F为EA上一点且FD⊥BC于点D”,画出新的图形,并说明∠EFD=12(∠C-∠B).(3)若把问题(2)中的“F为EA上一点”改为“F为AE延长线上的一点”,则问题(2)中的结论成立吗?说明你的理由.图11-2-1214.(题型一)如图11-2-13,在Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=α.(注:四边形的内角和是360°)(1)若点P在线段AB上,如图11-2-13(1),且α=50°,则∠1+∠2= .(2)若点P在边AB上运动,如图11-2-13(2),则α,∠1,∠2之间的关系为 .(1)(2)(3)(4)图11-2-13(3)若点P运动到边AB的延长线上,图11-2-13(3),则α,∠1,∠2之间有何关系?请写出你的猜想,并说明理由.(4)若点P运动到△ABC外,如图11-2-13(4),则α,∠1,∠2之间的关系为.答案基础巩固1. D 解析:如图D11-2-1,∵BC∥DE,∴∠CBD=∠2=50°.又∵∠CB D为△ABC的外角,∴∠CBD=∠1+∠3,即∠3=∠CBD-∠1=50°-30°=20°.故选D.图D11-2-12. B 解析:∵DE∥BC,∠B=40°,∴∠A DE=∠B=40°.又∵∠A=80°,∴在△ADE中,∠AED=180°-∠A-∠A DE=180°-80°-40°=60°(三角形的内角和定理).故选B.3. B 解析:设此三角形的三个内角分别是∠1,∠2,∠3(其中∠3最大),根据题意,得∠1=∠3-∠2,∴∠1+∠2=∠3.又∵∠1+∠2+∠3=180°,∴2∠3=180°,∴∠3=90°,∴这个三角形是直角三角形.故选B.4. B 解析:∵∠A+∠AMN+∠ANM=180°,∠A=30°,∴∠AMN+∠ANM=180°-∠A=180°-30°=150°.∵∠AMN=∠CME,∠ANM=∠BNF,∴∠CME+∠BNF=∠AMN+∠ANM=150°.故选B.5. C 解析:在△BCE中,∵∠BEC=145°,∴∠EBC+∠ECB=180°-145°=35°.∵∠DBE=∠EBC,∠DCE=∠ECB,∴∠DBC+∠DCB=2(∠EBC+∠ECB)=2×35°=70°.在△BCD中,∠BDC=180°-(∠DBC+∠DCB)=180°-70°=110°.故选C. 6. 75°解析:如图D11-2-2,∠1=90°-60°=30°,所以α=45°+∠1=45°+30°=75°.图D11-2-2 图D11-2-37. 50°解析:∵EF∥BC,∴∠BAF=180°-∠B=100°.∵AC平分∠BAF,∴∠CAB=12∠BAF=50°.∴∠C=180°-∠B-∠CAB=50°.8. 4 解析:由直角三角形的两个锐角互余,得∠ACD+∠A=90°,∠BCD+∠B=∠90°,∠A+∠B=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°.∴互余的角有4对.9. 220解析:如图D11-2-3,∠1+∠2=(∠A+∠4)+(∠A+∠3)=∠A+(∠A+∠3+∠4)=∠A+180°.∵∠A=40°,∴∠1+∠2=40°+180°=220°.10. 解:在△ABC中,∠B=40°,∠C=60°,∴∠BAC=80°.∵AE平分∠BAC,∴∠BAE=40°.又∵AD⊥BC,∠B=40°,∴∠BAD=90°-40°=50°.∴∠DAE=∠BAD-∠BAE=50°-40°=10°.能力提升11. ∠3>∠1>∠2 解析:如图D11-2-4,∵∠3=∠1+∠5,∴∠3>∠1.∵∠1=∠2+∠4,∴∠1>∠2.∴∠3>∠1>∠2.图D11-2-412. 解:(1)∵∠A=30°,∴∠ABC+∠ACB=180°-∠A=150°.∵∠X=90°,∴∠XBC+∠XCB=90°.(2)不变化.∵∠A=30°,∴∠ABC+∠ACB=150°.∵∠X=90°,∴∠XBC+∠XCB=90°.∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.13.(1)证明:在Rt△ADE中,∵∠AED+∠DAE=90°,∴∠DAE=90°-∠AED.∵∠AED=180°-∠C-∠CAE,且AE平分∠BAC,∴∠CAE=12∠BAC=12(180°-∠C-∠B).∴∠EAD=90°-180°-∠C-1/2(180°-∠C-∠B)=12(∠C-∠B).(2)解:如图D11-2-5(1),由三角形的内角和定理的推论,得∠FED=∠B+12∠BAC,故∠B+12∠BAC+∠EFD=90°①.在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即12∠C+12∠B+12∠BAC=90°②.②-①,得∠EFD=12(∠C-∠B).(3)解:成立.理由:如图D11-2-5(2),由三角形的内角和定理的推论,得∠FED=∠AEC=∠B+12∠BAC,故∠B+12∠BAC+∠EFD=90°①.在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即12∠C+12∠B+12∠BAC=90°②.②-①,得∠EFD=1(∠C-∠B).2(1)(2)图D11-2-514. 解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+α.∵∠C=90°,α=50°,∴∠1+∠2=140°.(2)由(1)得α+∠C=∠1+∠2,∴∠1+∠2=90°+α.(3)∠1=90°+∠2+α.理由如下:如图D11-2-6(1),∵∠2+α=∠DME,∠DME+∠C=∠1,∴∠1=∠C+∠2+α=90°+∠2+α.(4)如图D11-2-6(2),∵∠PFC=∠DFE,∴α+180°-∠1=∠C+180°-∠2,∴∠2=90°+∠1-α.(1)(2)图D11-2-6。
人教版八年级数学上册《11.2与三角形有关的角》同步练习题-含有答案

人教版八年级数学上册《11.2与三角形有关的角》同步练习题-含有答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.三角形的内角和等于A .100°B .150°C .180°D .360°2.三角形的三个内角( ) A .至少有两个锐角B .至少有一个直角C .至多有两个钝角D .至少有一个钝角 3.如图,在ABC 中85B ∠=︒,40ACD ∠=︒和AB ∥CD ,则ACB ∠的度数为( )A .90°B .85°C .60°D .55°4.如图.在ABC 中,AD 平分BAC ∠交BC 于点D .30,80B C ∠=︒∠=︒则ADC ∠的度数是( )A .65︒B .70︒C .75︒D .80︒5.如图,DEF 的顶点D ,E 在ABC 的边BC 上EF AC ∥,DFAB 若55A ∠=︒,则F ∠的度数为( )A .35°B .45°C .55°D .65°6.如图,ABC 是直角三角形90ACB ∠=︒,沿CD 折叠ABC ,使点B 恰好与AC 边上的点E 重合,若18A ∠=︒,则CDE ∠的度数为( )A .63︒B .68︒C .72︒D .78︒ 7.如图AB CD ,12560A CED ∠=︒∠=︒,则D ∠的度数为( )A .45︒B .60︒C .65︒D .75︒8.如图,一副三角形板按如图所示的位置摆放,其中AB CD ∥,45A ∠=︒和60C ∠=︒,90AEB CED ∠=∠=︒则AEC ∠的度数为( )A .70︒B .90︒C .105︒D .1?20︒9.如图,将三角形纸片ABC 沿BD 折叠,若290∠=,50A ∠=则1∠的度数为( )A .30︒B .25︒C .20︒D .35︒10.如图A ABC CB =∠∠,BD 、CD 、AD 分别平分ABC ∠、ACF ∠和EAC ∠.以下结论,A .①①B .①①①C .①①①D .①①①①二、填空题11.在ABC 中35A ∠=︒,45B ∠=︒则C ∠为 .12.如图,在ABC 中57A ∠=︒,40B ∠=︒和DE BC ∥,则AED ∠的度数为 ︒.13.如图,将一张三角形纸片沿着DE 折叠(点D 、E 分别在边AB 、AC 上),点A 落在点A '的位置,若70A ∠=︒,则12∠+∠= ︒.14.在ABC 中,BO 平分ABC ∠,CO 平分ACB ∠,当50A ∠=︒时,BOC ∠= ︒.15.将一副三角尺按如图所示的位置摆放,则1∠的度数是 .三、解答题 16.如图,已知75A ∠=︒,25B ∠=︒和35C ∠=︒,求BDC ∠和1∠的度数.17.如图,在ABC 中,三个内角的平分线交于点O ,过点O 作OD OB ⊥,交边BC 于点D .(1)若50ABC ∠=︒,则AOC ∠=________°,ODC ∠=________°.(2)猜想AOC ∠与ODC ∠的数量关系,并说明你的理由.18.如图,在ABC 中90ACB ∠=︒,点E ,F 在边AB 上,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处,再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B '处(1)求ECF ∠的度数;(2)若4CE =,1B F '=求BCE 的面积.参考答案:1.C2.A3.D4.A5.C6.A7.C8.C9.C10.D11.100︒ 12.8313.140 14.115 15.15︒ 16.110BDC ∠=︒ 1135∠=︒ 17.(1)115, 115(2)AOC ODC ∠=∠ 18.(1)45ECF ∠=︒(2)10。
人教版八年级数学11.2 和三角形有关的角(含答案 )

11.2 与三角形有关的角知识要点:1.三角形内角和定理:三角形三个内角的和等于180︒.(1)三角形内角和定理适用于任意三角形.(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.2.直角三角形的性质与判定(1)性质:直角三角形的两个锐角互余.在Rt ABC∠=︒,则90∠+∠=︒.A B△中,90C(2)判定:有两个角互余的三角形是直角三角形.3.三角形的外角三角形内角的一边与另一边的反向延长线组成的角,叫做三角形的外角.4.三角形外角的性质(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于与它不相邻的任意一个内角.一、单选题1.如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1=()A.30°B.25°C.20°D.15°【答案】D【解析】解:∵AB∵CD,∵∵A=∵FDE=45°,又∵∵C=30°.∵∵1=∵FDE﹣∵C=45°﹣30°=15°,故选:D.2.如图,直线a∠b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为()A.20°B.25°C.30°D.35°【答案】B解:由三角形的外角性质可得,∵3=∵1+∵B=65°,∵a∵b,∵DCB=90°,∵∵2=180°﹣∵3﹣90°=180°﹣65°﹣90°=25°.故选:B.3.已知∠ABC中,∠A=30°,则下列结论正确的是()A.0°<∠B<60°B.90°<∠B<150C.0°<∠B<60°或90°<∠B<150°D.以上都不对【答案】D解:∵∵A+∵B+∵C=180°,∵A=30°,∵∵B+∵C=150°,∵0°<∵B<150°,故选:D.4.若一个三角形三个内角度数的比为1:3:4,则这个三角形是( )A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形【答案】A设三个内角度数分别为:x、3x、4x由三角形内角和定理得,x+3x+4x=180°解得, x=22.5°则3x=67.5°、4x=90°∵这个三角形是直角三角形故选:A5.在ABC △中,如果1126A B C ∠=∠=∠,则这个三角形一定是( ). A .直角三角形B .等腰三角形C .锐角三角形D .钝角三角形 【答案】D∵在∵ABC 中,∵A =12∵B =16∵C ,∵A+∵B+∵C=180°, ∵16∵C+13∵C+∵C=180°, ∵∵C=120°,∵∵A=20°,∵B=40°,所以此三角形是钝角三角形.故选:D .6.如图,在∠ABC 中,∠BAC=56°,∠ABC=74°,BP 、CP 分别平分∠ABC 和∠ACB ,则∠BPC=( )A .102°B .112°C .115°D .118°【答案】D 解:∵在∵ABC 中,∵BAC=56°,∵ABC=74°,∵∵ACB=180°-∵BAC -∵ABC=50°,∵BP、CP分别平分∵ABC和∵ACB,∵∵PBC=37°,∵PCB=25°,∵∵BCP中,∵P=180°-∵PBC-∵PCB=118°,故选:D.7.如图,小丽画了一个三角形,不小心被墨水污染了,只剩下一个角(锐角). 小丽画的三角形可能是()A.锐角三角形B.直角三角形C.钝角三角形D.以上都有可能【答案】D∵此三角形只知道一个角为锐角,其它角可能有钝角或直角也可能是都是锐角,∵三角形可能为:锐角三角形、直角三角形、钝角三角形都有可能.故选:D.8.如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE等于()A.105°B.120°C.110°D.115°【答案】D由三角形的外角的性质可知:∵ADB=∵B+∵C=45°+38°=83°,∵DFE=∵ADB+∵A=83°+32°=115°,故选D.9.如图,把∠ABC纸片沿着DE折叠,当点A落在四边形BCED内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是()A.∠A=∠1+∠2B.2∠A=∠1+∠2C.3∠A=2∠1+∠2D.3∠A=2(∠1+∠2)【答案】B解:∵把∵ABC纸片沿着DE折叠,点A落在四边形BCED内部,∵∵1+∵2=180°−∵ADA′+180°−∵AEA′=180°−2∵ADE+180°−2∵AED=360°−2(∵ADE+∵AED)=360°−2(180°−∵A)=2∵A.故选:B.10.∠ABC中,∠A=50°,∠B=60°,则∠C=()A.50°B.60°C.70°D.90°【答案】C解:∵C=180°-50°-60°=70°,故选:C.11.如图,已知AB∠DE,∠ABC=75°,∠CDE=155°,则∠BCD的值为()A.50°B.40°C.30°D.20°【答案】A解:延长ED交BC于F,如图所示:∵AB∵DE,∵ABC=75°,∵∵MFC=∵B=75°,∵∵CDE=155°,∵∵FDC=180°-155°=25°,∵∵C=∵MFC-∵MDC=75°-25°=50°,故选:A.12.已知直线l1∠l2,一块含30°角的直角三角板如图所示放置,∠1=22°,则∠2等于()A.30°B.38°C.28°D.48°【答案】B解:∵∵3是∵ADG 的外角,∵∵3=∵A+∵1=30°+22°=52°,∵l 1∵l 2,∵∵3=∵4=52°,∵∵4+∵EFC=90°,∵∵EFC=90°-52°=38°,∵∵2=38°.故选:B .二、填空题13.如图所示,请将12A ∠∠∠、、用“>”排列__________________.【答案】21A ∠∠∠>>解:根据三角形的外角的性质得,∵2>∵1,∵1>∵A∵∵2>∵1>∵A ,故答案为:∵2>∵1>∵A .14.在∠ABC 中,∠B =40°,过点A 的直线将这个三角形分成两个等腰三角形,则∠C 的度数为______________.【答案】20°或50°或80°解:应分四种情况进行讨论:当AD=AC,AD=BD时,如图∵所示,∵BAD=∵B=40°,∵C=∵ADC.∵∵BAD+∵B+∵ADB=180°,∵∵ADB=180°-2×40°=100°,∵∵ADC=180°-∵ADB=80°,∵∵C=80°;当AC=DC,BD=AD时,如图∵所示,∵DAC=∵ADC=180°-∵ADB=∵B+∵BAD=80°,∵∵C=180°-∵ADC-∵DAC=20°;当AD=DC,AB=AD时,如图∵所示,∵C=∵DAC,∵ADB=∵B=40°.∵∵ADC=180°-∵ADB=140°,∵∵C=12(180°-∵ADC)=20°;当AD=BD,AD=CD时,如图∵所示,∵BAD=∵B=40°,∵ADC=180°-∵ADB=∵B+∵BAD=80°,∵C=∵DAC=12(180°-∵ADC)=12×(180°-80°)=50°.综上所述,∵C的度数为80°或20°或50°.15.如图,在∠ABC中,CD、BE分别是AB、AC边上的高,并且CD、BE交于点P,若∠A= 050,则∠BPC=_______.【答案】130°∵CD,BE分别是AB,AC边上的高,∵∵BDC=∵AEB=90°,∵∵ABE=90°-50°=40°,∵∵BPC=∵ABE+∵BDP=40°+90°=130°.故答案为:130°.16.将一副直角三角板如图放置,使两直角重合,则∠1=_____°.【答案】165°如图,根据题意知∵2=45°,∵3=60°,∵∵4=360°-90°-∵2-∵3=165°,∵∵1=∵4=165°17.如图所示,∠1=50°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为________【答案】260°.解:如图,∵D+∵F=∵2,∵A+∵E=∵3,∵∵A+∵D+∵E+∵F=∵2+∵3,∵∵1=50°,∵∵2+∵3=180°-50°=130°,∵4=50°,∵∵B+∵C=180°-50°=130°,∵∵A+∵B+∵C+∵D+∵E+∵F=260°.故答案为260°.18.已知∠A与∠B的两边一边平行,另一边垂直,∠A=x°,那么∠B等于_____.【答案】(90-x)°或(90+x)°.如图,∵DF∵AM,∵∵BDC=∵A=x.∵BC∵AN,∵∵BCA=90°,∵∵EBF=∵DBC=90°-∵BDC=90°-x°,∵FBC=90°+∵BDC=90°+x°.故答案为:(90-x)°或(90+x)°.19.一个正三角形和一副三角板(分别含30°和45°)摆放成如图所示的位置,且AB∠CD.则∠1+∠2=__________.【答案】75°解:连接AC,∵AB∵CD,∵∵BAC+∵ACD=180°,∵∵BAG=30°,∵ECD=60°,∵∵EAC+∵ACE=180°-30°-60°=90°,∵∵CED=60°,∵∵GEF=180°-90°-60°=30°,同理∵EGF=180°-∵1-90°=90°-∵1,∵GFE=180°-45°-∵2=135°-∵2,∵∵GEF+∵EGF+∵GFE=180°,即30°+90°-∵1+135°-∵2=180°,解得∵1+∵2=75°.故答案为:75°.三、解答题20.如图,在∠ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=60°,求∠DAC的度数.【答案】20°解:设∵1=∵2=x,则∵3=∵4=2x因为∵BAC=60°所以∵2 +∵4=120°即x+2x=120°所以x=40°所以∵3=∵4=80°,∵DAC=180°-∵3-∵4=20°21.如图,在∠ABC中,AD∠BC于点D,BE是∠ABC的平分线,已知∠ABC=040,求∠AOB 的度数。
人教版八年级数学 上 册 11.2与三角形有关的角同步练习题(含答案)

人教版八年级数学(上)第十一章《三角形》11.2与三角形有关的角同步练习题学校:___________姓名:___________班级:___________得分:___________一、选择题(本大题共10小题,共30分)1.如图,下列各角为△ABC 的外角的是( )。
A.∠1B.∠2C.∠3D.∠42.在△ABC 中,,则此三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形3.如图,∠DBA 和∠ACE 是△ABC 的外角,则∠DBA+∠ACE 等于( )。
A.180°B.180°-∠AC.180°+∠AD.以上答案都不对第3题图第5题图 4.已知a ∥b ,一块含30°角的直角三角尺按如图所示的方式放置,∠2=45°,则∠1的度数为( )。
A.100°B.135°C.155°D.165°5.如图,AB // CD ,∠A=50°,∠C=30°,则∠AEC 等于( )。
A.20°B.50°C.80°D.100°6.如图,在锐角三角形ABC 中,CD 和BE 分别是AB 和AC 边上的高,且CD 和BE 交于点P ,若∠A =50°,则∠BPC 的度数是( )。
A.100°B.120°C.130°D.150°第6题图 第7题图7.如图,CE 是△ABC 的外角∠ACD 的平分线,若∠B =35°,∠ACE =60°,则∠A 等于( )。
A.35°B.95°C.85°D.75°8.如图,在△ABC 中,∠A =60°,∠B =40°则∠C 的度数为( )。
A.100°B.80°C.60°D.40°9.下列说法正确的是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.2与三角形有关的角
专题一利用三角形的内角和求角度
1.如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分
线相交于D点,∠A=50°,则∠D=()
A.15°B.20°C.25°D.30°
2.如图,已知:在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D. 若AP平分∠BAC 且交BD于P,求∠BP A的度数.
3.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB 和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:__________;
(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数;(写出解答过程)
(3)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系.(直接写出结论即可)
专题二利用三角形外角的性质解决问题
4.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,
∠D=10°,则∠P的度数为()
A.15°B.20°C.25°D.30°
5.如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上
的高,若∠A=40°,∠B=72°.
(1)求∠DCE的度数;
(2)试写出∠DCE与∠A、∠B的之间的关系式.(不必证明)
6.如图:
(1)求证:∠BDC=∠A+∠B+∠C;
(2)如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠ABD、∠ACD这4个角之间有怎样的关系,并证明你的结论.
状元笔记
【知识要点】
1.三角形内角和定理
三角形三个内角的和等于180°.
2.直角三角形的性质及判定
性质:直角三角形的两个锐角互余.
判定:有两个角互余的三角形是直角三角形.
3.三角形的外角及性质
外角:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
性质:三角形的外角等于与它不相邻的两个内角的和.
【温馨提示】
1.三角形的外角是一边与另一边的延长线组成的角,而不是两边延长线组成的角.
2.三角形的外角的性质中的内角一定是与外角不相邻的内角.
【方法技巧】
1.在直角三角形中已知一个锐角求另一个锐角时,可直接使用“直角三角形的两个锐角互余”.
2.由三角形的外角的性质可得出:三角形的外角大于任何一个与它不相邻的内角.
参考答案
1.C解析:∵∠ABC的平分线与∠ACB的外角平分线相交于点D,∴∠1=1
2
∠ACE,
∠2=1
2
∠ABC.又∵∠D=∠1-∠2,∠A=∠ACE-∠ABC,∴∠D=
1
2
∠A=25°.故选C.
2.解:(法1)因为∠C=90°,所以∠BAC+∠ABC=90°,
所以1
2
(∠BAC+∠ABC)=45°.
因为BD平分∠ABC,AP平分∠BAC,
∠BAP=1
2
∠BAC,∠ABP=
1
2
∠ABC,
即∠BAP+∠ABP=45°,
所以∠APB=180°-45°=135°.
(法2)因为∠C=90°,所以∠BAC+∠ABC=90°,
所以1
2
(∠BAC+∠ABC)=45°,
因为BD平分∠ABC,AP平分∠BAC,
∠DBC=1
2
∠ABC,∠P AC=
1
2
∠BAC,
所以∠DBC+∠P AD=45°.
所以∠APB=∠PDA+∠P AD =∠DBC+∠C+∠P AD
=∠DBC+∠P AD+∠C =45°+90°=135°.
3.解:(1)∠A+∠D=∠B+∠C;
(2)由(1)得,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠1-∠3=∠P-∠D,∠2-∠4=∠B-∠P,
又∵AP、CP分别平分∠DAB和∠BCD,
∴∠1=∠2,∠3=∠4,
∴∠P-∠D=∠B-∠P,
即2∠P=∠B+∠D,
∴∠P=(40°+30°)÷2=35°.
(3)2∠P=∠B+∠D.
4.B解析:延长DC,与AB交于点E.根据三角形的外角等于不相邻的两内角和,可得∠ACD=50°+∠AEC=50°+∠ABD+10°,整理得∠ACD-∠ABD=60°.设AC与BP相交于
点O,则∠AOB=∠POC,∴∠P+1
2
∠ACD=∠A+
1
2
∠ABD,即∠P=50°-
1
2
(∠ACD-
∠ABD)=20°.故选B.
5.解:(1)∵∠A=40°,∠B=72°,
∴∠ACB=68°.
∵CD平分∠ACB,
∴∠DCB=1
2
∠ACB=34°.
∵CE是AB边上的高,
∴∠ECB=90°-∠B=90°-72°=18°.∴∠DCE=34°-18°=16°.
(2)∠DCE=1
2
(∠B-∠A).
6.(1)证明:延长BD交AC于点E,
∵∠BEC是△ABE的外角,
∴∠BEC=∠A+∠B.
∵∠BDC是△CED的外角,
∴∠BDC=∠C+∠DEC=∠C+∠A+∠B.
(2)猜想:∠BDC+∠ACD+∠A+∠ABD=360°.证明:∠BDC+∠ACD+∠A+∠ABD
=∠3+∠2+∠6+∠5+∠4+∠1
=(∠3+∠2+∠1)+(∠6+∠5+∠4)
=180°+180°=360°.。
