中考数学经典总复习专题多解题完美
2025年中考数学总复习专题07 二元一次方程组(附答案解析)
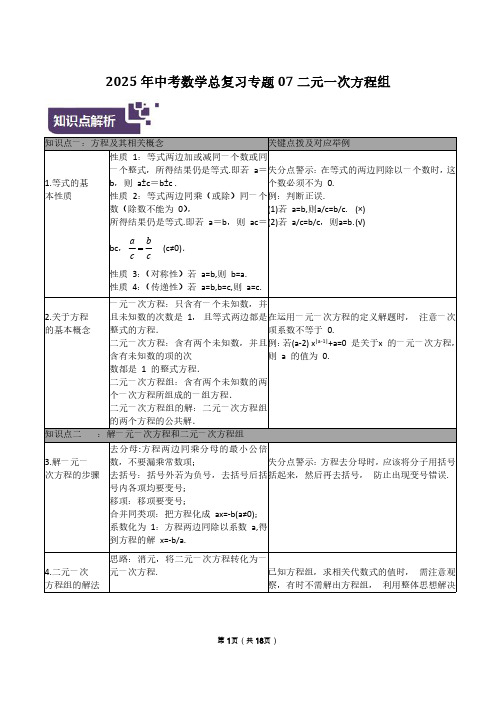
数(除数不能为 0),
(1)若 a=b,则a/c=b/c. (×)
所得结果仍是等式.即若 a=b,则 ac=(2)若 a/c=b/c,则a=b.(√)
bc, a b (c≠0). cc
性质 3:(对称性)若 a=b,则 b=a. 性质 4:(传递性)若 a=b,b=c,则 a=c.
2.关于方程 的基本概念
2025 年中考数学总复习专题 07 二元一次方程组
知识点一:方程及其相关概念
关键点拨及对应举例
1.等式的基 本性质
性质 1:等式两边加或减同一个数或同
一个整式,所得结果仍是等式.即若 a=失分点警示:在等式的两边同除以一个数时,这
b,则 a±c=b±c .
个数必须不为 0.
性质 2:等式两边同乘(或除)同一个例:判断正误.
根据题意,列出的方程组是()
8y x 3 A. 7 y x 4
8y x 3 B. 7 y x 4
y 8x 3
C.
7
y
x
4
8y x 3
D.
7
y
x
4
【答案】B
【分析】
设该物品的价格是 x 钱,共同购买该商品的由 y 人,根据题意每人出 8 钱,则多 3 钱;每人出 7 钱,则差 4
钱列出二元一次方程组.
【详解】
设该物品的价格是 x 钱,共同购买该商品的由 y 人,
8y x 3 依题意可得 7 y x 4
故选:B
【点睛】
本题考查由实际问题抽象出二元一次方程组以及数学常识,找准等量关系,正确列出二元一次方程组.
二、解答题 3.某工厂计划生产 A、B 两种产品共 60 件,需购买甲、乙两种材料.生产一件 A 产品需甲种材料 4 千克, 乙种材料 1 千克;生产一件 B 产品需甲、乙两种材料各 3 千克.经测算,购买甲、乙两种材料各 1 千克共 需资金 60 元;购买甲种材料 2 千克和乙种材料 3 千克共需资金 155 元. (1)甲、乙两种材料每千克分别是多少元? (2)现工厂用于购买甲、乙两种材料的资金不能超过 10000 元,且生产 B 产品要超过 38 件,问有哪几种 符合条件的生产方案?
中考数学总复习教材过关(试卷版+解析版)十八 勾股定理(附答案)

教材过关十八 勾股定理一、填空题1.一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是________________.2.在△ABC 中,若AB=17,AC=8,BC=15,则根据______________可知∠ACB=_______________.3.一座垂直于两岸的桥长15米,一艘小船自桥北头出发,向正南方向驶去,因水流原因,到达南岸后,发现已偏离桥南头9米,则小船实际行驶了______________米.4.若三角形中相等的两边长为10 cm,第三边长为16 cm,则第三边上的高为_____________cm.5.如图8-41,矩形ABCD,AB=5 cm,AC=13 cm,则这个矩形的面积为______________cm 2.图8-416.等边三角形的边长为4,则其面积为_______________.7.如图8-42,在高3米,坡面线段距离AB 为5米的楼梯表面铺地毯,则地毯长度至少需____________米.图8-428.若13 c +|a-12|+(b-5)2=0,则以a 、b 、c 为三边的三角形是______________三角形. 二、选择题9.下列是勾股数的一组是A.4,5,6B.5,7,12C.12,13,15D.21,28,35 10.下列说法不正确的是A.三个角的度数之比为1∶3∶4的三角形是直角三角形B.三个角的度数之比为3∶4∶5的三角形是直角三角形C.三边长度之比为3∶4∶5的三角形是直角三角形D.三边长度之比为5∶12∶13的三角形是直角三角形11.一个圆桶底面直径为24 cm,高32 cm,则桶内所能容下的最长木棒为A.20 cmB.50 cmC.40 cmD.45 cm12.一职工下班后以50米/分的速度骑自行车沿着东西马路向东走了5.6分,又沿南北马路向南走了19.2分到家,则他的家离公司距离为______________米.A.100B.500C.1 240D.1 000 三、解答题13.如图8-43,在四边形ABCD 中,AB=12 cm,BC=3 cm,CD=4 cm,∠C=90°.图8-43(1)求BD的长;(2)当AD为多少时,∠ABD=90°?14.有一块土地形状如图8-44所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,请计算这块地的面积.图8-4415.甲、乙两船上午11时同时从港口A出发,甲船以每小时20海里的速度向东北方向航行,乙船以每小时15海里的速度向东南方向航行,求下午1时两船之间的距离.图8-4516.已知:a、b、c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.解:∵a2c2-b2c2=a4-b4,①∴c2(a2-b2)=(a2+b2)(a2-b2).②∴c2=a2+b2.③∴△ABC是直角三角形.问:(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ______________;(2)错误的原因为_________________________________________________________________;(3)本题正确的解题过程:17.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图8-46所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.图8-46教材过关十八 勾股定理 一、填空题1.一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是________________. 答案:24提示:根据勾股定理,两直角边的平方和等于斜边的平方,设其中一条直角边为x ,另两条分别为(x-2),(x+2),则有(x-2)2+x 2=(x+2)2,解得x=0或x=8,x=0不合题意舍去,所以三边长为6、8、10,周长为24.2.在△ABC 中,若AB=17,AC=8,BC=15,则根据______________可知∠ACB=_______________.答案:勾股定理逆定理 90°提示:勾股定理逆定理是判定一个角是直角的重要方法,AC 2+BC 2=82+152=289=172=AB 2,根据勾股定理的逆定理说明AB 的对角是90度.3.一座垂直于两岸的桥长15米,一艘小船自桥北头出发,向正南方向驶去,因水流原因,到达南岸后,发现已偏离桥南头9米,则小船实际行驶了______________米. 答案:334提示:桥长、偏离桥南头的距离、实际行驶的路程构成一个直角三角形,利用勾股定理,可得实际行驶的路程的平方=152+92=306,所以实际行驶了334米.4.若三角形中相等的两边长为10 cm,第三边长为16 cm,则第三边上的高为_____________cm. 答案:6提示:等腰三角形三线合一,底边上的高也是底边的中线,所以底边的一半为8,则高为22810-=36=6.5.如图8-41,矩形ABCD,AB=5 cm,AC=13 cm,则这个矩形的面积为______________cm 2.图8-41答案:60提示:根据勾股定理求出BC 的长,BC 2=132-52=144,则BC=12,面积为5×12=60. 6.等边三角形的边长为4,则其面积为_______________. 答案:43提示:根据勾股定理求出高为2224-=23,面积为底×高×21=4×232=43.7.如图8-42,在高3米,坡面线段距离AB 为5米的楼梯表面铺地毯,则地毯长度至少需____________米.图8-42答案:7提示:由勾股定理求出另一直角边为4,将楼梯表面向下和右平移,则地毯的总长=两直角边的和=3+4=7.8.若13-c +|a-12|+(b-5)2=0,则以a 、b 、c 为三边的三角形是______________三角形. 答案:直角提示:满足a 2+b 2=c 2. 二、选择题9.下列是勾股数的一组是A.4,5,6B.5,7,12C.12,13,15D.21,28,35 答案:D提示:满足a 2+b 2=c 2的正整数是勾股数,只有212+282=352,所以选D. 10.下列说法不正确的是A.三个角的度数之比为1∶3∶4的三角形是直角三角形B.三个角的度数之比为3∶4∶5的三角形是直角三角形C.三边长度之比为3∶4∶5的三角形是直角三角形D.三边长度之比为5∶12∶13的三角形是直角三角形 答案:B提示:三个角的度数之比中有两个之和等于另一个,可以判定是直角三角形,另外两边的平方和=第三边的平方,也可以判定是直角三角形,三个角的度数之比为3∶4∶5的三角形,三个角分别是45度、60度和75度,不是直角三角形.11.一个圆桶底面直径为24 cm,高32 cm,则桶内所能容下的最长木棒为A.20 cmB.50 cmC.40 cmD.45 cm 答案:C提示:根据勾股定理,最长木棒长的平方=242+322,解得40 cm.12.一职工下班后以50米/分的速度骑自行车沿着东西马路向东走了5.6分,又沿南北马路向南走了19.2分到家,则他的家离公司距离为______________米.A.100B.500C.1 240D.1 000 答案:D提示:由于东西方向与南北方向互相垂直,两段路程与家离公司距离形成直角三角形,根据勾股定理求得家离公司距离=22)502.19()506.5(⨯+⨯=1 000米.三、解答题13.如图8-43,在四边形ABCD 中,AB=12 cm,BC=3 cm,CD=4 cm,∠C=90°.图8-43(1)求BD 的长;(2)当AD 为多少时,∠ABD=90°? (1)答案:5.提示:在△BDC 中,∠C=90°,BC=3 cm ,CD=4 cm ,根据勾股定理,BD 2=BC 2+CD 2,求得BD=5 cm. (2)答案:13.提示:根据勾股定理的逆定理,三角形两边的平方和等于斜边的平方,则三角形是直角三角形,所以AD=13时,可满足AD 2=BD 2+AB 2,可说明∠ABD=90°,AD=22512+=13. 14.有一块土地形状如图8-44所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,请计算这块地的面积.图8-44答案:234米2.提示:连结AC ,将四边形分割成两个三角形,其面积为两个三角形的面积之和,根据勾股定理求出AC ,进而求出AD.AC=221520+=25,AD=22725-=24,面积为21AB ×BC+21AD ×CD=234米2.15.甲、乙两船上午11时同时从港口A 出发,甲船以每小时20海里的速度向东北方向航行,乙船以每小时15海里的速度向东南方向航行,求下午1时两船之间的距离.图8-45答案:50海里.提示:东北方向航行,东南方向航行,则夹角为90度,根据勾股定理,相距=22)215()220(⨯+⨯=50.16.已知:a 、b 、c 为△ABC 的三边,且满足a 2c 2-b 2c 2=a 4-b 4,试判断△ABC 的形状. 解:∵a 2c 2-b 2c 2=a 4-b 4,①∴c 2(a 2-b 2)=(a 2+b 2)(a 2-b 2).② ∴c 2=a 2+b 2.③∴△ABC 是直角三角形. 问:(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ______________; (2)错误的原因为_________________________________________________________________; (3)本题正确的解题过程:答案:(1)③ (2)除式可能为零 (3)∵a 2c 2-b 2c 2=a 4-b 4,∴c 2(a 2-b 2)=(a 2+b 2)(a 2-b 2). ∴a 2-b 2=0或c 2=a 2+b 2. 当a 2-b 2=0时,a=b ;当c 2=a 2+b 2时,∠C=90度,∴△ABC 是等腰三角形或直角三角形.提示:(1)(2)两边都除以a 2-b 2,而a 2-b 2的值可能为零,由等式的基本性质,等式两边都乘以或除以同一个不为0的整式,等式仍然成立.(3)根据等式的基本性质和勾股定理,分情况加以讨论.17.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图8-46所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.图8-46提示:如图,作厂门的对称轴,求出PR 的长,只要PR >车高2.5,就说明卡车能通过厂门. 在Rt △OPQ 中,由勾股定理得PQ=228.01-=0.6米, ∴PR=0.6+2.3=2.9>2.5. ∴这辆卡车能通过厂门.。
2022-2023学年九年级下学期数学中考复习《轴对称最短路径问题》解答题专题训练

2022-2023学年九年级数学中考复习《轴对称最短路径问题》解答题专题训练(附答案)1.如图,在△ABC中,AB=AC,D是BC的中点,EF垂直平分AC,交AC于点E,交AB 于点F,M是直线EF上的动点.(1)当MD⊥BC时.①若ME=1,则点M到AB的距离为;②若∠CMD=30°,CD=3,求△BCM的周长;(2)若BC=8,且△ABC的面积为40,则△CDM的周长的最小值为.2.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交AC于点M.(1)若∠B=70°,求∠BAC的大小.(2)连接MB,若AB=8cm,△MBC的周长是14cm.①求BC的长;②在直线MN上是否存在点P,使PB+CP的值最小,若存在,标出点P的位置并求PB+CP的最小值,若不存在,说明理由.3.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点的坐标分别为;(2)△ABC的面积是;(3)在x轴上作一点P,使P A+PB的值最小.(保留作图痕迹,不写作法)4.在平面直角坐标系xOy中,已知点A(1,1),B(3,2).(1)如图1,在y轴上是否存在一点P,使P A+PB最小,若存在求出点P的坐标;若不存在,请说明理由.(2)如图2,点C坐标为(4,1),点D由原点O沿x轴正方向以每秒1个单位的速度运动,求点D运动几秒时,四边形ABCD是平行四边形.5.如图,在矩形ABCD中,AB=2,∠ABD=60°,G,H分别是AD,BC边上的点,且AG =CH,E,O,F分别是对角线BD上的四等分点,顺次连接G,E,H,F,G.(1)求证:四边形GEHF是平行四边形;(2)填空:①当AG=时,四边形GEHF是矩形;②当AG=时,四边形GEHF是菱形;(3)求四边形GEHF的周长的最小值.6.如图,C为线段BD上﹣动点,分别过点B、D作AB⊥BD于点B,ED⊥BD于点D,连接AC、EC,已知AB=3、DE=2、BD=12,设CD=x.(1)直接写出用含x的代数式表示的AC+CE的长(无需化简);(2)观察图形并说明在什么情况下AC+CE的值最小?最小值是多少?写出计算过程;(3)综上,直接写出代数式的最小值.7.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠BCE=β.(1)如图(1),点D在线段BC上移动时,①角α与β之间的数量关系是;②若线段BC=2,点A到直线BC的距离是3,则四边形ADCE周长的最小值是;(2)如图(2),点D在线段BC的延长线上移动时,①请问(1)中α与β之间的数量关系还成立吗?如果成立,请说明理由;②线段BC、DC、CE之间的数量是.8.问题提出我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小.例如:(1)对于任意两个代数式M,N的大小比较,有下面的方法:当M﹣N>0时,M>N;当M﹣N=0时,M=N;当M﹣N<0时,M<N.反过来也成立.因此,我们把这种比较两个代数式大小的方法叫做“作差法”.(2)对于比较两个正数a,b的大小,我们还可以用它们的平方进行比较:∵a2﹣b2=(a+b)(a﹣b),a+b>0,∴(a2﹣b2)与(a﹣b)的符号相同.当a2﹣b2>0时,a﹣b>0,得a>b;当a2﹣b2=0时,a﹣b=0,得a=b;当a2﹣b2<0时,a﹣b<0,得a<b.问题解决(3)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x >y,张丽同学的用纸总面积为S1,李明同学的用纸总面积为S2,回答下列问题:①S1=(用含x,y的代数式表示);S2=(用含x,y的代数式表示);②试比较谁的用纸总面积更大?(4)如图1所示,要在燃气管道l上修建一个泵站,向A,B两镇供气,已知A,B到l 的距离分别是3km,4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P 处,该方案中管道长度a2=AP+BP.①在方案一中,a1=km(用含x的代数式表示);②在方案二中,a2=km(用含x的代数式表示);③请分析说明哪种方案铺设的输气管道较短?(5)甲、乙两位采购员同去一家饲料公司购买两次饲料,两次购买的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000kg,乙每次用去1000元,而不管购买多少饲料.设两次购买的饲料单价分别为m元/kg和n元/kg(m,n是正数,且m≠n),试分析哪位采购员的购货方式合算?9.在平面直角坐标系xOy中,点A、B分别在y轴和x轴上,已知点A(0,4),以AB为直角边在AB左侧作等腰直角△ABC,∠CAB=90°.(1)当点B在x轴正半轴上,且AB=8时,①求AB解析式;②求C点坐标;(2)当点B在x轴上运动时,连接OC,求AC+OC的最小值及此时B点坐标.10.如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.(1)求证:∠ACB=∠ACD;(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.①连接PE,交AM于点N,证明AM垂直平分PE;②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合.11.如图,菱形ABCD的边长为1,∠ABC=60°,点E是边AB上任意一点(端点除外),线段CE的垂直平分线交BD,CE分别于点F,C,AE,EF的中点分别为M,N.(1)求证:AF=EF;(2)求MN+NG的最小值.12.已知点P在∠MON内.(1)如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.①若∠MON=50°,则∠GOH=;②若PO=5,连接GH,请说明当∠MON为多少度时,GH=10;(2)如图2,若∠MON=60°,A、B分别是射线OM、ON上的任意一点,当△P AB的周长最小时,求∠APB的度数.13.如图,四边形ABCD是菱形,对角线AC和BD相交于点O、点E是CD的中点,过点C 作AC的垂线,与OE的延长线交于点F,连接FD.(1)求证:四边形OCFD是矩形;(2)若四边形ABCD的周长为4,△AOB的周长为3+,求四边形OCFD的面积;(3)在(2)问的条件下,BD上有一动点Q,CD上有一动点P,求PQ+QE的最小值.14.如图1,在△ABC中,∠ABC的平分线与边AC的垂直平分线相交于点D,过点D作DF ⊥BC于点F,DG⊥BA交BA的延长线于点G.(1)求证:AG=CF;=5,求MN+AN (2)如图2,点M,N分别是线段AB,射线BD上的动点,若BC=5,S△ABC 的最小值.15.如图,在平面直角坐标系中,点A(﹣2,0),B(2,0),点C是y轴正半轴上一点,点P在BC的延长线上.(1)若点P的坐标为(﹣1,2),①求△P AB的面积;②已知点Q是y轴上任意一点,当△P AQ周长取最小值时,求点Q的坐标;(2)连接AC,若∠APC=∠ACP,∠APC比∠P AB大20°,求∠ABC的度数.16.已知如图,在平行四边形ABCD中,点E是AD边上一点,连接BE,CE,BE=CE,BE ⊥CE,点F是EC上一动点,连接BF.(1)如图1,当BF⊥AB时,连接DF,延长BE,CD交于点K,求证:FD=DK;(2)如图2,以BF为直角边作等腰Rt△FBG,∠FBG=90°,连接GE,若DE=,当点F在运动过程中,求△BEG周长的最小值.17.如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC、BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若,AC=4,求OE的长;(3)若点P是BD上一动点,在(2)的条件下,请求出△PCE周长的最小值.18.如图,在平面直角坐标系中,OA=OB=6,OD=1,点C为线段AB的中点.(1)直接写出点C的坐标为;(2)点P是x轴上的动点,当PB+PC的值最小时,求此时点P的坐标;(3)在平面内是否存在点F,使得以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.19.如图,在正方形ABCD中,F为BC为边上的定点,E、G分别是AB、CD边上的动点,AF和EG交于点H且AF⊥EG.(1)求证:AF=EG;(2)若AB=6,BF=2.①若BE=3,求AG的长;②连结AG、EF,求AG+EF的最小值.20.如图1,在△ABC中,AB=AC,点E为边AB上一点,连接CE.(1)如图1,以CE为边作等腰三角形DCE,DE=DC,连接AD,且满足条件AB⊥AD,∠B=∠ADE,∠ACD=3∠B,求证:DE⊥DC.(2)如图2,∠BAC=120°,过点A作直线AM⊥BC交BC于点M,点F为直线M上一点,BE=AF,连接CF,当CE+CF最小时,直接写出∠ECF的度数.参考答案1.解:(1)①∵MD⊥BC,AB=AC,D是BC的中点,∴A、M、D共线,∴AD是△ABC的对称轴,∵ME=1,∴点M到AB的距离为1,故答案为:1;②∵D是BC的中点,MD⊥BC,∴MB=MC,∴MD平分∠BMC,∴∠BMC=2∠CMD=60°,∴△BCM是等边三角形,∴BC=BM=MC,∵D是BC的中点,∴BC=2CD=6,∴BM=MC=BC=6,∴△BCM的周长为BC+BM+MC=18;(2)连接AD交EF于点M,∵EF是AC的垂直平分线,∴AM=CM,∴CM+MD=AM+MD=AD,此时△CMD的值最小,最小值为AD+CD,∵BC=8,△ABC的面积为40,∴AD=10,∵D是BC的中点,∴CD=4,∴AD+CD=14,∴△CMD的周长最小值为14,故答案为:14.2.解:(1)∵AB=AC,∠B=70°,∴∠BAC=180°﹣70°×2=40°;(2)∵MN垂直平分AB.∴MB=MA,又∵△MBC的周长是14cm,∴AC+BC=14cm,∴BC=6cm.(3)当点P与点M重合时,PB+CP的值最小,为AC长,最小值是8cm.3.解:(1)如图A1(﹣1,1)B1(﹣4,2)C1(﹣3,4),故答案为:(﹣1,1)、(﹣4,2)、(﹣3,4);(2)△A1B1C1的面积=(2+3)×3÷2﹣=7.5﹣1﹣3=3.5.(3)如图所示,作点A关于x轴的对称点A',再连接A'B,与x轴的交点P即为所求.4.解:(1)作A点关于y轴的对称点M(﹣1,1),连接BM后与y轴的交点即为所求的点P,如下图所示:设直线BM的解析式为y=kx+b,代入M(﹣1,1),B(3,2),,解之得,∴直线BM解析式为,令x=0,解得y=,∴存在点P的坐标,且P(0,);(2)当四边形ABCD是平行四边形,只能是AC为一条对角线,另一条对角线为BD,设D(m,0),由中点坐标公式可知:线段AC的中点坐标为,即,线段BD的中点坐标为,即,又线段AC与BD中点为同一个点,∴,解得m=2,故四边形ABCD是平行四边形,D点的坐标为(2,0),又速度为1个单位每秒,∴经过2秒后,四边形ABCD是平行四边形.5.(1)证明:∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∴∠GDF=∠HBE,∵AG=CH,∴DG=BH,∵E,O,F分别是对角线BD上的四等分点,∴DF=BE,在△DGF和△BHE中,,∴△DGF≌△BHE(SAS),∴GF=HE,∠DFG=∠BEH,∴∠EFG=∠FEH,∴GF∥HE,∴四边形GEHF是平行四边形;(2)①当AG=时,四边形GEHF是矩形.理由如下:连接GH,如下图,∵∠BAD=90°,∠ABD=60°,∴∠ADB=30°,∴BD=2AB=4,∴AD=,∵AG=CH=,AD=BC=2,∴,∵AG∥BH,∴四边形ABHG是平行四边形,∵GH=AB=2,∵E,O,F分别是对角线BD上的四等分点,∴EF=BD=2,∴EF=GH,∵四边形GEHF是平行四边形,∴四边形GEHF是矩形,故答案为:;②当AG=时,四边形GEHF是菱形.理由如下:连接BG、DH、GH,如下图,∵AG=CH,AD=BC,∴DG=BH,∵DG∥BH,∴四边形BHDG是平行四边形,∵AG=,AB=2,∠A=90°,∴DG=AD﹣AG=,BG=,∴BG=DG,∴四边形BHDG是菱形,∴GH⊥BD,即GH⊥EF,∵四边形GEHF是平行四边形,∴四边形GEHF是菱形.故答案为:;(3)解:过E作EM⊥AD于M,延长EM到点N,使得MN=EM,连接FN,NG,过F 作FP⊥EM于点P,如下图,则MN=EM=DE=,FP∥AD,EG=NG,∴∠EFP=∠ADB=30°,∴EP=EF=1,∴PN=EM+MN﹣EP=2,PF=,∵EG+FG=NG+FG≥FN,当F、G、N三点共线,EG+FG=NG+FG=FN的值最小,其值为FN=,∴四边形GEHF的周长的最小值为:2(EG+FG)=2.6.解:(1)∵AB⊥BD,AB=3,CD=x,∴BC=12﹣x,在Rt△ABC中,AC==,∵ED⊥BD,DE=2,在Rt△DEC中,CE==,∴AC+CE=,故答案为:;(2)如图,当C是AE和BD交点时,延长ED与AB的垂线AF交于点F,∴AC+CE=AE===13,∴AC+CE的最小值为13;(3)如图,AB=3,ED=2,DB=4,连接AE交BD于点C,∴AE=的最小∴AE的长即为代数式的最小值,∵四边形ABDF为矩形,∴AB=DF=1,AF=BD=4,在Rt△AEF中,由勾股定理得,AE===5,即代数式的最小值为5.7.解:(1)①α+β=180°;理由如下:∵∠DAE=∠BAC,∴∠DAE﹣∠DAC=∠BAC﹣∠DAC∴∠CAE=∠BAD,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠BAC+∠ABD+∠ACB=180°,∴∠BAC+∠ACE+∠ACB=180°,∴∠BAC+∠BCE=180°,即α+β=180°,故答案为:α+β=180°;②由①知,△ABD≌△ACE,∴BD=CE,AD=AE,∴CD+CE=BD+CD=BC=2,当AD⊥BC时,AD最短,即四边形ADCE周长的值最小,∵点A到直线BC的距离是3,∴AD=AE=3,∴四边形ADCE周长的最小值是2+3+3=8,故答案为:8;(2)①成立,理由如下:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠ACD=∠ABD+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∴∠BAC+∠BCE=∠DCE+∠BCE=180°,即α+β=180°;②∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,BD=CE,∵BD=BC+CD,∴CE=BC+CD,故答案为:CE=BC+CD.8.解:(3)①S1=3x+7y,S2=2x+8y.故答案为:3x+7y,2x+8y.②S1﹣S2=(3x+7y)﹣(2x+8y)=x﹣y,∵x>y∴x﹣y>0∴S1﹣S2>0∴S1>S2∴张丽同学的用纸总面积更大.(4)①a1=AB+AC=(3+x)km,故答案为:(3+x).②作BF⊥A′A于点F,在Rt△BAF中,由勾股定理得BF2=AB2﹣AF2=x2﹣1,在Rt△BF A′中,由勾股定理得A′B=A′P+BP=AP+BP==km,∴a2=km,故答案为:.③a12﹣a22=(x+3)2﹣()2=6x﹣39,由6x﹣39=0,得,此时a12﹣a22=0,即a1=a2,两种方案铺设的输气管道一样长;由6x﹣39>0,得,此时a12﹣a22>0,即a1>a2,方案二铺设的输气管道较短;由6x﹣39<0,得,此时a12﹣a22<0,即a1<a2,方案一铺设的输气管道较短.(5)===∵m≠n∴所以乙采购员的购货方式合算.9.解:(1)①∵A(0,4),AB=8,∴OB==4,∴B(4,0),设直线AB的解析式为y=kx+4,∴0=4k+4,k=﹣,∴AB解析式:y=﹣x+4;②过点A作x轴的平行线,分别过点C、B作y轴的平行线,交于G、H.则△AHB≌△CGA(AAS)∴AG=HB=4,CG=AH=4,∴C(﹣4,4﹣4);(2)由△AGC≌△BHA可知AG=4,(B在x轴负半轴同理可说明)点C在直线x=﹣4上运动,作点O关于直线x=﹣4的对称点O',∴OC=O'C=4,OO'=4+4=8,∴AC+OC=AC+O'C.AC+OC的最小值为AO'===4,此时OB=AH=CG=2,∴B(2,0).10.证明:(1)∵∠ABC=∠ADC=90°,BC=CD,AC=AC,∴Rt△ABC≌Rt△ADC(HL),∴∠ACB=∠ACD;(2)①∵Rt△ABC≌Rt△ADC,∴∠BAC=∠CAD,∵CA=CE,∴∠CAE=∠CEA,∵∠EBA=90°,∴∠BEA=∠BAC=∠CAE=30°,∵PD⊥AE,MP⊥PD,∴AE∥MP,∴∠PMC=∠MAE=30°,∵ME∥AB,∴∠MEB=∠ABE=90°,∴∠MEA=90°+30°=120°,∵∠MAE=30°,∴∠EMA=30°,∵CP⊥MP,CE⊥ME,∠MCP=∠MCE=60°,∴△NEC≌△NPC(SAS),∴EN=PN,∴N是EP的中点,NC⊥PE,∴AM垂直平分PE;②延长PD、ME交于Q点,由①知,∠BEA=30°,∠MEB=90°,∴∠MEA=120°,∴∠DEQ=60°,∵PD⊥AE,∴∠EDQ=90°,∴∠EQD=30°,∵∠CPN=30°,∴∠EPD=∠DQE,∴PE=EQ,∴ME+PE=QE+ME≥MQ,此时ME+PE的值最小,∵点O是直线AE上的动点,∴当MO+PO的值最小时,E点与O点重合.11.解:(1)证明:连接CF,∵FG垂直平分CE,∴CF=EF,∵四边形ABCD为菱形,∴A和C关于对角线BD对称,∴CF=AF,∴AF=EF;(2)连接AC,∵M和N分别是AE和EF的中点,点G为CE中点,∴MN=AF,NG=CF,即MN+NG=(AF+CF),当点F与菱形ABCD对角线交点O重合时,AF+CF最小,即此时MN+NG最小,∵菱形ABCD边长为1,∠ABC=60°,∴△ABC为等边三角形,AC=AB=1,即MN+NG的最小值为;12.解:(1)①∵点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,∴OG=OP,OM⊥GP,∴OM平分∠POG,同理可得ON平分∠POH,∴∠GOH=2∠MON=2×50°=100°,故答案为:100°;②∵PO=5,∴GO=HO=5,当∠MON=90°时,∠GOH=180°,∴点G,O,H在同一直线上,∴GH=GO+HO=10;(2)如图所示:分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A、B,连接P A、PB,则AP=AP',BP=BP“,此时△P AB周长的最小值等于P′P″的长.由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,∴∠P′OP″=2∠MON=2×60°=120°,∴∠OP′P″=∠OP″P′=(180°﹣120°)÷2=30°,∴∠OP A=∠OP'A=30°,同理可得∠BPO=∠OP″B=30°,∴∠APB=30°+30°=60°.13.(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°,∵AC⊥CF,CF∥BD∴∠ODE=∠FCE,∵E是CD中点,∴CE=DE,在△ODE和△FCE中,,∴△ODE≌△FCE(ASA);∴OD=FC,∵CF∥BD,∴四边形OCFD是平行四边形,∴四边形OCFD是矩形;(2)解:∵菱形ABCD的周长为4,∴AB=BC=CD=DA=,∠COD=90°,AO=CO,BO=DO,∵△AOB的周长为3+,∴AB+AO+BO=3+,∴AO+BO=3,∴CO+DO=3,在Rt△COD中,CO2+DO2=(CO+DO)2﹣2CO•DO=CD2,∴32﹣2CO•DO=()2,∴CO•DO=2,∴四边形OCFD的面积=CO•DO=2;(3)解:如图,过点O作OG⊥AD于点G,过点E作EH⊥AD于点H,则四边形OGHE 是矩形.∴OG=EH,由(2)可知,OA•OD=2,AD=,∴•OA•OD=•AD•OG,∴OG=,∴EH=OG=∵四边形ABCD是菱形,∴BD平分∠ADC,作点P关于DB的对称点P′,连接QP′,∴PQ+QE=EQ+QP′≥EH=,∴PQ+QE的最小值为.14.(1)证明:如图1,连接AD,DC,∵BD平分∠ABC,DG⊥BA,DF⊥BC,∴DG=DF.又∵点D在边AC的垂直平分线上,∴DA=DC.在Rt△DGA和Rt△DFC中,,∴Rt△DGA≌Rt△DFC(HL).∴AG=CF.(2)解:∵BD平分∠ABC,点M在线段AB上,∴点M关于BD的对称点M′在边BC上.如图2,作点M关于BD的对称点M′,连接M′N,过点A作AP⊥BC于点P,∴MN=M′N.∴MN+AN=M′N+AN≥AP.∴当点A,N,P在同一条直线上且AP⊥BC时,MN+AN的值最小,最小值即为AP的长.=5,∵S△ABC∴.∵BC=5,∴AP=2.∴MN+AN的最小值为2.15.解:(1)①∵点A(﹣2,0),B(2,0),P(﹣1,2),∴△P AB的面积为4×2=4;②如图,连接QB,∵A和B关于y轴对称,∴QA=QB,∴QA+QP=QB+QP,∴当P、Q、B三点共线时QB+QP最小,即△P AQ周长取最小,∴点Q为直线PB与y轴的交点,设直线PB为y=kx+b,直线过点B(2,0),P(﹣1,2),∴,解得,∴y=﹣x+,∵当x=0时,y=,∴Q(0,),∴当△P AQ周长取最小值时,点Q的坐标(0,);(2)如图,连接AC,设∠ABC=x,∵CA=CB,∴∠CAB=∠ABC=x,∴∠PCA=∠CAB+∠ABC=2x,∴∠APC=∠ACP=2x,∴∠P AB=2x﹣20°,∵∠P AB+∠PBA+∠APB=180°,∴2x﹣20°+2x+x=180°,解得x=40°,∴∠ABC的度数为40°.16.(1)证明:如图1中,延长BF交CD于点T.∵EB=EC,∠BEC=90°,∴∠ECB=∠EBC=45°,∵四边形ABCD是平行四边形,∴AD∥CB,AB∥CD,∴∠DEC=∠ECB=45°,∵∠CEK=90°,∴∠DEK=∠DEF,∵AB⊥BF,AB∥CD,∴BT⊥CD,∴∠BEF=∠CTF=90°,∵∠EFB=∠TFC,∴∠EBF=∠ECK,在△BEF和△CEK中,,∴△BEF≌△CEK(ASA),∴EF=EK,在△DEK和△DEF中,,∴△DEK≌△DEF(SAS),∴DK=DF;(2)解:如图2,作BK⊥BE,GK⊥BK于点K,延长KG交射线CE于点P,∵∠EBK=∠FBG=90°,∴∠KBG=∠EBF=90°﹣∠GBE,∵∠K=∠BEF=90°,BG=BF,∴△BKG≌△BEF(AAS),∴BK=BE;∵∠EBK=∠K=∠BEP=90°,∴四边形BEPK是正方形,∴PE=BE=CE,∴当点F在CE上运动时,点G在PK上运动;延长EP到点Q,使PQ=PE,连接BQ交PK于点G,∵PK垂直平分EQ,∴点Q与点E关于直线PK对称,∵两点之间,线段最短,∴此时GE+GB=GQ+GB=BQ最小,∵BE为定值,∴此时GE+GB+BE即△BEG的周长最小;作DH⊥CE于点H,则∠DHE=∠DHC=90°,∵∠ECB=∠EBC=45°,∴∠HED=∠ECB=45°,∴∠HDE=45°=∠HED,∴DH=EH,∴DH2+EH2=2DH2=DE2=()2,∴DH=EH=1;∴CH===2,∴BE=CE=EH+CH=1+2=3,∴EQ=2PE=2BE=6,∵∠BEQ=90°,∴BQ==3,∴GE+GB+BE=3+3,∴△BEG周长的最小值为3+3.17.(1)证明:∵AD∥BC,∴∠ADB=∠CBD,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AD=AB,∵AB=BC,∴AD=BC,∵AD∥BC,∴四边形ABCD是平行四边形,又∵AB=BC,∴四边形ABCD是菱形;(2)解:∵四边形ABCD是菱形,∴AC⊥BD,OB=OD,OA=OC=AC=2,在Rt△OCD中,由勾股定理得:OD=4,∴BD=2OD=8,∵DE⊥BC,∴∠DEB=90°,∵OB=OD,∴OE=BD=4.(3)如图,连接AE交BD于点P,连接PC,∵A,C关于BD对称,∴PC+PE=P A+PE=AE,此时PC+PE最小,即△PCE周长的最小,根据菱形ABCD的面积得BC•DE=BD•AC,∴2DE=8×4×,∴DE=,∴AE=,∵CE=,∴△PCE周长的最小值为+.18.解:(1)∵OA=OB=6,∴A(6,0),B(0,6),∵点C为线段AB的中点,∴点C的坐标为(3,3);故答案为:(3,3).(2)作点B关于x轴的对称点B',连接CB'交x轴于点P,此时PB+PC的值最小,由已知得,点B的坐标为(0,6),∴点B关于x轴的对称点B'(0,﹣6),由(1)知,C(3,3),可设直线CB'的解析式为y=kx+b,∴,解得∴直线CB'的解析式为y=3x﹣6,令y=0,∴3x﹣6=0,∴x=2,∴P(2,0);(3)存在点F,使以A、C、D、F为顶点的四边形为平行四边形,分三种情况考虑,如图所示:①当AC为对角线时,∵A(6,0),C(3,3),D(1,0),CF1=AD=5,CF1∥DA,∴点F1的坐标为(8,3);②当AD为对角线时,∵A(6,0),C(3,3),D(1,0),AC=DF2,AC∥DF2,∴点F2的坐标为(4,﹣3);③当CD为对角线时,∵A(6,0),C(3,3),D(1,0),CF3=AD=5,CF3∥DA,∴点F3的坐标为(﹣2,3).综上所述,点F的坐标是(8,3),(4,﹣3)或(﹣2,3).19.(1)证明:如图1,过点G作GP⊥AB交于P,∵AH⊥EG,∴∠AEH+∠DAH=90°,∵∠PEG+∠PGC=90°,∴∠EAH=∠PGE,∵PG=AB,∴△ABF≌△GPE(AAS),∴AF=EG;(2)①∵BF=2,∴PE=2,∵AB=6,BE=3,∴AE=3,∴AP=1,在Rt△APG中,AP=1,PG=6,∴AG==;②过点F作FQ∥EG,过点G作GQ∥EF,∴四边形EFQG为平行四边形,∴GQ=EF,∴AG+EF=AG+GQ≥AQ,∴当A、G、Q三点共线时,AG+EF的值最小,∵EG=AF,EG=FQ,∴AF=FQ,∵AF⊥EG,∴AF⊥FQ,∴△AFQ是等腰直角三角形,∵AF==2,∴AQ=4,∴AG+EF的最小值为4.20.(1)证明:设AD与BC交于点O,∵∠AOB=∠COD,∴∠B+∠BAO=∠ADC+∠OCD,∵AB⊥AD,∴∠BAO=90°,∵AB=AC,∴∠B=∠ACB,∵∠ACD=3∠B=∠ACB+∠OCD,∴∠OCD=2∠B,∴∠ADC=90°+∠B﹣2∠B=90°﹣∠B,∵∠ADE=∠B,∴∠EDC=∠ADE+∠ADC=90°,∴DE⊥DC;(2)解:作∠GBA=∠BAM,且BG=AB,连接BE,GA,CG,∵AB=AC,AM⊥BC,∴∠BAM=∠CAM=,∠ACB=∠ABC=30°,∴∠GBE=∠EAC=60°,∵BE=AF,BG=AC=AB,∴△GBE≌△CAF(SAS),∴GE=CF,∴CE+CF=GE+CE,当C,G,E在一条直线上时,CE+CF最短,∵∠GBA=60°,AB=BG,∴△GBA是等边三角形,∴∠GAB=60°,∵∠BAC=120°,∴C,G,A在一条直线上,∴当CE+CF最小时,E与A重合,∴BE=AF=AB=AC,∵∠F AC=60°,∴△AF'C是等边三角形,∴∠ACF=60°,即∠ECF=60°.。
中考数学总复习《45多边形与平行四边形》试题训练及解析.doc

第五节多边形与平行四边形基础训练1.(2017苏州中考)如图,在正五边形ABCDE中,连接BE,贝iJZABE的度数为(B)A.30°B.36°C.54°D.72°“(第1题图)2.(湘西屮考)下列说法错误的是(D)A.对角线互相平分的四边形是平行四边形2两组对边分别相等的四边形是平行四边形C 一组对边平行冃相等的四边形是平行四边形D.一组对边相等,另一组对边平行的四边形是平行四边形3・(2015石家屮四十三屮模拟)如图,在口ABCD屮,延长AB到点E,使BE = AB,连接DE交BC于点F,则下列结论不一定成立的是(D)A. ZE=ZCDF B・ EF=DFC. AD = 2BFD. BE=2CF4.(2017 丽水中考)如图,在口ABCD 中,连接AC, ZABC= ZCAD=45° , AB =2,则BC的长是(C)A.y[2B. 2C. 2^2 D・ 45.(荷泽中考)在口ABCD中,AB = 3, BC=4,当口ABCD的面积最大时,下列结论正确的有(B)①AC = 5;②ZA+ZC=180° ;③AC丄BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④6・(孝感中考)在口ABCD中,AD = 8, AE平分ZBAD交BC于点E” DF平分ZADC 交BC于点F,且EF=2,则AB的长为(D)儿 3 B. 5C 2或3 〃・3或57.平行四边形ABCD与等边AAEF如图放置,如果ZB = 45° ,那么ZBAE 的大小是(A)A.75°B.70°C.65°D.60°8.(北京中考)如图是由射线AB, BC, CD, DE, EA组成的平面图形,则Z1 + Z2+Z3+Z4+Z5= 360°9・(江西中考)如图所示,在oABCD中,ZC = 40° ,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则ZBEF的度数为§0。
中考数学专题复习一题多变与多解试题

无棣县埕口中学中考数学专题复习 一题多变与多解 新人教版制卷人:打自企; 成别使; 而都那。
审核人:众闪壹; 春壹阑; 各厅…… 日期:2022年二月八日。
一、一题多解,拓宽思路,培养思维的多向性,发散性,采用一题多解的方法可以训练同学们应用多种方法,以多种角度去认识、解决问题. 例 :如图1,直线AB ∥CD ,P 是AB 和CD 之间的一点.试说明∠ABP +∠PDC =∠BPD .该题证明思路较多,主要有以下几种:证法一:如图1,过点P 向右作PE ∥AB ,那么有∠ABP =∠BPE .又∵ AB ∥CD ,∴ PE ∥CD ,∴ ∠EPD =∠PDC .因此,∠ABP +∠PDC =∠BPE +∠EPD =∠BPD .证法二:如图2,过点P 向左作PE ∥AB ,那么有∠ABP +∠BPE =180°. 易得PE ∥CD ,∴∠EPD +∠PDC =180°. 故有∠ABP +∠BPE +∠EPD +∠PDC =360°.又∵ ∠BPE +∠EPD +∠BPD =360°,∴ ∠ABP +∠PDC =∠BPD . 证法三:如图3,延长BP ,交CD 于点E ,那么∠BPD =∠PED +∠PDC . ∵ AB ∥CD ,∴ ∠ABP =∠PED . ∴ ∠ABP +∠PDC =∠BPD . 证法四:如图4,过点P 作直线EF ,分别交AB 、CD 于点E 、F . 那么∠EPB +∠BPD =∠EPD =∠PFD +∠PDC .又∵ AB ∥CD ,∴ ∠PFD =∠AEF =∠ABP +∠EPB , ∴ ∠EPB +∠BPD =∠ABP +∠EPB +∠PDC . ∴ ∠ABP +∠PDC =∠BPD .二、题多变,同中求异,培养思维的敏捷性、深入性.ACDP图1 E B ACD 图2E BP图3C D E AP BP E 图4A CD F B一题多变指改变同一问题中的条件或者题目改变求解目的,或者加深题目难度,从而训练同学生举一反三,以不变应万变的才能。
中考数学备考专题复习反比例函数含解析

反比例函数一、单选题(共12题;共24分)1、(2016•龙东)已知反比例函数y= ,当1<x<3时,y的最小整数值是()A、3B、4C、5D、62、如果等腰三角形的底边长为x,底边上的高为y,则它的面积为定植S时,则x与y的函数关系式为()A、y=B、y=C、y=D、y=3、(2016•大庆)已知A(x1, y1)、B(x2, y2)、C(x3, y3)是反比例函数y= 上的三点,若x1<x2<x3, y2<y1<y3,则下列关系式不正确的是()A、x1•x2<0B、x1•x3<0C、x2•x3<0D、x1+x2<04、将一次函数y=x图象向下平移b个单位,与双曲线y=交于点A,与x轴交于点B,则OA2-OB2=( )A、-2B、2C、-D 、5、如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A、y=B、y=C、y=D、y=6、如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=(k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为()A、-B、-C、-3D、-67、教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的()A、7:20B、7:30C、7:45D、7:508、(2015•玉林)如图,反比例函数y=的图象经过二次函数y=ax2+bx 图象的顶点(﹣,m)(m >0),则有()A、a=b+2kB、a=b﹣2kC、k<b<0D、a<k<09、如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y= (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是()A 、B 、C 、D 、10、(2016•济宁)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于()A、60B、80C、30D、4011、(2016•湖北)一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为()A 、B 、C 、D 、12、(2016•天津)若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1, y2, y3的大小关系是()A、y1<y3<y2B、y1<y2<y3C、y3<y2<y1D、y2<y1<y3二、填空题(共5题;共6分)13、如果函数y=x2m-1为反比例函数,则m的值是________.14、(2015•黄石)反比例函数y=的图象有一支位于第一象限,则常数a的取值范围是________ .15、(2016•宁波)如图,点A为函数y= (x>0)图象上一点,连结OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为________.16、(2016•丽水)如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.(1)b=________(用含m的代数式表示);(2)若S△OAF+S四边形EFBC=4,则m的值是________.17、(2016•绍兴)如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为________.三、解答题(共3题;共15分)18、当m 取何值时,函数是反比例函数?19、(2016•苏州)如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.20、已知与是反比例函数图象上的两个点.(1)求m和k的值(2)若点C(-1,0),连结AC,BC,求△ABC的面积(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.四、综合题(共4题;共45分)21、(2016•曲靖)在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”.(1)直接写出函数y= 图象上的所有“整点”A1, A2, A3,…的坐标;(2)在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.22、(2015•广州)已知反比例函数y=的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.23、(2016•枣庄)如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= (k>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EFA的面积最大,最大面积是多少?24、(2016•雅安)已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y= 交于点C(1,a).(1)试确定双曲线的函数表达式;(2)将l1沿y轴翻折后,得到l2,画出l2的图象,并求出l2的函数表达式;(3)在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.答案解析部分一、单选题【答案】A【考点】反比例函数的性质【解析】【解答】解:在反比例函数y= 中k=6>0,∴该反比例函数在x>0内,y随x的增大而减小,当x=3时,y= =2;当x=1时,y= =6.∴当1<x<3时,2<y<6.∴y的最小整数值是3.故选A.【分析】根据反比例函数系数k>0,结合反比例函数的性质即可得知该反比例函数在x>0中单调递减,再结合x的取值范围,可得出y的取值范围,取其内的最小整数,本题得解.本题考查了反比例函数的性质,解题的关键是找出反比例函数y= 在1<x<3中y的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的系数结合反比例函数的性质得出该反比例函数的单调性是关键.【答案】C【考点】根据实际问题列反比例函数关系式,三角形的面积【解析】【解答】∵S=xy,∴y=.故选C.【分析】考查列反比例函数关系式,得到三角形高的等量关系是解决本题的关键.三角形的面积= 1 2 底×高,那么高=,把相关数值代入即可求解.【答案】A【考点】反比例函数图象上点的坐标特征【解析】【解答】解:∵反比例函数y= 中,2>0,∴在每一象限内,y随x的增大而减小,∵x1<x2<x3, y2<y1<y3,∴点A,B在第三象限,点C在第一象限,∴x1<x2<0<x3,∴x1•x2<0,故选A.【分析】根据反比例函数y= 和x1<x2<x3, y2<y1<y3,可得点A,B在第三象限,点C在第一象限,得出x1<x2<0<x3,再选择即可.本题考查了反比例函数图象上点的坐标特征,解答此题的关键是熟知反比例函数的增减性,本题是逆用,难度有点大.【答案】B【考点】一次函数图象与几何变换,反比例函数与一次函数的交点问题【解析】【解答】∵平移后解析式是y=x+b,代入y=得:x+b=,即x2+bx=,y=x+b与x轴交点B的坐标是(-b,0),设A的坐标是(x,y),∴OA2-OB2=x2+y2+(-b)2=x2+(x+b)2-b2=2x2+2xb=2(x2+xb)=2×=2,故选B.【分析】本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力的能力.【答案】D【考点】反比例函数图象的对称性【解析】【解答】由于函数图象关于原点对称,所以阴影部分面积为圆面积,则圆的面积为10π×4=40π.因为P(3a,a)在第一象限,则a>0,3a>0,根据勾股定理,OP=于是π=40π,a=±2,(负值舍去),故a=2.P点坐标为(6,2).将P(6,2)代入y=,得:k=6×2=12.反比例函数解析式为:y=.故选D.【分析】根据P(3a,a)和勾股定理,求出圆的半径,进而表示出圆的面积,再根据圆的面积等于阴影部分面积的四倍,求出圆的面积,建立等式即可求出a的值,从而得出反比例函数的解析式.【点评】此题是一道综合题,既要能熟练正确求出圆的面积,又要会用待定系数法求函数的解析式.【答案】C【考点】反比例函数系数k的几何意义,待定系数法求反比例函数解析式,三角形的面积【解析】【解答】如图,连接AC,∵点B的坐标为(4,0),△AO B为等边三角形,∴AO=OB=4.∴点A的坐标为(2,-2).∵C(4,0),∴AO=OC=4,∴∠OCA=∠OAC.∵∠AOB=60°,∴∠ACO=30°.又∵∠B="60°." ∴∠BAC=90°.∵S△ADE=S△DCO, S△AEC=S△ADE+S△ADC, S△AOC=S△DCO+S△ADC,∴∴S△AEC=S△AOC =×AE•AC=•CO•2,即•AE•2=×2×2,∴E点为AB的中点(3,-).把E点(3,-)代入y=中得:k=-3故选C.【分析】连接AC,由B的坐标得到等边三角形AOB的边长,得到AO与CO,得到AO=OC,利用等边对等角得到一对角相等,再由∠AOB=60°,得到∠ACO=30°,可得出∠BAC为直角,可得出A的坐标,由三角形ADE与三角形DCO面积相等,且三角形AEC面积等于三角形AED与三角形ADC面积之和,三角形AOC面积等于三角形DCO面积与三角形ADC面积之和,得到三角形AEC与三角形AOC面积相等,进而确定出AE的长,可得出E为AB中点,得出E的坐标,将E坐标代入反比例解析式中求出k的值,即可确定出反比例解析式。
中考数学总复习经典(代数)试题
中考数学总复习经典(代数)题(一)代数试题1、小高从家门口骑车去单位上班,先走平路到达点A ,再走上坡路到达点B ,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是( ) A .12分钟 B .15分钟 C .25分钟 D .27分钟2、小强从如图所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:(1)0a <;(2)1c >;(3)0b >;(4)0a b c ++>;(5)0a b c -+>.你认为其中正确信息的个数有( )A .2个B .3个C .4个D .5个3、. 在同一直角坐标系中,函数y mx m =+和函数222y mx x =-++(m 是常数,且0m ≠)的图象可能..是知αβ、是关于x 的一4、已元二次方程22(23)0x m x m +++=的两个不相等的实数根,且满足111αβ+=-,则m 的值是( ) A.3或-1 B.3 C. 1 D. –3或15、下列图形都是二次函数y=ax2+bx+a2-1的图象,若b >0,则a 的值等于( )A 、B 、-1C 、D 、16、如图,已知函数y ax b =+和y kx =的图象交于点P, 则根据图象可得,关于y ax b y kx=+⎧⎨=⎩的二元一次方程组的解是7、如图,已知点F 的坐标为(3,0),点A B ,分别是某函数图象与x 轴、y 轴的交点,点P 是此图象上的一动点...设点P 的横坐标为x ,PF 的长为d ,且d 与x 之间满足关系:355d x =-(05x ≤≤),则结论:①2AF =;②5BF =;③5OA =;④3OB =中,正确结论的序号是_ . 8、二次函数c bx ax y ++=2的图象如图6所示,则下列关系式不正确的是( )A .a <0B.abc >0C.c b a ++>0D.ac b 42->09、已知二次函数y=ax 2+bx+c(a ≠0)的图象如图所示,则下列结论中不正确的有( )个.①abc>0②2a+b=0③方程ax 2+bx+c=0(a ≠0)必有两个不相等的实根 ④a+b+c>0⑤当函数值y 随x 的逐渐增大而减小时,必有x ≤1A 、1B 、2C 、3D 、410、如图101,二次函数2y ax bx c =++的图象开口向上,图象经过点(-1,2)和(1,0),且与y 轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)第(1)问:给出四个结论:① 0a >;② 0b >;③ 0c >;④ 0a b c ++=.其中正确结论的序号是 (答对得3分,少选、错选均不得分).第(2)问:给出四个结论:① 0abc <;② 20a b +>;③ 1a c +=;④1a >.其中正确结论的序号是 (答对得5分,少选、错选均不得分). 11、如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数的图象上.若点A 的坐标为(-2,-2),则k 的值为( )(11题图)A 、1B 、-3C 、4D 、1或-3 (第7题) 图1018题12、如图8,点A 、B 、C 、D 为圆O 的四等分点,动点P 从圆心O 出发, 沿O-C-D-O 的路线作匀速运动.设运动时间为t 秒, ∠APB 的度数 为y 度,则下列图象中表示y 与t 之间函数关系最恰当的是13、 如图11,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 1y x=(0x >)的 图象上,则点E 的坐标是( , ).14、如图所示的二次函数y=ax 2+bx+c 的图象中,刘星同学观察得出了下面四条信息: (1)b2-4ac >0;(2)c >1;(3)2a-b <0;(4)a+b+c <0.你认为其中错误的有( )14题 A 、2个 B 、3个 C 、4个 D 、1个15、已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1,与x 轴交于A 、B 两点,交y 轴于点C ,且OB=OC ,则下列结论正确的个数是 . ①b=2a ②a-b+c>-1 ③0<b 2-4ac<4 ④ac+1=bA.1个B.2个C.3个D.4个16、阅读材料:设一元二次方程ax 2+bx +c =0(a ≠0)的两根为x 1,x 2,则两根与方程系数之间有如下关系:x 1+x 2=-b a ,x 1·x 2=ca.根据该材料填空:已知x 1、x 2是方程x 2+6x +3=0的两实数根,则21x x +12x x 的值为 . 17、已知二次函数2(0)y ax bx c a =++≠的图象如图(1)所示,则直线y ax b =+与反比例函数acy x=,在同一坐标系内的大致图象为( ) (18题图)xA .xB .D .xC .18、二次函数y=ax 2+bx+c(a ≠0)的图像如图所示,下列结论正确的是( )A.ac <0B.当x=1时,y >0C.方程ax 2+bx+c=0(a ≠0)有两个大于1的实数根D.存在一个大于1的实数x 0,使得当x <x 0时,y 随x 的增大而减小; 当x >x 0时,y 随x 的增大而增大. 19、甲、乙两个工程队完成某项工程,首先是甲单独做了10天,然后乙队加入合做,完成剩下的全部工程,设工程总量为单位1, 工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲单独完成这项工程所需时间少( )A.12天B.14天C.16天D.18天20、关于x 的一次函数21y kx k =++的图象可能正确的是( )21、(2010年杭州月考)如图,C 为⊙O 直径AB 上一动点,过点C 的直线交⊙O 于D 、E 两点, 且∠ACD=45°,DF ⊥AB 于点F,EG ⊥AB 于点G ,当点C 在AB 上运动时,设AF=x ,DE=y ,下列中图象中,能表示y 与x 的函数关系式的图象大致是( )22、如图所示是二次函数.2y ax bx c =++图象的一部分,图象过A 点(3,0),二次函数图象对称轴为1x =,给出四个结论:①24b ac >;②0bc <;③20a b +=;④0a b c ++=,其中正确结论是( ) A .②④B .①③C .②③D .①④23、如图6所示的计算程序中,y 与x 之间的函数关系所对应的图象应为( )24、若A (1,413y -),B (2,45y-),C (3,41y )为二次函数245y x x =+-的图象上的三点,则1,y 2,y 3y的大小关系是A .123y y y <<B .213y y y <<C .312y y y <<D .132y y y <<xxxxD.第20题图ADCB图6(第1925、已知αβ,为方程2420x x ++=的二实根,则31450αβ++= . 26、在反比例函数4y x=的图象中,阴影部分的面积不等于4的是( )A .B .C .D .27、如图4,直线24y x =-+与x 轴,y 轴分别相交于A B ,两点,C 为OB 上一点,且12∠=∠,则ABC S =△ ( ) A .1 B .2 C .3 D .428、 如图已知一次函数y=kx+b 和y=mx+n 的图象交于点P ,则根据图象可得不等式组0<mx+n <kx+b 的 解集是-29、如图,直线y 1=kx+b 过点A (0,2),且与直线y 2=mx 交于点P (1,m ),则不等式组mx>kx+b>mx-2的解集是------29题图 30题图 31题图 30、如图,已知A (-4,2)、B (2,-4)是一次函数y=kx+b 的图象和反比例函数的图象上的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线AB 与y 轴的交点C 的坐标及△AOB 的面积; (3)直接写出方程kx+b=0的解; (4)直接写出不等式kx+b >0的解.31、如图:已知A (-4,n )、B (2,-4)是一次函数y 1=kx+b 的图象与反比例函数 的图象的两个交点.(1)求反比例函数和一次函数的解折式.(2)求直线AB 与x 轴的交点C 的坐标及△AOB 的面积. (3)求不等式y 1<y 2的解集(请直接写出答案).图432题图32、如图,已知一次函数y=kx+b 的图象过点(1,-2),则关于x 的不等式kx+b+2≤0的解集是 33、已知一次函数y=kx+b 的图象经过点(1,2),且不经过第三象限,那么关于x 的不等式kx+b >2的解集是34、小明从图5所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:①0c <;②0abc >;③0a b c -+>;④230a b -=;⑤40c b ->,你认为其中正确信息的个数有( )A .2个B .3个C .4个D .5个35、小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象l 1、l 2,如图所示,他解的这个方程组是( )A 、B 、C 、D 、136、如图,直线y kx b =+经过A (-2,-1)和B (-3,0)两点,则不等式组102x kx b <+< 的解集为 .37、如图,半径为5的⊙P 与轴交于点M (0,-4),N (0,-10),函数(0)ky x x=<的图像过点P ,则k = . 38、已知点(-1,y 1),(2,y 2),(3,y 3)在反比例函数y= 的图象上.下列结论中正确的是( )A 、y 1>y 2>y 3B 、y 1>y 3>y 2C 、y 3>y 1>y 2D 、y 2>y 3>y 139、已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①240b ac ->;②0abc >;③80a c +>;④930a b c ++<. 其中,正确结论的个数是(A )1 (B )2 (C )3(D )4第37题第39题图540、 抛物线c bx ax y ++=2图像如图所示,则一次函数24b ac bx y +--=与反比例函数 a b cy x++=在同一坐标系内的图像大致为(41题图)C. D . 41、二次函数y=x 2-x-2的图象如图所示,则函数值y <0时x 的取值范围是( )A 、x <-1B 、x>2 C 、-1<x <2 D 、x <-1或x >242、如图,已知正方形ABCD 的边长为4 ,E 是BC 边上的一个 动点,AE ⊥EF , EF 交DC 于F , 设BE =x ,FC =y ,则当 点E 从点B 运动到点C 时,y 关于x 的函数图象是( ).43、(1)已知点A(2,3),将线段OA 绕点O 逆时针旋转900得到对应线段OA ’,则点A ’关于直线y=1对称的点的坐标是 ;(2)将直线y=2x+3向右平移2个单位长度得到直线L 1,则直线L 1关于直线y=1对称的直线的解析式为 ;(3)写出直线y=kx+b 关于直线y=1对称的直线的解析式 。
中考数学专题复习之一题多解题

三角形,分为三种情况:DA=DP,PA=PD,AP=AD(此时点P在边AB的延长
线上,不合题意).①如解图,当DA=DP=8时(点P为图中的点P1,E为图中的点
E1),由题意得BD= AB2 AD2= 62 82=10,BP1=BD-DP1=10-8=2,由
△P1BE1∽△DBC得
P1E1 =
DC
例3解题图
专题三 多解题
类型三 裁剪、拼接
例4 在一张三角形纸片上,取其一边的中点,沿着过这点的两条中位线分别剪去 两个小三角形,剩下的部分就是如图所示的平行四边形ABCD,经测量这个平行四 边形的相邻两边长为5、3,一条对角线的长为4,则原三角形纸片的周长是 __2_4_或__1_6_+_4___13__.
33
n),抛物线y=ax2-x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围
是_a_≤_-__1_或____14_≤_a_<__13__.
【解析】∵直线y=-1 x+5 经过点M(-1,m)和点N(2,n),∴m=-1 ×(-1)
+5
1
35 3
3
3
=2,n=-
3
×2+
3
=1,∴M(-1,2)1,N(25,1),∵抛物线y=ax2-x+2
例4题图
专题三 多解题
【解析】如解图①,当以过点A的中位线AB、AD剪去两个小三角形时,有EC= 2AB=2×5=10,FC=2AD=2×3=6,EF=2DB=2×4=8,∴原三角形纸片 的周长为10+6+8=24;如解图②,当以过点B的中位线BA、BC剪去两个小三 角形时,有DF=2AB=2×5=10,DE=2BC=2×3=6,∵DC2=52=BC2+DB2 =32+42,∴∠DBC=90°,∴∠EDB=90°,∴BE= DB2 DE2 =2 13, ∴EF=24BE1=3 ,∴原三角形纸片的周长为10+4 61+3 =41613+ .综上所述, 原三角形纸片的周长为24或4161+3 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
图形变换不确定型多解题
• 特征与方法:图形变换不确定型多解题,常见有图形的旋转及轴对称 (翻折)等变换,在图形的变换中产生不明确的因素,需要进行分类讨论, 从而产生多解.解决此类问题首先要弄清变换前后哪些量发生变化,哪 些没有变化,找出变化后的数量关系,明确分类讨论的对象,全面考虑, 建立数学模型,从而解决问题.
4
图1 图2
③当∠ABP=90°时,如图 3, ∵∠AOC=∠BOP=60°,∴∠BPO=30°, ∴BP=taOn3B0°= 23=2 3,在直角三角形 ABP 中,AP= 2 32+42=2 7.
3 综上所述,AP 的长为 2 或 2 3或 2 7.
图3
5
(2016 江西模拟)如图,已知点 A 是反比例函数 y=1x的图象与一次函数 y=2x-1 的图象在第一象限的交点,点 P 是 x 轴上一动点,当△OAP 是等腰三角形时,点 P 的坐标为_(-____2_,__0_)或__(_1_,0_)_或__(__2_,__0_)_或__(2_,_0_)___ .
• 【考查内容】本题考查反比例函数和一次函数的性质、 解二元一次方程组、等腰三角形的判定和性质,勾股定 理,坐标与图形,分类讨论思想.本题有两个不确定对 象,一是点P是x轴上正半轴还是负半轴上;二是△OAP 是等腰三角形哪两边为腰.不重不漏进行分类讨论是解 决本题的关键.
6
【解析】解方程组y=1x, y=2x-1,
得x1=-12, y1=-2,
x2=1, y2=1,
则点 A(1,1),OA=2.①如图 1,当点 P 在 x 轴负半轴上且 OA=OP 时,点 P 的坐标为(- 2,0);
②如图 2,当点 P 在 x 轴正半轴上且 OA=OP 时,点 P 的坐标为( 2,0);
7
③如图 3,当点 P 在 x 轴正半轴上且 AO=AP 时,点 P 的坐标为(2,0);
9
• 【例2】 (2016吉安九校联考)如图,△ABC中,∠ACB=90°, ∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角 时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的 值为___________________.
40°或70°或100°
10
【思路点拨】 本题考查旋转的性质:对应点到旋转中心的距离相等;对应点 与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.连接 AP,由旋转 的性质得 OP=OB,则可判断点 P,C 在以 AB 为直径的圆上,利用圆周角定理得∠ BAP=12∠BOP=12α,∠ACP=∠ABP=90°-12α,∠APC=∠ABC=70°,然后分类 讨论:当 AP=AC 时,∠APC=∠ACP,即 90°-12α=70°;当 PA=PC 时,∠PAC =∠ACP,即12α+20°=90°-12α;当 CP=CA 时,∠CAP=∠CAP,即12α+20°=70°, 再分别解关于 α 的方程即可.
3
【解答】 分三种情况讨论: ①当∠APB=90°,点 P 在线段 CO 上时,如图 1, ∵AO=BO,∠APB=90°,∴PO=AO, ∵∠AOC=60°,∴△AOP 为等边三角形, ∴AP=AO=2; ②当∠APB=90°,点 P 在线段 CO 延长线上时,如图 2, ∵AO=BO,∴PO=BO,∵∠AOC=60°, ∴∠BOP=60°, ∴△BOP 为等边三角形, ∵AB=BC=4,∴AP=AB·sin60°=4× 23=2 3;
①如图 1,当 AP=AC 时,∠APC=∠ACP,
即 90°-12α=70°,解得 α=40°.
图1
12
②如图 2,当 PA=PC 时,∠PAC=∠ACP, 即12α+20°=90°-12α,解得 α=70°. ③如图 3,当 CP=CA 时,∠CAP=∠CPA,即12α+20°=70°,解得 α=100°. 综上所述,α 的值为 40°或 70°或 100°.
11
【解答】 连接 AP,如图,
∵点 O 是 AB 的中点,∴OA=OB.∵OB 绕点 O 顺时针旋转 α 角时(0°<α<180°),
得到 OP,∴OP=OB.∴点 P 在以 AB 为直径的半圆上.∴∠BAP=12∠BOP=12α.
∵∠ACB=90°,∴点 P,C 在以 AB 为直径的圆上.
∴∠ACP=∠ABP=90°-12α,∠APC=∠ABC=90°-20°=70°.
2
• 【例1】 (2015江西)如图,在△ABC中,AB=BC=4, AO=BO,P是射线CO上的一个动点,∠AOC=60°,则 当△PAB为直角三角形时,AP的长为_______________ .
2 或 2 3或 2 7
【思路点拨】 本题主要考查等边三角形的判定与性质、含30°角的直角三角形的性质和直角三角形斜边 的中线的性质、勾股定理及点运动型问题.当△PAB为直角三角形时,哪一个内角是直角呢?点P在线段CO上还 是在线段CO延长线上?就需要分情况讨论了,当∠APB=90°时,分两种情况讨论,情况一:利用直角三角形斜 边的中线等于斜边的一半得出结论;情况二:易得∠ABP=60°,利用锐角三角函数得AP的长;当∠ABP=90° 时,易得BP,利用勾股定理可得AP的长.因此分类讨论及数形结合是解答此题的关键.
第二部分 专题综合强化
专题一 多解题
重点类型 ·突破
点运动型多解题
• 特征与方法:满足条件的多解型试题是江西省2013年中考试题开始创设 的一类独创性题型,一直放在填空题的最后一题,考查宗旨主要是进一 步强调分类讨论这一思想方法运用.点运动型多解题,是江西省近几年 来常考的类型,常见于某点在射线、直线、多边形的边上或直角坐标系 的坐标轴上运动,与之相关的图形的边或角产生变化而不明确,从而导 致分情况讨论产生多解.解决此类问题时,利用数形结合方法,采取 “动中求静,静中求解”的策略,以相对静止的瞬间,发现量与量之间 的关系.而在图形的变化中不重不漏地进行分类讨论是解决此类问题的 关键.
