抛物线与面积专题复习学案
学案2:2.3.1抛物线及其标准方程

2.3.1 抛物线及其标准方程学习目标:1.掌握抛物线的定义及其标准方程.2.了解抛物线的实际应用.3.能区分抛物线标准方程的四种形式.预习提示:1.我们知道,二次函数的图象是抛物线,那么抛物线上的点应满足什么条件呢?2. 抛物线的定义中,l能经过点F吗?为什么?3.比较椭圆、双曲线标准方程的建立过程,你认为应如何选择坐标系,建立的抛物线方程才能更简单?4.抛物线方程中p有何意义?标准方程有几种类型?抛物线的开口方向由什么决定?5.抛物线与二次函数有何关系?课堂探究:例1、(1)抛物线y2=2px(p>0)上一点A(6,y0),且点A到焦点的距离为10,则焦点到准线的距离是()A.4 B.8C.13 D.16(2)若点P到定点F(4,0)的距离比它到定直线x+5=0的距离小1,则点P的轨迹方程是()A.y2=-16xB.y2=-32xC.y2=16xD.y2=16x或y=0(x<0)变式训练:(1)抛物线x2=4y上一点A的纵坐标为4,则A点到抛物线焦点的距离为() A.2B.3 C.4 D.5(2)若动圆与圆(x-2)2+y2=1外切,又与直线x+1=0相切,则动圆圆心的轨迹方程是()A.y2=8x B.y2=-8x C.y2=4x D.y2=-4x例2、分别求适合下列条件的抛物线的标准方程.(1)过点M(-6,6).(2)焦点在直线l:3x-2y-6=0上.(3)已知抛物线的焦点在x轴上,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的标准方程.变式训练:若把本例题目改为:(1)过点(1,2).(2)焦点在直线x-2y-4=0上.试求抛物线的标准方程.例3、设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.(1)求点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值;(2)若点B的坐标为(3,2),求|PB|+|PF|的最小值.变式训练:定长为3的线段AB的端点A、B在抛物线y2=x上移动,求AB的中点M 到y轴的距离的最小值.例4、如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程;(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米(精确到0.1米)?变式训练:某河上有座抛物线形拱桥,当水面距拱顶5 m时,水面宽8 m,一木船宽4m ,高2 m ,载货后木船露在水面上的部分高为34 m ,问水面上涨到与拱顶相距多少时,木船开始不能通航?当堂达标:1.抛物线y 2=-8x 的焦点坐标是( ) A .(2,0) B .(-2,0) C .(4,0)D .(-4,0)2.设抛物线的顶点在原点,准线方程为x =-2,则抛物线的方程是( ) A .y 2=-8x B .y 2=8x C .y 2=-4x D .y 2=4x 3.已知动点M (x ,y )的坐标满足x -22+y 2=|x +2|,则动点M 的轨迹是( )A .椭圆B .双曲线C .抛物线D .以上均不对4.抛物线y 2=-2px (p >0)上有一点M 的横坐标为-9,它到焦点的距离为10,求此抛物线方程和M 点的坐标. 答案:1.【提示】 抛物线上的点满足到定点的距离等于它到定直线的距离.2. 【提示】 不能,若l 经过点F ,满足条件的点的轨迹不是抛物线,而是过点F 且垂直于l 的一条直线.3.【提示】 根据抛物线的几何特征,可以取经过点F 且垂直于直线l 的直线为x 轴,以F 到l 的垂线段的中垂线为y 轴建系.4.【提示】 p 是抛物线的焦点到准线的距离 抛物线的标准方程有四种类型:①焦点在x 轴的正半轴上,其标准方程为y 2=2px (p >0); ②焦点在x 轴的负半轴上,其标准方程为y 2=-2px (p >0); ③焦点在y 轴的正半轴上,其标准方程为x 2=2py (p >0); ④焦点在y 轴的负半轴上,其标准方程为x 2=-2py (p >0). 抛物线的方程中一次项决定开口方向.5.【提示】 二次函数的解析式为y =ax 2+bx +c (a ≠0),当b ,c 为0时,y =ax 2表示焦点在y 轴上的抛物线,标准方程为x 2=1a y ,a >0时抛物线开口向上,a <0时,抛物线开口向下,当抛物线的开口方向向左或向右时,方程为y 2=2px ,这是一条曲线,不能称为函数.课堂探究:例1、 【自主解答】 (1)由题意6+p2=10,∴p =8.(2)因为点F (4,0)在直线x +5=0的右侧,且P 点到点F (4,0)的距离比它到直线x +5=0的距离小1,所以点P 到F (4,0)的距离与到直线x +4=0的距离相等.故点P 的轨迹为抛物线,且顶点在原点,开口向右,p =8,故P 点的轨迹方程为y 2=16x .【答案】 (1)B (2)C变式训练:【解析】 (1)由抛物线的定义,点A 到焦点的距离等于它到准线的距离,而A 到准线的距离为4+p2=4+1=5.(2)由题意,动圆圆心到定圆圆心的距离比它到直线x +1=0的距离大1,故动圆圆心的轨迹是以(2,0)为焦点,x =-2为准线的抛物线,其方程为y 2=8x .【答案】 (1)D (2)A例2、 【自主解答】 (1)由于点M (-6,6)在第二象限, ∴过M 的抛物线开口向左或开口向上. 若抛物线开口向左,焦点在x 轴上, 设其方程为y 2=-2px (p >0),将点M (-6,6)代入,可得36=-2p ×(-6), ∴p =3.∴抛物线的方程为y 2=-6x ;若抛物线开口向上,焦点在y 轴上,设其方程为x 2=2py (p >0), 将点M (-6,6)代入可得,36=2p ×6,∴p =3, ∴抛物线的方程为x 2=6y .综上所述,抛物线的标准方程为y 2=-6x 或x 2=6y . (2)①∵直线l 与x 轴的交点为(2,0), ∴抛物线的焦点是F (2,0), ∴p2=2,∴p =4, ∴抛物线的标准方程是y 2=8x . ②∵直线l 与y 轴的交点为(0,-3), 即抛物线的焦点是F (0,-3), ∴p2=3,∴p =6, ∴抛物线的标准方程是x 2=-12y .综上所述,所求抛物线的标准方程是y 2=8x 或x 2=-12y .(3)法一:设抛物线方程为y 2=-2px (p >0),则焦点为F ⎝⎛⎭⎫-p2,0, 由题设可得⎩⎨⎧m 2=6p ,m 2+⎝⎛⎭⎫3-p22=5, 解得{ p =4,m =26或{ p =4,m =-26,故所求的抛物线方程为y 2=-8x .法二:设抛物线方程为y 2=-2px (p >0),则焦点F ⎝⎛⎭⎫-p 2,0,准线方程为x =p 2, 根据抛物线的定义,点M 到焦点的距离等于5,也就是M 到准线的距离为5, 则3+p2=5,∴p =4,∴抛物线方程为y 2=-8x .变式训练:【解】 (1)点(1,2)在第一象限,分两种情形: 当抛物线焦点在x 轴上时,设其方程为y 2=2px (p >0), 则22=2p ·1,解得p =2, 抛物线标准方程为y 2=4x ;当抛物线焦点在y 轴上时,设其方程为x 2=2py (p >0), 则12=2p ·2,解得p =14,抛物线标准方程为x 2=12y .(2)令方程x -2y -4=0的x =0得y =-2,令y =0得x =4. ∴抛物线的焦点为(4,0)或(0,-2), 当焦点为(4,0)时,p2=4,∴p =8,这时抛物线标准方程为y 2=16x ; 当焦点为(0,-2)时,p2=2,∴p =4,这时抛物线标准方程为x 2=-8y .例3、 【自主解答】 (1)如图,易知抛物线的焦点为F (1,0),准线方程是x =-1,由抛物线的定义知:点P 到直线x =-1的距离等于点P 到焦点F 的距离.于是问题转化为:在曲线上求一点P ,使点P 到点A (-1,1)的距离与点P 到F (1,0)的距离之和最小.显然,连接AF ,AF 与抛物线的交点即为点P ,故最小值为22+12=5,即点P 到点A (-1,1)的距离与点P 到直线x =-1的距离之和的最小值为 5.①(2)如图,把点B 的横坐标代入y 2=4x 中,得y =±12.因为12>2,所以点B 在抛物线内部,过点B 作BQ 垂直于准线,垂足为点Q ,交抛物线于点P 1,连接P 1F .此时,由抛物线定义知:|P 1Q |=|P 1F |.②所以|PB |+|PF |≥|P 1B |+|P 1Q |=|BQ |=3+1=4,即|PB |+|PF |的最小值为4.变式训练:【解】 如图,F 是抛物线y 2=x 的焦点,过A 、B 两点分别作准线的垂线AC 、BD ,过AB 的中点M 作准线的垂线MN ,C 、D 、N 为垂足,则|MN |=12(|AC |+|BD |).由抛物线的定义可知 |AF |=|AC |,|BD |=|BF |, ∴|MN |=12(|AF |+|BF |)≥12|AB |=32.设M 点的坐标为(x ,y ),则|MN |=x +14.又|MN |≥32,∴x ≥32-14=54,当且仅当AB 过抛物线的焦点时等号成立.此时点M 到y 轴的距离的最小值为54.例4、【自主解答】 如图所示(1)依题意,设该抛物线的方程为x 2=-2py (p >0), 因为点C (5,-5)在抛物线上, 所以该抛物线的方程为x 2=-5y .(2)设车辆高h ,则|DB |=h +0.5,故D (3.5,h -6.5), 代入方程x 2=-5y ,解得h =4.05, 所以车辆通过隧道的限制高度为4.0米.变式训练:【解】 以拱桥拱顶为坐标原点,拱高所在直线为y 轴,建立如下图所示的直角坐标系,设抛物线方程为x 2=-2py (p >0).由题意知,点A (4,-5)在抛物线x 2=-2py (p >0)上.所以16=-2p ×(-5),2p =165. 所以抛物线方程为x 2=-165y (-4≤x ≤4).设水面上涨船面两侧与抛物线拱桥接触于B 、B ′时,船开始不能通航. 设B (2,y ),由于22=-165×y ,所以y =-54.所以水面与抛物线拱顶相距|y |+34=2(m).答:水面上涨到与抛物线拱顶相距2 m 时,船开始不能通航.当堂达标:1.【解析】 由y 2=-8x ,得2p =8,∴p2=2.从而抛物线的焦点为(-2,0). 【答案】 B2.【解析】 由准线x =-2及顶点在原点, ∴焦点F (2,0),p =4. ∴抛物线的方程为y 2=8x . 【答案】 B3.【解析】 由条件知M 点轨迹满足抛物线定义.即M 到定点(2,0)与到定直线x =-2的距离相等,所以点M 的轨迹是抛物线. 【答案】 C4.【解】 设焦点为F ⎝⎛⎭⎫-p2,0,M 点到准线的距离为d . 则d =|MF |=10,即9+p2=10.∴p =2,∴抛物线方程为y 2=-4x , 将M (-9,y )代入抛物线的方程,得y =±6. ∴M 点坐标为(-9,6)或(-9,-6).。
抛物线学案-2023届高三数学一轮复习

第7节 抛物线考试要求 1.了解抛物线的实际背景,了解抛物线在刻画现实世界和解决实际问题中的作用;2.掌握抛物线的定义、几何图形、标准方程及简单几何性质. 知识梳理 1.抛物线的定义(1)平面内与一个定点F 和一条定直线l (F ∉l )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的 .(2)其数学表达式:{M ||MF |=d }(d 为点M 到准线l 的距离). 2.抛物线的标准方程与几何性质图形标准方程y 2=2px(p >0)y 2=-2px(p >0)x 2=2py(p >0)x 2=-2py(p >0)p 的几何意义:焦点F 到准线l 的距离性质顶点对称轴焦点离心率准线方程 y =p2 范围 开口方向向左3.设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则 (1)x 1·x 2=p 24.(2)y 1·y 2=-p 2.(3)|AB |=x 1+x 2+p =2psin 2α(α是直线AB 的倾斜角).(4)1|AF |+1|BF |=2p 为定值(F 是抛物线的焦点). 自主检测1.顶点在原点,且过点P (-2,3)的抛物线的标准方程是________________.2. 抛物线y 2=8x 上到其焦点F 距离为5的点的个数为________.3.若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p =( ) A.2 B.3 C.4 D.84.已知F 是抛物线y 2=x 的焦点,A ,B 是抛物线上的两点,且|AF |+|BF |=3,则线段AB 的中点到y 轴的距离为( )A.34B.1C.54D.745.已知抛物线方程为y 2=8x ,若过点Q (-2,0)的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是________. 典型例题考点一 抛物线的定义、标准方程及其性质【例1】 (1)已知抛物线C 与双曲线x 2-y 2=1有相同的焦点,且顶点在原点,则抛物线C 的方程是( ) A.y 2=±22x B.y 2=±2x C.y 2=±4x D.y 2=±42x(2)设抛物线y 2=4x 的焦点为F ,准线为l ,P 为该抛物线上一点,P A ⊥l ,A 为垂足,若直线AF 的斜率为-3,则△P AF 的面积为( ) A.2 3 B.4 3 C.8 D.8 3(3)动圆过点(1,0),且与直线x =-1相切,则动圆的圆心的轨迹方程为__________.【训练1】 (1)设抛物线y 2=2px 的焦点在直线2x +3y -8=0上,则该抛物线的准线方程为( ) A.x =-4 B.x =-3 C.x =-2 D.x =-1(2)已知抛物线x 2=2py (p >0)的焦点为F ,准线为l ,点P (4,y 0)在抛物线上,K 为l 与y 轴的交点,且|PK |=2|PF |,则y 0=________.考点二 与抛物线有关的最值问题 角度1 到焦点与定点距离之和(差)最值问题【例2-1】 点P 为抛物线y 2=4x 上的动点,点A (2,1)为平面内定点,F 为抛物线焦点,则: (1)|P A |+|PF |的最小值为________;(2)(多填题)|P A |-|PF |的最小值为________,最大值为________. 角度2 到点与准线的距离之和最值问题【例2-2】 设P 是抛物线y 2=4x 上的一个动点,则点P 到点A (-1,1)的距离与点P 到直线x =-1的距离之和的最小值为________.角度3 动弦中点到坐标轴距离最短问题【例2-3】 已知抛物线x 2=4y 上有一条长为6的动弦AB ,则AB 的中点到x 轴的最短距离为( ) A.34 B.32 C.1 D.2角度4 焦点弦中距离之和最小问题【例2-4】 已知抛物线y 2=4x ,过焦点F 的直线与抛物线交于A ,B 两点,过A ,B 分别作y 轴的垂线,垂足分别为C ,D ,则|AC |+|BD |的最小值为________.角度5 到定直线的距离最小问题【例2-5】 抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是________.【训练2】 (1)若在抛物线y 2=-4x 上存在一点P ,使其到焦点F 的距离与到A (-2,1)的距离之和最小,则该点的坐标为( ) A.⎝⎛⎭⎫-14,1 B.⎝⎛⎭⎫14,1 C.(-2,-22) D.(-2,22)(2)已知P 为抛物线y 2=4x 上一个动点,Q 为圆C :x 2+(y -4)2=1上一个动点,那么点P 到点Q 的距离与点P 到抛物线准线的距离之和的最小值是________. 考点三 直线与抛物线的综合问题【例3】 已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求直线l 的方程; (2)若AP →=3PB →,求|AB |.【训练3】 如图所示,抛物线关于x 轴对称,它的顶点在坐标原点,点P (1,2),A (x 1,y 1),B (x 2,y 2)均在抛物线上.(1)写出该抛物线的方程及其准线方程;(2)当P A 与PB 的斜率存在且倾斜角互补时,求y 1+y 2的值及直线AB 的斜率.当堂检测1.已知抛物线y 2=2px (p >0),点C (-4,0),过抛物线的焦点作垂直于x 轴的直线,与抛物线交于A ,B 两点,若△CAB 的面积为24,则以直线AB 为准线的抛物线的标准方程是( ) A.y 2=4x B.y 2=-4x C.y 2=8x D.y 2=-8x2.设抛物线C :y 2=3x 的焦点为F ,点A 为C 上一点,若|F A |=3,则直线F A 的倾斜角为( ) A.π3 B.π4 C.π3或2π3 D.π4或3π43.设F 为抛物线y 2=2x 的焦点,A ,B ,C 为抛物线上三点,若F 为△ABC 的重心,则|F A →|+|FB →|+|FC →|的值为________.4.已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2.若抛物线C 2:x 2=2py (p >0)的焦点到双曲线C 1的渐近线的距离为2,则抛物线C 2的方程为________.5.已知P 为抛物线C :y =x 2上一动点,直线l :y =2x -4与x 轴、 y 轴交于M ,N 两点,点A (2,-4)且AP →=λAM →+μAN →,则λ+μ的最小值为________.6.设A ,B 为曲线C :y =x 24上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.7.已知过抛物线y 2=2px (p >0)的焦点,斜率为22的直线交抛物线于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点,且|AB |=9.(1)求该抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若OC →=OA →+λOB →,求λ的值.。
抛物线与面积专题复习学案
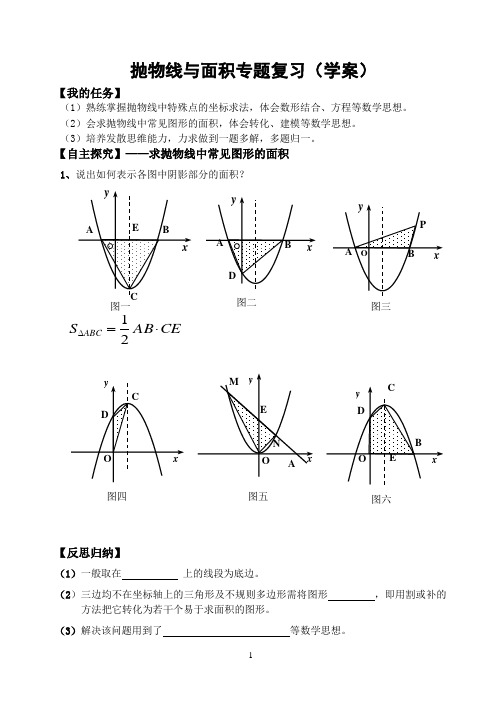
抛物线与面积专题复习(学案)【我的任务】(1)熟练掌握抛物线中特殊点的坐标求法,体会数形结合、方程等数学思想。
(2)会求抛物线中常见图形的面积,体会转化、建模等数学思想。
(3)培养发散思维能力,力求做到一题多解,多题归一。
【自主探究】——求抛物线中常见图形的面积1、说出如何表示各图中阴影部分的面积?【反思归纳】(1)一般取在 上的线段为底边。
(2)三边均不在坐标轴上的三角形及不规则多边形需将图形 ,即用割或补的方法把它转化为若干个易于求面积的图形。
(3)解决该问题用到了 等数学思想。
图五图四 图六图二图一CE AB S ABC⋅=∆21图三【尝试应用】——知识整合2、已知二次函数322--=x x y 与x 轴交于A 、B 两点(A 在B 的左边),与y 轴交于点C ,顶点为P.(1)结合图形,提出几个面积问题,并思考解法;(2)求A 、B 、C 、P 的坐标,并求出一个刚刚提出的图形面积; (3)在抛物线上(除点C 外),是否存在点N ,使得ABC NAB S S ∆∆=,若存在,请写出点N 的坐标;若不存在,请说明理由。
变式一:在抛物线的对称轴上是否存点N ,使得ABC NAB S S ∆∆=,若存在直接写出N 的坐标;若不存在,请说明理由.变式二:在双曲线3y x=上是否存在点N ,使得ABC NAB S S ∆∆=,若存在直接写出N 的坐标;若不存在,请说明理由.【反思归纳】——万变不离其宗同底 高的三角形面积相等,平行线间的距离处处 ;该类问题最终可转化为方程组是否有解的问题.【拓展提高】——中考真题改编3、已知二次函数322--=x x y 与x 轴交于A 、B 两点(A 在B 的左边),与y 轴交于点C.在抛物线上是否存在点N ,使得NBC ABC S S ∆∆=.【硕果累累】——感受收获的喜悦通过本节课的复习,我学会了……体会到了 的数学思想.【走进考场】——锲而不舍,金石可镂(2011,日照)如图,抛物线y=ax 2+bx (a 0)与双曲线y =xk相交于点A ,B . 已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan ∠AOx =4. 过点A 作直线AC ∥x 轴,交抛物线于另一点C .(1)求双曲线和抛物线的解析式;(3分) (2)计算△ABC 的面积;(4分)(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABC 的面积.若存在,请你写出点D 的坐标;若不存在,请你说明理由.(3(郯城五中 孟祥飞)。
[初中数学]抛物线复习教案 人教版
![[初中数学]抛物线复习教案 人教版](https://img.taocdn.com/s3/m/4865546133687e21af45a954.png)
拓展:
过抛物线 的焦点的直线交抛物线于 两点,且直线OA、OB的斜率分别为 ,则 , , 中有几个定值?
解:设直线AB的方程为 ,
联立
;
又 ;
而 ,所以 , , 均为定值。
课后练习:(高考·全国卷)设抛物线 的焦点为F,经过点F 的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC//x轴,证明:直线AC经过原点。
解:如图所示,因为抛物线 的焦点为
,所以经过F点的直线AB的方程可设为:
,联立 消去x可得
.若记 ,则
是该方程的两个根,所以 .
因为BC//x轴,且点C在准线 上,所以点C的坐标为 ,故直线CO的斜率为 ,即k也是直线OA的斜率,所以直线AC经过原点O.
三、课时小结
1.抛物线的定义、方程、几何性质;
,
所以 ,
此时即AB于y轴垂直(如图)。
变式:若该题中将A点的坐标改为 ,求 的最小值。
析:经判断A点在抛物线外,所以连接AF则
的长即为 的最小值,即
②设过定点M的直线方程为 ,
显然, ,直线交抛物线于点B、C。
,把直线方程带入抛物线,得
所以动直线方程为 ,即 ,必过定点(8,0);
当 不存在时,直线x=8交抛物线于点B(8,-8)、C(8,8),仍有 。
解析: 得, ,又焦点坐标为(1,0),所以直线方程为: 。
例4:已知抛物线 ,焦点为F,P为抛物线上一动点,定点A坐标为(4,2),
①求 的最小值。②(2)若点O为坐标原点,问是否存在点M,使过M的动直线与抛物线交与B、C两点,且 ,证明你的结论。
解:①因为点P为抛物线上的点,由抛物线的定义知:
抛物线复习学案

《抛物线》复习学案【基础知识】1. 抛物线定义:平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线 定点F 叫做抛物线的________,定直线l 叫做抛物线的________2、抛物线的标准方程、类型及其几何性质 (0>p ):3.弦长公式:),(11y x A ,),(22y x B 是抛物线上两点,则AB =||11||1212212y y kx x k -+=-+= 【基础自测】1、抛物线24x y =上的一点M 到焦点的距离为1,则点M 的纵坐标是( )A .1617 B .1615 C .87D .02、抛物线2ax y =的准线方程是2=y ,则a 的值为 ( )A .81B .-81C .8D .-83、设a ≠0,a ∈R ,则抛物线y=4ax 2的焦点坐标为 .4、若抛物线y 2=2px 的焦点与椭圆62x +22y =1的右焦点重合,则p 的值为 .二、例题讲析考点1 抛物线的定义(抛物线上的点到焦点的距离与到准线的距离之间的转换)例1 .设抛物线2y =8x 的焦点为F ,A 为抛物线上的一点,且F A =6,则点A 的坐标是__ 例2:已知点P 在抛物线y2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和的最小值为变式训练:1.已知点),4,3(A F 是抛物线x y 82=的焦点,M 是抛物线上的动点,当MF MA +最小时,M 点坐标( )A. )0,0(B. )62,3(C. )4,2(D. )62,3(- 考点2 抛物线的标准方程(要注意焦点位置和开口方向)例3:顶点在原点、焦点在坐标轴上且经过点(3,2)的抛物线的条数有例4、求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程: (1)过点(-3,2) (2)焦点在直线240x y --=上变式训练3.若抛物线22y px =的焦点与双曲线的右焦点2213x y -=重合,则p 的值4. 对于顶点在原点的抛物线,给出下列条件:①焦点在y 轴上; ②焦点在x 轴上; ③抛物线上横坐标为1的点到焦点的距离等于6; ④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为y 2=10x 的条件是____________.(要求填写合适条件的序号) 考点3 抛物线的几何性质例5 如果1P ,2P ,…,8P 是抛物线24y x =上的点,它们的横坐标依次为1x ,2x ,…,8x ,F 是抛物线的焦点,若)(,,,21*∈N n x x x n 成等差数列且45921=+++x x x ,则||5F P =( ). A .5 B .6 C . 7 D .9变式训练6、若直线10ax y -+=经过抛物线24y x =的焦点,则实数a =7、如图,已知O 是坐标原点,过点)0,5(P 且斜率为k 的直线l 交 抛物线x y 52=于),(11y x M 、),(22y x N 两点.(1)求21x x 和21y y 的值; (2)求证:ON OM .考点4 有关于直线与抛物线问题例6.过抛物线2y =4x 的焦点作直线交抛物线与于A (1x ,1y )、B(2x ,2y )两点, 若1x +2x =6,则AB 的值为( )(A )10 (B)8 (C)6 (D)4 例7 .过点(0,-2)和抛物线C: 2y = 2x 只有一个公共点的直线有_______条.例8、过抛物线2y =4x 的焦点F 的一条直线l 与这条抛物线相交于A (1x ,1y )、B(2x ,2y )两点,求21x x +21y y 的值。
初三数学一轮复习面积问题综合教案(含练习)

Presented by Csuzzy,All Rights Reserved.7面积问题§7-1铅锤法如图,抛物线2y x bx c =++(b ,c 为常数)与x 轴相交于点()1,0A -,()3,0B ,与y 轴相交于点C ,其对称轴与x 轴相交于点D ,作直线BC .(1)求抛物线的解析式.(2)设点P 为抛物线对称轴上的一个动点.①如图1,若点P 为抛物线的顶点,求PBC △的面积.②是否存在点P 使PBC △的面积为6?若存在,求出点P 坐标;若不存在,请说明理由.面积定值1Presented by Csuzzy ,All Rights Reserved. 1.如图,长方形OABC 的OA 边在x 轴的正半轴上,OC 在y 轴的正半轴上,抛物线2y ax bx =+经过点()1,4B 和点()3,0E 两点.(1)求抛物线的解析式;(2)若点D 在线段OC 上,且BD DE ⊥,BD DE =,求D 点的坐标;(3)在条件(2)下,在抛物线的对称轴上找一点M ,使得BDM △的周长为最小,并求BDM △周长的最小值及此时点M 的坐标;(4)在条件(2)下,从B 点到E 点这段抛物线的图象上,是否存在一个点F ,使得FAD △的面积最大?若存在,请求出FAD △面积的最大值及此时F 点的坐标;若不存在,请说明理由.2面积最大如图,曲线1y 抛物线的一部分,且表达式为()()2132333y x x x =--≤,曲线2y 与曲线1y 关于直线3x =对称.(1)求A ,B ,C 三点的坐标和曲线2y 的表达式;(2)过点C 作CD x 轴交曲线1y 于点D ,连接AD ,在曲线2y 上有一点M ,使得四边形ACDM 为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M 的横坐标;(3)在(2)的条件下,设直线CM 与x 轴交于点N ,试问在线段MN 下方的曲线2y 上是否存在一点P ,使PMN △的面积最大?若存在,求出点P 的坐标;若不存在,请说明理由.Presented by Csuzzy ,All Rights Reserved.如图1,抛物线2y x bx c =-++经过()1,0A -,()4,0B 两点,与y 轴相交于点C ,连接BC .点P 为抛物线上一动点,过点P 作x 轴的垂线l ,交直线BC 于点G ,交x 轴于点E .(1)求抛物线的表达式;(2)当P 位于y 轴右边的抛物线上运动时,过点C 作CF ⊥直线l ,F 为垂足.当点P 运动到何处时,以P ,C ,F 为顶点的三角形与OBC △相似?并求出此时点P的坐标;(3)如图2,当点P 在位于直线BC 上方的抛物线上运动时,连接PC ,PB .请问PBC △的面积S 能否取得最大值?若能,请求出最大面积S ,并求出此时点P 的坐标;若不能,请说明理由.3§7-2面积综合(2018福建)如图,直线与双曲线相交于,两点,轴,轴,则面积的最小值为.如图,OAC△和BAD△都是等腰直角三角形,90ACO ADB∠=∠= ,反比例函数6yx=在第一象限的图象经过点B,则OAC△与BAD△的面积之差OAC BADS S-△△为()A.36B.12C.6D.3 1Presented by Csuzzy ,All Rights Reserved.(2018盐城)如图①,在平面直角坐标系中,抛物线经过点,两点,且与轴交于点.(1)求抛物线的表达式;(2)如图②,用宽为个单位长度的直尺垂直于轴,并沿轴左右平移,直尺的左右两边所在的直线与抛物线相交于,两点(点在点的左侧),连接,在线段上方抛物线上有一动点,连接,.(Ⅰ)若点的横坐标为面积最大值,并求此时点的坐标;(Ⅱ)直尺在平移过程中,面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.2如图,已知抛物线交x 轴于A ,B 两点,交y 轴于C 点,A 点坐标为()1,0-,2OC =,3OB =,点D 为抛物线的顶点.(1)求抛物线的解析式;(2)P 为坐标平面内一点,以B ,C ,D ,P 为顶点的四边形是平行四边形,求P点坐标;(3)若抛物线上有且仅有三个点1M ,2M ,3M 使得1M BC △,2M BC △,3M BC △的面积均为定值S ,求出定值S 及1M ,2M ,3M 这三个点的坐标.Presented by Csuzzy ,All Rights Reserved.(2017苏州)如图,二次函数的图象与轴交于,两点,与轴交于点,.点在函数图象上,轴,且,直线是抛物线的对称轴,是抛物线的顶点.(1)求,的值;(2)如图①,连接,线段上的点关于直线的对称点恰好在线段上,求点的坐标;(3)如图②,动点在线段上,过点作轴的垂线分别与交于点,与抛物线交于点.试问:抛物线上是否存在点,使得与的面积相等,且线段的长度最小?如果存在,求出点的坐标;如果不存在,说明理由.3如图①,己知抛物线2239y ax ax a =--与坐标轴交于A ,B ,C 三点,其中()0,3C ,BAC ∠的平分线AD 交BC 于点D ,交第一象限的抛物线于点E .(1)求a 的值;(2)如图①,抛物线上两点C ,E 间的一动点F 关于AD 的对称点F '恰好落在线段BD 上,求F 点坐标;(3)若动点P 在线段OB 上,过点P 作x 轴的垂线分别与BC 交于点M ,与抛物线交于点N .试问:抛物线上是否存在点Q ,使得PQN △的面积是APM △面积的2倍,且线段NQ 的长度最小?如果存在,求出点Q 的坐标;如果不存在,说明理由.Presented by Csuzzy ,All Rights Reserved.如图(1),在平面直角坐标系中,抛物线212y x bx c =-++与x 轴交于点()4,0A -,与y 轴交于点()0,4B .(1)求抛物线的函数解析式;(2)在x 轴上有一点P ,点P 在直线AB 的垂线段为PC ,C 为垂足,且2PC =求点P 的坐标;(3)如图(2),将原抛物线向左平移,使平移后的抛物线过原点,与原抛物线交于点D ,在平移后的抛物线上是否存在点E ,使APE ACD S S =△△?若存在,请求出点E的坐标,若不存在,请说明理由.4如图,在平面直角坐标系中,二次函数223y x x =--的图象与x 轴交于A 、B 两点,与y 轴交于点C ,连接BC ,点D 为抛物线的顶点,点P 是第四象限的抛物线上的一个动点(不与点D 重合).(1)求OBC ∠的度数;(2)连接CD 、BD 、DP ,延长DP 交x 轴正半轴于点E ,且OCE OCDB S S =△四边形,求此时P 点的坐标;(3)过点P 作PF x ⊥轴交BC 于点F ,求线段PF 长度的最大值.Presented by Csuzzy ,All Rights Reserved.第7次课同步练习1.如图,在平面直角坐标系中,抛物线经过点()0,4A ,()1,0B ,()5,0C ,其对称轴与x 轴相交于点M .(1)求此抛物线的解析式和对称轴;(2)在此抛物线的对称轴上是否存在一点P ,使PAB △的周长最小?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)连接AC ,在直线AC 下方的抛物线上,是否存在一点N ,使NAC △的面积最大?若存在,请求出点N 的坐标;若不存在,请说明理由.2.如图,在平面直角坐标系xOy 中,抛物线2y x bx c =-++经过点()3,0A 和点()2,3B ,过点A 的直线与y 轴的负半轴相交于点C ,且1tan 3CAO ∠=.(1)求这条抛物线的表达式及对称轴;(2)连接AB ,BC ,求ABC ∠的正切值;(3)若点D 在x 轴下方的对称轴上,当DBC ADC S S =△△时,求点D 的坐标.Presented by Csuzzy ,All Rights Reserved.第7次课作业1.如图,在平面直角坐标系中,已知抛物线2y x bx c =++经过A ,B ,C 三点,已知()4,0B ,()2,6C -.(1)求该抛物线的解析式和点A 的坐标;(2)点()(),12D m n m -<<在抛物线图象上,当ACD △的面积为278时,求点D 的坐标;2.如图,在平面直角坐标系中,抛物线21y ax bx =++交y 轴于点A ,交x 轴正半轴于点()4,0B ,与过A 点的直线相交于另一点53,2D ⎛⎫ ⎪⎝⎭,过点D 作DC x ⊥轴,垂足为C .(1)求抛物线的表达式;(2)点P 在线段OC 上(不与点O ,C 重合),过P作PN x ⊥轴,交直线AD 于M ,交抛物线于点N ,连接CM ,求PCM △面积的最大值。
九年级中考数学复习北师大版《函数与面积》大单元复习教学设计

3.导入新课:今天我们将学习如何运用函数知识解决面积问题,让大家在实际问题中更好地理解函数与面积的关系。
(二)讲授新知
在这一环节中,我们将结合教材内容,详细讲解函数与面积的相关知识。
-对于重点知识,通过例题精讲、变式训练等方式,帮助学生巩固基础知识,形成解题技能;
-针对难点问题,设计梯度性的练习题,由浅入深,逐步提高学生的解题能力;
-引导学生总结解题思路和方法,形成个性化的解题策略,提高解题效率。
3.教学过程:
-导入新课:通过回顾已学的函数知识,引入函数与面积的关系,激发学生的学习兴趣;
【例题】给定一次函数y=2x+1,求该函数图像与x轴正半轴围成的三角形面积。
解答:首先,我们需要找到函数图像与x轴的交点,即令y=0,解得x=-1/2。然后,我们可以画出这个函数的图像,发现它与x轴正半轴围成一个直角三角形。利用三角形面积公式,我们可以计算出这个三角形的面积为1/4。
(二)过程与方法
(三)情感态度与价值观
在本章节的学习过程中,我们希望学生能够:
1.增强对数学学科的兴趣,相信自己能够掌握函数与面积的知识。
2.认识到数学与现实生活的紧密联系,体会数学在解决实际问题中的价值。
3.培养勇于挑战困难、追求卓越的品质,形成良好的学习习惯。
4.学会在合作中尊重他人,倾听他人意见,提高人际交往能力。
1.分组:将学生分成若干小组,每个小组针对某一特定问题进行讨论。
2.讨论主题:如一次函数图像与三角形面积的关系、二次函数图像与四边形面积的关系等。
3.交流分享:各小组汇报讨论成果,分享解题思路和方法,互相学习,共同提高。
学案1:2.7.1 抛物线的标准方程

2.7.1抛物线的标准方程学习目标核心素养1.理解抛物线的定义、标准方程及其推导过程.(重点)2.掌握抛物线的定义及其标准方程的应用.(难点)1.通过抛物线的定义、标准方程的学习,培养数学抽象、直观想象素养.2.借助于标准方程的推导过程,提升逻辑推理,数学运算素养.【情境导学】情境引入在某电视剧中敌我双方都曾使用一种单兵便携式火炮——击炮,击炮是一种曲射炮,发射后炮弹先飞向空中,飞过一个抛物线形的弹道后再砸向地面,很难防,地面上要防击炮的工事就必须是有顶盖的.对于躲在战壕中的敌人,击炮的密集发射无疑是一场灾难.因此研究抛物线是很有必要的,这节课我们就要“走入”抛物线看一看追击炮的弹道曲线.新知初探1.抛物线的定义思考1:平面内到一定点距离与到一定直线距离相等的点的轨迹是抛物线吗?2.抛物线的标准方程 图形标准方程焦点坐标准线方程⎝⎛⎭⎫p 2,0 x =-p 2⎝⎛⎭⎫-p 2,0 x =p 2⎝⎛⎭⎫0,p 2 y =-p 2⎝⎛⎭⎫0,-p 2y =p2思考2:确定抛物线的标准方程时,一般需要确定几个量?思考3:已知抛物线的标准方程,怎样确定抛物线的焦点位置和开口方向? 初试身手1.思考辨析(正确的打“√”,错误的打“×”)(1)标准方程y 2=2px (p >0)中的p 的几何意义是焦点到准线的距离.( ) (2)抛物线的焦点位置由一次项及一次项系数的正负决定.( )(3)平面内到一定点距离与到一定直线距离相等的点的轨迹是抛物线.( ) 2.抛物线y =ax 2的准线方程是y =2,则实数a 的值为( ) A .18 B .-18 C .8 D .-83.抛物线y 2=-16x 的焦点坐标为( ) A .(-4,0) B .(4,0) C .(0,4) D .(0,-4)4.抛物线x 2=16y 的准线方程为 .【合作探究】【例1】求满足下列条件的抛物线的标准方程.(1)过点M(-6,6);(2)焦点F在直线l:3x-2y-6=0上.[思路探究][规律方法]求抛物线的标准方程主要利用待定系数法,其步骤为:(1)依据条件设出抛物线的标准方程的类型;(2)求参数p的值;(3)确定抛物线的标准方程.提醒:当焦点位置不确定时,应分类讨论,也可以设y2=ax或x2=ay(a≠0)的形式,以简化讨论过程.[跟进训练]1.已知抛物线顶点在原点,对称轴是x轴,点P(-5,25)到焦点的距离为6,求抛物线的标准方程.[探究问题]1.抛物线定义的实质可归结为“一动三定”,这句话的含义是什么?2.如何看待抛物线中焦点和准线的位置?3.抛物线方程中参数p 的几何意义是什么?【例2】 若位于y 轴右侧的动点M 到F ⎝⎛⎭⎫12,0的距离比它到y 轴的距离大12.求点M 的轨迹方程.[思路探究] 把|MF |比M 到y 轴的距离大12,转化为|MF |与点M 到x =-12的距离相等,从而利用抛物线定义求解.[母题探究]1.(变换条件、改变问法)若本例中点M 所在轨迹上一点N 到点F 的距离为2,求点N 的坐标.2.(变换条件、改变问法)若本例中增加一点A(3,2),其他条件不变,求|MA|+|MF|的最小值,并求出点M的坐标.[规律方法]抛物线定义的两种应用(1)实现距离转化,根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距与点线距的相互转化,从而简化某些问题.(2)解决最值问题,在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.【例3】(1)探照灯反光镜的纵断面是抛物线的一部分,光源在抛物线的焦点处,已知灯口直径是60 cm,灯深40 cm,则光源到反光镜顶点的距离是()A.11.25 cm B.5.625 cmC.20 cm D.10 cm(2)某抛物线形拱桥跨度是20米,拱桥高度是4米,在建桥时,每4米需用一根支柱支撑,求其中最长支柱的长.[规律方法]求抛物线实际应用的五个步骤(1)建立适当的坐标系.(2)设出合适的抛物线方程.(3)通过计算求出抛物线的标准方程.(4)求出需要求出的量.(5)还原到实际问题中,从而解决实际问题.[跟进训练]2.河上有一抛物线形拱桥,当水面距拱桥顶5 m 时,水面宽为8 m ,一小船宽4 m ,高2 m ,载货后船露出水面上的部分高0.75 m ,则水面上涨到与抛物线形拱桥顶相距多少米时,小船开始不能通航?【课堂小结】1.抛物线的定义中不要忽略条件:点F 不在直线l 上.2.确定抛物线的标准方程,从形式上看,只需求一个参数p ,但由于标准方程有四种类型,因此,还应确定开口方向,当开口方向不确定时,应进行分类讨论.有时也可设标准方程的统一形式,避免讨论,如焦点在x 轴上的抛物线标准方程可设为y 2=2mx (m ≠0),焦点在y 轴上的抛物线标准方程可设为x 2=2my (m ≠0).【学以致用】1.抛物线y 2=4x 上的点M (4,y 0)到其焦点F 的距离为( ) A .3 B .4 C .5D .62.抛物线的准线方程为x =-4,则抛物线方程为( ) A .x 2=16y B .x 2=8y C .y 2=16x D .y 2=8x 3.若抛物线y 2=2px (p ≠0)的焦点与椭圆x 26+y 22=1的右焦点重合,则实数p = . 4.抛物线y 2=-2px (p >0)上有一点M 的横坐标为-9,它到焦点的距离为10,求此抛物线方程和M 点的坐标.【参考答案】【情境导学】新知初探 1. 抛物线的定义 相等定点F定直线l思考1:[提示] 不一定.当直线l 经过点F 时,点的轨迹是过定点F 且垂直于定直线l 的一条直线;l 不经过点F 时,点的轨迹是抛物线. 2. 抛物线的标准方程 y 2=2px (p >0) y 2=-2px (p >0) x 2=2py (p >0) x 2=-2py (p >0)思考2:[提示] 确定两个量,一个是p ,另一个是一次项系数的正负. 思考3:[提示] 一次项变量为x (或y ),则焦点在x 轴(或y 轴)上;若系数为正,则焦点在正半轴上;系数为负,则焦点在负半轴上.焦点确定,开口方向也随之确定. 初试身手1.[答案] (1)√ (2)√ (3)×[提示] (1)√ 抛物线的标准方程中p (p >0)即为焦点到准线的距离.(2)√ 一次项决定焦点所在的坐标轴,一次项系数的正负决定焦点是在正半轴还是负半轴上. (3)× 当定点在直线上时,不表示抛物线. 2.B [由y =ax 2,得x 2=1a y ,14a =-2,a =-18.]3.A [y 2=-16x ,∴p =-8,∴p2=-4,开口方向向左,∴焦点坐标为(-4,0).]4.y =-4 [抛物线的焦点在y 轴上,开口方向向上,故准线方程为y =-p2,且2p =16,∴p2=4,∴准线方程为y =-4.] 【合作探究】【例1】[解] (1)由于点M (-6,6)在第二象限, ∴过M 的抛物线开口向左或开口向上. 若抛物线开口向左,焦点在x 轴上, 设其方程为y 2=-2px (p >0),将点M (-6,6)代入,可得36=-2p ×(-6), ∴p =3,∴抛物线的方程为y 2=-6x .若抛物线开口向上,焦点在y 轴上,设其方程为x 2=2py (p >0), 将点M (-6,6)代入可得,36=2p ×6,∴p =3, ∴抛物线的方程为x 2=6y .综上所述,抛物线的标准方程为y 2=-6x 或x 2=6y . (2)①∵直线l 与x 轴的交点为(2,0), ∴抛物线的焦点是F (2,0), ∴p2=2,∴p =4, ∴抛物线的标准方程是y 2=8x . ②∵直线l 与y 轴的交点为(0,-3), 即抛物线的焦点是F (0,-3), ∴p2=3,∴p =6, ∴抛物线的标准方程是x 2=-12y .综上所述,所求抛物线的标准方程是y 2=8x 或x 2=-12y . [跟进训练]1.[解] 设焦点F (a,0),|PF |=(a +5)2+20=6, 即a 2+10a +9=0,解得a =-1,或a =-9.当焦点为F (-1,0)时,p =2,抛物线的开口向左,其方程为y 2=-4x ; 当焦点为F (-9,0)时,p =18,抛物线开口向左,其方程为y 2=-36x .[探究问题]1.[提示] 抛物线定义的实质可归结为“一动三定”,一个动点,设为M ;一个定点F ,即抛物线的焦点;一条定直线l ,即为抛物线的准线;一个定值,即点M 与点F 的距离和M 到l 的距离之比等于1.定点F 不能在直线上,否则,动点M 的轨迹就不是抛物线.2.[提示] 焦点在抛物线开口方向的内部,而准线在外部,即“怀抱焦点,背着准线”. 3.[提示] 抛物线的标准方程中参数p 的几何意义是:抛物线的焦点到准线的距离(即焦准距),所以p 的值永远大于0.当抛物线标准方程中一次项的系数为负值时,不要出现p <0的错误. 【例2】[解] 由于位于y 轴右侧的动点M 到F ⎝⎛⎭⎫12,0的距离比它到y 轴的距离大12, 所以动点M 到F ⎝⎛⎭⎫12,0的距离与它到直线l :x =-12的距离相等. 由抛物线的定义知动点M 的轨迹是以F 为焦点,l 为准线的抛物线(不包含原点), 其方程应为y 2=2px (p >0)的形式,而p 2=12,所以p =1,2p =2,故点M 的轨迹方程为y 2=2x (x ≠0). [母题探究]1.[解] 设点N 的坐标为(x 0,y 0),则|NF |=2,即⎝⎛⎭⎫x 0-122+y 20=4 ①, 又由例题的解析知点M 的轨迹方程为y 2=2x (x ≠0),故y 20=2x 0 ②, 由①②可得⎩⎪⎨⎪⎧ x 0=32,y 0=3,或⎩⎪⎨⎪⎧x 0=32,y 0=-3,故点N 的坐标为⎝⎛⎭⎫32,3或⎝⎛⎭⎫32,-3. 2.[解] 如图,由于点M 在抛物线上,所以|MF |等于点M 到其准线l 的距离|MN |, 于是|MA |+|MF |=|MA |+|MN |,所以当A 、M 、N 三点共线时, |MA |+|MN |取最小值,亦即|MA |+|MF |取最小值,最小值为3+12=72.这时点M 的纵坐标为2,可设M (x 0,2), 代入抛物线方程得x 0=2,即M (2,2).类型三抛物线的实际应用【例3】(1)B[如图,建立直角坐标系,设抛物线方程是y2=2px(p>0).∵A(40,30)在抛物线上,∴302=2p×40,∴p=454,∴光源到反光镜顶点的距离为p2=4542=458=5.625(cm).](2)解:如图,建立直角坐标系,设抛物线方程为x2=-2py(p>0).依题意知,点P(10,-4)在抛物线上,∴100=-2p×(-4),2p=25.即抛物线方程为x2=-25y.∵每4米需用一根支柱支撑,∴支柱横坐标分别为-6,-2,2,6.由图知,AB是最长的支柱之一.设点B的坐标为(2,y B),解得y B=-425,点A的坐标为(2,-4),∴|AB|=y B-(-4)=-425+4=3.84,∴最长支柱的长为3.84米.[跟进训练]2.[解]如图所示,以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x 轴,建立平面直角坐标系.设抛物线方程为x 2=-2py (p >0),由题意可知点B (4,-5)在抛物线上,故p =85,得x 2=-165y . 当船面两侧和抛物线接触时,船不能通航,设此时船面宽为AA ′,则A (2,y A ),由22=-165y A ,得y A =-54. 又知船面露出水面上的部分高为0.75 m ,所以h =|y A |+0.75=2(m).所以水面上涨到与抛物线形拱桥顶相距2 m 时,小船开始不能通航.【学以致用】1.C [由抛物线y 2=4x ,得F (1,0),如图,|FM |=4+p 2=4+1=5. ]2.C [抛物线的准线为x =-4,易知抛物线是开口向右的抛物线.设方程为y 2=2px (p >0),则p 2=4,p =8,抛物线方程为y 2=16x .] 3.4 [因为椭圆x 26+y 22=1,所以a 2=6,b 2=2, 所以c 2=a 2-b 2=4,故c =2,所以右焦点为(2,0),所以p 2=2,p =4.] 4.[解] 设焦点为F ⎝⎛⎭⎫-p 2,0,M 点到准线的距离为d , 则d =|MF |=10,即9+p 2=10,∴p =2, ∴抛物线方程为y 2=-4x .将M (-9,y )代入抛物线的方程,得y =±6.∴M 点坐标为(-9,6)或(-9,-6).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线与面积专题复习(学案)
【我的任务】
(1)熟练掌握抛物线中特殊点的坐标求法,体会数形结合、方程等数学思想。
(2)会求抛物线中常见图形的面积,体会转化、建模等数学思想。
(3)培养发散思维能力,力求做到一题多解,多题归一。
【自主探究】——求抛物线中常见图形的面积
1、说出如何表示各图中阴影部分的面积?
【反思归纳】
(1)一般取在 上的线段为底边。
(2)三边均不在坐标轴上的三角形及不规则多边形需将图形 ,即用割或补的
方法把它转化为若干个易于求面积的图形。
(3)解决该问题用到了 等数学思想。
图五
图四 图六
图二
图一
CE AB S ABC
⋅=∆2
1
图三
【尝试应用】——知识整合
2、已知二次函数322--=x x y 与x 轴交于A 、B 两点(A 在B 的左边),与y 轴交于点C ,顶点为P.
(1)结合图形,提出几个面积问题,并思考解法;
(2)求A 、B 、C 、P 的坐标,并求出一个刚刚提出的图形面积; (3)在抛物线上(除点C 外),是否存在点N ,使得ABC NAB S S ∆∆=,
若存在,请写出点N 的坐标;若不存在,请说明理由。
变式一:在抛物线的对称轴上是否存点N ,使得ABC NAB S S ∆∆=,若存在直接写出N 的坐
标;若不存在,请说明理由.
变式二:在双曲线3
y x
=
上是否存在点N ,使得ABC NAB S S ∆∆=,若存在直接写出N 的坐标;若不存在,请说明理由.
【反思归纳】——万变不离其宗
同底 高的三角形面积相等,平行线间的距离处处 ;该类问题最终可转化为方程组是否有解的问题.
【拓展提高】——中考真题改编
3、已知二次函数322--=x x y 与x 轴交于A 、B 两点(A 在B 的左边),与y 轴交于
点C.在抛物线上是否存在点N ,使得NBC ABC S S ∆∆=.
【走进考场】——锲而不舍,金石可镂
(2011,日照)如图,抛物线y=ax 2+bx (a 0)与双曲线y =
x
k
相交于点A ,B . 已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan ∠AOx =4. 过点A 作直线AC ∥x 轴,交抛物线于另一点C .
(1)求双曲线和抛物线的解析式;(3分) (2)计算△ABC 的面积;(4分)
(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABC 的面积.
若存在,请你写出点D 的坐标;若不存在,请你说明理由.(3
4:如图,已知在同一坐标系中,直线22
k
y kx =+-
与y 轴交于点P ,抛物线k x k x y 4)1(22++-=与x 轴交于)0,(),0,(21x B x A 两点。
C 是抛物线的顶点。
(1)求二次函数的最小值(用含k 的代数式表示); (2)若点A 在点B 的左侧,且021<⋅x x 。
①当k 取何值时,直线通过点B ;
②是否存在实数k ,使ABC ABP S S ∆∆=?如果存在,请求出此时抛物线的解析式;如果不存在,请说明理由。
5:已知抛物线)1(3)4(2-+---=m x m x y 与x 轴交于A 、B 两点,与y 轴交于C 点,
(1)求m 的取值范围;
(2)若0<m ,直线1-=kx y 经过点A ,与y 轴交于点D ,且25=⋅BD AD ,求抛物线的解析式;
(3)若A 点在B 点左边,在第一象限内,(2)中所得的抛物线上是否存在一点P ,使直线P A 平分ACD ∆的面积?若存在,求出P 点的坐标;若不存在,请说明理由。
6.已知矩形ABCD中,AB=2,AD=4,以AB的垂直平分线为x轴,AB所在的直线为y轴,建立平面直角坐标系(如图)。
(1)写出A、B、C、D及AD的中点E的坐标;
(2)求以E为顶点、对称轴平行于y轴,并且经过点B、C的抛物线的解析式;
(3)求对角线BD与上述抛物线除点B以外的另一交点P的坐标;
(4)△PEB的面积S△PEB与△PBC的面积S△PBC具有怎样的关系?证明你的结论。
7.如图1,已知直线
1
2
y x
=-与抛物线2
1
6
4
y x
=-+交于A B
,两点.
(1)求A B
,两点的坐标;
(2)求线段AB的垂直平分线的解析式;
(3)如图2,取与线段AB等长的一根橡皮筋,端点分别固定在A B
,两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A B
,构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.
图2
图1。
