21光的量子性习题解答
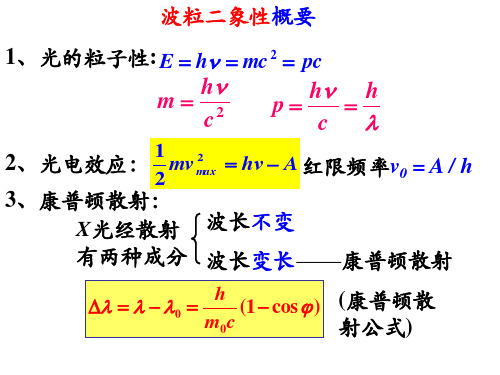
第21章_量子光学基础

例4:以一定频率的单色光照射在某种金属上,测出其 光电流曲线在图中用实线表示。⑴ 保持照射光的强度 不变,增大频率;测出其光电流曲线在图中用虚线表示。 满足题意的图,是_______。
I
o (A) U
I
o (B) U
I
o (C) U
I
o (D) U
⑵ 保持照射光的频率不变,增大强度。测出其光电流曲 线在图中用虚线表示。满足题意的图,是_______。
瑞利—金斯公式
实验曲线和普朗克公式
6 5 4 3 2 1 0
1 2 3
T=2000K
维恩公式
10-14Hz
由经典理论导出的 M (T)~ 公式都与实验曲线不 完全符合!
这正所谓是“ 物理学晴朗天空中的一朵乌云!”
四.普朗克的量子论的诞生 1900年德国物理学家普朗克为了得到与实验曲线相 一致的公式,摒弃了经典物理能量连续概念,提出了 一个与经典物理学概念截然不同的“能量子”假设. 他指出 :辐射物质中存在着带电谐振子,这些谐振 子吸收或辐射的能量是间断的不连续的,辐射“能量子 ”的能量
实验曲线
维恩公式
维恩公式在高频段与实 验曲线符合得很好, 但在低频段明显偏离 实验曲线。
10-14Hz
▲
著名公式之二: 瑞利 —金斯公式
1900年瑞利和金斯从经典电动力学和 统计物理学理论(能量均分)推导得:
2 2 M (T ) 2 kT c k 1.380658 1023 J K 1
I
O U
I
O (B) U
I
O (C) U
I
O (D) U
(A)
例5:关于光电效应有下列说法中正确的是________。 (1)任何波长的可见光照射到任何金属表面都能产生 光 电效应; (2)若入射光的频率均大于一给定金属的红限,则该 金属分别受到不同频率的光照射时,释出的光电子的 最大初动能也不同; (3)若入射光的频率均大于一给定金属的红限,则该 金属分别受到不同频率、强度相等的光照射时,单位 时间释出的光电子数一定相等; (4)若入射光的频率均大于一给定金属的红限,则当 入射光频率不变而强度增大一倍时,该金属的饱和光 电流也增大一倍。
量子力学练习题答案

Wmk =| am (t) |2
∫ ∫ 其中
am
(t)
=
1 i=
t 0
eiωmkτ
H
′
mk
dτ
,
H
′
mk
=
ϕm* Hl ′(t)ϕkdτ ,ωmk = (Em − Ek ) / =
二、 证明题 1. 证明黑体辐射的辐射本领 E(ν ,T ) 与 E(λ,T ) 之间的关系。 证明:黑体的辐射本领是指辐射体单位面积在单位时间辐射出来的、单位 频率间隔内的能量,用 E(ν ,T ) 表示。由于ν = c / λ ,所以黑体的辐射本领也 可以表示成 E(λ,T ) 。由定义得单位面积、单位时间内辐射的能量为
的同时决定,也使得它们的分布同时制约,这种制约就是不确定性原理,
它是任何两个力学量在任何状态下的涨落(用均方差表示)必须满足的相
互制约关系,公式表示为
ΔA⋅ ΔB ≥ 1 ⋅ [lA, Bl] 2
23. 如果算符 Aˆ 的本征值分别为 A1, A2, A3,",在算符 Aˆ 的自身表象中写出
算符 Aˆ 的矩阵形式。
下,所有力学量的概率分布不随时间改变;在一切状态下,守恒量的概率
分布不随时间改变。
25. 在 Sz 表象下,写出算符 Sˆz 及其本征态|↑〉 和|↓〉 的矩阵表达式。
答:在 Sz 表象下,算符 Sˆz 的矩阵表达式为
Sz
=
= ⎛1
2
⎜ ⎝
0
0⎞ − 1⎟⎠
其本征态|↑〉 和|↓〉 的矩阵表达式分别为
v∫ 答: pkdqk = nkh (nk = 1, 2,3,")
其中 (qk , pk ) 代表一对共轭的正则坐标和动量。 7. 利用光波的双缝干涉实验,说明 Born 的概率波解释。 答:Born 认为,微观粒子的运动状态用“波函数”来描述,粒子通过双缝 时,每一个缝都有一个所谓的“波”通过,只不过与经典波的强度对应的, 是粒子在某点附近出现的相对概率。对通过双缝的粒子,其概率“分成” 了两束(波动性),但对某个具体的粒子,它只能通过其中的一个缝(粒子
量子习题解答
n 0,1,2,3...
8、氢原子: 氢原子能级:
me4 1 1 En 2 13.6 2 (e V) 2 2 2 (4 0 ) n n
轨道角动量
L l (l 1)
轨道角动量沿磁场方向分量:Lz m 主量子数 轨道量子数 轨道磁量子数
n=1,2,3…
l=0,1,2,3…,n-1 ml=-l,-(l-1),…,0,1,..,l
h 0 ( 1 cos ) m0 c
4、不确定关系(1927):
h 2
x p x (或, 或h) 位臵动量不确定关系: 2
能量时间不确定关系:Et / 2
5、氢原子光谱(1913) 谱线的波数
1 1 R ( 2 2 ) T ( m) T ( n) m n
玻尔磁子
电子自旋磁矩在磁场中的能量 Es B B
e B 9.27 10 24 J / T 2me
10、多电子原子的电子组态 电子的状态用4 个量子数n,l,ml,ms确定。n相同 的状态组成一壳层,可容纳2n2个电子;l相同 的状态组成一次壳层,可容纳2(2l+1)个电子。 基态原子电子组态遵循两个规律: (1)能量最低原理,即电子总处于可能最 低的能级。一般n越大,l越大,能量就越高。 (2)泡利不相容原理(1921),不可能有两个 或两个以上的电子处在同一量子状态。即不 能有两个电子具有相同的n, l, ml , ms。
解: 光子的散射角 θ π 时电子获得的能量最大, v 电子的反冲速度沿入射光子的运动方向.设 为入 pe 射光的频率,为散射光的频率, 为反冲电子的动 v 量。 1 由能量守恒有: h(v v) Ek
由动量守恒有: 2 式得 由1 、
21光的量子性习题解答

第二十一章 光的量子性一 选择题1. 所谓绝对黑体,是指:( D )A. 不吸收不反射任何光的物体;B. 不反射不辐射任何光的物体;C. 不辐射而能全部吸收所有光的物体;D. 不反射而能全部吸收所有光的物体。
2. 若一黑体的绝对温度增加一倍,则它的总辐射能是原来的: ( C )A. 4倍B. 8倍C. 16倍D. 32倍3.用频率为ν的单色光照射某种金属时,逸出光电子的最大动能为E k ;若改用频率为2ν的单色光照射此金属时,则逸出光电子的最大初动能为:( D )A. 2E kB. 2h ν - E kC. h ν - E kD. h ν + E k4.光电效应和康普顿效应都包含有电子与光子的相互作用过程。
对此,在以下几种理解中,正确的是: ( C )A. 两种效应都相当于电子与光子的弹性碰撞过程。
B. 两种效应都属于电子吸收光子的过程。
C. 光电效应是电子吸收光子的过程,而康普顿效应则相当于光子和自由电子的弹性碰撞过程。
D. 康普顿效应是电子吸收光子的过程,而光电效应则相当于光子和自由电子的弹性碰撞过程。
5.用强度为I ,波长为λ的X 射线分别照射锂(Z = 3)和铁(Z =26)。
若在同一散射角下测得康普顿散射的X 射线波长分别为λLi 和λFe (λLi ,λFe >λ),它们对应的强度分别为I Li 和I Fe ,则 ( C )A .λLi >λF e ,I Li < I FeB .λLi =λFe ,I Li = I FeC .λLi =λFe ,I Li > I FeD .λLi <λFe ,I Li > I Fe解:因为散射角θ 确定时,波长的增加量∆λ与散射物质的性质无关;原子序数小的散射物质,康普顿散射较强。
故选C 。
6.根据玻尔氢原子理论,氢原子中的电子在第一和第三轨道上运动时速度大小之比v 1 / v 3是: ( C )A. 1 / 3B. 1 / 9C. 3D. 9解: 33311==v v mr mr ,,3)3/(/1331==r r v v7.将处于第一激发态的氢原子电离,需要的最小能量为:( B )A. 13.6eVB. 3.4eVC. 1.5eVD. 0eV二 填空题1. 大爆炸宇宙论预言存在宇宙背景辐射,其温度为2.7K ,则对应这种辐射的能谱峰值的波长为_1.06mm 。
光的量子性

光的量子性
(2)入射光频率ν一定时,反向截止电压U0取决于阴极材料,与 入射光强无关.若外加电压是A负K正,则为反向电压.对于固定的入射光 频率和入射光强,随着反向电压的增加,从阴极K逸出并能到达阳极A的 电子会越来越少,A、K间的电流就会越来越小,电流变为0时的电压就 称为反向截止电压.图15- 4(c)中的U0即为不同阴极材料的反向截止电压.
(3)对于给定的阴极材料,反向截止电压正比于入射光频率ν,且 存在一个最低频率,称为红限频率.当入射光频率低于此值时,就不会产 生电流.
光的量子性
(4)光电效应具有瞬时响应特性,即从光照射到阴极表面到产生 电流(有电子从阴极K发出)的时间间隔不大于纳秒数量级.
以上实验结果,除(1)之外的另外三点都无法用经典物理理予 以解释.按照经典物理理论,金属阴极中的电子在光线(电磁波)的照射 下做受迫振动,并吸收电磁场的能量.只要电子吸收足够多的能量,就可 能从金属表面逸出,产生光电效应.因此,只要光强足够强,或者照射的 时间足够长,电子就会积累到足够的能量并从表面逸出,从而发生光电 效应现象.这样,首先,反向截止电压应该与入射光强有关;其次,光电 效应不应该受到频率的限制;最后,电子要积累到足够的能量所需要的 时间应该在毫秒量级,并且这个时间应该随着光强的增加而缩短.
光的量子性
(15- 11) 式(15- 9)和式(15- 11)合在一起称为爱因斯坦关系式, 它们是爱因斯坦光子学说的核心.有趣的是,这两式的左边是能量和 动量,反映了光子粒子性的一面;而右边却与波长和频率相联系, 代表了光子波动性的一面.
光的量子性
三、 康普顿散射
当光照射到某物体时,光线就会向各个方向散开,这 种现象称为光散射.通常而言,光在散射过程中的波长不会 发生变化,这种普通的散射现象在经典物理学中可以得到圆 满解释.1923年,康普顿在用X射线(比紫外线波长更短的 光)进行光散射实验时发现,散射光中除原波长的光线外, 还会出现一些波长更长的光线,这就是康普顿效应.
光的量子性

光子的动量
p h h cc
引入 h 2
k 2 n
2
h
p h n k
11
光子具有动量,显示其有粒子性; 光子具有波长,又说
明其有波动性;这说明,光具有波粒二象性,即在传播过程中
显示它的波动性(如干涉,衍射等),而在光与实物粒子相互
作用时,又显示它的粒子特性。光的波粒二重特性,充分地包
答[ D ]
25
例 15 - 5 设用频率为1,2的两种单色光,先后照射同一种 金属均能产生光电效应,已知金属的红限频率为0 ,测得两次照 射时的遏止电压 |Ua2|=2| Ua1| ,则这两种单色光的频率有如下 关系:
(A)2 10, (B) 2 1+0, (C)2 210, (D) 2 120,
在光子流中,光的能量集中在光子上,电子与光子相遇, 只要hv足够大,电子就可以立刻吸收一个光子的能量而逸出金 属表面,因而不会出现滞后效应。
10
四、光的波粒二象性
描述光的波动性:波长λ,频率ν
描述光的粒子性:能量ε,动量 P
每个光子的能量
h
按照相对论的质能关系 光子无静质量 m0=0
2 p2c2 m02c4
一、光电效应
金属及其化合物在光波的照射下 发射电子的现象称为光电效应,所发 射的电子称为光电子。
1 、实验装置
2 、光电效应的实验规律 ( 1 )饱和光电流强度 Im 与入射 光强成正比(ν不变)。
当光电流达到饱和时,阴极 K 上 逸出的光电子全部飞到了阳极上。
单位时间内从金属表面逸出的光电子 数和光强成正比
4
二、经典物理学所遇到的困难
1、逸出功,初动能与光强、频率的关系
按照经典的物理理论,金属中的自由电子是处在晶格上正电
曾谨言量子力学(卷1)习题答案

目次第二章:波函数与波动方程………………1——25 第三章:一维定态问题……………………26——80 第四章:力学量用符表达…………………80——168 第五章:对称性与守衡定律………………168——199 第六章:中心力场…………………………200——272 第七章:粒子在电磁场中的运动…………273——289 第八章:自旋………………………………290——340 * * * * * 参考用书1.曾谨言编著:量子力学上册 科学。
1981 2.周世勋编:量子力学教程 人教。
19793.L .I .席夫著,李淑娴,陈崇光译:量子力学 人教。
19824.D .特哈尔编,王正清,刘弘度译:量子力学习题集 人教。
1981 5.列维奇著,李平译:量子力学教程习题集 高教。
1958 6.原岛鲜著:初等量子力学(日文) 裳华房。
19727.N.F.Mott.I.N.Sneddon:Wave Mechanics and its Applications 西联影印。
1948 8.L.Pauling.E.B.Wilson:Introduction to Quantum- Mechanics(有中译本:陈洪生译。
科学) 19519. A.S.Davydov: Quantum Mechanics Pergamon Press 1965 10. SIEGFRIED.Fluegge:Practical Quantum- Mechanics(英译本) Springer Verlag 197311. A.Messian:Quantum Mechanics V ol I.North.Holland Pubs 1961 ndau,E.Lifshitz:Quantum-Mechanics1958 量子力学常用积分公式 (1)dx e x an e x a dx e x axn ax n ax n ∫∫−−=11 )0(>n (2) )cos sin (sin 22bx b bx a ba e bxdx e axax−+=∫ (3) =∫axdx e axcos )sin cos (22bx b bx a ba e ax++ (4)ax x a ax a axdx x cos 1sin 1sin 2−=∫(5) =∫axdx x sin 2ax a xaax a x cos )2(sin 2222−+(6)ax a xax aaxdx x sin cos 1cos 2+=∫ (7) ax aa x ax a x axdx x sin )2(cos 2cos 3222−+=∫))ln(2222c ax x a ac c ax x ++++ (0>a ) (8)∫=+dx c ax 2)arcsin(222x c a ac c ax x −−++ (a<0) ∫20sin πxdx n2!!!)!1(πn n − (=n 正偶数)(9) =∫20cos πxdx n!!!)!1(n n − (=n 正奇数) 2π(0>a )(10)∫∞=0sin dx xax2π− (0<a )(11))1!+∞−=∫n n ax an dx x e (0,>=a n 正整数) (12)adx e ax π2102=∫∞− (13) 121022!)!12(2++∞−−=∫n n ax n an dx e x π(14)1122!2+∞−+=∫n ax n an dx e x (15)2sin 022adx xax π∫∞= (16)∫∞−+=222)(2sin b a abbxdx xe ax (0>a )∫∞−+−=022222)(cos b a b a bxdx xeax(0>a )第一章量子力学的诞生1.1设质量为m 的粒子在谐振子势2221)(x m x V ω=中运动,用量子化条件求粒子能量E 的可能取值。
光的量子性习题及答案

第七章光的量子性1.在深度远大于表面波波长的液体中,表面波的传播速度满足如下规律:v = 式中g 为重力加速度,ρ为液体密度,F为表面波的波长.试计算表面波的群速度.解:由任何脉动的一般瑞利公式u = v - λvδδλ= v-λdvdλ-λ3g F λπ+2. 测量二硫化碳的折射率实验数据为:当λ=589 nm .n' = 1.629:当"λ=656nm时,n''=1.620 试求波长589nm的光在二氧化硫的相速度、群速度和群折射率。
解:由v = cn得v1=2997924581.629= 1.840×108 m/s.v2 =2997924581.620=1.8506×108 m/s所以△v = v2– v1 = 1.057×106 m/s由一般瑞利公式u = v - λvλ∂∂=1.840×108- 589 ×1.507×106/(656 –589) = 1.747×108 m/sn = c/v = 299792458 /1.747×108 = 1.7163. 在测定光速的迈克尔逊旋转棱镜法中,设所用棱镜为正n 面棱柱体。
试导出:根据棱镜的转速、反射镜距离等数据计算光速公式。
解:设反射镜间距离为L 转速V0则n 面棱柱每转过一个面,光往返一个来回。
所用时间t = 1n/V= 01nV所以c = 2L /t = 021LnV= 2LnV04.试用光的相速度v 和dvdλ来表示群速度u=ddkω,再用v 和dndλ表示群速度u =ddkω解:(1) 由 u = d dk ω= v - λv λ∂∂(2) 由 u = v - λvλ∂∂<1> v = c /n <2>→ dv d λ= ()c d nd λ = -223,(1)c dnn d c dn v dn v dvv v v dn n d n d n d λλλλλλλ<>=+=+=+把〈3〉代入〈1〉得dv u =v -d5.计算在下列各种色散介质中的传播的各种不同性质的波的群速度:(1)v = 常量 (2)v = , ( a 为常量) (3)v = a(在水面上的表面张力波) (4)v = a /λ(5)v =(电离层的电磁波,其中c 是真空中的光速,λ是介质中的波长) (6)v =(在充满色散介质的直波导管中的电磁波,式中c 为真空中的光速,a 是与波导管有关的常量,()εεω=是介质的介电常数,()μμω=是介质的磁导率)解:(1)λλd dvv u -= ,0,==dv v 常量 所以常量==v u(2)λλd dv v u -=, λλλd a dv a v 2,==,所以222v a a a u ==-=λλλλ (3)λλλ2/32,ad dv av -==,所以va v u 2322/3=+=λλ(4)dv u v d λλ=-=()2ad aa d λλλλλ-=v 2=(5)dv u v d λλ=-=2d d λλ=v c 2= (6)kv dk d u ==ωω,,)1(11ωωωd dvv vd dk u -== 而)(),(,222ωμμωεεεμωω==-=ac c v2/3222)(])(2[a c d d v v d dv -+-=εμωωεμωεμωωω所以])(21[1ωεμεμωεμd d v cu +=6.利用维恩公式求:辐射的最概然频率v m ,辐射的最大光谱密度()mλε辐射出射度M 0(T)与温度的关系.解: 由维恩位移定律T T b b T m m m 1⋅⇒=⇒=λλλ由斯沁藩公式()()4040T T M T T M ⋅⇒=σ7.太阳光谱非常接近于480m nm λ=的绝对黑体的光谱.试求在1 s 内太阳由于辐射而损失的质量,并估算太阳的质量减少1% (由于热辐射)所经历的时间(太阳的质量m 0为2.0×1030千克,太阳的半径r 是7.0×108m) 解:由维恩位移公式m m bT b T λλ=⇒=:由斯沁藩公式34484()92.897810() 5.6705110()48010b b M T m σσλ---⨯===⨯⨯⨯=7.35×107瓦()()()瓦总262872106357.4100.714.341053.74⨯=⨯⨯⨯⨯⨯==⋅=r T M S T M P b b π由方程 P 总t =m 0×1%×c 221800.01 3.8810m c t sP ⨯⨯⇒==⨯总所以在1s 内kg 1015.5109106357.41916262⨯=⨯⨯=⋅=∆c s P m 总损8.地球表面每平方厘米每分钟由于辐射而损失的能量平均值为0.546J.如有有一黑体,它在辐射相同的能量时,温度应为多少? 解:4()0.546109160b M =⨯=()s m W ⋅/ 由斯沁藩公式11()444()891()()()200.145.670510b b M M T T T K σσ-=⇒===⨯9.若有一黑体的辐出度等于5.70W /cm 2,试求该辐射最大光谱强度相对应的波长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十一章 光的量子性
一 选择题
1. 所谓绝对黑体,是指:( D )
A. 不吸收不反射任何光的物体;
B. 不反射不辐射任何光的物体;
C. 不辐射而能全部吸收所有光的物体;
D. 不反射而能全部吸收所有光的物体。
2. 若一黑体的绝对温度增加一倍,则它的总辐射能是原来的: ( C )
A. 4倍
B. 8倍
C. 16倍
D. 32倍
3.用频率为ν的单色光照射某种金属时,逸出光电子的最大动能为E k ;若改用频率为2ν的单色光照射此金属时,则逸出光电子的最大初动能为:( D )
A. 2E k
B. 2h ν - E k
C. h ν - E k
D. h ν + E k
4.光电效应和康普顿效应都包含有电子与光子的相互作用过程。
对此,在以下几种理解中,正确的是: ( C )
A. 两种效应都相当于电子与光子的弹性碰撞过程。
B. 两种效应都属于电子吸收光子的过程。
C. 光电效应是电子吸收光子的过程,而康普顿效应则相当于光子和自由电子的弹性碰撞过程。
D. 康普顿效应是电子吸收光子的过程,而光电效应则相当于光子和自由电子的弹性碰撞过程。
5.用强度为I ,波长为λ的X 射线分别照射锂(Z = 3)和铁(Z =26)。
若在同一散射角下测得康普顿散射的X 射线波长分别为λLi 和λFe (λLi ,λFe >λ),它们对应的强度分别为I Li 和I Fe ,则 ( C )
A .λLi >λF e ,I Li < I Fe
B .λLi =λFe ,I Li = I Fe
C .λLi =λFe ,I Li > I Fe
D .λLi <λFe ,I Li > I Fe
解:因为散射角θ 确定时,波长的增加量∆λ与散射物质的性质无关;原子序数小的散射物质,康普顿散射较强。
故选C 。
6.根据玻尔氢原子理论,氢原子中的电子在第一和第三轨道上运动时速度大小之比v 1 / v 3是: ( C )
A. 1 / 3
B. 1 / 9
C. 3
D. 9
解: 33311==v v mr mr ,,3)3/(/1331==r r v v
7.将处于第一激发态的氢原子电离,需要的最小能量为:( B )
A. 13.6eV
B. 3.4eV
C. 1.5eV
D. 0eV
二 填空题
1. 大爆炸宇宙论预言存在宇宙背景辐射,其温度为
2.7K ,则对应这种辐射的能谱峰值的波长为_1.06mm 。
2. 频率为100MHz 的一个光子的能量是 6.626⨯10-26J ,动量的大小是
2.21⨯10-34kg.m / s 。
3. 在光电效应实验中,测得某金属的截止电压U c
与入射光频率ν的关系曲线如图所示,由此可知该金
属的红限频率ν0 = 5⨯1014 Hz ;逸出功A = 2.1 eV 。
4. 在光电效应中,当频率为3⨯1015 Hz 的单色光照射在逸出功为4.0eV 的金属表面时,金属中逸出的光电子的最大初速率为 1.72⨯106 m /s 。
5. 康普顿散射中,当出射光子与入射光子方向成夹角θ = π 时,光子的频率减少得最多;当θ = 0 时,光子的频率保持不变。
6. 根据玻尔氢原子理论,若大量氢原子处于主量子数n = 5的激发态,则跃迁辐射的谱线可以有 10 条,其中属于巴耳末系的谱线有 3 条。
7.在氢原子光谱的巴耳末系中,波长最长的谱线和与其相邻的谱线的波长比值是:
1.35 解:)141(1
2n R -==λσ,365)3141(12max min R R =-==λσ,163)4141(1
222R R =-==λσ,所以 35.120
272max ==λλ
三 计算题
1. 在加热黑体的过程中,单色辐出度的峰值波长由0.69µm 变化到0.50µm, 其辐出度增加了多少倍?
解:由斯忒蕃——玻耳兹曼定律得
12M M =414
2T T σσ=(41
2)T T 由维恩位移定律得
2
112M M T T λλ=
-14Hz)
故得 4412)50.0/69.0()(2
1==M M M M λλ=3.63 故其辐出度增加了2.63倍。
2. 功率为P 的点光源,发出波长为λ的单色光,在距光源为d 处,每秒钟落在垂直于光线的单位面积上的光子数为多少?若λ=66
3.0nm ,则光子的质量为多少?
解:设光源每秒钟发射的光子数为n ,每个光子的能量为h ν
则由P = n h ν= n h c /λ
得: n = P λ / ( h c )
令每秒钟落在垂直于光线的单位面积的光子数为n 0,则
n 0 = n / S = n / (4πd 2 ) = P λ / (4πd 2 h c )
光子的质量
m = h ν/ c 2 = h c / ( c 2λ) = h / ( c λ) =3.33×10-36kg 。
3. 图中所示为在一次光电效应实验中得出的曲线,(1)求证对不同材料的金属,AB 线的斜率相同。
(2)由图上数据求出普朗克常量h 。
解:(1)由光电效应的爱因斯坦方程:A h m eU -==ν2m e c 21v ,得 c e A h U -=ν 所以AB 线的斜率
)( d d c 恒量h U =ν
由此可知,对不同金属,曲线的斜率相同。
(2)根据曲线的斜率,得到
() J.s 104.6 10
0.50.1000.2 tan 3414-=--==××e e h θ 4. 试证明:静止的自由电子不可能吸收一个光子,即对于自由电子不可能有光电效应。
解:假如静止的自由电子吸收了一个光子,光子的频率为ν,电子的静止质量为m 0,电子吸收光子后的动量为p e ,则根据动量守恒有
e p c
h =ν (1) 而根据能量守恒有
22022e 20)(c m c p c m h +=+ν (2)
将上式两边平方,有
22022e 202202)()(2)()(c m c p c m h c m h +=++νν
利用(1)式得到
0=ν
U Hz) 计算题3图
这要求光子的频率为0,这就证明了静止的自由电子不可能吸收一个光子。
5. 处于基态的氢原子被外来单色光激发后发出的仅有三条谱线,问此外来光的频率为多少?
解:由于发出的光线仅有三条,按
)11( 22n
k cR c -=⋅=σν
当n =3,k =2得一条谱线;当n =3,k =1得一条谱线;当n =2,k =1得一条谱线,可见如果氢原子吸收外来光子后,处于n =3的激发态,发出的谱线将仅有以上三条。
这三条光谱线中,频率最大的一条是 Hz 1092.2)3
111( 1522×=-=cR ν 这也就是外来光的频率。
6. 处于基态的氢原子吸收了一个能量为h ν = 15 eV 的光子后,其电子成为自由电子,求该电子的速率。
解:把一个基态氢原子电离所需最小能量为
E min = 13.6 eV
则根据能量守恒有
2
1 2e min v m E h +
=ν 该电子获得的速度大小为 ()[] s m 100.72=521e min ×=-m E h νv。
