一阶电路的零输入响应101103
合集下载
4-1一阶电路的零输入响应101103
t
iL(t)I0et t0
t
Geq L
L Req
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RL电路
I0 iL(t)
0.368I0
0
iL(t) τ
uL(t)
0
-ReqI0
τ uL(t)
电流曲线
Rt
iL(t) I0e L
t 0
t
uL(t)
LdiL(t) dt
Rt
ReqI0e L ReqiL(t)
S(t=0) 0.02μF
2）求时间常数τ
+
Req6040100
200V
t R e q C 1 0 0 0 .0 2 1 0 6 2 1 0 6 s
+ uC 60Ω 80Ω 40Ω
20Ω
+ 60Ω uO
-
3）求uC(t)
u Ct 1e 2 5 1 050 t t0
Req 20Ω
60Ω 80Ω 60Ω
i(t) uC (t)
t
R eq
i(t)
U0一定 C一定，q一定 Req大，i 小，衰减越慢； Req小，i 大，衰减越快。
+C
Req
uC(t)
-
uc(0+)=U0
t ≥ 0+ 时等效电电路路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
uC(t) U0
C
0
t
uC(t)U0eReqC t0
i(t) uC (t)
60Ω
i(t) i(0 ＋ )e tt16 .2 5 e 1 2 0 tA t0
+ u - 3Ω
0.5H
+ 6Ω
iL(t)I0et t0
t
Geq L
L Req
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RL电路
I0 iL(t)
0.368I0
0
iL(t) τ
uL(t)
0
-ReqI0
τ uL(t)
电流曲线
Rt
iL(t) I0e L
t 0
t
uL(t)
LdiL(t) dt
Rt
ReqI0e L ReqiL(t)
S(t=0) 0.02μF
2）求时间常数τ
+
Req6040100
200V
t R e q C 1 0 0 0 .0 2 1 0 6 2 1 0 6 s
+ uC 60Ω 80Ω 40Ω
20Ω
+ 60Ω uO
-
3）求uC(t)
u Ct 1e 2 5 1 050 t t0
Req 20Ω
60Ω 80Ω 60Ω
i(t) uC (t)
t
R eq
i(t)
U0一定 C一定，q一定 Req大，i 小，衰减越慢； Req小，i 大，衰减越快。
+C
Req
uC(t)
-
uc(0+)=U0
t ≥ 0+ 时等效电电路路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
uC(t) U0
C
0
t
uC(t)U0eReqC t0
i(t) uC (t)
60Ω
i(t) i(0 ＋ )e tt16 .2 5 e 1 2 0 tA t0
+ u - 3Ω
0.5H
+ 6Ω
4-1一阶电路的零输入响应
τ 同,变化进程相同
不同, r(0+)不同,起点不同 不同 所以r 值不同. 所以 zi(t1)值不同. 值不同
τ
f) 由波形图,可通过作图法求τ 由波形图,
t ′(0+ ) τ1 r′(t1) r′(t1) ′ r dr (t1) = e = = dt τ τ t2 t1
∴ =t2 t1 τ
1 1 S= = RC τ
(t ≥ 0 + )
R一定时:τ ∝ C 即R一定,C越大,τ越大,rzi ↓ 越慢
∵ R一定, U 0 一定,放电电流一定
τ
U 0一定, C越大, q(0 + ) = CU 0大
C一定时:τ ∝ R 即C一定,R越大,τ越大,rzi ↓ 越慢
∵C一定, 0一定, (0+ ) = CU0一定 U q U 0一定,R越大,放电电流越小
1.2 u0 (0+ ) = ( × 60) V = 36V 2
80 Req = (60 + ) = 100 2
τ = ReqC = (100× 0.02 × 106 ) s = 2 s
i ( 0 + ) = 1 .2 A
u0 (0+ ) = 36 V
rzi (t ) = r (0+ )e
t
电路的r 一,RC电路的 zi(t) 电路的 求:换路后的i(t) 换路后的
duC 解:RC + uC = 0 (t > 0) dt
RCS + 1 = 0
S = 1 RC
t RC
uC (t ) = uct (t) = Ae
uC (t) = uct (t) = Ae
uC (0+ ) = uC (0 ) =U0
一阶电路的零输入响应
dt
50 1 e1500t 0.05 1500 e1500t
50 25e1500tV
第17页/共26页
§10.4 一阶电路的全响应 一、全响应的分解
全响应：电路中输入激励和储能元件的储能共同产生的响应。
R
+
+ uR – i
–US
C
uC 0 U0
电路方程
ui US
+u US-U0 C
一、RC电路的零输入响应
12 i
uC i
特征根
p
1
+ U0
—
R0
+ C uC
—
+ R uR
—
U0
U0
R
uC
i
0
RC
t
uC Ae RC t 0
确定积分常数
t
uC 0 U0
uC 0 U0
电路方程
uR uC 0
电压与电流的关系
u R iR
电路方程
RC
duC dt
uC
0
t＞0
通解
uC Aept
二、全响应的分解
1.全响应可分解为稳态分量和瞬态分量。
t
uC = uC′+ uC″ = US + （U0 - US）e
τ
稳态分量 瞬态分量
强制分量 自由分量
2.全响应可分解为零输入响应和零状态响应。
t
t
uc = uc1 + uc2 = U0e τ + US（1-e τ ）
零输入响应 零状态响应
uC US
+ uR –
uR uC i
+
R+i
(电路分析)一阶电路的零输入响应
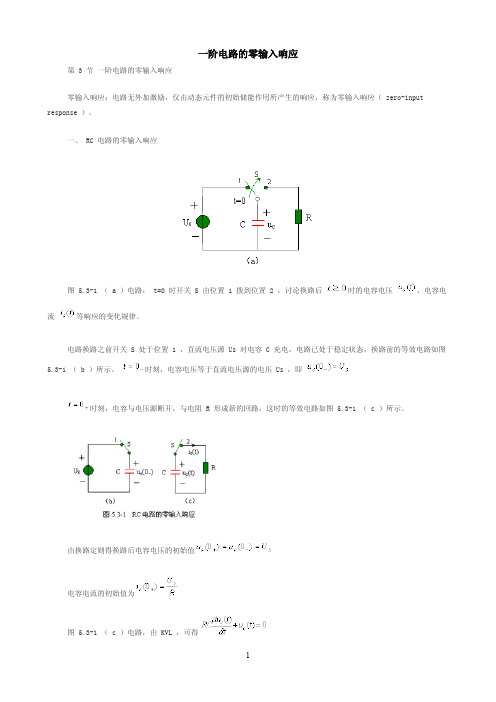
一阶电路的零输入响应第 3 节一阶电路的零输入响应零输入响应：电路无外加激励，仅由动态元件的初始储能作用所产生的响应，称为零输入响应（ zero-input response ）。
一、 RC 电路的零输入响应图 5.3-1 （ a ）电路， t=0 时开关 S 由位置 1 拨到位置 2 ，讨论换路后时的电容电压、电容电流等响应的变化规律。
电路换路之前开关 S 处于位置 1 ，直流电压源 Us 对电容 C 充电，电路已处于稳定状态，换路前的等效电路如图5.3-1 （ b ）所示。
时刻，电容电压等于直流电压源的电压 Us ，即时刻，电容与电压源断开，与电阻 R 形成新的回路，这时的等效电路如图 5.3-1 （ c ）所示。
由换路定则得换路后电容电压的初始值电容电流的初始值为图 5.3-1 （ c ）电路，由 KVL ，可得用积分变量分离法进行求解，得式中，为 RC 电路的时间常数（ time constant ），当 R 的单位为Ω， C 的单位为 F 时，τ的单位是秒（ s ）。
时间常数：时间常数是反映一阶电路过渡过程进展快慢的一个重要的参数，其大小仅取决于电路的结构和参数。
τ越大，响应衰减的速度就越慢；τ越小，响应衰减的速度就越快。
用表示电路换路后的响应，用表示该响应的初始值，则 RC 一阶电路的零输入响应可表示为RC 电路零输入响应的规律RC 电路换路后，各处的零输入响应都是从初始值开始，按指数规律衰减。
衰减得快慢由时间常数τ决定。
二、 RL 电路的零输入响应图 5.3-3 （ a ）是 RL 动态电路。
电路换路之前开关 S 处于位置 1 ， t=0 时开关 S 由位置 1 拨到位置 2 。
下面讨论换路后时的电感电流、电感电压等响应的变化规律。
时刻，电路换路之前开关 S 处于位置 1 ，直流电流源 Is 对电感 L 充电，电路已处于稳定状态，换路前的等效电路如图 5.3-3 （ b ）所示。
t=0 时，开关 S 拨到位置 2 ，时，电感与电流源断开，而与电阻 R 形成新的回路，这时的等效电路如图5.3-3 （ c ）所示。
一阶RC电路的零状态与零输入响应
关S。求：电感电流 iL (t) 和电感电压 uL (t) 。
2022/9/10
2022/9/10
一 四、一过阶渡R过C程电路零输入响应的实例
解： 在开关由位置1拨向位置2的瞬间，电容电压不能越变，因此可得
uC (0 ) uC (0 ) 6V
将连接于电容两端的电阻等效为一个电阻，其阻值为
R 8 6 3 10k 63
的电流为 I0 US R1，
电感中储存一定的 能量。在 t 0，开 关S由位置1拨向位 置2处。
一 三、一过阶渡R过L程电路的零输入响应的分析
一阶RL电路的零输入响应的定性分析
在换路的瞬间，由于电感的电流不能突变，即 iL (0 ) iL (0 ) I0 ， 此时电阻 端电压 uR (0 ) I 0 R 。根据KVL可知，电感上的电压立即从换路前的零值突变
得到如图(b)所示电路，其时间常数为
RC 10103 5106 5102 s 0.05s
uC
t
U0e
6e V 20t
iC
U0
t
e
R
- 6 e20t 10 10 3
0.6e20t mA
一 四、一过阶渡R过C程电路零输入响应的实例
例：电路如下图所示，t 0 时开关由位置1拨向位置2，求 t 0 时
而电阻消耗的能量为
Q
0 uC dq
U 0
S
CuC
duC
1 2
CU
2 S
WR
i 2 Rdt
0
U
2 S
0R
2t
e RC dt
1 2
CU
2 S
由此可见，在充电过程中电源所提供的能量，一半储存在电容的电场中， 一半消耗在电阻上。且电阻上消耗的能量与R无关，充电效率总是50%。
2022/9/10
2022/9/10
一 四、一过阶渡R过C程电路零输入响应的实例
解： 在开关由位置1拨向位置2的瞬间，电容电压不能越变，因此可得
uC (0 ) uC (0 ) 6V
将连接于电容两端的电阻等效为一个电阻，其阻值为
R 8 6 3 10k 63
的电流为 I0 US R1，
电感中储存一定的 能量。在 t 0，开 关S由位置1拨向位 置2处。
一 三、一过阶渡R过L程电路的零输入响应的分析
一阶RL电路的零输入响应的定性分析
在换路的瞬间，由于电感的电流不能突变，即 iL (0 ) iL (0 ) I0 ， 此时电阻 端电压 uR (0 ) I 0 R 。根据KVL可知，电感上的电压立即从换路前的零值突变
得到如图(b)所示电路，其时间常数为
RC 10103 5106 5102 s 0.05s
uC
t
U0e
6e V 20t
iC
U0
t
e
R
- 6 e20t 10 10 3
0.6e20t mA
一 四、一过阶渡R过C程电路零输入响应的实例
例：电路如下图所示，t 0 时开关由位置1拨向位置2，求 t 0 时
而电阻消耗的能量为
Q
0 uC dq
U 0
S
CuC
duC
1 2
CU
2 S
WR
i 2 Rdt
0
U
2 S
0R
2t
e RC dt
1 2
CU
2 S
由此可见，在充电过程中电源所提供的能量，一半储存在电容的电场中， 一半消耗在电阻上。且电阻上消耗的能量与R无关，充电效率总是50%。
一阶电路的零输入响应零状态响应全响应.
零状态响应
全响应
t t uC U 0e RC U (1 e RC ) (t 0) t U (U 0 U )e RC (t 0)
稳态分量
稳态值
初始值
暂态分量
结论： 全响应 = 稳态响应 +暂态响应
第四章 动态电路的时域分析
例1：电路如图，开关S闭合前电路已处于稳态。 t=0时S闭合，试求：t >0时电容电压uC和电流iC、 1 2 i1和i2 2 。 C + 1 解：用三要素法求解 Su+ 6V 3 C 求初始值 uC (0 ) - 5μ F t=0 由t=0-时电路
+
uR -
U e A R
R t L
t0
第四章 动态电路的时域分析
U i L (1 e ) R t R t di L uL L Ue Ue dt R t uR i L R U (1 e L ) uL、 uR变化曲线 2. i L、
R t L
第四章 动态电路的时域分析
(3) 求τ
R3 R4 3 6 R R2 2 4 R3 R4 3 6
RC 4 0.5 2 s
第四章 动态电路的时域分析
(4) 求uC和i。
uC 2 (6 2)e
t 2
2 4e V
t 2
t 2
t 2
第四章 动态电路的时域分析
3.3 一阶电路的零输入响应、 零状态响应和全响应
3.3.1 一阶电路的零输入响应: 一、一阶RC电路的零输入响应
实质：RC电路的放电过程。
第四章 动态电路的时域分析
定性分析：
6.4 一阶电路的零输入响应 电路原理第一版课件
RI0
t
令 =L/R RL电路的时间常数 3 5 过渡过程结束。
例.
35V
S(t=0)
iL
+
V
RV 5k
–
R=0.2 L=0.4H
iL (0+)=iL(0)=35/0.2=175 A= I0
L 0.481 0 5s8μ0 s
RR V 5000
R t
iL I0e L
R
R
t
t
u V R L i R V I0eL 8e 7L5 kV (t0)
6.4 一阶电路的零输入响应
零输入响应(Zeroinput response )：激励(电源)为零，由初 始储能引起的响应。
一、 RC电路的零输入响应 (C对R放电)
S(t=0) i
+
C uC
–
+
R uC
–
i C duC dt
uC
RCduC dt
0
uC (0)=U0
解答形式 uC(t)=uC"=Aept (特解 uC'=0)
由特征方程
Lp+R=0
得
pR L
由初值 i(0+)=i(0)= I0 得 i(0+)=A= I0
R
解 答iL(t)I0eLt
(t 0)
Rt
iL(t) I0e L
(t 0)
I0 iL
uL(t)LdditL
Rt
R0IeL
(t
0)
O uL
t
O
(1) iL, uL 以同一指数规律衰减到零；
(2)衰减快慢取决于L/R。
uV (0+)= 875 kV !
3-4 一阶电路的零输入响应
X
几个定义
如果已知电容电压和电感电流在初始时刻的值，则 根据该时刻的输入就能确定电路中的任何变量在随 后时刻的值。 将具有这种特性的量，即电容电压和电感电流，称 为状态变量。 动态电路中，通常以状态变量作为未知量来列写方 程。
X
几个定义
S (t 0)
R i(t)
C
us(t)
+ uC (0 ) U 0
X
例题
求t 0 时电路的时间常数 。
解： 开关闭合后电路变成两
联，所以有： L R2
个独立的部分，即 us 与 R1 的串联和 L 与R2 的串
R1
us
+ S (t 0)
R2
L
X
求t 0 时的 iC (t ) 和u(t )。 420 us (t ) uC (0 ) 120 V 解： t 0时电容开路： 70 420 20 70 i (t ) t 0, uC (0 ) uC (0 ) 120 V
t 0时，电感通过电阻放电， 电感释放能量 电阻消耗能量 电感释放能量，电阻消耗能量； 电感电流 ，电感电压 t 时，电感放电结束： i L () 0, uL () 0, uR () 0。
S (t 0)
uR
L
R
R0
U0
iL (t )
uL ( t ) L
§3-4 一阶电路的零输入响应
北京邮电大学电子工程学院 2012.1
退出
开始
内容提要
几个定义 一阶RC电路的零输入响应 一阶RL电路的零输入响应
X
几个定义
动态电路中，动态元件电压电流之间存在微积分关系， 因此电路方程就需要用微分方程进行描述。线性、非 时变动态电路用线性、常系数常微分方程描述。 含有一个独立的动态元件的线性、非时变动态电路 用线性、常系数一阶常微分方程描述，称其为一阶 动态电路。 二阶动态电路：用二阶微分方程描述的动态电路。 高阶动态电路：二阶以上的动态电路。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R2
R3
本章主要内容
问题2：研究什么样的一阶电路全响 应（包括零输入响应、零状态响应） 更具一般性？
零输入响应 零状态响应
全响应 三要素法
电路原理
问题
线性有 源二端 电阻网 络
uc (0 ) uS1 +
+
C uC
uS2
-
-
线性有源二
R2
R3
C L 端电阻网络
t ≥0+时的电路
Req + us -
t 0 Req
i(t)
+C uC(t)
- uc(0+)=U0
回路电流
i(t)
U0
t
e ReqC
Req
指数衰减 0
t ≥ 0+ 时的等效电路
t 0
衰减快慢由什么决定？ Uo和Uo/Req ？ReqC
×
√
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
uC(t) U0
Req
Req
+C uC(t)
- uc(0+)=U0
t
uC (t) U0e ReqC
t 0 t ≥ 0+ 时的等效电路
i(t)
uC (t)
U0
t
e ReqC
Req Req
t 0
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
电容电压
t
uC (t) U0e ReqC
指数衰减 0
的uS非1e零初R2 始tR3状C态和u输S2入1激 e励共R2同tR引3 C起的。（t ≥0+）
电路原理
问题
uc (0 ) uS1 +
+
C uC
uS2
-
-
问题1：一阶电路全响应（包括零输 入响应、零状态响应）的求解是否有 比上述“输入-输出法”更简单的方法？
+
C uC
uS2
-
-
R2
R3
t ≥0+时的电路
因uc此(0零电 )输路入中uS响的1 应响：应是换由路储后零能无暂输元输态入件入分分的激量量非励++零的零稳初作状态始用态分状，分量量= 全响应
A u态S1而引u起S2的。
uc 零为u零状S1，态电响uS路应2 中：e的换R响2路tR应后3 是储C 由能u输元S2入件激的（励初t ≥引始0起状+）的态。 全响应：换路后电路中的响应是储能元件
C
0
t
uC (t) U0e ReqC
t 0
i(t) uC (t)
t
Req
i(t)
U0一定 Req一定，i一定 C大，q 大，衰减越慢； C小，q小，衰减越快。
+C
Req
uC(t)
-
uc(0+)=U0
t ≥ 0+ 时等效电电路路原理
§4-1 一阶电路的零输入响应∙ 时间常数
时间常数：
0
t
uC (t) U0e ReqC
t 0
i(t) uC (t)
t
Req
i(t)
U0一定 C一定，q一定 Req大，i 小，衰减越慢； Req小，i 大，衰减越快。
+C
Req
uC(t)
-
uc(0+)=U0
t ≥ 0+ 时等效电电路路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
uC(t) U0
uct
Ae
R2
t R3
C
R2 R3
A为待定系数
C
t ≥0+时的电路
duC dt
uC
uS2
非齐次微分方程的特解
ucf uc uS2
电路原理
引例
非齐次微分方程的通解
uc
uct ucf
Ae
R2
t R3
C
uS2
由于
uc (0 ) uS1 +
uC(t)
U0
U0e-1=0.368U0
U0e-2=0.135U0
t
uC (t) U0e ReqC
t ReqC
t 0
U0e-3=0.05U0
U0e-4=0.0184U0 U0e-5=0.0068U0
t
0 t 2t 3t 4t
0
时间常数 t 愈小，放电过程进行得愈快，暂态过程需要的时 间越短；反之， t 愈大，放电过程进行得愈慢，暂态过程需要的 时间越长。工程上认为，大约经过4t－ 5t后暂态过程结束。
t ReqC
t 单位: s
V/A∙A ∙s/V=s
t
uC (t) U0e ReqC
t 0
电压(V) 电压 无量纲
t 和t 同量纲
电路的时间常数(time constant)
具有时间的量纲; 由电路的结构和参数决定。
τ 的大小表征了电容电压衰减的慢快
电路原理
§4-1 一阶电路的零输入响应∙时间常数
+C
Req
uC(t)
- uc(0+)=U0
t ≥ 0+ 时的等效电路
带电电容(初始储能)的放电过程，电阻耗能过程。
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
2.定量分析
t ≥ 0+时电路的微分方程
ReqC
duC (t dt
)
uC
(t
)
0
Req
uC(0 ) uC(0) U0
等效 is
Req
Req
+ us
-
C 对偶 is
uc (0 )
Req L
iL(0 )
一阶RC电路
一阶RL电路
具有一般性
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
1.定性分析(零输入响应)
t ≥ 0+
uc(t): uc(0+)=U0 0
i(t) : i(0+)=U0/Req 0
i(t)
i(t)
+C uC(t)
- uc(0+)=U0
特征方程为 特征根为
ReqCs 1 0
s 1 ReqC
t ≥ 0+ 时的等效电路
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
t
通解为 uC (t) Aes t Ae ReqC i(t)
代入初始条件得 A = U0
零输入响应
3) 列输出输出方程
C uC -
+ uS2 -
t=0-时的电路
R2
R3
C
duC dt
uC
uS 2
R2
R3
t≥0+时的电路
电路原理
引例
特征方程
R2 R3 CS 1 0
uc (0 ) uS1 +
+
C uC
uS2
-
-
特征值
R2
R3
1
S
R2 R3 C 对应齐次微分方程的通解
电路原理
§4-1 一阶电路的零输入响应∙ 一阶RC电路
U0 uC(t)
0.368U0
uC(t)
0τ
t
uC (t) U0e ReqC
第四章 一阶电路和二阶电路
引例：图示的电路在换路前已达到稳态，
求换路后的电容电压 uC。
S(t=0)
解： 1) t = 0- 时
uC 0 uS1
+
+
+
uS1
C uC
uS2
-
-
-
R1
R2
R3
+
+
2) 根据换路定则
uS1
uC(0-)
-
-
R1
R2
uC 0 uC 0 uSu1c (0 ) uS1 +