一、选择题下列每小题给出的四个选项中,只有一项符合
选择题在每题给出的四个选项中只有一项是符合题

一、选择题(在每题给出的四个选项中,只有一项是符合题目要求,每小题2分,共50分)图1中心为极点,外圆为50°纬线图,图中数字表示经度度数,P 、Q 之间和M 、N 之间为陆地,完成1~2题。
1、P 点附近的盛行风向是A 、东北风B 、西南风C 、西北风D 、东南风 2、关于P 、Q 、M 、N 四地气候的叙述,正确的是 A 、P 、M 两地的气候类型相同 B 、Q 、N 两地的气候类型相同C 、P 地夏季炎热干燥,冬季温和多雨D 、N 地为亚热带常绿阔叶林带读图2所示的气候统计资料,回答第3题:3.下列我国的省区中,哪个有该气候类型的分布读图3“我国部分省区七月平均气温分布图”,完成4~6题。
4.影响图中28℃等温分布的主要因素是 ①太阳辐射 ②海陆分布 ③地形因素 ④大气环流 A .①② B .②③ C .③④ D .①④5.此时沿图中海岸分布的28℃等温线自南向北观察到的现象,最可信的是 A .正午太阳高度逐渐增大 B .河流汛期逐渐变长 C .降水量越来越大 D .白昼时间越来越大 6.有关图示地区最大河流的叙述,正确的是 A .是我国水量最大、汛期最长的河流 B .是我国水能资源最丰富的河流 C .水运发达,航运里程仅次于长江,居全国第二位D .其流经地区全部属于我国经济发达地区 下图为某地地形剖面图,,完成7~9题。
图2图1图 37.若甲地位于乙地的正南方,则图示区域可能位于A .南纬30°附近B .北纬45°附近C .北纬25°附近D .南纬20°附近 8.若甲地位于乙地正西方,且甲地西侧临近海洋,盛行西风,则A .太阳辐射量:甲地>乙地B .气温:甲地=乙地C .水汽含量:甲地<乙地D .气温:甲地<乙地9.若丙地位于青藏高原,丁地位于云贵高原,丙地年太阳辐射量大于丁地的主要原因A .丙地白昼时间长,日照充足B .丙地海拔高,空气稀薄,对太阳辐射削弱少C .丙地纬度低,丁地纬度高D .丁地海拔低,降水丰富,太阳高度角小下图“沿经度20°线上某大洲地形剖面图及大气环流形势图”,完成10~11题。
2024广东省高考政治真题卷及答案

2024广东高考真题政治本试卷满分100分,考试时间75分钟一、选择题(本大题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是最符合题目要求的)。
1. 邓小平同志在1979年要求深圳“杀出一条血路来",之后进一步提出“走自己的路”,建设有中国特色的社会主义,强调要“摸着石头过河”。
2012年12月,习近平总书记在广东考察时作出“改革已经进入攻坚期和深水区”的重要论断。
对此,如下解读正确的是()①“杀出一条血路来”指明了打破帝国主义封锁的方向②“走自己的路”指明了我国改革开放的方向③“摸着石头过河”说明改革伊始就明确了发展蓝图④“改革已经进入攻坚期和深水区“要求加强全面深化改革的顶层设计A. ①②B. ①③C. ②④D. ③④2. 党的二十大报告提出,深入实施人才强国战略,强化现代化建设人才支撑。
2023年,中办、国办印发《关于进一步加强青年科技人才培养和使用的若干措施》,强调要激励引导青年科技人才,在以中国式现代化全面推进中华民族伟大复兴的进程中奉献青春和智慧。
作出这一举措是因为()①青年是实现中华民族伟大复兴的先锋力量②人才越来越成为推动经济社会发展的战略性资源③人力资源大国优势是实施人才强国战略的决定性因素④培养高素质人才是全面建设社会主义现代化国家的首要任务A. ①②B. ①③C. ②④D. ③④3. 习近平总书记指出:“中国人民历来具有深厚的天下情怀,当代中国文艺要把目光投向世界、投向人类。
”“广大文艺工作者要紧跟时代步伐.展现中华历史之美、山河之美、文化之美,抒写中国人民奋斗之志、创造之力、发展之果,全方位全景式展现新时代的精神气象。
”以上重要论述表明()①坚定文化自信是中国特色社会主义最本质的特征②习近平文化思想要求坚持以人民为中心的创作导向③面向世界是中国特色社会主义文化发展的根本方向④文艺创作要坚持不忘本来、吸收外来、面向未来相统一A. ①②B. ①③C. ②④D. ③④4. 随着无人机广泛应用于地理测绘、影视航拍、山地救援等领域,“联飞快送”“空中观光”等“无人机技术+”业务涌现,低空经济成为发展新引擎。
2017法律硕士(法学)联考专业综合课真题及答案

2017法律硕士(法学)联考专业综合课真题及答案一、单项选择题(每小题1 分,下列每题给出的四个选项中,只有一项是符合试题要求的)1、债权属于( )A.公权利B.对人权C.对世权D.绝对权2、法律事实包括行为和( )A.事件B.物质财富C.精神财富D.法律权利3、社会主义民主与社会主义法治的关系表现为( )A.社会主义法治是社会主义民主的目的B.社会主义法治是社会主义民主的力量源泉C.社会主义民主是社会主义法治的一项原则D.社会主义法治是社会主义民主的前提4、国务院根据宪法和法律,有权制定( )A.法律法规B.行政法规C.部门规章D.自治条例和单行条例5、以下诸项中,关于法学产生和特征的正确描述是( )A.法学随着法的出现而出现,有法就有了法学B.法学是超阶级的、超政治的C.职业法学家的出现是法学产生的标志D.法学是超历史的、永恒存在的6、关于公、私法的表述,正确的是( )A.公、私法的划分是普通法法系划分部门法的方法B.罗马法学家帕比尼安首先提出划分公法和私法的学说C.公法一般是指宪法、行政法、民法和程序法D.私法包括商法7、法律条文与法律规范的关系是( )A.法律规范是法律条文的载体B.一个法律规范就等于一个法律条文C.一个法律规范不能包括在几个法律条文中D.一个法律条文可以包括几个法律规范8、以下法典中,突出地反映法律社会化精神的是( )A.法国民法典B.德国民法典C.英国宪法D.美国宪法9、在阶级对立的社会中,法的实施主要是靠( )A.社会舆论B.领导的威信C.自觉遵守D.国家强制力的保证10、按照法的效力、内容和制定程序的不同,法可分为 ( )A.国内法和国际法B.根本法和普通法C 一般法和特别法D.成文法和不成文法11、贯彻以事实为根据、以法律为准绳这一原则,适用法律时( )A.就不应以党的政策为指导B.有时也要以党的政策为指导C 仍然要以党的政策为指导D.法律应无条件地服从党的政策12、美国的法属于( )A.法典法系B.罗马一一日耳曼法系C.大陆法系D.英美法系13、法的本质是()决定的A.社会生产力水平B.社会经济基础C 全体社会的共同意志D.执政党的意志14、甲是法学院教授.在某律师事务所担任兼职律师。
2024年高考数学真题试卷(天津卷)附详细解答
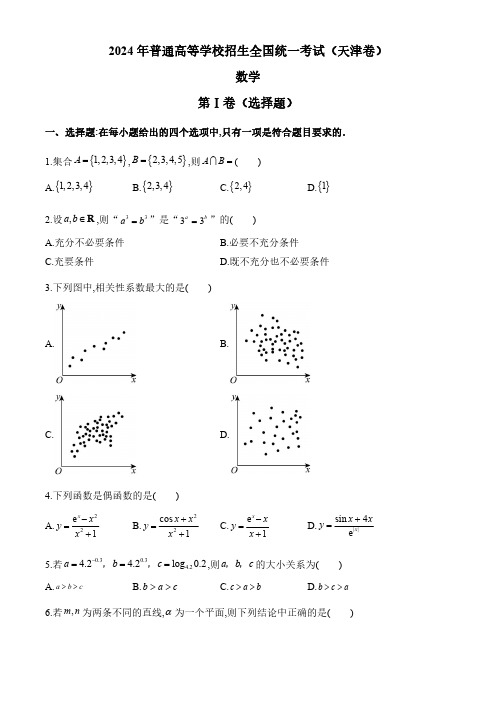
2024年普通高等学校招生全国统一考试(天津卷)数学第Ⅰ卷(选择题)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}1,2,3,4A =,{}2,3,4,5B =,则A B = ()A.{}1,2,3,4 B.{}2,3,4 C.{}2,4 D.{}12.设,a b ∈R ,则“33a b =”是“33a b =”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.下列图中,相关性系数最大的是()A. B.C. D.4.下列函数是偶函数的是()A.22e 1x x y x -=+ B.22cos 1x x y x +=+ C.e 1x x y x -=+ D.||sin 4e x x x y +=5.若0.30.3 4.24.2 4.2log 0.2a b c -===,,,则a b c ,,的大小关系为()A.a b c>> B.b a c>> C.c a b>> D.b c a>>6.若,m n 为两条不同的直线,α为一个平面,则下列结论中正确的是()A.若//m α,n ⊂α,则//m nB.若//,//m n αα,则//m nC.若//,αα⊥m n ,则m n⊥ D.若//,αα⊥m n ,则m 与n 相交7.已知函数()()πsin303f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π.则函数在ππ,126⎡⎤-⎢⎥⎣⎦的最小值是()A.32-B.32-C.0D.328.双曲线22221()00a x y a bb >-=>,的左、右焦点分别为12.F F P 、是双曲线右支上一点,且直线2PF 的斜率为2.12PF F △是面积为8的直角三角形,则双曲线的方程为()9.一个五面体ABC DEF -.已知AD BE CF ∥∥,且两两之间距离为1.并已知123AD BE CF ===,,.则该五面体的体积为()A.6B.33142+ C.32D.33142-第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.10.已知i 是虚数单位,复数))i 2i ⋅=______.11.在63333x x⎛⎫+ ⎪⎝⎭的展开式中,常数项为______.12.22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合,A 为两曲线的交点,则原点到直线AF 的距离为______.13.,,,,A B C D E 五种活动,甲、乙都要选择三个活动参加.(1)甲选到A 的概率为______;已知乙选了A 活动,他再选择B 活动的概率为______.14.在边长为1的正方形ABCD 中,点E 为线段CD 的三等分点,1,2CE DE BE BA BC ==+uur uur uuu r λμ,则λμ+=______;若F 为线段BE 上的动点,G 为AF 中点,则AF DG ⋅的最小值为______.15.若函数()21f x ax =--+有唯一零点,则a 的取值范围为______.三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.在ABC 中,92cos 5163a Bbc ===,,.(1)求a ;(2)求sin A ;(3)求()cos 2B A -.17.已知四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AB CD ,1A A ⊥平面ABCD ,AD AB ⊥,其中12,1AB AA AD DC ====.N 是11B C 的中点,M 是1DD 的中点.(1)求证1//D N 平面1CB M ;(2)求平面1CB M 与平面11BB CC 的夹角余弦值;(3)求点B 到平面1CB M 的距离.18.已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =.左顶点为A ,下顶点为B C ,是线段OB 的中点,其中ABC S =△.(1)求椭圆方程.(2)过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ,.在y 轴上是否存在点T 使得0TP TQ ⋅≤ 恒成立.若存在求出这个T 点纵坐标的取值范围,若不存在请说明理由.19.已知数列{}n a 是公比大于0的等比数列.其前n 项和为n S .若1231,1a S a ==-.(1)求数列{}n a 前n 项和n S ;(2)设11,2,kn n k k k n a b b k a n a -+=⎧=⎨+<<⎩,11b =,其中k 是大于1的正整数.(ⅰ)当1k n a +=时,求证:1n k n b a b -≥⋅;(ⅱ)求1nS i i b =∑.20.设函数()ln f x x x =.(1)求()f x 图象上点()()1,1f 处的切线方程;(2)若()(f x a x ≥-在()0,x ∞∈+时恒成立,求a 的取值范围;(3)若()12,0,1x x ∈,证明()()121212f x f x x x -≤-.2024年普通高等学校招生全国统一考试(天津卷)数学答案解析一、选择题.1.【答案】B【解析】因为集合{}1,2,3,4A =,{}2,3,4,5B =所以{}2,3,4A B = 故选:B 2.【答案】C【解析】根据立方的性质和指数函数的性质,33a b =和33a b =都当且仅当a b =,所以二者互为充要条件.故选:C.3.【答案】A【解析】观察4幅图可知,A 图散点分布比较集中,且大体接近某一条直线,线性回归模型拟合效果比较好,呈现明显的正相关,r 值相比于其他3图更接近1.故选:A 4.【答案】B【解析】对A,设()22e 1x x f x x -=+,函数定义域为R ,但()112e 1f ---=,()112e f -=,则()()11f f -≠,故A 错误;对B,设()22cos 1x x g x x +=+,函数定义域为R 且()()()()()2222cos cos 11x x x x g x g x x x -+-+-===+-+,则()g x 为偶函数,故B 正确;对C,设()e 1x xh x x -=+,函数定义域为{}|1x x ≠-,不关于原点对称,则()h x 不是偶函数,故C 错误;对D,设()||sin 4e x x x x ϕ+=,函数定义域为R,因为()sin141e ϕ+=,()sin141eϕ---=则()()11ϕϕ≠-,则()x ϕ不是偶函数,故D 错误.故选:B.5.【答案】B【解析】因为 4.2x y =在R 上递增,且0.300.3-<<所以0.300.30 4.2 4.2 4.2-<<<所以0.30.30 4.21 4.2-<<<,即01a b <<<因为 4.2log y x =在(0,)+∞上递增,且00.21<<所以 4.2 4.2log 0.2log 10<=,即0c <所以b a c >>故选:B 6.【答案】C【解析】对于A,若//m α,n ⊂α,则,m n 平行或异面,故A 错误.对于B,若//,//m n αα,则,m n 平行或异面或相交,故B 错误.对于C,//,αα⊥m n ,过m 作平面β,使得s βα= 因为m β⊂,故//m s ,而s α⊂,故n s ⊥,故m n ⊥,故C 正确.对于D,若//,αα⊥m n ,则m 与n 相交或异面,故D 错误.故选:C.7.【答案】A【解析】()()πsin3sin 3πsin 33f x x x x ωωω⎛⎫=+=+=- ⎪⎝⎭,由2ππ3T ω==得23ω=即()sin2f x x =-,当,126⎡⎤∈-⎢⎣⎦ππx 时,ππ2,63x ⎡⎤∈-⎢⎥⎣⎦画出()sin2f x x =-图象,如下图由图可知,()sin2f x x =-在ππ,126⎡⎤-⎢⎥⎣⎦上递减所以,当π6x =时,()min πsin 32f x =-=-故选:A 8.【答案】C【解析】如下图:由题可知,点P 必落在第四象限,1290F PF ∠=︒,设2PF m=211122,PF F PF F θθ∠=∠=,由21tan 2PF k θ==,求得12sin 5θ=因为1290F PF ∠=︒,所以121PF PF k k ⋅=-,求得112PF k =-,即21tan 2θ=21sin 5θ=由正弦定理可得:121212::sin :sin :sin 902:1:5PF PF F F θθ=︒=则由2PF m =得1122,25PF m F F c m ===由1212112822PF F S PF PF m m =⋅=⋅= 得2m =则21122,2,210,10PF PF F F c c =====由双曲线第一定义可得:1222PF PF a -==222,8a b c a ==-=所以双曲线的方程为22128x y -=.故选:C 9.【答案】C【解析】用一个完全相同的五面体HIJ LMN -(顶点与五面体ABC DEF -一一对应)与该五面体相嵌,使得,D N ;,E M ;,F L 重合因为AD BE CF ∥∥,且两两之间距离为1.1,2,3AD BE CF ===则形成的新组合体为一个三棱柱该三棱柱的直截面(与侧棱垂直的截面)为边长为1的等边三角形,侧棱长为1322314+=+=+=2132211311422ABC DEF ABC HIJ V V --==⨯⨯⨯⨯=.故选:C.第Ⅱ卷二、填空题.10.【答案】7【解析】))i 2i 527+⋅=+-+=-.故答案为:7.11.【答案】20【解析】因为63333x x ⎛⎫+ ⎪⎝⎭的展开式的通项为()63636216633C 3C ,0,1,,63rr r r r r r x T x r x ---+⎛⎫⎛⎫===⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭令()630r -=,可得3r =所以常数项为0363C 20=.故答案为:20.12.【答案】45【解析】圆22(1)25-+=x y 的圆心为()1,0F ,故12p =即2p =由()2221254x y y x⎧-+=⎪⎨=⎪⎩可得22240x x +-=,故4x =或6x =-(舍)故()4,4A ±,故直线()4:13AF y x =±-即4340x y --=或4340x y +-=故原点到直线AF 的距离为4455d ==故答案为:4513.【答案】①.35②.12【解析】设甲、乙选到A 为事件M ,乙选到B 为事件N则甲选到A 的概率为()2435C 3C 5P M ==;乙选了A 活动,他再选择B 活动的概率为()()()133524351C 2C C P MN C P N M P M ===故答案为:35;1214.【答案】①.43②.518-【解析】因为12CE DE =,即23CE BA =uur uur ,则13BE BC CE BA BC =+=+uuu r uur u uu ur r uuu r 可得1,13λμ==,所以43λμ+=;由题意可知:1,0BC BA BA BC ==⋅= 因为F 为线段BE 上的动点,设[]1,0,13BF k BE k BA k BC k ==+∈ 则113AF AB BF AB k BE k BA k BC ⎛⎫=+=+=-+ ⎪⎝⎭又因为G 为AF 中点,则1111112232DG DA AG BC AF k BA k BC ⎛⎫⎛⎫=+=-+=-+- ⎪ ⎪⎝⎭⎝⎭可得11111113232AF DG k BA k BC k BA BC ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⋅=-+⋅-+- ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 22111563112329510k k k k ⎛⎫⎛⎫⎛⎫=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又因为[]0,1k ∈,可知:当1k =时,AF DG ⋅ 取到最小值518-;15.【答案】()(1- 【解析】令()0f x =,即21ax =--由题可得20x ax -≥当0a =时,x ∈R ,有211=--=,则2x =±,不符合要求,舍去;当0a >时,则23,2121,ax x a ax ax x a ⎧-≥⎪⎪=--=⎨⎪-<⎪⎩即函数()g x =与函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩有唯一交点由20x ax -≥,可得x a ≥或0x ≤当0x ≤时,则20ax -<,则211ax ax=--=-即()22441x ax ax -=-,整理得)()()2242121210a x ax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦当2a =时,即410x +=,即14x =-当()0,2a ∈,12x a =-+或102x a =>-(正值舍去)当()2,a ∈+∞时,102x a =-<+或102x a=<-,有两解,舍去即当(]0,2a ∈时,210ax -+=在0x ≤时有唯一解则当(]0,2a ∈时,210ax -+=在x a ≥时需无解当(]0,2a ∈,且x a ≥时由函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩关于2x a =对称,令()0h x =,可得1x a =或3x a =且函数()h x 在12,a a ⎛⎫ ⎪⎝⎭上单调递减,在23,a a ⎛⎫ ⎪⎝⎭上单调递增令()g x y ==,即2222142a x y a a⎛⎫- ⎪-⎭=⎝故x a ≥时,()g x 图象为双曲线()222214y x a a-=右支的x 轴上方部分向右平移2a 所得由()222214y x a a -=的渐近线方程为22a y x xa =±=±即()g x 部分的渐近线方程为22a y x ⎛⎫=- ⎪⎝⎭,其斜率为2又(]0,2a ∈,即()23,21,ax x a h x ax x a⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a ≥时的斜率(]0,2a ∈令()0g x ==,可得x a =或0x =(舍去)且函数()g x 在(),a +∞上单调递增故有13aaaa ⎧<⎪⎪⎨⎪>⎪⎩,解得1a <<,故1a <<符合要求;当a<0时,则23,2121,ax x aax ax x a⎧-≤⎪⎪=--=⎨⎪->⎪⎩即函数()g x =与函数()23,21,ax x a h x ax x a⎧-≤⎪⎪=⎨⎪->⎪⎩有唯一交点由20x ax -≥,可得0x ≥或x a ≤当0x ≥时,则20ax -<,则211ax ax=--=-即()22441x ax ax -=-,整理得()()()2242121210a x ax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦当2a =-时,即410x -=,即14x =当()2,0a ∈-,102x a =-<+(负值舍去)或102x a =-当(),2a ∈-∞时,102x a =->+或102x a =>-,有两解,舍去即当[)2,0a ∈-时,210ax --+=在0x ≥时有唯一解则当[)2,0a ∈-时,210ax --+=在x a ≤时需无解当[)2,0a ∈-,且x a ≤时由函数()23,21,ax x a h x ax x a ⎧-≤⎪⎪=⎨⎪->⎪⎩关于2x a =对称,令()0h x =,可得1x a =或3x a =且函数()h x 在21,a a ⎛⎫ ⎪⎝⎭上单调递减,在32,a a ⎛⎫ ⎪⎝⎭上单调递增同理可得:x a ≤时,()g x 图象为双曲线()222214y x a a -=左支的x 轴上方部分向左平移2a 所得()g x 部分的渐近线方程为22a y x ⎛⎫=-+ ⎪⎝⎭,其斜率为2-又[)2,0a ∈-,即()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a <时的斜率[)2,0a ∈-令()0g x ==,可得x a =或0x =(舍去)且函数()g x 在(),a -∞上单调递减故有13a a a a⎧>⎪⎪⎨⎪<⎪⎩,解得1a <<-,故1a <<-符合要求;综上所述,()(11,a ∈- .故答案为:()(1-⋃.三、解答题.16.【答案】(1)4(2)74(3)5764【小问1详解】设2,3a t c t ==,0t >,则根据余弦定理得2222cos b a c ac B=+-即229254922316t t t t =+-⨯⨯⨯,解得2t =(负舍);则4,6a c ==.【小问2详解】因为B 为三角形内角,所以57sin 16B ===再根据正弦定理得sin sin a b A B =,即4sin 5716A =,解得7sin 4A =【小问3详解】因为9cos 016B =>,且()0,πB ∈,所以π0,2B ⎛⎫∈ ⎪⎝⎭由(2)法一知57sin 16B =因为a b <,则A B <,所以3cos 4A ==则7337sin 22sin cos 2448A A A ==⨯⨯=,2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭()19573757cos 2cos cos 2sin sin 281616864B A B A B A -=+=⨯+⨯=.17.【答案】(1)证明见解析(2)22211(3)21111【小问1详解】取1CB 中点P ,连接NP ,MP由N 是11B C 的中点,故1//NP CC ,且112NP CC =由M 是1DD 的中点,故1111122D M DD CC ==,且11//D M CC 则有1//D M NP 、1D M NP=故四边形1D MPN 是平行四边形,故1//D N MP又MP ⊂平面1CB M ,1D N ⊄平面1CB M故1//D N 平面1CB M ;【小问2详解】以A为原点建立如图所示空间直角坐标系有()0,0,0A 、()2,0,0B 、()12,0,2B 、()0,1,1M 、()1,1,0C 、()11,1,2C 则有()11,1,2CB =- 、()1,0,1CM =- 、()10,0,2BB = 设平面1CB M 与平面11BB CC 的法向量分别为()111,,m x y z = 、()222,,n x y z = 则有111111200m CB x y z m CM x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ,1222122020n CB x y z n BB z ⎧⋅=-+=⎪⎨⋅==⎪⎩ 分别取121x x ==,则有13y =、11z =、21y =,20z =即()1,3,1m = 、()1,1,0n =则cos ,11m n m n m n ⋅===⋅ 故平面1CB M 与平面11BB CC 的夹角余弦值为22211;【小问3详解】由()10,0,2BB = ,平面1CB M 的法向量为()1,3,1m =则有111BB m m ⋅== 即点B 到平面1CB M 的距离为21111.18.【答案】(1)221129x y +=(2)存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭,使得0TP TQ ⋅≤ 恒成立.【小问1详解】因为椭圆的离心率为12e =,故2a c =,b =,其中c 为半焦距所以()()32,0,0,,0,2A c B C ⎛⎫-- ⎪ ⎪⎝⎭,故13332222ABC S c c =⨯⨯=△故c =所以a =,3b =,故椭圆方程为:221129x y +=.【小问2详解】若过点30,2⎛⎫- ⎪⎝⎭的动直线的斜率存在,则可设该直线方程为:32y kx =-设()()()1122,,,,0,P x y Q x y T t 由22343632x y y kx ⎧+=⎪⎨=-⎪⎩可得()223412270k x kx +--=故()222Δ144108343245760k k k =++=+>且1212221227,,3434k x x x x k k+==-++而()()1122,,,TP x y t TQ x y t =-=- 故()()121212123322TP TQ x x y t y t x x kx t kx t ⎛⎫⎛⎫⋅=+--=+---- ⎪⎪⎝⎭⎝⎭ ()()22121233122k x x k t x x t ⎛⎫⎛⎫=+-++++ ⎪ ⎪⎝⎭⎝⎭()22222731231342342k k k t t k k ⎛⎫⎛⎫⎛⎫=+⨯--+⨯++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭()2222222327271812332234k k k t t t k k ⎛⎫----++++ ⎪⎝⎭=+()22223321245327234t t k t k ⎛⎫⎡⎤+--++- ⎪⎣⎦⎝⎭=+因为0TP TQ ⋅≤ 恒成立,故()223212450332702t t t ⎧+--≤⎪⎨⎛⎫+-≤⎪ ⎪⎝⎭⎩,解得332t -≤≤.若过点30,2⎛⎫- ⎪⎝⎭的动直线的斜率不存在,则()()0,3,0,3P Q -或()()0,3,0,3P Q -此时需33t -≤≤,两者结合可得332t ≤≤.综上,存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭,使得0TP TQ ⋅≤ 恒成立.19.【答案】(1)21n n S =-(2)①证明见详解;②()131419n n S i i n b =-+=∑【小问1详解】设等比数列{}n a 的公比为0q >因为1231,1a S a ==-,即1231a a a +=-可得211q q +=-,整理得220q q --=,解得2q =或1q =-(舍去)所以122112nn n S -==--.【小问2详解】(i )由(1)可知12n n a -=,且N*,2k k ∈≥当124k k n a +=≥=时,则111221111k k k k k a n n a a -++⎧=<-=-⎨-=-<⎩,即11k k a n a +<-<可知12,1k k n a b k -==+()()()1111222121k k k n a k k b b a a k k k k --+=+--⋅=+-=-可得()()()()1112112122120k n k n k k k k k k k k b k a b ---=--+=--≥--=-⋅≥-当且仅当2k =时,等号成立所以1n k n b a b -≥⋅;(ii )由(1)可知:1211n n n S a +=-=-若1n =,则111,1S b ==;若2n ≥,则112k k k a a -+-=当1221k k i -<≤-时,12i i b b k --=可知{}i b 为等差数列可得()()()111211112221122431434429k k k k k k k k i i b k k k k k -------=-⎡⎤=⋅+=⋅=---⎣⎦∑所以()()()232113141115424845431434499n n S n n i i n b n n -=-+⎡⎤=+⨯-⨯+⨯-⨯+⋅⋅⋅+---=⎣⎦∑且1n =,符合上式,综上所述:()131419n n S i i n b =-+=∑.20.【答案】(1)1y x =-(2){}2(3)证明过程见解析【小问1详解】由于()ln f x x x =,故()ln 1f x x ='+.所以()10f =,()11f '=,所以所求的切线经过()1,0,且斜率为1,故其方程为1y x =-.【小问2详解】设()1ln h t t t =--,则()111t h t t t'-=-=,从而当01t <<时()0h t '<,当1t >时()0h t '>.所以()h t 在(]0,1上递减,在[)1,+∞上递增,这就说明()()1h t h ≥,即1ln t t -≥,且等号成立当且仅当1t =.设()()12ln g t a t t =--,则()((ln 12ln f x a x x x a x x a x g ⎛⎫-=-=-=⋅ ⎪⎭⎝.当()0,x ∞∈+时的取值范围是()0,∞+,所以命题等价于对任意()0,t ∞∈+,都有()0g t ≥.一方面,若对任意()0,t ∞∈+,都有()0g t ≥,则对()0,t ∞∈+有()()()()112012ln 12ln 1212g t a t t a t a t at a t t t ⎛⎫≤=--=-+≤-+-=+-- ⎪⎝⎭取2t =,得01a ≤-,故10a ≥>.再取t =,得2022a a a ≤--=--=-,所以2a =.另一方面,若2a =,则对任意()0,t ∞∈+都有()()()212ln 20g t t t h t =--=≥,满足条件.综合以上两个方面,知a 的取值范围是{}2.【小问3详解】先证明一个结论:对0a b <<,有()()ln 1ln 1f b f a a b b a -+<<+-.证明:前面已经证明不等式1ln t t -≥,故ln ln ln ln ln ln ln 1ln 1b b b a a a b a a a b b b b b a b a a--=+=+<+---且1lnln ln ln ln ln ln ln 1ln 11a a b b a a b b b a b b a a a a a a b a b a b b ⎛⎫--- ⎪--⎝⎭=+=+>=+----所以ln ln ln 1ln 1b b a a a b b a -+<<+-,即()()ln 1ln 1f b f a a b b a-+<<+-.由()ln 1f x x ='+,可知当10e x <<时()0f x '<,当1ex >时()0f x '>.所以()f x 在10,e ⎛⎤ ⎥⎝⎦上递减,在1e ,⎡⎫+∞⎪⎢⎣⎭上递增.不妨设12x x ≤,下面分三种情况(其中有重合部分)证明本题结论.情况一:当1211e x x ≤≤<时,有()()()()()()122122121ln 1f x f x f x f x x x x x x -=-<+-<-<结论成立;情况二:当1210ex x <≤≤时,有()()()()12121122ln ln f x f x f x f x x x x x -=-=-.对任意的10,e c ⎛⎤∈ ⎥⎝⎦,设()ln ln x x x c c ϕ=--则()ln 1x x ϕ=++'由于()x ϕ'单调递增,且有1111111ln 1ln 11102e 2e e c c ϕ⎛⎫ ⎪=++<+=-= ⎪⎝⎭'且当2124ln 1x c c ≥-⎛⎫- ⎪⎝⎭,2c x >时,2ln 1c ≥-可知()2ln 1ln ln 102c x x c ϕ⎛⎫=++>++=-≥ ⎪⎝⎭'.所以()x ϕ'在()0,c 上存在零点0x ,再结合()x ϕ'单调递增,即知00x x <<时()0x ϕ'<,0x x c <<时()0x ϕ'>.故()x ϕ在(]00,x 上递减,在[]0,x c 上递增.①当0x x c ≤≤时,有()()0x c ϕϕ≤=;②当00x x <<时,112221e e f f c ⎛⎫=-≤-=< ⎪⎝⎭,故我们可以取1,1q c ⎫∈⎪⎭.从而当201c x q <<-时,>可得()1ln ln ln ln 0x x x c c c c c c q c ϕ⎫=--<--<--=-<⎪⎭.再根据()x ϕ在(]00,x 上递减,即知对00x x <<都有()0x ϕ<;综合①②可知对任意0x c <≤,都有()0x ϕ≤,即()ln ln 0x x x c c ϕ=--.根据10,e c ⎛⎤∈ ⎥⎝⎦和0x c <≤的任意性,取2c x =,1x x =,就得到1122ln ln 0x x x x --≤.所以()()()()12121122ln ln f x f x f x f x x x x x -=-=-≤.情况三:当12101ex x <≤≤<时,根据情况一和情况二的讨论,可得()11e f x f ⎛⎫-≤≤ ⎪⎝⎭,()21e f f x ⎛⎫-≤≤ ⎪⎝⎭而根据()f x 的单调性,知()()()1211e f x f x f x f ⎛⎫-≤- ⎪⎝⎭或()()()1221e f x f x f f x ⎛⎫-≤- ⎪⎝⎭.故一定有()()12f x f x -≤成立.综上,结论成立.。
在每小题给出的四个选项中只有一项是符合题目要求的

一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.i 为虚数单位,607i=( )A .iB .-iC .1D .-1 【答案】A 【解析】试题分析:i i i i -=⋅=⨯31514607,选 B . 考点:复数概念.2.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( ) A .134石 B .169石 C .338石 D .1365石 【答案】B 【解析】试题分析:依题意,这批米内夹谷约为169153425428=⨯石,选B. 考点:用样本估计总体.3.已知(1)n x +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.122B .112 C .102 D .92 【答案】D考点:1.二项式系数,2.二项式系数和. 4.设211(,)XN μσ,222(,)Y N μσ,这两个正态分布密度曲线如图所示.下列结论中正确的是( )A .21()()P Y P Y μμ≥≥≥B .21()()P X P X σσ≤≤≤C .对任意正数t ,()()P X t P Y t ≤≥≤D .对任意正数t ,()()P X t P Y t ≥≥≥【答案】C考点:正态分布密度曲线. 5.设12,,,n a a a ∈R ,3n ≥.若p :12,,,n a a a 成等比数列;q :22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件 【答案】A 【解析】试题分析:对命题p :12,,,n a a a 成等比数列,则公比)3(1≥=-n a a q n n且0≠n a ; 对命题q ,①当0=n a 时,22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++成立; ②当≠n a 时,根据柯西不等式,等式22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++成立,则nn a a a a a a 13221-=⋅⋅⋅==,所以12,,,n a a a 成等比数列, 所以p 是q 的充分条件,但不是q 的必要条件.考点:1.等比数列的判定,2.柯西不等式,3.充分条件与必要条件.6.已知符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩()f x 是R 上的增函数,()()()(1)g x f x f ax a =->,则( )A .sgn[()]sgn g x x =B .sgn[()]sgn g x x =-C .sgn[()]sgn[()]g x f x =D .sgn[()]sgn[()]g x f x =- 【答案】B 【解析】试题分析:因为()f x 是R 上的增函数,令x x f =)(,所以x a x g )1()(-=,因为1>a ,所以)(x g 是R 上的减函数,由符号函数1,0s g n0,01,0x x x x >⎧⎪==⎨⎪-<⎩知,1,0s g n [()]0,0s g n1,0x g x x x x ->⎧⎪===-⎨⎪<⎩. 考点:1.符号函数,2.函数的单调性.7.在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“1||2x y -≤”的概率,3p 为事件“12xy ≤”的概率,则 ( ) A .123p p p << B .231p p p << C .312p p p <<D .321p p p <<【答案】B(1) (2) (3) 考点:几何概型.8.将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则( ) A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e > 【答案】D考点:1.双曲线的性质,2.离心率.9.已知集合22{(,)1,,}A x y x y x y =+≤∈Z ,{(,)||2,||2,,}B x y x y x y =≤≤∈Z ,定义集合12121122{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为( )A .77B .49C .45D .30 【答案】C 【解析】试题分析:因为集合22{(,)1,,}A x y x y x y =+≤∈Z ,所以集合A 中有9个元素(即9个点),即图中圆中的整点,集合{(,)||2,||2,,}B x y x y x y =≤≤∈Z 中有25个元素(即25个点):即图中正方形ABCD 中的整点,集合12121122{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈的元素可看作正方形1111D C B A 中的整点(除去四个顶点),即45477=-⨯个.考点:1.集合的相关知识,2.新定义题型.10.设x ∈R ,[]x 表示不超过x 的最大整数. 若存在实数t ,使得[]1t =,2[]2t =,…,[]n t n = 同时成立....,则正整数n 的最大值是( ) A .3 B .4 C .5 D .6 【答案】B考点:1.函数的值域,2.不等式的性质.二、填空题:本大题共6小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号.......的位置上.答错位置,书写不清,模棱两可均不得分.(一)必考题(11—14题)11.已知向量OA AB ⊥,||3OA =,则OA OB ∙=. 【答案】9 【解析】试题分析:因为OA AB ⊥,||3OA =,所以OA OB ∙=93||||)(222===∙+=+∙. 考点:1.平面向量的加法法则,2.向量垂直,3.向量的模与数量积. 12.函数2π()4cos cos()2sin |ln(1)|22x f x x x x =---+的零点个数为.【答案】2考点:1.二倍角的正弦、余弦公式,2.诱导公式,3.函数的零点.13.如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75的方向上,仰角为30,则此山的高度CD =m.【答案】6100 【解析】试题分析:依题意, 30=∠BAC ,105=∠ABC ,在A B C ∆中,由180=∠+∠+∠ACB BAC ABC ,所以45=∠ACB ,因为600=AB ,由正弦定理可得30sin 45sin 600BC=,即2300=BC m ,在BCD Rt ∆中,因为30=∠CBD ,2300=BC ,所以230030tan CD BC CD == ,所以6100=CD m.考点:1.三角形三内角和定理,2.三角函数的定义,3.有关测量中的的几个术语,4.正弦定理.14.如图,圆C 与x 轴相切于点(1,0)T ,与y 轴正半轴交于两点,A B (B 在A 的上方), 且2AB =.(Ⅰ)圆C 的标准..方程为; (Ⅱ)过点A 任作一条直线与圆22:1O x y +=相交于,M N 两点,下列三个结论:①NA MA NBMB=; ②2NB MA NAMB-=; ③NB MA NAMB+=其中正确结论的序号是. (写出所有正确结论的序号)【答案】(Ⅰ)22(1)(2x y -+=;(Ⅱ)①②③所以11)2NB MA NAMB-==-=,11NB MA NAMB+=+=正确结论的序号是①②③.考点:1.圆的标准方程,2.直线与圆的位置关系.(二)选考题(请考生在第15、16两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑.如果全选,则按第15题作答结果计分.)15.(选修4-1:几何证明选讲)如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且3BC PB =,则ABAC=.【答案】21考点:1.圆的切线、割线,2.切割线定理,3.三角形相似. 16.(选修4-4:坐标系与参数方程)在直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系. 已知直线l 的极坐标方程为(sin 3cos )0ρθθ-=,曲线C 的参数方程为1,1x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩( t 为参数) ,l与C 相交于A ,B 两点,则||AB =. 【答案】52考点:1.极坐标方程、参数方程与普通方程的转化,2.两点间的距离.三、解答题:本大题共5小题,共65分,解答应写出文字说明、证明过程或演算步骤。
2020考研高数(一)真题及答案解析

2020全国硕士研究生入学统一考试数学一试题详解一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)当0x +→时,下列无穷小量中最高阶是( )(A )()21xt e dt -⎰(B )(0ln 1xdt +⎰(C )sin 20sin xt dt ⎰(D )1cos 0-⎰【答案】(D )【解析】由于选项都是变限积分,所以导数的无穷小量的阶数比较与函数的比较是相同的。
(A )()()222011x t x e dt e x '-=-~⎰(B )(()(0ln 1ln 1x dt x'+=⎰(C )()()sin 2220sin sin sin xt dt x x '=⎰(D )()1cos 3012xx x-'=⎰经比较,选(D )(2)设函数()f x 在区间()1,1-内有定义,且()0lim 0,x f x →=则( )(A )当0x →=时,()f x 在0x =处可导。
(B )当0x →=时,()f x 在0x =处可导。
(C )当()f x 在0x =处可导时,0x →=。
(D )当()f x 在0x =处可导时,0x →=【答案】(C )【解析】当()f x 在0x =处可导,且()0lim 0x f x →=,则有()00f =,0()lim 0x f x x→=(()f x为x 的高阶无穷小量),所以00x →=,选(C )。
(3)设函数(),f x y 在点()0,0处可微,()0,00,00,,,1f f f n x y ()⎛⎫∂∂==- ⎪∂∂⎝⎭,非零向量n与α垂直,则( ) (A )()(,0,0lim0x y →存在(B )()(,0,0lim0x y →=存在(C )()(,0,0lim0x y →存在(D )()(,0,0lim0x y →存在【答案】(A ) 【解析】由题意可知,(,)(,)limlimx y x y →→(,)limx y →=由于函数(),f x y 在点()0,0处可微,所以(,)lim0x y →,选(A )。
在每小题给出的四个选项中只有一项是最符合题目要求

一、单项选择题(在每小题给出的四个选项中,只有一项是最符合题目要求的)1.文化发展的实质,在于文化创新。
没有创新,文化就会萎缩,就会失去生机和活力。
而社会实践是文化创新和发展的基础,对此理解正确的有()①文化创新的需要来自社会实践②文化创作的灵感最终来自社会实践和创作者的聪明才智③文化创作的动力来自社会实践④社会实践是产生优秀文化作品的源泉A.①②③B.①③④C.②③④D.①②③④解析:本题主要考查社会实践与文化创新的关系,①③④正确阐明了社会实践是文化创新和发展的基础,文化创作的灵感最终来源于社会实践。
②观点表述不正确。
故选B。
答案:B2.首届“创造新的文化遗产”论坛指出,“我们应站在文化继承和创新的高度上审视历史和未来,力争在实践中多留遗产,少留遗憾,为后人创造出更多‘新’的文化遗产。
如《亮剑》《闯关东》《士兵突击》《中国地》等原创作品的热播就突出了‘新’”。
这里突出强调“新”,是因为()①文化创新可以不断推动社会实践的发展②文化创新是社会实践发展的内在动力③文化创新可以促进民族文化的繁荣④离开了文化创新,文化就会成为无源之水、无本之木A.①④B.②③C.①③D.②④解析:社会实践是文化创新的源泉和动力,离开了社会实践,文化就会成为无源之水、无本之木,所以②④说法错误;之所以要强调“新”,是因为文化创新具有巨大作用,所以选①③。
答案:C3.连环画《地球的红飘带》的作者沈荛尹为了再现历史,甚至历时六年重走长征路;在连环画《野火春风斗古城》的再版后记中,作者之一陈云华这样总结:“闭门造车、冥思苦想是画不出有生活气息的作品的。
”这说明()A.文化对人的影响来自于特定的文化环境B.文化感染力在于创作者的精益求精C.优秀的文化作品只能来自于生产实践D.文化作品中只有源于社会实践,才有感染力解析:本题考查的知识重点是文化创作的来源,为了进行文化创作,作者重走长征路,在实践活动中感悟历史,体会历史,依此作为文化创作的依据。
2024年山西省中考数学试卷(Word版含解析)

2024年山西省中考数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.中国空间站位于距离地面约400km的太空环境中.由于没有大气层保护,在太阳光线直射下,空间站表面温度可高于零上150℃,其背阳面温度可低于零下100℃.若零上150℃记作+150℃,则零下100℃记作()A.+100℃B.﹣100℃C.+50℃D.﹣50℃2.1949年,伴随着新中国的诞生,中国科学院(简称“中科院”)成立.下列是中科院部分研究所的图标,其文字上方的图案是中心对称图形的是()A.山西煤炭化学研究所B.东北地理与农业生态研究所C.西安光学精密机械研究所D.生态环境研究中心3.下列运算正确的是()A.2m+n=2mn B.m6÷m2=m3C.(﹣mn)2=﹣m2n2D.m2•m3=m54.斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为()A.B.C.D.5.一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为A.155°B.125°C.115°D.65°第5题第7题第1 2题第13题6.已知点A(x1,y1),B(x2,y2)都在正比例函数y=3x的图象上,若x1<x2,则y1与y2的大小关系是()A.y1>y2B.y1<y2C.y1=y2D.y1≥y27.如图,已知△ABC,以AB为直径的⊙O交BC于点D,与AC相切于点A,连接OD.若∠AOD=80°,则∠C的度数为()A.30°B.40°C.45°D.50°8.一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是()A.B.C.D.9.生物学研究表明,某种蛇在一定生长阶段,其体长y(cm)是尾长x(cm)的一次函数,部分数据如下表所示,则y与x之间的关系式为()尾长(cm)6810体长y(cm)45.560.575.5A.y=7.5x+0.5B.y=7.5x﹣0.5C.y=15x D.y=15x+45.510.在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,EG,FH交于点O.若四边形ABCD的对角线相等,则线段EG与FH一定满足的关系为()A.互相垂直平分B.互相平分且相等C.互相垂直且相等D.互相垂直平分且相等二、填空题(本大题共5个小题,每小题3分,共15分)11.比较大小:2(填“>”、“<”或“=”).12.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边MN,PQ上,且AB∥NP,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且,若NP=2cm,则BC的长为cm(结果保留根号).13.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m (kg)的反比例函数.已知一款机器狗载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=90kg时,它的最快移动速度v=m/s.14.如图1是小区围墙上的花窗,其形状是扇形的一部分,图2是其几何示意图(阴影部分为花窗).测量得到扇形AOB的圆心角为90°,OA=1m,C,D分别为OA,OB中点,花窗面积为m2.15.如图,在▱ABCD中,AC为对角线,AE⊥BC于点E,点F是AE延长线上一点,且∠ACF=∠CAF,线段AB,CF的延长线交于点G.若AB=,AD=4,tan∠ABC=2,则BG的长为.三、解答题(本大题共8个小题,共75分.解答应写出文字说明,证明过程或演算步骤)16.(1)计算:(﹣6)×﹣()﹣2+[(﹣3)+(﹣1)];(2)化简(+)÷.17.为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元,则最多可购买这种型号的水基灭火器多少个?18.为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.数据分析:小夏对这两个小组的成绩进行了如下分析:平均数(分)中位数(分)众数(分)方差优秀率甲组7.625a7 4.4837.5%乙组7.6257b0.73c请认真阅读上述信息,回答下列问题:(1)填空:a=,b=,c=;(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).19.当下电子产品更新换代速度加快,废旧智能手机数量不断增加.科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源.据研究,从每吨废旧智能手机中能提炼出的白银比黄金多760克.已知从2.5吨废旧智能手机中提炼出的黄金,与从0.6吨废旧智能手机中提炼出的白银克数相等.求从每吨废旧智能手机中能提炼出黄金与白银各多少克.20.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.数据采集:如图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角∠ACD=18.4°;然后沿CN 方向继续飞行,飞行方向与水平线的夹角∠NCD=37°,当到达点A正上方的点E处时,测得AE=9米;……数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计算纪念碑顶部点A到地面的距离AB的长(结果精确到1米.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin18.4°≈0.32,cos18.4°≈0.95,tan18.4°≈0.33).21.阅读与思考下面是博学小组研究性学习报告的部分内容,请认真阅读,并完成相应任务.关于“等边半正多边形”的研究报告博学小组研究对象:等边半正多边形研究思路:类比三角形、四边形,按“概念﹣性质﹣判定”的路径,由一般到特殊进行研究.研究方法:观察(测量、实验)﹣猜想﹣推理证明研究内容:【一般概念】对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形…【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:概念理解:如图2,如果六边形ABCDEF是等边半正六边形,那么AB=BC=CD=DE=EF=F A,∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B.性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:内角:等边半正六边形相邻两个内角的和为▲°.对角线:…任务:(1)直接写出研究报告中“▲”处空缺的内容:.(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想∠BAD与∠F AD的数量关系,并说明理由;(3)如图4,已知△ACE是正三角形,⊙O是它的外接圆.请在图4中作一个等边半正六边形ABCDEF(要求:尺规作图,保留作图痕迹,不写作法).22.综合与实践问题情境:如图1,矩形MNKL是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段AB组成的封闭图形,点A,B在矩形的边MN上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校面向全体同学征集设计方案.方案设计:如图2,AB=6米,AB的垂直平分线与抛物线交于点P,与AB交于点O,点P是抛物线的顶点,且PO=9米.欣欣设计的方案如下:第一步:在线段OP上确定点C,使∠ACB=90°,用篱笆沿线段AC,BC分隔出△ABC区域,种植串串红;第二步:在线段CP上取点F(不与C,P重合),过点F作AB的平行线,交抛物线于点D,E.用篱笆沿DE,CF将线段AC,BC与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.方案实施:学校采用了欣欣的方案,在完成第一步△ABC区域的分隔后,发现仅剩6米篱笆材料.若要在第二步分隔中恰好用完6米材料,需确定DE与CF的长.为此,欣欣在图2中以AB所在直线为x轴,OP所在直线为y轴建立平面直角坐标系.请按照她的方法解决问题:(1)在图2中画出坐标系,并求抛物线的函数表达式;(2)求6米材料恰好用完时DE与CF的长;(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图2设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段AC,BC上.直接写出符合设计要求的矩形周长的最大值.23.综合与探究问题情境:如图1,四边形ABCD是菱形,过点A作AE⊥BC于点E,过点C作CF⊥AD于点F.猜想证明:(1)判断四边形AECF的形状,并说明理由;深入探究:(2)将图1中的△ABE绕点A逆时针旋转,得到△AHG,点E,B的对应点分别为点G,H.①如图2,当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.猜想线段CH与MD 的数量关系,并说明理由;②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点Q.若AB=5,BE=4,直接写出四边形AMNQ的面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题下列每小题给出的四个选项中,只有一项符合题目要求.1.设f(x)是连续函数,F(x)是f(x)的原函数,则______.A.当f(x)是奇函数时,F(x)必是偶函数B.当f(x)是偶函数时,F(x)必是奇函数C.当f(x)是周期函数时,F(x)必是周期函数D.当f(x)是单调增函数时,F(x)必是单调增函数2.已知=0,其中a,b是常数,则______.A.a=1,b=1 B.a=-1,b=1C.a=1,b=-1 D.a=-1,b=-13.当x→0时,x-sinx是x2的{______.A.低阶无穷小B.高阶无穷小C.等价无穷小D.同阶但非等价的无穷小4.设f(x)=则在点x=1处函数f(x)______.A.不连续B.连续,但不可导C.可导,但导数不连续D.可导,且导数连续5.设f(x)和φ(x)在(-∞,+∞)内有定义,f(x)为连续函数,且f(x)≠0,φ(x)有间断点,则______.A.φ[f(x)]必有间断点B.[φ(x)]2必有间断点C.f[φ(x)]必有间断点D.必有间断点6.设函数y=f(x)具有二阶导数,且f'(x)>0,f"(x)>0,△x为自变量x在点x0处的增量,△y与dy分别为f(x)在点x0处对应的增量与微分,若△x>0,则______.A.0<dy<△y B.0<△y<dyC.△y<dy<0 D.dy<△y<07.设A是任-n(n≥3)阶方阵,A*是其伴随矩阵,又k为常数,且k≠0,±1,则必有(kA)*=______.A.kA* B.k n-1A* C.k n A* D.k-1A*8.设λ1,λ2是矩阵A的两个不同的特征值,对应的特征向量分别为α1,α2,则α1,A(α1+α2)线性无关的充分必要条件是______.A.λ1≠0 B.λ2≠0 C.λ1=0 D.λ2=0二、填空题9.______.10.曲线在t=2处的切线方程为______.11.______.12.设矩阵A=,E为二阶单位矩阵,矩阵B满足BA=B+2E,则|B|=______.13.设3阶矩阵A的特征值λ是2,3.若行列式|2A|=-48,则λ=______.14.微分方程yy'+y'2=0满足初始条件y|x=0=1,y'|x=0=的特解是______.三、解答题15.求16.计算17.设函数f(x)在(-∞,+∞)上有定义,在区间[0,2]上,f(x)=x(x2-4).若对任意的x 都满足f(x)=kf(x+2),其中k为常数.(1) 写出f(x)在[-2,0]上的表达式.(2)问k为何值时,f(x)在x=0处可导.18.设ρ=ρ(x)是抛物线y=上任一点M(x,y)(x≥1)的曲率半径,S=S(x)是该抛物线上介于点A(1,1)与M之间的弧长,计算的值(在直角坐标系下曲率公式为k=19.计算20.已知函数z=f(x,y)的全微分dz=2xdx-2ydy,并且f(1,1)=2.求f(x,y)在椭圆域D={(x,y)|x2+≤1}上的最大值和最小值.21.设矩阵A=,矩阵X满足A*X=A-1+2X.其中A*是A的伴随矩阵.求矩阵X.22.已知α1=(1,4,0,2)T,α2=(2,7,1,3)T,α3=(0,1,-1,a)T,β=(3,10,b,4)T.问:(1) a,b取何值时,β不能由α1,α2,α3线性表示?(2) a,b取何值时,β可由α1,α2,α3线性表示?并写出此表示式。
23.设,A=αβT,B=βTα,其中βT是β的转置.求解方程2B2A2x=A4x+B4x+γ.24.设矩阵A=的特征方程有一个二重根,求a的值,并讨论A是否可相似对角化.参考答案与解析一、选择题1.[考点提示] 原函数.[解题分析] 由已知f(x)是连续函数,则(t)dt是f(x)的一个原函数,从而f(x)的任一原函数F(x)可表示为(t)dt+C,即F(x)=(t)dt+C,其中C为任意常数,且有当f(x)是奇函数时,即F(x)为偶函数,A成立.当f(x)是偶函数时,所以B不成立.关于选项C,D可举反例予以排除,如令f(x)=1+cosx,则周期为2π,F(x)=x+sinx+C不是周期函数.又令f(x)=x,为单调增函数,但不是单调函数.综上,选A.2.[考点提示] 极限中常数的确定.[解题分析] 由于是有1-a=0,a+b=0,得a=1,b=-1.故应选C.3.[考点提示] 根据的值进行判断即可.[解题分析] 因为故应选B.4.[考点提示] 函数的连续性.[解题分析] 因为而可见f(x)在x=1处不连续,应选A.5.[考点提示] 间断点的判定.[解题分析] 用反证法.设无间断点,即连续,又已知f(x)连续,于是·f(x=一φ(x)连续.这与题设矛盾,故应选D.[评注] 本题也可举反例用排除法判定:设f(x)=1,φ(x)=,则有φ[f(x)]=1,[φ(x)]2=1,f[φ(x)]=1,都处处连续,可排除A,B,C,知应选D.6.[考点提示] 凹函数的性质.[解题分析] 由已知条件知,曲线y=f(x)单调上升且是凹的,根据凹函数的性质,有f(x0+△x)>f(x0)+f'(x0)△x(△x≠0),从而f(x0+△x)-f(x0)>f'(x0)△x>0(△x>0),所以△y>dy>0(△x>0).故选A.7.[考点提示] 伴随矩阵A*的定义.[解题分析] 题设未给出A-1存在的条件,所以公式A*=|A|A-1不可直接应用.但由题意知结论对A可逆应该也成立,即假没A可逆,则从而知只有B成立.题设中k≠0,±1的条件是为保证正确选项的唯一性.严格的做法是由伴随矩阵的定义出发,设A=(a ij),a ij的代数余子式为A ij,则A*=(A ij)T.令kA=(ka ij),ka ij 的代数余子式记为B ij,则B ij=k n-1A ij.因此(kA)*=(B ij)T=(k n-1A ij)T=k n-1(A ij)T=k n-1A*.8.[考点提示] 特征值与特征向量.[解题分析] 根据特征值特征向量的定义,有A(α1+α2)=Aα1+Aα2=λ1α1+λ2α2,α1,A(α1+α1)线性无关k1α1+k2A(α1+α2)=0.k1,k2恒为0(k1+λ1k2)α1+λ2k2α2=0,k1,k2恒为0.所以k1,k2恒为0.而齐次方程组只有零解所以选B.二、填空题9.[考点提示] 函数求极限.[解题分析][评注] 一般地,若a>0,b>0,则10.[考点提示] 曲线的切线方程.[解题分析] 按照参数方程求导得切线斜率,代入点斜式即得切线方程.当t=2时,x0=5,y0=8,且可知过曲线上对应于t=2处的切线斜率为3,切点为点(5,8).因此切线方程为y-8=3(x-5),即3x-y-7=0.11.[考点提示] 不定积分.[解题分析] 被积函数为幂函数与指数函数的乘积,因此采用分部积分法,将幂函数看作u.[评注] 此题为明了起见,也可以先令x2=t,原式化为后,再分部积分.12.[考点提示] 行列式、矩阵的计算.[解题分析] 由已知BA=B+2E,有B(A-E)=2E,两边取行列式,得|B|·|A-E|=4.因为|A-E|==2,所以|B|=2.13.[考点提示] 矩阵的特征值及其与矩阵的行列式之间的关系.[解题分析] 因为矩阵的行列式等于它所有特征值的积,且|2A|=23|A|=-48,所以23|A|=23×λ×2×3=-48,则λ=-1.14.[考点提示] 二阶微分方程.[解题分析] 由题设,令y'=u,则y"=代入原方程,得由初始条件知u≠0,所以化为+u=0.分离变量得两边积分得lnu=lnC-lny.由已知y=1时,u=,可解得C=于是lnu=ln,即u=.将y'=u代入上式,有,分离变量并积分得y2=c+C1.由初始条件x=0,y=1,解得C1=1,所以y2=x+1.此即所求特解.三、解答题15.[考点提示] 函数求极限.[解题分析][评注] 注意本题x为负,因此分子分母同除以x时,将x放入根式内应小心符号.16.[考点提示] 三角函数求极限.[解题分析] 本题为“1∞”型未定式,除可以利用第二类重要极限进行计算或化为指数函数计算外,由于已知数列的表达式,也可将n换为x转化为函数极限进行计算.一般地.若因为故原极限=e4.17.[考点提示] 分段函数、导数的定义.[解题分析] 由题设,f(x)=x(x2-4),x∈[0,2].当x∈[-2,0)时,x+2∈[0,2),则由f(x)=kf(x+2)知f(x)=kf(x+2)=k(x+2)[(x+2)2-4]=k(x+2)(x2+4x)=kx(x+2)(x+4),x∈[-2,0).由导数定义及f(0)=0.有令f'(0+)=f'(0-),则k=-.所以当k=-时,f(x)在x=0处可导.18.[考点提示] 曲率、弧长公式、参数方程求导.[解题分析] 由题设,且抛物线在点M(x,y)处的曲率半径为抛物线上的弧长为因此得到ρ(x)与S(x)都是x的函数,从而由知且因此19.[考点提示] 本题主要考查三角函数有理式不定积分的计算技巧和方法,由于三角函数的变形公式非常多,相应地,本题也有多种解法.[解题分析][详解1] 分子、分母同乘以某一三角函数.[详解2] 用万能代换.今t=tan则sinx=cosx=x=2arctant,dx=于是[详解3] 用半角公式.[详解4] 用半角公式.[评注] 不定积分的最后结果表达式,采用不同的计算方法可能在形式上不完全一致,这是正常的.最后结果是否正确只需对其求导即可验证.若求导后等于被积函数,说明一定是正确的.20.[考点提示] 多元函数的最值.[解题分析](1) 求f(x,y)的表达式.由已知有dx=dx2-dy2=d(x2-y2)z=x2-y2+C.又因为f(1.1)=2,所以C=2,从而z=f(x,y)=x2-y2+2.(2) 求f(x,y)在D内驻点及相应函数值.解得(x,y)=(0,0),即f(x,y)在D内有唯一驻点(0,0),且f(0,0)=2.(3) 求f(x,y)在D的边界y2=4(1-x2)上的最大值和最小值.将y2=4(1-x2)(|x|≤1)代入z=x2-y2+2,得z(x)=x2-4(1-x2)+2=5x2-2.显然,z(x)在[-1,1]上的最大值为3,最小值为-2.综上所述,z=f(x,y)在D上的最大值是max{2,3,-2}=3,最小值是min{2,3,-2}=-2.21.[考点提示] 矩阵方程.[解题分析] 根据已知A*X=A-1+2X,得(A*-2E)X=A-1,由A左乘该式,并利用公式A*=|A|A-1,则得(|A|E-2A)X=E,其中从而因此22.[考点提示] 线性代数方程组解的性质.[解题分析] 向量β能否由α1,α2,α3线性表示,实质上等价于下述方程组有解或无解的问题:Ax=β,其中从而相应的增广矩阵为利用初等行变换,将B化为阶梯形如下(1) 当b≠2时,r(A)<r(B),此时方程组Ax=β无解,即β不能由α1,α2,α3线性表示.(2) 当b=2,a≠1时,r(A)=r(B)且r(A)=3,此时方程组Ax=β有唯一解,且相应的行简化阶梯形为因此该唯一解为x=因此β可由α1,α2,α3唯一表示为β=-α1+2α2.当b=2,a=1时,r(A)=r(B)且r(A)=2<3,此时方程组Ax=β有无穷解,相应的行简化阶梯形为其导出组的基础解系为(-3,3,1)T,原方程组特解为(-1,2,0)T,则通解为C(-3,3,1)T+(-1,2,0)T,其中C为任意常数.此时β可由α1,α2,α3表示为β=-(3C+1)α1+(3C+2)α2+cα3.23.[考点提示] 矩阵方程.[解题分析] 由题设,不难求得而 A2=(αβT)(αβT)=α(βTα)βT=αβT=2A,则A4=4A2=8A.由此可将原矩阵方程化简为16Ax=8Ax+16x+γ,即8(A-2E)x=γ,其中E为三阶单位矩阵.令x=(x1,x2,x3)T,代入上式,得此方程组的增方矩阵为经由初等行变换化为行简化阶梯形为则导出组的基础解系为而原方程组有特解所以其中C为任意常数.24.[考点提示] 矩阵对角化、相似矩阵.[解题分析] 由题设,A=,则|A-λE|=0,即其行列式可得出(λ-2)(λ2-8λ+18+3a)=0.若λ=2是特征方程的二重根,则22-8·2+18+3a=0,解之得a=-2,此时λ1=λ2=2,λ3=6,且A-2E=.显然r(A-2E)=1,所以对应特征值2有两个线性无关的特征向量,因此A可相似对角化.若λ=2不是特征方程的二重根,则λ2-8λ+18+3a=0有二重根,即64-4(18+3a)=0,解之得a=-.此时λ1=2,λ2=λ3=4,且显然r(A-4E)=2,所以对应于特征值4只有一个线性无关的特征向量,所以A不可相似对角化.。
