2014年秋季新版苏科版八年级数学上学期2.5、等腰三角形的轴对称性同步练习7
苏科版八年级数学上册第二章2. 5 等腰三角形的轴对称性课时作业
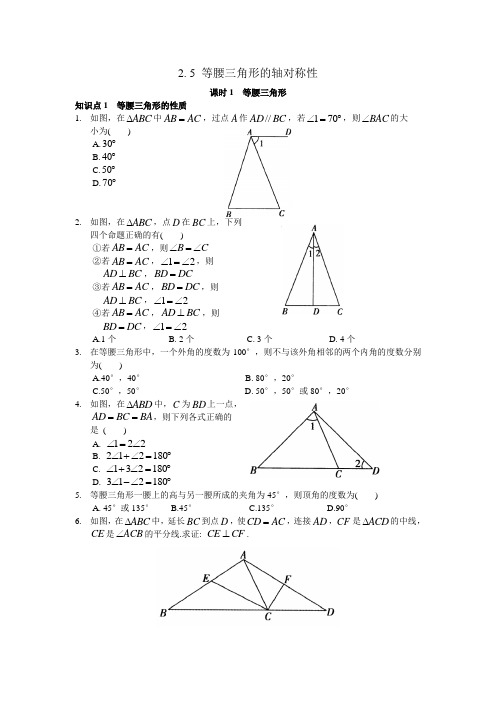
2. 5 等腰三角形的轴对称性课时1 等腰三角形知识点1 等腰三角形的性质1. 如图,在ABC ∆中AB AC =,过点A 作//AD BC ,若170∠=︒,则BAC ∠的大 小为( )A.30︒B.40︒C.50︒D.70︒2. 如图,在ABC ∆,点D 在BC 上,下列四个命题正确的有( )①若AB AC =,则B C ∠=∠②若AB AC =,12∠=∠,则AD BC ⊥,BD DC =③若AB AC =,BD DC =,则AD BC ⊥,12∠=∠④若AB AC =,AD BC ⊥,则BD DC =,12∠=∠A.1个B. 2个C. 3个D. 4个3. 在等腰三角形中,一个外角的度数为100°,则不与该外角相邻的两个内角的度数分别为( )A.40°,40°B. 80°,20°C.50°,50°D. 50°,50°或80°,20°4. 如图,在ABD ∆中,C 为BD 上一点,AD BC BA ==,则下列各式正确的是 ( )A. 122∠=∠B. 212180∠+∠=︒C. 132180∠+∠=︒D. 312180∠-∠=︒5. 等腰三角形一腰上的高与另一腰所成的夹角为45°,则顶角的度数为( )A. 45°或135°B.45°C.135°D.90°6. 如图,在ABC ∆中,延长BC 到点D ,使CD AC =,连接AD ,CF 是ACD ∆的中线,CE 是ACB ∠的平分线.求证: CE CF ⊥.7. 如图,点D ,E 是ABC ∆的边BC 上,AB AC =,AD AE =,BD 与CE 相等吗?请说明你的理由.知识点2 等腰三角形的判定8. 在ABC ∆中,已知下列条件,能判定ABC ∆为等腰三角形的是( )A. 40A ∠=︒,50B ∠=︒B. 40A ∠=︒,60B ∠=︒C. 20A ∠=︒,80B ∠=︒D. 40A ∠=︒,80B ∠=︒9. 如图,两个全等的直角三角形中都有一个锐角为30°,且较长的直角边在同一直线上,则图中的等腰三角形有 A.4个 B. 3个C. 2个D. 1个 10. 如图,在ABC ∆中,ABC ∠和ACB ∠的平分线交于点F ,过点F 作//DE BC ,分别交AB ,AC 于点D ,E .求证:(1)BD DF =;(2) ADE ∆的周长等于AB AC +.11. 如图,在ABC ∆中,AB AC =,点E 在CA 的延长线上,EP BC ⊥于点P ,交AB 于点F .(l)求证: E AFE ∠=∠;(2)若3AF =,5BF =,求CE 的长,并写出ABC ∆周长的取值范围.【精选作业】1. 如图,在PAB ∆中,PA PB =,M ,N ,K 分别是PA ,PB ,AB 上的点,且AM BK =,BN AK =,若44MKN ∠=︒,则P ∠的度数为( )A. 44°B. 66°C. 88°D. 92° 2. 如图,在ABC ∆中,36A ∠=︒,AB AC =,AB 的垂直平分线OD 交AB 于点O ,交AC 于点D ,连接BD .则下列结论错误的是( )A. 2C A ∠=∠B. BD 平分ABC ∠C. BCD BOD S S ∆∆=D. BD BC =3. 如图,在ABC ∆中,90ACB ∠=︒,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,作直线MN 交AB 于点D ,交AC 于点E ,连接CD ,下列结论错误的是( )A. AD CD =B. A DCE ∠=∠C. ADE DCB ∠=∠D. 2A DCB ∠=∠4. 如图,在ABC ∆中,36A ∠=︒,AB AC =,BD 是ABC ∠的平分线.若在边AB 上截取BE BC =,连接DE ,则图中的等腰三角形共有( )A. 2个B. 3个C. 4个D. 5个 5. 已知,,a b c 为ABC ∆的三边长,且()()()0a b a c b c ---=,则ABC ∆一定是 .6. 如图,在ABC ∆中,AB AC =,点,,D E F 分别在,,BC AB AC 上,且DE BE =,DF DC =,若40A ∠=︒,则EDF ∠的度数为 .7. 如图,60BOC ∠=︒,点A 是BO延长线上的一点,10OA =cm ,动点P 从点A 出发沿AB 以2 cm/s 的速度移动,动点Q 从点O 出发沿OC 以1 cm/s 的速度移动,点P ,Q 同时出发,用()t s 表示移动的时间,当t = 时,POQ ∆是等腰三角形.8. 如图,已知点,A C 分别在,BG BE 上,且AB AC =,//AD BE ,GBE ∠的平分线与AD 交于点D ,与AC 交于点F .连接CD .(1)求证:①AB AD =;②CD 平分ACE ∠.(2)猜想BDC ∠与BAC ∠之间有何数量关系?并对你的猜想加以证明.9. 如图,在ABC ∆中,90ABC ∠=︒,,D E 分别在边,BC AC 上,AD DE ⊥,且AD DE =.点F 是AE 的中点,FD 的延长线与AB 的延长线相交于点M ,连接CM .(1)求证: FMC FCM ∠=∠;(2)AD 与MC 垂直吗?请说明理由.10. 如图,在ABC ∆中,2AB AC ==,40B C ∠=∠=︒,点D 为BC 上一动点(点D 不与点B ,C 重合),连接AD ,作40ADE ∠=︒ ,DE 交AC 于点E .(1)当115BDA ∠=︒时,EDC ∠= ,DEC ∠= ,点D 从点B 向点C 运动的过程中,BDA ∠逐渐变 ;(填“大”或“小”)(2)当DC 的长为多少时,ABD DCE ∆≅∆,并给予证明;(3)在点D 的运动过程中,ADE ∆可以是等腰三角形吗?若可以,请直接写出BDA ∠的度数,若不可以,请说明理由.11. 问题情境:将一副直角三角板Rt ABC ∆和Rt DEF ∆按图1所示的方式摆放,其中90ACB FDE ∠=∠=︒,CA CB =,O 是AB 的中点,点D 与点O 重合,DF AC ⊥于点M ,DE BC ⊥于点N ,试判断线段OM 与ON 的数量关系,并说明理由. 探究展示:小宇同学展示出如下正确的解法:OM ON =,理由如下:连接CO ,则CO 是AB 边上的中线,∵CA CB =,∴CO 是ACB ∠的平分线,(依据1)∵OM AC ⊥,ON BC ⊥,∴OM ON =.(依据2)反思交流:(1)①依据1是 ;②依据2是 ;(2)你有与小宇不同的方法吗?请写出你的方法;(3)将图1中的Rt DEF ∆沿着射线BA 的方向平移至如图2的位置,使点D 落在BA 的延长线上,FD 的延长线与CA 的延长线相交于点M ,且FM CM ⊥,BC 的延长线与DE 相交于点N ,且BN DE ⊥,连接OM ,ON ,试判断线段OM ,ON 的数量关系和位置关系,并说明理由.2. 5等腰三角形的轴对称性课时1等腰三角形1.B2.D3.D4.B5.A6. ,CD CA CF =是ACD ∆的中线,CF ∴是ACD ∠的平分线,ACF DCF ∴∠=∠ CE 是ACB ∠的平分线,90ACE ACF ∴∠+∠=︒CE CF ∴⊥7. BD CE =8.C 9.B10. (1) BF 是ABC ∠的平分线,ABF FBC ∴∠=∠//,DE BC FBC BFD ∴∠=∠DBF DFB ∴∠=∠DB DF ∴=(2)由(1)知DB DF =,同理可得CE EF =.DE DF EF =+DE DB CE ∴=+ADE ∴∆的周长为AB AC +.11.(1) ,AB AC B C =∴∠=∠,,90,90EP BC C E B BFP ⊥∴∠+∠=︒∠+∠=︒E BFP ∴∠=∠又BFP AFE ∠=∠,E AFE ∴∠=∠.(2) 11CE =,16<ABC ∆的周长<32.【精选作业】1.D2.C3.D4.D5. 等腰三角形6. 70°7.103或10 8. (1)①//,AD BE ADB DBC ∴∠=∠, BD 平分,GBE ABD DBC ∠∴∠=∠,,ABD ADB AB AD ∴∠=∠∴=②//,AD BE ADC DCE ∴∠=∠,由①知AB AD =,又,AB AC AC AD =∴=,,ACD ADC ACD DCE ∴∠=∠∴∠=∠,CD ∴平分ACE ∠. (2) 12BDC BAC ∠=∠ 9. (1)由题意,知ADE ∆是等腰直角三角形,又F 是AE 的中点,DF AE ∴⊥,易得DF AF EF ==.90,ABC DF AE ∠=︒⊥90,90DCF MAC AMF MAC ∴∠+∠=︒∠+∠=︒,DCF AMF ∴∠=∠.又90,DFC AFM DF AF ∠=∠=︒=,()DFC AFM ASA ∴∆≅∆,CF MF ∴=,FMC FCM ∴∠=∠(2) AD MC ⊥10.(1)25° 115° 小(2)当DC =2时(3)在点D 的运动过程中,ADE ∆可以是等腰三角形,此时BDA ∠的度数为110°或80°11. (1)①等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合)②角平分线的性质(或角平分线上的点到角两边的距离相等)(2)有.方法如下:,CA CB A B =∴∠=∠. O 是AB 的中点,OA OB ∴=. ,,90DF AC DE BC AMO BNO ⊥⊥∴∠=∠=︒.在OMA 和ONB ∆中,OA OB A B AMO BNO =⎧⎪∠=∠⎨⎪∠=∠⎩(),OMA ONB AAS OM ON ∴∆≅∆∴=(3),OM ON OM ON =⊥1、Be honest rather clever 20.7.157.15.202017:4617:46:12Jul-2017:462、By reading we enrich the mind; by conversation we polish it.二〇二〇年七月十五日2020年7月15日星期三3、All things are difficult before they areeasy.17:467.15.202017:467.15.202017:4617:46:127.15.202017:467.15.20204、By other's faults, wise men correct theirown.7.15.20207.15.202017:4617:4617:46:1217:46:125、Our destiny offers not the cup of despair, but the chalice of opportunity. So let us seize it, not in fear, but in gladness. Wednesday, July 15, 2020July 20Wednesday, July 15, 20207/15/20206、I have no trouble being taken seriously as a woman and a diplomat [in Ghana].。
初中数学苏科版八年级上册第2章 轴对称图形2.5 等腰三角形的轴对称性-章节测试习题(8)

章节测试题1.【题文】如图,AD是等边三角形ABC的中线,E是AB上的点,且AE=AD,求∠EDB的度数.【答案】15°【分析】由AD是等边△ABC的中线,根据等边三角形中:三线合一的性质,即可求得又由根据等边对等角与三角形内角和定理,即可求得的度数,继而求得答案.【解答】解:∵AD是等边△ABC的中线,∴AD⊥BC,∠BAD=∠BAC=60°=30°,∴∠ADB=90°.∵AE=AD.∴∠ADE=∠AED==75°.∴∠EDB=∠ADB-∠ADE==15°.2.【题文】如图,等边三角形的边长为4,点是边上一动点(不与点重合),以为边在的下方作等边三角形,连接.(1)在运动的过程中,与有何数量关系?请说明理由.(2)当时,求的度数.【答案】(1) ,理由见解析;(2) .【分析】(1)AE=CD,证明△ABE≌△CBD,即可解决问题.(2)证明AE⊥BC;证明∠BDC=∠AEB,即可解决问题.【解答】解:(1)AE=CD;理由如下:∵△ABC和△BDE等边三角形∴AB=BC,BE=BD,∠ABC=∠EBD=60°;在△ABE与△CBD中,,∴△ABE≌△CBD(SAS),∴AE=CD.(2)∵BE=2,BC=4∴E为BC的中点;又∵等边三角形△ABC,∴AE⊥BC,由(1)知△ABE≌△CBD,∴∠BDC=∠AEB=90°.3.【题文】如图点D、E分别在等边ΔABC边BC、CA上,且CD=AE,联结AD、BE.(1)求证:BE=AD;(2)延长DA交BE于F,求∠BFD的度数.【答案】(1)证明见解析;(2)60°【分析】(1)根据等边三角形的性质可以得到∠BAC=∠ACB=60°,AC=AB,则∠EAB=∠ACD,根据SAS即可证得△ABE≌△CAD,然后根据全等三角形的对应边相等,即可证得:AD=BE.(2)易证∠AFE=∠ACD,从而∠BFA=∠ACB=60°.【解答】解:证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,AC=AB,∴∠EAB=∠ACD=120°,∵在△ABE和△CAD中,,∴△ABE≌△CAD(SAS),∴AD=BE.(2)如图,∵△ABE≌△CAD∴∠E=∠D∵∠EAF=∠DAC∴∠BFD=∠E+∠EAF=∠D+∠DAC=60°4.【题文】如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.说明:△ADE是等边三角形.【答案】详见解析.【分析】要证△ADE为等边三角形,可以先证它为等腰三角形,再证该等腰三角形的一个内角为60°. 综合分析已知条件可知,可以利用△ABD和△ACE全等证明AD=AE. 根据已知条件和等边三角形的性质,不难证明∠B=∠ACE,进而利用SAS 证明△ABD和△ACE全等. 利用全等三角形的性质可以得到△ADE是等腰三角形. 利用全等三角形的性质,通过相关角之间的和差关系,不难证明∠DAE=∠BAC=60°,从而证明△ADE为等边三角形.【解答】证明:∵△ABC为等边三角形,∴∠B=∠ACB=∠BAC=60°,AB=AC.∵∠ACB=60°,∴∠ACD=180°-∠ACB=180°-60°=120°,∵CE平分∠ACD,∴.∴∠B=∠ACE.∵在△ABD和△ACE中,,∴△ABD≌△ACE (SAS),∴AD=AE,∠BAD=∠CAE.∵∠BAD=∠CAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAC=∠DAE=60°.∵∠DAE=60°,AD=AE,∴△ADE为等边三角形.5.【题文】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);(2)猜想AE与DB的数量关系,并证明你的猜想.【答案】(1)=;(2)AE=BD.【分析】(1)△BCE中可证,∠BCE=30°,又EB=EC,则∠D=∠ECB=30°,所以△BCE 是等腰三角形,结合AE=BE即可;(2)过E作EF∥BC交AC于F,用AAS证明△DEB≌△ECF.【解答】解:(1)∵△ABC是等边三角形,∴∠ABC=60°,AB=AC=BC.∵E为AB的中点,所以∠BCE=30°.∵ED=EC,∴∠D=∠BCE=30°,∴∠BED=30°,∴∠D=∠BED,∴BD=BE,∴BD=AE.(2)当点E为AB上任意一点时,AE与DB的大小关系不会改变.理由如下:过E作EF∥BC交AC于F,∵△ABC是等边三角形,∴∠ABC=∠ACB=∠A=60°,AB=AC=BC.∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°.∴△AEF是等边三角形.∴AE=EF=AF.∵∠ABC=∠ACB=∠AFE=60°,∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°.∵DE=EC,∴∠D=∠ECD.∴∠BED=∠ECF.在△DEB和△ECF中,∴△DEB≌△ECF(AAS).∴BD=EF=AE,即AE=BD.6.【题文】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,①求证:△BCE≌△ACD;②求证:CF=CH;③判断△CFH的形状并说明理由。
苏科版八年级数学上册《2.5等腰三角形的轴对称性》同步练习题-带答案

苏科版八年级数学上册《2.5等腰三角形的轴对称性》同步练习题-带答案一、单选题1.如图,在Rt△ABC 中,△ACB =90°,△CAB=36°,以C 为原点,C 所在直线为y 轴,BC 所在直线为x 轴建立平面直角坐标系 ,在坐标轴上取一点M 使△MAB 为等腰三角形,符合条件的 M 点有( )A .6个B .7个C .8个D .9个2.如图,等腰△ABC ,AB=AC ,∠BAC=120°,AD ⊥BC 于点D .点P 是BA 延长线上一点,O 点是线段AD 上一点,OP=OC ,下面的结论:△AC 平分△PAD ;△△APO=△DCO ;△△OPC 是等边三角形;△AC=AO+AP.其中正确结论的个数为( )A .4B .3C .2D .13.如图,在四边形ABCD 中,△BAD =△BCD =90°,△ADC =45°,BD =2a ,E 为BD 中点,给出下列结论:△AE =a , △△CAE =45°,△AC = 2a ,△取AC 的中点F , 则EF △AC , 其中正确的个数是( )A .1个B .2个C .3个D .4个4.如图,在ABC 中,AB=AC ,分别以点A 、点B 为圆心,以大于12AB 长为半径画弧,两弧交点的连线交AC 于点D ,交AB 于点E ,连接BD ,若40A ∠=︒,则DBC ∠=( )A.40︒B.50︒C.20︒D.30︒∠的度数为()5.如图,ABC中,已知AB AC=,DE垂直平分AC,40∠=︒则BCDAA.15︒B.30︒C.50︒D.65︒6.已知A和B两点在线段EF的中垂线上,且△EBF=100°,△EAF=70°,则△AEB等于() A.95°B.15°C.95°或15°D.170°或30°7.等腰三角形的顶角是50°,则它的底角是()A.65°B.80°C.50°或65°D.50°或80°8.已知等腰三角形的一个内角是50︒,则这个三角形顶角的度数是()A.130︒B.50︒C.80︒D.50︒或80︒⊥于D点,点E、F分别是AD的三等分点,若ABC的面积为9.如图,在ABC中,AB=AC,AD BC18,则图中阴影部分面积为()A.6B.8C.9D.10∠,若AB=m,10.如图,ABC中,∠B=2∠C,AD是BC边上的高,E是BA延长线上一点,AC平分DAEBC=p,BD=q,则下列等式一定成立的是()A .m q p +=B .2m q p +=C .2m q p +=D .12q m p +=二、填空题11.在等边三角形ABC 中,点E 在直线AB 上,点D 在直线BC 上,且ED =EC ,若三角形ABC 的边长为1,AE =2,则CD 的长为 .12.若等腰三角形的周长为30cm ,一边长为6cm ,则腰长为 .13.如图,CA 1是等腰Rt △ABC 斜边AB 上的高,以CA 1为直角边构造等腰Rt △CA 1B 1(点C ,A 1,B 1按顺时针方向排列),△A 1CB 1=90°,称为第一次构造;CA 2是Rt △CA 1B 1斜边上的高,再以CA 2为直角边构造等腰Rt △CA 2B 2(点C ,A 2,B 2按顺时针方向排列),△A 2CB 2=90°,称为第二次构造…,以此类推,当第n 次构造的Rt △CAnBn 的边CBn 与△ABC 的边CB 第二次重合时,构造停止,若S △ABC =1,则构造出的最后一个三角形的面积为 .14.等腰三角形的一个角的度数是36︒,则它的底角的度数是 .15.如图,在ABC 中,AB=AC ,AD 是BC 边上的中线,ABC ∠的平分线交AD 于点E ,EF AB ⊥于点F ,若5EF =,则ED 的长度为 .三、解答题16.已知等腰三角形的周长为15cm ,一腰上的中线把等腰三角形分成周长之差为3cm 的两个三角形,求等腰三角形的腰长.17.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒,OA OB 组成,两根棒在O 点相连并可绕O 转动、C 点固定OC CD DE ==点D E 、可在槽中滑动.若75BDE ∠=︒,请求出CDE ∠的度数.18.(1)如图1,在四边形ABCD 中,AD//BC ,G 为CD 上一点,连接AG ,BG .△若AG 平分DAB ∠,BG 平分ABC ∠,求AGB ∠的度数;△若90ABC ∠=︒,AD+BC=AB ,G 为CD 中点,求证:ABG 为等腰直角三角形;(2)某工程队需要在A ,B 两棵树的前方建立一座八角亭.按如下方法选址:如图2,甲工人从C 点直走到树A 处,然后向右转90后再直走一段路等于AC 的长度到点D 处;乙工人从C 点直走到树B 处,然后向左转90后再直走一段路等于BC 的长度到点E 处.工程队队长打算把八角亭建在DE 的中点G 处.过几天,工程队带着建筑材料来施工,却发现忘记标记起始点C ,正当大家懊恼时,队长说:别急,只要找到A ,B 两棵树连线的中点F ,由点F 引AB 的垂线,再往A ,B 两棵树前方量出AB 的长度的一半,就能找到之前的G 点(如图3所示).你觉得队长的方法对吗?为什么?19.如图,一条船上午6时从海岛A 出发,以15海里/时的速度向正北方向航行,上午8时到达海岛B 处,分别从A ,B 处望灯塔C ,测得30NAC ∠=︒ 60NBC ∠=︒.(1)求海岛B到灯塔C的距离;(2)若这条船继续向正北航行,问上午几时小船与灯塔C的距离最短?20.某中学八年级学生到野外开展数学综合实践活动,在营地看到一个不规则的建筑物,为测量该建筑物两端A,B间的距离,但同学们给出了以下建议:(1)甲同学的方案如下:先在平地上取一个可直接到达A,B的点O,连接AO,BO,并分别延长AO至点C,,DO=BO,最后测出CD的长即为A,B间的距离,请你说说该方案可行的理延长BO至点D,使CO AO由;(2)由于在EF处有一堵墙阻挡了路线,使得无法按照甲同学的方案直接测量出A,B间的距离,但同学们测得∠EOC=65°,∠C=80°,∠OEF=145°,CF=127m,EF=78m,请求出该建筑物两端A,B之间的距离.参考答案1.C2.B3.D4.D5.B6.C7.A8.D9.C10.B11.1或3/3或112.12cm13.1612 14.36︒或72°15.516.4cm 或6cm17.80︒18.(1)△90︒△略;(2)队长说法正确,略 19.(1)海岛B 到灯塔C 的距离为30海里(2)上午9时小船与灯塔C 的距离最短 20.(1)甲同学的方案可行;略(2)该建筑物两端A ,B 之间的距离为205m .。
初中数学苏科版八年级上册第二章2.5等腰三角形的轴对称性同步练习(解析版)

初中数学苏科版八年级上册第二章2.5等腰三角形的轴对称性同步练习一、选择题1.如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,如果∠BEC=80°,那么∠GHE等于()A. 5°B. 10°C. 20°D. 30°AB,则下列结论2.如图,CD是△ABC的边AB上的中线,且CD=12错误的是()A. AD=BDB. CD=BDC. △ABC是直角三角形D. ∠B=60°3.如图,AD、CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是()A. 20°B. 35°C. 40°D.70°4.如图,在△ABC中,AB=AC,∠C=70°,△AB′C′与△ABC关于直线EF对称,∠CAF=10°,连接BB′,则∠ABB′的度数是()A. 30°B. 35°C. 40°D. 45°5.有一直角三角板,30°角所对直角边长是6cm,则斜边的长是()A. 3cmB. 6cmC. 10cmD. 12cm6.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为()A. 13B. 17C. 13或17D. 13或107.若一个等腰三角形的两边长分别为2,4,则第三边的长为()A. 2B. 3C. 4D. 2或48.如图,△ABC是等边三角形,DE//BC,若AB=10,BD=6,则△ADE的周长为()A. 4B. 30C. 18D. 129.已知△ABC中,AB=6,AC=8,BC=11,任作一条直线将△ABC分成两个三角形,若其中有一个三角形是等腰三角形,则这样的直线最多有()A. 3条B. 5条C. 7条D. 8条10.等腰△ABC的底角若为顶角的1,过底边上的一点D作底边BC的垂线交AC于点E,4交BA的延长线于点F,则△AEF是()A. 等边三角形B. 直角三角形C. 钝角三角形D. 等腰但非等边三角形二、填空题11.如图,在△ABC中,AB=AC,∠A=36°,将△ABC中的∠A沿DE向下翻折,使点A落在点C处.若AE=3,则BC的长为________.12.如图,在△ABO中,∠AOB=90°,C是AB的中点,若AB=10cm,则OC=_______;若OC=2.5cm,则AB=_______。
苏科版八年级数学上册 2.5 等腰三角形的轴对称性 同步测试题(无答案)

2.5 等腰三角形的轴对称性同步测试题(满分120分;时间:120分钟)班级____________姓名___________成绩_________一、选择题(本题共计9小题,每题3 分,共计27分,)1. 若等腰三角形的底角为,则顶角为()A. B. C. D.2. 如图,在中,,,于,则等于()A. B. C. D.3. 如图,,,为了使图中的是等边三角形,再增加一个条件可以是()A. B.C. D.4. 的三边长分别,,,且=,则是()A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形5 如图,的面积为,垂直的平分线于,则的面积为()A. B. C. D.6. 如图,在中,,点是上一点,,则的大小是()A. B. C. D.7. 是等边的外接圆,的半径为,则等边的边长为()A. B. C. D.8. 是等边三角形,,,为各边中点,则图中共有正三角形A.个B.个C.个D.个9. 如图,正方形网格中,网格线的交点称为格点,已知,是两格点,如果也是图中的格点,且使得为等腰三角形,则点的个数是()A. B. C. D.二、填空题(本题共计7 小题,每题3 分,共计21分,)10. 已知:在中,,垂足为点,若,,则________.11 等腰三角形的底角为,则一腰上的高与另一腰的夹角为________.12. 在矩形中,对角线,相交于点,若,,则________.13. 如图,以,两点为其中两个顶点作位置不同的等边三角形,最多可以作出________个.14. 已知等腰三角形的一个内角是,则其余两个角的度数分别是________度,________度.15 如图,已知在矩形中,对角线,相交于点,且,,则图中长度为的线段有________条.16. 如图,在中,为直角顶点,,为斜边的中点.将绕着点逆时针旋转至,当恰为轴对称图形时,的值为________.三、解答题(本题共计8 小题,共计72分,)17. 画一个,在射线上任选一点,画,与交于点,试判断的形状.18. 如图所示,,,试证明是等腰三角形.19. 如图,在等边中,点,分別在边,上,,过点作丄,交的延长线于点.求的度数;若,求,的长.20. 已知:如图,在中,,,于点,且,试判断的形状,并说明理由.21. 如图,在中,为中点,,,在上,且.求证:.22. 如图,已知矩形的两条对角线相交于,,,求此矩形的面积.。
初中数学苏科版八年级上册第2章 轴对称图形2.5 等腰三角形的轴对称性-章节测试习题

章节测试题1.【答题】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=()A. B. 2 C. 3 D. +2【答案】C【分析】根据角的平分线的性质解答即可.【解答】解:根据角平分线的性质可得CD=DE=1,根据Rt△ADE可得AD=2DE=2,根据题意可得△ADB为等腰三角形,则DE为AB的中垂线,则BD=AD=2,则BC=CD+BD=1+2=32.【答题】如图所示,已知OC平分∠AOB,CD∥OB,若OD=3cm,则CD等于()A. 3cmB. 4cmC. 1.5cmD. 2cm【答案】A【分析】根据角的平分线的性质解答即可.【解答】解:根据角平分线的性质可得:∠DOC=∠COB,根据平行线的性质可得:∠DCO=∠COB,则∠DOC=∠DCO,则CD=OD=3cm,选A.3.【题文】如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC 于D,求证:AD=DC.【答案】答案见解析【分析】连接BD,根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,然后求出∠A=∠C=∠ABD=30°,再求出∠DBC=90°,再根据直角三角形30°所对的直角边等于斜边的一半即可得证.【解答】解:如图,连接DB.∵BA=BC,∠B=120°,∴∠A=∠C=30°,∵MN是AB的垂直平分线,∴AD=DB,∴∠A=∠ABD=30°,又∵∠ABC=120°,∴∠DBC=120°-30°=90°,Rt△CBD中,∠C=30°∴∴4.【题文】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,(1)若△CMN的周长为21cm,求AB的长;(2)若∠MCN=50°,求∠ACB的度数.【答案】(1)AB=21 (cm);(2)∠ACB=115°【分析】(1)本题利用垂直平分线的性质即可解决,(2)利用等腰三角形的性质和外角性质得出.【解答】解:(1)∵DM、EN分别垂直平分AC和BC∴AM=MC, CN=NB∵△CMN的周长= CM+CN+MN =21∴AB=AM+MN+NB=CM+MN+CN=21 (cm)(2)∵∠MCN=50°∴∠CMN+∠CNM=180°-50°=130°∵AM=MC, CN=NE∴∠A=∠ACM, ∠B=∠BCN∵∠A+∠ACM=∠CMN, ∠B+∠BCN=∠CNM∴∠ACM=∠CMN, ∠BCN=∠CNM∴∠ACM +∠BCN= ( ∠CMN+∠CNM )=65°∴∠ACB=65°+50°= 115°5.【题文】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.(1)若△CDE的周长为4,求AB的长;(2)若∠ACB=100°,求∠DCE的度数;(3)若∠ACB=a(90°<a<180°),则∠DCE=___________.【答案】(1)4;(2)20°;(3)2α-180°.【分析】(1)根据线段的垂直平分线的性质得到DC=DA,EC=EB,根据三角形的周长公式计算即可;(2)根据三角形内角和定理求出∠A+∠B的度数,根据等腰三角形的性质求出∠DCA+∠ECB,根据题意计算即可;(3)根据(2)的方法解答.【解答】解:(1)∵D、E分别是AC、BC的垂直平分线上一点,∴DC=DA,EC=EB,∵△CDE的周长=DC+DE+EC=4,∴DA+DE+EB=4,即AB的长为4;(2)∵∠ACB=100°,∴∠A+∠B=80°,∵DC=DA,∴∠DCA=∠A,∵EC=EB,∴∠ECB=∠B,∴∠DCA+∠ECB=80°,∴∠DCE=100°-80°=20°;(3)∵∠ACB=α,∴∠A+∠B=180°-α,∵DC=DA,∴∠DCA=∠A,∵EC=EB,∴∠ECB=∠B,∴∠DCA+∠ECB=180°-α,∴∠DCE=α-180°+α=2α-180°,故答案为:2α-180°.6.【题文】已知:如图, AB=AC,DE∥AC,求证:△BDE是等腰三角形.【答案】见解答。
苏科版八年级上册数学第2章《轴对称图形》同步练习含答案2.5等腰三角形的轴对称性(2)

2.5等腰三角形的轴对称性(2)【基础训练】1.等边三角形是_______图形,并且有_______条对称轴;等边三角形的每个角等于_______.2.如果一个三角形是轴对称图形,且有一个角是60°,那么这个三角形是_______.3.如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=_______.4.在△ABC中,AB=AC,∠BAC=120°,点D、E在BC上,且BD=AD,CE=AE.判断△ADE的形状,并说明理由.5.如图,在等边三角形ABC中,点D是AC的中点,延长BC到点E,使CE=CD,AB =10 cm.(1)求BE的长;(2)BD=ED吗?为什么?6.如图,△ABC是等边三角形,O为△ABC内任意一点,OE∥AB,OF∥AC,分别交BC于点E、F.求证:△OEF是等边三角形.7.如图,D是等边△ABC内一点,DB=DA,BP=AB,∠DBP=∠DBC.求证:∠P=30°.8.如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.【提优拔尖】9.以正方形ABCD的一边CD为边作等边三角形CDE.连接AE、BE.(1)画出图形;(2)求∠AEB的度数.10.如图,在△ABC中,分别以AB、AC为边作等边三角形ABE、ACD,BD与CE相交于点O.(1)EC=BD吗?为什么?(2)如果要使△ABE和△ACD全等,那么还需要添加什么条件?在此条件下,整个图形是轴对称图形吗?此时∠BOC是多少度?11.如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B.求证:AB=AC+CD.12.如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( ).A.2 B.3 C.3D.3+113.如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A6BA7的边长为( ).A.6 B.12 C.32 D.64。
苏科版数学八年级上册(同步练习)《2.5等腰三角形的轴对称性》

《2.5等腰三角形的轴对称性》同步练习
一.选择题
1.如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是()
A.20 B.10 C.5 D.2.5
2.如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于点D,交AB于点E.当∠B=30°时,下列结论不正确的是()
A.AC=AE=BE B.AD=BD C.CD=BD D.CE=BE
3.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,若CD=2,那么BD等于()
A.6 B.4 C.3 D.2
4.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为()
A.20 B.12 C.14 D.13
二.填空题
5.若直角三角形斜边上的高和中线分别是5cm和6cm,则斜边长为______,面积为______.6.在△ABC中,∠C=90°,D是AB的中点,若CD=18cm,则AB=______.
7.在△ABC中,∠C=90°,∠A=30°,AB=10,则BC=______.
8.如图所示,已知:在△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=12cm,则BD=______cm.
9.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF=______.
三.解答题
10.已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.6等腰梯形的轴对称性
姓名_____________班级____________学号____________分数_____________
一、选择题
1 .如图,已知等腰梯形中, , ,则 ( )
A. B. C. D.
2 .如图2,等腰梯形ABCD中,AD∥BC,若将腰AB沿A→D的方向平移到DE的位置,则图中与∠C相等的角(不包括∠C)有( )。
A.1个
B.2个
C.3个
D.4个
3 .如图,把一张等腰梯形纸片沿中位线剪开,拼成一个新的图形, 这个新的图形可以是下列
图形中的
A.三角形
B.平行四边形
C.矩形
D.正方形
4 .如图,直线l为等腰梯形ABCD的对称轴,点P在直线l上,且PC+PB最小,则点P应位于
A.点P1处
B.点P2处
C.点P3处
D.点P4处
5 .在梯形中,∥,那么可以等于( )
()4:5:6:3 ()6:5: 4:3 ()6:4:5:3 ()3:4:5:6
6 .如图,在等腰梯形ABCD中, ,对角线于点O, ,垂足分别为E、F,设AD=a,BC=b,则四边形
AEFD的周长是( )
A. B. C. D.
二、填空题
7 .等腰梯形的上底与高相等,下底是上底的3倍,则底角(锐角)等于______度
8 .如图,在四边形ABCD中,已知AB不平行CD,∠ABD=∠ACD,请你添加一个条
件:______________,使得加上这个条件后能够推出AD∥BC且AB=CD.
9 .如图,等腰梯形ABCD中,AD∥BC,AD=3,AB=6,BC=8.若DE∥AB,则△DEC的周长是 _____.
10.如图,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是____度.
三、解答题
11.如图8,在梯形ABCD中, ,对角线AC,BD交于点O, ,请说明四边形ABCD为等腰梯形.
12.如图所示,已知等腰梯形ABCD中,AD∥BC, AB=CD,点E为梯形外一点,且AE=DE。
求证:BE=CE.
13.如图,在等腰梯形ABCD中,AB∥DC,AB=8,DC=3,∠A=60°,求CB的长.
14.如下图,在□ABCD中,∠BAD、∠BCD的平分线分别交BC、AD于点E、F,AE、DC的延长线交于点G.试说明四边形AFCG为等腰梯形.
15.图①是等腰梯形ABCD,其中AD∥BC,AB=DC.图②是与图①完全相同的图形.
(1)请你在图①、图②的梯形ABCD中各画一个
....与△ABD全等但位置不同的三角形,使三角形的各顶点在梯形的边(含顶点)上;
(2)选择(1)中所画的一个
..三角形说明它与△ABD全等的理由.
16.如图甲,四边形ABCD是等腰梯形,AB∥DC,由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
(1)求梯形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
1.6等腰梯形的轴对称性参考答案
一、选择题 1 .C 2 .C 3 .B
4 .C
5 .A
6 .A 二、填空题
7 .45
8 .∠DAC =∠ADB ,∠BAD =∠CDA ,∠DBC =∠ACB ,∠ABC =∠DCB ,OB =OC ,OA =OD ; 9 .17 10.
三、解答题 11.解:,
.
所以梯形ABCD 是等腰梯形.
12.证明:在等腰梯形ABCD 中, AB=CD,
∴∠BAD=∠CDA,∵EA=ED,∴∠EAD=∠EDA,∴∠EAB=∠EDC.在△ABE 和△DCE 中, ∵AB=DC,∠EAB=∠EDC,EA=ED,∴△ABE≌△DCE,∴EB=EC. 13.作辅助线 ;说明平行四边形 ;说明等边三角形 ;求得=5 . 14.因为AE 、CF 分别为∠BAD 、∠BCD 的平分线,
所以∠1=12 ∠BAD ,∠2=∠4=1
2
∠BCD
由平行四边形性质可知,∠BAD =∠BCD
所以∠1=∠2=∠4
由AD ∥BC 可得∠1=∠3.又因为∠1=∠2,所以∠2=∠3.所以AG ∥FC . 因为AG ≠FC .所以四边形AFCG 为梯形
因为AG ∥FC ,所以∠4=∠G.又因为∠1=∠4,所以∠1=∠G. 又因为四边形AFCG 为梯形,所以四边形AFCG 为等腰梯形 15.略
16.(1)只要善于观察就不难看出底角的三倍等于180°或三个顶角拼成了一个周角,即
∠A=∠B=60°,∠C=∠D=120°; (2)AB=2BC=2CD=2AD.。
