点线面复习讲义
点线面复习
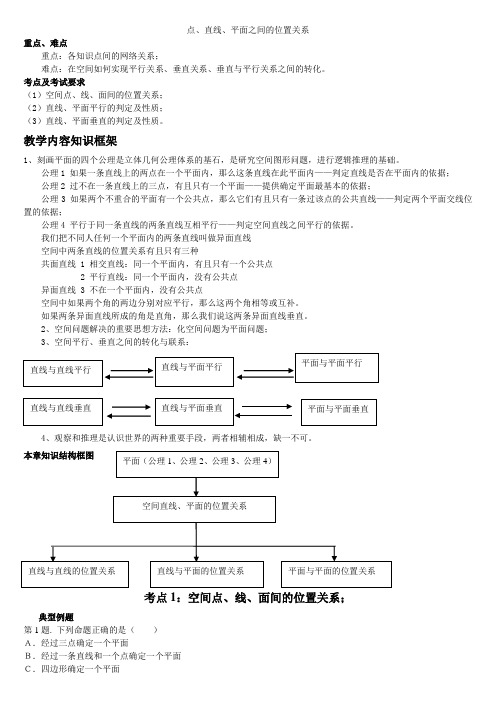
点、直线、平面之间的位置关系重点、难点重点:各知识点间的网络关系;难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
考点及考试要求(1)空间点、线、面间的位置关系; (2)直线、平面平行的判定及性质; (3)直线、平面垂直的判定及性质。
教学内容知识框架1、刻画平面的四个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内——判定直线是否在平面内的依据; 公理2 过不在一条直线上的三点,有且只有一个平面——提供确定平面最基本的依据;公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线——判定两个平面交线位置的依据;公理4 平行于同一条直线的两条直线互相平行——判定空间直线之间平行的依据。
我们把不同人任何一个平面内的两条直线叫做异面直线 空间中两条直线的位置关系有且只有三种共面直线 1 相交直线:同一个平面内,有且只有一个公共点 2 平行直线:同一个平面内,没有公共点 异面直线 3 不在一个平面内,没有公共点空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
如果两条异面直线所成的角是直角,那么我们说这两条异面直线垂直。
2、空间问题解决的重要思想方法:化空间问题为平面问题;3、空间平行、垂直之间的转化与联系:4、观察和推理是认识世界的两种重要手段,两者相辅相成,缺一不可。
本章知识结构框图考点1:空间点、线、面间的位置关系;典型例题第1题. 下列命题正确的是( ) A.经过三点确定一个平面B.经过一条直线和一个点确定一个平面 C.四边形确定一个平面直线与直线平行直线与平面平行平面与平面平行直线与直线垂直直线与平面垂直 平面与平面垂直 平面(公理1、公理2、公理3、公理4)空间直线、平面的位置关系 直线与直线的位置关系直线与平面的位置关系 平面与平面的位置关系D.两两相交且不共点的三条直线确定一个平面第2题. 如图,空间四边形ABCD 中,E ,F ,G ,H 分别 是AB ,BC ,CD ,DA 的中点. 求证:四边形EFGH 是平行四边形.第3题. 如图,已知长方体ABCD A B C D ''''-中,23AB =,23AD =,2AA '=.(1)BC 和A C ''所成的角是多少度?(2)AA '和BC '所成的角是多少度?第4题. 下列命题中正确的个数是( )①若直线l 上有无数个点不在平面α内,则l α∥.②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行.③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行. ④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点.A .0 B.1 C.2 D.3第5题. 若直线a 不平行于平面α,且a α⊄,则下列结论成立的是( ) A.α内的所有直线与a 异面 B.α内不存在与a 平行的直线 C.α内存在唯一的直线与a 平行 D.α内的直线与a 都相交第6题. 已知a ,b ,c 是三条直线,角a b ∥,且a 与c 的夹角为θ,那么b 与c 夹角为 . 第7题. 如图,AA '是长方体的一条棱,这个长方体中与AA '垂直的棱共 条.第8题. 如果a ,b 是异面直线,直线c 与a ,b 都相交,那么这三条直线中的两条所确定的平面共有 个. 第9题. 已知两条相交直线a ,b ,a α平面∥则b 与α的位置关系是 .第10题. 如图,三条直线两两平行且不共面,每两条确定一个平面,一共可以确定几个平面?如果三条直线相交于一点,它们最多可以确定几个平面?ADBCD 'C ' B 'A 'AEBHGCFDA DB CD 'C ' B 'A '第11题. 如图是正方体的平面展开图,则在这个正方体中:①BM 与ED 平行. ②CN 与BE 是异面直线.③CN 与BM 成60˚角. ④DM 与BN 垂直.以上四个命题中,正确命题的序号是( ) A.①,②,③B.②,④ C.③,④D.②,③,④第12题. 下列命题中,正确的个数为( )①两条直线和第三条直线成等角,则这两条直线平行;②平行移动两条异面直线中的任何一条,它们所成的角不变;③过空间四边形ABCD 的顶点A 引CD 的平行线段AE ,则BAE ∠是异面直线AB 与CD 所成的角; ④四边相等,且四个角也相等的四边形是正方形 A.0 B.1 C.2 D.3 第13题. 在空间四边形ABCD 中,N ,M 分别是BC ,AD 的中点,则2MN 与AB CD +的大小关系是 . 第14题. 已知a b ,是一对异面直线,且a b ,成70角,P 为空间一定点,则在过P 点的直线中与a b ,所成的角都为70的直线有 条.第15题. 已知平面αβ//,P 是平面αβ,外的一点,过点P 的直线m 与平面αβ,分别交于A C ,两点,过点P 的直线n 与平面αβ,分别交于B D ,两点,若698PA AC PD ===,,,则BD 的长为 .第16题. 空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,若AC BD a ==,且AC 与BD 所成的角为90,则四边形EFGH 的面积是 . 知识概括、方法总结与易错点分析四个定理的理解、认识与运用,空间感觉的形成针对性练习第1题. 已知下列四个命题: ① 很平的桌面是一个平面; ② 一个平面的面积可以是4m 2;③ 平面是矩形或平行四边形;④ 两个平面叠在一起比一个平面厚. 其中正确的命题有( ) A.0个 B.1个 C.2个 D.3个 第2题. 给出下列命题:和直线a 都相交的两条直线在同一个平面内; 三条两两相交的直线在同一平面内; 有三个不同公共点的两个平面重合; 两两平行的三条直线确定三个平面. 其中正确命题的个数是( ) A.0 B.1 C.2 D.3第3题. 直线12l l ∥,在1l 上取3点,2l 上取2点,由这5点能确定的平面有( )A FNDC B MEA.9个 B.6个 C.3个 D.1个第4题. 三条直线相交于一点,可能确定的平面有( ) A.1个 B.2个 C.3个 D.1个或3个 第5题. 下列命题中,不正确的是( )①一条直线和两条平行直线都相交,那么这三条直线共面; ②每两条都相交但不共点的四条直线一定共面; ③两条相交直线上的三个点确定一个平面; ④两条互相垂直的直线共面. A.①与② B.③与④ C.①与③ D.②与④ 第6题. 分别和两条异面直线都相交的两条直线一定是( ) A.异面直线 B.相交直线 C.不相交直线 D.不平行直线第7题. 在长方体1111ABCD A B C D -中,点O ,1O 分别是四边形ABCD ,1111A B C D 的对角线的交点,点E ,F 分别是四边形11AA D D ,11BB C C 的对角线的交点,点G ,H 分别是四边形11A ABB ,11C CDD 的对角线的交点. 求证:1OEG O FH △≌△.第8题. 若a ,b 是异面直线,b ,c 也是异面直线,则a 与c 的位置关系是( )N A.异面 B.相交或平行 C.平行或异面 D.相交或平行或异面第9题. a ,b 是异面直线,A ,B 是a 上两点,C ,D 是b 上的两点,M ,分别是线段AC 和BD 的中点,则MN 和a 的位置关系是( ) A.异面直线 B.平行直线 C.相交直线 D.平行、相交或异面 第10题. 如下图是正方体的平面展开图,在这个正方体中 ①BM 与ED 平行;②CN 与BE 是异面直线; ③CN 与BM 成60þ角;④DM 与BN 垂直.以上四个命题中,正确命题的序号是( )A.①②③ B.②④ C.③④ D.②③④第11题. 直线与平面平行的条件是这条直线与平面内的( ) A.一条直线不相交 B.两条直线不相交 C.任意一条直线不相交 D.无数条直线不相交第12题. 如果直线a 平行于平面α,则 ( ) A.平面α内有且只有一直线与a 平行 B.平面α内有无数条直线与a 平行 C.平面α内不存在与a 平行的直线 D.平面α内的任意直线与直线a 都平行1DA B1A 1C1B ED O G H 1O FC N DC E A BF M考点2:异面直线夹角典型例题1.在正方体ABCD—A1B1C1D1中,M、N、P、Q分别是棱AB、BC、CD、CC1的中点,直线MN与PQ所成的度数是()(A)(B)(C)(D)2.下列命题中,正确的命题是()(A)直线a、b异面,过空间任一点O,作OA∥a,OB∥a,则∠AOB叫做异面直线a和b所成的角(B)如果∠CBA=∠BAD,那么BC∥A D(C)和两条异面直线都垂直的直线,叫做这两条异面直线的公垂线(D)两条异面直线所成的角只能是锐角或直角知识概括、方法总结与易错点分析先把异面直线平移成共面的针对性练习1.正方体ABCD—A1B1C1D1的棱长为1,则BD1与CC1所成角的正切值为_____,BD1与CC1的距离为_____.2.2.长方体ABCD—A1B1C1D1中,AB=BC=2a,AA1=a,M、N分别是A1B1、BB1的中点,则A1D与MN所成角的余弦值是__________.巩固作业正方体ABCD—A1B1C1D1中,E、F、G分别为AB、BC、CC的中点,则EF与BG所成角的余弦值为()(A)(B)(C)(D)-考点3:直线与平面平行的求法典型例题例1如图所示,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F.求证:EF∥平面ABCD.证明方法一分别过E,F作EM⊥AB于M,FN⊥BC于N,连接MN.∵BB1⊥平面ABCD,∴BB1⊥AB,BB1⊥BC,∴EM∥BB1,FN∥BB1,∴EM∥FN.又∵B 1E=C 1F ,∴EM=FN ,故四边形MNFE 是平行四边形,∴EF ∥MN. 又MN ⊂平面ABCD ,EF ⊄平面ABCD , 所以EF ∥平面ABCD.方法二 过E 作EG ∥AB 交BB 1于G , 连接GF ,则BB GB A B E B 1111=, ∵B 1E=C 1F ,B 1A=C 1B , ∴BB GB BC E C 1111=,∴FG ∥B 1C 1∥BC , 又EG ∩FG=G ,AB ∩BC=B ,∴平面EFG ∥平面ABCD ,而EF ⊂平面EFG , ∴EF ∥平面ABCD.例2 已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC 的重心. (1)求证:平面G 1G 2G 3∥平面ABC ; (2)求S △321G G G ∶S △ABC .(1)证明 如图所示,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F , 连接DE 、EF 、FD ,则有PG 1∶PD=2∶3, PG 2∶PE=2∶3,∴G 1G 2∥DE. 又G 1G 2不在平面ABC 内,∴G 1G 2∥平面ABC.同理G 2G 3∥平面ABC.又因为G 1G 2∩G 2G 3=G 2, ∴平面G 1G 2G 3∥平面ABC. (2)解 由(1)知PE PG PD PG 21==32,∴G 1G 2=32DE. 又DE=21AC ,∴G 1G 2=31AC. 同理G 2G 3=31AB ,G 1G 3=31BC.∴△G 1G 2G 3∽△CAB ,其相似比为1∶3, ∴S △321G G G ∶S △ABC =1∶9.例3 (16分)如图所示,平面α∥平面β,点A ∈α,C ∈α,点B ∈β,D ∈β,点E ,F 分别在线段AB ,CD 上,且AE ∶EB=CF ∶FD.(1)求证:EF ∥β;(2)若E ,F 分别是AB ,CD 的中点,AC=4,BD=6,且AC ,BD 所成的角为60°, 求EF 的长.(1)证明 ①当AB ,CD 在同一平面内时, 由α∥β,平面α∩平面ABDC=AC ,平面β∩平面ABDC=BD ,∴AC ∥BD , ∵AE ∶EB=CF ∶FD ,∴EF ∥BD , 又EF ⊄β,BD ⊂β,∴EF ∥β.②当AB 与CD 异面时,设平面ACD ∩β=DH ,且DH=AC. ∵α∥β,α∩平面ACDH=AC ,∴AC ∥DH ,∴四边形ACDH 是平行四边形,在AH 上取一点G ,使AG ∶GH=CF ∶FD , 又∵AE ∶EB=CF ∶FD ,∴GF ∥HD ,EG ∥BH , 又EG ∩GF=G ,∴平面EFG ∥平面β.∵EF ⊂平面EFG ,∴EF ∥β.综上,EF ∥β.(2)解 如图所示,连接AD ,取AD 的中点M ,连接ME ,MF. ∵E ,F 分别为AB ,CD 的中点, ∴ME ∥BD ,MF ∥AC ,且ME=21BD=3,MF=21AC=2,∴∠EMF 为AC 与BD 所成的角(或其补角), ∴∠EMF=60°或120°,∴在△EFM 中由余弦定理得, EF=EMF MF ME MF ME ∠∙∙-+cos 222 =212322322⨯⨯⨯±+=613±, 即EF=7或EF=19.知识概括、方法总结与易错点分析 定理见解 总结针对性练习1.判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例: (1)如果a 、b 是两条直线,且a ∥b,那么a 平行于经过b 的任何平面; (2)如果直线a 和平面α 满足a ∥ α ,那么a 与α内的任何直线平行 (3)如果直线a 、b 和平面α 满足a ∥ α,b ∥ α,那么a ∥ b ;(4)如果直线a 、b 和平面α 满足a ∥ b,a ∥ α,b α, 那么 b ∥ α; (5)过平面外一点和这个平面平行的直线只有一条 1.下列命题中,正确命题的个数是 .①若直线l 上有无数个点不在平面α内,则l ∥α;②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行;③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点.2.下列条件中,不能判断两个平面平行的是 (填序号). ①一个平面内的一条直线平行于另一个平面 ②一个平面内的两条直线平行于另一个平面 ③一个平面内有无数条直线平行于另一个平面 ④一个平面内任何一条直线都平行于另一个平面3.对于平面α和共面的直线m 、n ,下列命题中假命题是 (填序号). ①若m ⊥α,m ⊥n ,则n ∥α ②若m ∥α,n ∥α,则m ∥n ③若m ⊂α,n ∥α,则m ∥n④若m 、n 与α所成的角相等,则m ∥n 4.已知直线a,b,平面α,则以下三个命题: ①若a ∥b,b ⊂α,则a ∥α; ②若a ∥b,a ∥α,则b ∥α; ③若a ∥α,b ∥α,则a ∥b.其中真命题的个数是 .5.如图所示,在三棱柱ABC —A 1B 1C 1中,M 、N 分别是BC 和A 1B 1的中点. 求证:MN ∥平面AA 1C 1.巩固作业1.下列命题,其中真命题的个数为 . ①直线l 平行于平面α内的无数条直线,则l ∥α;②若直线a 在平面α外,则a ∥α; ③若直线a ∥b,直线b ⊂α,则a ∥α;④若直线a ∥b,b ⊂α,那么直线a 就平行于平面α内的无数条直线. 2.对于不重合的两个平面α与β,给定下列条件: ①存在平面γ,使得α,β都垂直于γ; ②存在平面γ,使得α,β都平行于γ; ③存在直线l ⊂α,直线m ⊂β,使得l ∥m;④存在异面直线l 、m ,使得l ∥α,l ∥β,m ∥α,m ∥β.其中,可以判定α与β平行的条件有 (写出符合题意的序号).3.已知平面α⊥平面β,α∩β=l,点A ∈α,A ∉l,直线AB ∥l,直线AC ⊥l,直线m ∥α,m ∥β,则下列四种位置关系中,一定成立的是 .①AB ∥m ②AC ⊥m ③AB ∥β ④AC ⊥β4.设有直线m 、n 和平面α、β.下列命题不正确的是 (填序号). ①若m ∥α,n ∥α,则m ∥n②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β ③若α⊥β,m ⊂α,则m ⊥β ④若α⊥β,m ⊥β,m ⊄α,则m ∥α5.下列关于互不相同的直线m,l,n 和平面α,β的四个命题: ①若m ⊂α,l ∩α=A,点A ∉m ,则l 与m 不共面;②若m,l 是异面直线,l ∥α,m ∥α,且n ⊥l,n ⊥m,则n ⊥α; ③若l ∥α,m ∥β,α∥β,则l ∥m;④若l ⊂α,m ⊂α,l ∩m=A,l ∥β,m ∥β,则α∥β. 其中假命题的序号是 .考点4:二面角典型例题1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC是边长为 2的正三角形,求二面角 P-AB -C 的大小。
点线面课件

一.课标链接
点、线、面 通过丰富的实例,进一步认识点、线、 面(如交通图上用点表示城市,屏幕上的 画面是由点组成的).
二.系,了解线 段、直线、射线的概念、区别、联系及表示方 法.了解直线和线段的基本性质及两点间的距离 概念. 2.理解线段的中点的定义,会比较线段的大小. 3.了解角的概念、表示方法、度量及角的度、 分、秒的简单换算.了解角的分类及方向角的表 示方法,角的和与差,角的比较方法. 4.理解角的平分线的定义,角平分线的性质定 理、逆定理及其相关结论.
五.能力训练
4.如图(4)所示,从甲地到丙地,可供选择的方 案是水路、陆路、空中,从甲地到乙地有两条 水路,两条陆路,从乙地到丙地有3条陆路可 供选择,走空中从甲地到丙地不经过乙地就可 以到达,请设计出从甲地到丙地可供选择的方 案有( ) A.20种 B.8种 C.13种 D.5种
(4)
五.能力训练 (二)填空题 5.如图(5),观察图形,填空:包围着体的是 ______;面与面相交的地方形成______; 线与线相交的地方是_______.
nih16qfi
亮的诸人了。”“怎么,比爷的福晋还漂亮?”“那当然了!小四嫂美得,真是让妾身心服口服。”“福晋的评价真是高呢!既然福晋都心服 口服了,爷也信服。”“唉,您说,这老天爷为什么不能把好事让壹个人都占了去呢?小四嫂空有这么漂亮的模样,有什么用呀,她可真是可 怜呢!”“福晋何出此言?”“她居然连四哥都不认识,那他们是怎么成亲、怎么敬茶、怎么行礼、怎么归宁的呢?难道做这些事情的时候, 四哥都不在场?还是说四哥从来都没有……”“唉,这些事情,爷哪儿知道是怎么办的?你也就别瞎操心了,四哥这么做,壹定有他的道 理。”“再有道理,这么如花似玉的大姑娘整日里被冷落成这个样子,没几天,还不……。既然不喜欢,还不如不娶呢。”“谁让她姓年?你 知道有多少人抢着要娶她?先不说别人,光是十四弟,就已经跟四哥和额娘闹翻了。”“啊?十四叔也看上小四嫂了?”“谁知道怎么回事儿! 四哥不说,爷也不好问。”“唉,不知道小四嫂要是被指婚给十四叔会是什么结果?也被十四叔晾在壹边不理不睬?”“福晋!你今天的话实 在是太多了吧!这种话也是能从你的口中说出来的?”“爷息怒,爷息怒!妾身只是觉得小四嫂太可怜了,才口无遮拦,妾身知错了,望爷不 要治妾身的罪啊!”第壹卷 第111章 平息送完十三夫妇两人,众女眷眼巴巴地望向爷。可是王爷根本没有看任何人壹眼,目不斜视地走掉了。 大家壹看这个情形,只好极不甘心地就从霞光苑各自回了自家院子。不过,大家的心里都非常的不痛快!就这么结束了?本来还打算再继续看 壹出爷教训冰凝的重头戏呢,怎么除了那句“丢人现眼”以外,爷连句话都没有?这件事情就这么无声无息地结束了?凭什么啊!就因为她是 侧福晋,就可以特别优待,就可以不遵守王府的规矩吗?众人气愤难平,特别是淑清!虽然自己最得爷的宠爱,可是如果犯下这么天大的错, 爷哪里能轻饶了自己?罚跪佛堂壹定是跑不了的,额外的处罚肯定也还要有。可是,爷怎么能这么轻易地放过了她?第壹次,她对这个新嫁进 来的侧福晋有了危机感和愤恨感。王爷当然知道各位女眷气恨难平,不但她们,连他自己都是恨得咬牙切齿。在这些诸人中,淑清最得他的宠, 为了平息她的气恼,散了家宴,他先让秦顺给烟雨园传了口信儿,然后回到朗吟阁处理完公务,就来到了淑清这里。淑清得知爷要过来,激动 万分!爷好久都没有来她这里了,虽然爷对她还是壹如既入往地温柔体贴,珠宝首饰、绫罗绸缎就像流水似地进了她的烟雨园,看得别人既眼 谗不已,同时又心酸不已。可是这些东西哪儿比得上爷的大驾光临啊!她的烟雨园,爷都有两个多月没有歇过这里,好像就是从爷被赐婚那时 候开
高考冲刺必备立体几何专题·第2课点线面(一轮)

点、线、面位置关系一、必考基础知识梳理1、平面(1)平面的两个特征:①无限____________②没有____(2)平面的画法:通常画____________来表示平面(3)平面的表示:用一个小写的希腊字母_________等表示,;也能用表示平行四边形ABCD的两个相对顶点的字母表示,如平面____。
(4)点A在直线l上,记作:A___l;点A在平面α内,记作:A___α;直线l在平面α内,记作l___α2、平面的基本性质:公理1公理2公理3公理4图形表示自行表述公理2的推论:(1)经过一条直线和这条直线外的一点,______________;(2)经过两条相交直线,____________;(3)经过两条平行直线,_____________。
3、空间中两条直线的位置关系(1)按共不共面分类(2)按有没有交点分类4、异面直线的画法常用的有下列三种:5、空间等角定理:如果两个角的两边分别对应平行,那么这两个角__________6、异面直线所成的角①定义:直线a、b是异面直线,经过空间任意一点O,分别引直线a’∥a,b’∥b,则把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。
②异面直线所成角范围:____________③两条异面直线垂直的定义:两条异面直线角是________,记作a⊥b。
但是,两条直线垂直既包括________垂直,也包括________垂直。
④异面直线所成角的求法步骤:平移(一条或两条)、构造三角形、______定理7、直线与平面的位置关系①直线在平面内——有________个公共点②直线与平面相交——有______公共点③直线与平面平行——________公共点;但是,直线与平面相交或平行的情况统称为____________请将线面的位置关系分类(指出平面内各几条直线与已知直线平行、相交、异面、垂直):8、平面与平面的位置关系______——没有公共点,βα∥;______——有一条公共直线,a =⋂βα。
点线面关系复习课

1.如图所示,在四面体 ABCD 中,AD⊥底面 ABC,AB=3,AC=5,BC=4. 1) 2) 3) 在四面体 ABCD 中有几个直角三角形? 有几组平面垂直? 你能找出 A 点在面 BCD 上的射影吗?
例:在棱长为1的正方体ABCD—A1B1C1D1中,
(1)求异面直线A1B与B1C所成的角的大小; (2)求直线A1B与平面BB1D1D所成的角; (3)求二面角A—BD—A1的正切值; (4)求证:平面A1BD//平面CB1D1;
(5)线面平行、面面平行的性质定理 (当题目中的点没有给出具体位置时)
2.证明线面平行的方法:
(1)线线平行——利用判定定理(常用) (2) 面面平行——利用性质定理 (一般不建议这种方法)
3.证明面面平行的方法:
线线平行——线面平行——面面平行 (注意每个过程的条件都不能写漏!)
空间中的平行
定理应用
1.长方体ABCD-A1B1C1D1中,点E, F分别是BA1,BC1的中点。 求证:EF // 平面ABCD
D1 C1
看到中点找中点
A1 D A
E
B1
F
C B
空间中的平行
定理应用
方法一):构造平行四边形
D1 A1 D A
E
C1
B1
F
C
M
B
N
空间中的平行
定理应用 方法二):构造平行平面
D1 A1 D A
β α
a // b
α//β
a
α a
a //β
a b
β
性质5
线线平行 公理4
判定1 性质4
线面平行
判定2 定义3
面面平行
α
b
点线面知识点讲解

点线面知识点讲解点、线、面是几何学中的基本概念,也是数学、物理、工程学等领域中不可避免的基础概念。
这些基本概念的理解和运用在学习和实践中具有重要的作用。
下面将分别介绍点、线、面及其相关知识点。
1. 点点是几何学基本概念之一,通常定义为没有任何大小和形状的几何对象。
点用来表示位置,并且可以在图形中标识地图、建筑等位置。
点不具有长度、宽度和高度的属性,只是一个单独的位置。
沿一条确定的路径移动点可以创建线段和多边形等形状。
在解决几何问题时,点可以作为基本的构建要素使用。
在计算几何、拓扑学、物理学等科学中,点作为数学对象的表示方式被广泛应用。
在计算机图形学中,点一般表示为一个由数字值构成的二元组(x,y),可以用来表示屏幕上的所有像素。
2. 线线通常定义为在两个点之间的最短距离的路径,也可以视为延伸无限远的无限细的几何对象。
从另一个角度来看,线是由一序列的连续的点所构成的。
在数学上,线是一种数学对象,可以通过定义一条包含这条线的方程式来确定。
在几何中,线包括直线和曲线。
直线是由一组连续的无限点构成的,可以通过一个无限长的箭头来表示,箭头上选取的点表示线段的起点和终点。
曲线可能会伸出任意数量的点,但是从这些点的连通性中都可以看出它们属于同一条曲线。
在计算几何、拓扑学、图形学等领域中,线是一种常用的基本元素,通常作为分析、计算和设计的依据。
3. 面面是由大量的点和线围成的区域,并且满足一定的空间特征。
它是几何学中的基本概念之一,可以用于表示平面和曲面。
面可以是简单的图形,如多边形或圆形,也可以是复杂的三维几何体,如锥形或圆锥形。
它通常被用于计算和分析对象的表面积、体积和质量等方面。
在三维计算机图形学中,面是由一系列相邻点和边组成的多边形网格,也包括复杂的曲面构造。
这些表面可以由数字制图系统自动生成,也可以由手动输入数据创建。
此外,还有其他与点、线、面相关的知识点,例如:1. 平面几何:平面内的点、直线和圆,以及它们之间的关系和性质。
复习点线面体

条边.
12.生活中有许多立体图形,想象下列物体分别与哪 些图形相类似? (1)铅笔盒; (2)一堆沙子; (3)足球; (4)螺母.
(1)长方体; (3)球体; (2)圆锥; (4)棱柱.
13.如图 5 所示,把下面几何体的标号分别写在相对 应的括号里面.
长方体: { ②⑤⑧ } ;棱柱体: { ②④⑤⑧ } ; 圆柱体: { ①③⑥ } ;球 圆锥体: { 体: {
6.埃及金字塔类似于几何体( C ) . A.圆锥 C.棱锥 B.圆柱 D.棱柱
7.下列图形不是立体图形的是( A.球 C.圆锥 B.圆柱 D.圆
D
) .
8.小明为班级专栏设计一个图案,如图,主题是“我 们喜爱合作学习”,请你也尝试用圆、扇形、三角形、 四边形、直线等为环保专栏设计一个图案,并标明你 的主题.
连一连
请将下列的平面图形和将它如图绕虚线旋转 一周后得到的几何体连线.
练习:把下面第一行的平面图形绕线旋 转一周,便能形成第二行的某个几何体, 请用虚线连一连:
1
2
3
4
5
A
B
C
D
E
1.与易拉罐类似的几何体是( A.圆锥 B.圆柱
B
) . D.棱柱
C.棱锥
2.2008 年奥运会在我国举行,它的标志是五环,这 五环的每一个环的形状与下列哪个图形类似 (
B
A
C
D
探究:用下列图形能拼成怎样的立 体图形?
C
A
B
棱柱
圆柱
圆锥
谢
谢Hale Waihona Puke C) . B.正方形 D.长方形
A.三角形 C.圆
【问题 2】如图 2,将下列图形与对应的图形名称用 线连接起来:
点线面讲义
《空间中点、直线、平面之间的位置关系》讲义想一想:现有2个空水壶,容积分别为5升和6升。
问题是如何只用这2个水壶从池塘中取得三升水。
(不能直接量出3升)内容归纳总结:一、四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
符号语言:,,,A l B l A B l ααα∈∈∈∈ ⇒ ∈且。
公理2:过不在一条直线上的三点,有且只有一个平面。
三个推论:① 经过一条直线和这条直线外一点,有且只有一个平面 ② 经过两条相交直线,有且只有一个平面 ③ 经过两条平行直线,有且只有一个平面它给出了确定一个平面的依据。
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线)。
符号语言:,,P P l P l αβαβ∈∈⇒=∈且。
公理4:(平行线的传递性)平行与同一直线的两条直线互相平行。
符号语言://,////a l b l a b ⇒且。
二、空间中直线与直线之间的位置关系1、概念 异面直线及夹角:把不在任何一个平面内的两条直线叫做异面直线。
已知两条异面直线,a b ,经过空间任意一点O 作直线//,//a a b b '',我们把a '与b ' 所成的角(或直角)叫异面直线,a b 所成的夹角。
(易知:夹角范围090θ<≤︒) 定理: 空间中如果一个角的两边分别与另一个角的两边分别平行,那么这两个角相等或互补。
(注意:会画两个角互补的图形)2、位置关系:⎧⎧⎪⎨⎨⎩⎪⎩相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点三、空间中直线与平面之间的位置关系直线与平面的位置关系有三种://l l A l ααα⊂⎧⎪=⎧⎨⎨⎪⎩⎩直线在平面内()有无数个公共点直线与平面相交()有且只有一个公共点直线在平面外直线与平面平行()没有公共点四、空间中平面与平面之间的位置关系平面与平面之间的位置关系有两种://lαβαβ⎧⎨=⎩两个平面平行()没有公共点两个平面相交()有一条公共直线五、直线、平面平行的判定及其性质六、直线、平面平垂直的判定及其性质定理定理内容符号表示分析解决问题的常用方法直线与平面垂直的判定一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
立体几何点线面知识复习
知识探究 一、空间角的计算
1.异面直线所成角:
若异面直线l1与直线l2所成角为 (0
l2的方向向量CD ( x2 , y2 , z2 )
2
), l1的方向向量AB
( x1,
y1 ,
z1 )
AB
l1
C
l2
D
AB CD
cos cos AB,CD
AB CD
注意: 异面直线所成角的范围!!!
B 设平面OAB的法向量n ( x, y, z)
O
A x
y
由OA n OB n
0 0
x
y
y0 z0
令x 1,则y 1, z 1
n (1,1,1)
赋值
知识探究
平面的法向量
特别:有现存的线面垂直关系,直线向量就可以作为法向量。
z E F
O A
x
D G
C
B
平面OABC的法向量:OE (0,0,1) 平面OAFE的法向量:OC (0,1,0) y 平面ABGF的法向量:OA (1,0,0)
(1)点C1,点A1, BC1的中点M的坐标 C (2)AM的坐标
y
z
E
D
o
A
x
如图,平面AED ⊥平面ABCD,△AED是等边 三角形,四边形ABCD是矩形,若AD = 2
建 立 适 当 的 直 角 坐 标 系, 并 求 出CE的 坐 标
C
y
B
知识探究 利用空间向量解决立体几何问题
平面的法向量
aIα=A
a
直线上所有的点都在 平面内直线在平面内
a α
四、空间中面与面的位置关系
图形
文字语言
符号语言
点线面位置关系复习PPT课件
公理1:Al, B l,且A, B l .
作用:证明或者判断点或直线是否在平面内。
公理2:不共线的三点确定一个平面。
作用:确定一个平面的依据。
公理3:P ,且P l,且P l
作用:确定两平面相交的依据,判断多点共线的依据。
公理4:在空间平行于同一条直线的两 条直线
互相A.平行.Bα.
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
第10页/共24页
4.设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( ) A若l⊥m,m⊂α,则l⊥α
B
B若l⊥α,l∥m,则m⊥α C若l∥α,m⊂α,则l∥m D若l∥α,m∥α,则l∥m
D
第13页/共24页
10.已知m、n为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是 ()
A.m⊂α,n⊂α,m∥β,n∥β⇒α∥β
D
B.α∥β,m⊂α,n⊂β,⇒m∥n C.m⊥α,m⊥n⇒n∥α
D.n∥m,n⊥α⇒m⊥α
11.对于任意的直线l与平面α,在平面α内必有直线m,使m与l( )
垂直,那么该直线与此平面垂直. (线线垂直 线面垂直);
m ,n
a
mn P
a
a
n
Pm
a m, a n
第5页/共24页
2.判定两平面垂直的方法:
(1)定义法:平面与平面相交成直二面角则面面垂直;
(2)判定定理:如果一个平面经过另一个平面的垂线,
那么这两个平面互相垂直. (线面垂直 面面垂直);
a a
第6页/共24页
必修2点线面复习提纲及练习
必修2 点线面复习姓名一、点线面的关系:直线和直线有3种关系:相交、平行、异面;直线和平面有3种关系:相交、平行、在平面内;平面和平面有2种关系:相交、平行;二、平行垂直的判定:线面平行:线平行面内一条直线————线线平行面面平行:相交直线平行面——————线线平行×2线面垂直:线垂直面内两条相交直线——线线垂直×2面面垂直:过面的垂线————————线线垂直×2三、平行垂直的性质:线面平行:线与交线平行面面平行:面面交线平行线面垂直:(1)线垂直于面内任何一直线(2)两垂线平行面面垂直:垂直交线的垂直面典型例题:1、如图,在三棱锥A-BCD中,E、F是棱AB、AD的中点求证:EF∥平面BCD2、在正方体ABCD-A 1B1C1D1中,E为边DD1的中点,O为AC和BD的交点,求证:BD1∥平面AEC3、三棱锥A-BCD中,E、F、G分别是AB、AD、AC的中点求证:平面EFG∥平面BCD4、在正方体ABCD-A1B1C1D1中,E、F为A1D1和BC的中点求证:EF∥平面ABB1A15、三棱锥A-BCD中,AB=1,AD=2,求证:AB⊥平面BCD6、三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD求证:CD⊥平面ABC7、在四棱锥S-ABCD中,SD⊥平面ABCD,底面ABCD是正方形求证:AC⊥平面SBD8、ABCD和DCCD1是两个正方形,平面ABCD⊥平面DCC1D1(1)求证:AD⊥平面DCC1D1(2)求证:D1D⊥平面ABCD(3)CD⊥平面BCC1(4)AC⊥平面BDD19:、(湖北文)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,点E是线段SD上的任意一点,求证: AC⊥BE10、(江西文)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,M 为PD 上一点,求证:平面ABM ⊥平面A P D11、(10广州一模)如图,正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ,AE ⊥平面CDE ,求证:AB ⊥平面ADE ;12、在四面体ABCD 中,CB=CD ,AD BD ⊥,且E ,F 分别是AB ,BD 的中点, 求证(I )直线EF D 平面AC ;(II )EFC D ⊥平面平面BC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
//a α
//a b
//a b 点线面位置关系
知识梳理
一、直线与平面平行 1.判定方法
(1)定义法:直线与平面无公共点。
(2)判定定理:
(3)其他方法://a αβ
β⊂ 2.性质定理://a a b
α
βαβ⊂⋂= 二、平面与平面平行 1.判定方法
(1)定义法:两平面无公共点。
(2)判定定理:////a b a b a b P
β
β
α
α⊂⊂⋂= //αβ
(3)其他方法:a a αβ⊥⊥ //αβ; ////a γ
βγ
//αβ
2.性质定理://a b
αβ
γαγβ⋂=⋂=
三、直线与平面垂直
(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直。
(2)判定方法 ① 用定义.
② 判定定理:a b
a c
b c A b c αα
⊥⊥⋂=⊂⊂ a α⊥
③ 推论:
//a a b
α
⊥ b α⊥ (3)性质 ①
a b αα⊥⊂ a b ⊥ ②a b α
α
⊥⊥ 四、平面与平面垂直
(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直。
(2)判定定理a a α
β
⊂⊥ αβ⊥
(3)性质
①性质定理l a a l
αβ
αβα
⊥⋂=⊂⊥ αβ⊥
② l P PA A
αβαβα
β⊥⋂=∈⊥垂足为
A l ∈
④ l P PA αβ
αβαβ
⊥⋂=∈⊥ PA α⊂
“转化思想”
面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直 求二面角
1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.
2.在二面角
的棱上任取一点O ,在两半平面
内分别作射线OA ⊥l ,OB ⊥l ,则∠AOB 叫做二面角
的平面角
例1.如图,在三棱锥S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交AC 于D ,交SC 于E ,又SA=AB ,SB=BC ,求以BD 为棱,以BDE 和BDC 为面的二面角的度数。
解:
在RtΔSAC 中,SA=1,SC=2,∴∠ECA=30︒, 在RtΔDEC 中,∠DEC=90︒, ∴∠EDC=60︒, ∴ 所求的二面角为60︒。
//a b a b
αα
⊄⊂//a α//a b
求线面夹角
定义:斜线和它在平面内的射影的夹角叫做斜线和平面所成的角(或斜线和平面的夹角)
方法:作直线上任意一点到面的垂线,与线面交点相连,利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。
例:在棱长都为1的正三棱锥S -ABC 中,侧棱SA 与底面ABC 所成的角是________.
求线线距离
说明:求异面直线距离的方法有: (1)(直接法)当公垂线段能直接作出时,直接求.此时,作出并证明异面直线的公垂线段,是求异面直线距离的关键.
(2)(转化法)把线线距离转化为线面距离,如求异面直线a 、b 距离,先作出过a 且平行于b 的平面α,则b 与α距离就是a 、b 距离.(线面转化法).
也可以转化为过a 平行b 的平面和过b 平行于a 的平面,两平行平面的距离就是两条异面直线距离.(面面转化法).
(3)(体积桥法)利用线面距再转化为锥体的高用何种公式来求.
(4)(构造函数法)常常利用距离最短原理构造二次函数,利用求二次函数最值来解.
两条异面直线间距离问题,教科书要求不高(要求会计算已给出公垂线时的距离),这方面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.
例:在棱长为a 的正方体中,求异面直线BD 和C B 1之间的距离。
线面平行(包括线面距离)
例:已知点S 是正三角形ABC 所在平面外的一点,且SC SB SA ==,SG 为SAB ∆上的高,D 、E 、F 分别是AC 、BC 、SC 的中点,试判断SG 与平面DEF 内的位置关系,并给予证明
证法1:连结CG 交DE 于点H , ∵DE 是ABC ∆的中位线, ∴AB DE //.
在ACG ∆中,D 是AC 的中点,且AG DH //,
∴H 为CG 的中点.
∵FH 是SCG ∆的中位线,∴SG FH //. 又SG ⊄平面DEF ,FH ⊂平面DEF , ∴//SG 平面DEF .
证法2:∵EF 为SBC ∆的中位线, ∴SB EF //.
∵⊄EF 平面SAB ,⊂SB 平面SAB , ∴//EF 平面SAB .
同理://DF 平面SAB ,F DF EF = , ∴平面SAB //平面DEF ,又∵⊂SG 平面SAB , ∴//SG 平面DEF .
面面平行(包括面面距离) 例:在棱长为a 的正方体中,求异面直线BD 和C B 1之间的距离. 解:根据正方体的性质,易证:
1
111111//////D CB BD A C D B A D B BD 平面平面⇒⎭
⎬⎫
连结
1AC ,分别交平面BD A 1和平面
11D CB 于M 和N
因为
1CC 和1AC 分别是平面ABCD 的垂线和斜线,AC 在平面ABCD 内,BD AC ⊥
由三垂线定理:BD AC ⊥1,同理:D A AC 11⊥
∴
⊥1AC 平面BD A 1,同理可证:⊥1AC 平面11D CB
∴平面
BD A 1和平面11D CB 间的距离为线段MN 长度.
如图所示:
在对角面1AC 中,1O 为11C A 的中点,O 为AC 的中点 ∴
a AC NC MN AM 333111==
==.
∴BD 和C B 1的距离等于两平行平面BD A 1和1
1D CB 的距离为a 33.
面面垂直
例1:已知直线PA 垂直正方形ABCD 所在的平面,A 为垂足。
求证:平面PAC ⊥平面PBD 。
例2:
已知直线PA 垂直于⓪O 所在的平面,A 为垂足,AB 为⓪O 的直径,C 是圆周上异于A 、B 的一点。
求证:平面PAC ⊥平面PBC 。
点线面检测
一、选择题
1.互不同线l 、m 、n 和面α、β、γ的三个命题: ①若l 与m 为异面直线,l ⊂α,m ⊂β,则α∥β; ②若α∥β,l ⊂α,m ⊂β,则l ∥m;
③若α∩β=l,β∩γ=m,γ∩α=n,l ∥γ,则m ∥n. 其中真命题的个数为( )
A.3
B.2
C.1
D.0 2.设m 、n 是两条不同的直线,α、β是两个
不同的平面.考查下列命题,其中正确的命题是( )
A .βαβα⊥⇒⊥⊂⊥n m n m ,,
B .n m n m ⊥⇒⊥βαβα//,,//
C .n m n m ⊥⇒⊥⊥βαβα//,,
D .ββαβα⊥⇒⊥=⊥n m n m ,, 3.下列四个命题:
① 若//m α,//n β且//αβ,则//m n ;
② 若m α⊥,n β⊥且αβ⊥,则m n ⊥; ③ 若m α⊥,//n β且//αβ,则m n ⊥; ④ 若//m α,n β⊥且αβ⊥,则//m n 。
其中真命题的序号式( )
A .①②
B .③④
C .①④
D .②③ 4.如图,已知矩形ABCD 中,10=AB ,6=BC ,将矩形沿对角线BD 把ABD ∆折起,使A 移到
1A 点,且BCD O A 平面⊥1.(1)求证:D A BC 1⊥;
(2)求证:BD A BC A 11平面平面⊥;
(3)求三棱锥BCD A -1的体
积.A
B
C
D
A 1
O
⎫⇒⊥⎬⎭BC AC ⊥PA 平面ABC ⊂BC 平面ABC ⎫
⇒⊥⎬⎭BC PA ⊂⊂AC 平面PAC ,PA 平面PAC =AC PA A
⎫
⎪⎪⎬⎪⎪⎭⇒⊥BC 平面PAC ⊂BC 平面PBC
求角(线线角、线面角、二面角)。
例:如图,在三棱锥
P ABC -中,90APB ∠=,
60PAB ∠=,AB BC CA ==,平面PAB ⊥平面
ABC 。
(Ⅰ)求直线PC 与平面ABC 所成角的正弦值; (Ⅱ)求二面角B AP C --的余弦值。
解:(1)作PQ ⊥AB 于Q ,连CQ 。
ABC PQ ABC PAB AB PQ 面面面⊥⇒⎭
⎬⎫
⊥⊥ (证明)
所以直线PC 与平面ABC 所成的角即为∠PCQ (定角)
令AB=2,在△PAB 中,PQ=
23,在△ABC 中,CQ=2
13,
所以sin ∠PCQ=
4
3
(计算) 2)取AB 中点O ,连CO 、PO 。
过O 作ORAP 于R ,连CR (作图)
CR AP COR AP AP OR AP CO PAB CO ABC PAB AB CO AB O CA BC AB ⊥⇒⊥⇒⎪⎪
⎭
⎪
⎪⎬⎫⊥⊥⇒⊥⇒⎪
⎭⎪
⎬⎫⊥⊥⇒⎭⎬⎫
==面面面中点为(证明)所以二面角B AP C --的平面角∠CRO , (定角)
所以由CO=
3,OR=
23,得cos ∠CRO=5
5。
(计算。
P A C
B。
