一次函数导学案草案
八年级数学复习《一次函数》导学案.doc
八年级数学复习《一次函数》导学案.doc1、第十四章一次函数复习学习目标：1.了解本章的学问结构；2.把握一次函数的概念、图象和性质；能用待定系数法确定一次函数解析式。
学习重点：一次函数的概念、图象和性质；能用待定系数法确定一次函数解析式学习难点：一次函数学问的运用。
【学问提要】一、函数与函数的图象1.叫变量，叫常量.2.函数定义：在一个改变过程中，假如有两个变量x与y，并且对于x的每一个确定的值，y都有确定的值与其对应，那么我们就说x是自变量，y是x的函数.3.函数的图象：对于一个函数，假如把自变量与函数的每对对应值分别作为点的，那么坐标平面2、内由这些点组成的图形，就是这个函数的图象。
4、描点法画图象的步骤：5.函数的三种表示方法：6、自变量的取值范围：〔1〕分式类：分母不为0，〔2〕根式类：开偶次方的被开方数大于等于0，〔3〕整式类：全体实数。
〔4〕实际类：使实际问题有意义。
例1、求以下函数中自变量x的取值范围〔1〕；〔2〕；〔3〕；〔4〕。
例2、以下四组函数中，表示同一函数的是〔〕A、y=x与y=B、y=x与y=C、y=x与y=x2/xD、y=x与y=例3、如下图的图象分别给出了x与y的对应关系，其中y是x的函数的是〔〕xyoAxyo3、BxyoDxyoC二、一次函数1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。
当b_____时，函数y=____(k____)叫做正比例函数。
2、正比例函数y=kx(k≠0)的图象是过点〔_____〕，(______)的。
3、一次函数y=kx+b(k≠0)的图象是过点〔0，___),〔____，0)的__________。
4.一次函数y=kx+b的图象是一条直线，其中k确定直线性，b确定直线与轴的交点位置.k和b确定了直线所在的象限,k0时，图象必过象限 4、；k0时，图象必过象限；b0,b0时，图象过象限;k0,b0时，图象过象限;k0k0B0B.yx2时，y1y2，则m的范围是11、直线y=3x+b与y轴的交点的纵坐标为-2，则这条直线肯定不过象限12、一次函数y=(m2-3)x-1和y=(m+2)x+(m2-3)的图像与y轴分别交于P，Q两点，若P、Q点关于x轴对称，则m=。
《一次函数》导学案
《一次函数》导学案
一、基础知识自主盘点：研究课本或相关资料，自主复习，进一步理解、熟练掌握。
1.一次函数有关概念；
2.一次函数图象；
3.一次函数的性质；
4.会用待定系数法确定一次函数解析式；
5.会用一次函数解决实际问题，能用函数观点看方程（组）与不等式。
二、热点问题研究：（C组:1～5.B组:1～6.A组：5～7.)
1.m为何值时，关于x的函数y=(m+1)x2-m2+3是一次函数，并写出其函数关系式。
2.一次函数y=x+2的图象不经过第象限.
3.点P1（x1,y1),P2（x2,y2)是一次函数y=-4x+3图象上的两个点，且x1<</SPAN>x2，则y1与y2的大小关系是.
4.已知一次函数y=kx+b的图象经过点A（0，-2），B（1，0），则b=_____________，k=___________。
5.如图，已知函数y=x+b和y=ax+3的图象于点P,则不等式x+b>ax+3的解集为.
6.甲、乙两人骑自行车前往A地，。
14.2.2一次函数导学案(共3课时)
第十四章 14.2.2《一次函数》----（第1-2课时）导学案年级及科目：八年级数学备课：董成伟课型：展示课审核：陈泽念【学习内容】§14.2.2《一次函数》，教材第113—117页。
【学习目标】１．记住一次函数的概念；２．知道一次函数与正比例函数之间的关系；３．记住一次函数图象性质，知道性质与解析式的联系规律；４．会用简单方法画一次函数图象．【学习重点】一次函数的概念及一次函数图像的性质。
【学习难点】一次函数图像的性质和解析式中常数之间的关系。
【知识链接】1、正比例函数的概念：一般地，形如（）的函数，叫做正比例函数，其中k叫做。
2、正比例函数的性质:(1)正比例函数的图象是一条的，称它为。
y随x的增大(2)①当k>0时，直线y=kx经过象限，从左到右呈趋势，即而。
y随x的②当k〈0时，直线线y=kx经过象限，从左到右呈趋势，即增大反而。
【学习过程】一、探究活动1：（一）阅读课本：问题：（见课本第113页“问题”及分析过程）思考：下列问题中变量间的对应关系可用怎样的函数表示？这些函数有什么共同点？（1）有人发现，在20~25℃时蟋蟀每分钟鸣叫次数c与温度t（单位：℃）有关，即c的值约是t的7倍与35的差；（2）一种计算成年人标准体重G（单位：千克）的方法是，以厘米为单位量出身高值h减常数105，所得差是G的值；（3）某城市的市内电话的月收费额y（单位：元）包括：月租费22元，拨打电话x分的计时费按0.01元/分收取;(4)把一个长10cm、宽5cm的长方形的长减少xcm，宽不变，长方形的面积y（单位：cm2）随x的值而变化。
归纳：这些函数的形式都是的形式。
（二）学习概念：一般地，形如（）的函数，叫做一次函数。
特别的，当ｂ＝０时，y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数。
（三）当堂练习：见课本第114页的练习。
二、探究活动2：问题1：例2：请在同一坐标系中画出函数y=—6x与y=—6x+5的图象。
《一次函数》导学案
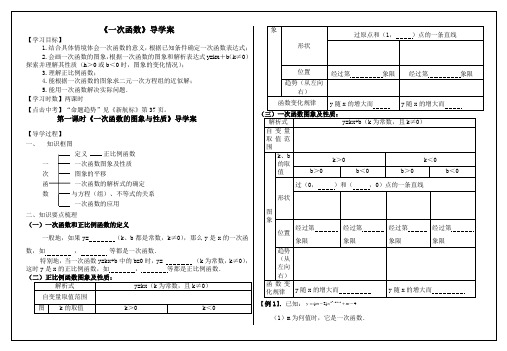
（2）当它是一次函数时，画出草图，指出它的图象经过哪几个象限？y是随x的增大而增大还是减小？（3）当图象不过原点时，求出图象与两轴所围成的三角形面积．解：（四）一次函数y=kx+b的图象与正比例函数y=kx的图象之间的位置关系：1.当b＞0时，直线y=kx+b由直线y=kx向平移个单位长度；2.当b＜0时，直线y=kx+b由直线y=kx向平移个单位长度．【例2】.将一次函数y=2x-3向下平移5个单位的表达式为__________。
（五）用待定系数法求一次函数的解析式：1.常见的直接条件：（1）、对于正比例函数，需要__________个点的坐标。
（2）、对于一次函数，需要__________个点的坐标。
【例3】．（1）、已知正比例函数经过点（-1,2），则其表达式为__________。
（2）、已知一次函数经过点（0,3）和（-2,5），则其表达式为__________。
2.间接条件：围成图形的面积；平行关系等．【例4】．已知一次函数y=kx+2的图象过第一、二、三象限且与x、y轴分别交于A、B两点，O为原点，若ΔAOB的面积为2，求（1）A点坐标.(2) 该一次函数的表达式．解：（六）用函数观点看方程（组）和不等式①一次函数y=kx+b的图象与x轴交点的横坐标-bk⇔一元一次方程kx+b=0的解x=②一次函数y=k1x+b与y=k2x+b两个图象的交点1122y kx by kx b=+⎧⇔⎨=+⎩二元一次方程组的．③使一次函数y=kx+b的函数值y＞0（或y＜0）的自变量的取值范围⇔一元一次不等式kx+b＞0（或kx+b＜0）的__________．【例4】.如图，已知函数y＝ax＋b和y＝kx的图象交于点P，则根据图象可得二元一次方程组⎩⎪⎨⎪⎧y＝ax＋b，y＝kx的解__________．三、综合演练见《新航标》P39（1——5、8）P40（3、8）P41( 1、3、7)四、课后提升见《新航标》P39——41其余题五、我的困惑第二课时《一次函数的应用》导学案【学习目标】能用一次函数解决实际问题．【点击中考】“命题趋势”见《新航标》第37页。
一次函数导学案1
一次函数导学案学习目标：1、了解一次函数图象的意义；体会一次函数与正比例函数的关系。
2、初步了解待定系数法确定自变量系数；3、能根据具体条件确定一次函数关系式中的未知数．学习重、难点：一次函数的意义与函数关系中未知数的确定.知识储备（10分钟）1、函数的定义。
2、画函数图象的步骤是①②③；3、前面所学的函数y=x+1，y=-2x-1，y=2.5x-2的图象都是什么图形？。
4、上面这几个函数关系式中的自变量的次数都是多少?它们具有什么样的一般形式？5、若点A（n，7 ）在函数y=2x+1 的图象上，则n=______。
（看书62页）新知探究一：（10分钟）一次函数的定义：上面我们讨论了这几个函数关系式都有的相同特点，即它们的自变量的次数都等于1这样的函数就是一次函数。
形如的函数叫做x的一次函数，其中，与是常数。
这里，系数k 不能为0，而b的值可以为0。
若b=0，则一次函数就变成，这样的函数也叫做正比例函数。
沙场练兵：1、下列函数关系式是一次函数的是：①y=32x-5 ( ) ②y=-0.5x ( )③y=ax+2 ( )④y=2.1x2-4 ( )⑤y=-32x( )⑥y=4-3x2( )⑦y=(a2+1)x-10( )2、判断：正比例函数是一次函数吗？一次函数是正比例函数吗？请举例说明。
新知探究二：（15分钟）自主学习课本例1. 思考：如何确定．．函数关系式（即确定函数关系式就是确定函数关系式中的的值）小组同桌讨论：确定函数关系式的一般步骤是什么？①因为y是x的一次（或正比例）函数；②所以设y=kx+b(或y=kx)(k≠0)；③把告诉的相关字母的值代入函数关系式，求出k的值；④所以函数关系式为；。
学以致用：已知一次函数y=kx-5的图象经过点M(-2,3)试求当x=4时的函数值y。
学生自主探究：如何根据函数关系式确定关系式中的未知数的值呢？。
请你来练习：已知函数y=kx-6当x=3时y的值为-5，求k的值。
一次函数(4)导学案.doc
课题 14.2.2 一次函数（4）课型 自学课—、导入（2分钟）P113实例引新课，，，，，，二、学习目标（2分钟）1 • 了解待定系数法，会用待定系数法求一次函数的解析式。
2. 探讨待定系数法求一次函数的解析式的一般过程。
3 .小组团结合作，激情讨论，大胆展示，勇于质疑。
二、导学程序（35分钟）1、 独学（课前完成）检查点评学习效果，达标率80%2、 对学（2分钟）了解学习效果，解决独学时存在的问题，达标率70 %3、 组学（12分钟）了解学习效果，解决对学时存在的问题，达标率85%4、 教师理清非大展示的内容（2分钟），达标率95%, 5展示（20分钟）点评学习效果，解决共性问题。
四、学法指导：1、 通读本章教材，进行知识梳理，归纳课本上重点内容。
2、 将学习中生成的问题记录下来。
3、 “观察一讨论一归纳一应用”为主线的学习模式。
五知识超市：1.一次函数的定义。
2 . 一次函数的图象和性质是什么？ 六导学内容：合作探究：（一）1、 一次函数的图象过点（1, 2）,且y 随x 的增大而增大，请你写出一个符合条件的函 数关系式.2、 如果正比例函数的图象经过点（-1, 2）,这个函数的解析式是,3、 已知一次函数的图象过点（3, 5）与（-4, -9）,求这个一次函数的解析式。
分析：求一次函数y=kx+b 的解析式，关键是求出k, b 的值，从已知条件可以列出 关J -k, b 的二兀一次方程组，并求出k, b.解：设这个一次函数解析式为。
因为 的图象过点（3, 5）与（一4, —9）,所以 {解得{这个一次函数的解析式为.归纳1：用 法确定一次函数的解析式的步骤：1. ----------------------------------------------------------------------------- 设一次函数的一般形式y=kx+b （kU0）； ------------------------------------- 设2. ----------------------------------------------------------------------------- 根据已知条件列出关于k , b 的二元一次方程组； ---------------------------- 列3. 解这个方程组，求出k, b ； ----------------------- 解4. ----------------------------------------------------------------------------- 据求出的k, b 的值，写出所求的解析式. ----------------------------------- 写象这样先设待求的—（其中含有未知的系数），再根据条件列出方程或方程组，求出未知系数，从而具体写出关系式的方法，叫做―合作探究：（二）【例1】：直线y=kx+b 的图像经过A （3, 4）和点B （2, 7）,求其解析式【例2] 一次函数的图象平行于直线y=-2x+7且与直线y=3x-4在y 轴上交于一点，求这 个函数的解析式。
一次函数的概念导学案
佃22 一次函数第1课时一次函数的概念一、新课导入1•导入课题2•学习目标(1 )知道什么样的函数是一次函数，能根据一次函数的定义求函数表达式中未知字母系数的值(2)知道正比例函数是特殊的一次函数.(3)根据等量关系列一次函数关系式.3•学习重、难点重点：一次函数的概念•难点：根据实际问题列一次函数表达式•二、分层学习第一层次学习1•自学指导(1)自学内容：P89到P90练习以上的内容•(2)自学时间：10分钟•(3 )自学要求：看书、动手、观察关系式的共同特点，尝试归纳一次函数的一般形式(4 )自学参考提纲：①思考中的四个解析式有什么共同特点？②请叙述一次函数的定义，注意不能忽视什么问题？③一次函数与正比例函数有什么联系和区别？④已知y=(a2—1)x+b - 2,a. 当土1, b丰2时，它是一次函数•b. 当土1, b=2时，它是正比例函数.⑤完成P90的练习•2. 自学：学生可参考自学参考提纲进行自学•3. 强化(1) 一次函数的定义及确定字母系数的依据•(2 )展示练习的答案，并点评•(3)正比例函数与一次函数的异同点•第二层次学习1•自学指导(1)自学内容：一次函数意义的应用•(2)自学时间：10分钟.(3 )自学要求：结合自学参考提纲进行自主学习，合作交流(4 )自学参考提纲：①下列函数中，是一次函数的是()281A.y=8xB.y=x+1C.y=D.y=x x+1②已知函数y=(m 3)x|m-2|+3是一次函数，求解析式.③已知函数y=(m —10)x+1 —2m,a. m为何值时，这个函数是一次函数；b. m为何值时，这个函数是正比例函数.④某报亭老板以每份0.5元的价格从报社购进某种报纸500份，以每份0.8元的价格销售x份(x< 500)，未销售完的报纸又以每份0.1元的价格由报社收回，这次买卖中该老板获利y元，求y与x的函数关系式.2•自学：学生可参考自学参考提纲进行自学.3•助学(1 )师助生：①明了学情：了解学生完成提纲时存在的问题和遇到的疑难②差异指导：对学生自学中的疑难问题进行针对性指导(2)生助生：相互交流，帮助矫正错误A.y=-x+25B.y=x+25C.y=-x+503. （10分）王明妈妈购进一批苹果，至憎货市场零售，已知卖出的苹果重量 表.重量（午克） 13 4 5 销售额（元）2 +0. 14+0.26 +0. 38+0.410 +0+ 5则y 关于x 的函数关系式是（）4.（10分）若点A （2 , 4）在函数y=kx-2的图象上，则下列各点在此函数图象上的是（）------------ 评价彳乍.j||f ■一、基础巩固（65分）1. （10分）下列说法中不正确的是（） A. 一次函数不一定是正比例函数 C.正比例函数是特殊的一次函数2. （10分）矩形的周长为50，设它的长为 （时间：12分钟满分：100分）B.不是一次函数就一定不是正比例函数 D.不是正比例函数就一定不是一次函数x ,宽为y ,则y 与x 的函数关系式为（） D.y=x+50x （千克）与销售额y （元）之间的对应关系如下 A.y = 2x+0.1B.y = 2x+0.1xC.y = 4x+0.2D.y = 4x+0.2xA.(1 , 1)B.(-1 , 1)C.(-2 , -2)D.(2 , -2)5. （15分）一盘蚊香长105cm，点燃时每小时缩短10cm.y（cm）与蚊香燃烧时间t（h）之间的函数关系式;（1 ）请写出点燃后蚊香的长（2）该蚊香可燃烧多长时间?、综合应用（15分）7. 某工厂加工一批产品，为了提前交货，规定：每个工人完成100个以内，每个产品付酬 1.5元；超过100个，超过部分每个产品付酬增加0.3元；超过200个，超过部分除按上述规定外，每个产品再增加0.4元.求一个工人: （1）完成100个以内所得报酬y（元）与产品数x（个）之间的函数关系式；（2）完成100个以上但不超过200个所得报酬y（兀）与产品数x（个）之间的函数关系式；（3）完成200个以上所得报酬y（元）与产品数x（个）之间的函数关系式.、拓展延伸（20分）8. 若5y+2与x-3成正比例，求证：y是x的一次函数。
6.2一次函数的导学案
一次函数导学案一．学习目标1、会说出一次函数概念，能判断两个变量间的关系是否可看作一次函数。
2、根据一次函数的关系式，给定其中一个量，相应地会求出另一个量的值。
3、会对一个具体实例进行概括抽象成为一次函数的数学问题。
二．自主学习 学习内容1、 独立完成课本182页问题的表格?2、 你能写出X 与Y 间的关系式吗？○1 ； ○2 ； ○3你能根据预习写出什么是一次函数和正比例函数吗？ 2、一次函数的概念：如果两个变量x 与y 之间的函数关系，可以表示为_________y =(其中________为常数，且____≠0）的形式，那么称y 是x 的一次函数。
x 是_____变量，y 是___变量。
特别地，当b=0时，一次函数_________y =就是____y =（____为常数，___≠0），则称y 是x 的正比例函数，所以______比例函数是一次函数的特例，即：正比例函数也是一次函数。
预习检测：1.下列函数中，一次函数有_____________，正比例函数有_______________。
① 5y x =-- ② 2y x = ③ 2y x π= ④ 2y x = ⑤ 4m n =- ⑥y = ⑦ 62y x =- ⑧ 23y x =2.若(1)5y m x =-+是一次函数, 则m _____；若2824a y x -=-是一次函数, 则a =____3.每人写两个一次函数，请同桌指出其中k 、b 的值。
比如25y x =-+ (k ＝___，b ＝___)三．先独立完成，再合作交流 1. 已知函数23(1)(2)my m x m -=-++（1）m 为何值时，该函数为一次函数？（2）m 为何值时，该函数为正比例函数？2. 已知1y -与x 成正比例，且x ＝2时，y ＝-8， 写出y 与x 之间的函数关系式.3、小组交流，把疑难问题写在黑板上。
四、展示解疑提出你的问题或不同的意见：五、课堂检测：1. 电信公司推出无线市话服务，收费标准为月租费25元，通话费为0.1元/min ，老张某月通话时间为x(min),应付费y 元.则y 与x 之间的函数关系式为_____________2. 已知函数2(1)1y m x m =++-（1）m 为何值时，该函数为一次函数？ （2）m 为何值时，该函数为正比例函数？3. 已知12y y y =+，其中1y 与x 成正比例，2y 与（x-2）成正比例，且当x=1时，y=2；当x=2时，y=5。
一次函数导学案
一次函数教案（一）教学目标（一）教学知识点１．掌握一次函数解析式的特点及意义．２．知道一次函数与正比例函数关系．３．理解一次函数图象特征与解析式的联系规律．４．会用简单方法画一次函数图象．（二）能力训练要求１．通过类比的方法学习一次函数，体会数学研究方法多样性．２．进一步提高分析概括、总结归纳能力．３．利用数形结合思想，进一步分析一次函数与正比例函数的联系，从而提高比较鉴别能力．教学重点１．一次函数解析式特点．２．一次函数图象特征与解析式联系规律．３．一次函数图象的画法．教学难点１．一次函数与正比例函数关系．２．一次函数图象特征与解析式的联系规律．教学方法合作─探究，总结─归纳．教具准备多媒体演示．教学过程一、创设情境、导入新课1、某登山队大本营所在地的气温为15℃，海拔每升高1km气温下降6℃．登山队员由大本营向上登高xkm时，他们所处位置的气温是y℃．试用解析式表示y•与x的关系．２．一种计算成年人标准体重G（kg）的方法是，以厘米为单位量出身高值h减常数105，所得差是G的值．３．某城市的市内电话的月收费额y（元）包括：月租费22元，拨打电话x 分的计时费（按0．01元／分收取）．４．把一个长10cm，宽5cm的矩形的长减少xcm，宽不变，矩形面积y（cm2）随x的值而变化．这些问题的函数解析式分别为：1、y=-6x+15（x≥0）2、G=h-105．3、y=0．01x+224、y=-5x+50它们的形式都是自变量x的k倍与一个常数的和．如果我们用b来表示这个常数的话．•这些函数形式就可以写成：y=kx+b（k≠0）归纳总结：一般地，形如y=kx+b（k、b是常数，k≠0•）的函数，•叫做一次函数．当b=0时，y=kx+b即y=kx．所以说正比例函数是一种特殊的一次函数．二、课堂练习：１．下列函数中哪些是一次函数，哪些又是正比例函数？（1）y=-8x．（2）y= 3+5x．（3）y=5x2+6．（3）y=-0．5x-1．三、活动探究：在同一直角坐标系中画出下列函数图象，并归纳y=kx+b（k、b是常数，k≠0）中k,b的符号与直线y=kx+b(k≠0) 的位置关系：1、y=x-1 y=x y=x+12、y=-2x+1 y=-2x y=-2x-1引导学生从图象形状，倾斜程度及与y轴交点坐标上比较两组图象，•从而认识图象的平移关系，进而了解解析式中k、b在图象中的意义，体会数形结合在实际中的表现．比较上面两组函数的图象的相同点与不同点。
《一次函数》导学案
19.2.2一次函数学案（3）学习目标： 1.会用待定系数法求一次函数解析式。
2.探讨待定系数法求一次函数的解析式的一般过程。
学习重点：待定系数法求一次函数解析式。
学习难点：用一次函数表达式解决有关实际问题。
学习过程：（一）情境导入：1：一次函数的图像过点（1，2），且y随x的增大而增大，请你写出一个符合条件的函数关系式。
2：一次函数的表达式、正比例函数的表达式分别是什么？3：如果正比例函数的图像经过点（-1，2），你能确定这个函数的解析式吗？（二）自主探究已知一次函数的图像过点（3，5）与（-4，-9），求这个一次函数的解析式。
分析：求一次函数y=kx＋b的解析式，关键是求出k，b的值，从已知条件可以列出关于k，b的二元一次方程组，并求出k，b．解：设这个一次函数解析式为。
因为的图象过点（3，5）与（－4，－9），所以{解得{这个一次函数的解析式为。
解题的步骤:1.设一次函数的一般形式y=kx+b(k≠0) ;2.根据已知条件列出关于k , b 的二元一次方程组3.解这个方程组,求出k, b ;4 .据求出的 k, b的值，写出所求的解析式.象刚才这样先设待求的_________(其中含有未知的系数)，再根据条件列出方程或方程组，求出未知系数，从而具体写出关系式的方法,叫做___________。
【问题】直线与一次函数表达式之间是怎样互相转化的？（三）课内检测1：根据下列条件，分别求一次函数解析式：（1）一次函数过点（2，4），（-2，2）；（2）一次函数经过直线y=2x-7且与直线y=0.25x+3交与y轴上同一点。
2．已知一次函数y＝kx＋2，当x＝5时y的值为4，求k的值．3．已知直线y=kx＋b经过点（9，0）和点（24，20），求k，b的值．4：已知一个正比例函数和一个一次函数，它们的图像都经过点p(-2, 1),且一次函数的图像与y轴交于点q (0 ,3 ).(1)求出这两个函数解析式。
人教版八年级数学上册《一次函数》导学案
人教版八年级数学上册《一次函数》导学案§复习课《一次函数》导学案学习目标：1. 会用待定系数法求一次函数的解析式2. 会用一次函数的图像和性质解决有关一一次方程（组）与不等式的问题3. 能用一次函数解决实际问题4. 从解题过程中体会“数形结合”思想学习过程：一、知识梳理：1、一次函数概念：函数 y= （k,b为常数，k ），叫一次函数。
当b= 时，函数 y= （k≠0），叫正比例函数。
2、正比例函数y=kx（k≠0）的图象必过点（，）和（，）的一条直线。
3、一次函数y=kx+b（k≠0）的图象必过点（0，）和（，0）的一条直线。
它可由正比例函数经过得到。
4、根据下列函数的草图判断k、b的意义及函数性质归纳性质：（1）(2) （3）（4） (5)（6）二、真题演练1、一次函数y=3x-4的图像不经过（）A、第一象限B、第二象限C、第三象限D、第四象限 2、（如图1）直线l 是一次函数y=kx+b的图像，则l1 （1）此函数的解析式为：（）（2）当x=4时，y=（）-2（3）当x＞0时，y （）当y＞0时，x （）图1 3、（如图2）已知函数y=ax+b与y=kx的图像交于点p，则由图像可知关于x、y的方程 ?y?ax?b 的解为：y?kx?y- -4 -y y=kx x x -2 p y=ax+b p三、巩固提高学习例、（如图3）在平面直角坐标系中点C（-3、0），点A、B分别在x轴和y轴的正半轴上且2满足O B??3OA??10（1）求A、B的坐标（2）若点P从C点出发，以每秒1个单位的速度沿射线CB方向运动，连接AP。
设△ABP的面积为S，点P运动的时间为t秒，求S与t的函数关系式，并写出自变量t的取值范围。
BPC O A四、练习1、已知一次函数的图像过点（1、3）和（-1、1）（1）求此函数的解析式，（2）求函数图像与坐标轴的交点坐标。
2、蜡烛燃烧时剩下的长度y (cm)是燃烧时间x(h)的一次函数。
一次函数导学案(新部编)草案
教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校19．1．1 变量和常量编写: 刘莉蓉挂联领导：何俊平使用者：学习目标：1.能举出一些变化的实例，指出什么随着什么的变化而变化，初步感受事物的变化性和事物变化的依存性.2.经历由简单实际问题列解析式的过程，感受量与量之间的对立关系，知道什么是变量什么是常量.学习重点和难点：1.重点：变量的意义.2.难点：列解析式.助学单阅读感知：阅读P70—71回答下列问题：1.仔细阅读70页彩页说明“函数”的意义与作用：____________________________________________________________________________________________________2.完成P71页的中思考的四个问题,根据题目要求与提示列出式子.(1)__________________ _________________________________________________(2) __________________ _________________________________________________(3) __________________ ________________________________________________(4) __________________ ________________________________________________3.分析说明“变量”与“常量”___________________________________________________________________________________________________________________4.完成P97“思考”。
一次函数教案(导学案)
教案一次函数的图像和性质（新授课）1. 重点：一次函数图象和性质的探究与简单运用．2. 难点：一次函数图象和性质的探究．【课时安排】一课时【教学设计】课前延伸1. 画一次函数)0(≠+=k b kx y 的图像，你认为最少取几个点？为什么？取什么样的点教容易画图？2. 一次函数25+=x y 的图像是一条经过第 象限的直线，它与x 轴的交点是 ，于y 轴的交点是 .3. 一次函数3+=kx y 的图像经过点（-1,5），则k = .〖设计说明〗设计基本题型，引导学生去预习要学习的内容，完成习题.课内探究一、 新课引入请你举出一个正比例函数.教师也举出一个正比例函数2y x =-．问题：你能从正比例函数2y x =-中获得哪些信息？教师把2y x =-改成2y x =又如何呢？〖设计说明〗简单从正比例函数的图象（形状，图象经过的象限，性质）复习.要求学生画出正比例函数2y x =-的图象，此时教师关注学生是否从两点（任一点和原点）来确定图象．教师把上述正比例函数解析式右边加上一个常数3，问：这又是什么函数？问：正比例函数是一次函数吗？（顺便说明正比例函数是一次函数的特殊情形）二、 探究一次函数图像和性质教师要求学生在同一坐标系内画出一次函数23y x =-+的图象.教师在表格中加上2y x =-.问题1：(1)当横坐标相等时，比较2y x =-与23y x =-+的各点坐标，你会发现什么？说明了什么？(2)那么2y x =-上所有的点都向上平移3个单位后都在23y x =-+的图象上吗？．〖设计说明〗由点的平移过渡到线的平移，学生便于理解，便于新知的形成.(3)让学生在同一坐标系中画出一次函数23y x =--，132y x =+，132y x =-的图象.〖设计说明〗让学生体会到用两点画一次函数图象的便捷性.问题2：(1) 直线23y x =--又怎样由直线2y x =-平移得到？（2）由此联想直线y kx b =+怎样由直线y kx =平移得到？教师补充：在画一次函数y kx b =+图象时其实也可以先画正比例函数y kx =的图象，然后向上平移b 个单位．思考：直线23y x =--又怎样由直线23y x =-+平移得到？问题3：比较23y x =-+与132y x =-的图象，它们还平行吗？那么132y x =+与132y x =-的图象呢？由此你能得到什么？ （也可以从倾斜程度的角度来说明）问题4：由这些函数图象联想：一次函数y kx b =+（k 、b 是常数，k ≠0）中，k 的正负对函数图象有什么影响？简单小结：根据k 相等，两直线平行，一次函数的增减性与正比例函数的性质是一致的，都是结合k 的正负考虑.问题5：观察32+-=x y 与132y x =+的图象，你会发现有什么共同之处？ 问题6：分别说出你所画函数图象经过的象限.试说出一次函数y kx b =+（k 、b 是常数，k ≠0，b ≠0）.教师简要说明数与形的结合辩证统一性，数形结合思想的重要作用.〖设计说明〗让学生在比较中形成认识上的冲突，关注到知识的联系与区别，便于新知的形成，锻炼了学生的归纳能力．同时又体现了数形结合的思想.另外通过特殊情况来联想一般情况，培养学生观察、交流、总结归纳的能力.练习：教师举一次函数34y x =-的解析式，提问：你能得到哪些信息？课后提升1．已知一次函数的图象与正比例函数3y x =-的图象平行，且经过点（0，-2），则该一次函数的解析式是 ．2．已知函数y kx b =+的图象如图：请画出函数y bx k =-的大致图象．3．已知一次函数()1321y k x k =-+-的图象经过一、三、四象限，则k 的取值范围是 ．〖设计说明〗锻炼学生综合运用知识的能力．通过本节课的学习你有哪些收获？课本120页5、10、11．〖设计说明〗让学生谈最终的收获，体现学习数学的价值．。
第十四章一次函数全章导学案
第十四章一次函数课题：变量与函数（1）主备人：初审人：终审人：中学理科教研组【导学目标】1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义。
2、学会用含一个变量的代数式表示另一个变量。
3、体会函数模型在数学中的应用。
【导学重点】了解常量与变量的意义。
【导学难点】较复杂问题中常量与变量的识别。
【导学过程】一、创设情境问题一：汽车以60千米／小时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时．１、请同学们根据题意填写下表：t/时12345ts/千米２、在以上这个过程中，变化的量是_____________．不变化的量是__________.３、试用含t的式子表示s: s=________,t的取值范围是 _________ .这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程．二、合作探究，（一）问题探究：问题二：每张电影票的售价为10元，如果早场售出票150张，午场售出205张，晚场售出310张，三场电影的票房收入各多少元？设一场电影售票x张，票房收入y元． １、请同学们根据题意填写下表：售出票数（张）早场150午场206晚场310x收入y (元)2、在以上这个过程中，变化的量是_____________．不变化的量是__________．3、试用含x的式子表示y: y=______ ,x的取值范围是 .这个问题反映了票房收入_________随售票张数_________的变化过程．问题三：在一根弹簧的下端悬挂重物，改变并记录重物的质量，观察并记录弹簧长度的变化，探索它们的变化规律．如果弹簧原长10cm ， 每1kg 重物使弹簧伸长0．5cm，设重物质量为mkg，受力后的弹簧长度为L cm.1、请同学们根据题意填写下表：所挂重物（kg）12345m受力后的弹簧长度L（cm）2、在以上这个过程中，变化的量是_____________．不变化的量是__________．3、试用含m的式子表示L: L=____________ ,m的取值范围是 .这个问题反映了_________随_________的变化过程．问题四：要画一个面积为10cm2的圆，圆的半径应取多少？圆的面积为20cm2呢？30 cm2呢?怎样用含有圆面积Ｓ的式子表示圆半径r？１、请同学们根据题意填写下表：(用含 的式子表示）面积s（cm2）102030s半径r(cm)２、在以上这个过程中，变化的量是_____________．不变化的量是__________．３、试用含s的式子表示r．r=_________，s的取值范围是 .这个问题反映了___ _ 随_ __的变化过程．问题五：用10m长的绳子围成长方形，试改变长方形的长度，观察长方形的面积怎样变化．记录不同的矩形的长度值，计算相应的矩形面积的值，探索它们的变化规律。
19.2 一次函数 导学案
第6课时 19.2.1 正比例函数 导学案（1）【学习目标】1．理解正比例函数的概念；2．经历用函数解析式表示函数关系的过程，进一步 发展符号意识； 3.会用待定系数法求正比函数的解析式。
【学习重点】正比例函数的概念、待定系数法 【学习难点】待定系数法求正比函数的解析式 一、学前准备1996年，鸟类研究者在芬兰给一只燕鸥（候鸟）套上标志环；大约128天后，人们在2.56万千米外的澳大利亚发现了它．(1)这只百余克重的小鸟大约平均每天飞行多少千米?(2) 这只燕鸥的行程y(单位：千米)与飞行时间x(单位：天)之间有什么关系？ (3)这只燕鸥飞行一个半月（一个月按30天计算．）的行程大约是多少千米？二、探索思考探究（一）1、下列问题中，变量之间的对应关系是函数关系吗？如果是，请写出函数解析式． （1）圆的周长 l 随半径 r 的变化而变化；（2）铁的密度为7.8 g/cm3，铁块的质量 m （单位：g ）随它的体积 V （单位：cm3）的变化而变化；（3）每个练习本的厚度为0.5 cm ，练习本摞在一起的总厚度 h （单位：cm ）随练习本的本数 n 变化而变化；（4）冷冻一个0 ℃ 的物体，使它每分下降2 ℃，物体的温度 T （单位：℃）随冷冻时间 t （单位：min ）的变化而变化．认真观察得到四个函数解析式，这些函数有什么共同点．2、一般地，形如 （k 是常数，k ≠0）的函数，叫做 ，其中k 叫做 ．练习1、下列函数中哪些是正比例函数？ （填序号） （1）y =2x （2）y = x+2 （3）3xy =（4）x y 3= （5）y=x 2+1 （6）121+-=x y三、典例分析 例1、（1）若 y =5x 3m-2是正比例函数， 求 m 的值（2）若32)2(--=mx m y 是正比例函数， 求 m 的值（3）若)2(32-+=-m x y m 是正比例函数，求 m 的值例2、已知正比例函数当自变量x 等于-4时，函数y 的值等于2。
《6.2一次函数》导学案
《6.2一次函数》导学案学习目标：1、理解一次函数和正比例函数的概念，能根据所给条件写出简单的一次函数表达式，发展数学应用能力2、经历一般规律的探索过程，发展抽象思维能力二、重点与难点重点：理解一次函数和正比例函数的概念；能根据所给条件写出简单的一次函数表达式难点：能根据所给条件写出简单的一次函数表达式,发展抽象思维能力前置学习：1.一般地，在某个变化过程中，有_______x和y, 如果给定一个x值,相应地就___________,那么我们称_____是________的函数.2.设地面气温是20℃，如果高度h每升高1千米，气温t就下降6℃，则______是_____的函数，其中_____是自变量，______是因变量.两个变量之间的关系式是__________________,当高空某位置的气温是－8℃时，这个位置的高度是_________米.二．探索新知：y与之间的函数关系式，并分别指出自变量与因变1.做一做：写出下列各题x中x量.（1）汽车以60千米∕时的速度匀速行驶，行驶路程y（千米）与行驶时间x（时）之间的关系；（2）圆的面积y(平方厘米)与它的半径x（厘米）之间的关系.（3）一棵树高50厘米，如果它每个月长高2厘米，x个月后这棵树的高度为y （厘米）.2.想一想：你列出的函数关系式及复习回顾中的函数关系式，它们的一般形式可以概括为),(o k b k b kx y ≠+=为常数，的形式吗？3.概念的生成：若两个变量y x , 间的关系式可以表示成),(o k b k b kx y ≠+=为常数，的形式，则称y 是x 的一次函数．．．．，特别地，当b 是0时，称y 是x 的正比例函数．．．．．. 4.思一思：（1）类比一元一次方程，你是如何理解“一次”的呢？理解一次函数的概念特别应注意什么？（2）你如何理解一次函数与正比例函数之间的关系？(3)前面你列出的函数关系式中哪些是一次函数？哪些是正比例函数？（三）学以致用：1.在下列函数中，x 是自变量，y 是因变量，哪些是一次函数？哪些是正比例函数？① 2x y =；②xy 5-=；③x y 2=；④13+-=x y . 2.已知函数3)3(2+-=-x x m y 是一次函数，试求m 的值及一次函数的解析式.3.已知一次函数关系式为y=kx+2，当x=2时y 值为4，求k 的值及一次函数关系式。
数学20章《一次函数》导学案.doc
数学20章《一次函数》导学案.doc1、导学引领，树梁中学对标检测”尝试教学导学案八年级上第二十章《一次函数》授课教师：主备教师：王继勇审核校对：初四数学组【学习目标】〔1〕理解具体问题中的数量关系及改变规律；〔2〕了解常量、变量的意义；〔3〕了解函数的概念及三种表示方法；〔4〕把握函数的自变量取值范围、会求出函数值；〔5〕把握一次函数及表达式；〔6〕把握一次函数的图象及性质；〔7〕理解正比例函数；〔8〕能依据一次函数的图象求二元一次方程组的近似解；〔9〕能用一次函数解决实际问题.【学问梳理】一、学问要点：1、一次函数：形如y=kx+b(k≠0,k,b 为常数)的函数。
留意：〔1〕k≠0,否则自变量x的最高次项的系数不为1；〔2〕当b=0时，2、y=kx，y叫x的正比例函数。
2、图象：一次函数的图象是一条直线，〔1〕两个常有的特别点：与y轴交于〔0，b〕；与x轴交于〔-，0〕〔2〕由图象可以知道，直线y=kx+b与直线y=kx平行，例如直线：y=2x+3与直线y=2x-5都与直线y=2x平行。
3．求一次函数解析式的方法求函数解析式的方法主要有三种(1)由已知函数推导或推证(2)由实际问题列出二元方程，再转化为函数解析式，此类题一般在没有写出函数解析式前无法〔或不易〕推断两个变量之间具有什么样的函数关系。
(3)用待定系数法求函数解析式。
“待定系数法”的基本思想就是方程思想，就是把具有某种确定形式的数学问题，通过引入一些待定的系数3、，转化为方程〔组〕来解决，题目的已知恒等式中含有几个等待确定的系数，一般就需列出几个含有待定系数的方程，本单元构造方程一般有以下几种状况：①利用一次函数的定义构造方程组。
②利用一次函数y=kx+b中常数项b恰为函数图象与y轴交点的纵坐标，即由b来定点；直线y=kx+b 平行于y=kx，即由k来定方向。
③利用函数图象上的点的横、纵坐标满足此函数解析式构造方程。
④利用题目已知条件直接构造方程。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
19．1．1 变量和常量学习目标：1.能举出一些变化的实例，指出什么随着什么的变化而变化，初步感受事物的变化性和事物变化的依存性.2.经历由简单实际问题列解析式的过程，感受量与量之间的对立关系，知道什么是变量什么是常量.学习重点和难点：1.重点：变量的意义.2.难点：列解析式.阅读感知：阅读P70—71回答下列问题：1.仔细阅读70页彩页说明“函数”的意义与作用：____________________________________________________________________________________________________2.完成P71页的中思考的四个问题,根据题目要求与提示列出式子.(1)__________________ _________________________________________________(2) __________________ _________________________________________________(3) __________________ ________________________________________________(4) __________________ ________________________________________________3.分析说明“变量”与“常量”___________________________________________________________________________________________________________________4.完成P97“思考”。
研习单交流探究:1.在小组内交流:你所知道的变量和常量,并举出和书上不一样的例子.2.思考行程问题中路程.速度和时间三者的关系:（1）当速度v保持不变时，行走的路程s的长短是随时间t的变化而变化，那么，（）是常量，而（）和（）是变量；（2）当路程s是个定值时，行走的时间t是随速度v的变化而变化的，那么，（）是常量，而（）和（）是变量。
注：变量和常量往往是相对的，相对于某一变化过程。
比如s、v、t三者之间，在不同的研究过程中，作为变量与常量的“身份”是可以相互转换的。
运用展示:一.1．关于l=2πr，下列说法正确的是（）A．2为常量，π，l，r为变量 B．2π为常量，l，r为变量C．2，l为常量，π，r为变量 D．2，r为常量，π，l为变量2．摄氏温度C与华氏温度F之间的对应关系为5(F-32)9C=℃，则其中的变量是（），常量是（）。
3．在△ABC中，它的底边是a，底边上的高是h，则三角形的面积ahS21=，当底边a的长一定时，在关系式中的常量是（），变量是（）。
4．设圆柱的底面半径R不变，圆柱的体积V与圆柱的高h的关系式是：（），其中（）是常量，（）是变量。
5．齿轮每分钟120转，如果n表示转数，t表示转动时间，那么用n表示t的关系是：（），其中（）为变量，（）为常量．二.1、写出下列各问题中的关系式，并指出其中的常量与变量。
（1）甲乙两地相距1000千米，一人骑自行车以15千米/小时的速度从甲地前往乙地，用行驶时间t(小时)表示自行车离乙地的距离S(千米)（2）直角三角形中一个锐角α与另一个锐角β之间的关系．（3）一盛满30吨水的水箱，每小时流出0.5吨水，试用流水时间t•（小时）表示水箱中的剩水量y（吨）．（4）小军用50元钱去买单价是8元的笔记本，则他剩余的钱Q•（元）与他买这种笔记本的本数x 之间的关系归纳延伸:变量常量变量和常量的关系检测单内化训练:1．汽车以60千米/时的速度匀速行驶，⑴行驶2小时，行驶里程为千米；⑵行驶5小时，行驶里程为千米；⑶行驶t小时，行驶里程为千米；⑷行驶里程为s千米，行驶时间为t小时，用含t的式子表示s，s= .分析此解析式中的变量：_____________,常量:__________2.李明家住在美丽的草原，养牛是家里收入的来源.李明家原有存款5万元，估计每卖掉一头牛增加存款0.2万元，(1)如果卖掉5头牛,李明家的存款是万元；(2)如果卖掉10头牛，李明家的存款是万元；(3)如果卖掉x头牛,李明家的存款是万元;(4)李明家的存款为y万元，卖掉的牛为x头，用含x 的式子表示y，y= . 此解析式中的变量：_____________,常量:__________3.长方形的宽为4米，(1)长为5米时，长方形的面积为平方米；(2)长为10米时，长方形的面积为平方米；(3)长为x米时，长方形的面积为平方米;(4)长方形的面积为y平方米，长为x米，用含x的式子表示y，y= ，其中，变量是，常量是.4.一个圆的面积为S平方厘米，它的半径为r厘米，用含r的式子表示S，S= ，其中，变量是，常量是.5．写出下列各问题中所满足的关系式，并指出各个关系式中，哪些量是变量，哪些量是常量？（1）用总长为60m的篱笆围成矩形场地，求矩形的面积S（m2）与一边长x(m)之间的关系式；（2）购买单价是0.4元的铅笔，总金额y（元）与购买的铅笔的数量n(支)的关系；（3）运动员在4000m一圈的跑道上训练，他跑一圈所用的时间t(s)与跑步的速度v(m/s)的关系；6.分别指出下列各式中的常量与变量.a.圆的面积公式S=πr2; 其中，变量是，常量是；b,正方形的周长L=4a; 其中，变量是，常量是；c.大米的单价为2.50元/千克，则购买的大米的数量x(kg)与金额与金额y的关系为y=2.5x.变量是，常量是；d.一个圆的半径为r厘米，它的面积为S平方厘米，用含S的式子表示r，r= 变量是，常量是.19．1．2 函数编写：刘莉蓉挂联领导：何俊平使用者：学习目标:1．函数概念以及自变量与函数值的关系。
2．会确定自变量取值范围。
学习重难点:函数概念；对函数中自变量取值范围的确定助学单知识链接:1．P71的每个问题中有几个变量；同一个问题中的变量之间有什么联系？（1）s=60t，当t=1，则s=60；当t=2，则s=120；……发现：当取定一个值时，就随之确定一个值。
（2）y=10x，当x=150，则y=1500；当x=205，则y=2050；……发现：当取定一个值时，就随之确定一个值。
（3）r=S，当S=10，则r= ；当S=20，则r=发现：当取定一个值时，就随之确定一个值。
（4）C=10+0.5m，当m=1，则l=10.5；当m=10，则l=发现：当取定一个值时，就随之确定一个值。
（5）S=x（5-x），当x=4，则S= ；当x=3，则S= ；当x=2.5，则S= ，当x=2，则S=发现：每当长方形长x取定一个值时，面积S就随之。
阅读感知:上面每个问题中的两个变量互相联系，当其中一个变量取定一个值时，另一个变量就。
2．认真阅读课本72.73页的“思考”．按要求完成思考题。
【概念】一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有确定的值与其对应，那么我们就说x是，y是x的．如果当x=a时y=b，那么b叫做当自变量的值为a时的．【练一练】在第1题中的关系式是函数关系式．请同学们指出上述函数关系式的两个变量中哪个是自变量？哪个是这个自变量的函数？研习单交流探究:1．请同学们阅读课本73页，细心理解自变量、函数、函数值三个概念。
并完成74页探究题（1）问题：显示的数y是x的函数吗？为什么？（2）y是x的函数吗？若是，写出它的表达式（用含x的式子表示y).一辆汽车的油箱中现有汽油50L，如果不再加油，那么油箱中的油量y（单位：L）随行驶里程x（单位：km）的增加而减少，平均耗油量为0.1L/km．（1）写出表示y与x的函数关系的式子．（2）指出自变量x的取值范围．（3）汽车行驶200km时，油箱中还有多少汽油？运用展示:1.下列各式中，y是x的函数的有：①4x-3y=2，②y=∣x∣，③y=，④y2=2x，⑤x =∣y∣2．全年级每个同学需要一本代数教科书，书的单价为6元，则总金额y(元)与学生数n(个)的关系是 。
其中 是 的函数， 是自变量。
3．学校计划购买50元的乒乓球，则所购买的乒乓球总数y (个)与单价x (元)的函数关系式是 ；其中 是 的函数， 是自变量。
4．已知三角形底边长为4，高为x ，三角形的面积为y ，则y 与x 的函数关系式为_______________；其中 是 的函数， 是自变量。
5．骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，自变量是（ ） A 、沙漠 B 、体温 C 、时间 D 、骆驼检 测 单归纳延伸:1.:函数 自变量 , 函数值2:函数值及自变量取值范围:函数自变量的取值：一是要符合 意义； 二是要使 有意义；(1).当含自变量的式子是 时，函数自变量取值范围 ． (2).当含自变量的式子是 时，函数自变量取值范围 ． (3).当含自变量的式子是 时，函数自变量取值范围 ． (4) 当自变量是 的数量时,函数自变量的取值必须 内化训练:1．已知函数y=x 2－x －2当x=2时，函数值为 。
2．当x= 时，函数y=3x-2与函数y=5x+1有相同的函数值。
3．函数3-=x y 的自变量x 的取值范围是 。
4．函数 431-+=x x y 中，自变量x 的取值范围是（ ） A ．34≠x B ．1≠x C ． 134-≠<x x 且 D ．34>x 5．函数112++--=x x x y 的自变量x 的取值范围为 （ ） A ．x≠1 B ．x ＞－1 C ．x≥－1 D ．x≥－1且 x≠16．汽车由北京驶往相距120千米的天津，它的平均速度是30千米/时，•则汽车距天津的路程S （千米）与行驶时间t （时）的函数关系及自变量的取值范围是（ • ） A ．S=120-30t （0≤t ≤4） B ．S=30t （0≤t ≤4） C ．S=120-30t （t>0） D ．S=30t （t=4）7．如图，在靠墙（墙长为18m ）的地方围建一个矩形的养鸡场，另三边用竹篱笆围成，.如果竹篱笆总长为35m ，求鸡场的一边长y （m ）与另一边长x （m ）的函数关系式，并求自变量的取值范围。
14.1.3函数的图象（1）编写： 刘莉蓉 挂联领导： 何俊平 使用者：学习目标：1.初步感知函数图象，根据函数图象，会由自变量的值求出函数值，会由函数值求出自变量的值，会对函数的变化情况作简单分析. 2.渗透数形结合思想，培养形象思维能力. 学习重点和难点：1.重点：感知函数图象.2.难点：根据函数图象，分析函数的变化情况.y x助 学 单知识链接:1.函数的表示方法有 2.解析式: 3.函数值及自变量取值范围应该注意的问题有:阅读感知：阅读P75—76（例2以上部分）回答下列问题：1．谈谈“函数图象”作用。