《运筹学》胡运权清华版-9-03网络计划的优化PPT资料31页
合集下载
清华大学运筹学教程胡运权主编课后习题答案
8 10
x1 , x2 0
目标函数最优值(下界)为:6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶 段法求解下列线性规划问题,并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0(, j 1,,3)
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
,
l.5 讨论c
,
上题(1)中,若目标函数变为max Z = d的值如何变化,使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述 线性规划问题,并对照指出单纯形表中的各 基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
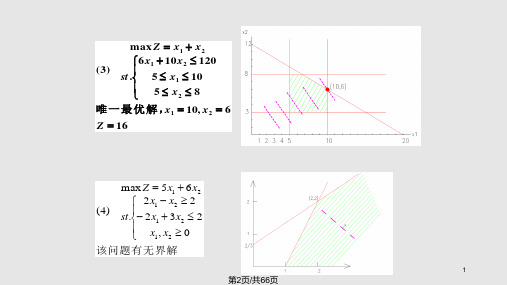
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
唯 一 最 优 解 ,x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2
清华大学《运筹学教程》胡运权主编课后习题答案
st
8x1 3x1
x2 x6
4x3 0
2 x5
10
x j 0(, j 1,,6)
基可行解
x1 x2 x3 x4 x5 x6 Z 0 3 0 0 3.5 0 3
0 0 1.5 0 8 0 3
0003500
page 10
0.7 0 0 0 2 2.2 2.2 10
5 13 April 2021
5 5 School of Management
运筹学教程
第一章习题解答
min Z 5x1 2x2 3x3 2x4
(2)
st
2x1x1 22x2x23xx33
4 x4 2 x4
7 3
x j 0, ( j 1,4)
x1 0 0 2/5
page 11 13 April 2021
基可行解
6 x2 2 x2
6 4
x1, x2 0
无穷多最优解,
x1
1, x2
1,Z 3
3是一个最优解
max Z 3x1 2x2
(2)
st.32xx11
x2 2 4x2 12
x1, x2 0
该问题无解
4
School of Management
运筹学教程
page 5 13 April 2021
a=3, j=5, k= -1.5
page 23 13 April 2021
23
School of Management
运筹学教程
第一章习题解答
1.9 若X(1)、X(2)均为某线性规划问题的
最优解,证明在这两点连线上的所有点也是
该问题的最优解。 max Z CT X
设X (1)和X (2)满足: AX b
运筹学胡运权PPT课件
第5页/共89页
§1多 阶段 决策 过程 的最 优化
2.多阶段决策问题举例
属于多阶段决策类的问题很多, 例如:
1)工厂生产过程:由于市场需 求是一随着时间而变化的因素,因此, 为了取得全年最佳经济效益,就要在 全年的生产过程中,逐月或者逐季度 地根据库存和需求情况决定生产计划 安排。
第6页/共89页
第24页/共89页
§2动 态规 划的 基本 概念 和基 本原 理
(1) 阶 段 指 标 函 数 ( 也 称 阶 段 效 应 ) 。 用
gk(sk,uk)表示第k段处于sk状态且所作决策 为uk(sk)时的指标,则它就是第k段指标函 数,简记为gk 。图7-1的gk值就是从状态 sk到状 态 sk+1的 距离。 譬如, gk(A,B1)=4, 即A到B1的距离为3。
第20页/共89页
§2动 态规 划的 基本 概念 和基 本原 理
(三)决策、决策变量和允许决策集合
所谓决策,就是确定系统过程发展的方 案。决策的实质是关于状态的选择,是决策者 从给定阶段状态出发对下一阶段状态作出的选 择。
用以描述决策变化的量称之决策变量和 状态变量一样,决策变量可以用一个数,一组 数或一向量来描述,也可以是状态变量的函数,
状态
x1
阶段1状x态 2
阶段2状x3态...状x态k
阶段k状x态k+1...状态
阶段n
状 态
T1
T2
Tk
xn
Tn xn+1
第4页/共89页
§1多 阶段 决策 过程 的最 优化
1.多阶段决策过程的最优化
动态规划方法与“时间”关系很密 切,随着时间过程的发展而决定各时段的 决策,产生一个决策序列,这就是“动态” 的意思。然而它也可以处理与时间无关的 静态问题,只要在问题中人为地引入“时 段”因素,就可以将其转化为一个多阶段 决策问题。在本章中将介绍这种处理方法。
2024版清华大学出版《运筹学》第三版完整版课件

要点三
金融服务与投资管理
在金融服务和投资管理中,存储论可用 于优化资金配置和投资组合,降低风险 和提高收益。例如,通过定期订货模型 的运用,可以制定合理的投资策略和资 产配置方案,实现资产的保值增值和风 险控制。
2024/1/28
31
07
排队论
2024/1/28
32
排队论的基本概念
2024/1/28
清华大学出版《运筹 学》第三版完整版课
件
2024/1/28
1
目录
2024/1/28
• 绪论 • 线性规划 • 整数规划 • 动态规划 • 图与网络分析 • 存储论 • 排队论
2
01
绪论
2024/1/28
3
运筹学的定义与发展
运筹学的定义
运筹学是一门应用数学学科,主要研究如何在有限资源下做出最优决策,以最 大化效益或最小化成本。
目标函数
表示决策变量的线性函数,需要最大化或最 小化。
约束条件
表示决策变量需要满足的线性等式或不等式。
2024/1/28
决策变量
表示问题的未知数,需要在满足约束条件的 情况下求解目标函数的最优值。
8
线性规划问题的图解法
01
可行域
表示所有满足约束条件的决策变量构成的集合。
2024/1/28
02
目标函数等值线
2024/1/28
34
单服务台排队系统
M/M/1排队系统
到达间隔和服务时间均服从负指数分布的单服务台排队系 统。
M/D/1排பைடு நூலகம்系统
到达间隔服从负指数分布,服务时间服从确定型分布的单 服务台排队系统。
表格。
10
运筹学第九章网络计划胡运权

b
3
0.445 g
4
0.445
c
2
0.111 h
4
0.111
d
2
0.028 i
2
0.028
e
1
0.028
15
二、时间参数
1、最早时间
从网络的发点开始,按顺序计算出每个工序的最早开始时间
(ES )和最早结束时间(EF)
ttEESS
(1, (i,
j) j)
0
maxt k
EF
(k , i)
tEF (i, j) tES (i, j) t(i, j)
运筹学--线性规划
25
例9.4 某公司装配一条新的生产线,具体过程如表1,求:完成 此工程的最少时间,关键路线及相应的关键工序,各工序的最 早开始时间和非关键工序在不影响工程完成时间的前提下,其 开始时间与结束时间可以推迟多久?
26
工序代号 a b c d e f g h i j
工序内容 生产线设计 外购零配件 下料、锻件 工装制造1 木模、铸件 机械加工1 工装制造2 机械加工2 机械加工3
9
在绘制统筹方法的网络图时,要注意图中不能有缺口和回路。
a
2
1 60
b 15
5
e
13 c
8 f
7
h 5
8
d 3
4
10 g
38
16 6
图4
避免交叉
节点标号:j > i i
j
10
第二节 时间参数的计算
在绘制出网络图之后,我们可以由网络图求出: 1、完成此工程项目所需的最少时间。 2、每个工序的开始时间与结束时间。 3、关键路线及其应用的关键工序。 4、非关键工序在不影响工程的完成时间的前提下,其开始时 间与结束时间可以推迟多久。
运筹学课程09-对策论(胡运权 清华大学)

18
设s i是第i个局中人的一个策略,则n个局中人的策略形成的 策略组合s=(s1,s2,…,sn) 就是一个局势。若记S为全部局势的集合,则 S=S1×S2×…×Sn
NEUQ
当一个局势s出现后,应该为每一局中人 i规定一个赢得值 (或所失值)Hi(s)。显然,Hi(s)是定义在S上的函数,称为局中 人i的赢得函数。在“齐王赛马”中,局中人集合I={1,2},齐 王和田忌的策略集可分别用 S1 {1 , 2 ,L , 6 }、S2 {1 , 2 ,L , 6 } 表示。这样 , 齐王的任一策略α i 和田忌的任一策略β j 就构成 了—个局势sij,如果α1=(上,中,下),βl=(上,中,下).则在 局势s11下,齐王的赢得为H1(s11)=3,田忌的赢得为H2(s11)= -3 当局中人、策略集和赢得函数这3个要素确定后,一个对策 模型也就给定了。 19
矩阵对策问题解的假设:
具有鞍点的矩阵对策
例:设有一矩阵博弈G={S1,S2;H},其中
-6 1 -8 3 2 4 9 - 1 - 10 -3 0 6
26
H=
NEUQ 如果双方部不想冒险、都不存在侥幸心理,而是考虑到 对方必然会设法使自己所得最少这一点,就应该从各自 可能出现的最不利的情形中选择一个最有利的情形作为 决策的依据,这就是所谓“理智行为”,也是对策双方 实际上可以接受并采取的一‘种稳妥的方法。 从各自可能出现的最不利的情形中选择一个最有利的 情形作为决策的依据
6
约翰· 福布斯· 纳什
NEUQ
7
NEUQ
《美丽心灵》是一部关于一个真实天才的极富人 性的剧情片。故事的原型是数学家小约翰-福布斯 -纳什(Nash),普林斯顿大学的著名教授,诺贝尔 经济学奖的获得者(1994年),他在博弈理论方面 的巨大发现甚至改变了我们的日常生活。但另一 方面,纳什也是一个悲剧人物,他的一生为精神 分裂症所困。在历经苦痛的人生里,纳什一方面 在运用自己那优美绝伦的大脑,另一方面也在与 他的大脑进行着顽强的抗争。最终理性为他带来 了心灵的和平,纳什终于摘取了科学事业上的桂 冠。
设s i是第i个局中人的一个策略,则n个局中人的策略形成的 策略组合s=(s1,s2,…,sn) 就是一个局势。若记S为全部局势的集合,则 S=S1×S2×…×Sn
NEUQ
当一个局势s出现后,应该为每一局中人 i规定一个赢得值 (或所失值)Hi(s)。显然,Hi(s)是定义在S上的函数,称为局中 人i的赢得函数。在“齐王赛马”中,局中人集合I={1,2},齐 王和田忌的策略集可分别用 S1 {1 , 2 ,L , 6 }、S2 {1 , 2 ,L , 6 } 表示。这样 , 齐王的任一策略α i 和田忌的任一策略β j 就构成 了—个局势sij,如果α1=(上,中,下),βl=(上,中,下).则在 局势s11下,齐王的赢得为H1(s11)=3,田忌的赢得为H2(s11)= -3 当局中人、策略集和赢得函数这3个要素确定后,一个对策 模型也就给定了。 19
矩阵对策问题解的假设:
具有鞍点的矩阵对策
例:设有一矩阵博弈G={S1,S2;H},其中
-6 1 -8 3 2 4 9 - 1 - 10 -3 0 6
26
H=
NEUQ 如果双方部不想冒险、都不存在侥幸心理,而是考虑到 对方必然会设法使自己所得最少这一点,就应该从各自 可能出现的最不利的情形中选择一个最有利的情形作为 决策的依据,这就是所谓“理智行为”,也是对策双方 实际上可以接受并采取的一‘种稳妥的方法。 从各自可能出现的最不利的情形中选择一个最有利的 情形作为决策的依据
6
约翰· 福布斯· 纳什
NEUQ
7
NEUQ
《美丽心灵》是一部关于一个真实天才的极富人 性的剧情片。故事的原型是数学家小约翰-福布斯 -纳什(Nash),普林斯顿大学的著名教授,诺贝尔 经济学奖的获得者(1994年),他在博弈理论方面 的巨大发现甚至改变了我们的日常生活。但另一 方面,纳什也是一个悲剧人物,他的一生为精神 分裂症所困。在历经苦痛的人生里,纳什一方面 在运用自己那优美绝伦的大脑,另一方面也在与 他的大脑进行着顽强的抗争。最终理性为他带来 了心灵的和平,纳什终于摘取了科学事业上的桂 冠。
第3节 最短路问题__运筹学__胡运权__清华大学出版社

0000
v2 6 0
2
-1 -5 -5 -5
v3
-3 0 -5
1
-2 -2 -2 -2
v4 8
0
2
3 -7 -7 -7
v5
-1
0
1 -3 -3
v6
1017
-1 -1 -1
v7
-1
0
5 -5 -5
v8
-3
-5 0
66
最短路算法—Warshall-Flod方法
v2
-1
-5
6
2
-1 -3
0 v1
-2
v3
2 [3, v1]
3
v3 6
12
v4
10
[1, v1]
[6, v2]
v5 2 v9
6 4 10 3
3
v8
v6 2
[10, v5]
4
v7
[9, v5]
[5, v3]
[6, v2]
[0, v1]
v1
16 v22 [3 v1]3v3 6
12
v5 2 v9
6 4 10 3
3 [12, v5]
v8
4
v4
10
v[34,v2/
v4]
5
[8,v5]
v6 5
[0,v1] 3
13
1
7
v4
5
[3,v1]
v5[7,v3]
[13,v6]
v7
[课堂练习] 无向图情形
答案(2):
v2 [2,v1]
v1
2
2
5
7
v[34,v2/
v4]
5
[8,v5]
16738-数学建模-运筹学PPT完整版胡运权

线性规划问题的数学模型
Page 18
3. 线性规划数学模型的一般形式
目标函数: max (min) z c1 x1 c2 x2 cn xn
a11 x1 a12 x2 a1n xn ( ) b1
约束条件: am1 x1 am2 x2 amn xn ( ) bm
x1 0 xn 0
a11 a1m
B
(
p1
pm
)
am1
amm
称 B中每个列向量Pj ( j = 1 2 … … m) 为基向量。与基向量Pj
对应的变量xj 为基变量。除基变量以外的变量为非基变量。
线性规划问题的数学模型
Page 29
基解:某一确定的基B,令非基变量等于零,由约束条件
方程②解出基变量,称这组解为基解。在基解中变量取非0
(5) 目标函数是最小值,为了化为求最大值,令z′=-z,得到max z′=-z,即当z达到最小值时z′达到最大值,反之亦然;
线性规划问题的数学模型
标准形式如下:
max Z
2 x1
x2
3(
x
3
x3)
0x4
0x5
5 x1
x2
(
x
3
x3)
x4
7
x1 x2 ( 5x1 x2
x3 2(
x
3
x3) x3)
真实系统
数据准备
系统分析 问题描述
模型建立 与修改
模型求解 与检验
结果分析与 实施
本课程授课方式与考核
讲授为主,结合习题作业
学科总成绩
平时成绩 (40%)
期末成绩 (60%)
课堂考勤 (50%)
平时作业 (50%)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 4
78 5
(天数)
9 10 11
9
1 6
20
15
10
9
10 7
9
10
5
0
(人数)
二、最低成本日程---工期-成本优化问题
(一)工程费用
费用
总费用 间接费用
O
最低成本日程
直接费用 工期
(二)工作 ( i, j )的直接费用与工作时间关系
直接费用
mij
极限
假定线性
Mij
正常
dij
Dij
工时
Cij =
16 70 2.5
18 102
1
18 48
2
24 103 1.5
20
90 2.5
18
54
/
10
68 0.5
间接费用:180(百元),每提前1天可省3.3 (百元)。 求:最低成本日程
解: 第一次调整
①选工序(1,3),可缩12天。
22 24 2
4 18
1
缩2160天即可
6
18 3
18 T=64(天) 5 24
(3)、在技术、章程允许条件下,可适当延长 时差大的工作的工时,或切断某些非关键工 作,以减少日总需求量。
根据日需求分时间段
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3
5
9 2
15
0
10
9 5
5
1
0
(人数)
按时差将工作排序
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
②
24 1
20
22
2
4
26
3
5
24
18 6 T=64(天)
18
③ 总直接费用 478+10×1=488(百元)
间接费用 180 -33=147(百元)
总费用
488 +147=635(百元)
第二次调整
①,
1246 1346
同时缩短
(1,3), (1,2) 同时缩小 2.5+1=3.5 可选方案: (1,3), (2,4) 同时缩小 1+2=3
3
第二次调整结果
23 4 56 7 8
9
7
5
2
3
5
4
4
(天数)
9 10 11
1 6
20
20
18
15
14
10
9
10
5
1
0
(人数)
以后各时间段类似处理,经过几次调整, 可得结果图。此时人力日需求量已满足不 超过10人的限制。总工期未受影响。必要 时总工期可能会延迟。
01
6 1
3
23 4 56
7 2
5 3
按时差将工作排序
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3假设:已进行5中非关键工作 6
3
4 不4允许中断
工作(1,4) , 总时差1,编为1#
20
19 20
18
工作(2,3) , 总时差0,编为2#
15
10
9
工作(1,6) ,5总时差5,编为3#
5
1
0
01
6 1
2 (1,3)(2,4) 2,4 2 494 140.4 634.4 62*
3 (3,4)(2,4) 2,2 2 501 133.8 634.8 60
mij - Mij Dij - dij
1500-1000
= 5-3 =250元/天
Cij:单位工时的直接费用变化率(成本斜率)
(三)、计算最低成本日程的基本步骤: (1)、选关键工序中成本斜率最低工序赶工, 确定可缩天数。
(2)、重新计算网络计划关键路线。
(3)、计算相应总费用
例:已知网络计划
2 22
4
24
26 1
30
3
5
24
18 6 T=74(天)
18
工序 正常工时 工时 费用
(1,2) 24 50 (1,3) 30 90 (2,4) 22 40 (3,4) 26 100 (3,5) 24 80 (4,6) 18 54 (5,6) 18 64 总直接费用 478
极限工时 工时 费用 Cij百元/天
18
15
10
9
5
0
(人数)
5 1
01
6 1
3
根据日需求分时间段
23 4 56 7 8
9
7
5
2
3
5
4
4
(天数)
9 10 11
1 6
20
19 20
18
15
10
9
5
0
(人数)
5 1
注意:如果已进行中非关键工作不允许 中断,则编号要优先考虑,把它们按照新的 总时差与最早开始时间之和的递增顺序排列。 否则同于第一段的编号规则。
间接费用 140.4–3.3×2=133.8(百元)
总费用
634.8(百元)
18
2
4
24
24 1
18
3
5
24
不能缩短,计算结束
18 6
18
计算 工序名称
可 缩短
实际 总 缩短 直接
过程
天数 天数 费用
间接 费用
总 成本
总 工期
0/
/ / 478 180 658 74
1 (1,3) 12 10 488 147 635 64
9
6
7
5
1
1
2
3
5
6
3
44
20
18
15
10
5 0
(人数)
19 工作2 (1,2) , 总时差0,编为1#
工作0 (1,49) , 总时差1,编为2# 工作(1,6) , 总时5 差7,编为1 3#
01
6 1
3
23
7 2
4
第一次调整结果
4 56 7 8
9
5
3
5
4
(天数)
9 10 11
1 6
20
19 20
总费用
634.4(百元)
第三次调整
①,
1246 1346
同时缩短
(3,4), (1,2) 同时缩小 1.5+2.5=4
可选方案:
(3,4), (2,4) 同时缩小 1.5+2=3.5
确定应在(3,4)、(2,4)各缩2天。
②
24 1
18
18
2
4
24
3
5
24
18 6 T=60(天)
18
③ 总直接费用 494+3.5×2=501(百元)
一、有限资源的合理利用
9 4
6 12
7 2
2
5 3
3
人数
天数 1
54 6
3 3
4
4 (单位:天)
3
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3
5
6
3
44
20
18 19 2
15
0
10
9 5
5
1
0
(人数)
调整的基本原则是:
(1)、尽量保证关键工作的日资源需求量。
(2)、利用非关键工作的时差错开各工作的 使用资源时间
(3,4), (1,2) 同时缩小 1.5+2.5=4 (3,4), (2,4) 同时缩小 1.5+2=3.5 确定应在(1,3)、(2,4)各缩2天。
②
24 1
18
20
2
4
26
3
5
24
18 6 T=62(天)
18
③ 总直接费用 488+3×2=494(百元)
间接费用 147 –3.3×2=140.4(百元)
78 5
(天数)
9 10 11
9
1 6
20
15
10
9
10 7
9
10
5
0
(人数)
二、最低成本日程---工期-成本优化问题
(一)工程费用
费用
总费用 间接费用
O
最低成本日程
直接费用 工期
(二)工作 ( i, j )的直接费用与工作时间关系
直接费用
mij
极限
假定线性
Mij
正常
dij
Dij
工时
Cij =
16 70 2.5
18 102
1
18 48
2
24 103 1.5
20
90 2.5
18
54
/
10
68 0.5
间接费用:180(百元),每提前1天可省3.3 (百元)。 求:最低成本日程
解: 第一次调整
①选工序(1,3),可缩12天。
22 24 2
4 18
1
缩2160天即可
6
18 3
18 T=64(天) 5 24
(3)、在技术、章程允许条件下,可适当延长 时差大的工作的工时,或切断某些非关键工 作,以减少日总需求量。
根据日需求分时间段
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3
5
9 2
15
0
10
9 5
5
1
0
(人数)
按时差将工作排序
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
②
24 1
20
22
2
4
26
3
5
24
18 6 T=64(天)
18
③ 总直接费用 478+10×1=488(百元)
间接费用 180 -33=147(百元)
总费用
488 +147=635(百元)
第二次调整
①,
1246 1346
同时缩短
(1,3), (1,2) 同时缩小 2.5+1=3.5 可选方案: (1,3), (2,4) 同时缩小 1+2=3
3
第二次调整结果
23 4 56 7 8
9
7
5
2
3
5
4
4
(天数)
9 10 11
1 6
20
20
18
15
14
10
9
10
5
1
0
(人数)
以后各时间段类似处理,经过几次调整, 可得结果图。此时人力日需求量已满足不 超过10人的限制。总工期未受影响。必要 时总工期可能会延迟。
01
6 1
3
23 4 56
7 2
5 3
按时差将工作排序
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3假设:已进行5中非关键工作 6
3
4 不4允许中断
工作(1,4) , 总时差1,编为1#
20
19 20
18
工作(2,3) , 总时差0,编为2#
15
10
9
工作(1,6) ,5总时差5,编为3#
5
1
0
01
6 1
2 (1,3)(2,4) 2,4 2 494 140.4 634.4 62*
3 (3,4)(2,4) 2,2 2 501 133.8 634.8 60
mij - Mij Dij - dij
1500-1000
= 5-3 =250元/天
Cij:单位工时的直接费用变化率(成本斜率)
(三)、计算最低成本日程的基本步骤: (1)、选关键工序中成本斜率最低工序赶工, 确定可缩天数。
(2)、重新计算网络计划关键路线。
(3)、计算相应总费用
例:已知网络计划
2 22
4
24
26 1
30
3
5
24
18 6 T=74(天)
18
工序 正常工时 工时 费用
(1,2) 24 50 (1,3) 30 90 (2,4) 22 40 (3,4) 26 100 (3,5) 24 80 (4,6) 18 54 (5,6) 18 64 总直接费用 478
极限工时 工时 费用 Cij百元/天
18
15
10
9
5
0
(人数)
5 1
01
6 1
3
根据日需求分时间段
23 4 56 7 8
9
7
5
2
3
5
4
4
(天数)
9 10 11
1 6
20
19 20
18
15
10
9
5
0
(人数)
5 1
注意:如果已进行中非关键工作不允许 中断,则编号要优先考虑,把它们按照新的 总时差与最早开始时间之和的递增顺序排列。 否则同于第一段的编号规则。
间接费用 140.4–3.3×2=133.8(百元)
总费用
634.8(百元)
18
2
4
24
24 1
18
3
5
24
不能缩短,计算结束
18 6
18
计算 工序名称
可 缩短
实际 总 缩短 直接
过程
天数 天数 费用
间接 费用
总 成本
总 工期
0/
/ / 478 180 658 74
1 (1,3) 12 10 488 147 635 64
9
6
7
5
1
1
2
3
5
6
3
44
20
18
15
10
5 0
(人数)
19 工作2 (1,2) , 总时差0,编为1#
工作0 (1,49) , 总时差1,编为2# 工作(1,6) , 总时5 差7,编为1 3#
01
6 1
3
23
7 2
4
第一次调整结果
4 56 7 8
9
5
3
5
4
(天数)
9 10 11
1 6
20
19 20
总费用
634.4(百元)
第三次调整
①,
1246 1346
同时缩短
(3,4), (1,2) 同时缩小 1.5+2.5=4
可选方案:
(3,4), (2,4) 同时缩小 1.5+2=3.5
确定应在(3,4)、(2,4)各缩2天。
②
24 1
18
18
2
4
24
3
5
24
18 6 T=60(天)
18
③ 总直接费用 494+3.5×2=501(百元)
一、有限资源的合理利用
9 4
6 12
7 2
2
5 3
3
人数
天数 1
54 6
3 3
4
4 (单位:天)
3
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3
5
6
3
44
20
18 19 2
15
0
10
9 5
5
1
0
(人数)
调整的基本原则是:
(1)、尽量保证关键工作的日资源需求量。
(2)、利用非关键工作的时差错开各工作的 使用资源时间
(3,4), (1,2) 同时缩小 1.5+2.5=4 (3,4), (2,4) 同时缩小 1.5+2=3.5 确定应在(1,3)、(2,4)各缩2天。
②
24 1
18
20
2
4
26
3
5
24
18 6 T=62(天)
18
③ 总直接费用 488+3×2=494(百元)
间接费用 147 –3.3×2=140.4(百元)
