相似中考难题
中考数学相似的综合题试题附详细答案

一、相似真题与模拟题分类汇编(难题易错题)1.如图,抛物线过点,.为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)求直线AB的解析式和抛物线的解析式;(2)如果点P是MN的中点,那么求此时点N的坐标;(3)如果以B,P,N为顶点的三角形与相似,求点M的坐标.【答案】(1)解:设直线的解析式为()∵,∴解得∴直线的解析式为∵抛物线经过点,∴解得∴(2)解:∵轴,则,∴,∵点是的中点∴∴解得,(不合题意,舍去)∴(3)解:∵,,∴,∴∵∴当与相似时,存在以下两种情况:∴解得∴∴ ,解得∴【解析】【分析】(1)运用待定系数法解答即可。
(2)由(1)可得直线AB的解析式和抛物线的解析式,由点M(m,0)可得点N,P用m 表示的坐标,则可求得NP与PM,由NP=PM构造方程,解出m的值即可。
(3)在△BPN与△APM中,∠BPN=∠APM,则有和这两种情况,分别用含m的代数式表示出BP,PN,PM,PA,代入建立方程解答即可。
2.如图,BD是□ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD—DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),□PQMN与□ABCD重叠部分图形的面积为S(cm2).(1)AP=________cm(同含t的代数式表示).(2)当点N落在边AB上时,求t的值.(3)求S与t之间的函数关系式.(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.【答案】(1)(10-5t)(2)解:如图①,当点N落在边AB上时,四边形PNBQ为矩形.∵PN∥DB,∴△APN∽△ADB,∴AP:AD=PN:DB,∴(10-5t):10=8t:8,120t=80,∴.(3)解:分三种情况讨论:a)如图②,过点P作PE⊥BD于点E,则PE=3t.当时,.b)如图③,过点P作PE⊥BD于点E,则PE=3t,设PN交AB于点F,则.当时,.c)如图④,当时,PF=8-4t,FB=3t,PN=DB=QM=8,∴FN=4t,DQ=6(t-1),∴BM=DQ=6(t-1).∵∠GBM=∠A,∠DBA=∠GMB,∴△BGM∽△ABD,∴GM:BM=DB:AB,解得:GM=8t-8,∴S=S平行四边形PNMQ-S△FMN-S△BMG=8(9t-6)- ×4t×(9t-6)- ×(6t-6)(8t-8)= .综上所述:(4)解:分三种情况讨论.①当NQ∥AB时,如图5,过P作PF⊥BD于F,则PF=3t,DF=4t,PN=FQ=BQ=8t,∴BD=8t+8t+4t=8,解得:.②当AD∥NQ,且Q在BD上时,如图6.∵PNQD和PNBQ都是平行四边形,∴PN=DQ=BQ,∴8t+8t=8,解得:.③当AD∥NQ,且Q在DC上时,如图7,可以证明当Q与C重合,即直线NQ与直线BC重合时,满足条件,如图8,此时DQ=AB= =6,t= =2.综上所述:或或.【解析】【解答】解:(1)(10-5t);【分析】(1)由题意可得,DP=5t,所以AP=AD-DP=10-5t;(2)由欧勾股定理的逆定理可得∠ABD=,所以根据有一个角是直角的平行四边形是矩形可得,当点N落在边AB上时,四边形PNBQ为矩形;由平行线分线段成比例定理可得比例式:,则可得关于t的方程,解方程即可求解;(3)由(2)知,当□PQMN全部在□ABCD中时,运动时间是秒,由已知条件可知,点Q 在BD边上的运动速度是8cm/s,在DC边上的运动速度是6cm/s,所以当点Q运动到C点时,点P也运动到了点A,所以分3种情况:a)如图②,过点P作PE⊥BD于点E,当0 < t ≤时, S=BQ PE;b)如图③,过点P作PE⊥BD于点E,设PN交AB于点F,当< t ≤ 1 时,S =(PF+BQ)PE;c)如图④,当 1 < t ≤ 2 时, S =平行四边形PNMQ的面积-三角形FNM的面积-三角形BMG 的面积;(4)由题意NQ与△ABD的一边平行可知,有3种情况:①当NQ∥AB;②当AD∥NQ,且Q在BD上时;③当AD∥NQ,且Q在DC上时。
中考数学总复习之图形的相似(15大题)

中考数学总复习之图形的相似(15大题)1.小明和小红学习了《利用相似三角形测高》一课后,对我国杰出数学家刘徽的著作《海岛算经》非常感兴趣,也想利用相同的方法测量广场上路灯的高度.如图所示,他们在广场上竖立两根长均为1.5米的标杆BC 和DE .测得标杆BC 在路灯AH 下的影长BF 为1米,标杆BF 在路灯AH 下的影长DG 为3米,两根标杆BC 和DE 之间的距离BD 为10.8米.已知AH ⊥HG ,CB ⊥BF ,ED ⊥DG ,点H 、B 、F 、D 、G 五点在同一直线上,求路灯的高AH .2.如图,点D 、E 、F 分别是三角形ABC 的边BC 、CA 、AB 上的点,DE ∥BA ,DF ∥CA . (1)求证:∠FDE =∠A .(2)若BD :DC =1:4,S △CDE =16,求S △ABC .3.(2023•镇海区校级一模)如图,在△ABC 中,BC AC=23,D ,M ,N 分别在直线AB ,直线AC ,直线BC 上.(1)若D 是AB 中点,∠MDN =∠A +∠B ,求MD ND ;(2)若点D ,M ,N 分别在AB ,CA ,CB 的延长线上,且ABBD=34,∠MDN =∠ACB ,求MD ND.4.(2023•工业园区校级模拟)如图,已知BF 是⊙O 的直径,A 为⊙O 上(异于B 、F )一点,过点A 的直线MA 与FB 的延长线交于点M ,G 为BF 上一点,AG 的延长线交⊙O 于点E ,连接BE ,∠MAE +∠AFM =90°. (1)求证:AM ∥EF ;(2)MA =6√2,BE =2,记△AMF 的面积为S 1,记△AEF 的面积为S 2,记△EFG 的面积为S 3,若S 1•S 3=35S 22,求⊙O 的半径.5.(2023•舟山一模)如图,在Rt △ABC 中,∠BAC =90°,∠ABC 的平分线交AC 于点E ,以A 为圆心,AE 为半径作⊙A 交BE 于点F ,直线AB 交⊙A 于G 、H 两点,AF 的延长线交BC 于点D ,作EK ⊥BC ,垂足为点K . (1)求证:AD ⊥BC ; (2)求证:BF BE=AD AC;(3)当BF •BE =BG •BH 且AH =BD 时,求证:BFBG=AC BE.6.(2023春•桐城市月考)如图,平面直角坐标系中点A (﹣3,3),B (﹣5,1),C (﹣2,0),P (a 、b )是△ABC 的边AC 上的任意一点.(1)以点M (﹣1,2)为位似中心,在M 点的右侧把△ABC 按2:1放大得△A 1B 1C 1,画出△A 1B 1C 1;直接写出△A 1B 1C 1的边A 1C 1上与点P (a 、b )的对应点P 1的坐标. (2)将△ABC 绕N (﹣1,﹣2)逆时针旋转90°得△A 2B 2C 2,画出△A 2B 2C 2,求旋转过程中线段BC在平面上扫过部分的面积.(用π表示)7.(2022秋•兴县期末)数学社团的同学们想用边长为20cm的正方形铝板,设计小组会徽下面是“兴趣小组”和“智慧小组”的设计方案,请认真阅读,并解决问题;“兴趣小组”:我们小组设计的会微如图1所示,它是由四个全等的“黄金矩形”组成的正方形图案,在该图案中“矩形的宽与长的比等于矩形的长与正方形的边长之比”.“智慧小组”:我们小组设计的会徽如图2所示,它是由四个全等的直角三角形组成的“赵爽弦图”,其中小正方形的面积为16cm2.解决问题:(1)“兴趣小组”设计的方案中,小正方形的边长约等于cm(精确到0.1 cm).(2)请你求出“智慧小组”设计的方案中,小直角三角形的两条直角边分别是多少cm?8.(2023•蜀山区校级模拟)如图,已知△ABC ,在已知的直角坐标系网格内画出下面图形: (1)画出△ABC 的位似图形△A 1B 1C ,其中点C 为位似中心,且A 1B 1AB=2.(2)画出△ABC 经过平移后得到的△A 2B 2C 2,其中△ABC 的一边上的点K (x ,y ),平移后的对应点为K 2(x +4,y ﹣4).9.(2023春•南岸区校级月考)如图,已知在直角△ABC 中,∠ABC =90°,E 为AC 边上一点,连接BE ,过E 作ED ⊥AC ,交BC 边于点D .(1)如图1,连接AD ,若CE =2,BD =3√2,∠C =45°,求△ADE 的面积; (2)如图2,作∠ABC 的角平分线交AC 于点F ,连接DF ,若∠BDE =∠CDF ,求证:AE +DE =√2BE ;(3)如图3,若∠C =30°,将△BCE 沿BE 折叠,得到△BEF ,且BF 与AC 交于点G ,连接AD ,DF ,点E 在AC 边上运动的过程中,当BF ⊥AC 时,直接写出DF DA的值.10.(2023春•西湖区校级期中)在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,过点D 作DE ⊥AC ,过点F 作DF ⊥BC ,其中AD =185,BC =8. (1)求证:AC 3BC 3=AE BF;(2)求BD 的值.11.(2023•普陀区一模)已知:如图,在四边形ABCD 中,E 为BC 上一点,AB •DE =AE •EC ,∠ABE =∠AED . (1)求证:△ABE ∽△ECD ;(2)如果F 、G 、H 分别是AE 、DE 、AD 的中点,联结BF 、HF 、HG 、CG .求证:BF •HF =CG •HG .12.(2022秋•辽宁期末)如图,在Rt △ABC 中,∠ABC =90°,点D ,E 分别在边BC ,AC 上,联结AD ,BE 交于点G ,且AD =CD . (1)如果BE =AB ,求证:BE •AG =BC •EG ;(2)如果射线CG 交AB 于点P ,且AD •AE =BD •CE ,求证:点P 是AB 中点.13.(2023•大连模拟)如图,在△ABC中,AB=BC,AD⊥BC于点D,AD=3cm,BD=4DC,点P是AB边上一动点(点P不与点A,B重合),过点P作PQ⊥BC于点Q,点M在射线QC上,且QM=BQ.设BQ=xcm,△PQM与△ABD重叠部分的面积为Scm2.(1)求AB的长;(2)求S关于x的函数解析式,并直接写出自变量x的取值范围.14.(2022秋•河西区校级期末)如图,D,E,F是Rt△ABC三边上的点,且四边形CDEF 为矩形,BC=6,∠A=30°.(1)求AB的长;(2)设AE=x,则DE=,EF=(用含x的表达式表示);(3)求矩形CDEF的面积的最大值.15.(2023•宝山区一模)已知:如图,四边形ABCD、ACED都是平行四边形,M是边CD 的中点,联结BM并延长,分别交AC、DE于点F、G.(1)求证:BF2=FM•BG;(2)联结CG,如果AB=√2CG,求证:∠BGC=∠BAC.。
中考压轴图形的相似问题综合(解析版)

的结论有(
)
A.①②③④
【标准答案】C
【思路点拨】
B.②③④
C.②③④⑤
D.②③⑤
①由特殊值法可判断,当点P与BD中点重合时,CM=0,显然FM≠CM;
②由SAS可证△ABP△CBP,可得AP=CP,由矩形的性质可得EF=PC=AP;
③由SSS可证△APD△CPD,可得∠DAP=∠DCP,由平行线的性质可得∠DCP=∠H,由
∴四边形GBED为平行四边形,
∴GD=BE,
1
∵BE=BC,
2
1
∴GD=AD,
2
即G是AD的中点,
故②正确,
∵BG//DE,
∴∠GBP=∠BPE,
故③正确.
∵BG//DG,AF⊥DE,
∴AF⊥BG,
∴∠ANG=∠ADF=90°,
∵∠GAM=∠FAD,
∴△AGM∽△AFD,
设AG=a,则AD=2a,AF=5a,
B.2个
C.3个
D.4个
【标准答案】C
【思路点拨】
1
根据正方形性质得出ADBCDC;ECDFBC;ADFDCE,证
2
ADF≌DCESAS,推出AFDDEC,求出DGF90即可判断
①;证明四边形
GBED为平行四边形,则可知②正确;由平行线的性质可得③正确;证明AGM∽AFD,
可得出SAGM:SDEC1:5.则④不正确.
D.5
【标准答案】D
【思路点拨】
①根据正方形的性质得到∠BAD=∠ADC=∠B=90°,根据旋转的性质得到∠NAD=∠BAM,
∠AND=∠AMB,根据余角的性质得到∠DAM+∠NAD=∠AND+∠NAD=90°,等量代换得
中考数学相似-经典压轴题含详细答案

一、相似真题与模拟题分类汇编(难题易错题)1.如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:(1)∠OAE=∠OBE;(2)AE=BE+ OE.【答案】(1)证明:在等腰Rt△ABC中,O为斜边AC的中点,∴OB⊥AC,∴∠AOB=90°,∵∠AEB=90°,∴A,B,E,O四点共圆,∴∠OAE=∠OBE(2)证明:在AE上截取EF=BE,则△EFB是等腰直角三角形,∴,∠FBE=45°,∵在等腰Rt△ABC中,O为斜边AC的中点,∴∠ABO=45°,∴∠ABF=∠OBE,∵,∴,∴△ABF∽△BOE,∴ = ,∴AF= OE,∵AE=AF+EF,∴AE=BE+ OE.【解析】【分析】(1)利用等腰直角三角形的性质,可证得∠AOB=∠AEB=90°,可得出A,B,E,O四点共圆,再利用同弧所对的圆周角相等,可证得结论。
(2)在AE上截取EF=BE,易证△EFB是等腰直角三角形,可得出BF与BE的比值为,再证明∠ABF=∠OBE,AB与BO的比值为,就可证得AB、BO、BF、BE四条线段成比例,然后利用两组对应边成比例且夹角相等的两三角形相似,可证得△ABF∽△BOE,可证得AF= OE,由AE=AF+EF,可证得结论。
2.已知线段a,b,c满足,且a+2b+c=26.(1)判断a,2b,c,b2是否成比例;(2)若实数x为a,b的比例中项,求x的值.【答案】(1)解:设,则a=3k,b=2k,c=6k,又∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12;∴2b=8,b2=16∵a=6,2b=8,c=12,b2=16∴2bc=96,ab2=6×16=96∴2bc=ab2a,2b,c,b2是成比例的线段。
中考数学压轴题之相似(中考题型整理,突破提升)含答案

一、相似真题与模拟题分类汇编(难题易错题)1.已知线段a,b,c满足,且a+2b+c=26.(1)判断a,2b,c,b2是否成比例;(2)若实数x为a,b的比例中项,求x的值.【答案】(1)解:设,则a=3k,b=2k,c=6k,又∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12;∴2b=8,b2=16∵a=6,2b=8,c=12,b2=16∴2bc=96,ab2=6×16=96∴2bc=ab2a,2b,c,b2是成比例的线段。
(2)解:∵x是a、b的比例中项,∴x2=6ab,∴x2=6×4×6,∴x=12.【解析】【分析】(1)设已知比例式的值为k,可得出a=3k,b=2k,c=6k,再代入a+2b+c=26,建立关于k的方程,求出kl的值,再求出2b、b2,然后利用成比例线段的定义,可判断a,2b,c,b2是否成比例。
(2)根据实数x为a,b的比例中项,可得出x2=ab,建立关于x的方程,求出x的值。
2.如图,在四边形ABCD中,AD//BC,,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设的面积为,直接写出与之间的函数关系式是________(不写取值范围).(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时的值.(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出 =________. (4)是否存在时刻,使得若存在,求出的值;若不存在,请说明理由.【答案】(1)(2)解:如图1,过点P作PH⊥BC于点H,∴∠PHB=∠PHQ=90°,∵∠C=90°,AD∥BC,∴∠CDP=90°,∴四边形PHCD是矩形,∴PH=CD=3,HC=PD=2t,∵CQ=t,BC=4,∴HQ=CH-CQ=t,BH=BC-CH=4-2t,BQ=4-t,∴BQ2= ,BP2= ,PQ2= ,由BQ2=BP2可得:,解得:无解;由BQ2=PQ2可得:,解得:;由BP2= PQ2可得:,解得:或,∵当时,BQ=4-4=0,不符合题意,∴综上所述,或;(3)(4)解:如图3,过点D作DM∥PQ交BC的延长线于点M,则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,∵AD∥BC,DM∥PQ,∴四边形PQMD是平行四边形,∴QM=PD=2t,∵QC=t,∴CM=QM-QC=t,∵∠BCD=∠MCD=90°,∴BD2=BC2+DC2=25,DM2=DC2+CM2=9+t2,∵BM2=(BC+CM)2=(4+t)2,∴由BM2=BD2+DM2可得:,解得:,∴当时,∠BDM=90°,即当时,PQ⊥BD.【解析】【解答】解:(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,∴S△PBQ= BQ×3= ;( 3 )解:如图2,过点P作PM⊥BC交CB的延长线于点M,∴∠PMC=∠C=90°,∵AD∥BC,∴∠D=90°,△OAP∽△OBQ,∴四边形PMCD是矩形,,∴PM=CD=3,CM=PD=2t,∵AD=6,BC=4,CQ=t,∴PA=2t-6,BQ=4-t,MQ=CM-CQ=2t-t=t,∴,解得:,∴MQ= ,又∵PM=3,∠PMQ=90°,∴tan∠BPQ= ;【分析】(1)点P作PM⊥BC,垂足为M,则四边形PDCM为矩形,根据梯形的面积公式就可以利用t表示,就得到s与t之间的函数关系式。
九年级相似较难题30题(有解析)

九年级相似较难题30题一、选择题(共15小题)1.梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向外作等腰直角三角形,其面积分别是S1、S2、S3,且S1+S3=4S2,则CD=()A.2.5AB B.3AB C.3.5AB D.4AB2.如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△B n+1D n C n面积为S n,则S n等于()A.B.C.D.3.如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC 交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②=;③AC•BE=12;④3BF=4AC.其中结论正确的个数有()A.1个B.2个C.3个D.4个4.如图,正方形ABCD中,在AD的延长线上取点E、F,使DE=AD,DF=BD;BF分别交CD,CE于H、G点,连接DG,下列结论:①∠GDH=∠GHD;②△GDH为正三角形;③EG=CH;④EC=2DG;⑤S△CGH:S△DBH=1:2.其中正确的是()A.①②③B.②③④C.③④⑤D.①③⑤5.如图,在矩形ABCD中,对角线AC,BD相交于点G,E为AD的中点.连接BE交AC于点F,连接FD.若∠BFA=90°,则下列四对三角形:(1)△BEA与△ACD;(2)△FED与△DEB;(3)△CFD与△ABG;(4)△ADF 与△CFB,其中相似的有()A.(1)(4)B.(1)(2)C.(2)(3)(4) D.(1)(2)(3)6.已知:△ABC中,∠ACB=90°,AC=BC,D为BC中点,CF⊥AD.下列结论:①∠ADF=45°;②∠ADC=∠BDF;③AF=2BF;④CF=3DF.正确的有()A.1个B.2个C.3个D.4个7.如图所示,△ABC中,点P,Q,R分别在AB,BC,CA边上,且AP=,BQ=BC,CR=CA,已知阴影△PQR的面积是19cm2,则△ABC的面积是()A.38 B.42.8 C.45.6 D.47.58.如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:①E为△ABP的外心;②△PBE为等腰直角三角形;③PC•OA=OE•PB;④CE+PC的值不变.A.1个B.2个C.3个D.4个9.如图,D为⊙O的直径AB上任一点,CD⊥AB,若AD、BD的长分别等于a和b,则通过比较线段OC与CD 的大小,可以得到关于正数a和b的一个性质,你认为这个性质是()A.B.C.D.10.如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为()A.B.C.D.11.如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B′处,点A落在点A′处.设AE=a,AB=b,BF=c,下列结论:①B′E=BF;②四边形B′CFE是平行四边形;③a2+b2=c2;④△A′B′E∽△B′CD;其中正确的是()A.②④B.①④C.②③D.①③12.如图,O为矩形ABCD的中心,将直角△OPQ的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是()A.B.C.D.13.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有()A.1个B.2个C.3个D.4个14.如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为()①OH=BF;②∠CHF=45°;③GH=BC;④DH2=HE•HB.A.1个B.2个C.3个D.4个15.如图,△ABC与△AFG是两个全等的等腰直角三角形,∠BAC=∠F=90°,BC分别与AF,AG相交于点D,E.则图中不全等的相似三角形有()A.0对B.1对C.2对D.3对二、填空题(共8小题)(除非特别说明,请填准确值)16.如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论:①=;②∠ADF=∠CDB;③点F是GE的中点;④AF=AB;⑤S△ABC=5S△BDF,其中正确结论的序号是_________.17.如图,直角梯形ABCD中,AD∥BC,∠BAC=∠ADC=90°,AB=AC,CE平分∠ACB交AB于点E,F为BC 上一点,BF=AE,连接AF交CE于点G,连接DG交AC于点H.下列结论:①AF⊥CE;②△ABF∽△DGA;③AF=DH;④.其中正确的结论有_________.18.如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…M n分别为边B1B2,B2B3,B3B4,…,B n B n+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△B n C n M n的面积为S n,则S n=_________.(用含n的式子表示)19.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论:①DE⊥EC;②点E是AB中点;③AD•BC=BE•DE;④CD=AD+BC.其中正确的有_________.20.如图,在正方形ABCD中,点E、F分别为AD、AB的中点,连接DF、CE,DF与CE交于点H,则下列结论:①DF⊥CE;②DF=CE;③=;④=.其中正确结论的序号有_________.21.在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、A n B n C n C n﹣1按如图所示的方式放置,其中点A1、A2、A3、…、A n均在一次函数y=kx+b的图象上,点C1、C2、C3、…、C n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点A n的坐标为_________.22.已知菱形ABCD中,对角线AC=8cm,BD=6cm,在菱形内部(包括边界)任取一点P,得到△ACP并涂成黑色,使黑色部分的面积大于6cm2的概率为_________.23.已知:在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是_________.三、解答题(共7小题)(选答题,不自动判卷)24.如图(1),直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由;(3)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由;(4)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值.(图(2)、图(3)供画图探究)25.已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC、CB于点E、F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断是否为定值?若是,请求出该定值;若不是,请说明理由.26.情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是_________,∠CAC′=_________°.问题探究如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE 和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.拓展延伸如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA 交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.27.如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接AA1,射线AA1分别交射线PB、射线B1B于点E、F.(1)如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在_________关系(填“相似”或“全等”),并说明理由;(2)如图2,设∠ABP=β.当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图3,当α=60°时,点E、F与点B重合.已知AB=4,设DP=x,△A1BB1的面积为S,求S关于x的函数关系式.28.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.(1)求证:AC平分∠DAB;(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);(3)若CD=4,AC=4,求垂线段OE的长.29.如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,(1)求证:△ABE∽△ADB;(2)求AB的长;(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.30.如图,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;(4)在(2)中x轴下方的抛物线上是否存在一点P,过点P作x轴的垂线,交直线AB于点D,线段OD把△AOB 分成两个三角形,使其中一个三角形面积与四边形BPOD面积比为2:3?若存在,求出点P的坐标;若不存在,请说明理由.参考答案与试题解析一、选择题(共15小题)1.梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向外作等腰直角三角形,其面积分别是S1、S2、S3,且S1+S3=4S2,则CD=()A.2.5AB B.3AB C.3.5AB D.4AB考点:勾股定理;等腰直角三角形;相似三角形的判定与性质.专题:计算题;证明题;压轴题.分析:过点B作BM∥AD,根据AB∥CD,求证四边形ADMB是平行四边形,再利用∠ADC+∠BCD=90°,求证△MBC为Rt△,再利用勾股定理得出MC2=MB2+BC2,在利用相似三角形面积的比等于相似比的平方求出MC即可.解答:解:过点B作BM∥AD,∵AB∥CD,∴四边形ADMB 是平行四边形,∴AB=DM,AD=BM,又∵∠ADC+∠B CD=90°,∴∠BMC+∠B CM=90°,即△MBC为Rt△,∴MC2=MB2+B C2,∵以AD、AB、BC为斜边向外作等腰直角三角形,∴△AED∽△A NB,△ANB∽△BF C,=,=,即AD2=,BC2=,∴MC2=MB2+B C2=AD2+BC2=+==,∵S1+S3=4S2,∴MC2=4AB2,CD=DM+MC=AB+2AB=3AB.故选B.点评:此题涉及到相似三角形的判定与性质,勾股定理,等腰直角三角形等知识点,解答此题的关键是过点B作BM∥AD,此题的突破点是利用相似三角形的性质求得MC=2AB,此题有一定的拔高难度,属于难题.2.(2012•深圳二模)如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△B n+1D n C n面积为S n,则S n等于()A.B.C.D.考点:相似三角形的判定与性质;等边三角形的性质.专题:压轴题;规律型.分析:由n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…B n在一条直线上,可作出直线B1B2.易求得积,然后由相似三角形的性质,易求得S1的值,同理求得S2的值,继而求得S n的值.解答:解:n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…B n在一条直线上,作出直线B1B2.∴S△AB1C1=×2×=,∵∠B1C1B2=60°,∴AB1∥B2C1,∴△B1C1B2是等边△,且边长=2,∴△B1B2D1∽△C1AD1,∴B1D1:D1C1=1:1,∴S1=,同理:B2B3:AC2=1:2,∴B2D2:D2C2=1:2,∴S2=,同理:B n B n+1:AC n=1:n,∴B n D n:D n C n=1:n,∴S n=.故选D.点评:此题考查了相似三角形的判定与性质以及等边三角形的性质.此题难度较大,属于规律性题目,注意辅助线的作法,注意数形结合思想的应用.3.如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC 交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②=;③AC•BE=12;④3BF=4AC.其中结论正确的个数有()A.1个B.2个C.3个D.4个考点:相似三角形的判定与性质;角平分线的性质;等腰三角形的判定与性质.专题:压轴题.分析:①∠AED=90°﹣∠EAD,∠ADC=90°﹣∠DAC,∠EAD=∠DAC;②易证△ADE∽△ACD,得DE:DA=DC:AC=3:AC,AC不一定等于4;③当FC⊥AB时成立;④连接DM,可证DM∥BF∥AC,得FM:MC=BD:DC=4:3;易证△FMB∽△CMA,得比例线段求解.解答:解:①∠AED=90°﹣∠EAD,∠ADC=90°﹣∠DAC,∵AD平分∠BAC∴∠EAD=∠DAC,∴∠AED=∠ADC.故本选项正确;②∵∠EAD=∠DAC,∠ADE=∠ACD=90°,∴△ADE∽△ACD,得DE:DA=DC:AC=3:AC,但AC的值未知,故不一定正确;③由①知∠AED=∠ADC,∴∠BED=∠BDA,又∵∠DBE=∠ABD,∴△BED∽△BDA,∴DE:DA=BE:BD,由②知DE:DA=DC:AC,∴BE:BD=DC:AC,∴AC•BE=BD•DC=12.故本选项正确;④连接DM,则DM=MA.∴∠MDA=∠MAD=∠DAC,∴DM∥BF∥AC,由DM∥BF得FM:MC=BD:DC=4:3;由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=4:3,∴3BF=4AC.故本选项正确.综上所述,①③④正确,共有3个.故选C.点评:此题重点考查相似三角形的判定和性质,综合性强,证明△ADE∽△ACD和△FMB∽△CMA是解决本题的关键.4.如图,正方形ABCD中,在AD的延长线上取点E、F,使DE=AD,DF=BD;BF分别交CD,CE于H、G点,连接DG,下列结论:①∠GDH=∠GHD;②△GDH为正三角形;③EG=CH;④EC=2DG;⑤S△CGH:S△DBH=1:2.其中正确的是()A.①②③B.②③④C.③④⑤D.①③⑤考点:正方形的性质;相似三角形的性质.专题:压轴题.分析:本题为选择题,做选择题是要有技巧,像排除法,假设法都可以用,先看选项因为都有③选项故③可作为已知条件求解,△DHB∽△CHG根据面积比等于相似比的平方可得S△CGH:S△DBH=1:2故选项有⑤,然后再看①④中间哪个正确,先看①过G作GO⊥CD于O,设正方形边长为1,则,可求得CH=,====所以OC=,OD=1﹣,又==所以DH=,DO=DH﹣OH=1﹣,可得DO=OH,△DGH为等腰三角形,∠GDH=∠GHD,①正确.解答:解:(1)∵选项都有③,故可确定EG=CH.(2)由题意可得四边形BCED为平行四边形,进而推出△DHB∽△CHG,==,∵面积比等于相似比的平方∴S△CGH:S△DBH=1:2.(3)先看①设正方形边长为1.则==可求得CH=,====所以OD=1﹣,又==∴DH=.DO=DH﹣OH=1﹣∴可得DO=OH,△DGH为等腰三角形,即得∠GDH=∠GHD,①正确故选D.点评:本题考查的知识点比较多,正方形四边相等的性质及等腰三角形两底角相等的性质,面积比等于相似比的平方,相似三角形的比例关系要熟练掌握,另外还要掌握做选择题的一些方法,可是选择题的解答即快又准.5.如图,在矩形ABCD中,对角线AC,BD相交于点G,E为AD的中点.连接BE交AC于点F,连接FD.若∠BFA=90°,则下列四对三角形:(1)△BEA与△ACD;(2)△FED与△DEB;(3)△CFD与△ABG;(4)△ADF 与△CFB,其中相似的有()A.(1)(4)B.(1)(2)C.(2)(3)(4) D.(1)(2)(3)考点:矩形的性质;相似三角形的判定与性质.专题:计算题;压轴题.分析:根据题意,分别寻找各对三角形相似的条件,运用判定方法判断.∠EFC=∠ADC=90°∴∠DCA+∠FED=180°∵∠FED+∠AEB=180°∴∠AEB=∠DCA,∠CDA=∠DAB=90°∵∠DAC=∠ABE∴△BEA∽△ACD.再利用相似三角形相似的判定证明△FED与△DEB,△CFD与△ABG相似,而(4)不成立.解答:解:(1)∵矩形ABCD,∴∠EAB=∠CDA=90°,∴∠BAF+∠CAD=90°,又∠BFA=90°,∴∠BAF+∠ABF=90°,∴∠CAD=∠ABF,∴△BEA与△ACD相似;故此选项正确;(2)△FED与△DEB相似.理由:DE2=AE2=EF•EB,∠DEF=∠BED;故此选项正确;(3)△CFD与△ABG相似.理由:∠CDF=90°﹣∠EDF,∠AGB=90°﹣∠EBG,由(2)的结论得:∠EDF=∠EBD,故∠CDF=∠AGB;∵AB∥CD,∴∠DCF=∠BAG;故此选项正确;(4)△ADF与△CFB不具备相似条件.故选D.点评:本题主要考查了三角形相似的判定.6.已知:△ABC中,∠ACB=90°,AC=BC,D为BC中点,CF⊥AD.下列结论:①∠ADF=45°;②∠ADC=∠BDF;③AF=2BF;④CF=3DF.正确的有()A.1个B.2个C.3个D.4个考点:相似三角形的判定与性质;全等三角形的判定与性质;等腰三角形的性质.专题:压轴题.分析:根据已知对结论进行分析,从而得到答案.解答:解:作BG⊥CG,交CF的延长线于点G,∵∠CGB=90°,CF⊥AD∴∠1=∠2∵AC=BC∴△ACD≌△CBG∴CD=BG,∠CDA=∠CBG∵CD=BD∴BG=BD∵∠3=∠4,BF=BF∴△BFG≌△BFD∴∠FGB=∠FDB∴∠ADC=∠BDF(故②正确)如图2,作GB⊥BC,交CF延长线于点G,∵∠ACB=90°,BG⊥BC∴AC∥BG,∠CAB=∠3,∠AFC=∠BFG∴△BFG∽△AFC∵BE=BD=BC=AC∴==∴AF=2BF(③正确)所以正确的有两个.故选B.点评:此题很复杂,解答此题的关键是作出辅助线,利用三角形全等及相似求解.7.如图所示,△ABC中,点P,Q,R分别在AB,BC,CA边上,且AP=,BQ=BC,CR=CA,已知阴影△PQR的面积是19cm2,则△ABC的面积是()A.38 B.42.8 C.45.6 D.47.5考点:三角形的面积;相似三角形的判定与性质.分析:通过求出△QPR的面积和△ABC面积的比,即可求出△ABC的面积.解答:解:过P作PM⊥BC于M,过A作AN⊥BC于N∴△BMP∽△BNA∴PM:AN=BP:BA=2:3设△ABC的面积为S,则S△BQP=BQ•PM=•(BC)•(AN)=BC•AN•=S同理可得出:S△QRC=S,同理,过P作PE⊥AC于E,过B作BF⊥AC于F.则S△APR=SS阴影=S﹣S△BQP﹣S△QRC﹣S△APR=S=19∴△ABC的面积S=12×19÷5=45.6.故选C.点评:已知部分求整体,可通过求得部分占整体的比重来求出整体的值.8.如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:①E为△ABP的外心;②△PBE为等腰直角三角形;③PC•OA=OE•PB;④CE+PC的值不变.A.1个B.2个C.3个D.4个考点:相似三角形的判定与性质;全等三角形的性质;全等三角形的判定;线段垂直平分线的性质;等腰三角形的性质;三角形的外接圆与外心.专题:几何综合题;压轴题.分析:①由于外心是三角形三边中垂线的交点,显然点E是AB、BP两边中垂线的交点,因此符合△ABP外心的要求,故①正确;②此题要通过连接AE,根据三角形的外心的性质可知:AE=PE=BE,即∠EPA=∠EAP,∠EAB=∠EBA,再结合三角形的内角和定理进行求解即可;③此题显然要通过相似三角形来求解,由于OA=OB,那么可通过证△OEB∽△CPB来判断③的结论是否正确;④此题较简单,过E作EM⊥OC,交AC于M,那么MC=CE,因此所求的结论可转化为证PM是否为定值,观察图形,可通过证△PEM、△BEC是否全等来判断.解答:解:①∵CO为等腰Rt△ABC斜边AB上的中线,∴CO垂直平分AB;又∵DE平分PB,即E点是AB、BP两边中垂线的交点,∴E点是△ABP的外心,故①正确;②如图,连接AE;由①知:AE=EP=EB,则∠EAP=∠EPA,∠EPB=∠EBP,;∵∠PAB=45°,即∠EAP+∠EPA+∠EAB+∠EBA =2(∠EAP+∠EA B)=2∠PAB=90°,由三角形内角和定理知:∠EPB+∠EBP= 90°,即∠EPB=∠EBP= 45°,∴△PEB是等腰直角三角形;故②正确;③∵∠PBE=∠ABC=45°,∴∠EBO=∠PB C=45°﹣∠CBE,又∵∠EOB=∠PC B=90°,∴△BPC∽△B EO,得:,即PC•OB=OE•BC ⇒PC•OA=OE•BC;故③错误;④过E作EM⊥OC,交AC于M;易知:△EMC 是等腰直角三角形,即MC=EC,∠PME=45°;∴∠PEM=∠B EC=90°+∠PEC ,又∵EC=ME,PE=BE,∴△PME≌△BPM=BC,即PM是定值;由于PM=CM+PC=EC+PC,所以CE+PC的值不变,故④正确;因此正确的结论是①②④,故选C.点评:此题主要考查了三角形的外接圆、等腰直角三角形的性质、全等三角形及相似三角形的相关知识等,综合性强,难度较大.9.如图,D为⊙O的直径AB上任一点,CD⊥AB,若AD、BD的长分别等于a和b,则通过比较线段OC与CD 的大小,可以得到关于正数a和b的一个性质,你认为这个性质是()A.B.C.D.考点:圆周角定理;垂径定理;射影定理.专题:压轴题.分析:连接AC,BC;根据射影定理求解.解答:解:连接AC,BC.根据AB是直是直角,CD是直角三角形斜边上的高线,因而CD2=AD•DB,即CD2=ab,CD=.而OC=,并且OC≥CD,则≥.故选A.点评:本题主要考查了圆中直径所对的弦是直径,并且考查了垂径定理.10.如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为()A.B.C.D.考点:勾股定理;全等三角形的性质;全等三角形的判定;相似三角形的判定与性质.专题:压轴题.分析:先求出△AEH与△BFE相似,再根据其相似比EF:FG=3:1设出AE、BF的长及AB、BC的即可.解答:解:∵四边形EFGH是矩形ABCD的内接矩形,EF:FG=3:1,AB:BC=2:1,∴∠HEA+∠FEB=90°,∵∠FEB+∠EFB=90°,∴∠HEA=∠EFB,∵∠HAE=∠B,∴Rt△HAE∽△EBF,∴===,同理可得,∠GHD=∠EFB,HG=EF,∴△GDH≌△EBF,DH=BF,DG=EB,设AB=2x,BC=x,AE=a,BF=3a,则AH=x﹣3a,AE=a,∴tan∠AHE=tan∠BEF,即=,解得:x=8a,∴tan∠AHE===.故选A点评:此题比较复杂,解答此题的关键是根据题意求出相似三角形的相似比,根关系列出方程解答.11.(2011•綦江县模拟)如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B′处,点A落在点A′处.设AE=a,AB=b,BF=c,下列结论:①B′E=BF;②四边形B′CFE是平行四边形;③a2+b2=c2;④△A′B′E∽△B′CD;其中正确的是()A.②④B.①④C.②③D.①③考点:翻折变换(折叠问题);勾股定理;平行四边形的判定;矩形的性质;相似三角形的判定.专题:几何综合题;压轴题.分析:由折叠前后对应线段相等可得①成立,那么只要判断③成立与否即可.解答:解:根据题意,结论①B′E=BF正确;连接BE,根据折叠可知:BF=B′F,∠BFE=∠B′FE,又∵EF=EF∴△B′EF≌△BEF(SAS),∴B′E=BE,∠B′FE=∠BFE,又∵AD∥BC,∴∠B'EF=∠BFE,∴∠B′FE=∠B′EF,∴B′F=B′E,∴BE=B′F=BF=c,在Rt△ABE中,根据勾股定理可得,a2+b2=c2;故选D.点评:此题主要考查图形的折叠问题,同时考查了平行线的性质和等角对等边等知识点.折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.12.如图,O为矩形ABCD的中心,将直角△OPQ的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是()A.B.C.D.考点:相似三角形的性质;动点问题的函数图象.专题:综合题;压轴题.分析:过点O分别作OE⊥BC与E,易证明△NOF∽△MOE,利用相似比作为相等关系即可得到关于x,y的方程,整理即可得到函数关系式从而判断图象.解答:解:过点O分别作OF⊥AB与F,OE⊥BC与E∵∠POQ=∠EOF=90°∴∠NOF=∠MOE∵∠NFO=∠MEO=90°∴△NOF∽△MOE∴=∵AB=4,AD=6,BM=x,AN=y∴NF=2﹣y,ME=3﹣x,OF=3,OE=2∴=∴y=x﹣(0<x<6)故选C.点评:解决有关动点问题的函数图象类习题时,关键是要根据条件找到所给的其是在几何问题中,更要注意基本性质的掌握和灵活运用.13.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有()A.1个B.2个C.3个D.4个考点:相似三角形的判定与性质;全等三角形的判定;正方形的性质;圆周角定理.专题:压轴题;动点型.分析:①由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;②若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45°,所以②的结论也是正确的.③此题要通过共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;④若BE平分∠DBC,那么H是DG的中点;易证得△ABH∽△BCE,得BD•BC=BE•BH,即BC2=BE•BH,因此只需求出BE•BH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BE•BH的值,由此得解.解答:解:①正确,证明如下:∵BC=DC,CE=CG,∠BCE=∠DCG=90°,∴△BEC≌△DGC,∴∠EBC=∠CDG,∵∠BDC+∠DBH+∠EBC=90°,∴∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,②由于∠BAD、∠BCD、∠BHD 都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;由圆周角定理知:∠DHA=∠ABD =45°,故②正确;③由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH ;又∵∠ABD=∠D BG=45°,∴△ABM∽△DBG,得AM:DG=AB:BD=1:,即DG=AM;故③正确;④过H作HN⊥CD于N,连接EG;若BH平分∠DBG,且BH⊥DG,已知:BH垂直平分DG;得DE=EG,H是DG中点,HN 为△DCG的中位线;设CG=x,则:HN=x,EG=DE=x,DC=BC=(+1)x;∴HN∥BC,∴∠NHB=∠EBC,∠ENH=∠ECB,∴△BEC∽△HEN,则BE:EH=BC:HN=2+2,即EH=;∴HE•BH=BH•=4﹣2,即BE•BH=4;∵∠DBH=∠CBE,且∠BHD=∠BCE=90°,∴△DBH∽△EBC,得:DB•BC=BE•BH=4,即BC2=4,得:BC2=4,即正方形ABCD的面积为4;故④正确;因此四个结论都正确,故选D.点评:本题主要考查三角形相似和全等的判定及性质、正方形的性质以及圆周角定理等知识的综合应用,能够判断出A、B、C、D、H五点14.(2013•蕲春县模拟)如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为()①OH=BF;②∠CHF=45°;③GH=BC;④DH2=HE•HB.A.1个B.2个C.3个D.4个考点:正方形的性质;全等三角形的判定与性质;角平分线的性质;三角形中位线定理;相似三角形的判定与性质.专题:几何综合题;压轴题.分析:根据已知对各个结论进行分析,从而确定正确的个数.①作EJ⊥BD于J,连接EF,由全等三角形的判定定理可得△DJE≌△ECF,再由平行线的性质得出OH是△DBF的中位线即可得出结论;②根据四边形ABCD是正方形,BE是∠DBC的平分线可求出Rt△BCE≌Rt△DCF,再由∠EBC=22.5°即可求出结论;线,得出GH=CF,由GH<BC,可得出结论;④由相似三角形的判定定理得出△DHG∽△BDH,根据相似三角形的对应边成比例即可得出结论.解答:解:作EJ⊥BD于J,连接EF①∵BE平分∠DBC∴EC=EJ,∴△DJE≌△ECF∴DE=FE∴∠HEF=45°+22.5°=67.5°∴∠HFE==22.5°∴∠EHF=180°﹣67.5°﹣22.5°=90°∵DH=HF,OH是△DBF的中位线∴OH∥BF∴OH=BF②∵四边形ABCD是正方形,BE是∠DBC的平分线,∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,∵CE=CF,∴Rt△BCE≌Rt△DCF,∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,∵OH是△DBF 的中位线,CD⊥AF,∴OH是CD的垂直平分线,∴DH=CH,∴∠CDF=∠D CH=22.5°,∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故②正确;③∵OH是△BFD的中位线,∴DG=CG=B C,GH=CF,∵CE=CF,∴GH=CF= CE∵CE<CG=BC,∴GH<BC,故此结论不成立;④∵∠DBE=4 5°,BE是∠DBF 的平分线,∴∠DBH=22.5°,由②知∠HBC=∠CDF =22.5°,∴∠DBH=∠CHD,∴△DHE∽△BHD,∴=∴DH=HE•HB,故④成立;所以①②④正确.故选C.点评:解答此题的关键是作出辅助线,构造等腰直角三角形,利用等腰直角三角形的性质结合角平分线的性质逐步解答.15.(2011•金平区二模)如图,△ABC与△AFG是两个全等的等腰直角三角形,∠BAC=∠F=90°,BC分别与AF,AG相交于点D,E.则图中不全等的相似三角形有()A.0对B.1对C.2对D.3对考点:相似三角形的判定;等腰直角三角形.专题:几何图形问题;压轴题.分析:根据已知及相似三角形的判定方法进行分析,从而得到答案.解答:解:∵△ABC与△AFG是两个∠BAC=∠F=90°∴∠C=∠B=∠FAG=∠G=45°∵∠CEA=∠B+∠EAB,∠DAB=∠FAG+∠EAB∴∠CEA=∠BAD,又∵AC=BC,∴△CAE≌△BAD;∴△BDA∽△ADE;∴△CAE∽△ADE;∴图中不全等的相似三角形有2对.故选:C.点评:此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线所组成的三角形与原三角形相似.二、填空题(共8小题)(除非特别说明,请填准确值)16.(2012•舟山)如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论:①=;②∠ADF=∠CDB;③点F是GE的中点;④AF=AB;⑤S△ABC=5S△BDF,其中正确结论的序号是①②④.考点:相似三角形的判定与性质;全等三角形的判定与性质;等腰直角三角形.专题:压轴题.分析:由△AFG∽△BFC,可确定结论①正确;由△ABG≌△BCD,△AFG≌△AFD,可确定结论②正确;由△AFG≌△AFD可得FG=FD>FE,所以点F不是GE中点,可确定结论③错误;由△AFG≌△AFD可得AG=AB=BC,进而由△AFG∽△BFC确定点F为AC的三等分点,可确定结论④正确;因为F为AC的三等分点,所以S△ABF=S△ABC,又S△BDF=S△ABF,所以S△ABC=6S△BDF,由此确定结论⑤错误.解答:解:依题意可得BC∥AG,∴△AFG∽△BFC,∴,又AB=BC,∴.故结论①正确;如右图,∵∠1+∠3=90°,∠1+∠4=90°,∴∠3=∠4.在△ABG与△BCD中,,∴△ABG≌△BCD(ASA),∴AG=BD,又BD=AD,∴AG=AD;在△AFG与△AFD中,,∴△AFG≌△AFD(SAS),∴∠5=∠2,又∠5+∠3=∠1+∠3=90°,∴∠5=∠1,∴∠1=∠2,即∠ADF=∠CDB .故结论②正确;∵△AFG≌△A FD,∴FG=FD,又△FDE为直角三角形,∴FD >FE,∴FG>FE,即点F不是线段GE的中点.故结论③错误;∵△ABC为等腰直角三角形,∴AC=AB;∵△AFG≌△A FD,∴AG=AD=A B=BC;∵△AFG∽△B FC,∴,∴FC=2AF,∴AF=AC=AB.故结论④正确;∵AF=AC,∴S△ABF=S△ABC;又D为中点,∴S△BDF=S△ABF,∴S△BDF=S△ABC,即S△ABC=6S△BDF .故结论⑤错误.综上所述,结论①②④正确,故答案为:①②④.点评:本题考查了等腰直角三角形中相似三角形与全等三角形的应用,有一定的难度.对每一个结论,需要仔细分析,严格论证;注意各结论之间并非彼此孤立,而是往往存在逻辑关联关系,需要善加利用.17.如图,直角梯形ABCD中,AD∥BC,∠BAC=∠ADC=90°,AB=AC,CE平分∠ACB交AB于点E,F为BC 上一点,BF=AE,连接AF交CE于点G,连接DG交AC于点H.下列结论:①AF⊥CE;②△ABF∽△DGA;③AF=DH;④.其中正确的结论有①②③④.考点:相似三角形的判定与性质;直角梯形.专题:压轴题.分析:先判断出△ABC是等腰直角三角形,过点E作EF′⊥BC于F′,根据角平分线上的点到角的两边的距离相等可得AE=EF′,再根据等腰直角三角形的性质可得BF′=EF′,从而确定点F、F′重合,再利用“HL”证明△ACE和△FCE全等,根据全等三角形对应边相等可得AC=CF,根据等腰三角形三线合一的可得AF⊥CE,判断出①正确;求出∠AFC=∠FAC=67.5°,再求出∠DAG=∠AFB=112.5°,∠BAF=∠ACE=22.5°,再根据点A、G、C、D四点共圆得到∠ADG=∠ACE,然后利用两组角对应相等,两三角形相似判断出②正确;求出△ACF和△HCD相似,利用相似三角形对应边成比例列式求解即可得到AF=DH,判断出③正确;根据S四边形ADCG=S△ACG+S△ADC,利用三角形的面积列出整理成AF•DG的形式,再把AF用DG表示,然后代入进行计算即可判断④正确.解答:解:。
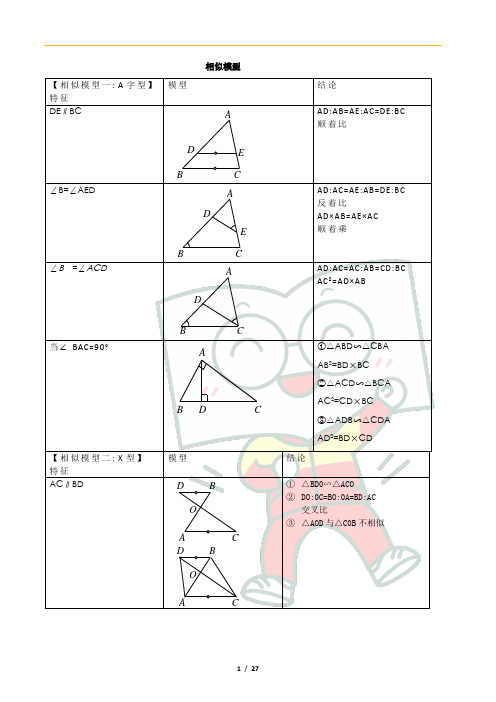
中考数学几何专项——相似模型(相似三角形)
相似模型【相似模型一: A 字型】 特征 模型 结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB C BDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD【相似模型二: X 型】 特征 模型 结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C(也叫蝴蝶型相似)A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D ③ 顺着比, 交叉乘 ④ △BOC∽△DOA【相似模型三: 旋转相似】 特征 模型结论成比例线段共端点① △ABC ∽△ADE ② △ABD∽△ACE【相似模型四: 三平行模型】 特征 模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=【相似模型五: 半角模型】 特征模型 结论ECD BAA BDC EEDCBA90度, 45度; 120度, 60度 120度,60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六: 三角形内接矩形模型】 特征模型 结论矩形EFGH 或正方形EFGH 内接与三角形H GFED C BA【相似模型七: 十字模型】 特征 模型结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE, 则AF=BE,②若AF ⊥BE ,则AF=BE,长方形PEAB CD矩形ABCD 中, CE ⊥BD, 则△CDE ∽△BCD,平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中, AB =AC,AB ⊥AC, ①D 为中点, ②AE ⊥BD, ③BE :EC =2:1, ④∠ADB =∠CDE, ⑤∠AEB =∠CED,⑥∠BMC =135°, ⑦ , 这七个结论中, “知二得五”【A 型, X 型, 三平行模型】1.如图, 在△ABC 中, EF ∥DC, ∠AFE=∠B, AE=6, ED=3, AF=8, 则AC=_________, _________.F E DCBABCDE FA2. 如图, AB ∥CD, 线段BC, AD 相交于点F, 点E 是线段AF 上一点且满足∠BEF=∠C, 其中AF=6, DF=3, CF=2, 则AE=_________.3.如图, 在Rt △ABD 中, 过点D 作CD ⊥BD, 垂足为D, 连接BC 交AD 于点E, 过点E 作EF ⊥BD 于点F, 若AB=15, CD=10, 则BF:FD=_____________.FEBCD AN MEDCBA4.如图, 在□ABCD中, E为BC的中点, 连接AE, AC, 分别交BD于M, N, 则BM:DN=_____________.5.如图所示, AB∥CD, AD, BC相交于点E, 过E作EF∥AB交BD于点F.则下列结论:①△EFD∽△ABD;②;③;④.其中正确的有___________.F EDCBA图26.在△ABC中, AB=9, AC=6, 点M在边AB上, 且AM=3, 点N在AC边上.当AN= 时, △AMN与原三角形相似.7.如图, 在△ABC中, ∠C=90°, AC=8, BC=6, D是边AB的中点, 现有一点P位于边AC上, 使得△ADP与△ABC相似, 则线段AP的长为.8.如图, 已知O是坐标原点, 点A.B分别在轴上, OA=1, OB=2, 若点D在轴下方, 且使得△AOB与△OAD相似, 则这样的点D有个.9.如图, 在Rt△ACB中, ∠C=90°, AC=16cm, BC=8cm, 动点P从点C出发, 沿CA方向运动;动点Q同时从点B出发, 沿BC方向运动,如果点P的运动速度均为4cm/s, Q点的运动速度均为2cm/s, 那么运动几秒时, △ABC与△PCQ相似.10.将△ABC的纸片按如图所示的方式折叠, 使点B落地边AC上, 记为点B', 折叠痕为EF, 已知AB=AC=8, BC=10,若以点B'.F.C为顶点的三角形与△ABC相似, 那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图, 四边形中, 平分, , , 为的中点.(1)求证: ;(2)与有怎样的位置关系?试说明理由;(3)若, , 求的值.13.如图, 在中, 为上一点, , , , 于, 连接.(1)求证:;(2)找出图中一对相似三角形, 并证明.14.如图, 在中, , 分别是, 上的点, , 的平分线交于点, 交于点.(1)试写出图中所有的相似三角形, 并说明理由(2)若, 求的值.15.如图, 在平行四边形ABCD中, 对角线AC.BD交于点O. M为AD中点, 连接CM交BD于点N, 且ON=1.(1)求BD的长;(2)若△DCN的面积为2, 求四边形ABNM的面积.16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB = _________.19.如图所示, AD=DF=FB, DE∥FG∥BC,则=__________.20.如图, 在矩形ABCD中, 对角线AC, BD相交于点O, OE⊥BC于点E, 连接DE交OC于点F, 作FG⊥BC于点G, 则线段BG与GC的数量关系是___.21.如图, 已知点C为线段AB的中点, CD⊥AB且CD=AB=4, 连接AD, BE⊥AB, AE是∠DAB的平分线, 与DC相交于点F, EH⊥DC于点G, 交AD 于点H, 则HG的长为 .22.如图1, 在△ABC 中, 点D.E 、Q 分别在边AB.AC.BC 上, 且DE ∥BC, AQ 交DE 于点P. (1)求证: ;(2)如图, 在△ABC 中, ∠BAC=90°, 正方形DEFG 的四个顶点在△ABC 的边上, 连接AG 、AF, 分别交DE 于M 、N 两点. 如图2, 若AB=AC=1, 直接写出MN 的长;如图3, 求证MN2=DM【母子型】1.已知: 如图, △ABC 中, ∠ACB=90°, CD ⊥AB 于D, S △ABC=20, AB=10。
中考数学相似难题压轴题精选

1.如图,在正三角形 【1 】中,,,分离是,,上的点,,,,则的面积与的面积之比等于()A .1∶3B .2∶3C .∶2D .∶32.如图,在中,的垂直等分线交的延伸线于点,则的长为()A .B .C .D .23.提出问题:如图,有一块散布平均的等腰三角形蛋糕(,且),在蛋糕的边沿平均散布着巧克力,小明和小华决议只切一刀将这块蛋糕等分(请求分得的蛋糕和巧克力质量都一样).布景介绍:这条朋分直线即等分了三角形的面积,又等分了三角形的周长,我们称这条线为三角形的“等分积周线”.测验测验解决:(1)小明很快就想到了一条朋分直线,并且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而等分蛋糕. (2) 小华认为小明的办法很好,所以本身模拟着在图1中过点C 画了一条直线CD 交AB于点D .你认为小华会成功吗?如能成功,说出肯定的办法;如不克不及成功,请解释来由. (3)经由过程上面的实践,你必定有了更深入的熟悉.请你解决下面的问题:若AB =BC =5 cm, AC =6 cm,请你找出△ABC 的所有“等分积周线”,并扼要的解释白定的办法.4.如图,点P 是菱形ABCD 的对角线BD 上一点,贯穿连接CP 并延伸,交AD 于E,交BA 的延伸线点F .问: (1) 图中△APD 与哪个三角形全等?并解释来由. (2) 求证:△APE ∽△FPA .(3) 猜测:线段PC.PE.PF 之间消失什么关系?并解释来由.5.如图1,在中,,于点,点是边AB C AB C B 图 1 C B 图 2 CBBAACO E DDECO F图1 图2F上一点,衔接交于,交边于点.(1)求证:;(2)当为边中点,时,如图2,求的值;(3)当为边中点,时,请直接写出的值.6.已知∠ABC=90°,AB=2,BC=3,AD ∥BC,P 为线段BD 上的动点,点Q 在射线AB 上,且知足(如图1所示).(1)当AD=2,且点与点重应时(如图2所示),求线段的长;(2)在图中,贯穿连接.当,且点在线段上时,设点之间的距离为,,个中暗示△APQ 的面积,暗示的面积,求关于的函数解析式,并写出函数界说域;(3)当,且点在线段的延伸线上时(如图3所示),求的大小. 7.如图1,在平面直角坐标系中,O 为坐标原点,点A 的坐标为,直线BC 经由点,,将四边形OABC绕点O 按顺时针偏向扭转度得到四边形,此时直线.直线分离与直线BC 订交于点P .Q .(1)四边形OABC 的外形是,当时,的值是;(2)①如图2,当四边形的极点落在轴正半轴时,求的值; ②如图3,当四边形的极点落在直线上时,求的面积.ADPCBQ 图1D APCB (Q )图2图3 C ADPB Q(3)在四边形OABC扭转进程中,当时,是否消失如许的点P和点Q,使?若消失,请直接写出点P的坐标;若不消失,请解释来由.8.如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上活动,设AP=,现将纸片折叠,使点D与点P重合,得折痕EF(点E.F为折痕与矩形边的交点),再将纸片还原.(1)当时,折痕EF的长为_______;当点E与点A重应时,折痕EF的长为_______;(2)请写出使四边形EPFD为菱形的的取值规模,并求出当时菱形的边长;(3)令,当点E在AD.点F在BC上时,写出与的函数关系式.当取最大值时,断定与是否类似?若类似,求出的值;若不类似,请解释来由.9.如图,在中,的面积为25,点为边上的随意率性一点(不与.重合),过点作,交于点.设,认为折线将翻折(使落在四边形地点的平面内),所得的与梯形重叠部分的面积记为.(1)用暗示的面积;(Q)CBA O xP(图3)yQCBA O xP(图2)yCBA Oyx(备用图)(第26题)EDB CA(2)求出时与的函数关系式;(3)求出时与的函数关系式;(4)当取何值时,的值最大?最大值是若干?10.如图,已知一个三角形纸片,边的长为8,边上的高为,和都为锐角,为一动点(点与点不重合),过点作,交于点,在中,设的长为,上的高为.(1)请你用含的代数式暗示.(2)将沿折叠,使落在四边形地点平面,设点落在平面的点为,与四边形重叠部分的面积为,当为何值时,最大,最大值为若干?11.如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延伸线与CB的延伸线交于点F.(1)求证:FD2=FB·FC.(2)若G是BC的中点,衔接GD,GD与EF垂直吗?并解释来由.12.正方形边长为4,.分离是.上的两个动点,当点在上活动时,保持和垂直, (1)证实:;(2)设,梯形的面积为,求与之间的函数关系式;当点活动到什么地位时,四边形面积最大,并求出最大面积;(3)当点活动到什么地位时,求的值.13.如图,在梯形ABCD中,,,,,点由B动身沿BD偏向匀速活动,速度为1cm/s;同时,线段EF由DC动身沿DA偏向匀速活动,速度为1cm/s,交于Q,衔接PE.若设活动时光为(s)().解答下列问题:(1)当为何值时,?(2)设的面积为(cm2),求与之间的函数关系式;(3)是否消失某一时刻,使?若消失,求出此时的值;若不消失,解释来由.(4)衔接,在上述活动进程中,五边形的面积是否产生变更?解释来由.14.如图,已知直线与直线订交于点分离交轴于两点.矩形的极点分离在直线上,极点都在轴上,且点与点重合.(1)求的面积;(2)求矩形的边与的长;(3)若矩形从原点动身,沿轴的反偏向以每秒1个单位长度的速度平移,设移动时光为秒,矩形与重叠部分的面积为,求关于的函数关系式,并写出响应的的取值规模.15.△ABC是一块等边三角形的废铁片,应用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,极点F.G分离落在AC.AB上.Ⅰ.证实:△BDG≌△CEF;Ⅱ. 探讨:如何在铁片上精确地画出正方形.小聪和小明各给出了一种设法主意,请你在Ⅱa和Ⅱb的两个问题中选择一个你爱好的问题解答. 假如两题都解,只以Ⅱa的解答记分.Ⅱa. 小聪想:要画出正方形DEFG,只要能盘算出正方形的边长就能求出BD和CE的长,从而肯定D点和E点,再画正方形DEFG就轻易了.设△ABC的边长为2 ,请你帮小聪求出正方形的边长(成果用含根号的式子暗示,不请求分母有理化) .Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:①在AB边上任取一点G’,如图作正方形G’D’E’F’;②贯穿连接BF’并延伸交AC于F;AB CD EFG图 (1)AB CD EFG图 (2)AB CD EFG图 (3)G′F′E′D′ADBEOCF xyy(G)GF ED CBA③作FE ∥F’E’交BC 于E,FG ∥F′G′交AB 于G,GD ∥G’D’交BC 于D,则四边形DEFG 即为所求. 你认为小明的作法精确吗?解释来由.16.如图11,在统一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一路,A 为公共极点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC 固定不动,∆AFG 绕点A 扭转,AF.AG 与边BC 的交点分离为D.E(点D 不与点B 重合,点E 不与点C 重合),设BE=m,CD=n.(1)请在图中找出两对类似而不全等的三角形,并拔取个中一对进行证实. (2)求m 与n 的函数关系式,直接写出自变量n 的取值规模.(3)以∆ABC 的斜边BC 地点的直线为x 轴,BC 边上的高地点的直线为y 轴,树立平面直角坐标系(如图12).在边BC 上找一点D,使BD=CE,求出D 点的坐标,并经由过程盘算验证BD +CE =DE .(4)在扭转进程中,(3)中的等量关系BD +CE =DE 是否始终成立,若成立,请证实,若不成立,请解释来由.GyxOF E DCBA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
01.如图,平行四边形ABCD 的面积是60,E 、F 分别是AB 、BC 的中点,AF 与DE 、DB 分别交于G 、H ,求四边形EBHG 的面积。
04.如图,在直线l 的同侧有三个相邻的等边三角形△ABC 、△ADE 、△AFG ,且G 、A 、B 都在直线l 上,设这三个三角形边长分别为a 、b 、c ,连结GD 交AE 于N ,连BN 交AC 于L ,求AL 的长。
09.如图207,正△ABC 和正△A 1B 1C 1,点O 既是AC 的中点又是A 1C 1的中点,则AA 1 : BB 1=________。
10.如图208,边长为1的等边△ABC ,BC 上有一点D ,BD=13
,AC 上有一点E ,∠ADE=60°,则EC=________,S △ADE =________。
08.如图206,在△ABC 中,∠A=90°,AD ⊥BC 于D ,P 为AD 的中点,BP 交AC 于E ,EF ⊥BC 于F 。
若AE=3,EC=12,则EF=________。
17、(2013•牡丹江)如图,在△ABC 中∠A=60°,BM ⊥AC 于点M ,CN ⊥AB 于点N ,P 为BC 边的中点,连接PM ,PN ,则下列结论:①PM=PN ;②
;③△PMN 为等边三角形;④当∠ABC=45°时,BN=PC .其
中正确的个数是( )
5、(2013•自贡)如图,在平行四边形ABCD 中,AB=6,AD=9,∠BAD 的平分线交BC 于E ,交DC 的延长线于F ,BG ⊥AE 于G ,BG=,则△EFC 的周长为( )
例2、已知在平行四边形ABCD 中,M 、N 为AB 的三等分点,DM 、DN 交于AC 于P 、Q 两点。
求AP :PQ :QC 的值。
8. (2012福建莆田,24,12分)
(1)(3分)如图①,在Rt △ABC 中,∠ABC=90°,BD ⊥AC 于点D .
求证:AC AD AB ∙=2;
(2) (4分)如图②,在Rt △ABC 中,∠ABC =90°,点D 为BC 边上的点,BE ⊥AD 于点E ,延长BE 交AC 于点F .1AB BD BC DC
==,求AF FC 的值; (3)(5分)在Rt △ABC 中,∠ABC =90°,点D 为直线BC 上的动点..
(点D 不与B 、C 重合),直线BE ⊥AD
于点E ,交直线AC 于点F .若
AB BD n BC DC
==,请探究并直接写出AF FC 的所有可能的值(用含n 的式子表示),不必证明. D B
A C E F C
B
A D
9.(2012湖北黄石,24, 9分)如图(10)所示:等边△ABC 中,线段AD 为其内角角平分线,过D 点的直线B 1C 1⊥AC 于C 1交AB 的延长线于B 1.
⑴请你探究:AC CD AB DB
=,1111AC C D AB DB =错误!未找到引用源。
是否都成立? ⑵请你继续探究:若△ABC 为任意三角形,线段AD 为其内角角平分线,请问AC CD AB DB
=一定成立吗?并证明你的判断.
⑶如图(11)所示Rt △ABC 中,∠ACB =900 ,AC =8,AB =403
,E 为AB 上一点且AE =5,CE
交其内角角平分线AD 于F .
试求DF FA 的值.
10.(2012四川攀枝花,24,12分)如图10所示,在形状和大小不确定的△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,P 在EF 或EF 的延长线上,BP 交CE 于D ,Q 在CE 上且BQ 平分∠CBP ,设BP =y ,PE =x .
(1)当EF x 3
1=
时,求D BC D PE S S ∆∆:的值; (2)当CQ =2
1CE 时,求y 与x 之间的函数关系式; (3)①当CQ =31CE 时,求y 与x 之间的函数关系式;②当CQ =n 1CE (n 为不小于2的常数)时,求直接y 与x 之间的函数关系式;
D F A B C
E P Q D
F A
B
C E P
Q
(1) (2)。
