高一数学空间几何体的结构2
高中数学必修2导学案

高中数学必修2导学案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN高一数学必修2 编制:廖信山审核:王育仁使用时间:2013年11月___日班级:__________ 组别:_________ 组号:_________ 姓名:___________空间几何体的结构(1)【学习目标】1.通过观察模型、图片,使学生理解并能归纳出棱柱、棱锥、棱台的结构特征。
2.通过对棱柱、棱锥、棱台的观察分析,培养学生的观察能力、空间想象能力和抽象概括能力。
3.通过教学活动,逐步培养学生探索问题的精神。
【自主学习】任务一阅读教材第2~3页,回答下列问题:1.空间几何体:____________________________________________________ 。
2.什么是多面体、多面体的面、棱、顶点?3.什么是旋转体、旋转体的轴?任务二阅读教材第3~4页,回答下列问题:1.什么是棱柱、棱柱的底、侧面、侧棱、顶点有什么特征如何表示如何分类思考:正方体、长方体是棱柱吗?2.什么是棱锥、棱锥的底、侧面、侧棱、顶点有什么特征如何表示如何分类思考:有一个面是多边形,其余各面是三角形的多面体是棱锥吗?3.什么是棱台、棱台的底、侧面、侧棱、顶点有什么特征如何表示如何分类2【合作探究】1.棱柱、棱锥、棱台都是多面体,当底面发生变化时,它们能否互相转化呢?【目标检测】A级:必做题1.一个多面体至少有________个面,面数最少的棱柱有_________个顶点。
2.在三棱锥A-BCD,可以当作棱锥底面的三角形的个数为()A.1B.2C.3D.43.在棱柱中()A、只有两个面平行B、所有的棱都平行C、所有的面都是平行四边形D、两底面平行,且各侧棱也互相平行4.棱台不具有的性质是()A.两底面平行且相似B.侧面都是梯形C.侧棱都平行D.侧棱延长后必交于一点B级:选做题1、若一个棱锥的侧面都是等边三角形,这个棱锥最多是()棱锥。
高一数学空间几何体的结构课件

探究问题
分别以直角三角形的不同的边所在的直线为 轴旋转三角形得到的旋转体形状相同吗? 如果不 同请你画出来。
1.1.1 柱、 锥、 台、 球
的结构特征
1. 棱柱的结构特征
什么叫棱柱? 有两个面互相平行, 其余各面都是四边形,并 且每相邻两个四边形的公 共边都互相平行,由这些 面围成的多面体叫做棱柱.
1.1 空间几何体的结构
奥运场馆
鸟巢
奥运场馆
水立方
世博场馆
中国馆 世博轴
演艺中心
在我们周围存在着各种各样的物体,它们 都占据着空间的一部分,如果我们只考虑 这些物体的形状和大小,而不考虑其它因 素,那么由这些抽象出来的空间图形就叫 做空间几何体.
11/12/2014
5
观察这八个几何体,说说它们有何共同的特 征?
思考 ? 这两个几何体与棱锥有什么关系?
S
截面A' B ' C ' D ' E '∽ 底面 ABCDE
E'
A' D' C' B'
D O
E A
C
B
3. 棱台的结构特征
什么是棱台? 一般地,用一个平行于棱锥底面的平面去截 棱锥,底面和截面中间的部分的多面体叫做棱台.
上底面 侧面
侧棱
下底面
顶点
三棱台
(2)侧面都是平行四边形. F
底面
18
(3)侧棱平行且相等.
11/12/2014
顶点
2.棱锥的结构特征
什么是棱锥?
一般地,有一个面是 多边形,其余各面都是有 一个公共点的三角形,由 这些面围成的多面体叫做 棱锥.
符号表示:四棱锥S-ABCD
高一数学必修2-第一章空间几何体知识点

第一章空间几何体1.1 空间几何体的结构1. 多面体与旋转体:(1)由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面.相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.(2)由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转体,这条定直线叫做旋转体的轴.2. 棱柱:(1)有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.棱柱中,两个互相平行的面叫做棱柱的底面(简称底),其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点.(2)侧棱垂直于底面的棱柱叫直棱柱,否则斜棱柱;底面是正多边形的直棱柱叫正棱柱。
(3)棱柱的分类:按底面的多边形的边数分,有三棱柱、四棱柱、五棱柱等.按侧棱与底面的关系分为直棱柱和斜棱柱。
(4)底面是平行四边形的四棱柱叫平行六面体;侧棱与底面垂直的平行六面体叫直平行六面体;底面为矩形的直平行六面体叫长方体;底面为正方形的长方体叫正四棱柱;棱长都相等的正四棱柱叫正方体。
(5)棱柱的性质:①两底面是对应边平行的全等多边形;②侧面、对角面都是平行四边形;③侧棱平行且相等;④平行于底面的截面是与底面全等的多边形。
3. 棱锥:(1)有一个面是多边形,其余各面都是有一公共点的三角形,由这些面所围成的几何体叫做棱锥.棱锥中,这个多边形面叫做棱锥的底面或底,有公共顶点的各个三角形面叫做棱锥的侧面,各侧面的公共顶点叫做棱锥的顶点,相邻侧面的公共边叫做棱锥的侧棱.(2)底面是正多边形,顶点在底面的射影是正多边形的中心的棱锥叫正棱柱。
正棱柱顶点与底面中心的连线段叫正棱锥的高;正棱锥侧面等腰三角形底边上的高叫正棱锥的斜高。
(3)棱锥的分类:按底面的多边形的边数分,有三棱锥、四棱锥、五棱锥等.(4)棱锥的性质:①侧面、对角面都是三角形;②平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方.(5)正棱锥的性质:①正棱锥各侧棱都相等,各侧面都是全等的等腰三角形。
高一数学知识点总结_空间几何体的结构知识点

⾼⼀数学知识点总结_空间⼏何体的结构知识点⾼⼀数学怎么学? 学⽣学习期间,在课堂的时间占了⼀⼤部分。
因此听课的效率如何,决定着学习的基本状况,今天⼩编在这给⼤家整理了⾼⼀数学知识点总结,接下来随着⼩编⼀起来看看吧!⾼⼀数学知识点总结(⼀)空间⼏何体的结构知识点1、静态的观点有两个平⾏的平⾯,其他的⾯是曲⾯;动态的观点:矩形绕其⼀边旋转形成的⾯围成的旋转体,象这样的旋转体称为圆柱。
2、定义:以矩形的⼀边所在直线为旋转轴,其余各边旋转⽽形成的的曲⾯所围成的旋转体叫做圆柱,旋转轴叫圆柱的轴;垂直于旋转轴的边旋转⽽成的圆⾯叫做圆柱的底⾯;平⾏于圆柱轴的边旋转⽽成的⾯叫圆柱的侧⾯,圆柱的侧⾯⼜称圆柱的⾯。
⽆论转到什么位置,不垂直于轴的边都叫圆柱侧⾯的母线。
表⽰:圆柱⽤表⽰轴的字母表⽰。
规定:圆柱和棱柱统称为柱体。
3、静态观点:有⼀平⾯,其他的⾯是曲⾯;动态的观点:直⾓三⾓形绕其⼀直⾓旋转形成的⾯围成的旋转体,像这样的旋转体称为圆锥。
4、定义:以直⾓三⾓形的⼀条直⾓边所在的直线为旋转轴,其余两边旋转⽽形成的⾯所围成的旋转体叫做圆锥。
旋转轴叫圆锥的轴;垂直于旋转轴的边旋转⽽成的圆⾯成为圆锥的底⾯;不垂直于旋转轴的边旋转⽽成的曲⾯叫圆锥的侧⾯,圆锥的侧⾯⼜称圆锥的⾯,⽆论旋转到什么位置,这条边都叫做圆锥侧⾯的母线。
表⽰:圆锥⽤表⽰轴的字母表⽰。
规定:圆锥和棱锥统称为锥体。
5、定义:以半直⾓梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转⽽形成的曲⾯所围成的⼏何体叫圆台。
还可以看成⽤平⾏于圆锥底⾯的平⾯截这个圆锥,截⾯于底⾯之间的部分。
旋转轴叫圆台的轴。
垂直于旋转轴的边旋转⽽形成的圆⾯称为圆台的底⾯;不垂直于旋转轴的边旋转⽽成的曲⾯叫做圆台的侧⾯,⽆论转到什么位置,这条边都叫圆台侧⾯的母线。
表⽰:圆台⽤表⽰轴的字母表⽰。
规定:圆台和棱台统称为台体。
6、定义:以半圆的直径所在的直线为旋转轴,将半圆旋转⼀周所形成的曲⾯称为球⾯,球⾯所围成的旋转体称为球体,简称为球。
空间几何体的结构_王素华.ppt

三棱柱
四棱柱
五棱柱
四、棱柱的表示
用底面各顶点的字母表示棱柱。
三棱柱ABC-A'B'C' 四棱柱ABCD-A'B'C'D'
六棱柱ABCDEF-A'B'C'D'E'F
常见的棱柱
长方体:侧面和底面都是矩形的棱柱. 正方体:侧面和底面都是正方形的棱柱.
棱柱的结构特征
思考:你能举出关于棱柱的生活实例吗?
么四边形?
平行四边形
理论迁移
例1、过BC的截面截长方体的一角,使 EF∥B’C’所得的几何体是不是棱柱,为 什么?
D' F C'
D' D C
A' D
E
B' C
A
F
C'
B
A
B
A'
E
B'
思考:有两个面互相平行, 其余各面都是四边形的几何体是 棱柱吗? 答:不一定是.如右图所 示,不是棱柱. 思考:有两个面互相平行, 其余各面都是平行四边形的几 何体是棱柱吗? 答:不一定是.如右图所 示,不是棱柱.
底 面
E
侧棱 F
D
C
A
侧面
B
顶点
思考:棱柱上、下两个底面的形状大小 如何?各侧面的形状如何?
两底面是全等的多边形, 各侧面都是平行四边形
三、棱柱的分类
思考:各种各样的棱柱,主要有什么不 同?你认为棱柱的三 角形、四边形、五边形、 …… 我们把这 样的棱柱分别叫做三棱柱、四棱柱、五棱 柱、……
二、棱柱的有关概念
两个互相平行的面 棱柱的底面:
H/
江苏省盐城中学高中数学立体几何知识点总结

高一立体几何知识梳理盐城中学高一数学组一、空间几何体(一)空间几何体的类型多面体:由若干个平面多边形围成的几何体.围成多面体的各个多边形叫做多面体的相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体.其这条直线称为旋转体的轴.(二)几种空间几何体的结构特征1 、棱柱的结构特征1.1 棱柱的定义:由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.1.2 棱柱的分类图1-1棱柱①棱柱,械垂直于底面》直棱柱 底山是多形)正棱柱其他棱柱…底面是四边形 棱柱 底面是平行四边形 四棱柱平行六面体 侧棱垂直于底面直平行底面是矩形底面是正方形 六面体长方体 性质:棱长都相等 正四棱柱正方体I 、II 、m 、1.3 侧面都是平行四边形,且各侧棱互相平行且相等;两底面是全等多边形且互相平行;平行于底面的截面和底面全等;棱柱的面积和体积公式s 二ch (c 是底周长,h 是高) 直棱柱侧S 直棱柱表面=C ・h+2S 底2.1(V 棱柱=S 底•h棱锥的结构特征棱锥的定义)棱锥:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥.()正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底f斜棱柱面的中心,这样的棱锥叫做正棱锥.2.2正棱锥的结构特征I、平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;II、正棱锥的各侧棱相等,各侧面是全等的等腰三角形;III、两个特征三角形:()A POH(包含棱锥的高、斜高和底面内切圆半径);()A POB(包含棱锥的高、侧棱和底面外接圆半径)正棱锥侧面积:S=1ch'(c为底周长,h,为斜高)P正棱椎2体积:V=1Sh(S为底面积,h为高)DC棱椎3OHAB正四面体:各条棱长都相等的三棱锥叫正四面体2对于棱长为a正四面体的问题可将它补成一个边长为—a的正方体问题.211正四面体的中心到底面与顶点的距离之比为1:3(=-/』舟3:/十6正方体体对角线2正方体体对角线3、棱台的结构特征3.1棱台的定义:用一个平行于底面的平面去截棱锥,我们把截面和底面之间的部分称为棱台.3.2正棱台的结构特征(1)各侧棱相等,各侧面都是全等的等腰梯形;(2)正棱台的两个底面和平行于底面的截面都是正多边形;(3)正棱台的对角面也是等腰梯形;(4)各侧棱的延长线交于一点.4、圆柱的结构特征4.1圆柱的定义:以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.4.2圆柱的性质(1)上、下底及平行于底面的截面都是等圆;(2)过轴的截面(轴截面)是全等的矩形.4.3圆柱的侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形.4.4圆柱的面积和体积公式S圆柱侧面=2n•r•h(r为底面半径,h为圆柱的高)V圆、=S h=nr2h5、圆锥的结构特征5.1圆锥的定义:以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆锥.5.2圆锥的结构特征(1)平行于底面的截面都是圆,截面直径与底面直径之比等于顶点到截面的距离与顶点到底面的距离之比;(2)轴截面是等腰三角形;(3)母线的平方等于底面半径与高的平方和:l2=r2+h25.3圆锥的侧面展开图:圆锥的侧面展开图是以顶点为圆心,以母线长为半径的扇形.6、圆台的结构特征6.1圆台的定义:用一个平行于底面的平面去截圆锥,我们把截面和底面之间的部分称为圆台.6.2圆台的结构特征⑴圆台的上下底面和平行于底面的截面都是圆;⑵圆台的截面是等腰梯形;⑶圆台经常补成圆锥,然后利用相似三角形进行研究.6.3圆台的面积和体积公式S圆台侧=n•(R+r)•l(r、R为上下底面半径)V1=1/3(n r2+n R2+n rR)h(h为圆台的高)7球的结构特征7.1球的定义:以半圆的直径所在的直线为旋转轴,半圆旋转一周形成的旋转体叫做球体.空间中,与定点距离等于定长的点的集合叫做球面,球面所围成的几何体称为球体.7-2球的结构特征⑴球心与截面圆心的连线垂直于截面;⑵截面半径等于球半径与截面和球心的距离的平方差:r2=R2-d2⑶注意圆与正方体的两个关系:球内接正方体,球直径等于正方体对角线;球外切正方体,球直径等于正方体的边长.7-3球的面积和体积公式S=4nR2(R为球半径);V=4/3nR3(三)空球面间几何体的表面积与体积球空间几何体的表面积棱柱、棱锥的表面积:各个面面积之和圆柱的表面积:S=2兀rl+2兀r2圆锥的表面积:S=兀rl+兀丫2圆台的表面积:S=兀r1+兀丫*兀Rl+兀R2球的表面积:S=4兀R2空间几何体的体积柱体的体积:V=S L X h;锥体的体积:v=1S X h底,3底1.T74〜台体的体积:V=-(S+JSS+S)X h;球体的体积:V二万兀R33上%’上下下3斜二测画法:(1)平行于坐标轴的线依然平行于坐标轴;(2)平行于y轴的线长度变半,平行于x,z轴的线长度不变;二、点、直线、平面之间的关系(一)、立体几何网络图:1、线线平行的判断:(1)平行于同一直线的两直线平行.(3)如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(6)如果两个平行平面同时和第三个平面相交,那么它们的交线平行.(12)垂直于同一平面的两直线平行.2、线线垂直的判断:(7)三垂线定理:在平面内的一条直线,如果和这个平面7的一条斜线的射影垂直,那么它也和这条斜线垂直.(8)三垂线逆定理:在平面内的一条直线,如果和这个平/:□力面的一条斜线垂直,那么它和这条斜线的射影垂直.人二L如图,已知PO ±a ,斜线PA 在平面a 内的射影为OA ,a 是平面a 内一条直线. ①三垂线定理:若a ^OA ,则a ^PA .即垂直射影则垂直斜线.②三垂线定理逆定理:若a ^PA ,则a ^OA .即垂直斜线则垂直射影.(10)若一直线垂直于一个平面,则这条直线垂直于平面内所有直线.补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条.3、线面平行的判断:(2)如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.(5)两个平面平行,其中一个平面内的直线必平行于另一个平面.判定定理:allb[线线平行n 线面平行)性质定理:aliauu/i〔线面平行n线线平行)CK H p-b★判断或证明线面平行的方法⑴利用定义(反证法):/I a=0,则l〃a(用于判断);⑵利用判定定理:线线平行0线面平行(用于证明);⑶利用平面的平行:面面平行n线面平行(用于证明);⑷利用垂直于同一条直线的直线和平面平行(用于判断).2线面斜交和线面角:/Aa=A2.1直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角0.2.2线面角的范围:0£[0°,90°]注意:当直线在平面内或者直线平行于平面时,0=0°;当直线垂直于平面时,0=90°4、线面垂直的判断:(9)如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面.(11)如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面.(14)一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.(16)如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面.判定定理:。
新课标人教A版-高一数学必修二定理总结
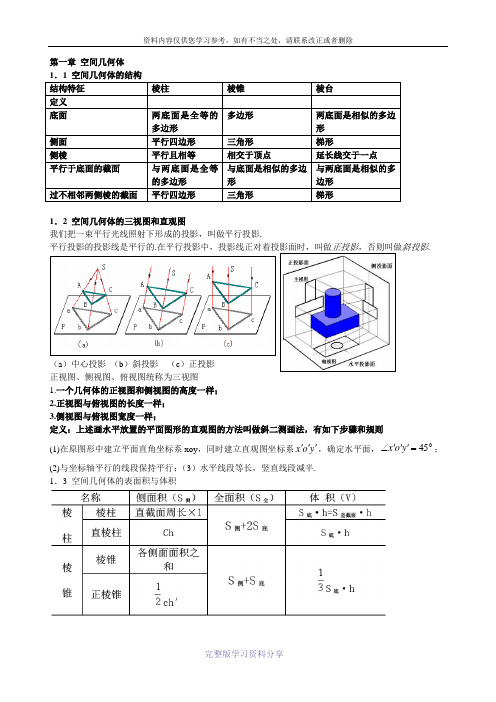
第一章 空间几何体 1.1 空间几何体的结构 结构特征 棱柱 棱锥 棱台 定义底面 两底面是全等的多边形 多边形 两底面是相似的多边形 侧面 平行四边形 三角形 梯形侧棱平行且相等 相交于顶点 延长线交于一点 平行于底面的截面 与两底面是全等的多边形 与底面是相似的多边形 与两底面是相似的多边形 过不相邻两侧棱的截面平行四边形三角形梯形1.2 空间几何体的三视图和直观图我们把一束平行光线照射下形成的投影,叫做平行投影.平行投影的投影线是平行的.在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影.(a )中心投影 (b )斜投影 (c )正投影 正视图、侧视图、俯视图统称为三视图1.一个几何体的正视图和侧视图的高度一样;2.正视图与俯视图的长度一样;3.侧视图与俯视图宽度一样;定义:上述画水平放置的平面图形的直观图的方法叫做斜二测画法,有如下步骤和规则(1)在原图形中建立平面直角坐标系xoy ,同时建立直观图坐标系y o x ''',确定水平面,045='''∠y o x ; (2)与坐标轴平行的线段保持平行;(3)水平线段等长,竖直线段减半. 1.3 空间几何体的表面积与体积表中S 表示面积,C ’、C 分别表示上、下底面周长,h 表示高,h ’表示斜高,l 表示侧棱长。
表示l 、h 分别表示母线、高,r 表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台上、下底面半径,R 表示半径。
第二章 点、直线、平面之间的位置关. 2.1 空间点、直线、平面之间的位.平面特征:平面没有大小、厚薄和宽窄,几何里的平面是无限延展的.平面内有无数个点,平面可以看成点的集合. 点A 在平面α内,记作A ∈α;点B 在平面α外,记作B ∉α.直线 l 在平面α内表示为α⊂l ;直线l 不在平面α内表示为α⊄m . 公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 公理2:过不在一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.公理2 推论1:经过一条直线和这条直线外一点,有且只有一个平面。
高一数学必修二

高一数学必修二第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积1.柱、锥、台、球的结构特征(1)柱棱柱:一般的,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱;棱柱中两个互相平行的面叫做棱柱的底面,简称为底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点。
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……圆柱:以矩形的一边所在的直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱;旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
棱柱与圆柱统称为柱体。
(2)锥棱锥:一般的有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥;这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱。
底面是三角锥、四边锥、五边锥……的棱柱分别叫做三棱锥、四棱锥、五棱锥……圆锥:以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥;旋转轴为圆锥的轴;垂直于轴的边旋转形成的面叫做圆锥的底面;斜边旋转形成的曲面叫做圆锥的侧面。
棱锥与圆锥统称为锥体。
(3)台棱台:用一个平行于底面的平面去截棱锥,底面和截面之间的部分叫做棱台;原棱锥的底面和截面分别叫做棱台的下底面和上底面;棱台也有侧面、侧棱、顶点。
圆台:用一个平行于底面的平面去截圆锥,底面和截面之间的部分叫做圆台;原圆锥的底面和截面分别叫做圆台的下底面和上底面;圆台也有侧面、母线、轴。
圆台和棱台统称为台体。
(4)球以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称为球;半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.圆柱的结构特征
以矩形的一边所在 问题 1:圆柱可以由什么 直线为旋转轴 ,其余边旋 平面图形旋转得到? 转形成的面所围成的旋 旋转体: 转体叫做圆柱。 所谓旋转体,就是把 问题 2: 模仿圆锥,表示 一个平面图形绕它所在 图中圆柱,并指出圆柱 平面内的一条定直线旋 的轴,底面,侧面,以 转,所形成的封闭几何 及它的一条母线, 体。这条定直线称为旋 转体的轴。如:圆锥
A’
母 线 O’ B’
轴 侧 面
A
O B
底面
圆柱SO
5.棱台的结构特征
用一个平行于棱锥 底面的平面去截棱锥, 底面与截面之间的部 分是棱台.
表示:用表示底面的各 顶点的字母表示。 如: 棱台ABCD-A’B’C’D’
侧棱 A 顶点 B’ 上 底 C’ 面
D’
D A’
C 侧面
下底面 B
底面是三角形,四边形,五边形----的棱台 分别叫三棱台,四棱台,五棱台---
※.有两个面互相平行 ※.其余各面都是平行四边形
E’ F’ A’
B’ D’ C’
※.每相邻两个四边形的公共 边互相平行
概念:凡是符合上述特 征的多面体都叫棱柱。
底 面
E
侧棱 F
D
C
A
侧面
表示:用表示底面的各顶点的字母表示。 如:棱柱ABCDEF-A’B’D’E’F’ 注:多面体指的是若干个平面 多边形围成的几何体。
返回
4.圆锥的结构特征:
以直角三角形的一 条直角边所在直线为 旋转轴, 两余边旋转形 成的面所围成的旋转 体叫做圆锥。 圆锥可以用它的轴来表示。 如:圆锥SO
A 顶点 S 母 线 轴 侧 面
O
B
底面
返回
思考1:倾斜后的 几何体还是柱体 吗?
E’ F’ A’
D’
B’
C’
E F A
D C B
思考2:这是一个 台体吗?(可看 课本P10.第二题 图(一))
小结: 棱柱 棱锥 圆锥
棱柱 棱台 台体 锥体 柱体
圆柱
棱台
圆台
考一考:
空 间 几 何 体 多面体
棱锥
圆锥 旋转体 圆柱
圆台
球(自主探究)
多谢指导!
作业:课本习题1.1 1-2, 预习球的结构特征
多面体:若干个平面多边 形围成 的几何体。如图所示: 多面体的面:围成多面体的 各个 E’ 多边形。如:面ABCDEF F’ A’ 多面体的棱:相邻两个面的公共 边。如:棱AA’ 多面体的顶点:棱与棱的公共点。 如:顶点A’ F
返回
; 绝地求生辅助
vfg80wiv
了救仁家老夫人,你早就挨板子了。”没得我帮老妇人盖好被子,鼠头人又责骂道,“仁老夫人不用你瞎操心,待会儿就会有 丫鬟来照料她,你做好你的本分就行。”听着鼠头人这么讲道,我也识趣的走了,但是我还是担心不知这傅家会怎么对待仁老 夫人。我已经答应了仁玉要好好照顾仁老夫人,但是自己在这里又没什么权利,得想个办法才行啊。9初到傅府|接新娘一事已 经完了,但我没有忘记我要粘着傅家过日子的目的。我赶紧向鼠头人身旁靠过去,恭敬地说道:“傅总管,那么现在我们是不 是也该动身回傅家了?”鼠头人用眼角瞄了我一眼,轻蔑地说道:“这事用不着你提醒,赶紧把你们家的下人叫过来,好了我 们就出发回去。”“那现在就可以走了,这仁家就我一个下人。”我应和道。“哟,就你一个下人啊?”鼠头人轻蔑中带着满 满地嘲笑意味反问道,“那也难怪,这烂屋子穷主人请不起仆人也是正常的。”这话听的我真不爽,心想,起码这一屋子人都 是能吃苦过活的好人,哪像你这只鼠头,仗势欺人,小心活命不长。也罢,我也就只有想想的份,现在的我可不敢当面说这货 的不是。过没多久,鼠头人叫上原先傅家的下人,再带上我这个新加入的下人,一同往傅家走去了。果真走了好远的路,我们 终于来到了傅家大宅门前。傅家大宅可真是雄伟啊!光是大宅的正门,就足足有两层楼这么高;两侧的围墙似乎在无限地伸延 着,完全看不见尽头;加之以摆在门口两侧的两头石狮子以及金光闪闪的写着“傅府”二字的巨大门牌,真是突出一个霸气。 霸气是挺霸气的,门面也是做得很光亮的,但是就是不知道里面的人是些怎么样的人儿。话说十个官员九个贪,贪得越多自家 的宅子也才建得越风光,倘若里面的傅家人们都是些权利之人,那么就算他们的物质生活有多丰富,也始终感受不到家人的关 爱,始终不会懂亲情是什么,因为他们只是靠着金钱与权利联系在一起,血缘之情想必已经被丢弃在不知何处了。随着鼠头人 一同踏入傅家大宅的正门,迎面扑来的是气场十分强大的喜庆情景。虽说这是傅家四少爷娶一个小老婆,但是这壮观的场面实 在是令人难以与之前在仁家门前发生的事情联想起来。大厅里坐满了达官贵人,他们的穿着打扮无不显得高贵,仔细瞅瞅,发 现有着各式各样的人儿;肚子大得吓人的中年男人们应该是傅家大老爷在朝中的大臣朋友;一些看起来稍微显得年轻帅气的要 不是官员们的儿子侄子什么的,就是来保护他们的保镖们;再要数的就是那一群聚在一起的女人们,她们个个穿着极其夸张, 胭脂水粉想必涂得满脸都是,她们围在一起有说有笑的,时不时还会传来一阵阵高音度的笑声。这时,从大厅里走出一位妇女。 我仔细打量着她,心中硬是吃了一大惊,这真是
B
顶点
1.棱锥的结构特征
※ .有一个面是多边形 ※.其余各面都是三角形 ※.这些三角形都有一个公共顶点 概念:凡是符合上述特 征的多面体都叫棱锥。
侧棱
A D 侧面 C 底面 B S 顶点
棱锥可以表示为:棱锥S-ABCD 底面是三角形,四边形,五边形----的棱锥 分别叫三棱锥,四棱锥,五棱锥---
6.圆台的结构特征
用一个平行于圆锥底面 的平面去截圆锥,底面与截面 之间的部分是圆台.
问题:圆台与圆柱,圆锥 类似,都是旋转体,请问 圆台还可以由哪个平面图 形旋转得到?
问题2: 模仿圆柱,表示图中圆 台,并指出圆台的轴,上下底面, 侧面,以及它的一条母线,
O’ O
A
B
(1)
(2)
(3)
(4)
(5)
A E
D’ B’
C’
D
C
B
返回
浓厚的兴趣和较好 的 思维让你灵气十足. 执著的创造力和丰富 的想象力 ,总是让你 在生活中事半功倍。 但灵性不等于知识也 不等于智慧。
返回
你是一个情商极高 的人,为人处事都很 随和,但遇上原则性 的事,你也绝不含糊。
返回
少有的个性可能让身 边的人不太理解你, 但你最要好的朋友依 然会支持你,即使她 很难明白你的思想。
湖州一中
沈立英
形 状 与 大 小
(1)
(2)
(3)
(4)
(5)
如果我们只考虑物体占用空 间部分的形状和大小,而不 考虑其它因素,那么由这些 物体抽象出来的空间图形, 就叫做空间几何体。
(6)
(7)
(8)
(9)
(10)
1.1.1柱、锥、台、球的结构特征
1.棱柱:
1.棱柱 棱柱的结构特征: 1. :
很好的心理测试,耐心做完会 有意外惊喜(仅供娱乐):请 你凭第一感觉按自己的心愿给 下列图形分组,然后把答案写 在纸上,再点击
(6)
(7) (8)
(9)
请选择相应的选项: A.(1)(2)(3)(7),(4)(6)(9),(5)(8)
B.(1)(2)(4)(7)(8)(9), (3)(5)(6)
C. 其它
