北师大版八年级数学上拓展习题.docx
北师大版初二数学上册拓展

拓展资源:拓展练习在教学中,根据学生的实际情况,在学有余力的情况下,可用以下的例题和练习题进行知识的拓展:内容:例 已知042=++-y x ,求x y 的值. 解:因为 2-x 和4+y 都是非负数,并且042=++-y x ,所以 02=-x ,04=+y ,解得x =2,y = -4,所以16)4(2=-=x y .意图:加深对算术平方根概念中两层含义的认识,会用算术平方根的概念来解决有关的问题. 效果:达到能灵活运用算术平方根的概念和性质的目的.课后还可以布置相应的拓展性习题:内容:1.已知()0232212=++++-z y x ,求x+y+z 的值. 2.若x ,y 满足52112=+-+-y x x ,求xy 的值.3.求55=-+x x 中的x .4.若115+的小数部分为a ,115-的小数部分为b ,求a +b 的值.5.△ABC 的三边长分别为a ,b ,c ,且a ,b 满足04412=+-+-b b a ,求c 的取值范围. 解:1.因为21-x ≥0,()22+y ≥0,23+z ≥0,且()0232212=++++-z y x , 所以21-x =0,()22+y =0,23+z =0,解得21=x ,2-=y ,23-=z ,所以x +y +z = 3-. 2.因为2x -1≥0,1-2x ≥0,所以 2x -1=0,解得 x =21 ,当 x =21时,y =5,所以 x y =21×5=25. 3.解:因为x -5≥0,x x -=-55≥0 ,所以 x =5 .4.解:因为4113<< ,所以115+的整数部分为8,115-的整数部分为1,所以115+的小数部分3118115-=-+=a ,115-的小数部分1141115-=--=b ,所以1114311=-+-=+b a .5.解:由04412=+-+-b b a ,可得0)2(12=-+-b a ,因为 1-a ≥0,2)2(-b ≥0, 所以1-a =0,2)2(-b =0,所以a = 1,b = 2,由三角形三边关系定理有:b- a < c < b +a ,即1 < c < 3.。
北师大版八年级(上)数学《一次函数》回顾与思考拓展习题(含答案)

一次函数 拓展训练1.若点(m ,n )在函数y=2x+1的图象上,则2m ﹣n 的值是( ) A .2B .﹣2C .1D .﹣12.一次函数y=mx+∣m-1∣的图象过点(0,2)且y 随x 的增大而增大,则m=( ) A .-1 B .3 C . 1 D .-1或33.下列四组点中,可以在同一个正比例函数图象上的一组点是( ) A .(2.-3),(-4,6) B .(-2,3),(4,6) C .(-2,-3),(4,-6) D .(2,3),(-4,6)4.面直角坐标系中,点O 为原点,直线y kx b =+交x 轴于点A(-2,0),交y 轴于点B .若△AOB 的面积为8,则k 的值为( )A .1B .2C .-2或4D .4或-45.面直角坐标系中,把直线y=2x 向左平移一个单位长度后,其直线解析式为( )A .y=2x+1 B.y=2x+2 C.y=2x D. y=2x-26.在平面直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( ) A .通过点(-1,0)的是①③ B .交点在y 轴上的是②④ C .相互平行的是①③ D .关于x 轴对称的是②④7.若函数222-+-=+n x y m 是正比例函数,则m 的值是 ,n 的值为 8.一次函数y=kx+b 中,y 随x 的增大而减小,且kb>0,则这个函数的图象一定不经过第 象限.9.如图,一次函数y=kx+b 的图象与正比例函数y=2x 的图象平行且经过点A (1,﹣2),则kb=10.一辆汽车在行驶过程中,路程 y (千米)与时间 x (小时)之间的函数关系如图所示 当时 0≤x ≤1,y 关于x 的函数解析式为 ,那么当 1≤x ≤2时,y 关于x 的函数解析式为 _ .11.如图,射线OA 、BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s 、t 分别表示行驶距离和时间,则这两人骑自行车的速度相差 _ km/h .12.如图,在平面直角坐标系中,A 、B 均在边长为1的正方形网格格点上.求线段AB 所在直线的函数解析式,并写出当0<y ≤1时,自变量x 的取值范围是 。
北师大版八年级(上)数学《一次函数》回顾与思考拓展习题(含答案)

一次函数 拓展训练1.若点(m ,n )在函数y=2x+1的图象上,则2m ﹣n 的值是( ) A .2B .﹣2C .1D .﹣12.一次函数y=mx+∣m-1∣的图象过点(0,2)且y 随x 的增大而增大,则m=( ) A .-1 B .3 C . 1 D .-1或33.下列四组点中,可以在同一个正比例函数图象上的一组点是( ) A .(2.-3),(-4,6) B .(-2,3),(4,6) C .(-2,-3),(4,-6) D .(2,3),(-4,6)4.面直角坐标系中,点O 为原点,直线y kx b =+交x 轴于点A(-2,0),交y 轴于点B .若△AOB 的面积为8,则k 的值为( )A .1B .2C .-2或4D .4或-45.面直角坐标系中,把直线y=2x 向左平移一个单位长度后,其直线解析式为( )A .y=2x+1 B.y=2x+2 C.y=2x D. y=2x-26.在平面直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( ) A .通过点(-1,0)的是①③ B .交点在y 轴上的是②④ C .相互平行的是①③ D .关于x 轴对称的是②④7.若函数222-+-=+n x y m 是正比例函数,则m 的值是 ,n 的值为 8.一次函数y=kx+b 中,y 随x 的增大而减小,且kb>0,则这个函数的图象一定不经过第 象限.9.如图,一次函数y=kx+b 的图象与正比例函数y=2x 的图象平行且经过点A (1,﹣2),则kb=10.一辆汽车在行驶过程中,路程 y (千米)与时间 x (小时)之间的函数关系如图所示 当时 0≤x ≤1,y 关于x 的函数解析式为 ,那么当 1≤x ≤2时,y 关于x 的函数解析式为 _ .11.如图,射线OA 、BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s 、t 分别表示行驶距离和时间,则这两人骑自行车的速度相差 _ km/h .12.如图,在平面直角坐标系中,A 、B 均在边长为1的正方形网格格点上.求线段AB 所在直线的函数解析式,并写出当0<y ≤1时,自变量x 的取值范围是 。
北师大版-数学-八年级上册--6.1函数课后拓展训练

6.1函数1.如图6-5所示,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C →D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致是(如图6-6所示) ( )2.已知函数y=51xx++,当x=-2时,函数y的值为( )A.3 B.-3 C.13D.-133.已知x,y满足等式x=213y+,则y等于( )A. 2133x+B.312x+C.312x-D.3122x-4.等腰三角形的底角y与顶角x之间的函数关系式是.5.菱形的周长为80 cm,各边长都减少x cm(x>0)后,得到的新菱形的周长为y cm,则y 与x的函数关系式为.6.当x=2时,函数y=kx+2与y=2x-k的值相等,则k的值是7.当x=2时,函数y=2x+k和y=3kx-2的值相等,则k=;当x=3时,两函数的函数值分别是,.8.写出函数关系式,并指出自变量的取值范围.(1)如果每盒圆珠笔有12支,售价为18元,求圆珠笔的售价y(元)与圆珠笔的支数x之间的函数关系式;(2)如果高度每升高1 km,气温就下降6℃,求气温降低数T(℃)与高度增加数h(km)之间的函数关系式;(3)设正方形ABCD的边长为5,P是DC边上一动点(不与D,C重合),设DP的长为x,求梯形ABCP的面积y与x的函数关系式.参考答案1.B2.B3.D4.y=-12x+90°(0°<x<180°)5.y=-4x+80(0<x<20)6.2 37.1.2 7.2 8.88.解:(1)每支圆珠笔的价格为1812=32元,∴y=32x,x为自然数.(2)由题意得T=6h,h≥0.(3)由梯形的面积公式,得y=12×5×(5+5-x)=25-52x,0<x<5.。
北师大版八年级上册 第二章 实数 解答题拓展专题

北师大版八年级上册第二章实数解答题拓展专题1. 求解:(1)设+|b 3-27|=0,求(a +b )2的值;a 3+64(2)已知225的算术平方根是a ,-512的立方根是b ,求的值.2a ‒12b +22. 已知(x -12)2=169,(y -1)3=-0.125,求的值.x ‒2xy ‒34y +x 3. 若实数a ,b 互为相反数,c ,d 互为倒数,m 是9的平方根,求-+(m -1)2的值.a +b +3cd 4. 比较a ,的大小.1a ,a 5. 已知x ,y 都是有理数,且y =+3,求2x -y 的值.x ‒2+2‒x 6. 国际比赛的足球场长在100m 和110m 之间,宽在64m 和75m 之间.现在有一个长方形足球场,其长是宽的1.5倍,面积是7560m 2,问这个足球场能否作国际比赛场地?7. 已知|x +2|+=0,求的算术平方根.y ‒2(x y )1008. 已知a >b >0,a +b =6,求的值.ab a ‒b a +b 9. 观察=2=3=4…2‒2525,3‒310310,4‒417417(1)等于什么? (2)写出符合这一规律的一般等式.6‒63710. 类比平方根(二次方根)、立方根(三次方根)的定义可给出四次方根、五次方根的定义:①如果x 4=a (a ≥0),那么x 叫做a 的四次方根;②如果x 5=a ,那么x 叫做a 的五次方根.请根据以上两个定义,解答下列问题:(1)求81的四次方根;(2)求-32的五次方根;(3)若有意义,则a 的取值范围为 ;若有意义,有a 的取值范围为 ; 4a 5a (4)解方程:①x 4=16;②100 000x 5=243.11. 已知x ,y 均为正数,且()=3(+5),求的值.x x +y y x y 2x +xy +3yx +xy ‒y12. 已知a -b =,b -c =,求a 2+b 2+c 2-ab -ac -bc 的值.5+35‒313. 已知实数x ,y 满足x 2+y 2-4x -2y +5=0,求的值.x ‒y3y ‒2x 14. 阅读理解:我们知道=3,=7,反过来,得到3=,7=,由此我们可以将式子9和4进行化简,即93272327212718,4.127=9227=318=428=2 仿照上面的方法,化简下列各式:(1)3;13(2)5;25(3)12.12415. 已知实数x ,y ,a 满足:,试问长度分别为x ,y ,a 的三条x +y ‒8+8‒x ‒y =3x ‒y ‒a +x ‒2y +a +3线段能否组成一个三角形?如果能,说明理由.16. 已知a +b =-3,ab =2,求的值.ba +ab 17. 已知x 为实数,化简+2.x 2‒4x +41+2x +x 218. 在如图所示的两个集合中各有一些实数,请你分别从中选出2个有理数和2个无理数,再用“+、-、×、÷”中的3种符号将选出的4个数进行3次运算使得运算的结果是一个正整数.19. 同学们已经学习了不少关于二次根式的知识,老师为了解同学们掌握知识的情况,请同学们根据所给条件求式子的值,可达达却把题目看错了,根据条件他得到=2,你能利用达达的结论25‒x 2+15‒x 225‒x 2‒15‒x 2求出的值吗?25‒x 2+15‒x 220. 观察下列各式:①=2 ②=32+23233+3838③=4 ④=54+4154155+524524……(1)写出分数中分母与式子序号n 之间的关系;(2)猜想写出第⑥个关系式;(3)用字母n (n 为自然数,且n ≥2)表示上述规律.21. 在八年级上册我们学习了整式的乘法,其中对于完全平方公式(a ±b )2=a 2±2ab +b 2,至今我们还记忆犹新. 利用这个公式可把3+2配成完全平方的形式:2 3+2=()2+2××1+12=(+1)2.2222(1)请你把下列各式都配成完全平方的形式:①8+2;②1-;③8-4;④14-5;⑤9+4;⑥x +y -2(x ≥0,y ≥0).1532335xy (2)已知x =8+4,求的值.3x ‒x ‒1(3)计算:.3‒22+5‒26+7‒21222. 阅读材料,并解决问题.定义:将分母中的根号化去的过程叫做分母有理化. 如:将分母有理化.25‒3 解:原式=.2·(5+3)(5‒3)(5+3)=5+3 运用以上方法解决问题:(1)将分母有理化;13+2(2)比较大小:(在横线上填“>”“<”或“=”) ; (n ≥2,且n 为整数);16‒517‒61n ‒n ‒11n +1‒n (3)化简:+…+.11+2+12+3+13+412015+201623. 观察下列各式及其验证过程.=2,验证:=2.2+23232+23=83=22×2323=3,验证:=3.3+38383+38=278=32×3838(1)按照上述两个等式及其验证过程,猜想的变形结果并进行验证.4+415(2)针对上述各式反映的规律,写出用a (a 为任意自然数,且a ≥2)表示的等式,并给出验证.24. 先阅读下面的解答过程,然后再解答:对于的化简,只要我们找到两个数a ,b ,使a +b =m ,ab =n ,使得()2+()2=m ,·,那么便有:m ±2n a b a b =n (a >b ).m ±2n =(a ±b )2=a ±b 例如:化简.7+43 解:首先把化为,这里m =7,n =12,由于4+3=7,4×3=12,7+437+212 即()2+()2=7,,434×3=12 ∴=2+.7+43=7+212=(4+3)23 利用上面的方法化简:(1); (2).13‒2428+4325. 已知·,且x 为偶数,求(1+x )的值.(9‒x )(x ‒7)=9‒x x ‒7x 2‒5x +4x 2‒126. 比较下面四个算式结果的大小.(在横线上填“<”,“>"或“=”)(1)42+52 2×4×5; (2)(-1)2+22 2×(-1)×2;(3)()2 2; (4)32+32 2×3×3.3+(13)2×3×13 通过观察归纳,写出反映这种规律的一般性结论.27. 阅读并回答下列问题.我们知道2,2,3,3.22=(‒2)2=32=(‒3)2= 思考:等于什么?a 2 观察例子,用分类讨论的思想分析的结果.a 228. 利用平方根去根号可以用一个无理数构造一个整系数方程.例如:a =+1时,移项a -1=,两项平方得(a -1)2=(22)2,所以a 2-2a +1=2,即a 2-2a -1=0,仿照上述方法完成下面的题目.己知a =求:25‒12(1)a 2+a 的值; (2)a 3-2a +2 015的值.29. 先化简,再求值;(1)若a +=4(0<a <1),求的值;1a a ‒1a (2)己知x =,y =,求的值.17+517‒5xy +y x 30. 在进行二次根式化简时,我们有时会碰上如,,这样的式子,其实我们还可以将其进一步化简:532323+1 .(一)53=5×33×3=533 .(二)23=2×33×3=63 -1.(三)23+1=2×(3‒1)(3+1)(3‒1)=2(3‒1)(3)2‒12=3 以上这种化简的方法叫做分母有理化. 还可以用如下方法化简:23+1 -1.(四)23+1=3‒13+1=(3)2‒123+1=(3+1)(3‒1)3+1=3(1)请用不同的方法化简.25+3 ①参照(三)式化简:②参照(四)式化简.(2)化简:+…+.13+1+15+3+17+512n +1+2n ‒1。
北师大版八年级(上)数学拓展资源:分层练习1(含答案)
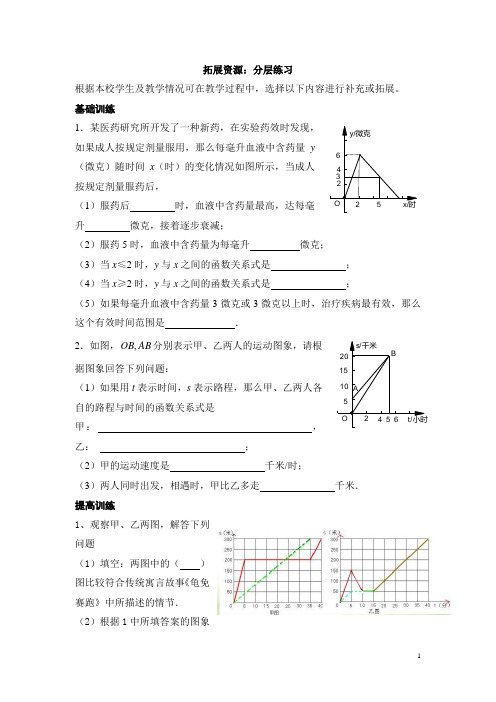
拓展资源:分层练习根据本校学生及教学情况可在教学过程中,选择以下内容进行补充或拓展。
基础训练1.某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y (微克)随时间x (时)的变化情况如图所示,当成人按规定剂量服药后,(1)服药后 时,血液中含药量最高,达每毫升 微克,接着逐步衰减;(2)服药5时,血液中含药量为每毫升 微克; (3)当x ≤2时,y 与x 之间的函数关系式是 ; (4)当x ≥2时,y 与x 之间的函数关系式是 ;(5)如果每毫升血液中含药量3微克或3微克以上时,治疗疾病最有效,那么这个有效时间范围是 .2.如图,AB OB ,分别表示甲、乙两人的运动图象,请根据图象回答下列问题:(1)如果用t 表示时间,s 表示路程,那么甲、乙两人各自的路程与时间的函数关系式是甲: ,乙: ;(2)甲的运动速度是 千米/时;(3)两人同时出发,相遇时,甲比乙多走 千米. 提高训练1、观察甲、乙两图,解答下列问题(1)填空:两图中的( )图比较符合传统寓言故事《龟免赛跑》中所描述的情节. (2)根据1中所填答案的图象265432y/微克x/时O26542015105t/小时s/千米BA O填写下表:项目主人公(龟或兔)到达时间(分)最快速度(米/分)平均速度(米/分)实线虚线(3)根据1中所填答案求:○1龟免赛跑过程中的函数关系式(要注明各函数的自变量的取值范围);○2乌龟经过多长时间追上了免子,追及地距起点有多远的路程?2、某电视机厂要印刷产品宣传材料,甲印刷厂提出:每份材料收1元印刷费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.(1)分别写出两厂的收费y(元)与印制数量x(份)之间的关系式;(2)在同一直角坐标系内作出它们的图象;(3)根据图象回答下列问题:①印制800份宣传材料时,选择哪家印刷厂比较合算?②电视机厂拟拿出3000元用于印刷宣传材料,找哪家印刷厂印刷宣传材料能多些?3、生态公园计划在园内的坡地上造一片有A B,两种树的混合林,需要购买这两种树苗2000棵.种植A B,两种树苗的相关信息如下表:设购买A种树苗x棵,造这片林的总费用为y元.解答下列问题:(1)写出y(元)与x(棵)之间的函数关系式;线型S (千米)t (时)O 1022.57.50.5 31.5l Bl A(2)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?4、如图,l A 与 l B 分别表示A 步行与B 骑车同一路上行驶的路程S 与时间t 的关系.(1)B 出发时与A 相距多少千米?(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时? (3)B 出发后经过多少小时与A 相遇?(4)若B 的自行车不发生故障,保持出发时的速度前进,那么经 过多少时间与A 相遇?相遇点离B 的出发点多远?你能用哪些方法 解决这个问题?在图中表示出这个相遇点C . 视野拓展抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A ,B 两仓库。
北师大版八年级(上)数学拓展资源:分层练习1(含答案)
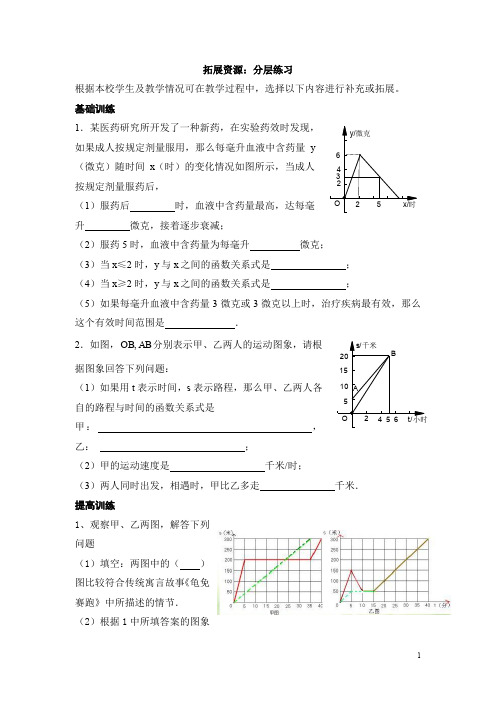
拓展资源:分层练习根据本校学生及教学情况可在教学过程中,选择以下内容进行补充或拓展。
基础训练1.某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y (微克)随时间x (时)的变化情况如图所示,当成人按规定剂量服药后,(1)服药后 时,血液中含药量最高,达每毫升 微克,接着逐步衰减;(2)服药5时,血液中含药量为每毫升 微克; (3)当x ≤2时,y 与x 之间的函数关系式是 ; (4)当x ≥2时,y 与x 之间的函数关系式是 ;(5)如果每毫升血液中含药量3微克或3微克以上时,治疗疾病最有效,那么这个有效时间范围是 .2.如图,AB OB ,分别表示甲、乙两人的运动图象,请根据图象回答下列问题:(1)如果用t 表示时间,s 表示路程,那么甲、乙两人各自的路程与时间的函数关系式是甲: ,乙: ;(2)甲的运动速度是 千米/时;(3)两人同时出发,相遇时,甲比乙多走 千米. 提高训练1、观察甲、乙两图,解答下列问题(1)填空:两图中的( )图比较符合传统寓言故事《龟免赛跑》中所描述的情节. (2)根据1中所填答案的图象265432y/微克x/时O26542015105t/小时s/千米BAO填写下表:项目主人公(龟或兔)到达时间(分)最快速度(米/分)平均速度(米/分)实线虚线(3)根据1中所填答案求:○1龟免赛跑过程中的函数关系式(要注明各函数的自变量的取值范围);○2乌龟经过多长时间追上了免子,追及地距起点有多远的路程?2、某电视机厂要印刷产品宣传材料,甲印刷厂提出:每份材料收1元印刷费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.(1)分别写出两厂的收费y(元)与印制数量x(份)之间的关系式;(2)在同一直角坐标系内作出它们的图象;(3)根据图象回答下列问题:①印制800份宣传材料时,选择哪家印刷厂比较合算?②电视机厂拟拿出3000元用于印刷宣传材料,找哪家印刷厂印刷宣传材料能多些?3、生态公园计划在园内的坡地上造一片有A B,两种树的混合林,需要购买这两种树苗2000棵.种植A B,两种树苗的相关信息如下表:设购买A种树苗x棵,造这片林的总费用为y元.解答下列问题:(1)写出y(元)与x(棵)之间的函数关系式;线型S (千米)t (时)O 1022.57.50.5 31.5l Bl A(2)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?4、如图,l A 与 l B 分别表示A 步行与B 骑车同一路上行驶的路程S 与时间t 的关系.(1)B 出发时与A 相距多少千米?(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时? (3)B 出发后经过多少小时与A 相遇?(4)若B 的自行车不发生故障,保持出发时的速度前进,那么经 过多少时间与A 相遇?相遇点离B 的出发点多远?你能用哪些方法 解决这个问题?在图中表示出这个相遇点C . 视野拓展抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A ,B 两仓库。
北师大版八年级数学上册勾股定理拓展.doc
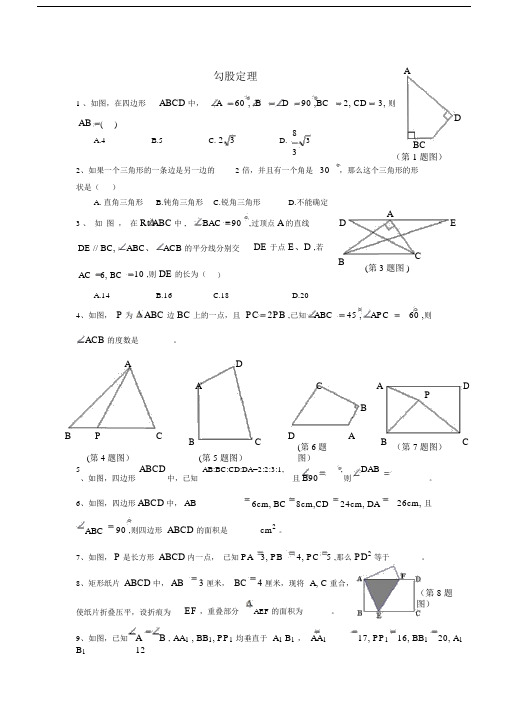
勾股定理A1 、如图,在四边形ABCD 中, A60 , BD90 ,BC2, CD3, 则AB ( )DA.4B.5C. 2 3D.83BC3(第 1题图)2、如果一个三角形的一条边是另一边的 2 倍,并且有一个角是 30 ,那么这个三角形的形状是()A. 直角三角形B.钝角三角形C.锐角三角形D.不能确定A3 、 如 图 , 在 Rt ABC 中 , BAC 90 ,过顶点 A 的直线 DEDE // BC, ABC 、 ACB 的平分线分别交DE 于点 E 、D ,若CBAC 6, BC10 ,则 DE 的长为((第3题图 ))A.14B.16C.18D.204、如图, P 为 ABC 边 BC 上的一点,且 PC 2PB ,已知 ABC 45 , APC60 ,则ACB 的度数是 _____ 。
ADACAPDBB PCBC DAB (第 7题图)C(第 4题图)(第5题图)(第 6题图)5ABCD 中,已知 AB:BC:CD:DA=2:2:3:1, 且B90 ,则 DAB ______。
、如图,四边形6、如图,四边形ABCD 中, AB6cm, BC 8cm,CD 24cm, DA26cm, 且ABC90 ,则四边形 ABCD 的面积是 _____ cm 2 。
7、如图, P 是长方形 ABCD 内一点, 已知 PA 3, PB 4, PC 5 ,那么 PD 2 等于 _____ 。
8、矩形纸片 ABCD 中, AB3 厘米, BC 4厘米,现将 A, C 重合,使纸片折叠压平,设折痕为 EF ,重叠部分AEF 的面积为 ____ 。
(第 8题图)9、如图,已知AB , AA 1 , BB 1, PP 1 均垂直于 A 1 B 1 , AA 1 17, PP 1 16, BB 1 20, A 1B 112则 AP PB _____ 。
BA PA1P1 B1 (第11题图)(第9题图)(第 10题图)10、如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是______ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学试卷
桑水出品
拓展习题
例1已知:如图,DE∥BC,分别交AB、AC于点D、E。
求证:
BC
DE
AC
AE
AB
AD
=
=。
分析:
BC
DE
中的DE不在△ABC的边BC上,但从比例
AC
AE
AB
AD
=可以看出,除DE外,其
它线段都在△ABC的边上,因此我们只要将DE移到BC边上得CF=DE,然后再证明
BC
CF
AB
AD
=就可以了。
这只要过D作DF∥AC交BC于F,CF就是平移DE后所得的线段。
结论:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
例2已知:△ABC中,E、G、D、F分别是边AB、CB上的点,且GF∥ED∥AC,EF∥AD。
求证:
BC
BD
BE
BG
=。
例3已知:在△ABC中,AD为BC边上的中线,过C任作一直线交AD于E,交AB于F。
求证:
FB
AF
ED
AE2
=。
例4如图,已知:D为BC的中点,AG∥BC。
求证:
FC
AF
ED
EG
=。
例5 已知:在△ABC 中,AD 平分∠BAC 。
求证:DC BD AC AB =。
例6 在△ABC 中,AD 平分∠BAC ,C M ⊥AD 交AD 于E ,交AB 于M 。
求证:AM
AB DC BD =。
