2、振动合成
合集下载
第6章 振动2(振动合成、其它振动)

A0e
−β⋅t
A0e-β t o 阻尼振动曲线
T=
t
2π
ω
=
2π
2 ω0 − β 2
> T0
阻尼振动周期
19
时间常量与品质因数: 时间常量与品质因数: 在欠阻尼情况下, 在欠阻尼情况下, 振幅 振动能量E: 振动能量 : E = E0e−2β⋅t 时间常量
A = A0e
−βt
(QE ∝ A2 )
1 τ= 2β
1
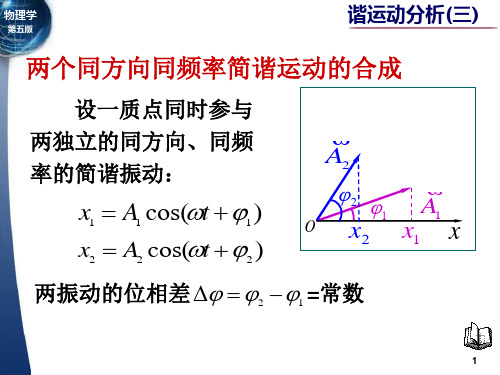
旋转矢量法处理谐振动的合成 1. 分振动 x1 = A cos(ω t +ϕ1) 1 x2 = A2 cos(ω t +ϕ2 ) 2. 合振动
O
ω
A2
ϕ2
x2
ϕ
A ϕ −ϕ 2 1 A1
x = x1 + x2 = Acos(ω t +ϕ)
2 A = A2 + A2 + 2A A2 cos(ϕ2 −ϕ1) 1 1
(5)ϕ2 −ϕ1 = 其 值 它
15
二、李萨如图: 李萨如图:
如果两个振动的频率相差较大,但有简单的整数比, 如果两个振动的频率相差较大,但有简单的整数比,则合成运 动具有稳定的封闭的运动轨迹。 动具有稳定的封闭的运动轨迹。
Tx : Ty =1: 2
Tx : Ty = 2 : 3
Tx : Ty = 3: 4
ω2 −ω1
2
)t
x
ω=
ω2 +ω 1
2
t
拍的现象: 3.拍的现象:
合振动忽强忽弱的现象. 合振动忽强忽弱的现象.
拍频 : 单位时间内强弱变化的次数
ν =|ν2-ν1|
ω拍 = ω2 −ω1 或: = T
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
(2)相位差 (2k 1) π(k 0,1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
(1)相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0,1, ) 加强
(2)相位差
2
1
(2k 1) π
(k 0,1, )
A A A
1
2
减弱
(3)一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气(室温为 20C)中来 回摆动. 摆线长l 1.0 m,摆锤是半径r 5.0103 m 的铅球.求(1)摆动周期;(2)振幅减小 10%所需的时间;(3)能量减小10%所需 的时间;(4)从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
6-2简谐振动的叠加

x1 = A cos(ω1t + ϕ )
ν =ν2 −ν1
x2 = A cos(ω 2t + ϕ )
合振动为 x = x1 + x2 = A cos(ω1t + ϕ ) + A cos(ω 2t + ϕ )
= 2 A cos(
ω 2 − ω1
2
t )cos(
ω 2 + ω1
2
t +ϕ)
4
拍的振幅为 振幅的周期为
′ A 2 ′ A 1
ω2
A
A ω 2 1 A 1
x
A′
O
ω2
A = A 2 + A 2 + 2A A cos[(ω2 −ω1)t + (ϕ2 −ϕ1)] 1 2 1 2
3
由于两个分振动频率的微小差异而 产生的合振 动振幅时强时弱的现象称为拍现象。 动振幅时强时弱的现象称为拍现象。 合振动在1s内加强或减弱的次数称为拍频。 合振动在 内加强或减弱的次数称为拍频。 内加强或减弱的次数称为拍频 拍频为 三角函数法 设两个简谐振动的振幅和初相位相同
9
*四、振动的分解 四 一个复杂的振动可以是由两个或两个以上的 简谐振动所合成。 简谐振动所合成。 把有限个或无限个周 期分别为T ,T/2,T/3,… 期分别为 … (或角频率分别为ω ,2ω, 3ω,…)的简谐振动合成 …)的简谐振动合成 起来, 起来,所得合振动也一 定是周期为T 的周期性 振动。 振动。
5
x = cosω t cos α − sinω t sin α 改写为 A y = cos ω t cos β − sin ω t sin β B
(3) ) (4) )
乘以(3)式 乘以(4)式 以cos β 乘以 式,cosα 乘以 式,后相减得
ν =ν2 −ν1
x2 = A cos(ω 2t + ϕ )
合振动为 x = x1 + x2 = A cos(ω1t + ϕ ) + A cos(ω 2t + ϕ )
= 2 A cos(
ω 2 − ω1
2
t )cos(
ω 2 + ω1
2
t +ϕ)
4
拍的振幅为 振幅的周期为
′ A 2 ′ A 1
ω2
A
A ω 2 1 A 1
x
A′
O
ω2
A = A 2 + A 2 + 2A A cos[(ω2 −ω1)t + (ϕ2 −ϕ1)] 1 2 1 2
3
由于两个分振动频率的微小差异而 产生的合振 动振幅时强时弱的现象称为拍现象。 动振幅时强时弱的现象称为拍现象。 合振动在1s内加强或减弱的次数称为拍频。 合振动在 内加强或减弱的次数称为拍频。 内加强或减弱的次数称为拍频 拍频为 三角函数法 设两个简谐振动的振幅和初相位相同
9
*四、振动的分解 四 一个复杂的振动可以是由两个或两个以上的 简谐振动所合成。 简谐振动所合成。 把有限个或无限个周 期分别为T ,T/2,T/3,… 期分别为 … (或角频率分别为ω ,2ω, 3ω,…)的简谐振动合成 …)的简谐振动合成 起来, 起来,所得合振动也一 定是周期为T 的周期性 振动。 振动。
5
x = cosω t cos α − sinω t sin α 改写为 A y = cos ω t cos β − sin ω t sin β B
(3) ) (4) )
乘以(3)式 乘以(4)式 以cos β 乘以 式,cosα 乘以 式,后相减得
大学物理教案(第五版)下册马文蔚改编09--2振动合成

应用程序
求合振动只需求矢量和即可. 求合振动只需求矢量和即可.
讨论: 讨论:
A = A + A + 2A A2 cos(2 1) 1
2 1 2 2
1)两振动同相 )
A= A + A 1 2
2)两振动反相 )
2 1 = 2kπ
合振幅最大
2 1 = (2k +1)π
A= A A 1 2
合振幅最小
A =A 1 2
每秒产生三个拍 加上一些泥土 拍频减少
ν拍 =ν1 ν2
ν 384 = 3
ν = 387 ν = 381
傅立叶定理: 傅立叶定理:任何一个周期振动都可以看成是由 各种频率不同的谐振动的合成. 各种频率不同的谐振动的合成.
x
x = x1 + x2
x1
x2
t
f (t) = a0 + a1 cosωt + a2 cos 2ωt +
x2 y2 xy + 2 2 cos(2 1) = sin 2 (2 1) A2 A2 A A2 1 1 Y
A2 S
x y =0 A A2 1
A1
X
S= x +y
2 2 1
2 2 2
= A + A cos(ωt +)
Y
2 1 = π
x y + =0 A A2 1
X
x2 y2 xy + 2 2 cos(2 1) = sin 2 (2 1) A2 A AA 1 2 1 2
归纳: 归纳:
m 2mπ 当δ = ≠ k) A = 0 时: ( N N 1) m =1.2.3....N 1 N +1 N + 2,2N 1 , 2N +1 2N + 2,2N 1 , ……………………………... A = 0
求合振动只需求矢量和即可. 求合振动只需求矢量和即可.
讨论: 讨论:
A = A + A + 2A A2 cos(2 1) 1
2 1 2 2
1)两振动同相 )
A= A + A 1 2
2)两振动反相 )
2 1 = 2kπ
合振幅最大
2 1 = (2k +1)π
A= A A 1 2
合振幅最小
A =A 1 2
每秒产生三个拍 加上一些泥土 拍频减少
ν拍 =ν1 ν2
ν 384 = 3
ν = 387 ν = 381
傅立叶定理: 傅立叶定理:任何一个周期振动都可以看成是由 各种频率不同的谐振动的合成. 各种频率不同的谐振动的合成.
x
x = x1 + x2
x1
x2
t
f (t) = a0 + a1 cosωt + a2 cos 2ωt +
x2 y2 xy + 2 2 cos(2 1) = sin 2 (2 1) A2 A2 A A2 1 1 Y
A2 S
x y =0 A A2 1
A1
X
S= x +y
2 2 1
2 2 2
= A + A cos(ωt +)
Y
2 1 = π
x y + =0 A A2 1
X
x2 y2 xy + 2 2 cos(2 1) = sin 2 (2 1) A2 A AA 1 2 1 2
归纳: 归纳:
m 2mπ 当δ = ≠ k) A = 0 时: ( N N 1) m =1.2.3....N 1 N +1 N + 2,2N 1 , 2N +1 2N + 2,2N 1 , ……………………………... A = 0
第2节_简谐振动的合成

2
x = ( A1 cosϕ1 + A2 cosϕ2 ) cosωt − ( A1 sinϕ1 + A2 sinϕ2 ) sinωt = A cos ϕ ⋅ cos ωt − A sin ϕ ⋅ sin ωt = A cos(ωt + ϕ ) ∴ x = A cos(ωt + ϕ )
两个同方向、 两个同方向、同频率的简谐振动合成后仍然是一个 简谐振动,且频率不变。 简谐振动,且频率不变。 由
若 A1 = A2 , A = 2A1
= A1 + A2
合振动振幅最大。 合振动振幅最大。
( ) 2.当 ∆ϕ=ϕ2 −ϕ1 = 2k +1 π ( k = 0,±1,±2,⋯) 时, 当
2 2 A = A1 + A2 + 2A1A2 cos( 2 −ϕ1 ) ϕ
A2
=| A1 − A2 |
A
A2 A1
2 2
ϕ 2 − ϕ1 = π / 2
2 2
x y + =1 A1 A2
•当 当
16
A1 = A2 ,
x +y =A
2
为圆方程
2.
∆ϕ = π / 2
y
8
1 2
y
7 6 5
4
7 6 5
4
8
1 2 2 1
x
3
3
4
播 放 动 画
17
3
5 6 7
x
8
4.
3π (ϕ 2 − ϕ1 ) = 2
9
由于余弦函数绝对值的周期为π。 ω 2 − ω1 t ) 的频率的两倍。 所以, 的频率的两倍。 所以,拍频是振动 cos( 2 即拍频为: 即拍频为:
x = ( A1 cosϕ1 + A2 cosϕ2 ) cosωt − ( A1 sinϕ1 + A2 sinϕ2 ) sinωt = A cos ϕ ⋅ cos ωt − A sin ϕ ⋅ sin ωt = A cos(ωt + ϕ ) ∴ x = A cos(ωt + ϕ )
两个同方向、 两个同方向、同频率的简谐振动合成后仍然是一个 简谐振动,且频率不变。 简谐振动,且频率不变。 由
若 A1 = A2 , A = 2A1
= A1 + A2
合振动振幅最大。 合振动振幅最大。
( ) 2.当 ∆ϕ=ϕ2 −ϕ1 = 2k +1 π ( k = 0,±1,±2,⋯) 时, 当
2 2 A = A1 + A2 + 2A1A2 cos( 2 −ϕ1 ) ϕ
A2
=| A1 − A2 |
A
A2 A1
2 2
ϕ 2 − ϕ1 = π / 2
2 2
x y + =1 A1 A2
•当 当
16
A1 = A2 ,
x +y =A
2
为圆方程
2.
∆ϕ = π / 2
y
8
1 2
y
7 6 5
4
7 6 5
4
8
1 2 2 1
x
3
3
4
播 放 动 画
17
3
5 6 7
x
8
4.
3π (ϕ 2 − ϕ1 ) = 2
9
由于余弦函数绝对值的周期为π。 ω 2 − ω1 t ) 的频率的两倍。 所以, 的频率的两倍。 所以,拍频是振动 cos( 2 即拍频为: 即拍频为:
振动的合成公式(一)

振动的合成公式(一)
振动的合成公式
1. 角频率和周期的关系
•角频率ω与周期T的关系公式为:
–ω = 2π/T
•例如:
–假设有一个周期为秒的振动,可以通过以上公式计算出该振动的角频率:
•ω = 2π/ = 4π rad/s
2. 周期和频率的关系
•周期T与频率ν的关系公式为:
–T = 1/ν
•例如:
–假设有一个频率为5 Hz的振动,可以通过以上公式计算出该振动的周期:
•T = 1/5 = s
3. 多个振动的合成公式
•当存在两个或多个不同频率的振动时,它们可以通过以下合成公式进行合成:
1.同频振动的叠加(同频振动合成):
–对于两个频率相同但振幅不同的振动A和B,它们可以通过简单相加来合成:
–合成振动 = A + B
2.不同频率振动的合成(异频振动合成):
–对于两个频率不同的振动A和B,它们可以通过以下公式进行合成:
–合成振动= A cos(ω1t) + B cos(ω2t)
–其中,ω1和ω2分别为两个振动的角频率,t为时间。
•例如:
–假设有一个频率为3 Hz,振幅为2的振动A,以及一个频率为5 Hz,振幅为4的振动B。
可以通过以上公式计算出
两个振动的合成:
•合成振动 = 2 cos(3t) + 4 cos(5t)
总结
•振动的合成公式包括角频率和周期的关系公式、周期和频率的关系公式,以及同频振动的叠加和不同频率振动的合成公式。
这些公式可以帮助我们计算和理解振动的特性和变化。
2 谐振动的合成

A1
•当2- 1= /2,
2 y x 正椭圆 (b) 2 2 1 A1 A2 2
A2 x 直线(c) •当2- 1= y = A1 2 2 y •当2- 1=- /2 x 正椭圆(d) 1 2 2 A1 A2
y y y y
o
x
o
x
o
x
o
x
Δφ= 0
(a)
Δφ= /2
y 88
5 6 1 y6
x
x
A
A1
A2
2. 若Δ =2-1=(2k+1) k=0,±1,±2 ..….
A A A 2A1A2
2 1 2 2
两分振动反相位
3.若 Δ≠
= |A1- A2| x 合振幅最小 振动减弱 x 2
2k (2k+1) x
t x1
则 A1 - A 2 < A < A1 + A 2
拍- 频率差异而引起振幅时强时弱的现象
ν=
1 T拍
ν 2 -ν 1 次 单位时间里 •2与1“同相”和“反相”各 •合振幅加强和减弱各 ν 2 - ν 1 次;
*9-6 阻尼振动
受迫振动
共振
• 观看插播片
21
作
P.39~41
业
9-17,18,25,28
下次课§10 - 1,2
*多个同方向同频率谐振动的合成 设: x1 = A0 cost B x2 = A0 cos(t+ ) A4 R x3 = A0 cos(t + 2 ) N o'· A x4 = A0 cos(t + 3 ) A … R 3 xN = A4cos[t + (N-1) ] A
医用物理学教学课件 第二节 两个简谐振动的合成

A12 A22 2A1A2[cos01 cos02 sin01 sin02]
A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注:cos( ) cos cos sin sin ]
t4 t3
t2
t1 Y超前π /2
右旋振动
t1 t2
t3
t4 Y落后π /2
左旋振动
例七
一质点同时参与相互垂直的两个振动:
X
8c
os(
t
)
cm
36
Y 6cos( t ) cm
33
请你画出合振动运动轨迹图。
解:
36
2
2B ∵Y落后π/2,左旋振动
2
2
A0
cos
2
O
X
2 A0
cos 2
1
2
t
注: 2t 1t
1 2
(1
cos
)
cos
2
从角度可分析:
t
2
1
2
t
1t
AA
2 1 t
2
O
X
将A与ωt表达式代入 x Acost
x
2
A0
cos 1
∴画一个2A*2B的矩形,内切
画椭圆,标出左旋箭头即可
2A
(2) 2 m 的情况: 1 n
若频率不相等,但是整数比,则合振动的轨迹 是有规则的稳定的闭合曲线-------李萨如图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= /2
= 3/4
=
= 5/4
= 3/2
= 7/4
4.相互垂直的(不同频率) 简谐振动的合成
• 两分振动频率相差很小 = ( 2- 1) t + ( 2- 1) 可看作两频率相等而 2- 1随t 缓慢变化,合运动轨迹将按上页 图依次缓慢变化。 • 两振动的频率相差较大,且成简 单的整数比 轨迹称为李萨如图形 观看
第一种:受到周围介质如空气、液体的摩擦
阻力的作用;
第二种:振动带动周围的介质中的振点振动,
将振动系统的能量传播出去(击鼓 )
阻尼分类
第一种:过阻尼
振动系统在过大阻尼的作用下,连一次振 动都不能完成就停止在平衡位置
以非周期运动方式
第二种:小(弱、欠)阻尼 振动系统可以在较长的时间内作振动
第三种:临界阻尼 特点:离开平衡位置的物体能最快 地回到平衡位置 ,而不发生振动 (刚能做周期性运动)
阻尼较小 阻尼较大
O
0
了解:简谐振动的合成(P247-253)
1 、同方向同频率的简谐振动的合成
代数方法:设两个振动具有相同频率,
结论:
仍 然 是 同 频 率
同一直线上运动,有不同的振幅和初相位 的 x1 (t ) A1 cos( t 1 ) 简 x2 (t ) A2 cos( t 2 ) 谐 振 x(t ) x1 (t ) x2 (t ) 动 。 ( A cos A cos ) cost
了解:过阻尼、欠阻尼和临界阻尼
1. 欠阻尼 2. 过阻尼 3. 临界阻尼
0
0
0
x
o
t
了解:受迫振动 共振
(P245-247)
物体在周期性外力的持续作用下发 生的振动称为受迫振动。
共振
A
阻尼=0
对于受迫振动,当外力幅 值恒定时,稳定态振幅随驱动 力的频率而变化。当驱动力的 角频率等于某个特定值时 ,位 移振幅达到最大值的现象称为 位移共振。
可见:
2 1 2k
A A1 A2
合振幅最大。
k 0,1,2,
A A2 A1
观看同频率振动的矢量合成
观看同频率振动的合成
2. 同方向不同频率的简谐振动的合成 1. 分振动 2. 合振动
x1 A cos1t
x 2 A cos2 t
1 1 2 2
( A1 sin 1 A2 sin 2 ) sin t 合振幅 A cos cost A sin sin t A cos( t )
式中:
A A A 2 A1 A2 cos( 2 1 )
2 1 2 2
A1 sin 1 A2 sin 2 arctg A1 cos1 A2 cos 2
x x1 x 2
2 2 2 1 x 2A cos t t cos 2 2
合振动不是简谐振动
拍:
两简谐振动的角频率都较大而两者之差 很小时,同方向简谐振动的合成结果。 观看“拍” 合振动忽强忽弱的现象 调音
3.相互垂直的(同频率)简谐振动的合成
目录 一、简谐振动的描述(P238-243全部) 二、(了解)共振等及振动的合成 (P244-254部分内容)
三、平面简谐波的表述(P255-260)
四、声波及其简单应用 (含P260-264部分内容) 五、惠更斯原理及波的衍射与干涉概念 (P265-268)
阻尼振动 概念:有回复力的存在,并有阻力作用而 无外界能量去补充的振动 振幅随时间减小的原因
1.分振动
x=A1cos( t+ 1) y=A2cos( t+ 2)
2. 合运动
x y x y 2 2 cos( 2 1 ) sin 2 ( 2 1 ) 2 A1 A2 A1 A2
2 2
观看垂直同频率振动的合成1
观看垂直同频率振动的合成2
= 0
= /4
x
方 波 的 分 解
0 x0 0 x1 0 x3 0 x5 0 x1+x3+x5+x0 0
t
t t
t
振 动 的 逆 过 程 _ 分 解
ቤተ መጻሕፍቲ ባይዱ
t
t
