自动控制原理(非自动化)1-3章答案
自动控制原理(非自动化)1-3章答案

自动控制原理(非自动化类)教材书后第1章——第3章练习题1。
2 根据题1。
2图所示的电动机速度控制系统工作原理图 (1) 将a ,b 与C,d 用线连接成负反馈系统; (2) 画出系统框图。
解:1)由于要求接成负反馈系统,且只能构成串联型负反馈系统,因此,控制系统的净输入电压△U 与U ab 和U cd 之间满足如下关系: 式中,U ab 意味着a 点高,b 点低平,所以,反馈电压U cd 的c 点应与U ab 的a 点相连接,反馈电压U cd 的d 点应与U ab 的b 点相连接.2)反馈系统原理框图如图所示。
1.3题1.3图所示为液位自动控制系统原理示意图。
在任何情况下,希望液面高度c 维持不变,说明系统工作原理并画出系统框图。
题1.3图第二章 习 题2.1 试求下列函数的拉氏变换,设f<O 时,z(f)=0: (1) (2)(3) (4)2。
2试求下列象函数x(s )的拉氏反变换X (t ): 解:(1) 其中(2)2.3 已知系统的微分方程为式中,系统输入变量r(f )=6(£),并设,,(O)=),(0)=O ,求系统的输出y (£)。
题1.2图2.4 列写题2。
4图所示RLC 电路的微分方程。
其中,u i 为输入变量,u o 为输出变量。
解:根据回路电压方程可知2.5 列写题2。
5图所示RLC 电路的微分方程, 其中,u.为输入变量,u 。
为输出变量。
解:由电路可知, 2。
6设运算放大器放大倍数很大,输入阻抗很大,输出阻抗很小。
求题2。
6图所示运 算放大电路的传递函数。
其中,u i 为输入变量,u o 为输出变量.解:根据运算放大器的特点有2.7 简化题2.7图所示系统的结构图,并求传递函数C (s ) / R (s )。
题2.7图解:根据梅逊公式得: 前向通道传递函数P K :回路传递函数L K :(注意到回路中含有二个负号)特征方程式: 余子式:于是闭环传递函数为:2.8 简化题2.8图所示系统的结构图,并求传递函数C (s ) / R (s )。
自动控制原理(梅晓榕)习题答案第1_4章
习题参考答案第1章1-1 工作原理当水位达到规定值时,浮子使电位器活动端处于零电位,放大器输出电压和电机电枢电压是零,电机停转,进水阀门开度不变。
水位高于规定值时,浮子使电位器活动端电位为正,放大器输出电压和电机电枢电压是正,电机正转,阀门开度减小,进水量减小,水位下降。
而水位低于规定值时,浮子使电位器活动端电位为负,电机反转,阀门开度变大,水位上升。
参考输入是电位器中的零电位,扰动量包括出水量和进水管压力的变化等,被控变量是水位,控制器是放大器,控制对象是水箱。
1-2 当水位处于规定值时,阀门开度正好使进水量和出水量相等,水位不变。
当水位高于规定值,浮子通过杠杆使阀门开度减小,进水减小,水位下降。
当水位低于规定值,浮子通过杠杆使阀门开度变大,进水增加,水位上升。
1-3 系统的目的是使发射架转到希望的角度。
电压u代表希望的角度,电1位器输出电压u表示发射架的实际转角。
它们的差值称为偏差电压,放大后加2到电机电枢绕组上成为电压u。
当发射架没有转到希望的角度时,偏差电压和a电机电枢电压不是零,它们使电机转动,转动方向是使偏差角减小至零。
该系统是伺服系统。
参考输入信号是电压u,被控变量是发射架转角 。
反1馈信号是电位器活动端电压2u ,控制变量是放大和补偿环节的输出电压3u 。
测量元件是电位器,执行元件是直流电动机。
1-4 程序控制系统,控制器是计算机,执行元件是步进电动机,被控变量是刀具位移x 。
1-5 (1)线性定常系统;(2)线性时变系统;(3)非线性系统;(4)线性时变系统;(5)线性定常系统;(6)线性时变系统。
第2章2-1 a)k ms s F s X t F t kx tt x m +==+2221)()( )()(d )(d b)取m 的平衡点为位移零点,列微分方程。
k fs ms l l s F s X t F l l t kx t t x f t t x m ++==++2212122/)()( )()(d )(d d )(d 2-2 设A 、B 点及位移x 见图中(b),(d)。
《自动控制原理》课后习题章节测试满分答案

绪论单元测试1【判断题】(100 分)自动控制理论经历了经典控制理论、现代控制理论和近代控制理论三个发展阶段。
A.错B.对第一章测试1【单选题】(10 分)下列系统中属于开环控制的为()。
A.家用空调器B.普通车床C.无人驾驶车D.自动跟踪雷达2【单选题】(10 分)下列系统属于闭环控制系统的为()。
A.家用电冰箱B.传统交通红绿灯控制C.自动流水线D.普通车床3【单选题】(10 分)下列系统属于定值控制系统的为()。
A.自动跟踪雷达B.自动化流水线C.家用空调D.家用微波炉4【单选题】(10 分)下列系统属于随动控制系统的为()。
A.火炮自动跟踪系统B.家用空调器C.自动化流水线D.家用电冰箱5【单选题】(10 分)下列系统属于程序控制系统的为()。
A.传统交通红绿灯控制B.火炮自动跟踪系统C.家用空调器D.普通车床6【单选题】(10 分)()为按照系统给定值信号特点定义的控制系统。
A.连续控制系统B.离散控制系统C.线性控制系统D.随动控制系统7【单选题】(10 分)下列不是对自动控制系统性能的基本要求的是()。
A.准确性B.快速性C.稳定性D.复现性8【单选题】(10 分)下列不是自动控制系统基本方式的是()。
A.开环控制B.复合控制C.闭环控制D.前馈控制9【单选题】(10 分)下列不是自动控制系统的基本组成环节的是()。
A.测量变送器B.控制器C.被控变量D.被控对象10【单选题】(10 分)自动控制系统不稳定的过度过程是()。
A.发散振荡过程B.其余选择都不是C.单调过程D.衰减振荡过程第二章测试1【单选题】(10 分)自动控制系统的数学模型为()。
A.热学方程B.梅森公式C.微分方程、传递函数、动态结构框图、信号流图D.状态方程、差分方程2【单选题】(10 分)以下关于传递函数的描述,的是()。
A.传递函数取决于系统和元件的结构和参数,并与外作用及初始条件有关B.传递函数是一种动态数学模型C.传递函数是复变量的有理真分式函数D.一定的传递函数有一定的零极点分布图与之相对应3【单选题】(10 分)系统的传递函数是由系统的()决定的。
自动控制原理(非自动化类)习题答案_第二版(孟庆明)

自动控制原理(非自动化类)习题答案第一章习题1-1(略)1-2(略)1-3解:受控对象:水箱液面。
被控量:水箱的实际水位h c 执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位h 。
给定值为希望水位h (与电位器设定c r 电压u r 相对应,此时电位器电刷位于中点位置)。
当h c =h r 时,电位器电刷位于中点位置,电动机不工作。
一但h c ≠h r 时,浮子位置相应升高(或电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值h r 。
出水h rh c水位自动控制系统的职能方框图1-4解:受控对象:门。
执行元件:电动机,绞盘。
放大元件:放大器。
受控量:门的位置测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动,使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
开(闭)门的位置门实际仓库大门自动控制开(闭)的职能方框图1-5解:系统的输出量:电炉炉温给定输入量:加热器电压被控对象:电炉_大门位置绞盘电动机放大器电位器_浮子杠杆水箱阀门减速器电动机放大器电位器放大元件:电压放大器,功率放大器,减速器比较元件:电位计测量元件:热电偶职能方框图:给定炉温炉温—第二章习题2-1解:对微分方程做拉氏变换:⎧X 1(s )=R (s )−C (s )+N 1(s )⎪⎪X 2(s )=K 1X 1(s )⎪X 3(s )=X 2(s )−X 5(s )⎨⎪TsX 4(s )=X 3(s )⎪X 5(s )=X 4(s )−K 2N 2(s )⎪⎪K X (s )=s 2C (s )+sC (s )⎩35绘制上式各子方程的方块图如下图所示:N 1(s)R(s)+X 1(s)X 2(s)X 3(s)X 1(s)X 2(s)--C(s)X 5(s)N 2(s)X 3(s)X 4(s)X 5(s)C(s)X 4(s)-X 5(s)将方块图连接起来,得出系统的动态结构图:N 2(s)N 1(s)+X 1(s)_C(s)R(s)X 2(s)X 3(s)X 4(s)X 5(s)K 1K 3C (s )/R (s )=,Ts 3+(T +1)s 2+s +K K 13--K 3K 11s 2+s1TsK 2K 31Ts1s 2+sK 2K 1热电偶电炉加热器电机功率放大电压放大电位器C (s )/N 1(s )=C (s )/R (s ),K 2K 3TsC (s )/N (s )=−2Ts 3+(T +1)s 2+s +K K 132-2解:对微分方程做拉氏变换⎧X 1(s )=K [R (s )−C (s )]⎪⎪X 2(s )=⎜sR (s )⎪(s +1)X 3(s )=X 1(s )+X 2(s )⎨⎪(Ts +1)X 4(s )=X 3(s )+X5(s )⎪C (s )=X (s )−N (s )4⎪⎪⎩X 5(s )=(Ts +1)N (s )绘制上式各子方程的方块如下图:X 2(s)R(s)X 1(s)R(s)X 2(s)X 1(s)X 3(s)-C(s)X 5(s)N(s)N(s)X 5(s)—X 3(s)X 4(s)X 4(s)C(s)将方块图连接得出系统的动态结构图:N(s)X 2(s)X 5(s)—C(s)R(s)X 1(s)X 3(s)X 4(s)⎜s K+K +⎜s =(s +1)(Ts +1)(s +1)(Ts +1)=C (s )R (s )k Ts 2+(T +1)s +(K +1)1+(s +1)(Ts +1)C (s )N (s )=02-3解:(过程略)C (s )1C (s )=G 1+G 2(a)=R (s )ms 2+fs +K(b)R (s )1+G G −G G +G G −G G 13142324-K1Ts +11s +1τsTs+1Ts1Ts +1τsK1s +1C (s )=G 2+G 1G 2C (s )=G 1−G 2(c)(d)R (s )1+G 1+G 2G 1R (s )1−G 2G 3C (s )=G 1G 2G 3G 4(e)R (s )1+G 1G 2+G 2G 3+G 3G 4+G 1G 2G 3G 42-4解:(1)求C/R ,令N=0G (s )=K 1K 2K 3s (Ts +1)K 1K 2K 3G (s )C (s )/R (s )==1+G (s )Ts 2+s +K K K 123求C/N ,令R=0,向后移动单位反馈的比较点K 3K 2)Ts +1=K n K 3s −K 1K 2K 3G n C (s )/N (s )=(K −G K n n 1K K Ts 2+s +K K K s 1+32K 1231Ts +1s(2)要消除干扰对系统的影响C (s )/N (s )=K n K 3s −K 1K 2K 3G n=0Ts 2+s +K K K 123K n s G (s )=n K 1K 22-5解:(a )(1)系统的反馈回路有三个,所以有3∑La=L 1+L 2+L 3=−G 1G 2G 5−G 2G 3G 4+G 4G 2G 5a =1三个回路两两接触,可得⊗=1−∑La=1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5(2)有两条前向通道,且与两条回路均有接触,所以P 1=G 1G 2G 3,⊗1=1P 2=1,⊗2=1(3)闭环传递函数C/R 为C =G 1G 2G 3+1R 1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5(b )(1)系统的反馈回路有三个,所以有3∑La=L 1+L 2+L 3=−G 1G 2−G 1−G 1a =1三个回路均接触,可得⊗=1−∑L a=1+G 1G 2+(2)有四条前向通道,且与三条回路均有接触,所以P 1=G 1G 2,⊗1=1P 2=G 1,⊗2=1P 3=G 2,⊗3=1P 4=−G 1,⊗4=1(3)闭环传递函数C/R 为C =G 1G 2+G 1+G 2−G 1=G 1G 2+G 2R 1+G 1G 2+2G 11+G 1G 2+2G 12-6解:用梅逊公式求,有两个回路,且接触,可得⊗=1−∑La=1+G 1G 2G 3+G 2,可得C (s )=G 1G 2G 3+G 2G 3C (s )=C (s )/R (s )R (s )1+G 1G 2G 3+G 2N 1(s )(1+G 2)G 3C (s )=−1⋅(1+G 1G 2G 3+G 2)=−1C (s )=N 2(s )1+G 1G 2G 3+G 21+G 1G 2G 3+G 2N 3(s )E (s )=1+G 2−G 2G 3E (s )=−C (s )=−G 2G 3−G 1G 2G 3R (s )1+G 1G 2G 3+G 2N 1(s )N 1(s )1+G 1G 2G 3+G 2E (s )=−C (s )−(1+G 2)G 3E (s )=−C (s )==1N 2(s )N 2(s )1+G 1G 2G 3+G 2N 3(s )N 3(s )第三章习题103-1解:(原书改为G (s )=)0.2s +1采用K 0,K H 负反馈方法的闭环传递函数为10K 0⎫(s )=C (s )=K G (s )1+10K H =R (s )01+G (s )K 0.2s +1H1+10K H要使过渡时间减小到原来的0.1倍,要保证总的放大系数不变,则:(原放大系数为10,时间常数为0.2)10K 0⎧=10⎧K =10⎪0⎨1+10K ⇒⎨H⎩K =0.9⎪H 1+10K =10⎩H3-2解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)⎛%=e −⎩/1−⎩⋅100%=1.3−1⋅100%21t p ==0.11−⎩2⎤n解得:⎤=33.71n⎩=0.358所以,开环传递函数为:113647.1G(s)==s(s+24.1)s(0.041s+1) 3-3解:(1)K=10s−1时:100G(s)=s2+10s⎤2=100n2⎩⎤=10n解得:⎤n=10,⎩=0.5,⎛%=16.3%,t p=0.363(2)K=20s−1时:200G(s)=s2+10s⎤2=200n2⎩⎤=10n解得:⎤n=14.14,⎩=0.354,⎛%=30%,t p=0.238结论,K增大,超调增加,峰值时间减小。
自动控制原理第二版课后答案

自动控制原理第二版课后答案1. 介绍。
自动控制原理是现代自动化领域中的重要基础课程,它涉及到控制系统的设计、分析和应用,对于工程技术人员来说具有重要的意义。
本文档将针对自动控制原理第二版课后习题进行详细解答,帮助学习者更好地掌握课程内容。
2. 第一章。
2.1 课后习题1。
答,根据控制系统的基本结构,可以将其分为开环控制系统和闭环控制系统。
开环控制系统中,控制器的输出不受到被控对象的影响,而闭环控制系统中,控制器的输出受到被控对象的影响。
闭环控制系统具有更好的稳定性和鲁棒性,但也更加复杂。
2.2 课后习题2。
答,传递函数是描述控制系统输入和输出之间关系的数学模型,其形式为输出变量的拉普拉斯变换除以输入变量的拉普拉斯变换。
传递函数可以帮助我们分析控制系统的性能和稳定性,并进行控制器的设计。
3. 第二章。
3.1 课后习题1。
答,稳定性是控制系统设计中需要考虑的重要因素,它决定了系统在受到干扰或参数变化时的表现。
稳定性分析可以通过判据、根轨迹和频域等方法进行,其中判据法是最为直观和简单的方法,通过对系统的特征方程进行判别来判断系统的稳定性。
3.2 课后习题2。
答,根轨迹是一种描述控制系统特征方程根在复平面上运动规律的方法,它可以直观地反映系统的稳定性、过渡过程和静态误差等性能指标。
通过对根轨迹的分析,可以帮助我们设计合适的控制器来满足系统性能指标的要求。
4. 第三章。
4.1 课后习题1。
答,比例控制器是一种简单的控制器,它的输出与系统的误差成正比。
比例控制器可以改善系统的静态误差性能,但无法消除系统的稳定性问题和过渡过程中的振荡。
4.2 课后习题2。
答,积分控制器是一种消除系统静态误差的控制器,它的输出与系统的误差积分成正比。
积分控制器可以有效地消除系统的静态误差,但在实际应用中可能会导致系统的过度调节和振荡。
5. 总结。
通过对自动控制原理第二版课后习题的详细解答,我们可以更好地理解控制系统的基本原理和设计方法。
《自动控制原理》习题及答案

《自动控制原理》习题解答(教学参考用书)自动控制原理教学组西北工业大学自动化学院2009年7月前言这本《自动控制原理习题解答》与西北工业大学自动化学院自动控制原理教学组编写(卢京潮主编)、西北工业大学出版社出版的国家教委“十一五”规划教材《自动控制原理》配套使用。
供任课教师在备课和批改作业时参考。
新的“十一五”规划教材是在原《自动控制原理》教材基础上经修改完成的,新教材基本保留了原教材的体系结构,主要在具体内容上作了进一步的完善和充实,习题也做了相应调整。
这本习题解答的内容主要由负责各章编写任务的老师提供。
为方便教学,在习题解答之后编入了课程进程表和教学大纲(96学时),供任课教师参考查阅。
对教材或习题解答中发现的错误和不妥之处,恳请各位读者及时记录,并转告编者,以便尽快纠正。
谢谢!。
联系人:卢京潮电 话:88431302 (办公室)135******** (手机)Email: lujc0129@编者2009.5目录一.习题解答 (1)第1章习题及解答 (1)第2章习题及解答 (10)第3章习题及解答 (32)第4章习题及解答 (64)第5章习题及解答 (86)第6章习题及解答 (133)第7章习题及解答 (157)第8章习题及解答 (181)二.课程进程表 (208)三.自动控制原理教学大纲 ( 96时) (210)一、 习 题 及 解 答第1章习题及解答1-1 根据图1-15所示的电动机速度控制系统工作原理图,完成:(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:,d a ↔c b ↔;(2)系统方框图如图解1-1 所示。
1-2 图1-16是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开、闭的工作原理,并画出系统方框图。
图1-16 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
自动控制原理第3章 习题及解析

自动控制原理(上)习 题3-1 设系统的结构如图3-51所示,试分析参数b 对单位阶跃响应过渡过程的影响。
考察一阶系统未知参数对系统动态响应的影响。
解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式:111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时,系统响应速度变慢;当/0T K b -<<时,系统响应速度变快。
3-2 设用11Ts +描述温度计特性。
现用温度计测量盛在容器内的水温,发现1min 可指示96%的实际水温值。
如果容器水温以0.1/min C ︒的速度呈线性变化,试计算温度计的稳态指示误差。
考察一阶系统的稳态性能分析(I 型系统的,斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数,进一步得到时间响应函数为:()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温,由题意得到:600.961Te-=-推出18.64T =,此时求输入为()0.1r t t =⋅时的稳态误差。
由一阶系统时间响应分析可知,单位斜坡响应的稳态误差为T ,所以稳态指示误差为:lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10,并保证总的放大倍数不变,试选择H K 和0K 的值。
解 一阶系统的调节时间s t 与时间常数成正比,则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++)比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-)试求系统的超调量%σ,峰值时间p t ,上升时间r t 和调节时间s t 。
自动控制原理 孟华第3章习题解答
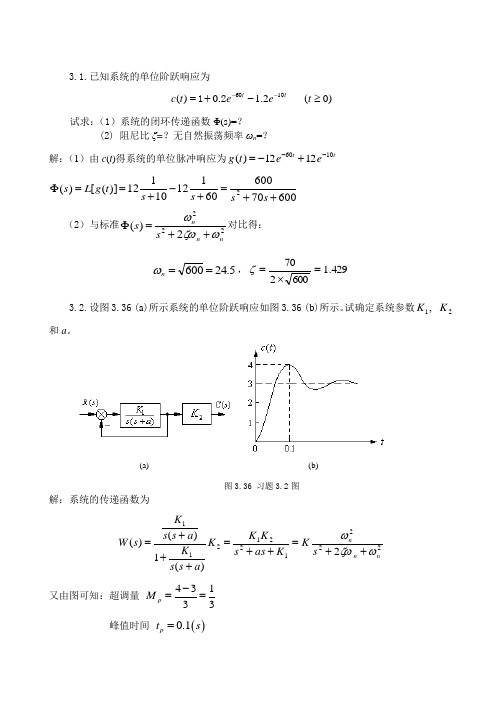
3.1.已知系统的单位阶跃响应为)0(2.1.0)(16≥-+=--t e e t c tt 0021试求:(1)系统的闭环传递函数Φ(s)=?(2) 阻尼比ζ=?无自然振荡频率ωn =? 解:(1)由c (t )得系统的单位脉冲响应为t te et g 10601212)(--+-=600706006011210112)]([)(2++=+-+==Φs s s s t g L s (2)与标准2222)(nn ns s ωζωω++=Φ对比得: 5.24600==n ω,429.1600270=⨯=ζ3.2.设图3.36 (a )所示系统的单位阶跃响应如图3.36 (b )所示。
试确定系统参数,1K 2K 和a 。
(a) (b)图3.36 习题3.2图解:系统的传递函数为22212212112)(1)()(nn n s K K as s K K K a s s K a s s K s W ωζωω++=++=+++= 又由图可知:超调量 43133p M -== 峰值时间 ()0.1p t s =代入得⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==-==--221121.01312K K eK n n ζωπωζζπ 解得:213ln ζζπ-=;33.0≈ζ,3.331102≈-=ζπωn ,89.110821≈=nK ω, 98.213.3333.022≈⨯⨯≈=n a ζω,32==K K 。
3.3. 给定典型二阶系统的设计性能指标:超调量p σ5≤%,调节时间 s t 3<s ,峰值时间1<p t s ,试确定系统极点配置的区域,以获得预期的响应特性。
解:设该二阶系统的开环传递函数为()()22nn G s s s ωξω=+ 则满足上述设计性能指标:⎪⎪⎪⎩⎪⎪⎪⎨⎧<-=<=≤=--113305.0212ζωπζωσζζπn p ns p t t e得:69.0≥ζ,1>n ζωπζω>-21n由上述各不等式得系统极点配置的区域如下图阴影部分所示:3.4.设一系统如图3.37所示。
