曲面积分习题课(供参考)
第四章 曲线积分与曲面积分 习题课(一)

2 [ a cos t ( a sin t ) b sin t ( b cos t )] dt 0
- 12 -
a b
2
2
2
习 题 课(一)
三 格林公式及其应用 设区域 D 是由分段光滑正向曲线 L 围成, 函数
第 十 章
在 D 上具有连续一阶偏导数, 则有
Q P x y d xd y D
y dx
L
2
2
2
-8-
习 题 课(一)
(3) L ( y z ) dx ( z x ) dy ( x y ) dz , 其中
2 2 2 2 2 2
L
为球面的一部分
x y z 1, x 0 , y 0 , z 0
2 2 2
第 的围线,其方向从 z 正向看去是逆时针的。 十 y2 z2 1 章 z 解 L L1 L 2 L 3 x 0 曲 L2 x2 z2 1 x cos t 线 积 L y 0 L3 t :0 1 y sin t 分 2 o 与 z 0 L1 曲 x x2 y2 1 面 积 z 0 分 y cos t z cos t t :0 L 3 x sin t L 2 z sin t t :0 2 2 x 0 y 0
Pd x Qd y
L
曲 在D 内具有一 线 设D 是单连通域 , 函数 积 分 阶连续偏导数, 则以下四个条件等价: 与 P Q . 曲 (1) 在 D 内每一点都有 y x 面 积 Pd x Qd y 0 . 分 (2) 沿D 中任意光滑闭曲线 L , 有 L
高数A(2)习题课(11)曲面积分

R( x, y, z )dxdy
D xy
R( x, y, z ( x, y) ) dxdy
Dxy
如果取下侧, 则
R( x, y, z)dxdy
R( x, y, z( x, y))dxdy
如果为x=x(y, z), (y, z)Dyz, P(x,y,z)C(), 则
2
2
2
2 a cos
0
r [cos sin cos sin ]rdr
2
o x
y
1 2 (cos sin cos sin ) (2a cos ) 4 d 2 4
8 2a
4
2
0
4 2 64 8 2a 2a 4 cos d 5 3 15
分记作2, 1在xoy面上投影为 1 2 于是, 2 2 Dx y {( x, y ) | x y a } 2
h
1
o
a
I ( x 2 y 2 )d S ( x 2 y 2 )d S
1 2
2 2
Dx y
ay
2
( x y )d S 0 D ( x y )
x
Dxy
y
2
R2 u 2 v2 dudv Dyz 2 所以, 2 2 2 3 u v R ,0v 2 3 R 类似地,有 ydzdx R I c R2 2 R3 3 3
(a R2 ( y b)2 ( z c)2 )dydz
课件制作:肖萍 赵庆华 李丹衡
一、 二、
内容总结 作业选讲
曲面积分-习题课2共35页文档

解 设(X,Y,Z)为上任意,一 则点 得 出的方程为
xX yYzZ1 22 由点O到平面的距离公式,得
(x, y,z)
1 x2 y2 z2 44
设 S为椭球 x2面 y2z21的上半部 22
由z 1 x2 y2
22
一、教学要求
1. 了解两类曲面积分的概念及高斯 Gauss) 斯托克斯(Stokes)公式, 并会 、 计算两类曲面积分.
2.了解散度、旋度的概念及其计算 方法.
3. 会用曲面积分求一些几何量与物 理量.
理论上的联系
1.定积分与不定积分的联系
b
a f ( x ) d F x ( b ) F ( a )( F ( x ) f ( x ))
牛顿--莱布尼茨公式
2.二重积分与曲线积分的联系
D( Q x P y)dx d L Py dQ xd (沿 y L 的)正向
格林公式
3.三重积分与曲面积分的联系
( P x Q y R z)d v P d Q yd d R zzd dx xd
高斯公式
4.曲面积分与曲线积分的联系
z
x
,
x
x2 y2
2 1
22
得
z
y
y 2 1 x2 y2
22
dS 1x z2 yz2dxdy 4 x2 y2 dxdy 2 1 x2 y2 22
所以
dS 4x2 y2 dxdy
z dS
S (x, y,z)
1 (4x2y2)dxdy
4 Dxy
2 1 x2 y2
22
(x, y,z)
(1 ) 若P,Q,R在闭曲面 所围成的空间 中域
高等数学《曲线积分与曲面积分》习题课

L( A,B)
b
f (x, y)
1 y2dx
a
曲顶柱体的表面积
如图曲顶柱体,
z z f (x, y)
S
(1
1
f2 x
f
2 y
)d
D
f ( x, y)ds L
o
y
x
D L
2
2
例 3 求柱面 x 3 y 3 1在球面 x2 y2 z 2 1内
的侧面积.
解 由对称性
S 8Lzds 1 x2 y2ds
2
解
z
y 1绕y轴旋转面方程为
x 0
y 1 z2 x2
(如下图)
欲求
I
(8
y
1) xdydz
2(1
2
y
)dzdx
4
yzdxdy
z
且有 I
* *
P Q R
*
(
x
y
z
)dxdydz
x
2
o1
*
y
3
(8 y 1 4 y 4 y)dxdydz dv
3
2
2
3
dxdz
D
8
a 0 dx (e x m) 0 0, OA 0
M
A(a,0) x
I
m a2 0 m a2.
AMOA OA
8
8
曲面面积的计算法
z
z f (x, y) S
z
z f (x, y)
o
Dxy
y
a
bo
A
s LB
y
x S dS
1
z
2 x
z
2 y
高中数学(人教版)曲面积分习题课课件

z x2 y2
其中Σ 为柱面 被锥 面 割下的 部分.
z
o
y
x
二 题型练习 (一) 对面积的曲面积分的计算
(二) 对坐标的曲面积分的计算
二 题型练习 (一) 对面积的曲面积分的计算
(二) 对坐标的曲面积分的计算
(二) 对坐标的曲面积分的计算 1.用高斯公式计算
2.添加曲面后用高斯公式计算 3.分项直接计算
1
1
Σ
2
2
1
Σ22源自2Σ22
Σ
Σ
(一) 对面积的曲面积分的计算 1.简化计算
2.Σ方程的选择与确定 3.Σ的投影的求法
(一) 对面积的曲面积分的计算 1.简化计算
2.Σ方程的选择与确定 3.Σ的投影的求法
例计 : x y z 2az. 3 算 y 注 确定Σ的方程需考虑 x z 结合所给条件 是否分片; 1 计算曲 例 简化计算. o 4 其中 1 y 是 面积分 1 x 与坐标面所围成的 由平面 Σ的方程需考虑 Σ的 注确定 z 四面体的表面 . x y z 1 ( x z )dS , 计 例 其中 1 1 投影面积非零. C ( , 0, ) 、 5 上以 Σ 为2 2 算 A(1,0,0) B o y 为顶点的球面 B (0,1,0)、 A 确定Σ的方程需考虑Σ x 注
n
0
i 1
i
i
i
i
n
0
i 1
i
i
i
i xy
曲面积分习题课
一 、内容小结
二 、题型练习
曲面积分习题课
高等数学第十一章习题课(二)曲面积分

z
B
o
dS
n C
y
z
x
3 2
y A x : x y z 1
n 1 (1, 1, 1)
3
1 3
(3) d S
答: 第一类曲面积分的特例.
2) 设曲面 问下列等式是否成立?
不对 ! 对坐标的积分与 的侧有关
练习: P185 题4(3)
计算 x d y d z y d z d x z d x d y, 其中 为半球面
的上侧. 提示: 以半球底面 0 为辅助面, 且取下侧 , 记半球域为 , 利用 高斯公式有 原式 =
x , 2 2 x y y , 2 2 x y
D
x y I y , x , z 2 , 2 ,1dxdy 2 2 x y x y
2
z 2dxdy
( x 2 y 2 )dxdy
D xy
[ Dxy : 1 x 2 y 2 4 ]
用重心公式
利用对称性
2( x z ) d S
0
例7. 设L 是平面
与柱面
的交线
从 z 轴正向看去, L 为逆时针方向, 计算 解: 记 为平面
上 L 所围部分的上侧,
D为在 xoy 面上的投影. 由斯托克斯公式
z
L
I
1 3 x
2z x y z 2 (4 x 2 y 3z )dS 3
2 2
1 3 y 2
2
3x y 2
1 3 z 2
dS
D
o x
y
曲面积分习题课

′x 2 + z ′y 2 dxdy = 1 + ( 2 x ) 2 + ( 2 y ) 2 dxdy dS = 1 + z 原式 = ∫∫ | xyz | dS = 4 ∫∫ xyz dS
= 4 ∫∫ xy ( x 2 + y 2 ) 1 + ( 2 x )2 + ( 2 y )2 dxdy
[ r 2 sin θ cos θ + r 2 (cos θ + sin θ )]rdr
=4
2 π 2a 4 2π (sin θ − 2
∫
cos 5 θ + cos 5 θ + sin θ cos 4 θ )dθ
y
64 = 2a 4 15
o
2a
x
或 ∫ ∫ ( xy + yz + zx )dS = 2 ∫ ∫ [ xy + ( x + y ) x 2 + y 2 ]dxdy
1. 若曲面Σ :
则
z = z( x, y)
′x 2 + z′y 2 dxdy; 1+ z
∫∫ f ( x , y , z )dS Σ = ∫∫ f [ x , y , z ( x , y )]
D xy
2. 若曲面 Σ: y = y( x, z)
则
∫∫
Σ
′ 2 + y′ 2dxdz f ( x , y , z )dS = ∫∫ f [ x, y( x, z),z] 1 + yx z
∫∫ Pdydz+Qdzdx+ Rdxdy = ∫∫(Pcosα+Qcosβ+ Rcosγ)dS
Σ Σ
§10.习题课(曲面积分)
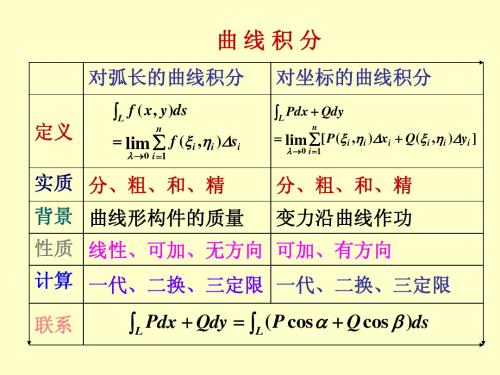
环流量 Pdx Qdy Rdz 旋度
R Q P R Q P rotA ( )i ( )j ( )k y z z x x y
线积分典型例题
例1 计算
e
L
x y
2
2
ds L : x y a , y x , y 0
2 2
其中L为
①不包围也不通过原点的任意闭曲线(可直接用格林公式) ②以原点为中心的正向单位圆周 ③包围原点的任意正向闭曲线(挖去小圆)
解 ① P x y2 2
x y
P y Q x
2
Q
2
y x x y
2
2 2
2
x y 2 xy (x y )
2
1) 因为
2
2
L l
-
l
-
l
-
D
(
Q x
P y
) dxdy
2
-
2
( x y ) dx ( x y ) dy
l
x y
2
( x y ) dx ( x y ) dy
l
这里的x,y就是小圆的
x y
2
2
0
(cos sin )( sin ) (sin cos )(cos ) cos sin
( 0 ,0 ) D
则由Green公式
Qdy 0
Pdx
L
②
I
L
2
x y 1
2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十二章曲面积分习题课
一 疑难问题与注意事项
1.第一型曲面积分的计算方法:
答 1)先把S 的方程代入,再利用
S
dS ⎰⎰为S 的表面积;
例如
,22⎰⎰+S y
x dS
其中S 为柱面222R y x =+被平面H z z ==,0所截取的部分; 解
222
21122S
S
dS H dS RH x y R R R
ππ==
=+⎰⎰⎰⎰. 2)利用公式
(1)设有光滑曲面
:(,),(,)S z z x y x y D =∈,
(,,)f x y z 为S 上的连续函数,则
(,,)(,,(,S
D
f x y z dS f x y z x y =⎰⎰⎰⎰.
注 一投------将曲面S 向xOy 面投影得D ;
二代------将(,)z z x y =代入到(,,)f x y z 中; 三变换------dS
.
(2)类似地,如果光滑曲面S 由方程(,),(,)x x y z y z D =∈,则
(,,)d ((,),,d S
D
f x y z S f x y z y z y z =⎰⎰
⎰⎰,
其中D 表示曲面S 在yOz 面上的投影.
(3)如果光滑曲面S 由方程(,),(,)y y x z x z D =∈,则
(,,)d (,(,),d S
D
f x y z S f x y x z z x z =⎰⎰⎰⎰.
其中D 表示曲面S 在xOz 面上的投影.
3)利用对称性
(1)若曲面∑关于xoy 坐标面对称,()z y x f ,,为∑上的连续函数,1∑为∑位于xoy 上
部的曲面,则
()()()()1
0,,,,,d 2,,d ,
,,f x y z z f x y z S f x y z S f x y z z ∑
∑⎧⎪
=⎨⎪⎩⎰⎰
⎰⎰为的奇函数,为的偶函数.
(2)若曲面∑关于yoz 坐标面对称,()z y x f ,,为∑上的连续函数,1∑为∑中0x ≥的
那部分曲面,则
()()()()1
0,,,,,d 2,,d ,
,,f x y z x f x y z S f x y z S f x y z x ∑
∑⎧⎪
=⎨⎪⎩⎰⎰
⎰⎰为的奇函数,为的偶函数.
(3)若曲面∑关于xoz 坐标面对称,()z y x f ,,为∑上的连续函数,1∑为∑中0y ≥的
那部分曲面,则
()()()()1
0,,,,,d 2,,d ,
,,f x y z y f x y z S f x y z S f x y z y ∑
∑⎧⎪
=⎨⎪⎩⎰⎰
⎰⎰为的奇函数,为的偶函数.
(4)若积分曲面∑关于,,x y z 具有轮换对称性,则有
[]1
(,,)(,,)(,,)3f x y z f y z x f z x y ds ∑
=
++⎰⎰. 2.第二型曲面积分的方法:
答 1)公式:
(1)设R 是定义在光滑曲面
上的连续函数, 以S 的上侧为正侧,则有
注一投-----曲面:(,)S z z x y =向xOy 面投影得D ;
二代----将(,)z z x y =代入到(,,)R x y z 中;
三定向—看S 的法线方向与z 轴的夹角,若夹角为锐角,则为正,否则为负. (2)类似地,当P 在光滑曲面 上连续时,有
这里S 是以S 的法线方向与x 轴的正向成锐角的那一侧为正侧,
(3)当Q 在光滑曲面 上连续时,有
这里S 是以S 的法线方向与y 轴的正向成锐角的那一侧为正侧. 2)若(,)z z x y =,则 3)高斯公式
注 高斯公式
(
),V
S
P Q R dxdydz Pdydz Qdzdx Rdxdy x y z
∂∂∂++=++∂∂∂⎰⎰⎰⎰⎰的适用条件是:
1)函数(,,)P x y z ,(,,)Q x y z ,(,,)R x y z 在V 上具有一阶连续的偏导数. 2)S 封闭,若S 不封闭需要补面,让它封闭,假如补面S *
后封闭,则有 3)S 取外侧;如果S 取内侧,则S -取外侧,则有 3.各种积分间的联系
τ
格林公式 n
二 1.计算第一型曲面积分
()S
x y z dS ++⎰⎰,其中S 是上半球面
2222x y z a ++=(0)a >,0z ≥.
解 把:S z
=xoy 面投影得222:D x y a +≤
(()
S
D
x y z dS x y ++=+⎰⎰⎰⎰3a π=.
注
(0D
x y +=⎰⎰,因为222
:D x y a +≤关于,x y 轴对称,且
(x y +
2.计算曲面积分
2
S
z dS ⎰⎰,其中S 是球面2
222x
y z a ++=.
解: ∵球面2
2
2
2
x y z a ++=关于x ,y ,z 具有对称性, ∴
222S
S
S
x dS y dS z dS ==⎰⎰⎰⎰⎰⎰ ∴
2
S
z dS ⎰⎰=2221
()3S
x y z dS ++⎰⎰ =22
133
S S
a a ds ds =⎰⎰⎰⎰
22214
.433
a a a ππ==. 3.计算曲面积分
⎰⎰∑
-+zdxdy dydz x z )(2
,其中∑是旋转抛物面)(2
122
y x z +=介于
平面0=z 及2=z 之间部分的下侧.
解 补平面2:1=∑z 的上侧,则1∑+∑为封闭曲面,在其上应用高斯公式:
π82)11(=+-=⎰⎰⎰⎰⎰Ω
xy
D dxdy dxdydz .
4.计算第二型曲面积分
S
xdydz ydzdx zdxdy -+⎰⎰,其中曲面S
为椭球面
222
222
1x y z a b c ++=的上半部分,其方向为下侧. 解:为求1S
I xdydz ydzdx zdxdy =
-+⎰⎰ (S 取下侧),只须求
2S
I xdydz ydzdx zdxdy =-+⎰⎰(S 取上侧),那么12I I =-.为求2I ,将S 与底面
'S (其中'S 是S 在xoy 坐标面上的投影)组成的封闭曲面记为total S ,即'total S S
S =,其
中S 方向取上侧,'S 方向取下侧.设total S 围成的区域为
()222
222,,|1,0x y z V x y z z a b c ⎧⎫=++≤≥⎨⎬⎩⎭
,
由高斯公式:
213
V
abc
dxdydz π==
⎰⎰⎰. 又由于
'
0S xdydz ydzdx zdxdy -+=⎰⎰,那么223
I abc π
=
,从而 123
S
abc
I xdydz ydzdx zdxdy π=-+=-
⎰⎰. 5.计算
S
xdydz ydzdx zdxdy ++⎰⎰,其中S
是上半球面z =
解:曲面S 不封闭,补上曲面222
1:0()S z x y a =+≤,取下侧
6.
⎰⎰
++S
dxdy z dzdx y dydz x 3
33,其中S 是单位球面1222=++z y x 的外侧. 解
333222()S
V
x dydz y dzdx z dxdy x y z dxdydz ++=++⎰⎰
⎰⎰⎰
21
40
12
3sin 5
d d r dr ππϕθϕπ==
⎰⎰⎰.
7.求222222
()()()C
I y z dx z x dy x y dz =-+-+-⎰
,其中C 是立方体{0,0,0,}x a y a z a ≤≤≤≤≤≤
的表面与平面3
2
x y z a ++=
的交线,取向从z 轴正向看去是逆时针方向. 解:可见交线若分为六段积分的计算量很大,且C 也不便于表示为一个统一的参数式,因C 为闭曲线,且2
2
P y z =-,2
2
Q z x =-,2
2
R x y =-连续可微,故考虑用斯托克斯公式,令∑为3
2
x y z a ++=被C 所围的一块,取上侧,则C 的取向与∑的取侧相容,应用斯托克斯公式得
23
394()2
42a x y z dS dS a a ∑∑=
-++==-⋅=-⎰⎰⎰⎰. 8.计算()d ()d ()d I z y x x z y x y z Γ
=-+-+-⎰,其中221
:2x y x y z ⎧+=Γ⎨-+=⎩,从z 轴正
向看为顺时针方向(图10-23).
解 用斯托克斯公式取:2x y z ∑-+=以Γ为边界所围有限部分的下侧,它在xOy 面上的投影区域为2
2
{(,)1}xy D x y x y =+≤,则
d d d d d d y z z x x y
I x y z z y
x z
x y
∑
∂∂
∂
=∂∂∂---⎰⎰
2d d 2d d 2xy
D x y x y π∑==-=-⎰⎰⎰⎰.。
