计算方法总复习word版
(完整word版)有理数和代数式的复习

有理数一(一)、正数和负数1、负数的意义负数是由实际的需要而产生的,如:某地气温是8℃,由于强冷空气南下,气温下降了12℃,则该地区这时的实际气温是(8-12)℃,但在算术中这个差是不存在的,实际上这个气温是客观存在的,为了解决这个“不够减”的矛盾,引入一个新数——负数,即(8-12)℃=-4℃,表示零下4℃.2、相反意义的量与正数为了表示具有相反意义的量,把其中一种意义的量规定为正,另一种与它意义相反的量规定为负,正的量记为“+”,如+6,+2。
5,…叫正数;负的量记做“-”,像-4,-6这类带有负号的数叫负数;“0”既不是正数,也不是负数,是正数与负数的界限,规定零是最小的自然数。
自然界有许多具有相反意义的量,如上升与下降,向东与向西、盈余与亏损等都可以用正负数来表示.3、有理数的概念及分类4、字母a的意义用字母 a表示有理数时:(1)a〉0时,a表示正数,-a表示负数;(2)a<0时,a表示负数,-a表示正数.(3)a≥0时,a表示非负数.(二)、数轴1、数轴的意义数轴是一种特定几何图形;原点、正方向、长度单位称数轴的三要素,这三者缺一不可.2、数轴的画法3、利用数轴比较有理数大小.建立了数轴后,就可以用数轴上的点表示有理数,原点表示的数是0,正有理数用原点右边的点表示,负有理数用原点左边的点表示,即用数轴上的点表示有理数的口诀为:左负右正,原为零,所有的有理数都可在数轴上找到对应的点。
由数轴知,数轴上的两个有理数中,右边的数总比左边的数大,因此有理数大小比较的规律是:正数大于 0,零大于一切负数,负数小于零,正数大于一切负数。
(三)、相反数1、相反数的意义(1)代数意义:只有符号不同的两个数叫互为相反数,其中一个数叫另一个数的相反数,0的相反数是0。
(2)几何意义:在数轴上的原点两旁,离原点的距离相等的两个点所表示的数互为相反数。
(3)性质:互为相反数的和为0,即a+b=0a、b两数互为相反数。
(完整word版)人教版六年级数学上册总复习教案

六年级数学上册总复习教案单元教学目标:通过总复习,系统、全面地复习和整理本学期所学知识,帮助学生构建合理的知识体系,以便学生更好地理解和掌握所学的概念、计算方法以及有关的规律性的知识,进一步发展学生的数概念、空间概念、统计概念,增强学生综合运用知识的能力,全面达到本学期的教学目标。
第一课时总复习——分数乘、除法教学内容:教材第118页总复习第1——5题。
教学目标:1、理解分数乘、除法的意义、倒数的意义,分数乘除法的关系,掌握分数乘、除的计算方法,能正确地进行分数乘除法的计算。
2、掌握比的意义,理解比与分数、除法的关系,比的基本性质,会求比值和化简比。
3、掌握解决分数乘除法问题的思路,能熟练地分析数量关系,正确地解决分数除法问题。
教学重点:概念和计算方法。
教学难点:掌握解决分数乘,除法问题的思路和方法。
教学过程:一、分步复习活动准备将学生课前就本节复习内容提出的知识性问题和难点问题分类整理,制成问题卡,交由3位学生主持复习.师:同学们,经历了将近一个学期的学习,大家都有不同程度的收获,为了帮大家更好地复习整理本节知识,我们请3位同学分别主持复习。
现在请第一位主持人出场。
二、复习分数乘除法的知识(1)主持人持知识问题卡提出问题,分别指名回答。
分数乘法的意义是什么?与整数乘法相同吗?分数除法的意义是什么?与整数除法相同吗?分数乘法的计算法则是怎样的?什么叫倒数?怎样求一个数的倒数?分数除法的计算方法是怎样的?(2)主持人持难点问题卡提出问题,指名回答。
分数乘、除法的关系是怎样的?分数除法的计算具体要注意几点?0有倒数吗?为什么?1呢?(3)教师组织学生活动计算。
3/4×2/5=2/3×5/6=7/9×18=3/10÷3/4=5/9÷5/6=21÷7/9=3/10÷2/5=5/9÷2/3=6/11÷5/12=(4)复习比的知识第二位主持人提出问题,学生回答。
(完整word版)《数值计算方法》试题集及答案

《计算方法》期中复习试题一、填空题:1、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f 。
答案:2.367,0.252、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L3、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;4、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( ); 答案)(1)(1n n n n n x f x f x x x '---=+5、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );6、计算方法主要研究( 截断 )误差和( 舍入 )误差;7、用二分法求非线性方程f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 );11、 两点式高斯型求积公式⎰10d )(x x f ≈(⎰++-≈1)]3213()3213([21d )(f f x x f ),代数精度为( 5 );12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0.5,0.75 。
(word完整版)6年级分数乘除法总复习

复习分数乘法7、已知比一个数多(少)几分之几是多少,求这个数1美术小组有25人,美术小组的人数比航模小组多1•问航模小组有多少人?4随堂检测11、甲数的2与乙数的3相等.甲数是3,乙数是多少?5 4 82、一个数的2等于120的1,这个数是多少?3 413、食堂运进540千克大米,大米比运进的面粉多.食堂运进大米和面粉共多少千克?91台笔记本电脑原价4200元,现在降价―,请问现在的售价是多少?34、四、解分数方程1、解方程2 3 5 3 53 484 62x 3x 3x2、应用题解方程的步骤找出单位“ 1”,设未知量为X.找出题中的数量关系式,转化为分数乘除法问题列出方程——解方程.指导训练21、食堂买了60千克的西红柿,西红柿的量是青菜的2,请问买了青菜多少千克?32、小明要下载一份稿件,已经下5,下载了1200字,请问这份稿件一共有多少字?13、农机厂10月份生产抽水机8000台,比9月份增长4,9月份生产的抽水机多少台?五、分数的混合运算分数混合运算的运算顺序和整数的运算顺序(相同)指导训练39 11 2240 5 546346 12 2372377、填空“一桶油的3重6千克”,把()看作单位“ 1”,()x 3=(44“男生占全班人数的4 5 ”,把()看作单位“ 1”,()X5=( 992“鸭只数的2等于鸡”把( )看作单位“ 1”,( )X 6 =(7745是( )的5, 7吨是()吨的1,()是3平方米的1910243二、应用题1、 X公顷玉米匸多少分?棉花」50公顷2、小红体重42千克,小云体重40千克,小新的体重相当于小红和小云体重总和的 千克?3、六年级三个班学生帮助图书室修补图书 的是二班的4/3.三班修补图书多少本?4、小丽比小兰多12张彩色画片,这个数目正好相当于小兰画片张数的 3/10.小兰有多少张彩色画片? 小丽有多少张?5、2009年9月份红星乡晴天有20天,雨天的天数比晴天少 4/5,阴天的天数比雨天多1/2.这个月阴 天有多少天?47、建一座厂房,计划投资 200万元,实际比计划节约了 —.实际比计划节约投资多少万元?实际投资5016、一套西服原价250兀,现在降价-.现在买这套西服要多少兀? 多少万元?8王阳期末数学成绩是96分,孙月的成绩比王阳低1/6,王华的成绩是王阳和孙月总分的1/2.王华得课内练习与训练1/2.小新体重多少.一班修补了 54本,二班修补的本数是一班的5/6,三班修补四、拓展题1、一种国产冰箱原来每台售价2700元,现在比原来降低了1/10,现在每台多少元?(1)应把_______________________ 作单位1.(2)2700X 1/10 求的是____________________________..(3)1-1/10 求的是__________________________________ .(4)2700X 9/10 求的是_____________________________ .2、有一批货物,第一天运走了这批货物的1/4,第二天运的是第一天的3/5,还剩下180吨没有运.这批货物有多少吨?3、小明三天看一本书,第一天看了全书的1/4,第二天看了余下的2/5 ,第二天比第一天多看了21页, 这本书共多少页?4、昆虫飞行时经常振动翅膀.蜜蜂每秒振动翅膀236次,蜱虫每秒振动次数比蜜蜂少.那么蝗虫每秒118能振动多少次?5、青山镇修一条公路,实际投资56万元,比计划节约1•修这条公路计划投资多少万元?86、商场销售一种学习机,它的原价是180元,,价格先上涨了1销售了一部分后,又下降了—,这种学9 10习机的现价是多少元?作业。
(完整word版)六年级数学总复习知识点梳理
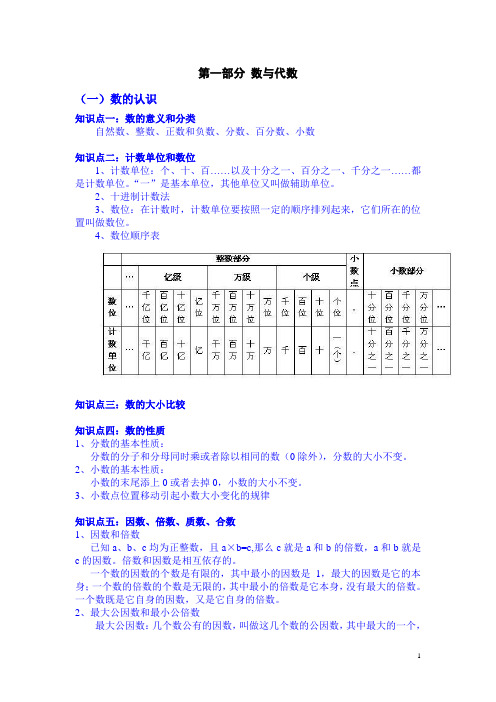
第一部分数与代数(一)数的认识知识点一:数的意义和分类自然数、整数、正数和负数、分数、百分数、小数知识点二:计数单位和数位1、计数单位:个、十、百……以及十分之一、百分之一、千分之一……都是计数单位。
“一”是基本单位,其他单位又叫做辅助单位。
2、十进制计数法3、数位:在计数时,计数单位要按照一定的顺序排列起来,它们所在的位置叫做数位。
4、数位顺序表知识点三:数的大小比较知识点四:数的性质1、分数的基本性质:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
2、小数的基本性质:小数的末尾添上0或者去掉0,小数的大小不变。
3、小数点位置移动引起小数大小变化的规律知识点五:因数、倍数、质数、合数1、因数和倍数已知a、b、c均为正整数,且a×b=c,那么c就是a和b的倍数,a和b就是c的因数。
倍数和因数是相互依存的。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它的本身;一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
一个数既是它自身的因数,又是它自身的倍数。
2、最大公因数和最小公倍数最大公因数:几个数公有的因数,叫做这几个数的公因数,其中最大的一个,叫做这几个数的最大公因数。
最小公倍数:几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数。
3、质数和合数质数:一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
最小的质数是2。
合数:一个数,如果除了1和它本身两个因数外还有别的因数,这样的数叫做合数。
最小的合数是4。
1既不是质数,也不是合数。
(二)数的运算知识点一:四则运算的意义1、加法的意义:把两个数合并成一个数的运算。
2、减法的意义:已知两个数的和与其中的一个加数,求另一个加数的运算。
3、整数乘法的意义:求几个相同加数的和的简便运算。
4、小数乘法的意义:小数乘整数与整数乘法的意义相同,也是求几个相同加数的和的简便运算;一个数乘小数求这个数的十分之几、百分之几……是多少。
(完整word版)数值计算方法期末复习答案终结版

一、 名词解释1.误差:设*x 为准确值x 的一个近似值,称**()e x x x =-为近似值*x 的绝对误差,简称误差。
2.有效数字:有效数字是近似值的一种表示方法,它既能表示近似值的大小,又能表示其精确程度。
如果近似值*x 的误差限是1102n -⨯,则称*x 准确到小数点后n 位,并从第一个不是零的数字到这一位的所有数字均称为有效数字。
3. 算法:是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。
计算一个数学问题,需要预先设计好由已知数据计算问题结果的运算顺序,这就是算法。
4。
向量范数:设对任意向量n x R ∈,按一定的规则有一实数与之对应,记为||||x ,若||||x 满足 (1)||||0x ≥,且||||0x =当且仅当0x =; (2)对任意实数α,都有||||||x αα=||||x ; (3)对任意,n x y R ∈,都有||||||||||||x y x y +≤+ 则称||||x 为向量x 的范数。
5. 插值法:给出函数()f x 的一些样点值,选定一个便于计算的函数形式,如多项式、分段线性函数及三角多项式等,要求它通过已知样点,由此确定函数()x ϕ作为()f x 的近似的方法。
6相对误差:设*x 为准确值x 的一个近似值,称绝对误差与准确值之比为近似值*x 的相对误差,记为*()r e x ,即**()()r e x e x x=7。
矩阵范数:对任意n 阶方阵A ,按一定的规则有一实数与之对应,记为||||A .若||||A 满足 (1)||||0A ≥,且||||0A =当且仅当0A =; (2)对任意实数α,都有||||||A αα=||||A ;(3)对任意两个n 阶方阵A ,B,都有||||||||||||A B A B +≤+; (4)||||||||AB A =||||B称||||A 为矩阵A 的范数.8. 算子范数:设A 为n 阶方阵,||||•是n R 中的向量范数,则0||||||||||||maxx Ax A x ≠=是一种矩阵范数,称其为由向量范数||||•诱导出的矩阵范数,也称算子范数.9。
(完整word版)小学数学复习备考方案(汇总)
让数学复习课堂具有生命活力——小学数学毕业班复习备考凤庆县第一完全小学陈树清课堂是教师职业幸福的生命,数学与生活息息相关。
作为数学教师,要学会做学生生命中的贵人,数学教学应该是生动的、寓于思维碰撞的心灵交流,通过建立信任、安全、民主、平等、有序的数学学习环境,沉淀到学生生命里的是数学思维和数学方法,达成人课合一、浑然一体,这是目标、是要求、更是境界;要实践、要思考、更要创新。
古语说得好:温故而知新,可以为师矣。
意思是说,在温习旧知识时,能有新体会、新发现、就可以当老师了。
这里强调的就是复习对于学习的重要作用。
某种意义上说,复习比学习更重要。
小学数学期末总复习,是学生对本学期数学学习的一个系统的整理,是对本学期数学知识的一个重构,更是一种提升。
此阶段复习效率的高低关系到本学期教学任务是否能圆满完成,影响到小学生今后在数学方面的发展。
因此,做好小学数学期末复习,提高复习效率尤其显得重要。
今天,我重点从小学数学复习课的定义、小学数学毕业总复习的任务、认清总复习的教学目标、掌握小学数学复习的方法及措施、小学数学复习应注意的问题和把握知识点进行有针对性地复习这六大方面来谈一谈。
一、小学数学复习课的定义数学是一门研究数量关系和空间形式的科学。
关于数学课的复习,我们先来重新认识复习课的定义:复习课是以复习巩固所学知识为主要内容,并借助板书形成知识网络的课型。
复习课的任务:加深学生对知识的理解并系统化。
复习课的结构:揭题——回忆——整理——沟通——练习——总结。
揭题——复习课一般直接揭示课题,有时还同时列出复习目标。
回忆——由学生对所复习的内容进行回顾,学生可翻阅课本、相互提示。
通常教师只是辅以提问或学生做基本的练习。
整理——分与合,即按一定的标准进行分类与合并,使知识条理化、系统化。
这种既求同又求异的环节通常与板书结合起来,形成线状、块状、网状、表格等形式的板书。
沟通——进行纵向联系和横向联系,构成网络,形成知识结构,并通过深化练习使之转化为学生的认知结构。
(完整word版)六年级下册简便运算总复习练习题和答案
运算定律练习题(1)乘法互换律: a× b= b× a乘法联合律:(a×b)× c=a×(b× c)38×25× 442×125×825×17× 4(25× 125)×(8× 4)49×4×538×125× 8× 3(125×25)×45 ×289×2 (125×12)× 8 125×( 12× 4)(2)乘法互换律和联合律的变化练习125× 64125× 8844×25125× 2425×28(3)加法互换律: a+ b= b+ a 加法联合律:(a+b)+ c=a+( b+ c)357+ 288+143 158+ 395+105 167+289+33 129+235+171+165 378+ 527+73169+ 78+2258+39+42+61138+293+62+107(4)乘法分派律:(a+b)× c= a× c+ b× c 正用练习(80+ 4)× 25 (20+4)×25 ( 125+17)×8 25×(40+4)15×(20+3)(5)乘法分派律正用的变化练习:36×3 25×41 39×101 125×88 201× 24(6)乘法分派律反用的练习:34×72+ 34×2835×37+65× 3785×82+85× 1825× 97+25× 376×25+25× 241(7)乘法分派律反用的变化练习:38× 29+3875× 299+ 7564× 199+ 6435×68+68+ 68×64☆思虑题:(8)其余的一些简易运算。
(完整word版)2019年中考专题复习第二讲实数的运算(含详细参考答案)
2019年中考专题复习 第二讲 实数的运算【基础知识回顾】一、实数的运算.1、基本运算:初中阶段我们学习的基本运算有 、 、 、 、 、 和 共六种,运算顺序是先算 ,再算 ,最后算 ,有括号时要先算 ,同一级运算,按照 的顺序依次进行. 2、运算法则:加法:同号两数相加,取 的符号,并把 相加,异号两数相加,取 的符号,并用较大的 减去较小的 ,任何数同零相加仍得 。
减法,减去一个数等于 。
乘法:两数相乘,同号得 ,异号得 ,并把 相乘。
除法:除以一个数等于乘以这个数的 。
乘方:(-a )2n +1= (—a ) 2n=3、运算定律:加法交换律:a+b= 加法结合律:(a+b )+c= 乘法交换律:ab= 乘法结合律:(ab )c= 分配律: (a+b )c= 二、零指数、负整数指数幂。
0a = (a≠0) a -p= (a≠0)【名师提醒:1、实数的混合运算在中考考查时经常与0指数、负指数、绝对值、锐角三角函数等放在一起,计算时要注意运算顺序和运算性质。
2、注意底数为分数的负指数运算的结果,如:(31)-1= 】三、实数的大小比较:1、比较两个有理数的大小,除可以用数轴按照的原则进行比较以外,,还有比较法、比较法等,两个负数大的反而小。
2、如果几个非负数的和为零,则这几个非负数都为。
【名师提醒:比较实数大小的方法有很多,根据题目所给的实数的类型或形可以式灵活选用。
22的大小,可以先确定10和65的取值范围,然后得结论:10+2 65—2。
】【重点考点例析】考点一:实数的大小比较。
例1 (2018•福建)在实数|-3|,—2,0,π中,最小的数是()A.|-3| B.-2 C.0 D.π【思路分析】直接利用利用绝对值的性质化简,进而比较大小得出答案.解:在实数|—3|,-2,0,π中,|—3|=3,则-2<0<|-3|<π,故最小的数是:—2.故选:B.【点评】此题主要考查了实数大小比较以及绝对值,正确掌握实数比较大小的方法是解题关键.考点二:估算无理数的大小例2 (2018•南京)下列无理数中,与4最接近的是()A B C D【点评】此题主要考查了估算无理数的大小,正确得出接近4的无理数是解题关键. 考点三:实数与数轴例3(2018•北京)实数a,b,c 在数轴上的对应点的位置如图所示,则正确的结论是( ) A .|a |>4 B .c —b >0 C .ac >0 D .a+c >0【思路分析】本题由图可知,a 、b 、c 绝对值之间的大小关系,从而判断四个选项的对错. 解:∵—4<a <-3,∴|a |<4,∴A 不正确; 又∵a <0,c >0,∴ac <0,∴C 不正确; 又∵a <—3,c <3,∴a+c <0,∴D 不正确; 又∵c >0,b <0,∴c-b >0,∴B 正确; 故选:B .【点评】本题主要考查了实数的绝对值及加减计算之间的关系,关键是判断正负. 考点四:实数的混合运算例4 (2018•怀化)计算:0112sin 3022|31|π-︒--+-+()()【思路分析】直接利用特殊角的三角函数值以及零指数幂的性质和负指数幂的性质分别化简得出答案.【解答】解:原式=1213122⨯-+-+ =1+3.【点评】此题主要考查了实数运算,正确化简各数是解题关键. 考点五:实数中的规律探索。
2022届高考化学大一轮复习课时作业:热点突破2 化学常用计算方法 Word版含解析
课时作业1.标准状况下,一个装满氯气的容器的质量为74.6 g,若装满氮气时总质量为66 g,则此容器的容积是()A.22.4 L B.44.8 LC.11.2 L D.4.48 L解析:22.4 L(标准状况下)Cl2换成22.4 L(标准状况下)N2的质量差是71 g-28 g=43 g,设氯气的体积为x L,则有Cl2~N2Δm22.4 L43 gx L74.6 g-66 g=8.6 g解得x=4.48。
答案:D2.含KCl和KBr的样品3.87 g,溶于水配成溶液,向溶液中加入过量AgNO3溶液,充分反应后,产生的沉淀质量为6.63 g,则原样品中钾元素的质量分数为()A.24.1% B.40.3%C.25.9% D.48.7%解析:KCl和KBr与AgNO3溶液反应生成AgCl和AgBr沉淀,固体的质量发生了变化,实质是由于K变成了Ag造成的,故可用差量法进行计算。
K~AgΔm3910869m 6.63 g-3.87 g=2.76 g解得m=1.56 g质量分数为1.56 g3.87 g×100%≈40.3%答案:B3.肯定质量的碳和8 g氧气在密闭容器中于高温下反应,恢复到原来的温度,测得容器内的压强变为原来的1.4倍,则参与反应的碳的质量为()A.2.4 g B.4.2 g C.6 g D.无法确定解析:由化学方程式:C+O2=====高温CO2和2C+O2=====高温2CO可知,当产物全部是CO2时,气体的物质的量不变,温度和体积不变时气体的压强不变;当产物全部是CO时,气体的物质的量增大1倍,温度和体积不变时压强增大1倍,现在气体压强变为原来的1.4倍,故产物既有CO2,又有CO。
n(O2)=8 g32 g·mol-1=0.25 mol,由阿伏加德罗定律可知,气体压强变为原来的1.4倍,气体的物质的量变为原来的1.4倍,即Δn(气体)=0.25 mol×(1.4-1)=0.1 mol。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算方法复习一、期末考试试题期末考试主要考核:●基本概念;●基本原理;●基本运算。
必须带简易计算器。
总成绩=平时成绩*30%+期末成绩*70%二、考核知识点、复习要求1 误差(一) 考核知识点●误差的来源类型;●绝对误差和绝对误差限,相对误差和相对误差限,有效数字;●绝对误差的传播。
(二) 复习要求1. 产生误差的主要来源。
2. 了解绝对误差和绝对误差限、相对误差和相对误差限和有效数字等概念以及它们之间的关系。
2 方程求根(一) 考核知识点二分法;迭代法;牛顿法;弦截法。
(二) 复习要求1. 知道有根区间概念,和方程f(x)=0在区间 (a,b)有根的充分条件。
2. 掌握方程求根的二分法,知道其收敛性;掌握二分法迭代次数公式;掌握迭代法,知道其收敛性。
3. 熟练掌握牛顿法。
掌握初始值的选择条件。
4. 收敛阶和收敛速度3 线性方程组的数值解法(一) 考核知识点高斯顺序消去法,列主元消去法,LU分解法;消去法消元能进行到底的条件;雅可比迭代法,高斯―赛德尔迭代法。
(二) 复习要求1. 掌握线性方程组雅可比迭代法和高斯――赛德尔迭代法。
2. 知道高斯消去法的基本思想,熟练掌握高斯顺序消去法和列主元消去法。
3. 知道解线性方程组的高斯消去法消元能进行到底的条件,迭代解收敛性的充分条件。
4. Cond(A)的概念和性质4 函数插值与最小二乘法(一) 考核知识点●插值函数,插值多项式;●拉格朗日插值多项式;插值基函数;●牛顿插值多项式;差商表;●分段线性插值、线性插值基函数(二) 复习要求1. 了解插值函数,插值节点等概念。
2. 熟练掌握拉格朗日插值多项式的公式,知道拉格朗日插值多项式余项。
3. 掌握牛顿插值多项式的公式,掌握差商表的计算,知道牛顿插值多项式的余项。
4. 掌握分段线性插值的方法和线性插值基函数的构造。
6. 了解曲线拟合最小二乘法的意义和推导过程,掌握法方程组的求法,以及线性拟合和二次多项式拟合的方法。
5 数值积分与微分(一) 考核知识点●数值求积公式,求积节点,求积系数,代数精度;●插值型求积公式,牛顿―科特茨求积公式,科特茨系数及其性质,●(复化)梯形求积公式,(复化)抛物线求积公式;●高斯型求积公式,高斯点,(二点、三点)高斯――勒让德求积公式;(二) 复习要求1. 了解数值积分和代数精度等基本概念。
2. 了解牛顿科茨求积公式和科茨系数的性质。
熟练掌握并推导(复化)梯形求积公式和(复化)抛物线求积公式。
3. 知道高斯求积公式和高斯点概念。
会用高斯勒让德求积公式求定积分的近似值。
4. 知道插值型求导公式概念,掌握两点求导公式和三点求导公式。
6 常微分方程的数值解法(一) 考核知识点欧拉公式,梯形公式,改进欧拉法,局部截断误差;龙格―库塔法,局部截断误差。
(二) 复习要求1. 掌握欧拉法和改进的欧拉法(梯形公式、预报-校正公式和平均形式公式),知道其局部截断误差。
2. 知道龙格库塔法的基本思想。
知道二阶、三阶龙格库塔法。
掌握四阶龙格――库塔法,知道龙格库塔法的局部截断误差。
三、重、难点分析例1 证明计算)0(>a a 的牛顿切线法迭代公式为:,1,0),(211=+=+n x ax x nn n并用它求2的近似值(求出1x 即可) 解(1) 因计算a 等于求02=-a x 正根,a x x f -=2)(,x x f 2)(='代入牛顿法迭代公式得)(21221nn n n n n x ax x a x x x +=--=+ ,1,0=n(2) 设2)(2-=x x f ,因,0121)1(2<-=-=f 025.1)5.1(2>-=f所以 []5.1,12*∈=x选5.10=x用上面导出的迭代公式计算得4167.11217)2(21001≈=+=x x x例2 用迭代法求0243=-+x x 的最小正根(求出2x 即可)。
解 (1)用迭代法因02)0(<-=f ,0125.0)5.0(>=f ,故[]5.0,0*∈x在[]5.0,0上将0243=-+x x ,同解变形为)()2(413x x x ϕ=-=则 [][]116343max)(max 25.0,05.0,0<=='=∈∈x x x x ϕρ取,5.00=x 应用迭代公式)2(4131n n x x -=+, ,1,0=n 计算得3215)812(411=-=x47425.0321524132≈⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=x例3 用列主元消元法的方程组⎪⎩⎪⎨⎧=++=++=++53368435532321321321x x x x x x x x x 注意:每次消元时主元的选取是各列中系数最大的。
解 第1列主元为3,交换第1、2方程位置后消元得,⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=-=++331351313168433232321x x x x x x x 第2列主35,元为交换第2、3方程位置后消元得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+=++5252331356843332321x x x x x x回代解得 2,2,1123==-=x x x例4 将矩阵A 进行三角分解(Doolittle 分解,Crout 分解,LDU 分解)其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=1332222224A 说明:一般进行矩阵的三角分解采用紧凑格式。
即应用矩阵乘法和矩阵相等原则进行矩阵的三角分解(或代入公式求得相应元素)。
在分解时注意矩阵乘法、矩阵求逆等代数运算。
解:9,2;1,121,21;2,2,43322123132321321232312212222113131112121131312121111=-=-=-=-==-=-====-======r r r l a l r l a r r l a r a a l a a l a r a r a r则矩阵的Doolittle 分解为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----911224122112111332222224因为对角阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=914D ,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--==-111212111R D U所以矩阵的LDU 分解为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----11121211914122112111332222224矩阵的Crout 分解为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----111212119221241332222224 例5 用LU 分解求解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----5481332222224321x x x 注意:消元过程是解方程组b LY =,和回代过程是解方程组Y RX =。
解:(1)将矩阵进行三角分解,由上例得: 矩阵的三角分解为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----911224122112111332222224(2)解方程组9,0,8,321====y y y b LY (3)解方程组1,1,2,321====x x x Y RX所以 T X )1,1,2(=例6 已知向量X=(1,-2,3),求向量X 的三种常用范数。
解 3max ==∞i ix X,14,612211====∑∑==ni ini i xXx X例7 证明 ,1∞∞≤≤Xn X X证明 因为 11max X x x x Xni i p i i=<==∑=∞∞=≤=≤∑Xn x n x n x i ip ni i max 1所以 ,1∞∞≤≤Xn X X例8 已知矩阵⎥⎦⎤⎢⎣⎡-=2212A ,求矩阵A 的三种常用范数。
解 4max 31==∑=∞j ij i a A,∑===ni ijjaA 114m ax,39)9)(4(36135228522822122122122===--=+-=--=-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-=λλλλλλλλAI A A A A TT例9 已知方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛121212212321x x x a a a (1)写出解此方程组的雅可比法迭代公式 (2)证明当4>a 时,雅可比迭代法收敛 (3)取5=a ,T X)101,51,101()0(=,求出)2(X 。
解 (1)对3,2,1=i ,从第i 个方程解出i x ,得雅可比法迭代公式为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=--=--=+++ ,1,0,)21(1)222(1)21(1)(2)(1)1(3)(3)(1)1(2)(3)(2)1(1m x x a x x x a x x x a x m m m m m m m m m (2)当4>a 时,A 为严格对角占优矩阵,所以雅可比迭代法收敛。
(3)取5=a ,T X)101,51,101()0(= 由迭代公式计算得 101)1(1=x , 258)1(2=x , 101)1(3=x 25013)2(1=x , 258)2(2=x , 25013)2(3=x 则 )(2X=(25013, 258,25013)T例10 用高斯——塞德尔迭代法解方程组⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛434510*********x x x(1)证明高斯——塞德尔迭代法收敛 (2)写出高斯——塞德尔法迭代公式 (3)取TX)()(0000=,求出)(2X解 (1)因为A 为严格对角占优矩阵,故高斯——塞德尔迭代收敛。
(2)对3,2,1=i ,从第i 个方程解出i x ,得高斯——塞德尔法迭代公式为⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=---=-=+++++ ,1,0,)4(51)3(51)4(51)1(2)13)(3)1(1)1(2)(2)1(1m x x x x x x x m m m m m m m ((3) 54)1(1=x , 2519)1(2-=x , 125119)1(3=x 125119)2(1=x , 625613)2(2-=x , 31251887)2(3=x 则)(2X=(125119, 625613-,31251887)T例11 已知,3)9(,2)4(==f f 用线性插值计算)5(f ,并估计误差。
解 取插值节点x 0= 4,x 1= 9,两个插值基函数分别为)9(51)(1010--=--=x x x x x x l )4(51)(0101-=--=x x x x x x l故有565)4(53)9(52)()()(11001+=-+--=+=x x x y x l y x l x L 2.25655)5()5(1=+=≈L f 误差为 )(2)95)(45(!2)()5(2ξξf f R ''-=--''=例12 已知函数)(x f 数数值表x1 2 3 y1 3 7用抛物插值法求近似值)8.1(f 。
