第十二章单元测试题(一)
人教版八年级物理下册 《第十二章 简单机械》单元测试试卷含答案解析(1)

人教版八年级物理下册《第十二章简单机械》单元测试卷学校:姓名:班级:考号:一、单选题1.如图所示的工具中,在使用时属于费力杠杆的是()A.天平B.核桃夹子C.瓶盖起子D.食品夹子2.如图所示,杠杆在水平位置平衡,按下列调整后杠杆仍然能保持平衡的是()A.左右两边的钩码均向外边移2格B.左右两边的钩码均向中间移1格C.左边的钩码向左移1格,右边的钩码向右移2格D.左边的钩码向中间移2格,右边的钩码向中间移1格3.下列关于滑轮和滑轮组的几种说法中不正确的是()A.定滑轮实质是个等臂杠杆B.动滑轮实质是动力臂为阻力臂2倍的杠杆C.使用动滑轮省力但费距离D.使用滑轮组既可以省力又可以省距离4.如图,杠杆在水平方向平衡,若将测力计缓慢地自位置1移到位置2,并保持杠杆始终水平平衡,则测力计的读数变化是()A.不断增大B.不断减小C.先增大,然后减小D.先减小,然后增大5.如图所示,用完全相同的滑轮组成甲、乙两装置,分别将重1N的物体匀速提升相同的高度,滑轮重0.2N,不计摩擦和绳重,机械效率分别是η甲、η乙,所用的拉力分别是F甲和F乙,则()A.η甲>η乙B.η甲<η乙C.F甲>F乙D.F甲=F乙6.工人用如图所示的甲、乙两种滑轮把同样一袋沙提升相同的高度,已知沙和袋总重为100N,滑轮重20N(绳重和摩擦力不计),则下列说法正确的是()A.甲比乙更省力B.甲做的总功比乙的多C.甲做的有用功比乙的多D.甲的机械效率比乙的高7.下列说法中正确的是()A.机械做的有用功越多,机械效率越大B.机械效率大的功率一定大C.机械做功可以省力或省距离,但不能省功D.机械做功时间短的,功率一定大8.如图所示,在斜面上将一个重4.5N的物体匀速拉到高处,沿斜面向上的拉力为1.8N,斜面长s=1.2m、高h=0.3m。
把重物直接提升h所做的功作为有用功,则()A.有用功为1.35J,机械效率为75%B.有用功为2.16J,机械效率为62.5%C.有用功为1.35J,机械效率为62.5%D.有用功为1.35J,机械效率为100%9.质量为m的同一物体,先用滑轮组(如图甲)匀速提升,后沿斜面(如图乙)匀速拉升,两次物体提升高度均为h,两次拉力大小均为0.8mg,斜面长AB=2h,则两次提升物体的机械效率()A.η甲>η乙B.η甲<η乙C.η甲=η乙D.条件不足无法判断10.“节约用水,人人有责”,我们应养成随手关闭水龙头的好习惯。
人教版八年级物理下册单元测试:第十二章简单机械(含答案)
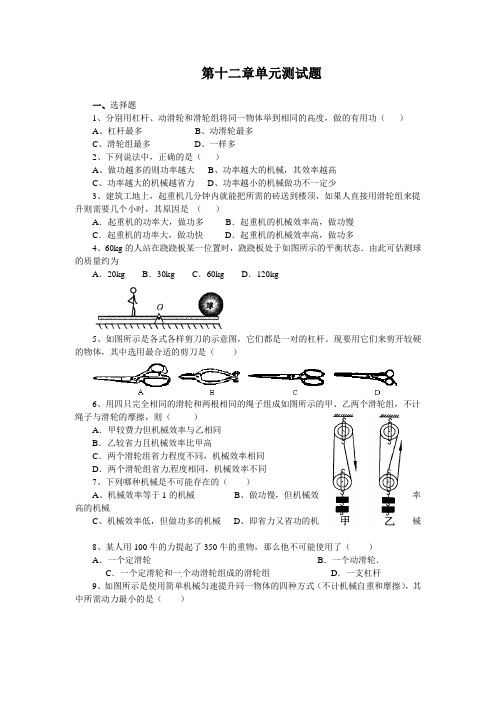
第十二章单元测试题一、选择题1、分别用杠杆、动滑轮和滑轮组将同一物体举到相同的高度,做的有用功()A、杠杆最多B、动滑轮最多C、滑轮组最多D、一样多2、下列说法中,正确的是()A、做功越多的则功率越大B、功率越大的机械,其效率越高C、功率越大的机械越省力D、功率越小的机械做功不一定少3、建筑工地上,起重机几分钟内就能把所需的砖送到楼顶,如果人直接用滑轮组来提升则需要几个小时,其原因是()A.起重机的功率大,做功多B.起重机的机械效率高,做功慢C.起重机的功率大,做功快D.起重机的机械效率高,做功多4、60kg的人站在跷跷板某一位置时,跷跷板处于如图所示的平衡状态.由此可估测球的质量约为A.20kg B.30kg C.60kg D.120kg5、如图所示是各式各样剪刀的示意图,它们都是一对的杠杆。
现要用它们来剪开较硬的物体,其中选用最合适的剪刀是()6、用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,不计绳子与滑轮的摩擦,则()A.甲较费力但机械效率与乙相同B.乙较省力且机械效率比甲高C.两个滑轮组省力程度不同,机械效率相同D.两个滑轮组省力程度相同,机械效率不同7、下列哪种机械是不可能存在的()A、机械效率等于1的机械B、做功慢,但机械效率高的机械C、机械效率低,但做功多的机械D、即省力又省功的机械8、某人用100牛的力提起了350牛的重物,那么他不可能使用了()A.一个定滑轮B.一个动滑轮.C.一个定滑轮和一个动滑轮组成的滑轮组D.一支杠杆9、如图所示是使用简单机械匀速提升同一物体的四种方式(不计机械自重和摩擦),其中所需动力最小的是()10.如图所示,将体积相同的物体G1、G2分别挂在杠杆的两端,杠杆处于平衡状态。
若将两个物体G1、G2同时浸没在水中,则A.杠杆仍能保持平衡B.杠杆不能平衡,A端下沉C.杠杆不能平衡,B端下沉D.无法确定杠杆的状态二、填空题11.指出图中所列工具分别属于那种简单机械,剪刀;扳手;钻头。
八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)
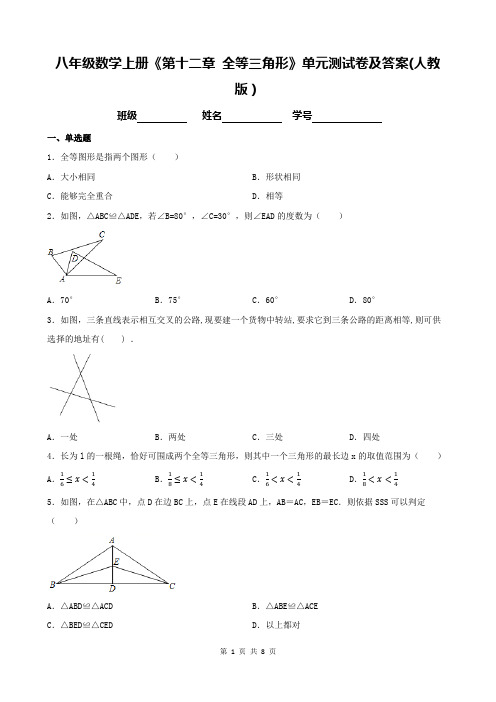
八年级数学上册《第十二章全等三角形》单元测试卷及答案(人教版)班级姓名学号一、单选题1.全等图形是指两个图形()A.大小相同B.形状相同C.能够完全重合D.相等2.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为()A.70°B.75°C.60°D.80°3.如图,三条直线表示相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) .A.一处B.两处C.三处D.四处4.长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为()A.16≤x<14B.18≤x<14C.16<x<14D.18<x<145.如图,在△ABC中,点D在边BC上,点E在线段AD上,AB=AC,EB=EC.则依据SSS可以判定()A.△ABD≌△ACD B.△ABE≌△ACEC.△BED≌△CED D.以上都对6.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是()A.2α+∠A=180°B.α+∠A=90°C.2α+∠A=90°D.α+∠A=180°7.如图,点O在△ABC内,且到三边的距离相等,∠A=64°,则∠BOC的度数为()A.58°B.64°C.122°D.124°8.如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是()A.②③④B.①②C.①④D.①②③④二、填空题9.已知△ABC≌△DEF,若∠B=40°,∠D=30°,则∠F=10.如图,已知B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件,可以判断△ABF≌△DCE.11.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC= cm.12.如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面AC•BD.正确的是(填写所有正确结论的序号)积S= 1213.如图,在△ABC中AC=BC,∠ACB=50°,AD⊥BC于点D,MC⊥BC于点C,MC=BC点E,点F分别在线段AD,AC上CF=AE,连接MF,BF,CE.(1)图中与MF相等的线段是;(2)当BF+CE取最小值时∠AFB=°三、解答题14.将Rt△ABC的直角顶点C置于直线l上AC=BC,分别过点A、B作直线l的垂线,垂足分别为点D、E连接AE若BE=3,DE=5求△ACE的面积.15.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.16.如图,已知AC∥BD、EA、EB分别平分∠CAB和△DBA,CD过点E,则线段AB与AC、BD有什么数量关系?请说明理由.17.如图,已知B,C,E三点在同一条直线上AC//DE,AC=CE,∠ACD=∠B .求证:△ABC≌△EDC .18.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.19.已知:AD=BC,AC=BD.(1)如图1,求证:AE=BE;(2)如图2,若AB=AC,∠D=2∠BAC,在不添加任何辅助线的情况下,请直接写出图2中四个度数为36°的角.参考答案 1.C 2.A 3.D 4.A 5.D 6.A 7.C 8.B 9.110° 10.AB=DC 11.5 12.①④ 13.(1)EC (2)9514.解:∵AD ⊥CE ,BE ⊥CE ∴∠ADC =∠CEB =90° ∵∠ACB =90°∴∠ACD =∠CBE =90°−∠ECB 在 △ACD 与 △CBE 中{∠ADC =∠CEB∠ACD =∠CBE AC =BC∴△ACD ≌△CBE (AAS) ∴CD =BE =3 AD =CE ∵CE =CD +DE =3+5=8 ∴AD =8 .S △ACE =12CE ·AD =12×8×8=32 . 15.证明:∵CE ∥DF ∴∠ACE=∠D 在△ACE 和△FDB 中{AC=FD ∠ACE=∠D EC=BD∴△ACE≌△FDB(SAS)∴AE=FB.16.解:AB=AC+BD理由是:在AB上截取AC=AF,连接EF∵AE平分∠CAB∴∠CAE=∠BAE在△CAE和△FAE中{AC=AF∠CAE=∠BAE AE=AE∴△CAE≌△FAE(SAS)∴∠C=∠AFE∵AC∥BD∴∠C+∠D=180°∴∠AFE+∠D=180°∵∠EFB+∠AFE=180°∴∠D=∠EFB∵BE平分∠ABD∴∠DBE=∠FBE在△BEF和△BED中{∠D=∠EFB∠FBE=∠DBEBE=BE∴△BEF≌△BED(AAS)∴BF=BD∵AB=AF+BF,AC=AF,BF=BD ∴AB=AC+BD.17.证明:∵AC//DE∴∠BCA =∠E ∠ACD =∠D . 又∵∠ACD =∠B ∴∠B =∠D .在 △ABC 和 △EDC 中{∠B =∠D∠BCA =∠E AC =EC∴△ABC ≌△EDC .18.解:过点D 作DE ⊥AB 于点E ,DF ⊥BC 于点F . ∴∠DEB =∠DFB =90°. 又∵BD 平分∠ABC ∴DE =DF .∵∠BMD+∠DME =180°,∠BMD+∠BND =180° ∴∠DME =∠BND . 在△EMD 和△FND 中{∠DEM =∠DFN∠EMD =∠FND DE =DF∴△EMD ≌△FND (AAS ). ∴DM =DN .19.(1)证明:在△ABD 和△BAC 中:{AB =BAAD =BC BD =AC∴△ABD ≌△BAC (SSS ) ∴∠ABD=∠BAC ∴AE=BE ;(2)∠BAC ,∠ABD ,∠DAC ,∠DBC。
八年级数学上册第12章全等三角形单元评价检测(精品测试卷)

12.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD 面积是_____.
三、解答题(共47分)
21.如图21所示,海岛上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸的距离相等吗?为什么?
22.如图22,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.
(Ⅱ)∠AOB是一个任意角,在边OA,OB上分别取OM=ON,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
A.5B.8C.10D.15
4.如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带哪块玻璃碎片去玻璃店?( )
A.①B.②C.③D.④
5.如图6所示,在△ABC和△ABD中,∠C=∠D=90°,要利用“HL”判定△ABC≌△ABD成立,还需要添加 条件是( )
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
第十二章 单元测试题(一)

第十二章单元测试题一、选择题1.以下关于机械波的几种说法中,正确的是:()A.有机械振动必定会有机械波B.机械波在介质中的传播速度由介质本身的性质决定C.在波传播方向上的某个质点的振动速度就是波的传播速度D.在波动的过程中,波上的质点是沿着波形曲线运动的2.在山中砍伐时发出的声音既含有频率较高的声波,也含有频率较低的声波,其中只有频率较低的“嘭”“嘭”声才能被远处的人听到。
这是因为()A.频率较低的“嘭”“嘭”声能量大,能传到很远B.频率较低的“嘭”“嘭”声速度快,最先到达C.频率较低的“嘭”“嘭”声波长较长,容易产生衍射D.以上说法均不对3.如图所示为一列简谐横波的图像,波速为0.2m/s,以下结论正确的是:()A.振源振动的频率为0.4HzB.若质点a比质点b先回到平衡位置,则波沿x轴正方向传播C.图示时刻质点a、b、c所受回复力大小之比为2∶1∶3D.经过0.5s质点a、b、c通过的路程为75cm4.图甲为一列简谐横波在某一时刻的波形图,图乙为质点P以该时刻为计时起点的振动图象,下列说法正确的是()A.从该时刻起经过0.15s时,质点P到达波峰B.从该时刻起经过0.25s时,质点Q的加速度小于质点P的加速度C.从该时刻起经过0.15s时,波沿x轴的正方向传播了3mD.从该时刻起经过0.35s时,质点Q距平衡位置的距离大于质点P距平衡位置的距离5.如图所示是利用水波槽观察到的水波衍射图象,从图象可知()A.B侧波是衍射波B.A侧波速与B侧波速相等C.减小挡板间距离,衍射波的波长将减小D.增大挡板间距离,衍射现象将更明显6.如图所示,甲、乙两平面波是振幅相同的相干波,甲波沿x轴正方向传播,乙波沿y轴正方向传播,图中实线表示某一时刻的波峰位置,虚线表示波谷位置,对图中正方形中央的a、b、c、d四点的振动情况,正确的判断是()A.a、b点振动加强,c、d点振动减弱B.a、c点振动加强,b、d点振动减弱C.a、d点振动加强,b、c点振动减弱D.a、b、c、d点的振动都加强7.如右图所示产生机械波的波源O做匀速运动的情况,图中圆表示波峰,已知波源的频率为f0,则下列说法正确的是:()A.该图表示波源正在向B点移动B.观察者在图中A点接收波的频率是定值,但大于f0C.观察者在图中B点接收波的频率是定值,但大于f0D.观察者在图中C点或D点接收波的频率是定值,但大于f08.如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分子位于x=-2×10-1m和x=12×10-1m处,两列波的波速均为v=0.4m/s,两波源的振幅均为A=2cm。
第十二章 运动和力 单元测试

第十二章《运动和力》单元测试题一、填空题(每空1分,共32分)1.“地球同步卫星总是静止在地球某处的上空”,这是以________为参照物的,若以太阳为参照物,这个卫星应是__________的.2.在平静的湖面上行驶的游船上坐着的乘客,以________为参照物他是运动的,以________为参照物他是静止的.3.一个做匀速直线运动的物体在2 min内通过了300 m的路程,它运动的速度是___ ___m/s,这个物体在前10 s内通过的路程是____m.4.用钢丝绳系上一个质量是50kg的物体,当钢丝绳拉着它匀速上升时,绳对物体的拉力是____N,当钢丝绳拉着物体静止时,绳对物体的拉力是______N,当钢丝绳拉着物体以2 m/s的速度匀速下降时,绳对物体的拉力是_____N.5.小明用刻度尺测物体的长度,如图所示,他所用的刻度尺的分度值是______,物体的长度是______.6.速度用来表示物体运动的;在匀速直线运动中,速度等于运动物体在__ 内通过的,写成公式是:。
108km/h=___ _m/s 5 m/s=_ ___km/h7.小明用手拍了一下小红,小明、小红都感到疼,这说明___ ___,使小明感觉疼的力的施力物体是______.8.物体在受几个力作用时,如果保持状态或状态,这几个力就彼此平衡。
9.作用在上的两个力,如果,,并且作用在上,这两个力就相互平衡。
10.力的、、、叫做力的三要素,它们都可以影响力的。
11.力可以改变物体的,也可以改变物体。
12.小明同学用刻度尺测量一个物体的长度,测得的四次结果如下:5.45cm、5.44cm、5.45cm、5.43cm,则这个物体的长度是。
二、选择题(每小题3分,共39分)13.一个物体沿直线运动,它在第1 min内、第2 min内、第3 min内的路程都是300 m,在这3 min内做的是()A.匀速直线运动B.变速直线运动C.变速运动D.无法确定14.坐在逆水航行的轮船中的乘客,认为自己是静止的,他选取的参照物是()A.河岸上的树B.船舱C.迎面驶来的船D.河水15.一辆长30 m的大型平板车,在匀速通过70 m长的大桥时,所用时间是10 s,它以同样的速度通过另一座桥,用了20 s的时间,那么这座桥的长度是()A.140 mB.170 mC.200 mD.230 m16.人在火车车厢里立定跳远,在下列情况中,如果人用力相同,则下列说法正确的是()A.在静止的火车里向前跳,跳得较远B.在匀速直线运动的火车里,向车行进的方向跳,跳得较远C.在匀速直线运动的火车里,向车行进的反方向跳,跳得较远D.在以上三种情况里人跳的距离均相同17.下图所指的四个力中,使受力物体运动状态发生改变的是()18.如图所示,一物体在外力F 的作用下,以5m/s 的速度做匀速直线运动,如果突然将力撤去,则物体 ( )A .立即停止B .继续以5m/s 的速度做匀速直线运动C .继续向右运动,但速度逐渐减小直至停止D .先向右运动,然后向左运动19.如下图所示,下列物体受力示意图中,物体处于二力平衡的是 ( )20.磁铁靠近铁钉的时下列说法中,正确的是 ( )A 、磁铁吸铁钉的力,此力的施力物体是铁钉。
第十二章 全等三角形单元测试卷(含解析)

第十二章全等三角形单元测试卷一.选择题(共10小题,满分30分,每小题3分)1.在△ABC和△DEF中,∠A=50°,∠B=70°,AB=3cm,∠D=50°,∠E=70°,EF=3cm.则△ABC与△DEF()A.一定全等B.不一定全等C.一定不全等D.不确定2.下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是()A.①②B.②③C.①③D.①②③3.某同学不小心把一块玻璃打碎了,变成了如图所示的三块,现在要到玻璃店配一块完全一样的玻璃,那么应带哪块去才能配好()A.①B.②C.③D.任意一块4.如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD;⑤BC=CE.()A.0个B.1个C.2个D.3个5.下列画图的语句中,正确的为()A.画直线AB=10cm B.画射线OB=10cmC.延长射线BA到C,使BA=BC D.画线段CD=2cm6.长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为()A.B.C.D.7.AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=()A.69°B.°C.°D.不能确定8.已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,对于上述的两个判断,下列说法正确的是()A.①正确,②错误 B.①错误,②正确 C.①,②都错误D.①,②都正确9.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为()A.1 B.2 C.5 D.无法确定10.如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A 折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP =S△APF.正确的个数是()A.1个B.2个C.3个D.4个二.填空题(共6小题,满分18分,每小题3分)11.如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由:或.12.如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,△ABD、△BCE均为等边三角形,DE、AB交于点F,AF=3,则△ACE的面积为.13.在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC 于E,连接DE,DF⊥BC于F,则∠EDC=°.14.如图:△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:,使△ABD≌△CEB.15.如图,线段AC、BD相交于点0,OA=OC,OB=OD,那么AB、CD的位置关系是.16.如图,将一张直角三角形纸片对折,使点B、C重合,折痕为DE,连接DC,若AC=6cm,∠ACB=90°,∠B=30°,则△ADC的周长是cm.三.解答题(共8小题,满分72分)17.(8分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠FAE的度数;(3)求证:CD=2BF+DE.18.(8分)如图,△ABC是等边三角形,AN=BM,BN,MC相交于O,CH⊥BN于点H,求证:2OH=OC.19.(8分)已知:如图,在△ABC中,AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证:(1)△ABD≌△ACE;(2)AF⊥DE.20.(8分)如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.(1)试判断B′E与DC的位置关系;(2)如果∠C=130°,求∠AEB的度数.21.(8分)如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC 于一点O,AC=AE,AD=AB,∠BAC=∠DAE.(1)求证:△ABC≌△ADE;(2)若∠BAD=20°,求∠CDE的度数.22.(10分)已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.(1)求证:∠AFC=120°;(2)若AD=6,CE=4,求AC的长?23.(10分)有一座锥形小山,如图,要测量锥形小山两端A、B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,量出DE的长为50m,你能求出锥形小山两端A、B的距离吗?24.(12分)探究问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为.拓展问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.推广问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.参考答案与试题解析1.解:∵在△ABC和△DEF中,∠A=50°,∠B=70°,∠D=50°,∠E=70°,EF=3cm,AB=3cm 若是AB=DE,则可以推出两三角形全等此处是EF与AB相等,设DE=3,则DE=EF,则∠D=∠E显然与已知相违背,所以此假设不成立所以两三角形一定不全等.故选C.2.解:①正确.可以用AAS或者ASA判定两个三角形全等;②正确.可以用“倍长中线法”,用SAS定理,判断两个三角形全等;如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,∴△ADC≌△EDB,∴BE=AC,同理:B′E′=A′C′,∴BE=B′E′,AE=A′E′,∴△ABE≌△A′B′E′,∴∠BAE=∠B′A′E′,∠E=∠E′,∴∠CAD=∠C′A′D′,∴∠BAC=∠B′A′C′,∴△BAC≌△B′A′C′.③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.故选:A.3.解:只有①中包含两角及夹边,符合ASA.故选A.4.解:∵AD∥BC,∴∠ABC+∠BAD=180°,∵AE 、BE 分别是∠BAD 与∠ABC 的平分线, ∴∠BAE=∠BAD ,∠ABE=∠ABC , ∴∠BAE +∠ABE=(∠BAD +∠ABC )=90°, ∴∠AEB=180°﹣(∠BAE +∠ABE )=180°﹣90°=90°, 故③小题正确;延长AE 交BC 延长线于F , ∵∠AEB=90°, ∴BE ⊥AF , ∵BE 平分∠ABC , ∴∠ABE=∠FBE , 在△ABE 与△FBE 中,,∴△ABE ≌△FBE (ASA ), ∴AB=BF ,AE=FE , ∵AD ∥BC , ∴∠EAD=∠F ,在△ADE 与△FCE 中,,∴△ADE ≌△FCE (ASA ), ∴AD=CF ,∴AB=BC +CF=BC +AD ,故①小题正确; ∵△ADE ≌△FCE ,∴CE=DE ,即点E 为CD 的中点,故②小题正确; ∵△ADE ≌△FCE , ∴S △ADE =S △FCE , ∴S 四边形ABCD =S △ABF , ∵S △ABE =S △ABF ,∴S △ABE =S 四边形ABCD ,故④小题正确;若AD=BC ,则CE 是Rt △BEF 斜边上的中线,则BC=CE ,∵AD与BC不一定相等,∴BC与CE不一定相等,故⑤小题错误.综上所述,不正确的有⑤共1个.故选:B.5.解:A、错误.直线没有长度;B、错误.射线没有长度;C、错误.射线有无限延伸性,不需要延长;D、正确.故选:D.6.解:∵围成两个全等的三角形可得两个三角形的周长相等∴x+y+z=,∵y+z>x∴可得x<,又因为x为最长边大于∴x≥综上可得≤x<故选:A.7.解:∵AD=AB,∴∠ADB=(180°﹣∠BAC)=90°﹣∠BAC,∴∠C=∠ADB﹣∠DAC=(180°﹣∠BAC)=90°﹣∠BAC﹣∠BAC=90°﹣∠BAC;∵BE=BC,∴∠C=∠BEC=∠BAC+∠ABE=∠BAC+(180°﹣∠BAC)=∠BAC+45°﹣∠BAC=45°+∠BAC,∴90°﹣∠BAC=45°+∠BAC,解得∠BAC=,∴∠C=90°﹣=.故选:C.8.解:∵△A1B1C1,△A2B2C2的周长相等,A1B1=A2B2,A1C1=A2C2,∴B1C1=B2C2,∴△A1B1C1≌△A2B2C2(SSS),∴①正确;∵∠A1=∠A2、∠B1=∠B2,∴△A1B1C1∽△A2B2C2,设相似比为k,即===k,∴=k,∵△A1B1C1,△A2B2C2的周长相等,∴k=1,即A1B1=A2B2,B1C1=B2C2,A1C1=A2C2,∴△A1B1C1≌△A2B2C2,∴②正确;故选:D.9.解:过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,∵∠EDF+∠FDC=90°,∠GDC+∠FDC=90°,∴∠EDF=∠GDC,于是在Rt△EDF和Rt△CDG中,,∴△DEF≌△DCG,∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,=(AD×EF)÷2=(2×1)÷2=1.所以,S△ADE故选:A.10.解:①正确.作EM ∥AB 交AC 于M . ∵CA=CB ,∠ACB=90°, ∴∠CAB=∠CBA=45°,∵∠CAE=∠BAE=∠CAB=22.5°, ∴∠MEA=∠EAB=22.5°,∴∠CME=45°=∠CEM ,设CM=CE=a ,则ME=AM=a ,∴tan ∠CAE===﹣1,故①正确,②正确.△CDA ≌△CDB ,△AEC ≌△AEF ,△APC ≌△APF ,△PEC ≌△PEF ,故②正确, ③正确.∵△PEC ≌△PEF , ∴∠PCE=∠PFE=45°, ∵∠EFA=∠ACE=90°, ∴∠PFA=∠PFE=45°,∴若将△PEF 沿PF 翻折,则点E 一定落在AB 上,故③正确. ④正确.∵∠CPE=∠CAE +∠ACP=67.5°,∠CEP=90°﹣∠CAE=67.5°, ∴∠CPE=∠CEP , ∴CP=CE ,故④正确, ⑤错误.∵△APC ≌△APF , ∴S △APC =S △APF ,假设S △APF =S 四边形DFPE ,则S △APC =S 四边形DFPE , ∴S △ACD =S △AEF ,∵S △ACD =S △ABC ,S △AEF =S △AEC ≠S △ABC , ∴矛盾,假设不成立. 故选:D .11.解:∵已知DE=AB,∠D=∠A,∴根据ASA判断全等添加∠B=∠E;根据AAS判断全等添加∠ACB=∠DFE;根据SAS判断全等添加AF=CD.故填空答案:∠B=∠E或∠ACB=∠DFE或AF=CD.12.解:如图所示,过D作DG⊥AB于G,EK⊥AC交AC的延长线于K.∵△ABD是等边三角形,DG⊥AB,∴AG=BG=AB,由勾股定理得:DG=AG,∵∠BAC=30°,∴AC=AB,∴AG=AC=AB,∵由勾股定理得:BC=AC,∴DG=BC=BE,∵∠EBA=60°+30°=90°,∴EB⊥AB.∴DG∥EB.∴∠BEF=∠GDF,∠DGB=∠EBF=90°,在△DGF与△EBF中,∵,∴△ADF≌△GEF(AAS),∴DF=EF,GF=BF,∵AG=BG,AF=3,∴FG=,AG=2,∴AB=4AC=2,EC=BC=AC=6,在Rt△CEK中,EK=EC=3,∴S=•AC•EK=•2•3=6.△ACE故答案为6.13.解:过D作DM⊥AC交CA的延长线于M,DN⊥AE,∵CD平分∠ACB,∴DF=DM,∵∠BAC=120°,∴∠DAM=60°,∵AE平分∠BAC,∴∠BAE=60°,∴∠DAM=∠BAE,∴DM=DN,∵DF⊥BC,∴DE平分∠AEB,∵AB=AC,AE平分∠BAC交BC于E,∴AE⊥BC,∴∠AEB=90°,∴∠DEF=45°,∵∠B=∠C=30°,∴∠DCF=15°,∴∠EDC=30°,故答案为:30.14.解:已知∠B=∠B,∠BDA=∠BEC=90°,则再添加一个边相等即可,所以可添加BD=BE或AD=CE或BA=BC,从而利用AAS或ASA来判定△ABD≌△CEB,故答案为:BD=BE或AD=CE或BA=BC.15.解:在△AOB和△COD中,,∴△AOB≌△COD(SAS),∴∠A=∠C,∴AB∥CD.故答案为:AB∥CD.16.解:根据折叠前后角相等可知,∠B=∠DCB=30°,∠ADC=∠ACD=60°,∴AC=AD=DC=6,∴ADC的周长是18cm.17.证明:(1)∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠E=45°,由(1)知△BAC≌△DAE,∴∠BCA=∠E=45°,∵AF⊥BC,∴∠CFA=90°,∴∠CAF=45°,∴∠FAE=∠FAC+∠CAE=45°+90°=135°;(3)延长BF到G,使得FG=FB,∵AF⊥BG,∴∠AFG=∠AFB=90°,在△AFB和△AFG中,,∴△AFB≌△AFG(SAS),∴AB=AG,∠ABF=∠G,∵△BAC≌△DAE,∴AB=AD,∠CBA=∠EDA,CB=ED,∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,∵∠GCA=∠DCA=45°,在△CGA和△CDA中,,∴CG=CD,∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.18.证明:∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠ABC=∠ACB=60°,在△BAN和△CBM中,,∴△BAN≌△CBM(SAS),∴∠ABN=∠BCM,∵∠ABN+∠OBC=60°,∴∠BCM+∠OBC=60°,∵∠NOC为△OBC的外角,∴∠NOC=∠BCM+∠OBC=60°,在Rt△OHC,∠HCO=30°,则2OH=OC.19.证明:(1)∵AB=AC,∠BAC=90°,∴∠B=∠BCA=45°,∵EC⊥BC,∴∠ACE=90°﹣45°=45°,∴∠B=∠ACE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)由(1)知,△ABD≌△ACE,∴AD=AE,等腰△ADE中,∵DF=FE,∴AF⊥DE.20.解:(1)由于AB′是AB的折叠后形成的,∠AB′E=∠B=∠D=90°,∴B′E∥DC;(2)∵折叠,∴△ABE≌△AB′E,∴∠AEB′=∠AEB,即∠AEB=∠BEB′,∵B′E∥DC,∴∠BEB′=∠C=130°,∴∠AEB=∠BEB′=65°.21.证明:(1)在△ABC和△ADE中,,∴△ABC≌△ADE(SAS);(2)∵△ABC≌△ADE,∴∠BAC=∠DAE,∠E=∠C,∵∠BAC=∠BAD+∠DAC,∠DAE=∠DAC+∠CAE,∠BAD=20°,∴∠CAE=∠BAD=20°,∵∠E=∠C,∠AOE=∠DOC,∴∠CAE=∠CDE,∴∠CDE=20°.22.解:(1)∵AE、CD分别为△ABC的角平分线,∴∠FAC=,∠FCA=,∵∠B=60°∴∠BAC+∠BCA=120°,∴∠AFC=180﹣∠FAC﹣∠FCA=180°﹣×120°=120°.(2)在AC上截取AG=AD=6,连接FG.∵AE、CD分别为△ABC的角平分线∴∠FAC=∠FAD,∠FCA=∠FCE,∵∠AFC=120°,∴∠AFD=∠CFE=60°,在△ADF和△AGF中,∴△ADF≌△AGF(SAS)∴∠AFD=∠AFG=60°,∴∠GFC=∠CFE=60°,在△CGF和△CEF中,∴△CGF≌△CEF(ASA),∴CG=CE=4,∴AC=10.23.解:在△ABC和△EDC中,∴△ABC≌△EDC,∴AB=DE=50.答:锥形小山两端A、B的距离为50m.24.解:(1)∵AE⊥BC,BF⊥AC∴△AEB和△AFB都是直角三角形∵D是AB的中点∴DE和DF分别为Rt△AEB和Rt△AFB的斜边中线∴DE=AB,DF=AB(直角三角形斜边中线等于斜边的一半)∴DE=DF∵DE=kDF∴k=1(2)∵CB=CA∴∠CBA=∠CAB∵∠MAC=∠MB∴∠CBA﹣∠MBC=∠CAB﹣∠MAC即∠ABM=∠BAM∴AM=BM∵ME⊥BC,MF⊥AC∴∠MEB=∠MFA=90又∵∠MBE=∠MAF∴△MEB≌△MFA(AAS)∴BE=AF∵D是AB的中点,即BD=AD又∵∠DBE=∠DAF∴△DBE≌△DAF(SAS)∴DE=DF(3)DE=DF如图1,作AM的中点G,BM的中点H,∵点D是边AB的中点∴DG∥BM,DG=BM同理可得:DH∥AM,DH=AM∵ME⊥BC于E,H 是BM的中点∴在Rt△BEM中,HE=BM=BH∴∠HBE=∠HEB∠MHE=∠HBE+∠HEB=2∠MBC又∵DG=BM,HE=BM∴DG=HE同理可得:DH=FG,∠MGF=2∠MAC∵DG∥BM,DH∥GM∴四边形DHMG是平行四边形∴∠DGM=∠DHM∵∠MGF=2∠MAC,∠MHE=2∠MBC 又∵∠MBC=∠MAC∴∠MGF=∠MHE∴∠DGM+∠MGF=∠DHM+∠MHE∴∠DGF=∠DHE在△DHE与△FGD中,∴△DHE≌△FGD(SAS),∴DE=DF21世纪教育网–中小学教育资源及组卷应用平台21世纪教育网。
第十二章_温度与物态变化单元测试题 最新沪科版九年级物理

第十二章 温度与物态变化单元测试题一、选择题(各2分,共18分)1、下列数据最接近实际的是( )A .教室的高约6m ;B .起重机的效率可以达到100%;C .洗热水澡时的水温约40℃;D .中学生在体测中跑完1000m 用时2min2、先在保温瓶中装入一定量0℃的水,再向保温瓶中放一小块-5℃的冰,盖上保温瓶盖,过一会儿,你的猜想是( )A 、冰的质量增加;B 、冰的质量减少;C 、冰的质量不会改变;D 、条件不足,无法确定。
3、新鲜的白菜放两天就“蔫”了。
对此,小明同学利用所学的物理知识,主要从防止水分蒸发的角度白菜保鲜的问题展开了探究。
他所采用的下列四项措施中,你认为可行的是( )A 、将白菜放在紫外线下照射;B 、不让白菜在太阳下晒即可;C 、将白菜直接放入冷冻室;D 、用塑料膜包好白菜放入冰箱冷藏室。
4、下列物态变化的过程中, 吸收热量的是( )( 1) 春天, 冰雪融化 ( 2) 夏天, 从冰箱里面拿出来的饮料罐“出汗”( 3) 秋天, 清晨出现的雾 ( 4) 冬天, 早晨在太阳照射下, 草地上的霜消失A. ( 1) ( 2);B. ( 1) ( 4);C. ( 2) ( 3);D. ( 2) ( 4)。
5、小芳吃雪糕时,看到雪糕周围冒“冷气”,由此她联想到了泡方便面时碗里冒“热气”的情景。
以下是她对“冷气”和“热气”的思考,其中正确的是( )A.“冷气”和“热气”本质是相同的,他们都是汽化成的水蒸气;B.“冷气”和“热气”本质是不同的,前者是小水珠,后者是水蒸气C.“冷气”和“热气”本质是不同的,前者是液化形成的,后者是汽化形成的D.“冷气”和“热气”本质是相同的,都是液化形成的小水珠6、加油站都有这样的提示:请“熄火加油”、“禁止抽烟”、“不要使用手机”等。
这是为了防止火花点燃汽油引起火灾,因为常温下液态的汽油容易发生的物态变化是 ( )A .液化B .汽化C .熔化D .凝固7、用体温计测得甲的体温为37.50℃,若没有甩过,又用它依次去量乙和丙的体温,已知它们的实际体温为36.90℃和38.60℃,那么两次测温后下列数据正确的是( )A.36.90℃和38.60℃;B.37.50℃和38.60℃;C.36.90℃和37.50℃ ;D.37.50℃和37.50℃8、如下图所示的四种物态变化的实例中,属于液化的是 ( )9、洗热水澡时,卫生间的玻璃镜面变得模糊不清,洗完后过一段时间,镜面又变得清晰起来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单机械 单元测试题
陕西 李云峰
(满分:100分)
一、单项选择题(每小题4分,共36分) 1.使用杠杆时,下列说法正确的是( ) A .力臂不变时,阻力越大,动力一定越小
B .阻力大小不变时,动力臂越长,动力一定越小
C .使用杠杆时,一定使用动力臂大于阻力臂的杠杆
D .阻力和阻力臂不变时,动力臂越长,动力一定越小
2.图1中是一种有把手的门锁,则门锁的把手实质上是一个( ) A .定滑轮 B .动滑轮 C .省力杠杆
D .费力杠杆 3.甲升降机比乙升降机的机械效率高,它们分别把相同质量的物体匀速提升相同的高度。
两者相比,甲升降机( )
A .做的总功较少
B .做的总功较多
C .提升重物做的有用功较少
D .提升重物做的有用功较多
4.如图2所示是我们日常工作生活中所使用到的机械,按图中所示的情景使用过程中没有省力的是( )
5.如图3所示,在用滑轮将同一物体沿相同水平地面匀速移动时,拉力分别为F 甲、F 乙、F 丙、F 丁,比较它们的大小(不计滑轮重及滑轮与细绳间的摩擦),正确的是( )
A .F 甲>F 乙
B .F 乙=F 丙
C .F 丙<F 丁
D .一样大
图
1
AA .抛石机 B .方向盘
C .辘轳
D .斜面
图 2
图3
6.如图4所示,不考虑滑轮与轻绳之间的摩擦,米袋总重为800N ,而绳上吊着的静止的“绅士”重500N ,则米袋对地面的压力为( )
A .500N
B .250N
C .300N
D .800N
7.如图5(不计绳重与摩擦,且动滑轮重G 动小于物重G ),用它们分别将重相同的甲、乙两物体匀速提升相同的高度,所用的拉力分别为F 甲、F 乙,它们的机械效率分别为η甲、η乙。
则下列关系正确的是( ) A .F 甲<F 乙 B .F 甲>F 乙 C .η甲<η乙
D .η甲=η乙
8.某人用100N 的力提起了350N 的重物,那么他可能使用了( ) A .一个定滑轮 B .一个动滑轮 C .一个定滑轮和一个动滑轮组成的滑轮组 D .一支杠杆
9.用一个定滑轮和一个动滑轮组成的滑轮组把重150N 的物体匀速提升1m ,不计摩擦和
绳重,滑轮组的机械效率为60%。
则下列选项错误的是( ) A .拉力一定是125N B .有用功一定是150J C .总功一定是250J D .动滑轮重一定是100N 二、填空题(每空2分,共20分)
10.如图6所示,一位母亲推着婴儿车行走,当前轮遇到障碍物时,母亲向下按扶把,
若把婴儿车视为杠杆,这时杠杆的支点是 ;当后轮遇到障碍物时,母亲向上抬起扶把,这时婴儿车可视为 杠杆(填“省力”或“费力”)。
11.如图7所示的A 、B 两个滑轮中A 是 滑轮,B 是 滑轮;当以F 为10N
的拉力拉物体匀速前进时,则物体与地面间的摩擦力为 N 。
12.如图8所示,用一根结实的绳子在两根光滑木棒上绕几圈,一小朋友用力一拉,两位
大力士竟撞在一起了。
这幅漫画说明了 。
13.如图9所示为一装配线上的一个“机械手”,其O 点为固定转动轴,先它水平抓住一
图
5
图
4
图 6
图
8
图7
只重40N 的工件G ,若它在0.5s 内匀速将这一工件提升了20cm ,而M 的功
率为20W ,则机械手做的有用功为 J ,机械效率为 。
14.将重物从长4m 、高1m 的斜面底部匀速
推上斜面的顶端。
已知沿斜面所用的推
力是300N ,斜面的机械效率是
75%,
则推力做的总功为
J ,物体所受的重力为
N 。
三、作图题(15题6分,16题4分,共10分)
15.如图10所示为钓鱼竿钓鱼的示意图。
O 为支点,A 为手握鱼竿的作用点,请在图中画
出鱼线对钓鱼竿拉力F 2的力臂,最小的动力F 1。
16.小红家住二楼,正装修房子,小红站在地面上,用如图11所示的器材,请帮她设计
一较省力的方法,把材料送到二楼窗口去。
四、实验与探究题(17题11分,18题13分,共24分) 17.在如图12所示的实验装置中:
(1)实验前没有挂钩码时,发现杠杆左端下倾,应将杠杆右端螺母向_______(选填“左”或“右”)边旋一些,使杠杆在水平位置平衡。
(2)实验时只有8个相同的钩码,杠杆上每格等距,当在A 点挂4个钩码时,则怎样挂钩码可以使杠杆在水平位置平衡?(请设计两种方案)
答:①_____________________________。
②____________________________。
18.某学习小组使用几个相同的滑轮分别进行机械效率的测定,如图13。
他们将测得钩
码重G 、拉力F 、钩码上升的髙度h 、测力计移动的距离S ,并将计算出的有用功W 有用总图12
图9 图10 图11
(1)表格中数据★= ;
(2)比较实验1、2,第2次的机械效率较低,主要原因是 ;
(3)比较实验2、3,影响这两次实验机械效率不同的主要因素是 ,使用滑轮组的优点是。
(4)在实验3的装置下再加挂一只相同的钩码,装置的机械效率将 (选填“变大”“变小”或“不变”)。
五、计算题(10分)
19.如图14所示是古书《天工开物》中描述人们用舂(chong )来捣谷时的情景。
若在A 点悬挂的物重为60N ,OA :OB=4:3,则捣谷人在B 点至少需施加竖直向下的多大的力?(不计杆自重)。
参考答案与提示
一、单项选择题
1.D 2.C 3.A 4.A 5.B 6.C 7.B 8.D 9.A 二、填空题
10.后轮;省力 11.定;动;30 12.滑轮组省力 13.8;80% 14.1200;900 三、作图题
15.如图1所示。
16.如图2所示。
图13
图14
四、实验与探究题
17.(1)右 (2)示例:①在右边第三格处挂上4个钩码 ②在右边第六格处挂上2个钩码
18.(1)74.1% (2)动滑轮有重力(或有用功相同时,使用动滑轮做的额外功多) (3)摩擦 可以省力或改变用力方向 (4)变大 五、计算题
19.根据刚刚平衡条件可知,捣谷人施加的力大小为: F =Gl OA l OB =43×60N =80N
图1。
