第2章 Excel在货币时间价值计算中的应用[25页]
Excel在货币时间价值计算中的应用(下)
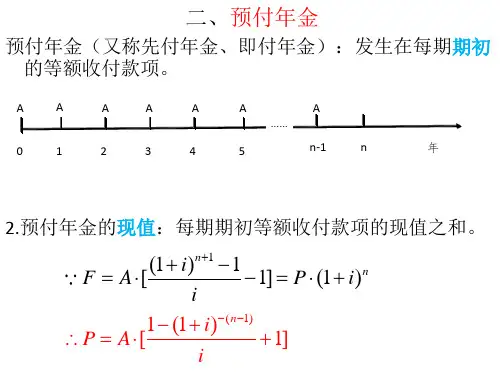
type 0或省略 1
付款时间 期末 期初
年金形式 普通年金 预付年金
思考
题目改为:小王自2001年1月初开始,每年年初都向一位 失学儿童捐款1000元,帮助这位失学儿童从小学1年级 读完9年义务教育。假设每年定期存款利率都是2%,则 小王9年捐款在2009年年底相当于多少钱?
2001年初
0
1
2
3
分析: 1.第一个方案的现值是4000元。
回忆:现值函数PV(rate, nper, pmt, fv, type) 2.第二个方案属于普通年金,现值=PV (10%, 5, -1150,, 0) 3.第三个方案属于预付年金,现值=PV (10%, 5, -1050,, 1) 哪个方案的现值最高,就选择哪个方案。
分析:只要未来5年所有收入的现值>现在支付的400000 元,该方案就可以接受。
回忆:现值函数PV(rate, nper, pmt, fv, type)
例2-14 企业欲用柴油机更新汽油机,柴油机比汽油机贵 20000元,但每年末可以节省燃油费6000元。当年利率为 12%时,如果使用柴油机,至少使用多少年才划算?
例2-7 小李打算购买一份保险,成本价500000元。合同约 定,在未来的10年间,保险公司会在每月的月末支付 5000元给小李,其间的利率为6%。请你帮小李评估一 下,可否购买这份保险?
分析: 回忆:现值函数PV(rate, nper, pmt, fv, type)
这份合同的年金现值=PV (6%/12, 12*10, 5000,,0)
2-3-4-1 年金函数PMT()
年金函数,又称每期付款函数,是各期所应给付(或所能 取得)的金额,在整个年金期间中,其金额是固定的。
Excel在财务管理中的应用第二章Excel在资金时间价值分析中的应用

内含报酬率和修正内含报酬率
(一)内含报酬率的概念
内含报酬率也称内部报酬率,是投资方案净现值为零时的贴现率,净现 值为零说明现金流入的现值等于现金流出的现值。
内含报酬率法是根据投资方案本身内含报酬率来评价方案优劣的一种方 法。如果内含报酬率大于资金成本率,则方案可行,且内含报酬率越高,方 案越优。
内含报酬率法的优点是能够把项目寿命期内的收益与其投资总额联系起 来,揭示这个项目的收益率,通过将它与同行业投资收益率对比,以确定这 个项目是否值得建设。
功能 基于一系列将来收支现金流和一贴现率,返回一项投资的净现值。
NPV(rate,value1,[value2],...)
语法 rate为某一期间的贴现率。 value1,value2,...为一系列现金流,在时间上必须具有相等间隔,并且
都发生在期末。现金流中,支出用负数表示,收入用正数表示。 Value1是必需的,后续值是可选的。
பைடு நூலகம்
【学习引例2-1】
某企业计划在5年后积累资金达到1 000 000元,假设年投资报酬率 为10%,现在应该一次性投入多少资金?
分析: 已知投资报酬率、投资期和投资终值,计算现值。
【学习引例2-2】
某基金的购买成本为80 000元,该基金可以在今后20年内于每月月 末回报600元,假定投资机会的最低年报酬率为8%,投资该项基金是否 合算?
使用借款进行建设,在利率还不很明确时,内含报酬率法可以避开借款 条件,先求得内含报酬率,作为可以接受借款利率的高限。
当然,内含报酬率表现的是比率,不是绝对值,一个内含报酬率较低的 方案,可能由于其规模较大而有较大的净现值,更值得建设。所以优选方案 时,必须将内含报酬率与净现值结合起来考虑。
Excel在货币时间价值中的综合运用
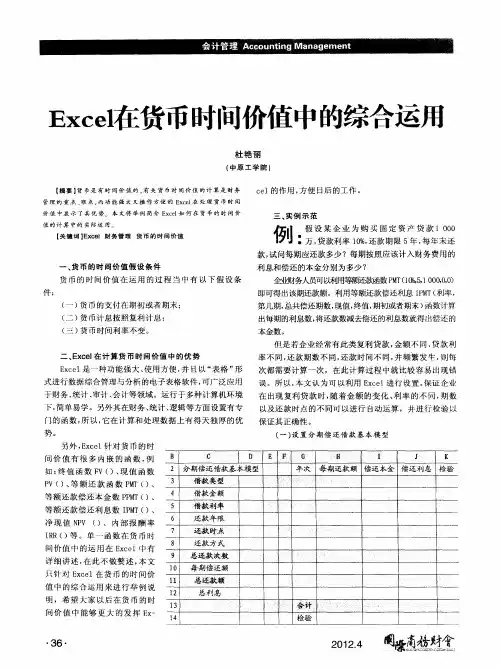
以检 验偿 还 的本金 合计 数 时候等 于借 款金 额 ( 注意 : 此 在 由 于 是一 正一 负 , 以要添 加 “ ”才能 够 相 等 ) 在 3 4 所 一 ; 1 单 元 格 输 入 = R U D(1 , ) R U D(1 , ) O N J 3 2 = O N D 2 2 以检 验 还 款 利 息 金 额 是 否 等 于 总 利 息 数 ; 在 K 4单 元 格 输 入 : 1 I 3 J 3 H 3 以检 验总 还 款数 是 否 等于 总还 款 本 金加 总 1 + 1= 1 , 偿还 利 息 。
本金 数 。
( ) 币的支 付在 期初 或者 期末 ; 一 货 ( ) 币计 息按照 复利 计 息; 二 货 ( ) 币 时间利 率不 变 。 三 货
二 、 xe 在 计算 货 币时 间价值 中的 优势 E cl
但 是若 企 业经 常有 此类 复 利贷 款 , 额 不 同 , 款 利 金 贷 率不 同 , 款 期数 不 同, 款 时 间不 同 , 频繁 发 牛 , 每 还 还 并 则 次 都需 要计 算一 次 ,在 此计 算过 程 中就 比较 容 易 出现 错
若 数 据 计 算 正 确 , 则 验 证 行 和 验 证 列 就 会 显 示
7 8
借款j 率 } 式
间价 值 中 的运 用 在 E c l中有 xe
详细 讲 述 , 此 不做 赘 述 , 文 在 本 只针 对 E c l在 货 币的 时 间 价 xe 值 中 的综 合 运用 来 进 行 举 例 说 明,希 望 大 家 以后 在货 币 的 时
9
1 O
总还款次数
每 期 偿 还 额
【税会实务】利用Excel 计算货币时间价值

我们只分享有价值的知识点,本文由梁老师精心收编,大家可以下载下来好好看看!【税会实务】利用Excel 计算货币时间价值货币时间价值是现代理财的基本观念之一‚ 也可以说是理财活动的“第一原则”。
根据货币时间价值原理‚ 在利率水平一定的条件下‚ 同等数额的资金在不同时点上的经济价值是不等的; 而数额不等的资金在不同时点上的经济价值又有可能是相等的。
因此我们在会计核算尤其是在进行理财分析与财务决策时‚ 对于跨期较大( 如跨年) 的收入或支出‚ 需要先把它们放到相同的时间基础上‚ 然后才能进行加减或比较。
在这方面‚ 巧妙地利用Excel 是最好的选择‚ 本文试图通过18 个精选案例来加以阐释。
大家若能以此为基础‚ 再加以灵活运用和深入研究‚ 也就具备了解决复杂问题的能力。
一、现值计算在Excel 中‚ 计算现值的函数是PV‚ 其语法格式为: PV( rate‚ nper‚ pmt‚[ fv] ‚[ type] ) 。
其中: 参数rate 为各期利率‚ 参数nper 为投资期( 或付款期) 数‚ 参数pmt 为各期支付的金额。
省略pmt 参数就不能省略fv 参数; fv 参数为未来值‚ 省略fv 参数即假设其值为0‚ 也就是一笔贷款的未来值为零‚ 此时不能省略pmt参数。
type 参数值为1 或0‚ 用以指定付款时间是在期初还是在期末‚ 如果省略type 则假设值为0‚ 即默认付款时间在期末。
学习情境二 Excel在货币时间价值计算中的应用

学习情境二 Excel 在货币时间价值计算中的应用复习思考题1. 一笔现金流如何计算单利终值?一笔现金流的单利终值是指现在的一笔资金按单利的方法只对最初的本金计算利息,而不对各期产生的利息计算利息,在一定时期之后所得到的本利和。
其计算公式如下:)(n i P n i P P F S S S ⋅+⋅=⋅⋅+=1 式中,S F 为单利终值;P 为现在的一笔资金;S i 为单利年利率;n 为计息期限。
2. 一笔现金流如何计算复利终值?一笔现金流的复利终值是指现在的一笔资金按复利的方法不仅对最初的本金计息,还对各期产生的利息计息,在一定时期以后所得到的本利和。
其计算公式如下:n i P F )1(+⋅= 或 n i F V I F P F ,⋅=式中,F 为复利终值;P 为现在的一笔资金;i 为复利年利率;n 为计息期限;n i FVIF ,=n i )1(+称为复利终值系数,表示现在的1元钱在n 年后的价值。
3. 一笔款项如何计算单利现值?单利现值的计算实质上是单利终值计算的逆运算过程,即在已知一定时期后单利终值的基础上,求其按给定贴现率计算的现在时刻的价值。
其计算公式为:P =F /(1+i ·n )式中,P 表示现值;F 表示未来值;i 为单利年利率;n 为计息期限。
4. 一笔款项如何计算复利现值?若已知现在收入或支出的一笔款项在n 年末的复利终值F 和贴现率i ,则可以计算求出这笔款项现在时刻的价值P 。
其计算公式为:n i F P )1/(+= 或 n i P V I F F P ,⋅=式中,n n i i PVIF )1/(1,+=称为复利现值系数。
5. 如何计算名义年利率与有效年利率?在给定了年利率i 且每年计息m 次的情况下,给定的年利率仅是名义年利率,而按一年的实际年利息与本金之比所计算的年利率称为有效年利率。
有效年利率r 与名义年利率之间的关系为:1-)1(m mi r += 式中,m 为每年计息次数。
第二章EXCEL货币时间价值应用
第2章 Excel在货币时间价值中的应用
2-3 年金及其在Excel中的应用
2-3-4 其它关于年金的函数
年金中的利息函数(IPMT):即各期所应给付(或 所能取得)的年金中剔除本金的利息部分。 功能:基于固定利率及等额分期付款方式,返回投 资或贷款的每期付款额中所含的利息部分。 语法:
第2章 Excel在货币时间价值中的应用
2-3 年金及其在Excel中的应用
2-3-2 年金终值 年金的终值计算 年金终值在Excel中的应用 例:小王自1995年12月底开始,每年末都要 向一位失学儿童捐款 1000元,帮助这位失学儿童 从小学1年级读完九年义务教育。假设每年定期存 款利率都是2%,则小王九年捐款在2003年底相当 于多少钱?
第2章 Excel在货币时间价值中的应用
2-2 利用Excel 函数计算现值和终值
2-2-3 在Excel中建立终值与现值模型
单利的终值计算 复利的终值计
第2章 Excel在货币时间价值中的应用
2-3 年金及其在Excel中的应用
2-3-1 年金分析
普通年金 预付年金 递延年金 永续年金
第2章 Excel在货币时间价值中的应用
第2章 Excel在货币时间价值中的应用
2-2 利用Excel 函数计算现值和终值
2-2-1终值的操作
例:小张将10000存入银行,年利率8%,每年计息一次,10 年后的复利终值为多少?
第2章 Excel在货币时间价值中的应用
2-2 利用Excel 函数计算现值和终值
2-2-2 现值的操作
例:如果小张希望10年后拥有21589.25元购买一套家具,假设年利率 8%,每年计息一次,那么他现在应该存入银行多少钱?
Excel在财务管理中的应用-第2章 货币时间价值
当复制公式到其他单元格时,Excel仅保持所引用单元格的行或列方向之一的绝对位置不变,而另一个方向位置发生变化
,这种引用方式称为混合引用。可分为对行绝对引用、对列相对引用和对行相对引用、对列绝对引用。
12
不同引用类型的特性
引用类型 绝对引用 行绝对引用、列相对引用
A1样式 =$A$1 =A$1
特性 公式向右向下复制时,都不会改变引用关系。 公式向下复制时,不改变引用关系。公式向右复制时,引用的列标发生变化。
15
认识图表元素
绘图区
图表区
标题
数据标签
图例项
网格线 趋势线 数据系列 纵坐标轴
横坐标轴
实际利率与名义利率之间关系为:
i m R (1 m ) 1
16
名义利率与实际利率
在经济分析中,复利计算通常以年为计息周期。但在实际经济活动中计息周期有半年、季、月、周、日等多种形式, 当利率的时间单位与计息期不一致时,就会出现名义利率和实际利率的问题。
07
FV函数
FV函数的作用是基于固定利率及等额分期付款方式,返回某项投资的未来值。该函数语法为: FV(rate,nper,pmt,[pv],[type]) 第一参数rate代表各期利率,本例中为6.25%。 第二参数nper代表期数,本例中为4年。 第三参数pmt代表每期等额支付金额,用于年金计算,本例使用0。 第四参数pv代表原始投资额。FV函数计算时,认定现值的现金流量方向与计算出的终值现金流量方向是相反的,
19
实际利率转为名义利率
实际利率转为名义利率的公式为:
其中I为名义利率,r为实际利率,m为一年内计息的次数。
NOMINAL函数 NOMINAL函数能够基于给定的实际利率和年复利期数,返回名义年利率。该函数语法为: NOMINAL(effect_rate, npery) 第一参数effect_rate为实际利率。 第二参数npery为每年的复利期数。
第2章 Excel在资金时间价值中的应用
2.1 普通年金的终值与现值
2.1.1普通年金终值系数 FVAn=A·[(1+i)n-1]/i=A·FVIFAi,n [(1+i)n-1]/i称之为年金终值系数或年金复 利系数,通常用符号FVIFAi,n来表示。 FVIFAi,n= [(1+i)n-1]/i
在20次迭代计算后,如果相邻两次结果没 有收敛于0.0000001,则返回错误值#NUM。
RATE(nper,pmt,pv,fv,type,guess) Guess为预期利率(估计值),如果省略
预期利率,则假设该值为10%,如果RATE 函数不收敛,则需要改变guess的值。通常 情况下当guess的值位于0和1之间时, RATE函数收敛。 利用RATE函数进行求解
系数,通常用符号PVIFAi,n来表示。 PVIFAi,n= [1-(1+i)-n]/I PV函数 计算年金现值通常用PV函数, PV函数的
功能是返回未来若干期资金的现值。
PV(rate,nper,pmt,fv,type) Rate: 每期利率 nper: 年金处理中的总期数 pmt: 年金 fv: 未来值,终值 type: 年金类型, 0(普通年金);1(先付年金)
例2-12:某人准备现在存入银行一笔钱, 希望能够在第6年至第10年末每年等额从银 行取出1000元钱,如果银行存款的年利率 为8%,且复利计息,那么此人现在应当一 次性存入银行多少钱?
按照第一种计算方法:
PV(8%,5,0,-PV(8%,5,-1000))= 按照第二种计算方法:
例2-10:某人准备在今后的5年中每 年年初等额存入银行8000元钱,如 果银行按4%的年利率复利计息,那 么5年末此人可一次性从银行取出多 少钱?
用Excel计算货币时间价值
单利和复利的对比
单利是指按照固定的本金计算的利息,而本金所产生的利息不再计算利息。 复利是指在每经过一个计息期后,都要将所生利息加入本金,以计算下期的利息。 如果分别使用单利和复利两种方式来计算收益,随着期数增多,两者的差异越大。
实际利率转为名义利率
实际利率转为名义利率的公式为:
其中I为名义利率,r为实际利率,m为一年内计息的次数。 NOMINAL函数 NOMINAL函数能够基于给定的实际利率和年复利期数,返回名义年利率。该函数语法为: NOMINAL(effect_rate, npery) 第一参数effect_rate为实际利率。 第二参数npery为每年的复利期数。
04 单利现值计算
单利现值计算相当于单利终值计算的逆运算过程,是在已知一定时期后单利终值的基础上,按照指定的利率计算出 的当前的价值。 单利计算的规则为: 现值=未来值/(1+年利率*期限)
05 普通复利现值计算
PV函数 PV函数用于返回普通复利情况下的投资现值,该函数语法为: PV(rate,nper,pmt,[fv],[type]) 第1个参数rate表示利率,本例中为6.25%。 第2个参数nper表示期限,本例中为3年。 第3个参数pmt代表每期等额支付金额,本例为0。 第4个参数fv代表未来值,与FV函数一样,如果希望计算结果为正数,则该参数应该用负数表示。 第5个参数type是可选参数,值为数字 0 或 1,用以指定各期的付款时间是在期初还是期末。本例中省略该参数,表示 期末。
Excel Home
Excel在财务中的应用
06
第六章
用Excel计算货币时间价值
PART 06
01 终值计算
终值是指现在的一笔资金在一定时期之后的本利或未来值。 单利终值是指对一笔资金按单利的方法对最初的本金计算利息,而不对各期产生的利息再次计算利息,在一定 时期内得到的本金利息之和。
Excel财务建模与应用教程第02章货币时间价值与财务估价
(A)普通年金
2.偿债基金 ——是指为了使年金终值达到既定金额,每年年末应支付的年金 数额。 注:偿债基金的计算实际上是年金终值的逆运算,其计算公式为:
i
A
F[ (1
i)n
] 1
(A)普通年金
i 上式中方括号内的部分 (1 i)n 1 是普通年金终值系数的倒数,
1
100
0.0795
7.95
即每年年末需存入银行7.95万元,才能到期用本利和偿 清借款。
(A)普通年金
3.普通年金现值 ——普通年金现值是指为在每期期末取得相等金额的款项, 现在需要投入的金额。
(A)普通年金
0 1 2 … n-1 n
A(1+i)-1 A(1+i)-2
AA ┇
AA
A(1+i)-(n-1) A(1+i)-n 普通年金现值计算原理图解
(A)普通年金
1、普通年金终值——是指一定时期内每期期末收付款项的复利终值之和。
0
1
2
3
100
100
100
普通年金图例
0 1 2 3…
n-1 n
AAA
AA ┇
A(1+i)0 A(1+I)1
A(1+I)n-3 A(1+i)n-2 A(1+i)n-1
普通年金终值计算原理图解
普通年金终值的计算
根据上图,普通年金终值计算如下所示:
相比,它是“期数加1,而系数减1”所得的结果。同样可通 过查“年金终值系数表”来获得其数值。不过查表前要把期 数先加1,得到(n+1)期的值,然后减去1后就得出1元先 付年金终值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
pmt参数不可省略。 type:指定各期的收款或付款时间(pmt的时间)是在期初还是在期末,
type为1表示期初,type为0表示期末。此参数可省略,省略时,其默认值 为0。
type为1表示期初,type为0表示期末。此参数可省略,省略该参数时,其 默认值为0。
2019/9/21
10
2.2.2 现值函数
注意,与FV函数一样,PV函数认定年金pmt和终值fv 现金流量的方向,与计算出的现值现金流量的方向相 反,即如果年金pmt和终值fv是付款,那么计算出的现 值为收款;反之,如果年金pmt和终值fv是收款,那么 计算出的现值为付款。因此,当pmt和fv参数都以正数 存放在工作表的单元格中时,为了使计算出的现值能 显示为正数,应在输入pmt和fv参数时加上负号。
(元)。
所谓复利,是指每次计算出利息后,将利息重新加入本金,从而 使下一次的利息计算在上一次的本利和的基础上进行,即通常所 说的利滚利。上例中,若张某和李某商定双方按复利计算利息, 则3年后应得的本利和计算如下。
若令PV为现值,FV为终值,存期为n年,年利率为i,则 单利终值计算公式为FV = PV(1 + i·n)。 复利终值计算公式为FV = PV(1 + i)n,其中(1+ i)n称为复利终值系
所谓单利,是指在计算利息时,每次都按照原先融资双方确认的 本金计算利息,每次计算的利息并不转入下一次本金中。比如, 张某借给李某1000元,双方商定年利率为5%,3年后归还。若按 单利计算,则张某3年后应收的利息为3 × 1000 × 5% = 150 (元)。
所谓复利,是指每次计算出利息后,将利息重新加入本金,从而 使下一次的利息计算在上一次的本利和的基础上进行,即通常所 说的利滚利。
第2章 Excel在货币时间价值计算中的应用 2.1 终值计算 2.2 现值计算 2.3 年金计算
2019/9/21
1
2.1 终值计算
2.1.1 单利终值和复利终值 2.1.2 终值函数 2.1.3 计算终值的操作
2019/9/21
2
2.1.1 单利终值和复利终值
终值是指现在存入一笔资金,按照一定的利率和利息计算方式, 到未来某一时刻的本利和。终值的计算方式有两种:单利和复利。
2019/9/21
11
2.2.3 计算现值的操作
例2.4 例2.5 例2.6
2019/9/21
12
2.3 年金计算
2.3.1 年金分析 2.3.2 年金终值 2.3.3 年金现值
2019/9/21
13
2.3.1 年金分析
年金是指在相同间隔期收到或支付的系列等额 款项。
年金按发生的时点不同,分为普通年金、预付 年金、递延年金和永续年金。
2019/9/21
14
2.3.1 年金分析
1.普通年金 2.预付年金 3.递延年金 4.永续年金
2019/9/21
15
2.3.2 年金终值
符号
说明
P 现值:发生在未来的现金流量相当于现在时刻的价值
F 终值:即一个或多个现金流量相当于未来时刻的价值
CFt 现金流量:第t期期末的现金流量 A 年金:在相同间隔期收到或支付的系列等额款项
上例中,若张某和李某商定双方按复利计算利息,则3年后应得的 本利和计算如下。
2019/9/21
3
2.1.1 单利终值和复利终值
第1年的利息为1000 × 5% = 50(元)。 转为本金后,第2年的利息为(1000 + 50) × 5% = 52.5(元)。 转为本金后,第3年的利息为(1050 + 52.5) × 5% = 55.125(元)。 加上本金,第3年的本利和为1000 + 50 + 52.5 + 55.125 = 1157.625
PV(rate, nper, pmt, fv, type) 其中的参数说明如下。 rate:各期利率。 nper:总投资期数。 pmt:各期应付(得到)的金额,其数值在整个年金期间(投资期内)保
持不变。此参数可省略,省略该参数时,fv参数不可省略。 fv:终值。若省略,则其默认值为0,此时pmt参数不可省略。 type:指定各期的收款或付款时间(pmt的时间)是在期初还是在期末,
2019/9/21
6
2.1.3 计算终值的操作
例2.1 例2.2 例2.3
2019/9/21
7
2.2 现值计算
2.2.1 单利现值和复利现值 2.2.2 现值函数 2.2.3 计算现值的操作
2019/9/21
8
2.2.1 单利现值和复利现值
现值(PV)是指将来的一笔款项相当于现在的价值。
数。
2019/9/21
4
2.1.2 终值函数
FV函数的功能是,基于固定利率及等额分期付款方式,返回某项投资的 未来值。FV函数的语法格式为
FV(rate, nper, pmt, pv, type) 其中的参数说明如下。 rate:各期利率,是一个固定值。 nper:总投资(或贷款)期数。 pmt:各期应付(或得到)的金额,其数值在整个年金期间(或投资期内)
设FV为终值,存期为n年,年利率为i,则单利现值计
算公式为
PV FV (1 i n)
复利现值计算公式为
FV PV
(1 i)n
式中, (1+i)-n称为复利现值系数。
2019/9/21
9
2.2.2 现值函数
函数的功能是根据固定利率及等额分期付款方式,返回某项投资的现 值,现值为一系列未来付款的当前值的累积和。PV函数的语法格式为
2019/9/21
5
2.1.2 终值函数
注意,FV函数认定年金pmt和现值pv现金流量的方向, 与计算出的终值现金流量的方向相反,即如果年金pmt 和现值pv是付款,那么计算出的终值为收款;反之, 如果年金pmt和现值pv是收款,那么计算出的终值为付 款。因此,当pmt和pv参数都以正数存放在工作表的单 元格中时,为使计算出的终值能显示为正数,应在输 入pmt和pv参数时加上负号。
