2018-2019湖工大高等数学-2
西安工业大学高数试题及答案

高等数学(Ⅱ)期末参考答案一、填空题(每小题3分,共30分)1.已知)2,1,0(),2,1,1(-=-=b a,则=⨯b a =--21211kj i )1,2,0(-- . 2.点)1,1,1(到平面014263=+-+z y x 的距离为 3.3.过点)1,0,3(-且与平面012573=-+-z y x 平行的平面方程为04573=-+-z y x .4.已知)2,(2y e x xy f z +=,则=∂∂xz 212f f y '+' .5.曲线2,3,4234tz ty tx ===在相应于1=t 处的法平面方程为0)21()31()41(=-+-+-z y x .6.交换积分dy y x f dx x ⎰⎰11),(的积分次序为dy y x f dy y ⎰⎰10),( .7.设∑:)10(22≤≤+=z yx z ,则⎰⎰∑=zdS dxdy yx y x 212222⋅+⎰⎰≤+π322=.8.设向量k xy z j zx y i yz x A )()()(222-+-+-=,则=A d i v=∂∂+∂∂+∂∂zR yQ xP)(2z y x ++.9.设函数)(x f 以π2为周期,且)()(ππ≤<-=x x x f ,其Fourier 级数为∑∞=++10)sin cos (2n n n nx b nx a a ,则=2b =⎰ππ02sin 2xdx x 1- .10.函数xx f +=21)(的麦克劳林级数为nn nnx ∑∞=-02)1(21.二、(8分)求函数1),(22--+++=y x y xy x y x f 的极值,并指出是极大值还是极小值. 解: 12),(++=y x y x f x , 12),(-+=x y y x f y ,令 ,0),(0),(⎩⎨⎧==y x f y x f yx 即 ⎩⎨⎧=-+=++012012x y y x ,得驻点)1,1(-.由于 2),(==y x f A xx , 1),(==y x f B xy , 2),(==y x f C yy ,且03221)(112<-=⨯-=-=-=y x AC B ,02>=A ,则)1,1(-为极小值点,极小值为2)1,1(-=-f .三、(8分)求级数n n x n ∑∞=+0)1(的收敛域及它的和函数.解:由于 1|1|lim ||lim 1=+=∞→+∞→n n a a n nn n ,则1=R ,当1±=x 时,级数n n n )1()1(0±+∑∞=均发散,所以收敛域为)1,1(-.设=)(x s nn xn ∑∞=+0)1(,则xx xdt t n dt t s n n xnn x -==+=∑⎰∑⎰∞=+∞=1])1[()(01,于是20)1(11)()(x x x dt t s dx d t s x -='⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎰. 四、(8分)计算dy y xyy x dx y xyx L)33()35(222324+-+-+⎰,其中L 是抛物线2x y =上自点)0,0(到点)1,1(的一段弧.解:32435),(y xyx y x P -+=,22233),(y xyy x y x Q +-=在xoy 面偏导数连续,且236y xy xQ yP -=∂∂=∂∂,则曲线积分与路径无关,取折线段)1,1()0,1()0,0(→→,则dy y xyy x dx y xyx L)33()35(222324+-+-+⎰dy y y y dx x x ⎰⎰+⋅⨯-⋅⨯+-⋅+=10222322104)1313()0035(611)31123(1=+-+=.五、(8分)计算曲面积分dxdy y x dzdx x z dydzz y x I )()()(-+-+-=⎰⎰∑,其中∑是由柱面122=+y x ,平面3,0==z z 所围立体表面的外侧.解:y x z y x R x z z y x Q z y x z y x P -=-=-=),,(,),,(),(),,(在柱面122=+y x ,平面3,0==z z 所围立体Ω上偏导数连续,则由高斯公式有dxdy y x dzdx x z dydzz y x I )()()(-+-+-=⎰⎰∑dv z y dv zR yQ xP ⎰⎰⎰⎰⎰⎰ΩΩ-=∂∂+∂∂+∂∂=)()(⎰⎰⎰⎰⎰⎰ΩΩ-=dv z dv y (第一个积分为0,想想为什么?)ππ29103230-=⋅-=-=⎰⎰⎰⎰dz z dxdy dz z zD .六、(8分)求下列方程的通解: 1.xy y y x ln='解:xy y y x ln ='xy x y y ln ='⇒,方程为齐次微分方程;设xy u =,则u x u y '+=',代入得xdx u u du=-)1(ln ,两端积分dx x u d u ⎰⎰=--1)1(ln 1ln 1即 C x u ln ln )1ln(ln +=- 或 1ln +=Cx u 将xy u =代回得 1+=Cx ex y2.xe y y y 234=+'+''.解:方程为二阶非齐次线性微分方程,对应齐次线性微分方程的特征方程0342=++r r 的特征根为3,121-=-=r r ;xex f 2)(=中2=λ不是特征方程的根,则特解形式为x Ae y 2*=,代入得151=A ,在由解的结构得方程的通解为xxxeeC eC y 2321151++=--七、(10分)设2nn n u u v +=,2nn n u u w -=,证明:1.若级数∑∞=1n n u 绝对收敛,则级数∑∞=1n n v 收敛;证:由于∑∞=1n n u 绝对收敛,即||1∑∞=n n u 收敛,则∑∞=1n n u 也收敛,又n n n u u v 21||21+=,由性质知∑∞=1n n v 收敛.2.若级数∑∞=1n n u 条件收敛,则级数∑∞=1n n w 发散.证:(反证)假设∑∞=1n n w 收敛,已知∑∞=1n n u 收敛,由2nn n u u w -=,即nn n u w u +=2||及性质知||1∑∞=n n u 收敛,即∑∞=1n n u 绝对收敛,与已知条件矛盾.所以∑∞=1n n w 发散.八、(10分)一均匀物体Ω是由抛物面22y x z +=及平面1=z 所围成. 1.求Ω的体积;解:Ω在xoy 面投影域1:22≤+y x D ,则所围体积为 d x d y y xV D])(1[22⎰⎰+-=dr r r d ⎰⎰-=πθ2012)1(2)4121(2ππ=-=.2.求Ω的质心.解:由于Ω是均匀物体及几何体关于yoz 面、xoz 面对称,则质心坐标应为),0,0(z ; 而3223101202====⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩππρθρρρπVdzz dr r d dvdvz z r,所以质心坐标为)32,0,0(.九、(10分)设{}]1[,0,0,2|),(2222y x y x y x y x D ++≥≥≤+=表示不超过221y x ++的最大整数,计算二重积分dxdy y x xy D⎰⎰++]1[22.解:设 }0,0,1|),{(221≥≥<+=y x y x y x D ,}0,0,21|),{(222≥≥≤+≤=y x yx y x D ,则21D D D +=,且当1),(D y x ∈时,1]1[22=++y x ,当2),(D y x ∈时,2]1[22=++y x ,所以dxdy y x xy D⎰⎰++]1[22=+++⎰⎰dxdy y x xy D 1]1[22dxdy y x xy D ⎰⎰++2]1[22⎰⎰⎰⎰+=212D D dxdyxy dxdyxy⎰⎰⎰⎰+=421320132cos sin 2cos sin dr r d dr r d θθθθθθππ8381281=⨯+=。
答案2018测试题(二)

守
(A)若 lim f (x) 存在,则 f (0) 0
(B) 若 lim f (x) 存在,则 f (0) 存在
考
x0 x
x0 x
试
(C)若 lim f (x) f (x) 存在,则 f (0) 存在 (D)若 lim f (x) f (x) 存在,则 f (0) 0
x0
x
x0
x
纪
请将选择题答案填入下面的表格中!(每题 2 分,共 30 分)
律
注
1
2
3
4
5
6
7
8
意
B
D
A
B
D
C
D
A
行
9
10 11 12 13 14 15
得分
为
B
D
D
B
A
B
B
规
范
姓名:
出题教师签字:
教研室主任签字:
第 1 页(共 2 页)
x f (t)
7.设
y
ห้องสมุดไป่ตู้
f
(e3t
,其中
1)
f
可导,且
f
'(0) 0 ,则 dy =( dx t0
D
)
(A) 0 (B) 1 (C) 2 (D) 3
第 2页(共 2 页)
2.函数 y arcsin(ln x) 在 x 1 点的微分 dy x1 =(D ) (A) 1 (B) 2 dx (C) 0 (D) dx
3.曲线 y x2 x(x 0) 上曲率为 2 的点的坐标是( A ) 2
(A) (1, 0) (B) (0, 0) (C) (2, 2) (D) (3, 6)
西北工业大学《高等数学2B》2019-2020学年第二学期期末试卷

.
∫∫ 5. 设曲面 Σ 是圆锥面=z x2 + y2 ( 0 ≤ z ≤ 2) , 则曲面积分 z dS 的值为 Σ
.
二、选择题(共 15 分,每小题 3 分)
1. 下列级数中收敛的是 (
).
∞
∑ (A) (−1)n n=1
∑ (B) ∞ tan π
n=3 n
∑∞ 4n −1
(C) n=1 n2 + n
2
2
的曲线段.
= 解: P
x= x2 ++ yy2 , Q
y x2
+= − yx2 , 则 ∂∂Py
x= 2( x−22+xyy 2−)2y 2
∂Q , 故曲线积分与路径无关, ∂x
选取= 圆弧 C : x π= cosθ , y π sinθ , θ: π → 0, 则
2
2
∫ ∫ L
(x
+
y)dx x2
六、证明题(本题 5 分)
设常数 a
>
0, 对 ∀ n ∈ N+ ,
un
>
0,
vn
>
0,
且
vn
un un+1
− vn+1
≥
a.
∞
∑ 证明: 级数 un 收敛.
n=1
证明:
vn
un un+1
−
vn+1
≥
a
>
0
即
unvn − un+1vn+1 ≥ a > 0 , un+1
于是
unvn − un+1vn+1 > 0,
合肥工业大学高数下部分课后习题参考答案

AB 7 , AC 7 , BC 7 2 ; 等腰直角三角形.
14 3. M 0, 0, . 9
4. 5.
2x 6 y 6z 3 0 .
a b a b a b a b ; ; ; . 2 2 2 2
1 2 1 , cos ; 7. AB 2 ; cos , cos 2 2 2
5. 8x 9 y 22 z 59 0 . 6.
3 2 . 2
习题 8-5
1. (1)直线,平面; (2)抛物线,抛物柱面; (3)圆,圆柱面; (4)双曲线,双曲柱面. 2. (1)将 xOy 平面上双曲线 x2 y2 1绕 x 轴旋转一周;
(2)将 yOz 平面上直线 z y a 绕 z 轴旋转一周.
12. (1)见图 8-9;
(2)见图 8-10;
图 8-9
图 8-10
(3)见图 8-11;
(4)见图 8-12.
图 8-11 习题 9-1
图 8-12
1. ( 1 )为有界开区域;聚点为集合 {(x, y ) | x 2 + y 2 1} ,边界点为集合 {(x, y ) | x 2 + y 2 =1} {(0, 0)} ;
4
x2 y 2 1, ( 2 ) 在 xOy 面 投 影 曲 线 方 程 : 在 yOz 面 投 影 曲 线 方 程 : z 0;
z z y sin , x cos , 2 在 zOx 面投影曲线方程: 2 y 0. x 0;
3020max21minminmaxmax上的点到原点的距离的最大值与最小值分别为15max16总复习题九11122sincoscossincos10
2018-2019-2本科补考缓考安排表(学生)
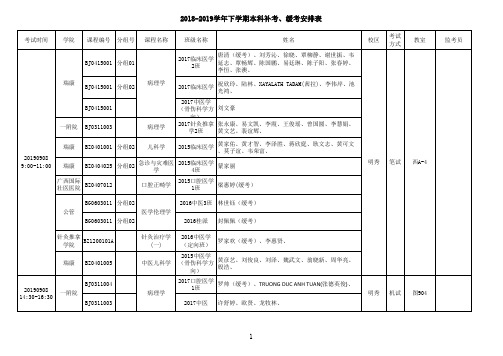
BZ0501004
耳鼻喉科学 方剂学 方剂学
2015口腔医学 1班
梁惠婷(缓考)
2017中医学 NGUYEN CUONG SON(阮强山)、陈国林、李祐为、彭宇
(国际传统中 忻、黄皓贤、陈雅焙、杨净钧、
2017医壮)医学1 班
吴文超
2017护理学3 班
李洁(缓考)
护理 BZ0501004
20501BZ001
李洁、李文楚、
人体系统解剖 学
2018中医学 (国际传统中
医)
武光松、胡海维、
眼科学
2015口腔医学 1班
梁惠婷(缓考)
影像数学2 (图像处理数
分组02 急诊与灾难医 学
2016中医3班
2016中医学 (定向班)
林世钰(缓考) 李惠贤
基础
BJ0104005 分组01 BJ0104005 分组03
金匮要略
2016中医1班 林均宇 2016中医3班 葛蓓莉
20190908 14:30-16:30 基础 BJ0104005
2016桂派 封佩佩(缓考)
班级名称
姓名
护理 BZ0502003
基础 BJ0107001
一附院 BZ0309004 药学院 BJ0211031
BZ0305001 20190910 19:00-21:00 一附院 BZ0301007B
BZ0301007A 瑞康 BZ0406005
一附院 BZ0315002
内科护理学I
2017护理学3 班
班级名称
姓名
20190908 14:30-16:30
基础
BJ0111012
医学免疫学与 微生物学
2017壮医学1 班
线性代数习题集第二章-湖北工业大学水印

1 2 1
1
学 1
,试求伴随矩阵
A*
的逆矩阵。
3
湖
大
业
工 四、求解下列方程组(每题 10 分,共 20 分)
北 x1 + 2x2 + 3x3 = 1
1、 2x1 + 2x2 + 5x3 = 2 3x1 + 5x2 + x3 = 3
湖
2 1 −1 1 −1 3
学 2、
X
1
1
1
=
4
3
2
3 2 1 2 −2 5
A
可逆,则下列结论中成立的是(
湖 大 (A) A1可逆
(B) A2 可逆
)
(C) A1 与 A2 的可逆性不定
业 (D) A1 与 A2 均可逆
3、设
A、B
为
n
阶方阵,则分块矩阵
C
=
A
O
北 工 (A)
A* O
O
B*
A A* (B) O
O B B*
O
B
的伴随矩阵 C*
=
(
)
湖
B A* (C) O
2
1
2
学 a11 a12 a13 x1
( ) 4、 x1
x2
x3
a12
a22
a23
x2
大 a13 a23 a33 x3
业
1 0
工
四、设
A
=
0
0
0
北 1
,
求
Ak
,
k
N
+
湖
学 大
3 1 1
工 五、已知
全国985重点大学-西北工业大学-高等数学第二学期期终考试试卷答案及评分标准

高等数学2009--2010第二学期期终考试试题答案及评分标准A卷一、1、-8,2、,3、,4、8π,5、,6、。
二、1, 2、,3、,4、,5、3,6、[]2121+-,,缺闭区间扣一分。
三、1、解:设切点…………………2分由已知条件得:,得到.………..4分切平面方程为即……………..6分2、解:……………..3分……………..6分3、解:………………4分………………6分四、1、解:g f fy xx u v∂∂∂=+∂∂∂,g f fx yy u v∂∂∂=-∂∂∂,…………….2分vfvfxvufxyufyx∂∂+∂∂+∂∂∂+∂∂=∂∂2222222222g,vfvfyvufxyufxy∂∂-∂∂+∂∂∂-∂∂=∂∂2222222222g, ………………..5分222222g gx yx y∂∂+=+∂∂………………6分2.解:设dydppyp=''=',y,………………………2分得到舍去)(,0y==+ppdydp,解得ycp1=,由初始条件yy21,21c1='=,………………………4分100(,)dy f x y dx⎰83π12eπ+1415-{}00000(,,),,2,1P x y z n x y=-224000sind d drππθϕϕ⎰⎰143π0021221x y-==-2230x y z+--=2200002,1, 3.2xx y z y===+=2(2)2(1)(3)0x y z-+---=231131()12yyyydy e dxy y e dy e∂=-=-⎰⎰⎰8232008222336dz d drz dzπθππ==⎰⎰⎰2y1=-22c x y +=, 由初12=c , 其特解为1,12+=+=x y x y 或。
……………………..6分3.、解:由xQ y p ∂∂=∂∂,得x e x f x f x f =-'-'')()()(,………………2分 x x x e y e c e c Y 21,221-=+=*-, 由初始条件61,3221-==c c , x x x e e e x f 216132)(2--=- ……….4分 (1,1)(0,0)()2()()x f x f x e ydx f x dy ''⎡⎤+++⎣⎦⎰ =⎰-+=-+--101212216134216134e e e dy e e e ). ……………….6分五、解:1151lim lim (1)55n n n n n na n a n ++→∞→∞⋅==+⋅, ∴收敛半径为5R =…………………..2分 当5x =-时, 15n n ∞=∑发散; 当5x =时,11(1)5n n n -∞=-⋅∑收敛 ∴收敛区间为(5,5]-…………………………………………………4分 设和函数1111111100110(1)()(1)55 [(1)][(1)()]5551 ln(1), (5,5]5515n n n n n n n n n x x n n n n n n x x S x x x n n t x t x dt dt n x x dt x x t -∞∞+-==∞∞---==-==-⋅⋅'=-=-⋅==+∈-+∑∑∑∑⎰⎰⎰………..…7分 …………………….8分六、解:设旋转曲面S 的方程为 12222=++z y x ,--------------------1分给定的方向 )0,21,21(0-=l方向导数函数 )(2c o s c o s c o s y x zf y f x f l f -=∂∂+∂∂+∂∂=∂∂γβα --------2分 设)12()(2222-+++-=z y x y x L λ, ---------------3分令 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++==∂∂=+-=∂∂=+=∂∂1202022042222z y x z zL y y L x x L λλλ ------------------4分 解之得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=02242z y x λλ 23±=λ ------------------6分 23=λ,得S 上的点为)0,36,66(-,此时3-=∂∂l f 23-=λ,得S 上的点为)0,36,66(-,此时3=∂∂lf 所以,所求的S 上的点为)0,36,66(- ------------------7分 七、解:……………………3分………………………6分………………………7分(2009)(1)2010ae f =000()()(x)lim ()(1)()lim lim x x x x x f x x f x f x f x e f x e x x ∆→∆∆→∆→+∆-'=∆-∆=+∆∆(x)()(0),(),(0)0,0..x x x f f x f e y ax c e f c y axe ''=+=+=∴== 111100(x)(1)(1)(1)!!x x x x n n n n f axe aexe ae x e aee x x ae ae n n ---+∞∞=====-+--=+∑∑n=100(1)(1)=ae (1)!!(1)(1),.!n nn nn x x ae n n n x ae x R n ∞∞=∞=--+-+-=∈∑∑∑。
武汉轻工大学18-19高数II1 a

设函数 f (x)在0,1上连续,且f (x) 1
证明F(x) 2x 1
x
f (t)dt 在(0,1)内只有一个零点。
0
第 2 页(共 ) 第 1 页(共 1 页)
x1
2
3
设
x y
ln(1 t 2 arctant
) ,
求
dy dx
,
d2 dx
y
2
.
4. 求y x 4 (12 ln x 7) 的凹凸区间与拐点,并求该曲线在拐点处的切线方程。
班级:
考试课程:
5. 设y y(x)由方程f (x 2 y) yex x 0所确定,其中f可导,且 2 f ex 0 , 求 dy. dx
武汉轻工大学 2018 –2019 学年第 1 学期 高等数学 II1 期末考试试卷 A
学号:
姓名 :
注:1、考生必须在《武汉轻工大学学生考试答题纸》上答题,答题时需注明大、小 题号;填空题只填答案,主观题要有必要的过程。
2、答题纸上要填写姓名、班级、学号,答题纸共 1 页。
3、只交答题纸。
-----------------------------------------------------------------------------------------------------------------------一、填空题(每小题 2 分,共 16 分)
1 y x 2 1 的可去间断点是 x = _________
x(x 1)
2 lim (sin x x sin 3)
x x
x
_。
3 若 y cos x2 , 则 dy
。
dx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收敛,其中
常数 0 .
3
(D) f (0,1) f (1, 0)
8.曲面 x 1 sin y z 1在点 (1, 1, 0) 处的法线方程为(
);
(A) x 1 y 1 z 1 1 1
(B) x 1 y 1 z 1 1 1
(C) x 1 y 1 z 1 1 1
(D) x 1 y 1 z 1 1 1
9. 已知曲线 L 为抛物线 y x2 的一部分( 0 x 1),则对弧长的曲线积分
注意
四三二一
、 试
、考意、姓:
、 密
卷生名封
印在、线
刷答准内 不题考不 清前证准
18.计算曲面积分 I (2x z)dydz zdxdy 其中 为有向曲面
楚应号答 。先不题
z x2 y2 (0 z 1) ,其法向量与 z 轴正向的夹角为锐角;
可将许。
举姓涂
手名改
向、, 监学否
封
考号则
;
(x, y)(0,0)
3.函数 z ln1 xy 在点 (0,1) 处的全微分 dz =
;
4.空间曲面 : x2 y2 z 2 1,则 (x3 z2 )dS =
;
5.
( 1)n1
n 1
n 2n
=
.
二、选择题(本题共 5 小题,每小题 3 分,共 15 分)
6.已知向量 b 与 a 共线,方向相反,且 | b | 5 | a | ,则 a+b 由 a 表示为(
教、试
师年卷
询级无
问和效
。 班。
级
填
写
在
指
定
的
方
框
内
。
19.将函数 f (x) 1 展开成 (x 2) 的幂级数,并指出其收敛域. 3 x
四、证明题(本题共 1 小题,每小题 7 分,共 7 分)
20.设 an =
4 tann xdx ,(1) 求
an an2
0
n1
n
的值;(2)试证:级数 an n1 n
(
专业用 闭卷)
题号 一 二 三 四 五 六 七 八 九 十 题分
得分
注意:学号、姓名和所在年级班级不写、不写全或写在密封线外者,试卷作废。
一、填空题(本题共 5 小题,每小题 3 分,共 15 分)
1.已知
a
(4,
1,
1),
b
(2,
1,
2)
,则
a
b
;
x2
2.二重极限 lim 1 x y xy
);
(A) 5a
(B) 4a
(C) 5a
(D) 4a
1
7.设 f (x, y) 具有一阶偏导数,且对任意的 (x, y) ,都有 f (x, y) 0 ,f (x, y) 0 ,
x
y
则(
);
(A) f (0, 0) f (1,1)
(B) f (0, 0) f (1,1)
(C) f (0,1) f (1, 0)
11.求通过点
4,
3,1
和直线
L
:
2x 5x 5
y 3z y 4z
20 30
的平面方程;
学号 姓名
12.设 z f (cos x, x2 y2) , f 具有二阶连续偏导数,求 2z ; xy
所在年级、班级 密
注意
四三二一
、 试
、考意、姓:
、 密
卷生名封
13.求点 (2,2,0) 到曲面 x2 y2 2z 0 的最短距离;
x 1 4 yds 等于( L
);
(A) 3 2
(B) 2 3
(C) 1 2
(D) 1 3
10.设级数 (1)n
n1
n
sin
1 n
绝对收敛,级数 (1)n n2
n1
条件收敛,则
(
).
(A) 0 1 (B) 1 1 (C) 3 2 (D)1 3
2
2
2
2
三、计算题(本题共 9 小题,每小题 7 分,共 63 分)
印在、线
刷答准内
不题考不
清前证准
楚应号答
。先不题
可将许。
举姓涂
手名改
向、, 监学否
封
考号则
教、试
师年卷
பைடு நூலகம்
询级无
问和效
。 班。
级
填
写
在
指
定
的
方
框
内
。
14.计算 I
1
dx
x sin y dy ;
0x y
15.求由 yoz 平面上曲线 2z y 2 绕 z 轴旋转一周而成的曲面被平面 z 1 截下的
学号 姓名
总分
卷号:A
所在年级、班级 密
注意
四三二一
、 试
、考意、姓:
、 密
卷生名封
印在、线
刷答准内
不题考不
清前证准
楚应号答
。先不题
可将许。
举姓涂
手名改
向、, 监学否
封
考号则
教、试
师年卷
询级无
问和效
。班。
级
填
写
在
指
定
的
方
框
内
。
核分人
二 O 一 八 — 二 O 一 九 学年第二学期期末考试
高等数学(下) 试题
部分曲面的面积;
16.计算三重积分 I zdxdydz ,其中 是由平面 x 0, y 0, z 0,
x y z 1围成的闭区域;
2
学号
17.计算曲线积分 I (x y)dx (x y)dy ,其中 L 是曲线 x y 2 ,
L
x y
取逆时针方向;
姓名
所在年级、班级 密
