【名师一号】2014-2015学年高中数学 第二章 平面向量双基限时练17(含解析)北师大版必修4
【名师一号】2014-2015学年高中数学 第二章 平面向量双基限时练17(含解析)新人教A版必修4

双基限时练(十七)1.给出下面三种说法:①一个平面内只有一对不共线的非零向量可作为表示该平面所有向量的基底; ②一个平面内有无数多对不共线的非零向量可作为表示该平面所有向量的基底; ③零向量不可为基底中的向量. 其中正确的说法是( ) A .①② B .②③ C .①③D .②解析 因为不共线的两个向量都可以作为一组基底,所以一个平面内有无数多个基底,又零向量和任何向量共线,所以基底中不含有零向量.因此本题中,①错,②、③正确,故选B.答案 B2.已知e 1和e 2是表示平面内所有向量的一组基底,那么下面四组向量中不能作为一组基底的是( )A .e 1和e 1+e 2B .e 1-2e 2和e 2-2e 1C .e 1-2e 2和4e 2-2e 1D .e 1+e 2和e 1-e 2解析 分析四个选项知,在C 中,4e 2-2e 1=-2(e 1-2e 2).∴e 1-2e 2与4e 2-2e 1共线,应选C.答案 C3.在△ABC 中,BC →=3BD →,则AD →等于( )A.13(AC →+2AB →) B.13(AB →+2AC →) C.14(AC →+3AB →) D.14(AC →+2AB →)解析 如图所示,AD →=AB →+BD →=AB →+13BC →=AB →+13(AC →-AB →)=23AB →+13AC →=13(AC →+2AB →),故选A. 答案 A4.已知四边形ABCD 是菱形,点P 在对角线AC 上(不包括端点A ,C ),则AP →等于( )A .λ(AB →+AD →),λ∈(0,1)B .λ(AB →+BC →),λ∈⎝ ⎛⎭⎪⎫0,22 C .λ(AB →-AD →),λ∈(0,1)D .λ(AB →-BC →),λ∈⎝ ⎛⎭⎪⎫0,22 解析 ∵ABCD 是菱形,且AC 是一条对角线,由向量加法的平行四边形法则知,AC →=AB →+AD →,而点P 在AC 上,∴三点A ,P ,C 共线,∴AP →=λAC →=λ(AB →+AD →),显然λ∈(0,1),故选A.答案 A5.平面内有四边形ABCD 和点O ,若OA →+OC →=OB →+OD →,则四边形ABCD 的形状是( )A .梯形B .平行四边形C .矩形D .菱形解析 因为OA →+OC →=OB →+OD →, 所以OA →-OB →=OD →-OC →, 即BA →=CD →.又A ,B ,C ,D 四点不共线,所以|BA →|=|CD →|,且BA ∥CD , 故四边形ABCD 为平行四边形. 答案 B6.如图所示,点P 在∠AOB 的对角区域MON 的阴影内,满足OP →=xOA →+yOB →,则实数对(x ,y )可以是()A.⎝ ⎛⎭⎪⎫12,-13B.⎝ ⎛⎭⎪⎫14,12C.⎝ ⎛⎭⎪⎫-23,-13D.⎝ ⎛⎭⎪⎫-34,25 解析 由图观察并根据平面向量基本定理,可知x <0,y <0,故选C. 答案 C7.已知a ,b 不共线,且c =λ1a +λ2b (λ1,λ2∈R ),若c 与b 共线,则λ1=________. 解析 ∵a ,b 不共线,∴a ,b 可以作为一组基底,又c 与b 共线,∴c =λ2b ,∴λ1=0.答案 08.设向量a ,b 不共线,且OC 1→=k 1a +k 2b ,OC 2→=h 1a +h 2b ,若OC 1→+OC 2→=m a +n b ,则实数m =________,n =________.解析 OC 1→+OC 2→=(k 1+h 1)a +(k 2+h 2)b =m a +n b . ∴m =k 1+h 1,n =k 2+h 2. 答案 k 1+h 1 k 2+h 29.已知e 1,e 2不共线,a =e 1+2e 2,b =2e 1+λe 2,要使a ,b 能作为平面内所有向量的一组基底,则实数λ的取值范围是________.解析 使a 、b 为基底,则使a 、b 不共线,∴λ-2×2≠0.∴λ≠4. 答案 {λ|λ≠4}10.若a ≠0,且b ≠0,且|a |=|b |=|a -b |,则a 与a +b 的夹角是________. 答案 30°11.设M ,N ,P 是△ABC 三边上的点,它们使BM →=13BC →,CN →=13CA →,AP →=13AB →,若AB →=a ,AC →=b ,试用a ,b 将MN →,NP →,PM →表示出来.解 如图所示,MN →=CN →-CM →=-13AC →-23CB →=-13AC →-23(AB →-AC →)=13AC →-23AB →=13b -23a . 同理可得NP →=13a -23b ,PM →=-MP →=-(MN →+NP →)=13a +13b .12.如图所示,在▱ABCD 中,M ,N 分别为DC ,BC 的中点.已知AM →=c ,AN →=d ,试用c ,d 表示AB →和AD →.解 设AB →=a ,AD →=b .由M ,N 分别为DC ,BC 的中点,得BN →=12b ,DM →=12a .在△ABN 和△ADM 中,⎩⎪⎨⎪⎧a +12b =d , ①b +12a =c . ②①×2-②,得a =23(2d -c ).②×2-①,得b =23(2c -d ).∴AB →=23(2d -c ),AD →=23(2c -d ).13.若a ,b 是两个不共线的非零向量,且a 与b 起点相同,则当t 为何值时,a 、t b 、13(a +b )(t ∈R )三向量的终点在同一直线上? 解 设a -t b =m ⎣⎢⎡⎦⎥⎤a -13a +b (m ∈R ),化简得⎝⎛⎭⎪⎫2m 3-1a =⎝ ⎛⎭⎪⎫m 3-t b ,∵a 与b 不共线, ∴⎩⎪⎨⎪⎧ 2m 3-1=0,m 3-t =0,∴⎩⎪⎨⎪⎧m =32,t =12.∴t =12时,a 、t b 、13(a +b )的终点在同一直线上.。
【名师一号】2014-2015学年高中数学人教b版必修1双基限时练12函数的奇偶性(第二章)(含答案)

双基限时练(十二) 函数的奇偶性基 础 强 化1.下列说法不正确的是( )A .图象关于原点成中心对称的函数是奇函数B .图象关于y 轴成轴对称的函数是偶函数C .奇函数的图象过原点D .对定义在R 上的奇函数f (x ),一定有f (0)=0解析 函数f (x )=1x 是奇函数,但它不过原点.答案 C2.下列函数中是偶函数的是( )A .y =x -2B .y =|3-x |C .y =x 2+2,x ∈(-3,3]D .y =-3x 2解析 D 选项中函数是偶函数.答案 D3.已知定义域为R 的奇函数f (x )满足:f (x )=f (4-x ),且当x ∈ 答案 C4.函数y =f (x )在(0,2)上是增函数,函数y =f (x +2)是偶函数,则下列结论中正确的是( )A .f (1)<f ⎝ ⎛⎭⎪⎫52<f ⎝ ⎛⎭⎪⎫72 B .f ⎝ ⎛⎭⎪⎫52<f (1)<f ⎝ ⎛⎭⎪⎫72 C .f ⎝ ⎛⎭⎪⎫72<f ⎝ ⎛⎭⎪⎫52<f (1)D .f ⎝ ⎛⎭⎪⎫72<f (1)<f ⎝ ⎛⎭⎪⎫52解析 ∵y =f (x +2)是偶函数,∴y =f (x )关于x =2对称.∵f (x )在(0,2)上是增函数,∴f (x )在(2,4)上是减函数.∵f (1)=f (3),且52<3<72,∴f ⎝ ⎛⎭⎪⎫52>f (3)>f ⎝ ⎛⎭⎪⎫72,即f ⎝ ⎛⎭⎪⎫72<f (1)<f ⎝ ⎛⎭⎪⎫52.答案 D5.若函数f (x )=x(2x +1)(x -a )为奇函数,则a =() A.12B.23C.34D .1解析 由题意知f (-x )=-f (x )恒成立,即-x 2⎝ ⎛⎭⎪⎫-x +12(-x -a )=-x2⎝ ⎛⎭⎪⎫x +12(x -a ),即⎝ ⎛⎭⎪⎫x -12(x +a )=⎝ ⎛⎭⎪⎫x +12(x -a )恒成立,所以a =12.答案 A6.若奇函数f (x )在区间上是增函数且最小值为5,那么在区间上是()A.增函数且最大值为-5B.增函数且最小值为-5C.减函数且最小值为-5D.减函数且最大值为-5解析根据奇函数的图象关于原点对称,且在y轴两侧单调性相同,∴f(x)在上是增函数,且有最大值-5.答案 A7.已知函数f(x)=ax3-bx+2,其中a,b为常数,若f(-2)=3,则f(2)的值为________.解析令g(x)=ax3-bx,则g(x)为奇函数,f(x)=g(x)+2. f(-2)=g(-2)+2=3,∴g(-2)=-8a+2b=1,∴g(2)=-1.f(2)=g(2)+2=-1+2=1.答案 18.设奇函数f(x)的定义域为,若当x∈时,f(x)的图象如图所示,则不等式f (x )<0的解集是________.答案 (-2,0)∪(2,5]能 力 提 升9.函数f (x )的定义域为R ,且x ≠1,已知f (x +1)为奇函数,当x <1时,f (x )=2x 2-x +1,那么当x >1时,f (x )的递减区间是________.解析 ∵y =f (x +1)为奇函数,∴y =f (x )关于点(1,0)对称,如图:当x >1时,f (x )在⎣⎢⎡⎭⎪⎫74,+∞递减.答案 ⎣⎢⎡⎭⎪⎫74,+∞ 10.判断下列函数的奇偶性:(1)f (x )=3,x ∈R ;(2)f (x )=5x 4-4x 2+7,x ∈;(3)f (x )=|2x -1|-|2x +1|;(4)f (x )=⎩⎪⎪⎨⎪⎪⎧ 1-x 2,x >0,0,x =0,x 2-1,x <0.)解 (1)f (-x )=3=f (x ),∴f (x )是偶函数.(2)∵x ∈,f (-x )=5(-x )4-4(-x )2+7=5x 4-4x 2+7=f (x ),∴f (x )是偶函数.(3)∵x ∈R ,f (-x )=|-2x -1|-|-2x +1|=-(|2x -1|-|2x +1|)=-f (x ),∴f (x )是奇函数.(4)当x >0时,f (x )=1-x 2,此时-x <0,∴f (-x )=(-x )2-1=x 2-1,∴f (-x )=-f (x );当x <0时,f (x )=x 2-1,此时-x >0,f (-x )=1-(-x )2=1-x 2,∴f (-x )=-f (x );当x =0时,f (-0)=-f (0)=0.综上,对x ∈R ,总有f (-x )=-f (x ),∴f (x )为R 上的奇函数.11.(1)已知函数f (x )=ax +b x 2+1是奇函数,且f (1)=2,求f (x )的解析式;(2)若f (x )=ax 2+bx +3a +b 是定义在上的偶函数,求f (x )的解析式. 解 (1)∵f (x )是奇函数,且定义域为R ,∴f (0)=0,∴b =0.∵f (1)=2,∴a 1+1=2,∴a =4. ∴f (x )=4xx 2+1. (2)∵f (x )是上的偶函数, ∴⎩⎨⎧ a -1+2a =0,b =0.∴⎩⎪⎨⎪⎧ a =13,b =0.∴f (x )=13x 2+1. 12.设f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )=x 2,若对任意的x ∈,不等式f (x +t )≤f (2x )恒成立,求实数t 的取值范围.解 由题意知f (x )=⎩⎨⎧ x 2(x ≥0),-x 2(x <0).所以f (x )在R 上为单调增函数.因为f (x +t )≤f (2x ),所以x +t ≤2x .所以t ≤(2-1)x .又x ∈,所以(2-1)x 的最小值为(2-1)(-2-2)=- 2.所以t ≤- 2.品 味 高 考13.已知函数f (x )为奇函数,且当x >0时,f (x )=x 2+1x ,则f (-1)=( )A .-2B .0C .1D .2解析 f (-1)=-f (1)=-2.答案 A。
【名师一号】2014-2015学年高中数学 模块检测试题二(含解析)新人教B版必修2

(1)求实数m的取值范围;
(2)若直线l:x+2y-4=0与圆C相交于M、N两点,且OM⊥ON,求m的值.
解(1)配方得(x-1)2+(y-2)2=5-m,
所以5-m>0,即m<5.
(2)设M(x1,y1),N(x2,y2),因为OM⊥ON,
10.已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=4 5°,则棱锥S-ABC的体积为()
A.B.C.D.
解析如图,设球心为O,由OS=OA=OC得∠SAC=90°,又∠ASC=45°,所以AS=AC=SC,同理BS=BC=SC,可得SC⊥面AOB,则VS-ABC=S△AOB·SC=××2××4=,故选C.
解过A点作BC边的高AE,交PQ于点F,
∵l∥BC,∴kl=kBC=.
∵=,∴=.
直线BC的方程为2x-3y-1=0,
∴|AE|==.
∴|AF|=,∴|EF|=|AE|-|AF|=.
设直线l的方程为2x-3y+b=0,
∵两条平行线间的距离为,
∴=,解得b=,或b=-(舍去),
∴直线l的方程是6x-9y+13=0.
模块检测试题二
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.空间直角坐标系中,点A(10,4,-2)关于点M(0,3,-5)的对称点的坐标是()
A.(-10,2,8)B.(-10,3,-8)
C.(5,2,-8)D.(-10,2,-8)
答案D
2.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是()
(2)由三视图可知,该平行六面体中,
【名师一号】2014-2015学年高中数学 第二章 解析几何初步双基限时练17(含解析)北师大版必修2
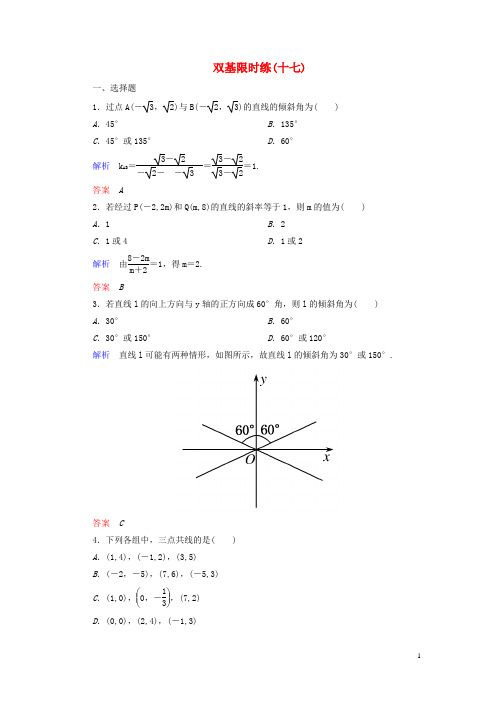
双基限时练(十七)一、选择题1.过点A(-3,2)与B(-2,3)的直线的倾斜角为( )A .45°B .135°C .45°或135°D .60°解析 k AB =3-2-2- -3 =3-23-2=1.答案 A2.若经过P(-2,2m)和Q(m,8)的直线的斜率等于1,则m 的值为( )A .1B .2C .1或4D .1或2解析 由8-2mm +2=1,得m =2.答案 B3.若直线l 的向上方向与y 轴的正方向成60°角,则l 的倾斜角为( )A .30°B .60°C .30°或150°D .60°或120°解析 直线l 可能有两种情形,如图所示,故直线l 的倾斜角为30°或150°.答案 C4.下列各组中,三点共线的是( )A .(1,4),(-1,2),(3,5)B .(-2,-5),(7,6),(-5,3)C .(1,0),⎝⎛⎭⎪⎫0,-13,(7,2)D .(0,0),(2,4),(-1,3)解析 利用斜率公式可知答案为C . 答案 C5.若经过A(2,1),B(1,m)的直线l 的倾斜角为锐角,则m 的取值范围是( )A .m<1B .m>1C .m<-1D .m>-1解析 由l 的倾斜角为锐角,可知k AB =m -11-2>0,即m<1. 答案 A6.若直线l 的斜率为k ,倾斜角为α,若60°<α<135°,则k 的取值范围是( )A .(-1,3)B .(-∞,-1)∪(3,+∞)C .[-1,3]D .(-∞,-1]∪[3,+∞)解析 由正切函数的图象可知,k∈(3,+∞)∪(-∞,-1). 答案 B 二、填空题7.若点A(4,2)和B(5,b)的连线与C(1,2),D(3,4)连线的斜率相等,则b 的值为________.解析 由题意,可得b -25-4=4-23-1=1,∴b=3.答案 38.若A(2,-3),B(4,3),C ⎝ ⎛⎭⎪⎫5,k 2在同一条直线上,则k =________. 解析 由题意,得k AB =3- -3 4-2=k 2-35-4,得k =12.答案 129.已知直线l 过原点,点M ,N 坐标分别为(3,1),(1,3),则当l 与线段MN 相交时l 的斜率的取值范围是______.解析 如图所示,当l 与线段MN 相交时,直线l 的倾斜角α∈[α1,α2],其中tan α1=13,tan α2=31=3, ∴直线l 的斜率k∈⎣⎢⎡⎦⎥⎤13,3.答案 ⎣⎢⎡⎦⎥⎤13,3三、解答题10.已知A(1,2),在直线y =x 上找一点P ,使PA 的斜率为 2.解 ∵点P 在直线y =x 上,∴设P(x ,x),由题意,得k PA =x -2x -1=2,得x =-2,∴P(-2,-2).11.已知直线过点A(2m,3),B(2,-1),根据下列条件求m 的值. (1)直线的倾斜角为135°; (2)直线的倾斜角为90°; (3)点C(3,m)也在直线上.解 (1)由题意,得3- -12m -2=tan 135°=-1,得m =-1.(2)由题意,得2m =2,得m =1.(3)由题意,得3- -1 2m -2=m - -13-2,得m =± 3.12.设A(m ,-m +3),B(2,m -1),C(-1,4),直线AC 的斜率等于直线BC 的斜率的3倍,求实数m 的值.解 由题意得直线AC 的斜率存在,∴m≠-1.由题意得k AC =3k BC ,∴4- 3-m-1-m=3²4- m-1-1-2,得m =4, ∴m 的值为4.思 维 探 究13.如图所示,已知点A(-2,3),B(3,2),P(0,-2),过点P 的直线l 与线段AB 有公共点,求直线l 的斜率的变化范围.解 直线l 是一组绕点P 转动而形成的直线,直线PA 和直线PB 是它的两个极端位置,k PB =43,k PA =-52.l 从PB 位置逆时针转到PA 位置的过程中,其倾斜角从α1连续变大到钝角α2,其斜率从正数k PB 逐渐变大到+∞,又从-∞逐渐增大到一个负数k PA ,其中当倾斜角为90°时,斜率不存在.所以斜率的变化范围为⎣⎢⎡⎭⎪⎫43,+∞∪⎝⎛⎦⎥⎤-∞,-52.。
【名师一号】高中数学 第二章 解析几何初步双基限时练17(含解析)北师大版必修2

双基限时练(十七)一、选择题1.过点A(-3,2)与B(-2,3)的直线的倾斜角为( )A .45°B .135°C .45°或135°D .60°解析 k AB =3-2-2--3=3-23-2=1. 答案 A2.若经过P(-2,2m)和Q(m,8)的直线的斜率等于1,则m 的值为( )A .1B .2C .1或4D .1或2解析 由8-2mm +2=1,得m =2.答案 B3.若直线l 的向上方向与y 轴的正方向成60°角,则l 的倾斜角为( )A .30°B .60°C .30°或150°D .60°或120°解析 直线l 可能有两种情形,如图所示,故直线l 的倾斜角为30°或150°.答案 C4.下列各组中,三点共线的是( )A .(1,4),(-1,2),(3,5)B .(-2,-5),(7,6),(-5,3)C .(1,0),⎝⎛⎭⎪⎫0,-13,(7,2)D .(0,0),(2,4),(-1,3)解析 利用斜率公式可知答案为C . 答案 C5.若经过A(2,1),B(1,m)的直线l 的倾斜角为锐角,则m 的取值范围是( )A .m<1B .m>1C .m<-1D .m>-1解析 由l 的倾斜角为锐角,可知k AB =m -11-2>0,即m<1. 答案 A6.若直线l 的斜率为k ,倾斜角为α,若60°<α<135°,则k 的取值范围是( )A .(-1,3)B .(-∞,-1)∪(3,+∞)C .[-1,3]D .(-∞,-1]∪[3,+∞)解析 由正切函数的图象可知,k∈(3,+∞)∪(-∞,-1). 答案 B 二、填空题7.若点A(4,2)和B(5,b)的连线与C(1,2),D(3,4)连线的斜率相等,则b 的值为________.解析 由题意,可得b -25-4=4-23-1=1,∴b=3.答案 38.若A(2,-3),B(4,3),C ⎝ ⎛⎭⎪⎫5,k 2在同一条直线上,则k =________. 解析 由题意,得k AB =3--4-2=k2-35-4,得k =12. 答案 129.已知直线l 过原点,点M ,N 坐标分别为(3,1),(1,3),则当l 与线段MN 相交时l 的斜率的取值范围是______.解析 如图所示,当l 与线段MN 相交时,直线l 的倾斜角α∈[α1,α2],其中tan α1=13,tan α2=31=3, ∴直线l 的斜率k∈⎣⎢⎡⎦⎥⎤13,3.答案 ⎣⎢⎡⎦⎥⎤13,3三、解答题10.已知A(1,2),在直线y =x 上找一点P ,使PA 的斜率为 2.解 ∵点P 在直线y =x 上,∴设P(x ,x),由题意,得k PA =x -2x -1=2,得x =-2,∴P(-2,-2).11.已知直线过点A(2m,3),B(2,-1),根据下列条件求m 的值. (1)直线的倾斜角为135°; (2)直线的倾斜角为90°; (3)点C(3,m)也在直线上. 解 (1)由题意,得3--2m -2=tan 135°=-1,得m =-1.(2)由题意,得2m =2,得m =1. (3)由题意,得3--2m -2=m --3-2,得m =± 3.12.设A(m ,-m +3),B(2,m -1),C(-1,4),直线AC 的斜率等于直线BC 的斜率的3倍,求实数m 的值.解 由题意得直线AC 的斜率存在,∴m≠-1.由题意得k AC =3k BC ,∴4---1-m=3·4---1-2,得m =4, ∴m 的值为4.思 维 探 究13.如图所示,已知点A(-2,3),B(3,2),P(0,-2),过点P 的直线l 与线段AB 有公共点,求直线l 的斜率的变化范围.解 直线l 是一组绕点P 转动而形成的直线,直线PA 和直线PB 是它的两个极端位置,k PB =43,k PA =-52.l 从PB 位置逆时针转到PA 位置的过程中,其倾斜角从α1连续变大到钝角α2,其斜率从正数k PB 逐渐变大到+∞,又从-∞逐渐增大到一个负数k PA ,其中当倾斜角为90°时,斜率不存在.所以斜率的变化范围为⎣⎢⎡⎭⎪⎫43,+∞∪⎝⎛⎦⎥⎤-∞,-52.。
【名师一号】2014-2015学年高中数学 第二章 平面向量双基限时练19(含解析)新人教A版必修4

双基限时练(十九)1.已知两点A (2,-1),B (3,1),与AB →平行且方向相反的向量a 可能是( ) A .(1,-2) B .(9,3) C .(-1,2)D .(-4,-8)解析 AB →=(3-2,1+1)=(1,2), ∵(-4,-8)=-4(1,2), ∴(-4,-8)满足条件. 答案 D2.已知A (3,-6),B (-5,2),且A ,B ,C 三点在一条直线上,则C 点坐标不可能是( ) A .(-9,6) B .(-1,-2) C .(-7,-2)D .(6,-9) 解析 设C (x ,y ),则AC →=(x -3,y +6),AB →=(-8,8). ∵A ,B ,C 三点在同一直线上,∴x -3-8=y +68,即x +y +3=0,将四个选项分别代入x+y +3=0验证可知,不可能的是C.答案 C3.若向量a =(1,1),b =(-1,1),c =(4,2)满足(k a +b )∥c ,则k =( ) A .3 B .-3 C.13D .-13解析 k a +b =(k -1,k +1),由(k a +b )∥c ,得2(k -1)-4(k +1)=0,解得k =-3. 答案 B4.若a =⎝ ⎛⎭⎪⎫32,sin α,b =⎝ ⎛⎭⎪⎫sin α,13,且a ∥b ,则锐角α为( ) A .30° B .45° C .60°D .75° 解析 由a ∥b ,得32³13-sin α²sin α=0,∴sin 2α=12,∴sin α=±22,又α为锐角,∴α=45°.故选B. 答案 B5.已知向量a =(1,2),b =(-2,m ),且a ∥b ,则2a +3b 等于( )A .(-5,-10)B .(-4,-8)C .(-3,-6)D .(-2,-4)解析 ∵a ∥b ,∴m +4=0,∴m =-4,b =(-2,-4).则2a +3b =2(1,2)+3(-2,-4)=(2,4)+(-6,-12)=(-4,-8). 答案 B6.已知向量a =(2,3),b =(-1,2),若m a +n b 与a -2b 共线,则m n等于( ) A.12 B .2 C .-12D .-2解析 m a +n b =m (2,3)+n (-1,2) =(2m -n,3m +2n ),a -2b =(2,3)-2(-1,2)=(4,-1),又m a +n b 与a -2b 平行,∴(2m -n )(-1)-(3m +2n )³4=0,即14m +7n =0,∴m n =-12.答案 C7.向量a =(n,1)与b =(4,n )共线且方向相同,则n =________.解析 ∵a ∥b ,∴n 2-4=0,∴n =2或n =-2,又∵a 与b 方向相同,∴n =2. 答案 28.已知向量a =(2,-1),b =(-1,m ),c =(-1,2),若(a +b )∥c ,则m =________. 解析 a +b =(2-1,-1+m )=(1,m -1),由(a +b )∥c ,得1³2-(m -1)³(-1)=0,解得m =-1.答案 -19.若点A ,B 的坐标分别为(2,-2),(4,3),向量a =(2k -1,7),且a ∥AB →,则k 的值为________.解析 AB →=(2,5),由a ∥AB →可得(2k -1)³5-7³2=0,解得k =1910.答案1910 10.已知△ABC 的顶点A (2,3)和重心G (2,-1),则BC 边上的中点的坐标是________. 解析 设BC 边上的中点为D (x ,y ),则AG →=2GD →,∴⎩⎪⎨⎪⎧2=2+2x 1+2,-1=3+2y1+2,解得⎩⎪⎨⎪⎧x =2,y =-3.答案 (2,-3)11.已知AB →=(6,1),BC →=(x ,y ),CD →=(-2,-3),且BC →∥DA →,试确定x ,y 的关系式.解 因为AB →=(6,1),BC →=(x ,y ),CD →=(-2,-3), 所以AD →=AB →+BC →+CD →, =(6,1)+(x ,y )+(-2,-3) =(4+x ,y -2).又因为BC →∥DA →,所以BC →∥AD →. 所以x (y -2)-y (4+x )=0,xy -2x -4y -xy =0,故x +2y =0.12.已知a =(3,2),b =(-1,2),c =(4,1). (1)求3a +b -2c ;(2)求满足a =m b +n c 的实数m 、n ; (3)若(a +k c )∥(2b -a ),求实数k . 解 (1)3a +b -2c =(0,6).(2)∵a =m b +n c ,∴(3,2)=m (-1,2)+n (4,1)=(-m +4n,2m +n ).∴⎩⎪⎨⎪⎧-m +4n =3,2m +n =2,∴⎩⎪⎨⎪⎧m =59,n =89.(3)由a +k c =(3+4k,2+k ),2b -a =(-5,2),(a +k c )∥(2b -a ),得2³(3+4k )-(-5)³(2+k )=0,∴k =-1613.13.如图,已知两点P (-1,6)和Q (3,0),延长线段QP 到A ,使|AP →|=13|PQ →|,求A 点坐标.解 解法一:若P 为终点,Q 为起点,则A (x ,y )分QP →所成的比λ=-4. ∴x =3-4³ -1 1-4=-73,y =0-4³61-4=8,∴A ⎝ ⎛⎭⎪⎫-73,8. 解法二:若Q 为起点,A 为终点,则P 分QA →所成的比λ=3.设A (x ,y ),则-1=3+3x 1+3,∴x =-73,6=3y 1+3,∴y =8,∴A ⎝ ⎛⎭⎪⎫-73,8.。
高中数学 第二章 平面向量双基限时练17(含解析)北师大版必修4

双基限时练(十七) 数乘向量一、选择题1.已知e 1,e 2是不共线向量,则下列各组向量中,是共线向量的有( ) ①a =5e 1,b =7e 1;②a =12e 1-13e 2,b =3e 1-2e 2;③a =e 1+e 2,b =3e 1-3e 2. A .①② B .①③ C .②③D .①②③解析 ①中a 与b 显然共线;②中,因为b =3e 1-2e 2=6(12e 1-13e 2)=6a ,故a 与b 共线;而③设b =3e 1-3e 2=k (e 1+e 2)无解,故a 与b 不共线,故共线的有①②,故选A.答案 A2.下列计算正确的个数是( )①(-2)(3a )=-6a ;②(a +3b )+(-a -3b )=0; ③2(a +b )-3(b -2a )=8a -b . A .0 B .1 C .2D .3解析 ②中,(a +3b )+(-a -3b )=0,故②不正确,①③均对. 答案 C3.△ABC 中,点D 是BC 边的中点,设AB →=a ,AC →=b ,用a ,b 表示AD →为( ) A. a +b B. 12a +b C. a +12bD. 12a +12b 解析 方法一:AD →=AB →+BD →=AB →+12BC →=AB →+12(AC →-AB →)=12AB →+12AC →=12a +12b ,故选D.方法二:以AB ,AC 为邻边作平行四边形ABEC ,则点D 是平行四边形对角线的中点,所以AD →=12AE →=12a +12b ,故选D.答案 D4.线段AB 的中点为C ,若AB →=λBC →,则λ的值是( ) A .2B .-2C .2或-2D.12或2 解析 ∵AC →=CB →,∴AB →=AC →+CB →=2CB →=-2BC →. 答案 B5.设e1,e2是两个不共线的向量,则a =e1+λe 2(λ∈R )与向量b =-(e 2-2e 1)共线的条件是( )A .λ=0B .λ=-1C .λ=-2D .λ=-12解析 由题可知,b =-e 2+2e 1=k (e 1+λe 2),得λ=-12.答案 D6.如图,已知AB →=a ,AC →=b ,BD →=3DC →,用a ,b 表示AD →,则AD →等于( ) A .a +34bB.14a +34bC.14a +14bD.34a +14b 解析 AD →=a +BD →=a +34BC →=a +34(b -a )=14a +34b ,故选B.答案 B7.已知向量e 1,e 2不共线,实数x ,y 满足(3x -4y )e 1+(2x -3y )e 2=6e 1+3e 2,则x -y 的值为( )A .3B .-3C .0D .2解析 由平面向量基本定理,得⎩⎪⎨⎪⎧3x -4y =6,2x -3y =3,,∴x =6,y =3.∴x -y =3.答案 A 二、填空题8.已知2(x -13a )-12(b +c +3x )+b =0,其中a ,b ,c 为已知向量,则x =________.解析 由已知得:12x -23a -12b -c2+b =0,得12x =23a -b 2+c 2, 得x =43a -b +c .答案 43a -b +c9.设AB →=22(a +5b ),BC →=-2a +8b ,CD →=3(a -b ),则共线的三点是__________.解析 BD →=BC →+CD →=a +5b ,∴AB →=22BD →,即A ,B ,D 三点共线. 答案 A ,B ,D10.已知O 是△ABC 内一点,OA →+OC →=-3OB →,则△AOB 与△AOC 的面积之比为________.解析 如图,在△ABC 中,设D 为AC 的中点,四边形OCEA 为平行四边形, ∴OC →+OA →=OE →. 且△ADE ≌△CDO , ∴S △AOC =S △AOE .又OA →+OC →=-3OB →,即OE →=-3OB →, ∴S △AOB S △AOE =|BO →||OE →|=|BO →|3|BO →|=13. 答案 13三、解答题 11.化简下列各式: (1)3(2a -b )-2(4a -3b ); (2)13(4a +3b )-12(3a -b )-32b ; (3)2(3a -4b +c )-3(2a +b -3c ). 解 本题可利用结合律和分配律进行化简. (1)3(2a -b )-2(4a -3b ) =6a -3b -8a +6b =-2a +3b .(2)13(4a +3b )-12(3a -b )-32b =43a +b -32a +12b -32b =⎝ ⎛⎭⎪⎫43-32a +⎝ ⎛⎭⎪⎫1+12-32b =-16a .(3)2(3a -4b +c )-3(2a +b -3c ) =6a -8b +2c -6a -3b +9c =(6-6)a +(-8-3)b +(2+9)c =-11b +11c =11(c -b ).12.已知向量m ,n 是不共线向量,a =3m +2n ,b =6m -4n ,c =m +x n . (1)判断a ,b 是否平行; (2)若a ∥c ,求x 的值.解 (1)若a ∥b ,则b =λa ,即6m -4n =λ(3m +2n ),∴⎩⎪⎨⎪⎧6=3λ,-4=2λ,⇒⎩⎪⎨⎪⎧λ=2,λ=-2,⇒λ不存在,∴a 与b 不平行. (2)∵a ∥c , ∴c =r a .∴m +x n =r (3m +2n ).即⎩⎪⎨⎪⎧1=3r ,x =2r ⇒⎩⎪⎨⎪⎧r =13,x =23,所以x =23.13.已知两个非零向量a 、b 不共线,OA →=a +b ,OB →=a +2b ,OC →=a +3b . (1)证明:A 、B 、C 三点共线;(2)试确定实数k ,使k a +b 与a +k b 共线.解 (1)由于OA →=a +b ,OB →=a +2b ,OC →=a +3b ,则AB →=OB →-OA →=a +2b -(a +b )=b . 而AC →=OC →-OA →=a +3b -(a +b )=2b , 于是AC →=2AB →,即AC →与AB →共线.又AC 与AB 有公共点A ,所以A 、B 、C 三点共线. (2)由于a 、b 为非零向量且不共线,所以a +k b ≠0. 若k a +b 与a +k b 共线,则必存在唯一实数λ, 使k a +b =λ(a +k b ),整理得(k -λ)a =(λk -1)b .因此⎩⎪⎨⎪⎧k -λ=0,λk -1=0,解得⎩⎪⎨⎪⎧k =1,λ=1,或⎩⎪⎨⎪⎧k =-1,λ=-1,即存在实数λ=1,使k a +b 与a +k b 共线,此时k =1;或存在实数λ=-1,使k a +b 与a +k b 共线,此时k =-1,因此k =±1都满足题意.。
【名师一号】2014-2015学年高中数学 第二章 平面向量双基限时练14(含解析)新人教A版必修4

双基限时练(十四)1.已知a ,b ,c 是非零向量,则(a +c )+b ,b +(a +c ),b +(c +a ),c +(a +b ),c +(b +a )中,与向量a +b +c 相等的向量的个数为( )A .5B .4C .3D .2解析 向量加法满足交换律, 所以五个向量均等于a +b +c . 答案 A2.向量(AB →+MB →)+(BO →+BC →)+OM →化简后等于( )A.CB →B.AB →C.AC →D.AM → 解析 (AB →+MB →)+(BO →+BC →)+OM →=(AB →+BC →)+(BO →+OM →+MB →)=AC →+0=AC →,故选C.答案 C3.向量a ,b 皆为非零向量,下列说法不正确的是( ) A .向量a 与b 反向,且|a |>|b |,则向量a +b 与a 的方向相同 B .向量a 与b 反向,且|a |<|b |,则向量a +b 与a 的方向相同 C .向量a 与b 同向,则向量a +b 与a 的方向相同 D .向量a 与b 同向,则向量a +b 与b 的方向相同解析 向量a 与b 反向,且|a |<|b |,则a +b 应与b 方向相同,因此B 错. 答案 B4.设P 是△ABC 所在平面内一点,BC →+BA →=2BP →,则( )A.PA →+PB →=0B.PB →+PC →=0C.PC →+PA →=0D.PA →+PB →+PC →=0解析 由向量加法的平行四边形法则易知,BA →与BC →的和向量过AC 边的中点,且长度是AC 边中线长的2倍,结合已知条件知,P 为AC 的中点,故PA →+PC →=0.答案 C5.正方形ABCD 的边长为1,AB →=a ,AC →=c ,BC →=b ,则|a +b +c |为( ) A .0 B. 2 C .3D .2 2解析 |a +b +c |=|2c |=2|c |=2 2.应选D. 答案 D6.在▱ABCD 中,若|BC →+B A →|=|B C →+AB →|,则四边形ABCD 是( )A .菱形B .矩形C .正方形D .不确定解析 |BC →+AB →|=|AB →+BC →|=|AC →|, |BC →+BA →|=|BD →|,由|BD →|=|AC →|知四边形ABCD 为矩形.答案 B 7.根据图示填空. (1)AB →+OA →=________; (2)BO →+OD →+DO →=________; (3)AO →+BO →+2OD →=________. 解析 由三角形法则知 (1)AB →+OA →=OA →+AB →=OB →;(2)BO →+OD →+DO →=BO →; (3)AO →+BO →+2OD →=AD →+BD →. 答案 (1)OB → (2)BO →(3)AD →+BD →8.在正方形ABCD 中,边长为1,AB →=a ,BC →=b ,则|a +b |=________.解析 a +b =AB →+BC →=AC →,∴|a +b |=|AC →|= 2. 答案29.若P 为△ABC 的外心,且PA →+PB →=PC →,则∠ACB =__________.解析 ∵PA →+PB →=PC →,则四边形APBC 是平行四边形. 又P 为△ABC 的外心, ∴|PA →|=|PB →|=|PC →|. 因此∠ACB =120°. 答案 120°10.设a 表示“向东走了2 km”,b 表示“向南走了2 km”,c 表示“向西走了2 km”,d 表示“向北走了2 km”,则(1)a +b +c 表示向________走了________km ; (2)b +c +d 表示向________走了________km ; (3)|a +b |=________,a +b 的方向是________. 解析 (1)如图①所示,a +b +c表示向南走了2 km.(2)如图②所示,b +c +d 表示向西走了2 km.(3)如图①所示,|a +b |=22+22=22,a +b 的方向是东南. 答案 (1)南 2 km (2)西 2 km (3)2 2 东南 11.如图,O 为正六边形ABCDEF 的中心,试通过计算用图中有向线段表示下列向量的和: (1)OA →+OC →; (2)BC →+FE →; (3)OA →+FE →.解 (1)因为四边形OABC 是平行四边形,所以OA →+OC →=OB →. (2)因为BC ∥AD ∥FE ;BC =FE =12AD ,所以BC →=AO →,FE →=OD →, 所以BC →+FE →=AO →+OD →=AD →.(3)因为|OA →|=|FE →|,且OA →与FE →反向. 所以利用三角形法则可知OA →+FE →=0.12.化简:(1)AB →+CD →+BC →; (2)(MA →+BN →)+(AC →+CB →); (3)AB →+(BD →+CA →)+DC →.解 (1)AB →+CD →+BC →=AB →+BC →+CD →=AD →.(2)(MA →+BN →)+(AC →+CB →) =(MA →+AC →)+(CB →+BN →) =MC →+CN →=MN →.(3)AB →+(BD →+CA →)+DC →=AB →+BD →+DC →+CA →=013.如右图所示,P ,Q 是△ABC 的边BC 上的两点,且BP →=QC →.求证:AB →+AC →=AP →+AQ →.证明 由图可知AB →=AP →+PB →,AC →=AQ →+QC →,∴AB →+AC →=AP →+AQ →+PB →+QC →.∵BP →=QC →,又PB →与BP →模相等,方向相反, 故PB →+QC →=PB →+BP →=0. ∴AB →+AC →=AP →+AQ →.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双基限时练(十七) 数乘向量
一、选择题
1.已知e 1,e 2是不共线向量,则下列各组向量中,是共线向量的有( ) ①a =5e 1,b =7e 1;②a =12e 1-1
3e 2,b =3e 1-2e 2;
③a =e 1+e 2,b =3e 1-3e 2. A .①② B .①③ C .②③
D .①②③
解析 ①中a 与b 显然共线;②中,因为b =3e 1-2e 2=6(12e 1-1
3e 2)=6a ,故a 与b 共
线;而③设b =3e 1-3e 2=k (e 1+e 2)无解,故a 与b 不共线,故共线的有①②,故选A.
答案 A
2.下列计算正确的个数是( )
①(-2)(3a )=-6a ;②(a +3b )+(-a -3b )=0; ③2(a +b )-3(b -2a )=8a -b . A .0 B .1 C .2
D .3
解析 ②中,(a +3b )+(-a -3b )=0,故②不正确,①③均对. 答案 C
3.△ABC 中,点D 是BC 边的中点,设AB →=a ,AC →=b ,用a ,b 表示AD →
为( ) A. a +b B. 1
2a +b C. a +12
b
D. 12a +12
b 解析 方法一:AD →=AB →+BD →=AB →+12BC →=AB →+12(AC →-AB →)=12AB →+12AC →
=12a +1
2b ,故选D.
方法二:以AB ,AC 为邻边作平行四边形ABEC ,则点D 是平行四边形对角线的中点,所以AD →=12AE →
=12a +1
2
b ,故选D.
答案 D
4.线段AB 的中点为C ,若AB →=λBC →
,则λ的值是( ) A .2
B .-2
C .2或-2
D.1
2
或2 解析 ∵AC →=CB →,∴AB →=AC →+CB →=2CB →=-2BC →
. 答案 B
5.设e1,e2是两个不共线的向量,则a =e1+λe 2(λ∈R )与向量b =-(e 2-2e 1)共线的条件是( )
A .λ=0
B .λ=-1
C .λ=-2
D .λ=-1
2
解析 由题可知,b =-e 2+2e 1=k (e 1+λe 2),得λ=-1
2.
答案 D
6.如图,已知AB →=a ,AC →=b ,BD →=3DC →,用a ,b 表示AD →,则AD →
等于( ) A .a +34b
B.14a +34b
C.14a +14b
D.34a +14
b 解析 AD →=a +BD →=a +34BC →
=a +34(b -a )=14a +3
4b ,故选B.
答案 B
7.已知向量e 1,e 2不共线,实数x ,y 满足(3x -4y )e 1+(2x -3y )e 2=6e 1+3e 2,则x -
y 的值为( )
A .3
B .-3
C .0
D .2
解析 由平面向量基本定理,得⎩⎪⎨
⎪⎧
3x -4y =6,
2x -3y =3,
,∴x =6,y =3.∴x -y =3.
答案 A 二、填空题
8.已知2(x -13a )-1
2(b +c +3x )+b =0,其中a ,b ,c 为已知向量,则x =________.
解析 由已知得:12x -23a -12b -c
2+b =0,
得12x =23a -b 2+c 2, 得x =4
3a -b +c .
答案 4
3
a -
b +c
9.设AB →=2
2(a +5b ),BC →=-2a +8b ,CD →
=3(a -b ),则共线的三点是__________.
解析 BD →=BC →+CD →=a +5b ,∴AB →=2
2BD →
,
即A ,B ,D 三点共线. 答案 A ,B ,D
10.已知O 是△ABC 内一点,OA →+OC →=-3OB →
,则△AOB 与△AOC 的面积之比为________.
解析 如图,在△ABC 中,设D 为AC 的中点,四边形OCEA 为平行四边形, ∴OC →+OA →=OE →. 且△ADE ≌△CDO , ∴S △AOC =S △AOE .
又OA →+OC →=-3OB →,即OE →=-3OB →, ∴S △AOB S △AOE =|BO →||OE →|=|BO →
|3|BO →|=13
. 答案 13
三、解答题 11.化简下列各式: (1)3(2a -b )-2(4a -3b ); (2)13(4a +3b )-12(3a -b )-32b ; (3)2(3a -4b +c )-3(2a +b -3c ). 解 本题可利用结合律和分配律进行化简. (1)3(2a -b )-2(4a -3b ) =6a -3b -8a +6b =-2a +3b .
(2)13(4a +3b )-12(3a -b )-32b =43a +b -32a +12b -32
b =⎝ ⎛⎭⎪⎫43-32a +⎝ ⎛⎭
⎪⎫1+12-32b =-16
a .
(3)2(3a -4b +c )-3(2a +b -3c ) =6a -8b +2c -6a -3b +9c =(6-6)a +(-8-3)b +(2+9)c =-11b +11c =11(c -b ).
12.已知向量m ,n 是不共线向量,a =3m +2n ,b =6m -4n ,c =m +x n . (1)判断a ,b 是否平行; (2)若a ∥c ,求x 的值.
解 (1)若a ∥b ,则b =λa ,即6m -4n =λ(3m +2n ),
∴⎩⎪⎨
⎪⎧
6=3λ,-4=2λ,⇒⎩
⎪⎨
⎪⎧
λ=2,
λ=-2,⇒λ不存在,
∴a 与b 不平行. (2)∵a ∥c , ∴c =r a .
∴m +x n =r (3m +2n ).
即⎩
⎪⎨
⎪⎧
1=3r ,x =2r ⇒⎩⎪⎨⎪⎧
r =1
3,x =2
3,
所以x =2
3
.
13.已知两个非零向量a 、b 不共线,OA →=a +b ,OB →=a +2b ,OC →
=a +3b . (1)证明:A 、B 、C 三点共线;
(2)试确定实数k ,使k a +b 与a +k b 共线.
解 (1)由于OA →=a +b ,OB →=a +2b ,OC →=a +3b ,则AB →=OB →-OA →
=a +2b -(a +b )=b . 而AC →=OC →-OA →
=a +3b -(a +b )=2b , 于是AC →=2AB →,即AC →与AB →
共线.
又AC 与AB 有公共点A ,所以A 、B 、C 三点共线. (2)由于a 、b 为非零向量且不共线,所以a +k b ≠0. 若k a +b 与a +k b 共线,则必存在唯一实数λ, 使k a +b =λ(a +k b ),整理得(k -λ)a =(λk -1)b .
因此⎩⎪⎨
⎪⎧
k -λ=0,λk -1=0,
解得⎩⎪⎨
⎪⎧
k =1,λ=1,
或⎩⎪⎨⎪⎧
k =-1,
λ=-1,
即存在实数λ=1,使k a +b 与a +k b 共线,此时k =1;或存在实数λ=-1,使k a +b 与a +k b 共线,此时k =-1,因此k =±1都满足题意.。
