第12章 结构动力计算
物理化学(第五版傅献彩)第12_化学动力学基础2

k
=ν
K
≠ c
=
kBT h
f fA
≠'
fBC
exp
−
E0 RT
一般基元反应 k 的计算式为
k
=
kBT h
f ≠' ΠfB
exp
−
E0 RT
常温
kBT ≈ 1013 s−1 h
36
A (单原子) + B(单原子) ‡ˆˆˆ†ˆ[ALB]≠ (双原子)
( ) k = kBT ( ) ( ) h
25
势能面
Ep
OT ≠
rAB
A+RBC
D
P
rBC
AB+C
A+B+C
26
R点:是反应物A+BC分子的基态。随A原子靠近, 势能沿RT 升高,到T点形成活化络合物 随C原子离去,势能沿TP线下降
P点:是生成物AB+C分子 的基态
D点:是离解为A,B,C原 子时的势能
OEP一侧是原子间 的相斥能,很高
f
3 t
fr2
≠
f
3 t
A
f
3 t
B
exp
−
E0 RT
1个振动自由度用于活化络合物的分解
37
A
(
N
,非线型多原子分子
A
)
+
B
(
N
,非线型多原子分子
B
)
‡ˆˆˆ†ˆ[ALB]≠ ( NA + NB,非线型多原子分子)
( ) k = kBT
( ) ( ) h
物理化学12章_化学动力学基础(二)
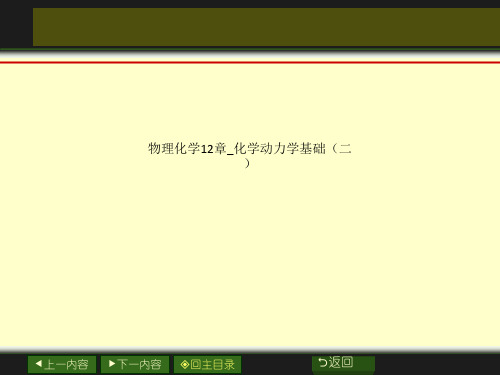
Eb。Eb。是活化络合物与反应物最 低势能之差,E0是两者零点能
之间的差值。
这个势能垒的存在说明了实验活化能的实质。
上一内容 下一内容 回主目录
返回
2021/1/16
势能面剖面图
上一内容 下一内容 回主目录
返回
2021/1/16
三原子系统振动方式
式中r0是分子中双原子分子间的平衡核间 距,De是势能曲线的井深,a为与分子结构有 关的常数.
上一内容 下一内容 回主目录
返回
2021/1/16
双原子分子的莫尔斯势能曲线
AB双原子分子根据该公式 画出的势能曲线如图所示。
当r>r0时,有引力,即化学键力。 当r<r0时,有斥力。 0时的能级为振动基态能级,E0为零点能。
物理化学12章_化学动力学基础(二 )
上一内容 下一内容 回主目录
返回
物理化学电子教案—第十二章
上一内容 下一内容 回主目录
返回
2021/1/16
第十二章 化学动力学基础(二)
§12.1 碰撞理论 *§12.2 过渡态理论
§12.3 单分子反应理论 * §12.4 分子反应动态学简介
§12.5 在溶液中进行的反应 * §12.6 快速反应的几种测试手段
Ea≈ E
上一内容 下一内容 回主目录
返回
2021/1/16
概率因子(probability factor)
由于简单碰撞理论所采用的模型过于简单, 没有考虑分子的结构与性质,所以用概率因子 来校正理论计算值与实验值的偏差。
P=k(实验)/k(理论)
概率因子又称为空间因子或方位因子。
上一内容 下一内容 回主目录
结构动力学【习题课】(单自由度体系1)

15.求图示体系的自振频率和周期,EI=常数. 15.求图示体系的自振频率和周期,EI=常数. 求图示体系的自振频率和周期 常数 解:
m
l
5l 3 δ 11 = ; 3EI
1 3EI = ω = mδ11 5ml3
2
l =1 l
ω=
3EI 3EI 5ml3
5ml3 = 2π T= ω 3EI
l
2π
10.图示体系,不计阻尼及杆件质量, 10.图示体系,不计阻尼及杆件质量,其振动微分方程为 图示体系
M 0 sin θ t单自由度体系在自由振动中惯性力与位移方向一致。 11.无阻尼单自由度体系在自由振动中惯性力与位移方向一致。 无阻尼单自由度体系在自由振动中惯性力与位移方向一致 12.计算自振频率时可以不计阻尼。 12.计算自振频率时可以不计阻尼。 计算自振频率时可以不计阻尼 13.任何体系均能发生自由振动。 13.任何体系均能发生自由振动。 任何体系均能发生自由振动 14.图示体系的动力自由度为多少? 14.图示体系的动力自由度为多少? 图示体系的动力自由度为多少
动荷载及其分类第12章小结自由度及其确定运动方程的建立运动方程的求解方法动力特性计算动力反应计算确定动力特性的试验方法阻尼力假定及阻尼的影响简谐荷载周期荷载阶跃荷载冲击荷载一般荷载经典解法频域解法时域解法数值解法公式法能量守恒幅值方程惯性力法虚功法动荷载及其分类第12章小结自由度及其确定运动方程的建立运动方程的求解方法动力特性计算动力反应计算确定动力特性的试验方法阻尼力假定及阻尼的影响简谐荷载周期荷载阶跃荷载冲击荷载一般荷载经典解法频域解法时域解法数值解法公式法能量守恒幅值方程惯性力法虚功法1
EA = ∞
7.体系的振幅和自振频率与初始条件有关. 7.体系的振幅和自振频率与初始条件有关. 体系的振幅和自振频率与初始条件有关
《结构设计原理》教案 第十二章 预用力混凝土受弯构件的应力损失
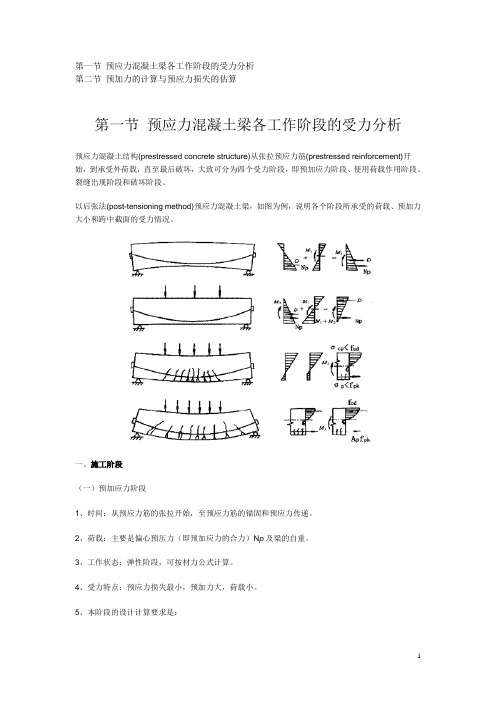
第一节预应力混凝土梁各工作阶段的受力分析第二节预加力的计算与预应力损失的估算第一节预应力混凝土梁各工作阶段的受力分析预应力混凝土结构(prestressed concrete structure)从张拉预应力筋(prestressed reinforcement)开始,到承受外荷载,直至最后破坏,大致可分为四个受力阶段,即预加应力阶段、使用荷载作用阶段、裂缝出现阶段和破坏阶段。
以后张法(post-tensioning method)预应力混凝土梁,如图为例,说明各个阶段所承受的荷载、预加力大小和跨中截面的受力情况。
一、施工阶段(一)预加应力阶段1、时间:从预应力筋的张拉开始,至预应力筋的锚固和预应力传递。
2、荷载:主要是偏心预压力(即预加应力的合力)N p及梁的自重。
3、工作状态:弹性阶段,可按材力公式计算。
4、受力特点:预应力损失最小,预加力大,荷载小。
5、本阶段的设计计算要求是:①控制梁的上、下缘混凝土的最大拉应力和压应力,及梁腹的主应力,不应超出《公桥规》的规定;②控制钢筋的最大张拉应力;③保证锚具下混凝土局部承压的容许承载能力,使其大于实际承载的压力,并有足够的安全度,以保证梁体不出现水平纵向裂缝。
6、有效预应力的概念:通常把扣除应力损失后钢筋中实际存余的应力称为有效预应力(effective Prestress)。
(二)运输、安装阶段此阶段混凝土梁所承受的荷载,仍是预加力和梁的自身恒载。
但由于引起预应力损失的因素相继增加,使要比预加应力阶段小;同时梁的自身恒载应根据《公桥规》的规定计入1.20或0.85的动力系数。
构件在运输中的支点或安装时的吊点位置常与正常支承点不同,故应按梁起吊时自身恒载作用下的计算图式进行验算,特别需注意验算构件支点或吊点处上缘混凝土的拉应力。
二、使用阶段1、时间:该阶段是指桥梁建成通车后整个使用阶段。
2、荷载:梁自重(称为Ⅰ期恒载),偏心预加力N p,车辆及人群等活载,和桥面铺装、人行道板、栏杆等后加桥梁恒载(称为Ⅱ期恒载)。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解(12-15章)【圣才出品】

阶方阵)。
十、地震作用计算 ★★ 整节非考研初试重点,但为考研复试的考察重点,需重点掌握基本概念。地震作用的基 本概念见表 12-1-14。
表 12-1-14 地震作用的基本概念
十一、计算频率的近似法 ★★ 本节掌握集中质量位置选择的基本思路即可,其他的为非重点。具体内容见表 12-1-15。
表 12-1-15 计算频率的近似法
11 / 150
圣才电子书 十万种考研考证电子书、题库视频学习平台
••
•
简写为 MY+cY+KY=F(t)。
式中,cij 为质点 j 处的运动速度引起质点 i 处的阻力系数;Fi(t)为作用在质点 i 处的
任意荷载;Y 为速度列向量;F(t)为任意荷载列向量(n×1 阶列矩阵);c 为阻尼矩阵(n×n
12 / 150
圣才电子书 十万种考研考证电子书、题库视频学习平台
12.2 课后习题详解 复习思考题
1.怎样区别动力荷载与静力荷载?动力计算与静力计算的主要差别是什么? 答:(1)静力荷载:指施力过程缓慢,不致使结构产生显著的加速度,因而可以略去 惯性力影响的荷载; 动力荷载:指将使结构产生不容忽视的加速度,因而必须考虑惯性力的影响的荷载。 主要差别在于是否考虑惯性力的影响。
圣才电子书
第 12 章 结构动力学
十万种考研考证电子书、题库视频学习平台
12.1 复习笔记
【知识框架】
1 / 150
圣才电子书 十万种考研考证电子书、题库视频学习平台
【重点难点归纳】 一、基本概念 ★★★ 1.动力载荷与静力载荷(见表 12-1-1)
图 12-1-1 (1)刚度系数与柔度系数(见表 12-1-5)
表 12-1-5 刚度系数与柔度系数
第12章结构动力学 ppt课件

§14-1 概 述
一、结构动力计算的特点 动力荷载作用下,结构将发生振动,各种量值均随时间而变化。
1、内容: (1)研究动力荷载作用下,结构的内力、位移等计算原理和计算方法。 求出它们的最大值并作为结构设计的依据。
(2)研究单自由度及多自由度的自由振动、强迫振动。 2、静荷载和动荷载 (1)静荷载:荷载的大小和方向不随时间变化(如梁板自重)。 (2)动荷载:荷载的大小和方向随时间变化,需要考虑惯性力。 3、特点 (1)必须考虑惯性力。 (2)内力与荷载不能构成静平衡。必须考据惯性力。依达朗伯原理, 加惯性力后,将动力问题转化为静力问题。
动力自由度的确定方法:加附加链杆约束质点位移,最少链杆数即为自 由度
图刚架上有四个集中质点,但只需要加三根链杆 便可限制全部质点的位置。如图e。
自由度=3 或
图示梁,其分布质量集度为m,可看作有无穷多 个mdx的集中质量,是无限自由度结构。
自由度的数目与结构是否静定或超静定无关
§14-2 结构振动的自由度
2、运动方程的解:
方程
y2y0
为一常系数线性齐次微分方程,其通解为
y (t) A 1 co t s A 2sitn
A1和A2为任意常数,可有初始条件来确定。
振动的初始条件为 t 0 时 y y , 0 , y y 0
式中y0—初位移, y0—初速度。则有Fra bibliotekA1y0,A2
y0
可得
yy0cots y0si nt
第十四章 结构动力学
§14-1 概 述 §14-2 结构振动的自由度 §14-3 单自由度结构的自由振动 §14-4 单自由度结构在简谐荷载作用下的强迫振动 §14-5 单自由度结构在任意荷载作用下的强迫振动 §14-6 多自由度结构的自由振动 §14-7 多自由度结构在简谐荷载作用下的强迫振动 §14-8 振型分解法 §14-9 无限自由度结构的振动 §14-10 计算频率的近似法
第12章 结构的动力计算(3)

l2 7m 12EI
w2
1
l2
1.309
EI 1 261 . 86 s m l3
(3)求主振型ri
第一主振型
ห้องสมุดไป่ตู้
r1
Y11 12 m2 1 Y21 11 m1 l1 1
第二主振型
Y12 12 m2 1 r2 Y22 11 m1 l 2 1
w1
1
l1
, w2
1
l2
(4)求主振型
(11m1 1 )Y1 12 m2Y2 0 1
w
2
21m1Y1 ( 22 m2
1) 第一主振型:将w w1代入
w
2
)Y2 0
Y11 12 m2 r1 Y21 11 m1 l1
2) 第二主振型:将w w2代入
y 0 [ ][M ] y
注意:[]与[K]虽然互为逆阵,但[]中之ij与[K]中之kij元素一般并不互 逆(仅单自由度体系例外)。
(2)运动方程的求解
设特解
1 11 m2 2 12 y1 m1 y y 1 21 m2 2 22 y 2 m1 y y
1 1
C C C
l /4
M 基1
1 1 B
图
C
M 2图
B B
13ll /64 13l /64 /4
解:(1)求柔度系数ij
A
1 A B 2 C
11
M1M 基 1 l /4 EI
23 dx 24EI
M 基2 图
l /4
22
M 2 M 基2 EI
dx
23 24EI
李廉锟《结构力学》(第5版)(下册)课后习题-第12章 结构动力学【圣才出品】

第12章 结构动力学复习思考题1.怎样区别动力荷载与静力荷载?动力计算与静力计算的主要差别是什么?答:(1)静力荷载:指施力过程缓慢,不致使结构产生显著的加速度,因而可以略去惯性力影响的荷载;动力荷载:指将使结构产生不容忽视的加速度,因而必须考虑惯性力的影响的荷载。
主要差别在于是否考虑惯性力的影响。
(2)计算上的差别:①计算式中是否加入惯性力的数值;②静力计算时,结构处于平衡状态,荷载的大小、方向、作用点及由它引起的结构的内力、位移等各种量值都不随时间而变化;而动力计算时,结构将发生振动,各种量值均随时间而变化;③动力分析方法常与荷载类型有关,而静力分析方法与荷载类型无关。
2.何谓结构的振动自由度?它与机动分析中的自由度有何异同?如何确定结构的振动自由度?答:(1)结构振动的自由度是指结构在弹性变形过程中确定全部质点位置所需的独立参数的数目。
(2)机动分析中的自由度简称静力自由度(又称动力自由度)。
①两者相同点:在数学意义上是一致的,都是强调体系空间质量所需的几何参量的个数。
②不同点:静力自由度是机构移动即刚体位移,排除了各个组成部件的变形运动;而动力自由度是变形位移导致机构位置改变,即体系变形过程质量的运动自由度。
(3)确定结构振动自由度的两种方法:①直接由确定质点位置所需的独立参数数目来判定;②加入最少数量的链杆以限制刚架上所有质点的位置,则该刚架的振动自由度数目即等于所加入链杆的数目。
3.建立振动微分方程有哪两种基本方法?每种方法所建立的方程代表什么条件?答:(1)建立振动微分方程的两种基本方法:刚度法和柔度法。
(2)刚度法代表力的平衡条件,柔度法代表变形协调条件。
4.为什么说结构的自振频率和周期是结构的固有性质?怎样改变它们?答:(1)自振频率和周期是结构的固有性质的原因:结构的自振频率和周期只取决于结构自身的质量和刚度,反映着结构固有的动力特性,而外部干扰力只能影响振幅和初相角的大小并不能改变结构的自振频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节概述一、动力计算的特点和内容1、动力计算的特点“静力荷载”是指其大小、方向和作用位置不随时间而变化的荷载。
这类荷载对结构产生的惯性力可以忽略不计,由它所引起的内力和变形都是确定的。
“动力荷载”是指其大小、方向和作用位置随时间而变化的荷载。
这类荷载对结构产生的惯性力不能忽略,因动力荷载将使结构产生相当大的加速度,由它所引起的内力和变形都是时间的函数。
与静力计算的对比:两者都是建立平衡方程,但动力计算,利用动静法,建立的是形式上的平衡方程。
力系中包含了惯性力,考虑的是瞬间平衡,荷载、内力都是时间的函数。
建立的平衡方程是微分方程。
2、动力计算的目的和内容结构动力计算的目的在于确定结构在荷载作用下产生的最大内力与最大位移,为设计提供可靠的依据。
此外还需求出结构在动力荷载作用下产生的最大速度和加速度,用以判别所设计的结构是否超过规范中的允许值,因为过大的速度和加速度对人工健康、工艺过程和建筑物不利。
结构在动力荷载作用下的计算,要涉及内外两个方面的因素,即结构本身的动力特性和干扰力的变化规律。
所谓结构的动力特性是指结构的自振频率、振型和阻尼,其中阻尼的大小取决于结构的物理性质,它是由试验测定的,而结构的自振频率和振型的计算就构成结构动力计算中一个很重要的组成部分。
至于干扰力的变化规律可事先设定或由统计得到。
结构的动力计算将分为两大类,即自由振动(结构自身的动力特性)和强迫振动(结构受到激励后的动力反应)。
3、动力计算的研究方法理论分析实验研究数学模型结构的质量是连续分布结构的质量离散化无限自由度体系多自由度体系材料性能的测定结构动力相似模型结构固有振动测定振动环境试验联机实验二、动力荷载分类(1) 简谐荷载按正弦函数或余弦函数变化的周期荷载,称为简谐荷载。
P (t )t (2) 一般周期荷载它是指除简谐荷载以外的其它型式的周期荷载。
tP (t )图12-1图12-2(3)冲击荷载这类荷载的特点是在很短的时间内,荷载值急剧增大或急别减小。
例如,锻锤对基础的撞击作用以及爆炸型荷载部属于这类荷载。
因为在冲击荷载作用下.结构很快就达到它的最大反应值,由阻尼所吸收的能量较小,所以阻尼对这类荷载的动力反应的影响是比较小的。
P t P (t )tt r Pt r P 图12-3它们不仅随时间作复杂变化,而且在基本条件不变的情况下,由于偶然因素的影响,两次荷载不会重现同一波形,因而不可能将荷载与时间的函数关系作出精确的数学描述。
如地震荷载、风荷载、海浪作用等。
(4)随机荷载-320-240-160-800801602403200246810时间(S)加速度(g a l )图12-4三、体系振动的自由度确定体系上全部质量位置所需独立参变数的数目称为该体系的振动自由度。
实际结构的质量都是连续分布的,严格地说来都是无限自由度体系。
计算困难,常作简化如下:1、集中质量法把连续分布的质量集中为几个质点,将一个无限自由度的问题简化成有限自由度问题。
m+αm柱mm>>m梁m+αm梁I I2I厂房排架水平振动时的计算简图水平振动时的计算体系θ(t )v (t )u (t )4个自由度m 1m 2m 32个自由度)(x m y (x,t )x无限自由度体系2、广义座标法如简支梁的变形曲线可用三角级数来表示∑==n k k l x k t a t x y 1sin )(),(π用几条函数曲线来描述体系的振动曲线就称它是几个自由度体系,其中l x k πsin ——是根据边界约束条件选取的函数,称为形状函数。
a k (t )——称广义座标,为一组待定参数,其个数即为自由度数,用此法可将无限自由度体系简化为有限自由度体系。
x y x )(.),........(),(21x x x n ϕϕϕa 1,a 2,…….. a n∑==n k k k x a t x y 1)(),(ϕy (x,t )图12-7四、动力计算的方法动力平衡法(达朗伯尔原理))()(t ym t F P =0)()(=-t ym t F P …………..运动方程m设其中)()(t F t y m I =-F P (t )=F I (t )…………..平衡方程F I (t )-惯性力,与加速度成正比,方向相反。
)()(t y m t F P =改写成虚功原理(拉格朗日方程)哈米顿原理(变分方程)}都要用到抽象的虚位移概念)(t y m-图12-9一、运动微分方程的建立1、刚度法m...yd静平衡位置质量m 在任一时刻的位移:k 11.ydmmW弹性力:)()()(1111d st e y k t y k t F +∆-=-=惯性力:)()()(d stI y m t y m t F+∆-=-=W y k y m d st d st=+∆++∆)()(11 (a )上式可以简化为:011=+d d y k y m 或011=+y k ym st∆)(t F I )(t F e dst y t y +∆=)(mgW k st ==∆11(b)刚度系数图12-10第二节单自由度体系的自由振动2、柔度法..m静平衡位置)(t F I 研究结构上质点的位移,建立位移协调方程。
)(t y ..静平衡位置11δ1根据比例关系可得到质点的位移为))(()()(1111t ym t F t y I -==δδ可进一步写成0)()(11=+t ym t y δ(c)由于,故式(b)与式(c)等效。
11111δ=k 上式平衡方程式,由于引用了柔度系数,称柔度法。
柔度系数图12-11二、自由振动微分方程的解它是二阶线性齐次微分方程,其一般解为:tC t B t y ωωsin cos )(+=积分常数B ,C 由初始条件确定。
单自由度体系的自由振动微分方程可改写为02=+y yω 其中11111δωm m k ==设在初始时刻t=0时:)0(y y =0)0(ν=y (d)(f)(e)则由式(e)可求出y B =ων0=C于是,式(e )可以写成tv t y t y ωωωsin cos )(00+=由式可知,动位移是由初位移y 0引起的余弦运动和由初速度v 0引起的正弦运动的合成,为了便于研究合成运动,令ϕωϕcos sin 00A v A y ==(g)式(g)改写成)sin()(ϕω+=t A t y 它表示合成运动仍是一个简谐运动。
其中A 和可由下式确定ϕ⎪⎪⎪⎪⎬⎫=⎪⎭⎫ ⎝⎛+=02020arct anv y v y A ωϕω(h)(i)ytTTTω0v ω0v -yty t∙∙ωϕA-Aty ωcos 0tv ωωsin 0⎪⎭⎫ ⎝⎛+ωϕωt A sin 0y 0y -图12-12三、结构的自振周期和频率由式)sin()(ϕω+=t A t y 及图可见位移方程是一个周期函数。
Ty t∙∙ωϕA-A周期-,2ωπ=T 工程频率-),(21Hz T f πω==园频率-T f ππω22==计算频率和周期的几种形式stgW g m m k ∆====1111111δδωgk mT st ∆==ππ2211图12-13[例12-1] 图示三种不同支承情况的单跨梁,EI =常数,在梁中点有一集中质量m ,当不考虑梁的质量时,试比较三者的自振频率。
ml/2l/2l/2l/2mm l/2l/2[解] 先按前面章节的方法算出此三种情况下的静力位移分别为EIm gl st4831=∆EImgl st768732=∆EImgl st19233=∆然后分别求得三种情况的自振频率为3148ml EI =ω327768ml EI =ω33192ml EI =ω据此可求得2:512.1:1::321=ωωω图12-14[例12-2]试求图示刚架的自振频率。
略去柱的质量。
II EI 1=∞m h1=∆k 1126hEI 26h EI 26h EI 26h EI 312h EI 312h EI 31124hEI k =[解] 先求刚架的刚度系数k 11。
为此,作出刚架横梁发生水平单位位移时的弯矩图,根据横梁的平衡条件可求得1124EI k ==ω于是刚架的自振频率为图12-15T当k 11较大或者m 较小时,周期T 取较低值。
Response Displacement Trace-0.002-0.00100.0010.002012345678910time(secs)Di s p l a c e m e n t (m )D i s p l a c e m e n t (m )四、自由振动反应讨论time (sec)TResponse Displacement Trace-3-2-10123012345678910time(secs)Di s p l a c e m e n t (m )D i s p l a c e m e n t (m )当k 11较小或者m 较大时,周期T 取较大值。
图12-18图12-19建筑物自振周期随着高度增加而增加,下表给出的是周期估计(按照美国规范IBC-2000中的经验公式推算)建筑高度(m)砼抗抗弯框架砼剪力墙180.640.4360 1.58 1.06120-- 1.8240-- 3.0420-- 4.6桥梁T = 6 -15 sec图12-20储水罐图12-21T = 3 -4 sec桥梁自振周期T = 0.5 sec图12-22 T = 1 secT = 2 secT = 5 secT = 10 sec五、简谐自由振动的特性由式)sin()(ϕω+=t A t y 可得,加速度为:)sin()(2ϕωω+-=t A t y )sin()()(2ϕωω+=-=t mA t ym t F I 在无阻尼自由振动中,位移、加速度和惯性力都按正弦规律变化,且作相位相同的同步运动,即它们在同一时刻均达极值,而且惯性力的方向与位移的方向一致。
它们的幅值产生于1)sin(=+ϕωt 时,其值分别为:Ay =02ωA y-= 2ωmA F I=既然在运动的任一瞬时质点都处于平衡状态,在幅值出现时间也一样,于是可在幅值处建立运动方程,此时方程中将不含时间t ,结果把微分方程转化为代数方程了,使计算得以简化。
惯性力为:[例12-3]计算图示体系的自振频率。
A BC D EI=∞l /2l /2lmm =1mm 312=k BC k 1m 2m α..A 1..A 2l k α01I F02I F[解]:单自由度体系,以α表示位移参数的幅值,各质点上所受的力为:αωω2212101l m A m F I ⋅==αωαωωl m l m A m F I ⋅=⋅==2222202212331建立力矩平衡方程0=∑B M 02320201=⨯-⨯+⨯l l k l F l F I I α0232122122=⨯-⨯+⨯l l k l l m l l m ααωαω化简后得km =2ωk =∴ω图12-23mk 11)(t F P (a))()(11t y k t F e -=)(t F P )()(t ym t F I -=(b))(11t F y k ym P =+ 所谓爱迫振动,是指体系在干扰力作用下所产生的振动。
