2013届全国中考数学3年中考2年模拟之15二次根式pdf版50

合集下载

中考试题届复习专题练1-5二次根式3.docx

§1.5二次根式A组2015年全国中考题组一、选择题1．(2015·重庆，3，3分)化简12的结果是() A．4 3 B．2 3 C．3 2 D．2 6解析化简得：23，故B正确．答案 B2．(2015·山东济宁，3，3分)要使二次根式x－2有意义，x必须满足() A．x≤2 B．x≥2 C．x＜2 D．x＞2解析由x－2≥0得：x≥2.故B正确．答案 B3．(2015·江苏淮安，4，3分)下列式子为最简二次根式的是()A. 3B. 4C.8D.1 2解析4＝2，8＝22，12＝22，4，8，12都不是最简二次根式，故选A.答案 A4．(2015·湖北孝感，9，3分)已知x＝2－3，则代数式(7＋43)x2＋(2＋3)x＋3的值是()A．0 B. 3 C．2＋ 3 D．2－ 3解析原式＝(7＋43)(2－3)2＋(2＋3)(2－3)＋3＝49－48＋4－3＋3＝2＋3.故选C.答案 C二、填空题5．(2015·贵州遵义，11，4分)27＋3＝________．解析原式＝33＋3＝4 3. 答案 4 36．(2015·江苏南京，12，3分)计算5×153的结果是________．解析5×153＝5×5＝5. 答案 57．(2015·江苏泰州，12，3分)计算：18－212等于________．解析原式＝32－2＝2 2. 答案 2 2 三、解答题8．(2015·四川凉山州，19，5分)计算：－32＋3×1tan 60°＋|2－3|.解－32＋3×1tan 60°＋|2－3|＝－9＋3×13＋3－2＝－5－ 2.9. (2015·山西，21，6分)阅读与计算：请阅读以下材料，并完成相应的任务．斐波那契(约1170～1250)是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列(按照一定顺序排列着的一列数称为数列)．后来人们在研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．斐波那契数列中的第n 个数可以用15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1＋52n －⎝ ⎛⎭⎪⎫1－52n 表示(其中，n ≥1)．这是用无理数表示有理数的一个范例．任务：请根据以上材料，通过计算求出斐波那契数列中的第1个数和第2个数．解第1个数，当n ＝1时，15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1＋52n －⎝ ⎛⎭⎪⎫1－52n ＝15⎝ ⎛⎭⎪⎫1＋52－1－52＝15×5＝1. 第2个数，当n ＝2时， 15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1＋52n －⎝ ⎛⎭⎪⎫1－52n＝15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1＋522－⎝ ⎛⎭⎪⎫1－522＝15⎝ ⎛⎭⎪⎫1＋52＋1－52⎝ ⎛⎭⎪⎫1＋52－1－52＝15×1×5＝1.B 组 2014～2011年全国中考题组一、选择题1．(2013·上海，1，4分)下列式子中，属于最简二次根式的是 ( ) A.9B.7C.20D.13解析 ∵9＝32＝3，20＝22×5＝25，13＝13＝33，∴9，20，13都不是最简二次根式，7是最简二次根式，故选B. 答案 B2．(2013·广东佛山，5，3分)化简2＋(2－1)的结果是( )A ．22－1B ．2－ 2C ．1－ 2D ．2＋ 2解析2＋(2－1)＝2＋2－1＝22－1，故选A.答案 A3．★(2013·江苏泰州，2，3分)下列计算正确的是( )A．43－33＝1 B.2＋3＝ 5C．212＝ 2 D．3＋22＝5 2解析43－33＝3，∴A错误；∵2与3被开方数不同，不能合并，∴B错误；212＝2×22＝2，∴C正确；3和22一个是有理数，一个是无理数，不能合并，∴D错误．综上所述，选C.答案 C4．(2013·山东临沂，5，3分)计算48－913的结果是 ()A．－ 3 B. 3 C．－113 3 D.113 3解析48－913＝43－33＝ 3.答案 B5．(2014·山东济宁，7，3分)如果ab＞0，a＋b＜0，那么下面各式：①ab＝ab，②a b·ba＝1，③ab÷ab＝－b，其中正确的是()A．①②B．②③C．①③D．①②③解析∵ab＞0，a＋b＜0，∴a，b同号，且a＜0，b＜0，∴ab＞0，ba＞0.ab＝ab.等号右边被开方数小于零，无意义，∴①不正确；ab·ba＝ab·ba＝1，②正确；ab÷ab＝ab·ba＝b2＝－b，∴③正确．故选B.答案 B二、填空题6．(2013·浙江舟山，11，4分)二次根式x－3中，x的取值范围为________．解析由二次根式有意义，得出x－3≥0，解得x≥3.答案x≥37．(2014·福建福州，13，4分)计算：(2＋1)(2－1)＝________.解析由平方差公式可得(2＋1)(2－1)＝(2)2－12＝2－1＝1. 答案 18．(2013·山东泰安，22，3分)化简：3(2－3)－24－︱6－3︱＝________．解析原式＝3×2－(3)2－26－3＋6＝6－3－ 26－3＋6＝－6. 答案－69．(2012·浙江杭州，14，4分)已知a (a －3)＜0，若b ＝2－a ，则b 的取值范围是________．解析由题意知，a >0，∴a >0，∴a －3<0，解得：0<a <3，∴2－3<2－a <2，即：2－3<b <2. 答案 2－3<b <2 三、解答题10．(2013·浙江温州，17，5分)计算：8＋(2－1)＋⎝ ⎛⎭⎪⎫120.解8＋(2－1)＋⎝ ⎛⎭⎪⎫120＝22＋2－1＋1＝3 2.11．(2013·湖北孝感，19，6分)先化简，再求值：1x －y ÷⎝ ⎛⎭⎪⎫1y －1x ，其中x ＝3＋2，y ＝3－ 2. 解1x －y ÷⎝⎛⎭⎪⎫1y －1x ＝1x －y ·xy x －y ＝xy （x －y ）2，当x ＝3＋2，y ＝3－2时，原式＝（3＋2）（3－2）（3＋2－3＋2）2＝18.初中数学试卷鼎尚图文**整理制作。

中考培优专题之二次根式

备战中考之二次根式习题一、单选题（共15题；）1.对于任意的正数m 、n 定义运算※为：m ※n={√m −√n (m ≥n )√m +√n (m <n )),计算（3※2）×（8※12）的结果为（）A. 2﹣4√6B. 2C. 2√5D. 20 2.要使二次根式√3−2x 有意义，则x 的取值范围是（）A. x ⩾32 B. x ⩽32 C. x ⩾23 D. x ⩽23 3.下列各实数中最大的一个是（） A. 5× √0.039 B.3.141πC.√14+√7D. √0.3 + √0.24.已知x 为实数，化简√−x 3−x√−1x的结果为（）A. (x −1)√−xB. (−1−x )√−xC. (1−x )√−xD. (1+x )√−x 5.若√x −1+√x +y =0 ，则x 2005+y 2005 的值为：（）A. 0B. 1C. -1D. 26.等式√xx−3=√x√x−3成立的条件是（） A. x≠3 B. x≥0 C. x≥0且x≠3 D. x>3 7.下列二次根式中，最简二次根式是( ).A. B.C.D.8.已知是正整数，则实数n 的最大值为（）A. 12B. 11C. 8D. 39.如果最简根式 √3a −8 与√17−2a 是同类二次根式,那么使√4a −2x 有意义的x 的取值范围是（） A. x≤10 B. x≥10 C. x ＜10 D. x ＞10 10.已知 y =√4−x +√x −4+3 ，则 yx 的值为（）A. 43 B. −43 C. 34 D. −34 11.若x +y ＝3+2 √2 ，x ﹣y ＝3﹣2 √2 ，则 √x 2−y 2 的值为（） A. 4 √2 B. 1 C. 6 D. 3﹣2 √2 12.函数 y =1x+1−√2−3x 中，自变量 x 的取值范围是（）A. x ≤23 B. x ≥23 C. x <23 且 x ≠−1 D. x ≤23 且 x ≠−113.利用计算器计算时，依次按键下：，则计算器显示的结果与下列各数中最接近的一个是（）A. 2.5B. 2.6C. 2.8D. 2.914.把代数式(a－1) √11−a的a－1移到根号内，那么这个代数式等于（）A. －√1−aB. √a−1C. √1−aD. －√a−115.一个三角形的三边长分别为1，k，4，化简|2k－5|－√k2−12k+36的结果是( )A. 3k－11B. k＋1C. 1D. 11－3k二、填空题（共15题；）16.若|1001−a|+√a−1002=a，则a−10012=________．17.观察下列运算过程：1+√2=√2+1=√2(√2+1)(√2−1)=√2(√2)2−12=√2−1√2+√3=√3+√2=√3√2(√3+√2)(√3−√2)=√3√2(√3)2−(√2)2=√3−√2……请运用上面的运算方法计算：1+√3+√3+√5√5+√7⋯+√2015+√2017√2017+√2019=________．18.如图，数轴上点A表示的数为a，化简：a+√a2−4a+4=________19.√12与最简二次根式5 √a+1是同类二次根式，则a=________．20.读取表格中的信息，解决问题．满足n n n√3+√2≥2014×(√3−√2+1)的n可以取得的最小整数是________．21.已知|6﹣3m|+（n﹣5）2=3m﹣6﹣√(m−3)n2，则m﹣n=________22.若m=√2012−1，则m5﹣2m4﹣2011m3的值是________．23.若√20n是整数，则正整数n的最小值为________．24.已知√a（a﹣√3）＜0，若b=2﹣a，则b的取值范围是________．25.如果（x﹣√x2−2008）（y﹣√y2−2008）=2008，求3x2﹣2y2+3x﹣3y﹣2007=________．26.已知a、b为有理数，m、n分别表示5−√7的整数部分和小数部分，且amn+bn2=1，则2a+b=________.27.若实数x，y，m满足等式√3x+5y−3−m+(2x+3y−m)2=√x+y−2−√2−x−y，则m+4的算术平方根为________．28.若x、y都为实数，且y=2008√x−5+2007√5−x+1，则x2+y=________。

2013届中考数学考前热点冲刺《第5讲数的开方及二次根式》课件新人教版

第5讲┃ 归类示例
此类有意义的条件问题主要是根据：①二次根式的被开方数大于或等于零；②分式的分母不为零等列不等式组，转化为求不等式组的解集．
第5讲┃ 归类示例 ► 类型之三根式的化简与计算
命题角度： 1. 二次根式的性质：两个重要公式，积的算术平方根，商的算术平方根； 2. 二次根式的加减乘除运算．
[点析] 在进行二次根式化简求值时，常常用到整体思想．把 x＋y、x－y、xy 当作整体进行代入．
第5讲┃ 回归教材
中考变式
a2－4a＋4 a＋1 2 [2012· 苏州] 先化简，再求值：＋ 2 · ，其 a－1 a －1 a－2 中 a＝ 2＋1.
a－22 a＋1 a－2 2 2 a 解：原式＝＋ · ＝＋＝ . a－1 a＋1a－1 a－2 a－1 a－1 a－1 2＋1 2＋ 2 当 a＝ 2＋1 时，原式＝＝ . 2 2
第5讲┃ 考点聚焦考点3 二次根式的性质
两个重要的性质 ( a)2＝a(a________) ≥0 a ＝a
2

二次根积的算术式平方根的性商的算术质平方根
＝
a -a
a≥0 a<0
ab＝ a· b(a______(a________， >0 a a b________) ≥0
立方一个数x的________等于a，那么x叫做立方根 3 数a的立方根，记作 a
第5讲┃ 考点聚焦考点2 二次根式的有关概念
二次根式最简二次根式
定义防错提醒
形如 a(________)的式子叫做二次根式 a≥0 a中的 a 可以是数或式， a 一定要大于但或等于 0

二次根式(优选真题60道)-三年(2021-2023)中考数学真题分项汇编(学生版)

专题03二次根式(优选真题60道)一．选择题(共24小题)1(2023•烟台)下列二次根式中，与2是同类二次根式的是()A.4B.6C.8D.122(2023•岳阳)对于二次根式的乘法运算，一般地，有a•b=ab．该运算法则成立的条件是()A.a>0，b>0B.a<0，b<0C.a≤0，b≤0D.a≥0，b≥03(2023•金华)要使x-2有意义，则x的值可以是()A.0B.-1C.-2D.24(2023•巴中)下列运算正确的是()A.x2+x3=x5B.3×2=6C.(a-b)2=a2-b2D.|m|=m5(2023•江西)若a-4有意义，则a的值可以是()A.-1B.0C.2D.66(2023•临沂)设m=515-45，则实数m所在的范围是()A.m<-5B.-5<m<-4C.-4<m<-3D.m>-37(2023•天津)sin45°+22的值等于()A.1B.2C.3D.28(2023•扬州)已知a=5，b=2，c=3，则a、b、c的大小关系是()A.b>a>cB.a>c>bC.a>b>cD.b>c>a9(2023•台州)下列无理数中，大小在3与4之间的是()A.7B.22C.13D.1710(2023•云南)按一定规律排列的单项式：a，2a2，3a3，4a4，5a5，⋯，第n个单项式是() A.n B.n-1a n-1 C.na n D.na n-111(2023•重庆)估计5×6-1 5的值应在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间12(2022•内蒙古)实数a在数轴上的对应位置如图所示，则a2+1+|a-1|的化简结果是()A.1B.2C.2aD.1-2a13(2022•安顺)估计(25+52)×15的值应在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间14(2022•广州)代数式1x+1有意义时，x应满足的条件为()A.x≠-1B.x>-1C.x<-1D.x≤-115(2022•聊城)射击时，子弹射出枪口时的速度可用公式v=2as进行计算，其中a为子弹的加速度，s为枪筒的长．如果a=5×105m/s2，s=0.64m，那么子弹射出枪口时的速度(用科学记数法表示)为()A.0.4×103m/sB.0.8×103m/sC.4×102m/sD.8×102m/s16(2022•青岛)计算(27-12)×13的结果是()A.33B.1C.5D.317(2022•绥化)若式子x+1+x-2在实数范围内有意义，则x的取值范围是() A.x>-1 B.x≥-1 C.x≥-1且x≠0 D.x≤-1且x≠018(2021•内江)函数y=2-x+1x+1中，自变量x的取值范围是()A.x≤2B.x≤2且x≠-1C.x≥2D.x≥2且x≠-119(2021•泰州)下列各组二次根式中，化简后是同类二次根式的是()A.8与3B.2与12C.5与15D.75与2720(2021•大连)下列计算正确的是()A.(-3)2=-3B.12=23C.3-1=1D.(2+1)(2-1)=321(2021•益阳)将452化为最简二次根式，其结果是()A.452B.902C.9102D.310222(2021•娄底)2、5、m是某三角形三边的长，则(m-3)2+(m-7)2等于() A.2m-10 B.10-2m C.10 D.423(2021•河北)与32-22-12结果相同的是()A.3-2+1B.3+2-1C.3+2+1D.3-2-124(2021•常德)计算：5+12-1•5+12=()A.0B.1C.2D.5-12二．填空题(共26小题)25(2023•滨州)一块面积为5m2的正方形桌布，其边长为 5m　．26(2023•陕西)如图，在数轴上，点A表示3，点B与点A位于原点的两侧，且与原点的距离相等．则点B表示的数是 -3　．27(2023•枣庄)计算(2023-1)0+12-1=　3　．28(2023•安徽)计算：38+1=　3　．29(2023•广安)16的平方根是．30(2023•自贡)请写出一个比23小的整数 4(答案不唯一)　．31(2023•天津)计算(7+6)(7-6)的结果为 1　．32(2023•永州)已知x为正整数，写出一个使x-3在实数范围内没有意义的x值是 1(答案也可以是2)　．33(2023•连云港)计算：(5)2=　5　．34(2022•朝阳)计算：63÷7-|-4|=　-1　．35(2022•日照)若二次根式3-2x在实数范围内有意义，则x的取值范围为 x≤32　．36(2022•青海)若式子1x-1有意义，则实数x的取值范围是．37(2022•北京)若x-8在实数范围内有意义，则实数x的取值范围是．38(2022•哈尔滨)计算3+313的结果是3　．39(2022•包头)若代数式x+1+1x在实数范围内有意义，则x的取值范围是．40(2022•荆州)若3-2的整数部分为a，小数部分为b，则代数式(2+2a)•b的值是．41(2022•常德)要使代数式xx-4有意义，则x的取值范围为．42(2022•随州)已知m为正整数，若189m是整数，则根据189m=3×3×3×7m=33×7m可知m有最小值3×7=21．设n为正整数，若300n是大于1的整数，则n的最小值为，最大值为．43(2022•天津)计算(19+1)(19-1)的结果等于．44(2022•泰安)计算：8•6-343=　23　．45(2022•遂宁)实数a、b在数轴上的位置如图所示，化简|a+1|-(b-1)2+(a-b)2=．46(2022•内蒙古)已知x，y是实数，且满足y=x-2+2-x+18，则x⋅y的值是　12　．47(2022•六盘水)计算：12-23=．48(2022•邵阳)若1x-2有意义，则x的取值范围是．49(2021•铜仁市)计算(27+18)(3-2)=．50(2021•荆州)已知：a=12-1+(-3)0，b=(3+2)(3-2)，则a+b=．三．解答题(共10小题)51(2023•内江)计算：(-1)2023+12-2+3tan30°-(3-π)0+|3-2|．52(2023•十堰)计算：|1-2|+12-2-(π-2023)0．53(2023•岳阳)计算：|-3|+4+(-2)×1．54(2023•上海)计算：38+12+5-13-2+|5-3|．55(2023•陕西)计算：5×(-10)-17-1+|-23|．56(2023•岳阳)计算：22-tan60°+|3-1|-(3-π)0．57(2023•眉山)计算：(23-π)0-|1-3|+3tan30°+-1 2-2．58(2023•武威)计算：27÷32×22-62．59(2022•陕西)计算：5×(-2)+2×8-13-1．60(2022•襄阳)先化简，再求值：(a+2b)2+(a+2b)(a-2b)+2a(b-a)，其中a=3-2，b=3 +2．。

全国各地名校2013年中考数学5月试卷分类汇编二次根式

二次根式一、选择题1、（2013年某某荆州模拟题）实数a 、b 在轴上的位置如图所示，且|a |＞|b |，则化简-2a ∣a +b ∣的结果为（ ▲ ）A ． 2a +bB ． ﹣2a +bC ．bD ．2a ﹣b答案：Ｃ2、(2013年某某省模拟六)计算221－631＋8的结果是…………………【】 A ．32－23 B ．5－2 C ．5－3D ．22答案：A3、(2013年某某省模拟七)4的算术平方根是…………………【】A ．2B ．±2C ．16D ．±16 答案：A4、(2013年某某省模拟七)实数a 、b 在轴上的位置如图所示，且|a |＞|b |，则化简-2a ∣a +b ∣的结果为……【】A ． 2a +bB ． ﹣2a +bC ．bD ．2a ﹣b 答案：B5、(2013年某某省模拟八)已知211a a a a--=，则a 的取值X 围是…………【】 A ．a ≤0； B ．a ＜0； C ．0＜a ≤1； D ．a ＞0 答案：C6、(2013年某某荆州模拟6)函数1y x =-的自变量x 的取值X 围是（ ▲ ）A ．x ≥1B ．x ≥1且x ≠2C ．x >1D ．x >1且x ≠2 答案：C7、（2013年某某奉贤区二模）下列二次根式中最简二次根式是（▲）第3题图A ．12-a ； B ．ba； C ．b a 2； D ．a 9；答案：A8、（2013年某某长宁区二模)下列二次根式中，最简二次根式是（）.A. 4B. 6C. 8D. 129、．（2013某某市景山中学模拟题）要使式子x -2有意义，则x 的取值X 围是（ ◆ ）A ．0>xB ．2-≥xC ．2≥xD ．2≤x 答案：C10、(2013年某某某某一模)的说法中，错误．．的是（） A是无理数B是15的算术平方根 C ．15D．34<<答案：C11C ）A ．2B ．4C ．2±D ．4±12.2-3)(的值是【 D 】A. －3B. 3或－3C. 9D. 313、（2013x 的取值X 围是( )A ．x ≥1B ．x ≤1C ．x ＞1D ．x ≠1答案：A14、(2013年某某省某某市一模)x 的取值X 围是（）A ．12x ≠ B ．x ≥12 C ．x ≤12 D ．x ≠-12答案：B15、（2013某某某某二模）1的结果是（）【答案】CCBA16、（2013某某一中一模）8．估算110+的值在A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间【答案】C17. （2013某某黄浦二摸）下列二次根式中，2的同类根式是（A ）4 （B ）6 （C ）8 （D ） 10答案：C18.．（2013年某某浦东新区二摸）如果()12212-=-a a ，那么（A ）21<a ；（B ）21≤a ；（C ）21>a ；（D ）21≥a ．答案：D19．（2013年某某徐汇区二摸）下列二次根式中与3是同类二次根式的是Ａ．6；Ｂ．8；Ｃ．12；Ｄ．18．答案：C20、（2013某某五校联考二模）若整数a ，m ，n 满足n m a -=-242，则这样的a ，m ，n 的取值（）A 有一组B 有两组C 多于两组D 不存在答案：B21、（2013某某某某特长展示）下列各式（题中字母均为正实数）中化简正确的是（）A ．213419=B ．x x 41421=C ．ab ab =2D =D22、（2013某某沁阳市九年级第一次质量检测）有意义,则x 的取值X 围是【】A.21≥xB.21≤xC.21-≤xD.21-≥x D23、（2013某某沁阳市九年级第一次质量检测）下列二次根式中属于最简二次根式的是【】A ．44+aB ．48C ．14D ．b aC24、（2013某某沁阳市九年级第一次质量检测）下列等式成立的是【】 A ． B.C ．D ． =9A25、（201324x -X 围内有意义，则x 的取值X 围为( ).≥2 B. x ≤2 C.x ≥-2≤-2 A26、（2013年某某某某模拟）下列说法中：①若式子x -2有意义，则x ≥2.②已知∠α=27°，则∠α的余角是63°. ③已知x=-1是方程x 2-bx+5=0 的一个实数根，则b 的值为6. ④在反比例函数xk y 2-=中，若x ＞0 时，y 随x 的增大而增大，则k 的取值X 围是k ＜2. 其中正确命题有（） A. 1个 B. 2个个 D. 4个答案：B27.（2013年某某某某市四模）下列计算结果正确的是： 257=3223=2510= 25105=答案：C28.（2013年某某拱墅区一模）下列计算或化简正确的是（）A ．2()a a b ab a ---=-B ．235a a a +=C ．4513833+=D ．93=± 答案：A二、填空题1、（2013年某某模拟二）若21(3)0x y y +-++=，则x y -的值为．答案：7 2.计算a22a－8a 3(a ＞0)＝．答案：－a 2a3．（2013年房山区一模）在函数1y x =+中，自变量x 的取值X 围是．答案：x ≥1-；4、(2013年某某省模拟七)函数31x y x -=+的自变量x 的取值X 围是__________________. 答案：3x ≥-且1x ≠5、(2013年某某荆州模拟5)对于X Y ，定义一种新运算“”：*X Y aX bY =+，其中a b ，为常数，等式右边是通常的加法和乘法的运算．若21482=+---b a a a 成立，那么2*3=▲ __．答案： 16、（2013年聊城莘县模拟）若代数式有意义，则的取值X 围为__________．答案：且a ≠17、（2013年某某长宁区二模)方程：31=-x 的解是. 答案：x =108、(2013年某某某某一模)计算(2＋1)(2－2)＝ ▲ ．答案： 29、(2013年某某某某一模)计算答案： 610、(2013年某某某某一模)计算：2＋8＝▲．答案：3 211、(2013年某某省某某市模拟) 与2的积为正整数的数是____________（写出一个即可）（原创）答案：2（答案不唯一）12、(2013北仑区一模)14. 当x ▲时，二次根式3-x 在实数X 围内有意义．【答案】3≥x三、解答题1、计算：()()0201320131-+-解：()()8120132013--+-2211--= ……………3分(每化对一个给1分) 22-=…………………2分2、（2013某某沁阳市九年级第一次质量检测）（8分）计算 32－512＋618解：原式=22322524+-=23.。

2013届全国中考数学3年中考2年模拟之专题突破：11实数pdf版

能力要求能记住各个概念，运用概念进行判断．能说明任意两个有理数之间的大小关系．能利用有理数运算法进行运算．能进行有理数的混合运算．利用有效数字、科学记数法表示当下热点问题．能利用根式概念进行判断．
能解释实数与数轴的一一对应关系．能利用估算思想估算一个无理数的大致大小．能利用运算律快速进行实数的运算．
１２２１ · 湖北鄂州）计算－２等于８．（２０１１＋（－２）－－２Ａ．５Ｂ．１（．）Ｃ．－１Ｄ．－５Ａ．２Ｂ．－２ ·浙江杭州）计算（））的结果是（７．（２０１２２－３＋（－１．）Ｃ．６Ｄ．１０Ａ．－２Ｂ．０小明家冰箱冷冻室温度为－５℃，调高１９．（２０１１· 四川乐山）Ｃ．１Ｄ．２４℃后的温度为（．） ·山东济宁）在数轴上到原点距离等于２的点所表示的８．（２０１２Ａ．４℃ Ｂ．９℃ 数是（．）Ｃ．－１℃ Ｄ．－９℃ Ａ．－２Ｂ．２２（ · 浙江舟山）的绝对值是（０．２０１１－６．）Ｃ．± ２Ｄ．不能确定Ａ．－６Ｂ．６ ·四川乐山）规定收入为正，支出为负，收入５９．（２０１２００元记作１１元，那么支出元记作（）５００２３７．Ｃ．Ｄ．－６６Ａ．－５００元Ｂ．－２３７２ ·浙江宁波）下列各数中是正整数的是（１．（２０１１．）Ｃ．２３７元Ｄ．５００元Ａ．－１Ｂ．２ ·陕西）如果零上５℃ 记作＋那么零下７℃ 可记１０．（２０１２５℃，Ｃ．０．５Ｄ．２槡作（．）３２２之值为（２ ·台北）计算（））２．（２０１１－３＋５－（－２．）Ａ．－７℃ Ｂ．＋７℃ Ａ．２Ｂ．５Ｃ．＋１２℃ Ｄ．－１２℃ Ｃ．－３Ｄ．－６２的值为（ ·广西玉林）计算２．（２０１２．１１）７ ·台北）计算４）．（２０１１ ÷（－１．６＋ ÷ ２．５之值为（．３）Ａ．１Ｂ．２２４Ｃ．４Ｄ．８Ａ．－１．１Ｂ．－１．８（ · 安徽）下面的数中，与和为的数是（）１２．２０１２－３０．Ｃ．－３．２Ｄ．－３．９Ａ．３Ｂ．－３（ · 贵州贵阳）如果盈利记为那么亏损６２４．２０１１１０％＋１０％，％１１记为（）．Ｃ．Ｄ．－３３Ａ．－１６％Ｂ．－６％ ·台湾）已知某公司去年的营业额为四千零七十亿元，１３．（２０１２Ｃ．＋６％Ｄ．＋４％则此营业额可用下列何者表示？（．）２（ ·上海）下列分数中，能化为有限小数的是（５．２０１１．）９元１０元Ａ．４．０７ × １０Ｂ．４．０７ × １０１１１１元１２元Ａ．Ｂ．Ｃ．４．０７ × １０Ｄ．４．０７ × １０３５（ · 天津）据某域名统计机构公布的数据显示，截止１４．２０１２２０１２１１Ｃ．Ｄ．７９年５月２我国“ ” 域名注册量约为５居全球１日，犖犈犜６００００个，（ · 湖南湘潭）下列等式正确的是（２６．２０１１．第三位，用科学记数法表示为（））．５４（）Ａ．－２＝２Ｂ．－－１＝－１｜｜Ｂ．５６ × １０Ａ．５６０ × １０５６１Ｃ．５．６ × １０Ｄ．０．５６ × １０）Ｃ．１ ÷（－３＝Ｄ．－２ × ３＝６３ ·北京）首届中国（北京）国际服务贸易交易会（京交１５．（２０１２２的结果是（ ·福建莆田）计算（）７．（２０１１－３．）于２本届京交会期间签订项目成交２会）０１２年６月１日闭幕，Ａ．－６Ｂ．６总金额为６将６０１１０００００００美元，０１１０００００００用科学记Ｃ．－９Ｄ．９数法表示为（）．（ · 湖南常德）年常德比上年８．２０１０２００８ＧＤＰ为１０５０亿元，２９９Ａ．６．０１１ × １０Ｂ．６０．１１ × １０增长１提前两年实现了市委、市政府在 “ 十一五规划 ” ３．２％，１０１１Ｃ．６．０１１ × １０Ｄ．０．６０１１ × １０中提出“ 到２的目标．如果按此增０１０年全年ＧＤＰ．（２０１２长速度，那么我市年的为（）２０１０ＧＤＰ．襄阳” ，能搜索到与之相关的结果个数约有２，这个数３６０００２２Ａ．１０５０ ×（１＋１３．２％）Ｂ．１０５０ ×（１－１３．２％）用科学记数法表示为（．）２Ｃ．１０５０ ×（１３．２％）Ｄ．１０５０ ×（１＋１３．２％）３３Ａ．２．３６ × １０Ｂ．２３６ × １０（ · 江苏南京）如图，下列各数中，数轴上点９．２０１０犃表示的可２５６Ｃ．２．３６ × １０Ｄ．２．３６ × １０能是（．） ·湖南衡阳）１７．（２０１２２０１２年我省各级政府将总投入５９４亿元教育经费用于教育强省战略，将５保留９４亿用科学记数法（（第２９题）两个有效数字）表示为（）．１０１０Ａ．５．９４ × １０Ｂ．５．９ × １０Ａ．４的算术平方根Ｂ．４的立方根１１１０的算术平方根Ｃ．５．９ × １０Ｄ．６．０ × １０Ｃ．８Ｄ．８的立方根

两年中考模拟2020年中考数学：二次根式(学生版)

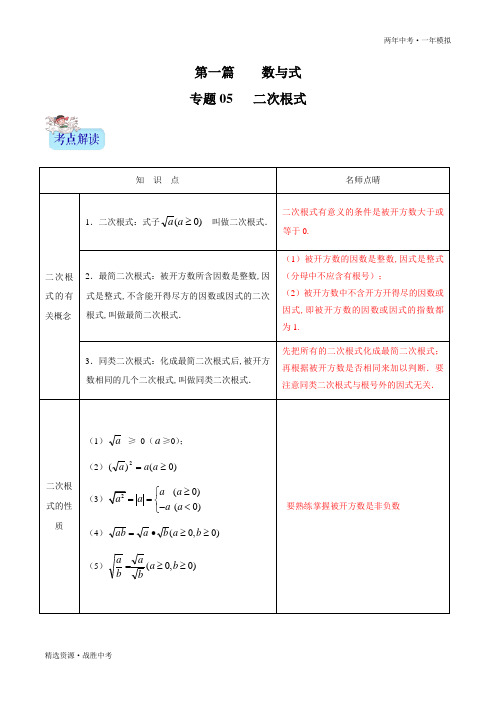
第一篇数与式专题05二次根式知识点名师点晴二次根式的有关概念1．二次根式：式子)0(≥aa叫做二次根式．二次根式有意义的条件是被开方数大于或等于0.2．最简二次根式：被开方数所含因数是整数,因式是整式,不含能开得尽方的因数或因式的二次根式,叫做最简二次根式．（1）被开方数的因数是整数,因式是整式（分母中不应含有根号）；（2）被开方数中不含开方开得尽的因数或因式,即被开方数的因数或因式的指数都为1.3．同类二次根式：化成最简二次根式后,被开方数相同的几个二次根式,叫做同类二次根式．先把所有的二次根式化成最简二次根式；再根据被开方数是否相同来加以判断．要注意同类二次根式与根号外的因式无关．二次根式的性质（1）a≥0（a≥0）；（2）)0()(2≥=aaa（3）2(0)(0)a aa aa a≥⎧==⎨-<⎩（4）)0,0(≥≥•=babaab（5）)0,0(≥≥=bababa要熟练掌握被开方数是非负数二次根式的运算（1）二次根式的加减法（2）二次根式的乘除法二次根式的乘法：a b⋅＝ab（a≥0,b≥0）．二次根式的除法：ab＝ba（a≥0,b＞0）1.二次根式的加减法就是把同类二次根式进行合并；2.二次根式的乘除法要注意运算的准确性．归纳1：二次根式的意义及性质基础知识归纳：二次根式有意义的条件是被开方数大于或等于0．注意问题归纳：1．首先考虑被开方数为非负数,其次还要考虑其他限制条件,这样就转化为解不等式或不等式组问题,如有分母时还要注意分式的分母不为0．2、利用二次根式性质时,如果题目中对根号内的字母给出了取值范围,那么应在这个范围内对根式进行化简,如果题目中没有给出明确的取值范围,那么应注意对题目条件的挖掘,把隐含在题目条件中所限定的取值范围显现出来,在允许的取值范围内进行化简．【例1】（2019云南,第10题,4分）要使12x+有意义,则x的取值范围为（）A．x≤0B．x≥﹣1C．x≥0D．x≤﹣1【例2】（2018四川省凉山州,第23题,5分）当﹣1＜a＜0时,则221144a aa a⎛⎫⎛⎫+---+=⎪ ⎪⎝⎭⎝⎭．归纳 2：最简二次根式与同类二次根式基础知识归纳： 1．最简二次根式被开方数所含因数是整数,因式是整式,不含能开得尽方的因数或因式的二次根式,叫做最简二次根式． 2．同类二次根式化成最简二次根式后,被开方数相同的几个二次根式,叫做同类二次根式．注意问题归纳：最简二次根式的判断方法：1．最简二次根式必须同时满足如下条件：（1）被开方数的因数是整数,因式是整式（分母中不应含有根号）；（2）被开方数中不含开方开得尽的因数或因式,即被开方数的因数或因式的指数都为1． 2．判断同类二次根式：先把所有的二次根式化成最简二次根式；再根据被开方数是否相同来加以判断．要注意同类二次根式与根号外的因式无关．【例3】（2019山西省,第4题,3分）下列二次根式是最简二次根式的是（） A ．12B ．127 C ．8 D ．3归纳 3：二次根式的运算基础知识归纳：（1）．二次根式的加减法：实质就是合并同类二次根式．合并同类二次根式：在二次根式的加减运算中,把几个二次根式化为最简二次根式后,若有同类二次根式,可把同类二次根式合并成一个二次根式．（2）．二次根式的乘除法二次根式的乘法：ab b a =⋅（a ≥0,b ≥0）．二次根式的除法：b a ba =（a ≥0,b ＞0）．注意问题归纳：正确把握运算法则是解题的关键【例4】（2018山东省聊城市,第8题,3分）下列计算正确的是（） A ．310﹣25=5 B ．711•（117÷111）=11 C ．（75﹣15）÷3=25 D ．1183﹣389=2归纳 4：二次根式混合运算基础知识归纳：先乘方,再乘除,最后加减,有括号的先算括号里的（或先去括号）．注意问题归纳：注意运算顺序．【例5】（2019辽宁省大连市,第17题,9分）计算：（3-2）212++613．【例6】（2019湖北省宜昌市,第14题,3分）古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式：如果一个三角形的三边长分别是a ,b ,c ,记p 2a b c++=,那么三角形的面积为S ()()()p p a p b p c =---．如图,在△ABC 中,∠A ,∠B ,∠C 所对的边分别记为a ,b ,c ,若a =5,b =6,c =7,则△ABC 的面积为（）A ．66B ．63C ．18D ．192归纳5：二次根式运算中的技巧基础知识归纳：1．二次根式的被开方数是非负数；2．非负数的性质．注意问题归纳：【例7】（2019湖北省随州市,第9题,3分）“分母有理化”是我们常用的一种化简的方法,如：()()()()232323232323+++==--+7+43,除此之外,我们也可以用平方之后再开方的方式来化简一些有特点的无理数,如：对于3535+--,设x3535=+--,易知3535+-＞,故x＞0,由x2=（3535+--）2=35++35--2()()3535+-=2,解得x2=,即35352+--=．根据以上方法,化简3263363332-+--++后的结果为（）A．5+36B．56+C．56-D．5﹣36【2019年题组】一、选择题1．（2019四川省泸州市,第5题,3分）函数y24x=-的自变量x的取值范围是（）A．x＜2B．x≤2C．x＞2D．x≥22．（2019广安,第2题,3分）下列运算正确的是（）A．a2+a3=a5B．3a2•4a3=12a6C．533-=5D．236⨯=3．（2019山东省淄博市,第7题,4分）如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为（）A2B．2C．2D．64．（2019聊城,第6题,3分）下列各式不成立的是（）A=B===5D=C5．（2019广西河池市,第3题,3分）下列式子中,为最简二次根式的是（）A B C D6．（2019南通,第2题,3的结果是（）A．B．C．D．7．（2019江苏省常州市,第6题,2分）下列各数中与2）A．2B．2C D．2在实数范围内有意义,则x的取值范围是（）8．（2019湖北省黄石市,第6题,3分）若式子2x-A．x≥1且x≠2B．x≤1C．x＞1且x≠2D．x＜1 9．（2019湖南省常德市,第3题,3分）下列运算正确的是（）=A=B=C=-2D10．（2019湖南省株洲市,第2题,3=（）A．B．4C D．二、填空题11．（2019吉林省长春市,第9题,3分）计算：=．12．（2019四川省巴中市,第11题,4分）函数y=的自变量x的取值范围．13．（2019天津,第14题,31）1）的结果等于．14．（2019安徽省,第11题,5的结果是．15．（2019山东省临沂市,第15题,3tan 45°= ．16．（2019滨州,第13题,5分）计算：（12-）﹣2﹣2|= ．17．（2019山东省菏泽市,第10题,3分）已知x =,那么x 2﹣x 的值是．18．（2019青岛,第9题,3-）0= ．19．（2019南京,第8题,2的结果是．20．（2019江苏省扬州市,第13题,3分）计算：2）20182）2019的结果是． 21．（2019湖南省益阳市,第18题,4分）观察下列等式：①3﹣=1）2,②5﹣=2,③7﹣=-2,… 请你根据以上规律,写出第6个等式．22．（2019辽宁省营口市,第13题,3和,则这个长方形的面积为．23．（2019四川省内江市,第22题,6分）若|1001﹣a |=a ,则a ﹣10012= ． 24．（2019枣庄,第18题,4分）观察下列各式：=1112+=⨯1+（112-=1123+=⨯1+（1123-=1134+=⨯1+（1134-）,… 请利用你发现的规律,计算：+L 其结果为．三、解答题25．（2019湖南省长沙市,第19题,6分）计算：|（12）﹣12cos 60°．26．（2019四川省南充市,第17题,6分）计算：（1﹣π）0）﹣1．27．（2019江苏省泰州市,第17题,12分）（1）计算：（182-）6⨯；（2）解方程：252x x -+-3332x x -=-． 28．（2019内蒙古呼和浩特市,第17题,10分）计算（1）计算（112）÷（34-）312+⨯-2()13--；（2）先化简,再求值：（2222532x y x x y y x ++--）()3x x y ÷-,其中x =33,y 12=． 29．（2019内蒙古赤峰市,第24题,12分）阅读下面材料：我们知道一次函数y =kx +b （k ≠0,k 、b 是常数）的图象是一条直线,到高中学习时,直线通常写成Ax +By +C =0（A ≠0,A 、B 、C 是常数）的形式,点P （x 0,y 0）到直线Ax +By +C =0的距离可用公式d 0022Ax By C A B++=+计算．例如：求点P （3,4）到直线y =﹣2x +5的距离．解：∵y =﹣2x +5,∴2x +y ﹣5=0,其中A =2,B =1,C =﹣5,∴点P （3,4）到直线y =﹣2x +5的距离为： d 002222231455521Ax By C A B ++⨯+⨯-====++ 根据以上材料解答下列问题：（1）求点Q （﹣2,2）到直线3x ﹣y +7=0的距离；（2）如图,直线y =﹣x 沿y 轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离．【2018年题组】一、选择题1．（2018四川省达州市,第2题,324x +x 的取值范围是（） A ．x ＜﹣2 B ．x ≤﹣2 C ．x ＞﹣2 D ．x ≥﹣22．（2018山东省日照市,第4题,3分）若式子22(1)m m +-有意义,则实数m 的取值范围是（） A ．m ＞﹣2 B ．m ＞﹣2且m ≠1 C ．m ≥﹣2 D ．m ≥﹣2且m ≠1 3．（2018云南省曲靖市,第6题,4分）下列二次根式中能与23合并的是（）A ．8B ．13C ．18D ．9 4．（2018内蒙古赤峰市,第7题,3分）代数式3x -+11x -中x 的取值范围在数轴上表示为（） A ． B ． C ．D ．5．（2018台湾省,第7题,3分）算式6×（3﹣1）之值为何？（） A ．26- B ．21- C ．26- D ．1 6．（2018四川省德阳市,第4题,3分）下列计算或运算中,正确的是（） A ．22aa = B ．1882-= C ．615÷23=345 D ．﹣3327= 7．（2018四川省绵阳市,第6题,3分）等式3311x x x x --=++成立的x 的取值范围在数轴上可表示为（） A ． B ．C ．D ．8．（2018江苏省无锡市,第1题,3分）下列等式正确的是（）A ．32=3B 2(3)-﹣3C 33=3D ．32=﹣39．（2018江苏省泰州市,第2题,3分）下列运算正确的是（）A ．235B ．183C ．235D ．21210．（2018浙江省临安区,第4题,3()22-的结果是（）A ．﹣2B ．±2C ．2D ．411．（2018兰州,第4题,4分）下列二次根式中,是最简二次根式的是（） A ．18B 13C 27D 12 ．．．12．（2018重庆市,第7题,4分）估计（230﹣24）•16的值应在（） A ．1和2之间 B ．2和3之间 C ．3和4之间 D ．4和5之间 13．（2018黑龙江省绥化市,第5题,3分）若y =12xx-有意义,则x 的取值范围是（） A ．x ≤12且x ≠0 B ．x ≠12 C ．x ≤12D ．x ≠0 二、填空题14．（2018北京,第10题,2分）若x 在实数范围内有意义,则实数x 的取值范围是．15．（2018四川省凉山州,第13题,4分）式子23x x --有意义的条件是． 16．（2018四川省巴中市,第13题,3分）已知|sinA 12-|2(3)tanB +-=0,那么∠A +∠B = ． 17．（2018天津市,第14题,3分）计算（6+3）（6﹣3）的结果等于．18．（2018山东省烟台市,第14题,3分）12与最简二次根式51a +是同类二次根式,则a = ． 19．（2018山东省莱芜市,第15题,4分）如图,正三角形和矩形具有一条公共边,矩形内有一个正方形,其四个顶点都在矩形的边上,正三角形和正方形的面积分别是23和2,则图中阴影部分的面积是．20．（2018山西省,第11题,3分）计算：（32+1）（32-1）= ．21．（2018广州,第15题,3分）如图,数轴上点A 表示的数为a ,化简：a +244a a -+= ．22．（2018山东省枣庄市,第15题,4分）我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a ,b ,c ,则该三角形的面积为S =2222221[)42a b c a b ⎛⎤+-- ⎥⎝⎦．现已知△ABC 的三边长分别为1,2,5,则△ABC 的面积为．23．（2018山东省滨州市,第20题,5分）观察下列各式：2211112++112⨯2211123++123⨯,2211134++134⨯,...... 请利用你所发现的规律,2211112++2211123++2211134++ (2211)1910++,其结果为．24．（2018贵州省毕节市,第20题,5分）观察下列运算过程：()()()()()222212112212121213232322332323232====+++----====+++--L L请运用上面的运算方法计算：1335572015201720172019++++++L = ．三、解答题25．（2018辽宁省大连市,第17题,9分）计算：3）248+2﹣2．26．（2018陕西省,第15题,5分）计算：36）2﹣1|+（5﹣2π）0．27．（2018湖北省襄阳市,第17题,6分）先化简,再求值：（x +y ）（x ﹣y ）+y （x +2y ）﹣（x ﹣y ）2,其中x 3y =2328．（2018广西玉林市,第20题,6分）先化简再求值：（a ﹣22ab b a -）÷22a b a-,其中a 2b =12．一、选择题1．（2019保定二模,第2题,32x -x 的取值范围是（） A ．x ＞2 B ．x ≥2 C ．x =2 D ．x ≠22．（2019东西湖区模拟,第2题,32x +,则x 的取值范围是（） A ．x ＞﹣2 B ．x ≥﹣2 C ．x ＜﹣2 D ．x ≤﹣2 3．（2019重庆八中模拟,第9题,422441(23)x x x -+-得（） A ．2 B ．﹣4x +4 C ．﹣2 D ．4x ﹣4二、填空题4．（2019丰台区一模,第9题,22x -,则x 的取值范围是． 5．（2019长春二模,第9题,317最接近的整数是． 6．（2019长春四模,第9题,326= ．7．（2019武侯区二诊,第21题,4分）已知x 135=,y 135=,则代数式x 2﹣2xy +y 2的值是．8．（2019玄武区二模,第10题,2133的结果是． 9．（2019高淳区二模,第9题,2分）23x -,则x 的取值范围是． 10．（2019高淳区二模,第10题,241233⨯的结果是． 11．（2019邢台二模,第17题,31273= ． 12．（2019河南省实验中学模拟,第11题,3分）化简：(0223242+= ． 13．（2019东西湖区模拟,第11题,316的结果是． 14．（2019松滋市三模,第11题,5分）计算：21）21）= ．三、解答题15．（2019大连二模）计算：)1111()3--16．（2019碑林区校级模拟）计算：2﹣1+（π﹣3）0﹣|4|．17．（2019鄂州模拟）计算：（1）⎛÷ ⎝（2）())2122+．18．（2019开平区一模）在学习二次根式时,===（1）假设说思发现的规律是正确的,=后面连续的两个等式；（2）用字母表示思思发现的规律；（3）请你给出这个结论的一般性的证明．19．（2019重庆模拟）我们将、）称为一对“对偶式”,因为+=2）2=a ﹣b ,）==23==+,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化根据以上材料,理解并运用材料提供的方法,解答以下问题：（1、“＜”或“=”填空）；（2）已知x=y =求x 2+y 2的值；（3++L=,求2a2﹣8a+1的值”时,小明是这样分析与解答的：20．（2019滦南县一模）在解决问题“已知a===2,∴a﹣2=∴（a﹣2）2=3,a2﹣4a+4=3,∴a2﹣4a=﹣1,∴2a2∵a﹣8a+1=2（a2﹣4a）+1=2×（﹣1）+1=﹣1．请你根据小明的分析过程,解决如下问题：（1=求3a2﹣6a﹣1的值．（2）若a21．（2019广水市模拟）阅读材料：小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+=（12．善于思考的小明进行了以下探索：设a+=（m+2（其中a,b,m,n均为整数）,则有a+=m2+2n2+2,∴a=m2+2n2,b=2mn．这样小明就找到了一种把类似a+的式子化为平方式的方法．请你仿照小明的方法解决下列问题：（1）当a,b,m,n均为正整数时,若a+=（m+2,用含m,n的式子分别表示a,b,得a= ,b= ；（2）利用所探索的结论,找一组正整数a,b,m,n填空：+ =（ + 2；（3）若a+=（m+2,且a,m,n均为正整数,求a的值．（4．22．（2019,小亮的解题过程如下：解：原式==L①=L②=（2﹣1L③10=L L ④（1）老师认为小亮的解法有错,请你指出：小亮是从第步开始出错的；（2）请你给出正确的解题过程．23．（2019杏花岭区校级三模）阅读下列材料,并完成相应的任务．古希腊的几何学家海伦在他的著作《度量论》一书中给出了利用三角形三边之长求面积的公式﹣﹣﹣﹣海伦公式S ()()()p p a p b p c =---（其中a ,b ,c 是三角形的三边长,2a b cp ++=,S 为三角形的面积）,并给出了证明例如：在△ABC 中,a =3,b =4,c =5,那么它的面积可以这样计算： ∵a =3,b =4,c =5,∴2a b cp ++==6,∴S ()()()6321p p a p b p c =---=⨯⨯⨯=6事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．根据上述材料,解答下列问题：如图,在△ABC 中,BC =7,AC =8,AB =9 （1）用海伦公式求△ABC 的面积；（2）如图,AD 、BE 为△ABC 的两条角平分线,它们的交点为I ,求△ABI 的面积．24．（2019九龙坡区校级模拟）先阅读,再解答问题．恒等变形,是代数式求值的一个很重要的方法,利用恒等变形,可以把无理数运算转化为有理数运算,可以把次数较高的代数式转化为次数较低的代数式．如当x 31=+时,求312x -x 2﹣x +2的值,为解答这题,若直接把x 31=代入所求的式中,进行计算,显然很麻烦．我们可以通过恒等变形,对本题进行解答．方法一将条件变形．因x 31=,得x ﹣13=x ﹣1）的表达式．原式12=（x 3﹣2x 2﹣2x ）+2 12=[x 2（x ﹣1）﹣x （x ﹣1）﹣3x ]+212=[x （x ﹣1）2﹣3x ]+2 12=（3x ﹣3x ）+2 =2方法二先将条件化成整式,再把等式两边同时平方,把无理数运算转化为有理数运算．由x ﹣1=可得x 2﹣2x ﹣2=0,即,x 2﹣2x =2,x 2=2x +2．原式12=x （2x +2）﹣x 2﹣x +2 =x 2+x ﹣x 2﹣x +2 =2请参以上的解决问题的思路和方法,解决以下问题：（1）若a 2﹣3a +1=0,求2a 3﹣5a 2﹣3231a ++的值；（2）已知x =2求432295543x x x x x x ---+-+的值．。

中考数学5年真题(2019-2023)专题汇总解析—二次根式

中考数学5年真题（2019-2023）专题汇总解析—二次根式考点1二次根式一、单选题1．（2023）A．25与30之间B．30与35之间C．35与40之间D．40与45之间【答案】D【详解】解∶∵160020232025<<．即4045<，40与45之间．故选D．【点睛】本题主要考查了估算无理数的大小，正确估算无理数的取值范围是解题关键．2．（2023年江苏省无锡市中考数学真题）实数9的算术平方根是（）A．3B．3±C．19D．9-【答案】A【分析】根据算术平方根的定义即可求出结果．3=，故选：A．【点睛】本题考查了平方根和算术平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．3．（2023年重庆市中考数学真题（A卷）的值应在（）A ．7和8之间B ．8和9之间C ．9和10之间D ．10和11之间【答案】B【分析】先计算二次根式的混合运算，再估算结果的大小即可判断．=4=+∵2 2.5<<，∴45<<，∴849<+<，故选：B ．【点睛】此题考查了二次根式的混合运算，无理数的估算，正确掌握二次根式的混合运算法则是解题的关键．4．（2019·广东·的结果是()A ．4-B ．4C ．4±D ．2【答案】B【分析】根据算术平方根的定义进行求解即可.，故选B.【点睛】本题考查了算术平方根，熟练掌握算术平方根的定义是解题的关键.5．（2020·广西贵港·在实数范围内有意义，则实数x 的取值范围是（）A ．1x <-B ．1x ≥-C ．0x ≥D ．1x ≥【答案】B【分析】根据二次根式的被开方数为非负数即可得出的取值范围．∴x＋1≥0∴x≥﹣1故选：B【点睛】本题考查了二次根式有意义的条件，解答本题的关键是掌握二次根式有意义：被开方数为非负数．6．（2020·山东聊城·÷）．A．1B．53C．5D．9【答案】A【分析】利用二次根式的乘除法则计算即可得到结果．÷==1=，故选：A．【点睛】本题主要考查了二次根式的乘除法，熟练掌握运算法则是解题的关键．7．（2023年辽宁省大连市中考数学真题）下列计算正确的是（）A．0=B．+=C=D)26=-【答案】D【分析】根据零指数幂，二次根式的加法以及二次根式的性质，二次根式的混合运算进行计算即可求解．【详解】解：A.)1=，故该选项不正确，不符合题意；B.=C.=D.)26=-，故该选项正确，符合题意；故选：D ．【点睛】本题考查了零指数幂，二次根式的加法以及二次根式的性质，二次根式的混合运算，熟练掌握二次根式的运算法则是解题的关键．8．（2021·广东·统考中考真题）若0a =，则ab =（）AB ．92C ．D ．9【答案】B【分析】根据一个实数的绝对值非负，一个非负实数的算术平方根非负，且其和为零，则它们都为零，从而可求得a 、b 的值，从而可求得ab 的值．【详解】∵0a ≥0≥，且0a =∴0a =0==即0a =，且320a b -=∴a =b∴92ab ==故选：B ．【点睛】本题考查了绝对值和算术平方根的非负性，一般地，几个非负数的和为零，则这几个非负数都为零．9．（2022·河北·统考中考真题）下列正确的是（）A23=+B 23=⨯CD 0.7=【答案】B【分析】根据二次根式的性质判断即可．【详解】解：23=≠+，故错误；=⨯，故正确；23=≠≠，故错误；0.7故选：B．【点睛】本题主要考查二次根式的性质，掌握二次根式的性质是解题的关键．10．（2023()A．点P B．点Q C．点R D．点S【答案】B<<【详解】解：∵479<<，<<23Q，故选：B．11．（2023年河北省中考数学真题）若a b===（）A．2B．4C D【答案】A【分析】把a b【详解】解：∵a b==2==，故选：A．【点睛】本题考查了求二次根式的值，掌握二次根式的乘方和乘除运算是解题的关键．12．（2019·四川资阳·统考中考真题）设x=x的取值范围是（）A．23x<<B．34x<<C．45x<<D．无法确定【答案】B【分析】根据无理数的估计解答即可．【详解】解：∵91516<<，∴34<<，故选B．【点睛】此题考查估算无理数的大小，关键是根据无理数的估计解答．13．（2021·广东·统考中考真题）设6a，小数部分为b，则(2a b+的值是（）A．6B．C．12D．【答案】A的整数部分可确定a的值，进而确定b的值，然后将a与b的值代入计算即可得到所求代数式的值．【详解】∵34<<，∴263<<，∴62a=，∴小数部分624b==∴(((22244416106a b+=⨯+-=+-=-=．故选：A．【点睛】本题考查了二次根式的运算，正确确定6a与小数部分b的值是解题关键．二、填空题14．（2019·江苏苏州·x的取值范围为.【答案】6x≥【分析】根据根式有意义的条件，得到不等式，解出不等式即可.-60x≥，解出得到6x≥.【点睛】本题考查根式有意义的条件，能够得到不等式是解题关键.15．（2020·广西·=．【分析】利用二次根式的性质化简，再相减．==【点睛】本题考查了二次根式的减法，解题的关键是掌握二次根式的化简及性质．16．（2021·天津·统考中考真题）计算1)的结果等于．【答案】9【分析】根据二次根式的混合运算法则结合平方差公式计算即可．【详解】21)19=-=．故答案为9．【点睛】本题考查二次根式的混合运算．掌握二次根式的混合运算法则是解答本题的关键．17．（2023年湖北省武汉市数学真题）写出一个小于4的正无理数是．【分析】根据无理数估算的方法求解即可．<4<．．【点睛】本题主要考查了无理数的估算，准确计算是解题的关键．18．（2023x 的取值范围是．【答案】13x ≥-【分析】根据二次根式有意义的条件得到130x +≥，解不等式即可得到答案．∴130x +≥，解得13x ≥-，故答案为：13x ≥-【点睛】此题考查了二次根式有意义的条件，熟知被开方式为非负数是解题的关键．19．（2019·河南·12--=＝．【答案】112【分析】本题涉及二次根式化简、负整数指数幂两个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．12--122=-112=．故答案为11 2．【点睛】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、二次根式等考点的运算．20．（2021·安徽·统考中考真题）埃及胡夫金字塔是古代世界建筑奇迹之一，其底面是正方形，侧面是全等的等腰三角形，1-，它介于整数n和1n+之间，则n的值是．【答案】11即可完成求解．2.236≈；1 1.236≈；因为1.236介于整数1和2之间，所以1n=;故答案为：1．分即可；该题题干前半部分涉及到数学文化，后半部分为解题的要点，考查了学生的读题、审题等能力．21．（20231+=．【答案】3【分析】根据求一个数的立方根，有理数的加法即可求解．1+=213+=，故答案为：3．【点睛】本题考查了求一个数的立方根，熟练掌握立方根的定义是解题的关键．22．（2023年上海市中考数学真题）已知关于x2=，则x=【答案】18【分析】根据二次根式的性质，等式两边平方，解方程即可．【详解】解：根据题意得，140x -≥，即14x ≥，2=，等式两边分别平方，144x -=移项，18x =，符合题意，故答案为：18．【点睛】本题主要考查二次根式与方程的综合，掌握含二次根式的方程的解法是解题的关键．23．（2023年黑龙江省绥化市中考数学真题）若式子x有意义，则x 的取值范围是．【答案】5x ≥-且0x ≠/0x ≠且5x ≥-【分析】根据分母不为零，二次根式的被开方数是非负数，列出不等式计算即可．【详解】∵式子∴50x +≥且0x ≠，∴5x ≥-且0x ≠，故答案为：5x ≥-且0x ≠．【点睛】本题考查了分母不为零，二次根式的被开方数是非负数，熟练掌握二次根式和分式有意义的条件是解题的关键．24．（2023年黑龙江省齐齐哈尔市中考数学真题）在函数12y x +-中，自变量x 的取值范围是．【答案】1x >且2x ≠【分析】根据分式有意义的条件，二次根式有意义的条件得出10,20x x ->-≠，即可求解．【详解】解：依题意，10,20x x ->-≠∴1x >且2x ≠，故答案为：1x >且2x ≠．【点睛】本题考查了求函数自变量的取值范围，熟练掌握分式有意义的条件，二次根式有意义的条件是解题的关键．三、解答题25．（2019·福建·统考中考真题）先化简，再求值：(x －1)÷(x －21xx-),其中x【答案】1x x -，1+2【分析】先化简分式，然后将x 的值代入计算即可．【详解】解：原式＝（x−1）÷221x x x-+()()211xx x =-⋅-1x x =-当x ＋1时，12=+【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算法则是解题的关键．26．（2022·福建·统考中考真题）先化简，再求值：2111aa a -⎛⎫+÷ ⎪⎝⎭，其中1a =．【答案】11a -．【分析】根据分式的混合运算法则化简，再将a 的值代入化简之后的式子即可求出答案．【详解】解：原式()()111a a a a a+-+=÷()()111a a a a a +=⋅+-11a =-．当1a =时，原式2=．【点睛】本题考查了分式的化简求值，熟练掌握运算法则是解题的关键．27．（2023年安徽中考数学真题）先化简，再求值：2211x x x +++，其中1x =．【答案】1x +【分析】先根据分式的性质化简，最后将字母的值代入求解．【详解】解：2211x x x +++()211x x +=+1x =+，当1x =-时，∴原式11+=．【点睛】本题考查了分式化简求值，解题关键是熟练运用分式运算法则进行求解．28．（20232133-⎛⎫- ⎪⎝⎭【答案】6-【分析】根据立方根、负整数指数幂及二次根式的运算可进行求解．【详解】解：原式2293=-+6=-．【点睛】本题主要考查立方根、负整数指数幂及二次根式的运算，熟练掌握立方根、负整数指数幂及二次根式的运算是解题的关键．29．（2023年吉林省长春市中考数学真题）先化简．再求值：2(1)(1)a a a ++-，其中3a =．【答案】31a +1+【分析】根据完全平方公式以及单项式乘以单项式进行化简，然后将字母的值代入进行计算即可求解．【详解】解：2(1)(1)a a a ++-2221a a a a =+++-31a =+当a =311==【点睛】本题考查了整式乘法的化简求值，实数的混合运算，熟练掌握完全平方公式以及单项式乘以单项式的运算法则是解题的关键．30．（2023年内蒙古通辽市中考数学真题）计算：21tan 453-⎛⎫+︒-⎪⎝⎭【答案】0【分析】根据负整数次幂、特殊角的三角函数值、算术平方根化简，然后在计算即可．【详解】解：21tan 453-⎛⎫+︒-⎪⎝⎭9110=+-，0=．【点睛】本题主要考查了负整数次幂、特殊角的三角函数值、算术平方根等知识点，掌握基本的运算法则是解答本题的关键．31．（2019·河南·统考中考真题）先化简，再求值：22121244x x x x x x +-⎛⎫-÷ ⎪--+⎝⎭，其中x =【答案】3x【分析】先根据分式的混合运算顺序和运算法则化简原式，再将x 的值代入计算可得．【详解】解：原式212(2)22(2)x x x x x x x +--⎛⎫=-÷ ⎪---⎝⎭322x x x-=⋅-3x=，当x ===．【点睛】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则．32．（2023年辽宁省营口市中考数学真题）先化简，再求值：524223m m m m-⎛⎫++⋅⎪--⎝⎭，其中tan 45m =︒．【答案】26--m ，原式16=-【分析】先根据分式的混合计算法则化简，然后根据特殊角三角函数值和二次根式的性质求出m 的值，最后代值计算即可．【详解】解：524223m m m m-⎛⎫++⋅⎪--⎝⎭()22245223m m m m m-⎛⎫-=-⋅⎪---⎝⎭()222923m m m m--=⋅--()()()332223m m m m m+--=⋅--()23m =-+26m =--，∵tan 45m =︒，∴415m =+=，∴原式25610616=-⨯-=--=-．【点睛】本题主要考查了分式的化简求值，求特殊角三角函数值，化简二次根式等等，正确计算是解题的关键．33．（2023·重庆九龙坡·的值应在（）A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间【答案】A【分析】根据二次根式的乘法进行计算，以及估算无理数的大小的方法解答即可．=6=∵91416<<，∴34<，∴43-<<-，∴263<<，故选：A ．【点睛】本题考查了估算无理数的大小和二次根式的运算．解题的关键是掌握二次根式的运算方法，以及估算无理数的大小的方法．34．（2023·辽宁丹东·统考二模）在函数y =x 的取值范围是（）A ．12x -<≤B ．21x -<≤C ．12x ≤≤D ．12x <≤【答案】D【分析】根据函数有意义的条件得到2010x x -≥⎧⎨->⎩,解不等式组即可得到自变量x 的取值范围．【详解】解：由题意得2010x x -≥⎧⎨->⎩，解不等式组得12x <≤，故选：D ．【点睛】此题考查了自变量的取值范围，熟练掌握二次根式和分式有意义的条件是解题的关键．35．（2023·安徽蚌埠·统考三模）下列运算正确的是（）A 3=B ．()3328a a -=-C =D ．112235+=【答案】B【分析】根据二次根式的性质，积的乘方法则，二次根式的加法运算法则，有理数的加法运算法则依次判断即可得出答案．【详解】解：A 333==B ．()3328a a -=-，故此选项符合题意；CD ．11522365+=≠，故此选项不符合题意．故选：B ．【点睛】本题考查二次根式的性质，积的乘方法则，二次根式的加法运算法则，有理数的加法运算法则．掌握相应的运算法则和性质是解题的关键．36．（2023·河北沧州·校考模拟预测）下列运算中，正确的是（）．A3=±B 2=C 2=D 8=-【答案】C【分析】利用二次根式的化简的法则对各项进行运算即可．【详解】解答：解：A 3=，故A 不符合题意；B 2=-，故B 不符合题意；C 2=，故C 符合题意；D 8=，故D 不符合题意；故选：C ．【点睛】本题主要考查二次根式的化简，解答的关键是对相应的运算法则的掌握．37．（2023·四川泸州·四川省泸县第一中学校考三模）实数2的平方根为（）A ．2B ．2±C D ．【答案】D【分析】利用平方根的定义求解即可．【详解】∵2的平方根是．故选D ．【点睛】此题主要考查了平方根的定义，注意一个正数的平方根有2个，它们互为相反数．38．（2023·西南大学附中校考三模）估计(3-）A ．0和1之间B ．2和3之间C ．3和4之间D ．4和5之间【答案】A【分析】由题意知(34-，由1.4 1.5=<<=，可得4.2 4.5<<，0.240.5<<，然后判断作答即可．【详解】解：(34-⨯，∵1.4 1.5=<<=，∴4.2 4.5<<，∴0.240.5<<，∴估算(3-0和1之间，故选：A ．39．（2023·河北石家庄·校联考一模）下列计算正确的是（）A =B1=-C =D 23=【答案】C【分析】根据二次根式加法、二次根式减法、二次根式乘法、二次根式除法分别进行判断即可．【详解】解：AB 0-=，故选项错误，不符合题意；C =D 1=，故选项错误，不符合题意．故选：C ．【点睛】此题考查了二次根式的加法、减法、乘法、除法，熟练掌握运算法则是解题的关键．40．（2023·江苏无锡·校考二模）函数y x的取值范围是（）A ．5x ≥-B ．5x ≤-C ．5x ≥D ．5x ≤【答案】C【详解】试题分析：求函数自变量的取值范围，就是求函数解析式有意义的条件，根据二次根式被开方数x 50x 5-≥⇒≥.故选C.考点：1.函数自变量的取值范围；2.二次根式有意义的条件.41．（2023·湖南长沙·校联考二模）4的算术平方根是（）A ．2B ．2±C ．8D ．16【答案】A【分析】如果一个数x 的平方等于(0)a a ≥，那么这个数x 叫做a 的平方根，可以表示为平方根叫做a 的算术平方根．正数的算术平方根是正数，0的算术平方根是0，负数没有算术平方根．【详解】解：42=，故选：A ．【点睛】本题考查算术平方根的定义，明确平方根与算术平方根的区别与联系是本题的关键．42．（2023·重庆九龙坡·重庆市育才中学校考一模）x）A ．0B ．2C ．3D ．5【答案】D【分析】根据二次根式有意义的条件进行求解即可．∴40x -≥，即4x ≥，∴四个选项中只有D 选项中的5符合题意，故选：D ．【点睛】本题主要考查了二次根式有意义的条件，熟知二次根式有意义的条件是被开方数大于等于零是解题的关键．43．（2023·甘肃平凉·的结果是．【答案】2【分析】根据二次根式的性质进行化简即可．2=．故答案为：2．()()(0000a a a a a a ⎧⎪===⎨⎪-⎩＞）＜．44．（2021·黑龙江大庆·=【答案】4【分析】先算4(2)-，再开根即可．==4=故答案是：4．【点睛】本题考查了求一个数的4次方和对一个实数开根号，解题的关键是：掌握相关的运算法则．45．（2023·广东茂名·校考一模）已知实数x，y |4|0y -=，则1x y -=⎛⎫⎪⎝⎭．【答案】2【分析】根据算术平方根的非负性，绝对值的非负性得出24x y ==，，进而根据负整数指数幂进行计算即可求解．40y -=0≥，40y -≥，∴20x -=，40y -=，∴24x y ==，，∴11112422x y ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭===．故答案为：2．【点睛】本题主要考查了算术平方根和绝对值的非负性、负整数次幂等知识点，根据非负性正确求得x 、y 的值是解答本题的关键．46．（2023·福建福州·校考二模）已知2a =2b =22a b ab -的值等于．【答案】【分析】先求出a b -=1ab =，再由()22a b ab ab a b -=-进行求解即可．【详解】解：∵2a =2b =∴22a b -=++=((22431ab =+⨯-=-=，∴22a b ab -()ab a b =-1=⨯=故答案为：【点睛】本题主要考查了二次根式的混合运算、求代数式的值，正确得到a b -=1ab =是解题的关键47．（2023·山东聊城·x 的取值范围是．【答案】12x ≥【分析】根据二次根式有意义的条件可得210x -≥，即可．【详解】解：由题意得：210x -≥，解得：12x ≥，故答案为：12x ≥．【点睛】此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．48．（2023·安徽滁州·校考模拟预测）计算)11-的结果等于．【答案】22【分析】直接利用平方差公式进行简便运算即可．【详解】解：)2211123122=-=-=，故答案为：22【点睛】本题考查的是二次根式的乘法运算，熟练的利用平方差公式进行简便运算是解本题的关键．49．（2023·陕西西安·校考模拟预测）－64的立方根是．【答案】-4【分析】直接利用立方根的意义，一个数的立方等于a ，则a 的立方根是这个数进行求解．【详解】解：根据立方根的意义，一个数的立方等于a ，则a 的立方根是这个数，可知-64的立方根为-4．故答案为：-4．【点睛】本题考查了立方根，解题的关键是掌握一个数的立方等于a ，则a 的立方根是这个数．50．（2023·云南昭通·x 的取值范围是．【答案】x＞8【分析】由分式的分母不等于零和二次根式的被开方数是非负数得到x﹣8＞0．【详解】解：由题意，得x﹣8＞0，解得x＞8．故答案是：x＞8．【点睛】考查了分式有意义的条件和二次根式有意义的条件，注意，二次根式在分母上，所以不能取到0．51．（2023·四川泸州·四川省泸县第一中学校考三模）函数y=x的取值范围是．【答案】x>3【分析】求函数自变量的取值范围，就是求函数解析式有意义的条件，根据二次根式被开方数必须是非负数和分式分母不为0的条件.x30x3x>3x30x3-≥≥⎧⎧⇒⇒⎨⎨-≠≠⎩⎩．52．（2023·河南洛阳·统考一模）计算：22-=．【答案】74-【分析】先计算22-，再算减法．【详解】解：原式17244=-=-．故答案为：74-．【点睛】本题考查了实数的计算，掌握负整数指数幂、二次根式的化简是解决本题的关键．53．（2023·安徽蚌埠·统考三模）计算：212022--=．【答案】2023【分析】根据有理数的乘方，二次根根式的性质，化简绝对值进行计算即可求解．【详解】解：212022--=122022-++2023=，故答案为：2023．【点睛】本题考查了有理数的乘方，二次根根式的性质，化简绝对值，正确的计算是解题的关键．54．（2022·新疆·x的取值范围是．【答案】x≥3【分析】直接利用二次根式有意义的条件得到关于x的不等式，解不等式即可得答案.【详解】由题意可得：x—3≥0，解得：x≥3，故答案为：x≥3【点睛】本题考查了二次根式有意义的条件，熟练掌握二次根式的被开方数是非负数是解题的关键.55．（2023·黑龙江哈尔滨·统考三模）计算=．【答案】【分析】先根据二次根式的性质化简，然后根据二次根式的加减法则求解即可．【详解】解：=-2=-=故答案为：【点睛】本题主要考查了二次根式的性质、二次根式的加减运算等知识点，灵活运用二次根式的的性质化简是解题的关键．x的取值范围是．56．（2023·云南昆明·一模）要使式子3有意义，x≥【答案】5【分析】二次根式中的被开方数是非负数，依此即可求解．x-≥，【详解】解：依题意有：50x≥．解得5x≥．故答案为：5【点睛】本题考查了二次根式有意义的条件，关键是熟悉二次根式中的被开方数是非负数的知识点．57．（云南省丽江市华坪县2020-2021=．【答案】6【分析】利用二次根式的乘法法则进行求解即可．==．6故答案为：6．【点睛】本题考查了二次根式的乘法，熟练掌握二次根式的乘法法则和二次根式的性质是解题的关键．58．（2023·山西·模拟预测）计算：=．【答案】【分析】先化简二次根式，再根据二次根式的加减计算法则求解即可．【详解】解：3=⨯=+=故答案为：【点睛】本题主要考查了二次根式的加减计算，二次根式的化简，正确计算是解题的关键．59．（2023·重庆沙坪坝·重庆八中校考模拟预测）如果2y=+，那么yx的值是．【答案】225【分析】根据二次根式有意义的条件，求出,x y的值，进而求出y x的值即可．【详解】解：∵2y=，∴150,150x x -≥-≥，∴15150x x -=-=，∴15,2x y ==，∴215225y x ==；故答案为：225．【点睛】本题考查二次根式有意义的条件，代数式求值．熟练掌握二次根式的被开方数是非负数，是解题的关键．60．（江西省崇仁县第二中学2016-2017学年八年级上学期第二次月考数学试题）计算:=【答案】61．（2015年初中毕业升学考试（山东滨州卷）数学（带解析））计算的结果为．【答案】﹣1【分析】此题用平方差公式计算即可.【详解】22=-23=-1=-62．（2023·黑龙江哈尔滨·=．【答案】3【分析】根据二次根式的化简方法和运算法则进行计算．【详解】解：原式33==【点睛】本题考查二次根式的计算，在化简二次根式的基础上再把同类二次根式合并．63．（福建省永春县第一中学2017【分析】根据二次根式乘法，加减法运算法则计算即可．【详解】解：原式＝【点睛】本题考查了二次根式的混合运算，熟练掌握二次根式的化简方法是解题的关键．64．（2023·广东茂名·校考一模）先化简，再求值：2121211x x x x +⎛⎫÷+ ⎪-+-⎝⎭其中1x +．【答案】11x -；2【分析】先通分算括号内的，把除化为乘，再约分，化简后将x 的值代入计算．【详解】解：212(1)211x x x x +÷+-+-211(1)1x x x x ++=÷--211(1)1x x x x +-=⋅-+11x =-，当1x =+时，原式=2=．【点睛】本题考查了分式化简求值，掌握分式的基本性质，将分式通分和约分进行化简是关键．65．（2023·四川泸州·011+()3-23－【答案】【分析】根据实数的混合运算法则即可求解．011+()3-23－=(1+32-=1+32-+【点睛】此题主要考查实数的运算，解题的关键是熟知实数的性质及运算法则．66．（2023·安徽六安·1+【分析】先计算算术平方根．化简绝对值，求解立方根，再合并即可．1+=+-413=【点睛】本题考查是算术平方根的含义，化简绝对值，求解立方根，实数的混合运算，掌握“算术平方根与立方根的含义”是解本题的关键．67．（2022·新疆·统考中考真题）计算：20-+(2)|(3【分析】分别计算有理数的乘方、绝对值、二次根式及零指数幂，再进行加减即可．【详解】解：原式451=++=【点睛】本题考查有理数的乘方，绝对值和二次根式的化简及零指数幂的性质，属于基础题，正确运算是=．解题的关键．要熟练掌握：任何一个不等于零的数的零次幂都等于1a。

2013年全国中考数学试题分类解析汇编专题6二次根式

2013年全国中考数学试题分类解析汇编专题6：二次根式一、选择题1. （2012天津市3分）6+1的值在【】（A ）2到3之间（B ）3到4之间（C ）4到5之间（D ）5到6之间【答案】B 。

【考点】估算无理数的大小。

【分析】利用”夹逼法“得出66的范围：∵4 ＜ 6 ＜ 9 469263。

∴36+14<。

故选B 。

2. （2012上海市4分）a b - 】 A a+b B a +b C a b -D a b【答案】C 。

【考点】有理化因式。

-【分析】a b a b=a b ---，a b -a b -C 。

3. （2012广东肇庆3分）2x -x 的取值范围是【】A ．x 0>B ．x 2≥-C ．x 2≥D ．x 2≤ 【答案】A 。

【考点】二次根式有意义的条件。

【分析】根据二次根式被开方数必须是非负数的条件，要使2x -在有意义，必须2x 0x 2-≥⇒≤。

故选A 。

4. （2012浙江杭州3分）已知(3m 221⎛=⨯- ⎝⎭，则有【】A ．5＜m ＜6B ．4＜m ＜5C ．﹣5＜m ＜﹣4D ．﹣6＜m ＜﹣5 【答案】A 。

【考点】二次根式的乘除法，估算无理数的大小。

【分析】求出m 的值，估算出经的范围5＜m ＜6，即可得出答案：(324m 2213213212839⎛=⨯-=⨯⨯⨯ ⎝⎭252836，∴5286，即5＜m ＜6。

故选A 。

5. （2012江苏南京2分）12的负的平方根介于【】 A. -5和-4之间 B. -4与-3之间 C. -3与-2之间 D. -2与-1之间【答案】B 。

【考点】估算无理数的大小，不等式的性质。

【分析】∵9 ＜ 12 ＜ 1691216。

∴-16-12-9-412-3<。

故选B 。

6. （2012江苏盐城3分）4的平方根是【】A ．2B ．16C ．2±D ．16± 【答案】C 。

【考点】平方根。

2013年中考数学专题复习题3一元二次方程根的判别式应用探讨

【2013年中考攻略】专题3：一元二次方程根的判别式应用探讨一元二次方程，就是只有一个未知数且未知数最高次数为2的整式方程，其一般形式为ax2+bx+c=0（a≠0）。

在系数a≠0的情况下，Δ=b2－4ac>0时，方程有2个不相等的实数根；Δ=b2－4ac =0时，方程有两个相等的实数根；Δ=b2－4ac <0时，方程无实数根。

反之，若方程有2个不相等的实数根，则Δ=b2－4ac>0；若方程有两个相等的实数根，则Δ=b2－4ac =0；若无实数根，则Δ=b2－4ac <0。

因此，Δ=b2－4ac称为一元二次方程根的判别式。

根的判别式b2-4ac的使用条件，是在一元二次方程中，而非别的方程中，因此，解题过程中要注意隐含条件a≠0。

使用判别式之前一定要先把方程变化为一般形式，以便正确找出a、b、c的值。

一元二次方程根的判别式在初中数学中有着广泛的应用，也是中考必考内容，并占有一定的份量。

锦元数学工作室将其应用归纳为直接应用和综合应用两方面，直接应用包括①不解一元二次方程，判断（证明）根的情况、②根据方程根的情况，确定待定系数的取值范围、③限制一元二次方程的根与系数关系的应用；综合应用包括④判断二次三项式是完全平方式时的待定系数、⑤判断双曲线与直线的公共点个数、⑥判断抛物线与直线（含x轴）的公共点个数。

下面通过近年全国各地中考的实例探讨其应用。

一.不解一元二次方程，判断（证明）根的情况：典型例题：例1：（2012广西河池3分）一元二次方程2x2x20++=的根的情况是【】A．有两个相等的实数根 B．有两个不相等的实数根C．只有一个实数根 D．无实数根【答案】D。

【考点】一元二次方程根的判别式。

【分析】∵2x2x20++=中，a=1，b=2，c=2，∴△22b4ac=2412=40<=--⨯⨯-。

∴2x2x20++=无实数根。

故选D。

例2：（2011江苏苏州3分）下列四个结论中，正确的是【】A．方程1x+=2x-有两个不相等的实数根B．方程1x+=1x有两个不相等的实数根C ．方程1x+=2x 有两个不相等的实数根D ．方程1x+=a x（其中a 为常数，且a 2>）有两个不相等的实数根【答案】D 。

2013年全国各地中考数学试卷分类汇编：二次根式

二次根式一、选择题1．（2013江苏苏州，3，3分）在实数范围内有意义，则x 的取值范围是（）． A ．x >1B ．x <1C ．x ≥1D ．x ≤1 【答案】C ．【解析】被开方数x －1≥0，可得x ≥1．所以应选C ．【方法指导】二次根式有意义的条件是被开方数为非负数．2．（2013山东临沂，5，3分））A ．BC ．D 【答案】B ．【解析】48－931=34－33=3，故选B. 【方法指导】分别对每个二次根式进行化简，然后合并被开方数相同的二次根式.【易错点分析】不会被开方数为分数的二次根式的化简．3．（2013四川宜宾，4，3分）二次根式2)3(-的值是( )A ．－3B ．3或－3C ．9D ． 3【答案】D ．【解析】根据93-2=）（=3得应选D. 【方法指导】本题考查了二次根式的化简a a =2，（1）当a >0时原式=a ；（2）当a<0时原式=－a;(3)当a=0时原式=0，解题时要注意性质符号.4．（2013四川南充，2，3分）0.49的算数平方根的相反数是（）A ．0.7B ．﹣0.7C ．±0.7D ．0【答案】：B ．【解析】根据算数平方根的定义得0.49的算术平方根为0.7，再根据相反数的定义得应选B .【方法指导】本题考查算术平方根及相反数的概念. 算术平方根的概念：一个正数a 的正的平方根叫做a 的算术平方根；0的算术平方根是0.相反数概念：只有符号不同的两个数互为相反数.5．（2013江苏泰州，2，3分）下列计算正确的是（）A ．-BC ．D ．3+【答案】C ．【解析】A.,错误在于合并时漏掉3;B ,因为本身不能够合并; C ．12=22计算正确; D ．322=52+错误,因为本身不能够合并. 【方法指导】本题考查了二次根式的运算.二次根式的加减关键在于合并同类二次根式,二次根式的乘除关键会正、逆用运算法则:)0,0(≥≥=⋅b a ab b a ,)0,0(>≥=b a ba b a . 6．（2013四川凉山州，5，4分）如果代数式x 有意义，那么x 的取值范围是 A ．x ≥0 B ．1x ≠ C ．0x > D ．x ≥0且1x ≠【答案】D.【解析】式子有意义的条件是分母不为0,分子的被开方数为非负数.由题意得0,10,x x ≥⎧⎨-≠⎩ 解得x ≥0且1x ≠. 【方法指导】本题考查代数式有意义的条件,当代数式是几种代数式组合而成的时候,要使每一个都得有意义才可以的.常见的代数式有意义的条件是:如果是二次根式时,则被开数为非负数,如果是分式时,分母不能为0,当出现0次幂时,底数不能为0,等.7．（2013广东湛江，8，4分）函数3y x =+中，自变量x 的取值范围是（）A ．3x >-B ．3x ≥-C ．3x ≠-D ．3x ≤-【答案】B.【解析】由30x +≥，解得3x ≥-，本题选B【方法指导】本题考查了函数自变量的取值范围。

全国2024年中考数学试题精选50题分式二次根式含解析

2024年全国中考数学试题精选50题：分式、二次根式一、单选题1.（2024·绵阳）若有意义，则a的取值范围是（）A. a≥1B. a≤1C. a≥0D. a≤﹣12.（2024·淄博）化简的结果是（）A. a+bB. a﹣b C.D.3.（2024·威海）人民日报讯，2024年6月23日，中国胜利放射北斗系统第55颗导航卫星．至此中国提前半年全面完成北斗三号全球卫星导航系统星座部署．北斗三号卫星上配置的新一代国产原子钟，使北斗导航系统投时精度达到了十亿分之一秒，十亿分之一用科学记数法可以表示为（）A. B.C.D.4.（2024·威海）分式化简后的结果为（）A. B.C.D.5.（2024·滨州）冠状病毒的直径约为80～120纳米，1纳米＝米，若用科学记数法表示110纳米，则正确的结果是（）A. 米B.米 C.米 D. 米6.（2024·鄂尔多斯）二次根式中，x的取值范围在数轴上表示正确的是（）A. B. C.D.7.（2024·赤峰）2024年6月23日9时43分，我国胜利放射了北斗系统第55颗导航卫星，其授时精度为世界之最，不超过0.000 000 009 9秒.数据“0. 000 000 009 9”用科学记数法表示为（）A. B.C.D.8.（2024·云南）下列运算正确的是（）A. B.C. D.9.（2024·南通）下列运算，结果正确的是（）A. B.C. D.10.（2024·上海）下列各式中与是同类二次根式的是（）A. B.C.D.11.（2024·呼和浩特）下列运算正确的是（）A.B.C. D.12.（2024·包头）的计算结果是（）A. 5B.C.D.13.（2024·包头）下列计算结果正确的是（）A. B.C. D.14.（2024·长沙）下列运算正确的是（）A. B.C. D.15.（2024·邵阳）下列计算正确的是（）A.B.C.D.16.（2024·郴州）下列运算正确的是（）A. B.C. D.17.（2024·郴州）年月日，北斗三号最终一颗全球组网卫星在西昌卫星放射中心点火升空．北斗卫星导航系统可供应高精度的授时服务，授时精度可达纳秒（秒= 纳秒）用科学记数法表示纳秒为（）A. 秒B.秒 C.秒 D. 秒18.若关于x的分式方程＝+5的解为正数，则m的取值范围为（）A. m＜﹣10B. m≤﹣10 C. m≥﹣10且m≠﹣6 D. m＞﹣10且m≠﹣6二、填空题19.（2024·眉山）关于x的分式方程的解为正实数，则k的取值范围是________．20.（2024·东营）2024年6月23日9时43分，“北斗三号”最终一颗全球组网卫星放射胜利，它的授21.（2024·永州）在函数中，自变量x的取值范围是________．22.（2024·南县）若计算的结果为正整数，则无理数m的值可以是________．（写出一个符合条件的即可）23.（2024·昆明）要使有意义，则x的取值范围是________.24.（2024·营口）（3 + ）（3 ﹣）＝________.25.（2024·山西）计算：________．26.（2024·呼和浩特）分式与的最简公分母是________，方程的解是________．27.（2024·包头）计算：________．28.（2024·包头）在函数中，自变量的取值范围是________．29.（2024·邵阳）在如图方格中，若要使横、竖、斜对角的3个实数相乘都得到同样的结果，则2个空格的实数之积为________．21 6330.（2024·郴州）若分式的值不存在，则________．31.（2024·黑龙江）在函数中，自变量x的取值范围是________．三、计算题32.（2024·眉山）先化简，再求值：，其中．33.（2024·烟台）先化简，再求值：÷ ，其中x＝+1，y＝﹣1．34.（2024·滨州）先化筒，再求值：其中35.（2024·呼伦贝尔）先化简，再求值：，其中．36.（2024·鄂尔多斯）（1）解不等式组，并求出该不等式组的最小整数解．（2）先化简，再求值：（）÷ ，其中a满意a2+2a﹣15＝0．37.（2024·赤峰）先化简，再求值：，其中m满意：.38.（2024·永州）先化简，再求值：，其中．39.（2024·南县）先化简，再求值：，其中40.（2024·云南）先化简，再求值：，其中.41.（2024·营口）先化简，再求值：（﹣x）÷ ，请在0≤x≤2的范围内选一个合适的整数代入求值.42.（2024·宿迁）先化简，再求值：÷（x﹣），其中x＝﹣2.43.（2024·南通）计算：（1）（2m+3n）2﹣（2m+n）（2m﹣n）；（2）44.（2024·娄底）计算：45.（2024·郴州）计算：46.（1）计算：sin30°+ ﹣（3﹣）0+|﹣|（2）因式分解：3a2﹣4847.（2024·长沙）先化简，再求值，其中48.（2024·娄底）先化简，然后从，0，1，3中选一个合适的数代入求值．49.（2024·山西）（1）计算：（2）下面是小彬同学进行分式化简的过程，请仔细阅读并完成相应任务．第一步其次步第三步第四步第五步第六步任务一：填空：①以上化简步骤中，第________步是进行分式的通分，通分的依据是________或填为________；②第________步起先出现不符合题意，这一步错误的缘由是________；（3）任务二：请干脆写出该分式化简后的正确结果；解；．任务三：除订正上述错误外，请你依据平常的学习阅历，就分式化简时还须要留意的事项给其他同学提一条建议．50.（2024·通辽）用※定义一种新运算：对于随意实数m和n ，规定，如：．（1）求；（2）若，求m的取值范围，并在所给的数轴上表示出解集．答案解析部分一、单选题1.【答案】 A【解析】【解答】解：若有意义，则，解得：．故答案为：A．【分析】干脆利用二次根式有意义的条件分析得出答案．2.【答案】 B【解析】【解答】解：原式＝＝＝＝a﹣b．故答案为：B．【分析】跟据同分母分式相加减的运算法则计算．同分母分式相加减，分母不变，分子相加减．3.【答案】 B【解析】【解答】，故答案为：B．【分析】依据科学记数法的表示形式(n为整数)进行表示即可求解．4.【答案】 B【解析】【解答】解：故答案为：B．【分析】依据异分母分式相加减的运算法则计算即可．异分母分式相加减，先通分，再依据同分母分式相加减的法则计算．5.【答案】 C【解析】【解答】解：110纳米=110×10-9米=1.1×10-7米．故答案为：C．【分析】肯定值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所运用的是负整数指数幂，指数n由原数左边起第一个不为零的数字前面的0的个数所确定．6.【答案】 D【解析】【解答】解：依据题意得3+x≥0，解得：x≥﹣3，故x的取值范围在数轴上表示正确的是．故答案为：D ．【分析】依据二次根式的性质，被开方数大于或等于0，可以求出x的范围．7.【答案】 C【解析】【解答】解：0. 000 000 009 9用科学记数法表示为．8.【答案】 D【解析】【解答】解：A. ，故本选项错误；B. ，故本选项错误；C. ，故本选项错误；D. ，故本选项正确；故答案为：D.【分析】依据一个正数的正的平方根就是该数的算术平方根即可推断A；依据与互为倒数即可推断B；依据积的乘方，等于把积中的每一个因式分别乘方，再把所得的幂相乘即可推断C；依据同底数幂的除法，底数不变，指数相减即可推断D.9.【答案】 D【解析】【解答】解：A. 与不是同类二次根式，不能合并，此选项错误；B.3与不是同类二次根式，不能合并，此选项错误；C. ，此选项错误；D. ，此选项计算正确.故答案为：D.【分析】（1）由同类二次根式的定义可知与不是同类二次根式，所以不能合并；（2）同理可知不能合并；（3）由二次根式的除法法则可得原式=；（4）由二次根式的乘法法则可得原式=.10.【答案】 C【解析】【解答】解：A、和是最简二次根式，与的被开方数不同，故A选项不符合题意；B、，3不是二次根式，故B选项不符合题意；C、，与的被开方数相同，故C选项符合题意；D、，与的被开方数不同，故D选项不符合题意；故答案为：C.【分析】依据同类二次根式的概念逐一推断即可.11.【答案】 C【解析】【解答】解：A、，不符合题意；B、，不符合题意；C、=== ，符合题意；D、，不符合题意；故答案为：C.【分析】分别依据二次根式的乘法，幂的乘方和积的乘方，分式的混合运算，分式的除法法则推断即可.12.【答案】 C【解析】【解答】= ,故答案为：C．【分析】依据二次根式的运算法则即可求解．13.【答案】 D【解析】【解答】解：A. ，故A选项不符合题意；B. ，故B选项不符合题意；C. ，故C选项不符合题意；D. ，故D选项符合题意．故答案为D．【分析】依据幂的乘方、积的乘方、单项式除法、分式加法以及分式乘除混合运算的学问逐项解除即可．14.【答案】 B【解析】【解答】解：A、，故本选项不符合题意；B、，故本选项符合题意；C、，故本选项不符合题意；D、，故本选项不符合题意．故答案为：B．【分析】依据合并同类项，系数相加字母和字母的指数不变；同底数幂的除法，底数不变指数相减；二次根式的乘法计算；幂的乘方，底数不变，指数相乘，利用解除法求解．15.【答案】 D【解析】【解答】解：A. ，故A选项不符合题意；B. ，故B选项不符合题意；C. ，故C选项不符合题意；D. ，故D选项符合题意．故答案为D．【分析】分别运用二次根式、整式的运算、分式的运算法则逐项解除即可．16.【答案】 A【解析】【解答】A. ，计算符合题意，符合题意；B. ，故本选项不符合题意；C. ，故本选项不符合题意；D. 不能计算，故本选项不符合题意；故答案为：A．【分析】依据积的乘方、同底数幂的乘法、二次根式的减法以及合并同类项法则进行计算得出结果进行推断即可．17.【答案】 A【解析】【解答】∵1秒=1000000000纳秒，∴10纳秒=10÷1000000000秒=0.000 00001秒=1×10-8秒．故答案为：A．【分析】肯定值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所运用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所确定．18.【答案】 D【解析】【解答】解：去分母得，解得，由方程的解为正数，得到，且，，则m的范围为且，二、填空题19.【答案】 k＞-2且k≠2【解析】【解答】解：方程两边同乘（x-2）得，1+2x-4=k-1，解得，，且故答案为：且【分析】利用解分式方程的一般步骤解出方程，依据题意列出不等式，解不等式即可．20.【答案】【解析】【解答】因为，故答案为：．【分析】依据科学记数法表示较小的数，一般形式为，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所确定，进而求解．21.【答案】x≠3【解析】【解答】∵在函数中，x-3≠0，∴x≠3．故答案是：x≠3．【分析】依据分式有意义的条件，即可求解．22.【答案】（答案不唯一）【解析】【解答】解：∵ ，∴ 时的结果为正整数，故答案为：（答案不唯一）．【分析】依据为12，即可得到一个无理数m的值．23.【答案】x≠﹣1【解析】【解答】解：要使分式有意义，需满意x+1≠0.即x≠﹣1.故答案为：x≠﹣1.【分析】依据分式的分母不能为0，建立不等式即可求解.24.【答案】 12【解析】【解答】解：原式＝（3 ）2﹣（）2＝18﹣6＝12.故答案为：12.【分析】干脆利用平方差公式去括号，再依据二次根式的性质化简，最终利用有理数的减法计算得出答案.25.【答案】 5【解析】【解答】原式=2+2 +3−2 =5.故答案为5.【分析】敏捷运用完全平方公式进行求解.26.【答案】；x=-4【解析】【解答】解：∵ ，∴分式与的最简公分母是，方程，去分母得：，去括号得：，移项合并得：，变形得：，解得：x=2或-4，∵当x=2时，=0，当x=-4时，≠0，∴x=2是增根，∴方程的解为：x=-4．【分析】依据最简公分母的定义得出结果，再解分式方程，检验，得解．27.【答案】【解析】【解答】解：=== ．故答案为．【分析】先将乘方绽开，然后用平方差公式计算即可．28.【答案】【解析】【解答】在函数中，分母不为0，则，即，故答案为：.【分析】在函数中，分母不为0，则x-3≠0，求出x的取值范围即可.29.【答案】【解析】【解答】解：由题意可知，第一行三个数的乘积为：，设其次行中间数为x ，则，解得，设第三行第一个数为y ，则，解得，∴2个空格的实数之积为．故答案为：．【分析】先将表格中最上一行的3个数相乘得到，然后中间一行的三个数相乘以及最终一行的三个数相等都是，即可求解．30.【答案】 -1【解析】【解答】∵分式的值不存在，∴x+1=0，解得：x=-1，故答案为：-1．【分析】依据分式无意义的条件列出关于x的方程，求出x的值即可．31.【答案】【解析】【解答】解：函数中：，解得：．故答案为：．【分析】干脆利用二次根式和分式有意义的条件列出不等式组求解即可．三、计算题32.【答案】解：原式，，．当时，原式【解析】【分析】首先计算小括号里面的分式的减法，然后再计算括号外分式的除法，化简后，再代入a 的值可得答案．33.【答案】解：÷＝÷＝×＝当x＝+1，y＝﹣1时原式＝＝2﹣．【解析】【分析】依据分式四则运算依次和运算法则对原式进行化简÷ ，得到最简形式后，再将x＝+1、y＝﹣1代入求值即可．34.【答案】解：，，，；∵ ，所以，原式．【解析】【分析】干脆利用分式的混合运算法则化简，再计算x，y的值，进而代入得出答案．35.【答案】解：原式== ，将代入得：原式=-4+3=-1，故答案为：-1.【解析】【分析】先依据分式混合运算的法则把原式进行化简，再把x=-4代入进行计算即可．36.【答案】（1）解：解不等式①，得：x＞﹣，解不等式②，得：x≤4，则不等式组的解集为﹣＜x≤4，∴不等式组的最小整数解为﹣2；（2）解：原式＝＝＝＝＝，∵a2+2a﹣15＝0，∴a2+2a＝15，则原式＝．【解析】【分析】（1）分别求出每一个不等式的解集，依据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集；（2）先依据分式的混合运算依次和运算法则化简原式，再由已知等式得出a2+2a＝15，整体代入计算可得．37.【答案】解：原式为==== ，又∵m满意，即，将代入上式化简的结果，∴原式= ．【解析】【分析】将分式运用完全平方公式及平方差公式进行化简，并依据m所满意的条件得出，将其代入化简后的公式，即可求得答案．38.【答案】解：当时，原式【解析】【分析】先依据分式的混合运算步骤进行化简，然后代入求值即可．39.【答案】解：时，原式=【解析】【分析】先利用分式的运算法则化简，然后代入计算即可．40.【答案】解：当上式【解析】【分析】先把分子、分母能分解因式的分解因式，再把除法转化为乘法，约分后再代入求值即可.41.【答案】解：原式＝＝＝﹣2﹣x.∵x≠1，x≠2，∴在0≤x≤2的范围内的整数选x＝0.当x＝0时，原式＝﹣2﹣0＝﹣2.【解析】【分析】先通分计算括号内异分母分式的减法，再将能分解因式的分子、分母分解因式，化除法为乘法进行约分化简，然后依据分式有意义的条件取x的值，代入求值即可.42.【答案】解：原式＝÷( ﹣)＝÷＝·＝，当x＝﹣2时，原式＝＝＝.【解析】【分析】先通分计算括号内异分母分式的减法，再将各个分式的分子、分母能分解因式的分别分解因式，同时将除法转变为乘法，约分化为最简形式，最终将x的值代入计算可得.43.【答案】（1）解：原式＝4m2+12mn+9n2﹣（4m2﹣n2）＝4m2+12mn+9n2﹣4m2+n2＝12mn+10n2；（2）解：原式＝＝＝＝.【解析】【分析】（1）依据完全平方公式，平方差公式去括号，再合并同类项即可；（2）括号内先通分计算，将各个分式的分子、分母能分解因式的分别分解因式，然后变除为乘，进行约分即可.44.【答案】原式．【解析】【分析】先计算肯定值运算、特别角的正切函数值、零指数幂、负整数指数幂，再计算实数的混合运算即可得．45.【答案】．【解析】【分析】依据负整指数幂的性质，特别角的三角函数值，肯定值，零指数幂的性质，干脆计算即可．46.【答案】（1）sin30°+ ﹣（3﹣）0+|﹣|＝+4﹣1+＝4；（2）3a2﹣48＝3（a2﹣16）＝3（a+4）（a﹣4）．【解析】【分析】（1）先用特别角的三角函数值、零指数幂的性质、肯定值的性质、算术平方根的学问化简，然后计算即可；（2）先提取公因式3，再运用平方差公式分解因式即可．四、解答题47.【答案】．将x=4代入可得:原式= ．【解析】【分析】先将代数式化简,再代入值求解即可．48.【答案】原式分式的分母不能为0解得：m不能为，0，3则选代入得：原式．【解析】【分析】先计算括号内的分式减法，再计算分式的除法，然后选一个使得分式有意义的x的值代入求值即可．五、综合题49.【答案】（1）原式（2）三；分式的基本性质；分式的分子与分母都乘（或除以）同一个不为零的整式，分式的值不变；五；括号前是“ ”号，去掉括号后，括号里的其次项没有变号（3）解：答案不唯一，如：最终结果应化为最简分式或整式；约分，通分时，应依据分式的基本性质进行变形；分式化简不能与解分式方程混淆，等．【解析】【解答】（2）任务一：①三；分式的基本性质；分式的分子与分母都乘（或除以）同一个不为零的整式，分式的值不变；故答案为：三；分式的基本性质；分式的分子与分母都乘（或除以）同一个不为零的整式，分式的值不变；②五；括号前是“ ”号，去掉括号后，括号里的其次项没有变号；故答案为：五；括号前是“ ”号，去掉括号后，括号里的其次项没有变号；【分析】（1）先分别计算乘方，与括号内的加法，再计算乘法，再合并即可得到答案；（2）先把能够分解因式的分子或分母分解因式，化简第一个分式，再通分化为同分母分式，依据同分母分式的加减法进行运算，留意最终的结果必为最简分式或整式．50.【答案】（1）===（2）∵ ，∴解得：将解集表示在数轴上如下：【解析】【分析】（1）依据新定义规定的运算法则列式，再由有理数的运算法则计算可得；（2）依据新定义列出关于x的不等式，解不等式即可得．。

中考数学总复习第05讲二次根式及其运算课件(考点精

考点2 二次根式的运算
【例2】（1）（2012·黔东南州）下列等式一定成立的是（ B ）
A. 9 4 5
B. 5 3 15
C. 9 3
D. 92 9
考点2 二次根式的运算
(2)计算： 24－ 23＋ 23－2
1 6
解原式＝2 6－12 6＋13 6－13 6＝32 6.
(3)(2012·南通) 计算： 48÷ 3－ 21× 12＋ 24 解原式＝ 16－ 6＋2 6＝4＋ 6.
求值问题“五招”
(1)巧用乘法公式；(2)巧用平方；(3)巧用配方； (4)巧用换元；(5)巧用倒数．
1.（2013·嘉兴）二次根式中 x 3 ，x的取值范围是 x≥3
2.（2011·杭州）下列各式中，正确的是（ B ）
A. 32 3
B. 32 3
C. 32 3
D. 32 3
3.（2012·金华）一个正方形的面积为15，估计它的边
(2)若几个非负数的和为零，则每一个非负数都等于零；
两个防范
(1)求 a2时，一定要注意确定 a 的大小，应注意利用等式 a2＝|a|，当问题中已知条件不能直接判定 a 的大小时就要分类讨论；
(2)一般情况下，我们解题时，总会习惯地把重点放在探求思路和计算结果上，而忽视了一些不太重要、不直接影响求解过程的附加条件．要特别注意，问题中的条件没有主次之分，都必须认真对待．
请完成考点跟踪突破
（3）（2012·安顺）计算 12 3 3 3 .
考点3 二次根式混合运算
【例 3】计算：(1)(3 2－1)(1＋3 2)－(2 2－1)2；解原式＝(3 2)2－1－[(2 2)2－4 2＋1] ＝18－1－8＋4 2－1＝8＋4 2.

2013届全国中考数学3年中考2年模拟之专题突破：3.3.2二次函数pdf版

上一动点（端点除外），过点犘作犘交犅连犇∥犃犆，犆于点犇，结犆犘．（）求该抛物线的解析式；１ ① 写出二次函数犔２与二次函数犔１有关图象的两条相同２（）当动点犘运动到何处时，的性质；犅犘＝犅犇·犅犆．２问线段犈８犽与抛物线犔２交于犈、犉两点，犉 ②若直线狔＝的长度是否发生变化？如果不会，请求出犈犉的长度；如果会，请说明理由．（第１２题）（第１０题）３２ ·广东）如图，抛物线狔＝１狓１１．（２０１２－狓－９与狓轴交于２２２ ·广东汕头）已知抛物线狔＝１狓３．（２０１１＋狓＋犮与狓轴没有与狔轴交于点犆，连结犅犃、犅两点，犆、犃犆．１２（）求犃交点．犅和犗犆的长；１（）点从点出发，沿轴向点运动（点与点、不（）求犮的取值范围；２犈犃狓犅犈犃犅１重合），过点犈作直线设犃交犃并说明理由．（）试确定直线狔＝犾平行犅犆，犆于点犇．犈的犮狓＋１经过的象限，２长为犿，的面积为，求关于的函数关系式，犇犈犛犛犿 △犃并写出自变量犿的取值范围．（第１１题）
化范围是（．）
２２ ·四川乐山）二次函数狔＝（ · 广西北海）二次函数狔＝狓）的图象的６１．（２０１２犪狓＋犫狓＋１犪≠ ．（２０１２－４狓＋５的顶点坐标为０顶点在第一象限，且过点（，）设狋，则狋值的变－１０．＝犪＋犫＋１．

二次根式2013年全国中考题

二次根式2013年全国中考题（2013•衡阳）计算的结果为（）A．B．C．3D．5考点：二次根式的乘除法；零指数幂．专题：计算题．分析：原式第一项利用二次根式的乘法法则计算，第二项利用零指数幂法则计算，即可得到结果．解答：解：原式=2+1=3．故选C点评：此题考查了二次根式的乘除法，以及零指数幂，熟练掌握运算法则是解本题的关键．（2013，娄底）式子有意义的的取值范围是（）A.B.C.D.（2013，永州）运用湘教版初中数学教材上使用的某种电子计算器求的近似值，其按键顺序正确的是()A.B.C.D.（2013，永州）已知,则的值为A.0B.C.1D.（2013凉山州）如果代数式有意义，那么x的取值范围是（）A．x≥0B．x≠1C．x＞0D．x≥0且x≠1考点：分式有意义的条件；二次根式有意义的条件．专题：计算题．分析：代数式有意义的条件为：x﹣1≠0，x≥0．即可求得x的范围．解答：解：根据题意得：x≥0且x﹣1≠0．解得：x≥0且x≠1．故选D．点评：式子必须同时满足分式有意义和二次根式有意义两个条件．分式有意义的条件为：分母≠0；二次根式有意义的条件为：被开方数≥0．此类题的易错点是忽视了二次根式有意义的条件，导致漏解情况．（2013•绵阳）的相反数是（）A．B．C．D．（2013鞍山）要使式子有意义，则x的取值范围是（）A．x＞0B．x≥﹣2C．x≥2D．x≤2考点：二次根式有意义的条件．分析：根据被开方数大于等于0列式计算即可得解．解答：解：根据题意得，2﹣x≥0，解得x≤2．故选D．点评：本题考查的知识点为：二次根式的被开方数是非负数．（2013•荆州）计算的结果是BA.+B.C.D.－（2013•武汉）式子在实数范围内有意义，则x的取值范围是（）A．答案：B解析：由二次根式的意义，知：x－1≥0，所以x≥1。

（2013•襄阳）使代数式有意义的x的取值范围是x≥且x≠3．考点：二次根式有意义的条件；分式有意义的条件．3801346分析：根据被开方数大于等于0，分母不等于0列式进行计算即可得解．解答：解：根据题意得，2x﹣1≥0且3﹣x≠0，解得x≥且x≠3．故答案为：x≥且x≠3．点评：本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．（2013•宜昌）若式子在实数范围内有意义，则的取值范围为（）A.=1B.≥1C.＞1D.＜12013•张家界）下列运算正确的是（D）A.3a-2a=1B.C.D.（2013•晋江）计算：.解：原式……………………………………………………………8分………（2013•龙岩）已知，则＝_________8___.．（2013•厦门）式子x－3在实数范围内有意义，则实数x的取值范围是x≥3．（2013•吉林省）计算：.（2013•苏州）若式子在实数范围内有意义，则x的取值范围是A．x>1B．x（2013•苏州）计算：．（2013•宿迁）计算的值是▲．（2013•南京）计算的结果是。

中考数学模拟题《二次根式》专项测试卷(附答案)

中考数学模拟题《二次根式》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________（36题）一单选题1．（2023·江苏徐州·2023 ） A ．25与30之间 B ．30与35之间C ．35与40之间D ．40与45之间2．（2023·黑龙江牡丹江·统考中考真题）函数1y x =+ 自变量x 的取值范围是（） A ．1x ≤B ．1x ≥-C ．1x <-D ．1x >3．（2023·江苏泰州·2(2)- ） A ．2±B ．2C ．4D 24．（2023·内蒙古赤峰·统考中考真题）如图 7的点可能是( )A ．点PB ．点QC ．点RD ．点S5．（2023·宁夏·23 ） A ．3.5和4之间 B ．4和4.5之间 C ．4.5和5之间D ．5和5.5之间6．（2023·山东潍坊·统考中考真题）在实数1 －1 0 2 最大的数是（）A ．1B ．－1C ．0D 27．（2023·四川绵阳·433x x -+x 有( ) A ．5个B ．3个C ．4个D ．2个二填空题8．（2023·吉林·统考中考真题）计算：5= . 9．（2023·湖北鄂州·16= ．10．（2023·江苏徐州·3x -x 的取值范围是． 11．（2023·辽宁营口·13x +x 的取值范围是．12．（2023·湖北恩施·= ．13．（2023·湖南娄底·统考中考真题）函数y x 的取值范围为．14．（2023·辽宁·a 的取值范围是．15．（2023= ．16．（2023·陕西·统考中考真题）如图在数轴上点A点B 与点A 位于原点的两侧且与原点的距离相等．则点B 表示的数是．17．（2023·湖南益阳· ．18．（2023·湖南常德·x 应满足的条件是．19．（2023·湖南·的点所表示的整数有．（写出一个即可）20．（2023·内蒙古·统考中考真题）若,a b 为两个连续整数且a b <，则a b += ．21．（2023·山东·统考中考真题）计算：211)3-⎛⎫+- ⎪⎝⎭．22．（2023·宁夏·统考中考真题）如图点A B C 在数轴上点A 表示的数是1- 点B 是AC 的中点线段AB =C 表示的数是．23．（2023·湖南湘西·统考中考真题）则x 的取值范围是．24．（2023·山东潍坊·统考中考真题）从中任意选择两个数分别填在算式()22+÷的“□”与“○”中计算该算式的结果是．（只需写出一种结果）三解答题25．（2023·湖南娄底·统考中考真题）计算：()020231tan 60π-+︒．26．（2023·甘肃兰州·36827．（2023·北京·统考中考真题）计算：114sin602123-⎛⎫︒++- ⎪⎝⎭28．（2023·湖南·统考中考真题）计算：()1120232sin 4522--⎛⎫+--︒- ⎪⎝⎭．29．（2023·黑龙江大庆·统考中考真题）计算：11122cos 452-⎛⎫-︒+ ⎪⎝⎭．30．（2023·辽宁沈阳·统考中考真题）计算：()()221202324sin 303-⎛⎫---︒ ⎪⎝⎭．31．（2023·湖南益阳·21313123⎛⎫--⨯- ⎪⎝⎭．32．（2023·四川德阳·统考中考真题）计算：0112cos302|2-⎛⎛⎫︒+-++ ⎪ ⎝⎭⎝33．（2023·宁夏·统考中考真题）计算：())21221tan 45--⨯-+︒34．（2023·江苏宿迁·()013tan 60π+--︒．35．（2023·山东济南·统考中考真题）计算：()1011tan 602π-⎛⎫++-︒ ⎪⎝⎭．36．（2023·陕西·(131()27--+-．参考答案一单选题1．（2023·江苏徐州·） A ．25与30之间 B ．30与35之间 C ．35与40之间D ．40与45之间【答案】D【详解】解∶∶160020232025<<．16002023202540202345< 202340与45之间．故选D ．【点睛】本题主要考查了估算无理数的大小正确估算无理数的取值范围是解题关键． 2．（2023·黑龙江牡丹江·统考中考真题）函数1y x =+ 自变量x 的取值范围是（） A ．1x ≤ B ．1x ≥-C ．1x <-D ．1x >【答案】B【分析】根据二次根式有意义的条件被开方数大于等于0知：10x +≥ 可求出x 的范围．【详解】解：根据题意得：10x +≥ 解得：1x ≥- 故选：B ．【点睛】本题考查的是函数自变量取值范围的求法．函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时自变量可取全体实数（2）当函数表达式是分式时考虑分式的分母不能为0 （3）当函数表达式是二次根式时被开方数非负．3．（2023·江苏泰州·2(2)- ） A ．2± B ．2C ．4D 2【答案】B【分析】直接利用二次根式的性质化简得出答案． 2(2)42-=．故选：B ．【点睛】此题主要考查了二次根式的性质与化简正确化简二次根式是解题关键． 4．（2023·内蒙古赤峰·统考中考真题）如图 7的点可能是( )A ．点PB ．点QC ．点RD ．点S【答案】B7 看它介于哪两个整数之间从而得解．【详解】解：∶479<<<<即23∶Q故选：B．【点睛】本题考查无理数的大小估算5．（2023·宁夏·）A．3.5和4之间B．4和4.5之间C．4.5和5之间D．5和5.5之间【答案】C【分析】先找到所求的无理数在哪两个和它接近的有理数之间然后判断出所求的无理数的范围．<23<【详解】∶1625∶45<排除A和D又∶23更接近2554.5和5之间故选：C．【点睛】此题主要考查了无理数的大小估算现实生活中经常需要估算估算应是我们具备的数学能力“夹逼法”是估算的一般方法也是常用方法．6．（2023·山东潍坊·统考中考真题）在实数1 －1 0 最大的数是（）A．1B．－1C．0D【答案】D【分析】正数大于0 负数小于0 两个正数较大数的算术平方根大于较小数的算术平方根．【详解】解：21>1>=101故选：D．【点睛】本题考查实数的大小比较二次根式的化简掌握二次根式的性质公式是解题的关键．7．（2023·四川绵阳·x有()【答案】C 【详解】∶433x x -+ ∶30430x x +>⎧⎨-≥⎩，，解得：433x -<≤又∶x 要取整数值 ∶x 的值为：-2 -1 0 1. 即符合条件的x 的值有4个. 故选C.二填空题8．（2023·吉林·统考中考真题）计算：5= . 5【分析】根据负数的绝对值是它的相反数可得答案．【详解】解：|55 59．（2023·湖北鄂州·16= ．【答案】4【分析】根据算术平方根的概念求解即可．算术平方根的定义：一个非负数的正的平方根即为这个数的算术平方根由此即可求出结果．【详解】解：原式24．故答案为4．【点睛】此题主要考查了算术平方根的定义算术平方根的概念易与平方根的概念混淆而导致错误． 10．（2023·江苏徐州·3x -x 的取值范围是．【答案】3x ≥/3x ≤3x -30x -≥ 再求出答案即可．【详解】解：∶3x -有意义∶30x -≥ 解得：3x ≥ 故答案为：3x ≥．【点睛】本题考查了二次根式有意义的条件 30x -≥是解此题的关键．11．（2023·辽宁营口·x 的取值范围是．【答案】13x ≥-【分析】根据二次根式有意义的条件得到130x +≥ 解不等式即可得到答案．【详解】解：∶ ∶130x +≥ 解得13x ≥-故答案为：13x ≥-【点睛】此题考查了二次根式有意义的条件熟知被开方式为非负数是解题的关键．12．（2023·湖北恩施·= ．【答案】6【分析】利用二次根式的乘法法则进行求解即可．6=．故答案为：6．【点睛】本题考查了二次根式的乘法熟练掌握二次根式的乘法法则和二次根式的性质是解题的关键．13．（2023·湖南娄底·统考中考真题）函数y x 的取值范围为．【答案】x≥－1【详解】由题意得 x+1≥0 解得x≥﹣1．故答案为x≥﹣1．14．（2023·辽宁·a 的取值范围是．【答案】2a ≥【分析】根据二次根式有意义则被开方数是非负数列式求解即可．【详解】解：∶2a-∶20a-≥a≥．∶2a≥．故答案为：2a a≥的式子叫二次根式二次根式中的被开方数必须是非【点睛】本题考查了二次根式的定义)0负数否则二次根式无意义熟练掌握二次根式有意义的条件是解题的关键．15．（20234=．【答案】2【分析】根据算术平方根进行计算即可求解．4=2故答案为：2．【点睛】本题考查了求一个数的算术平方根熟练掌握算术平方根的定义是解题的关键．16．（2023·陕西·统考中考真题）如图在数轴上点A3点B与点A位于原点的两侧且与原点的距离相等．则点B表示的数是．【答案】3-【分析】由绝对值的定义再根据原点左边的数是负数即可得出答案．【详解】解：由题意得：点B表示的数是3故答案为：3-【点睛】此题考查了数轴绝对值的意义掌握绝对值的意义是解本题的关键．17．（2023·湖南益阳·205=．【答案】10【分析】根据二次根式的乘法法则计算即可．⨯．205=20510010故答案为：10．a b ab．18．（2023·湖南常德·4x-x应满足的条件是．【答案】4x ≥/4x ≤【分析】根据二次根式有意义的条件求解即可．【详解】根据题意得：40x -≥ 解得：4x ≥ 故答案为：4x ≥．【点睛】本题考查二次根式有意义的条件熟练掌握二次根式有意义需被开方数大于等于0是解题的关键．19．（2023·湖南·的点所表示的整数有．（写出一个即可）【答案】2（答案不唯一）【分析】根据实数与数轴的对应关系且为整数再利用无理数的估算即可求解．【详解】解：设所求数为a a < 且为整数则a <即23<< ∶a 可以是2±或1±或0．故答案为：2（答案不唯一）．【点睛】本题考查了实数与数轴无理数的估算掌握数轴上的点到原点距离的意义是解题的关键．20．（2023·内蒙古·统考中考真题）若,a b 为两个连续整数且a b <，则a b += ．【答案】3【分析】根据夹逼法求解即可．【详解】解：∶2132<< 即22212<<∶12< ∶1,2a b == ∶3a b +=．故答案为：3．【点睛】题目主要考查无理数的估算熟练掌握估算方法是解题关键．21．（2023·山东·统考中考真题）计算：2031(21)83-⎛⎫+-⎪⎝⎭．【答案】8【分析】根据零次幂负整数指数幂和立方根的性质化简然后计算即可．【详解】解：原式192=+-8=故答案为：8．【点睛】本题考查了实数的混合运算熟练掌握零次幂负整数指数幂和立方根的性质是解题的关键．22．（2023·宁夏·统考中考真题）如图点A B C在数轴上点A表示的数是1-点B是AC的中点线段2AB=C表示的数是．【答案】221【分析】根据两点间的距离公式和中点平分线段进行计算即可．【详解】解：∶点B是AC的中点线段2AB=∶22AC=∶点C表示的数是：221故答案为：221．【点睛】本题考查数轴上两点间的距离以及线段的中点．熟练掌握线段中点的定义以及数轴上两点间的距离公式是解题的关键．23．（2023·湖南湘西·统考中考真题）210x-则x的取值范围是．【答案】5x≥【分析】根据二次根式有意义的条件可直接进行求解．210x-2100x-≥解得：5x≥故答案为5x≥．【点睛】本题主要考查二次根式有意义的条件熟练掌握二次根式有意义的条件是解题的关键．24．（2023·山东潍坊·统考中考真题）从2-36中任意选择两个数分别填在算式()22+÷的“□”与“○”中计算该算式的结果是．（只需写出一种结果）6 写出一种结果即可）【分析】先利用完全平方公式计算二次根式的乘法再计算二次根式的除法即可得．【详解】解：∶选择则(()223=-(5=-5==∶选择则(()226-(8=-8==∶则()236+(9=+9=6=．6 写出一种结果即可）．【点睛】本题考查了二次根式的乘除法熟练掌握二次根式的运算法则是解题关键．三解答题25．（2023·湖南娄底·统考中考真题）计算：()020231tan 60π-+︒．【答案】【分析】先计算零次幂化简绝对值化简二次根式求解特殊角的正切再合并即可．【详解】解：()02023138tan 60π-+︒ 13123=+22=【点睛】本题考查的是含特殊角的三角函数值的混合运算零次幂的含义化简绝对值二次根式熟记相关概念与运算法则是解本题的关键．26．（2023·甘肃兰州·368 2【分析】根据二次根式乘法加减法运算法则计算即可．【详解】解：原式＝32222【点睛】本题考查了二次根式的混合运算熟练掌握二次根式的化简方法是解题的关键．27．（2023·北京·统考中考真题）计算：114sin602123-⎛⎫︒++- ⎪⎝⎭【答案】5【分析】代入特殊角三角函数值利用负整数指数幂绝对值和二次根式的性质化简然后计算即可．【详解】解：原式343223=++-233223=+-5=．【点睛】本题考查了实数的混合运算牢记特殊角三角函数值熟练掌握负整数指数幂绝对值和二次根式的性质是解题的关键．28．（2023·湖南·统考中考真题）计算：()1120232sin 4522--⎛⎫+--︒- ⎪⎝⎭．【答案】1-【分析】分别根据绝对值零指数幂的运算法则及负整数指数幂的运算法则特殊角的三角函数值计算出各数再根据实数混合运算的法则进行计算即可．【详解】解：原式22122=- 2122=1=-．【点睛】本题考查绝对值零指数幂的运算法则负整数指数幂的运算法则特殊角的三角函数值熟知各个运算法则是解答此题的关键．29．（2023·黑龙江大庆·统考中考真题）计算：1112cos 452-⎛⎫-︒+ ⎪⎝⎭．【答案】1【分析】首先去绝对值符号代入特殊角的三角函数值以及负整数幂的运算然后进行加减法．【详解】解：原式＝﹣﹣＝﹣ =1．【点睛】本题考查实数的运算掌握负整数幂以及牢记特殊角的三角函数值是解决问题的关键．30．（2023·辽宁沈阳·统考中考真题）计算：()2120234sin 303-⎛⎫--︒ ⎪⎝⎭．【答案】10【分析】根据零指数幂和负整数指数幂运算法则二次根式性质特殊角的三角函数值进行计算即可．【详解】解：()2120234sin 303-⎛⎫--︒ ⎪⎝⎭2112342=++-⨯392=+-10=．【点睛】本题主要考查了实数混合运算解题的关键是熟练掌握零指数幂和负整数指数幂运算法则二次根式性质特殊角的三角函数值准确计算．31．（2023·湖南益阳·211123⎛⎫--⨯- ⎪⎝⎭．【分析】先化简绝对值计算二次根式的乘方运算有理数的乘法运算再合并即可．211123⎛⎫--⨯- ⎪⎝⎭134=-+【点睛】本题考查的是化简绝对值二次根式的乘方运算实数的混合运算掌握实数的混合运算的运算法则是解本题的关键．32．（2023·四川德阳·统考中考真题）计算：01192cos3032|924-⎛⎛⎫︒+-++ ⎪ ⎝⎭⎝【答案】4【分析】先计算锐角的余弦负整数指数幂化简绝对值零次幂算术平方根再合并即可．【详解】解：01192cos3032|2924-⎛⎛⎫︒+-++ ⎪ ⎝⎭⎝()3222313=-++ ()322313=-++ 4=．【点睛】本题考查的是实数的混合运算负整数指数幂的含义零次幂的含义求解算术平方根特殊角的三角函数值熟记运算法则与运算顺序是解本题的关键．33．（2023·宁夏·统考中考真题）计算：()()212231tan 45--⨯-+︒【答案】43【分析】先化简各式在按照运算顺序进行计算即可．【详解】解：原式143112=⨯+2311=+43=【点睛】本题考查特殊角三角函数值实数的混合运算．解题的关键是熟记特殊角的三角函数值掌握相关运算法则正确的进行计算．34．（2023·江苏宿迁·()0313tan 60π+--︒．【答案】0【分析】根据去绝对值运算零指数幂运算及特殊角的三角函数值分别计算后再根据二次根式加减运算法则求解即可得到答案．()0313tan 60π+--︒ 3113=+0=．【点睛】本题考查二次根式加减运算涉及去绝对值运算零指数幂运算及特殊角的三角函数值熟练掌握相关运算法则是解决问题的关键．35．（2023·山东济南·统考中考真题）计算：()1011tan 602π-⎛⎫++-︒ ⎪⎝⎭．【答案】3【分析】根据绝对值的意义负整数指数幂零指数幂以及特殊角的三角函数值分别计算后再根据二次根式加减运算法则求解即可得到答案．【详解】解：()1011tan 602π-⎛⎫+++-︒ ⎪⎝⎭21=+3=．【点睛】本题考查了绝对值的意义负整数指数幂运算零指数幂运算特殊角的三角函数值二次根式加减运算熟练掌握相关运算法则是解本题的关键．36．（2023·陕西·(131()27--+-．【答案】1-【分析】直接利用二次根式的乘法运算法则以及负整数指数幂的性质绝对值的性质分别化简进而得出答案．【详解】解：原式＝﹣7+|﹣8|78=-+＝﹣1．【点睛】此题主要考查了实数的运算正确化简各数是解题关键．。

2013届全国中考数学3年中考2年模拟之专题突破：1.5二次根式pdf版

一、选择题
槡
槡
（槡）
（）
（
）
（
）
V
在数学史上，瑞士的伯努利家族培养出很多优秀的数学家，其中最著名的数学家是雅可比 · 伯努利，他
发明了“ 等角螺线” 在等角螺线中，任意一点画出的连线与该点切线永远保持一定角度，故取此名．有一种说．法是雅可比·伯努利要求自己死后在墓碑上刻上等角螺线并写上 “ 纵然改变，依然故我（Ｅａｄｅｒｎｍｕｔａｔａｒｅ） ” 的碑文，不过错误理解等角螺线的雕刻师把旋涡状花纹刻了上去．ｓｕｒｏｇ
１．５二次根式 Nhomakorabea内容清单二次根式的概念二次根式的加、减运算法则二次根式的乘、除运算法则
能力要求能利用二次根式概念判断二次根式存在的可能性．会利用二次根式的加减法则进行加减运算．能根据先乘除后加减法则进行二次根式的混合运算．
*
香农在信息论领域中研究了８年后，发表了信息论的奠基之作— — —《通信的数学理论》次年，又发表了《噪声１９４８年，．下的通信》在这两篇文章中，他经典地阐明了通信的基本问题，提出了通信系统的模型，给出了信息量的数学表达式，解决．了信息容量、信源统计特性、信源编码、信道编码等有关精确地传送通信符号的基本技术问题．
方法、技巧．实数的运２．要特别注意二次根式运算的法则、趋势总揽三角函数等组成的混合算式的计算，一般考查时多算主要是由二次根式、２０１３年对二次根式的考查仍将以基本题型为主，难度不大，运算时要认真审题，确定符号，明确运算顺序，灵活运以填空题、选择题的形式出现，题目中包含若干个知识点，同时渗透数形结合的思想．其中重点考查最简二次根式、同类二次根

2013中考数学提高测试《二次根式》

《二次根式》提高测试（一）判断题：（每小题1分，共5分）1．ab 2)2(-＝－2ab ．…………………（）【提示】2)2(-＝|－2|＝2．【答案】×． 2．3－2的倒数是3＋2．（）【提示】231-＝4323-+＝－（3＋2）．【答案】×．3．2)1(-x ＝2)1(-x ．…（）【提示】2)1(-x ＝|x －1|，2)1(-x ＝x －1（x ≥1）．两式相等，必须x ≥1．但等式左边x 可取任何数．【答案】×． 4．ab 、31b a 3、ba x2-是同类二次根式．…（）【提示】31b a 3、ba x2-化成最简二次根式后再判断．【答案】√． 5．x 8，31，29x +都不是最简二次根式．（）29x +是最简二次根式．【答案】×．（二）填空题：（每小题2分，共20分）6．当x __________时，式子31-x 有意义．【提示】x 何时有意义？x ≥0．分式何时有意义？分母不等于零．【答案】x ≥0且x≠9． 7．化简－81527102÷31225a＝_．【答案】－2aa ．【点评】注意除法法则和积的算术平方根性质的运用．8．a －12-a 的有理化因式是____________．【提示】（a －12-a ）（________）＝a 2－22)1(-a ．a ＋12-a ．【答案】a ＋12-a ．9．当1＜x ＜4时，|x －4|＋122+-x x ＝________________．【提示】x 2－2x ＋1＝（）2，x －1．当1＜x ＜4时，x －4，x －1是正数还是负数？ x －4是负数，x －1是正数．【答案】3． 10．方程2（x －1）＝x ＋1的解是____________．【提示】把方程整理成ax ＝b 的形式后，a 、b 分别是多少？12-，12+．【答案】x ＝3＋22．11．已知a 、b 、c 为正数，d 为负数，化简2222dc abd c ab +-＝______．【提示】22d c ＝|cd |＝－cd ．【答案】ab ＋cd ．【点评】∵ ab ＝2)(ab （ab ＞0），∴ ab －c 2d 2＝（cd ab +）（cd ab -）．12．比较大小：－721_________－341．【提示】27＝28，43＝48．【答案】＜．【点评】先比较28，48的大小，再比较281，481的大小，最后比较－281与－481的大小．13．化简：(7－52)2000·(－7－52)2001＝______________．【提示】(－7－52)2001＝(－7－52)2000·（_________）[－7－52．]（7－52）·（－7－52）＝？[1．]【答案】－7－52．【点评】注意在化简过程中运用幂的运算法则和平方差公式． 14．若1+x ＋3-y ＝0，则(x －1)2＋(y ＋3)2＝____________．【答案】40．【点评】1+x ≥0，3-y ≥0．当1+x ＋3-y ＝0时，x ＋1＝0，y －3＝0．15．x ，y 分别为8－11的整数部分和小数部分，则2xy －y 2＝____________．【提示】∵ 3＜11＜4，∴ _______＜8－11＜__________．[4，5]．由于8－11介于4与5之间，则其整数部分x ＝？小数部分y ＝？[x ＝4，y ＝4－11]【答案】5．【点评】求二次根式的整数部分和小数部分时，先要对无理数进行估算．在明确了二次根式的取值范围后，其整数部分和小数部分就不难确定了．（三）选择题：（每小题3分，共15分）16．已知233x x +＝－x 3+x ，则………………（）（A ）x ≤0 （B ）x ≤－3 （C ）x ≥－3 （D ）－3≤x ≤0【答案】D ．【点评】本题考查积的算术平方根性质成立的条件，（A ）、（C ）不正确是因为只考虑了其中一个算术平方根的意义． 17．若x ＜y ＜0，则222y xy x +-＋222y xy x ++＝………………………（）（A ）2x （B ）2y （C ）－2x （D ）－2y【提示】∵ x ＜y ＜0，∴ x －y ＜0，x ＋y ＜0．∴222y xy x +-＝2)(y x -＝|x －y |＝y －x ．222y xy x ++＝2)(y x +＝|x ＋y |＝－x －y ．【答案】C ．【点评】本题考查二次根式的性质2a ＝|a |．18．若0＜x ＜1，则4)1(2+-xx －4)1(2-+xx 等于………………………（）（A ）x2 （B ）－x2 （C ）－2x （D ）2x 【提示】(x －x 1)2＋4＝(x ＋x1)2，(x ＋x1)2－4＝(x －x1)2．又∵ 0＜x ＜1，∴ x ＋x1＞0，x －x1＜0．【答案】D ．【点评】本题考查完全平方公式和二次根式的性质．（A ）不正确是因为用性质时没有注意当0＜x ＜1时，x －x1＜0．19．化简aa 3-(a ＜0)得………………………………………………………………（）（A ）a - （B ）－a （C ）－a - （D ）a【提示】3a -＝2a a ⋅-＝a -·2a ＝|a |a -＝－a a -．【答案】C ．20．当a ＜0，b ＜0时，－a ＋2ab －b 可变形为………………………………………（）（A ）2)(b a + （B ）－2)(b a -（C ）2)(b a -+- （D ）2)(b a ---【提示】∵ a ＜0，b ＜0，∴ －a ＞0，－b ＞0．并且－a ＝2)(a -，－b ＝2)(b -，ab ＝))((b a --．【答案】C ．【点评】本题考查逆向运用公式2)(a ＝a （a ≥0）和完全平方公式．注意（A ）、（B ）不正确是因为a ＜0，b ＜0时，a 、b 都没有意义．（四）在实数范围内因式分解：（每小题3分，共6分）21．9x 2－5y 2；【提示】用平方差公式分解，并注意到5y 2＝2)5(y ．【答案】（3x ＋5y ）（3x －5y ）．22．4x 4－4x 2＋1．【提示】先用完全平方公式，再用平方差公式分解．【答案】(2x ＋1)2(2x －1)2．（五）计算题：（每小题6分，共24分）23．（235+-）（235--）；【提示】将35-看成一个整体，先用平方差公式，再用完全平方公式．【解】原式＝(35-)2－2)2(＝5－215＋3－2＝6－215．24．1145-－7114-－732+；【提示】先分别分母有理化，再合并同类二次根式．【解】原式＝1116)114(5-+－711)711(4-+－79)73(2--＝4＋11－11－7－3＋7＝1．25．（a 2mn －mab mn ＋mn nm ）÷a 2b 2mn ；【提示】先将除法转化为乘法，再用乘法分配律展开，最后合并同类二次根式．【解】原式＝（a 2mn －m ab mn ＋m n n m ）·221ba nm＝21b nm mn ⋅－mab1nm mn ⋅＋22bma n nmn m ⋅ ＝21b －ab1＋221ba ＝2221ba ab a +-．26．（a ＋ba ab b +-）÷（bab a +＋aab b -－abb a +）（a ≠b ）．【提示】本题应先将两个括号内的分式分别通分，然后分解因式并约分．【解】原式＝ba abb ab a +-++÷))(())(()()(b a b a ab b a b a b a b b b a a a -+-+-+--＝ba b a ++÷))((2222b a b a ab ba b ab b ab a a -++----＝ba b a ++·)())((b a ab b a b a ab +-+-＝－b a +．【点评】本题如果先分母有理化，那么计算较烦琐．（六）求值：（每小题7分，共14分）27．已知x ＝2323-+，y ＝2323+-，求32234232yx y x y x xyx ++-的值．【提示】先将已知条件化简，再将分式化简最后将已知条件代入求值．【解】∵ x ＝2323-+＝2)23(+＝5＋26，y ＝2323+-＝2)23(-＝5－26．∴ x ＋y ＝10，x －y ＝46，xy ＝52－(26)2＝1．32234232yx y x y x xyx ++-＝22)())((y x y x y x y x x +-+＝)(y x xy y x +-＝10164⨯＝652．【点评】本题将x 、y 化简后，根据解题的需要，先分别求出“x ＋y ”、“x －y ”、“xy ”．从而使求值的过程更简捷． 28．当x ＝1－2时，求2222ax xa x x+-+＋222222ax x x ax x +-+-＋221ax +的值．【提示】注意：x 2＋a 2＝222)(a x +，∴ x 2＋a 2－x 22a x +＝22a x +（22a x +－x ），x 2－x22a x +＝－x （22a x +－x ）．【解】原式＝)(2222x a x a x x-++－)(22222x a x x ax x -++-＋221ax +＝)()()2(22222222222x ax a x xx ax x a x x a x x -++-+++-+-＝)()(22222222222222x a x a x x x a x x a x a x x x -++-+++++-=)()(222222222x a x a x x a x x a x -+++-+＝)()(22222222x a x a x xx a x a x -++-++＝x1．当x ＝1－2时，原式＝211-＝－1－2．【点评】本题如果将前两个“分式”分拆成两个“分式”之差，那么化简会更简便．即原式＝)(2222x a x a x x-++－)(22222x a x x ax x -++-＋221ax +＝)11(2222ax x a x +--+－)11(22xxa x --+＋221ax +＝x1．七、解答题：（每小题8分，共16分）29．计算（25＋1）（211+＋321+＋431+＋…＋100991+）．【提示】先将每个部分分母有理化后，再计算．【解】原式＝（25＋1）（1212--＋2323--＋3434--＋…＋9910099100--）＝（25＋1）[（12-）＋（23-）＋（34-）＋…＋（99100-）]＝（25＋1）（1100-）＝9（25＋1）．【点评】本题第二个括号内有99个不同分母，不可能通分．这里采用的是先分母有理化，将分母化为整数，从而使每一项转化成两数之差，然后逐项相消．这种方法也叫做裂项相消法． 30．若x ，y 为实数，且y ＝x 41-＋14-x ＋21．求xy yx ++2－xy yx +-2的值．【提示】要使y 有意义，必须满足什么条件？].014041[⎩⎨⎧≥-≥-x x 你能求出x ，y 的值吗？].2141[⎪⎪⎩⎪⎪⎨⎧==y x【解】要使y 有意义，必须⎩⎨⎧≥-≥-014041[x x ，即⎪⎪⎩⎪⎪⎨⎧≥≤.4141x x ∴ x ＝41．当x ＝41时，y ＝21．又∵x y y x ++2－xy yx +-2＝2)(xy yx +－2)(xy yx -＝|xy yx +|－|xy yx -|∵ x ＝41，y ＝21，∴ y x ＜x y ．∴ 原式＝xy yx +－yx xy +＝2yx 当x ＝41，y ＝21时，原式＝22141＝2．【点评】解本题的关键是利用二次根式的意义求出x 的值，进而求出y 的值．。

2013年历年全国初三数学中考1.5二次根式冲刺押题训练及答案

第1章数与式1.5二次根式1．16的平方根是（）． A ．±4 B ．4 C ．±2 D ．2答案：C 【解析】16＝4，4的平方根是±2． 2．若x ＝a －b ，y ＝a +b ，则xy 的值为（）．A ．2aB ．2bC ．a ＋bD ．a －b答案：D【解析】本题主要考查平方差公式．xy ＝（a －b ）（a +b ）＝（a ）2－（b ）2＝a －b.3．若化简｜1－x ｜－1682+-x x 的结果为2x －5，则x 的取值范围是（）．A ．x 任意实数B ．1≤x ≤4C ．x ≥1D ．x ≤4答案：B【解析】原式＝（x －1）－（4－x ）＝2x －5．∴ 1－x ≤0，x －4≤0，即 1≤x ≤4．4．实数a ，b 在数轴上的位置如图所示，化简2a －2b －2)(b a -答案：－2b【解析】本题主要考查无理数、二次根式及绝对值的知识，在计算时应灵活运用2a ＝｜a ｜．5．计算：2sin60°＋)21(--1－2)32(-÷0)212(-．答案：原式＝2×23＋（－2）－（3－2）÷1＝3－2－3＋2＝2－2． 6．计算：（－2）2－8 ＋（1－3 ）0．答案：原式＝4－22＋1＝5－22．7．计算：（1）（7）2－2)3(--3512.0×1691；（2）343x 3－38-=625．答案：（1）原式＝7－3－0．8×45＝3．（2）343x 3－38-=625，343x 3－（－2）＝－25，343x 3＝－27，x 3＝34327-， x ＝334327-＝－73． 8．判断下面各式是否成立：（1）322＝232；（2）833＝383；（3）1544＝4154．探究：（1）你判断完上面各题后，发现了什么规律？并猜想：2455＝；（2）用含有n 的代数式将规律表示出来，说明n 的取值范围，。