高考数学复习、高中数学 独立性检验附答案解析
新高考数学复习考点知识讲解11---列联表与独立性检验
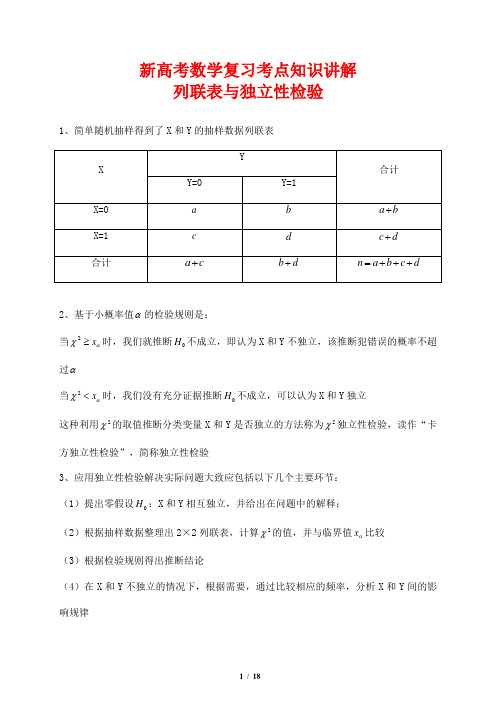
新高考数学复习考点知识讲解列联表与独立性检验1、简单随机抽样得到了X 和Y 的抽样数据列联表2、基于小概率值α的检验规则是:当αχx ≥2时,我们就推断0H 不成立,即认为X 和Y 不独立,该推断犯错误的概率不超过α当αχx <2时,我们没有充分证据推断0H 不成立,可以认为X 和Y 独立这种利用2χ的取值推断分类变量X 和Y 是否独立的方法称为2χ独立性检验,读作“卡方独立性检验”,简称独立性检验3、应用独立性检验解决实际问题大致应包括以下几个主要环节: (1)提出零假设0H :X 和Y 相互独立,并给出在问题中的解释; (2)根据抽样数据整理出2×2列联表,计算2χ的值,并与临界值αx 比较 (3)根据检验规则得出推断结论(4)在X 和Y 不独立的情况下,根据需要,通过比较相应的频率,分析X 和Y 间的影响规律题型一 变量关系例 1 为了判断两个分类变量X 、Y 是否有关系,应用独立性检验的方法算得2K 的观测值为5,则下列说法中正确的是( ) A .有95%的把握认为“X 和Y 有关系” B .有95%的把握认为“X 和Y 没有关系” C .有99%的把握认为“X 和Y 有关系” D .有99%的把握认为“X 和Y 没有关系” 【答案】A 【分析】利用2K 的观测值与临界值进行比较得解. 【详解】因为2( 3.841)0.050P K =≥,5 3.841>,所以有95%的把握认为“X 和Y 有关系”. 故选:A若由一个22⨯列联表中的数据计算得2 4.013K =,那么有( )把握认为两个变量有关系.知识典例巩固练习()20P K k ≥ 0.500.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.0010k0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828A .95%B .97.5%C .99%D .99.9%【答案】A 【分析】由2 3.841K >可对照临界值表得到结果. 【详解】2 4.013 3.841K =>,∴有()10.05100%95%-⨯=的把握认为两个变量有关系. 故选:A.题型二 列联表例 2 如表是一个2×2列联表:则表中a ,b 的值分别为( )y 1 y 2 合计x 1 a21 73x 2 22 25 47合计 b 46 120A .94,72B .52,50C .52,74D .74,52【答案】C 【分析】根据表中数据简单计算即可. 【详解】a =73-21=52,b =a +22=52+22=74. 故选:C.下面是一个22⨯列联表:1y 2y总计 1x35 a 70 2x15 1530 总计 50b100其中,a b 处填的值分别为_______. 【答案】35,50. 【分析】由列联表易得结果. 【详解】由3570a +=,得35a =,15a b +=,得50b =.巩固练习故答案为:35,50.题型三 独立性检验应用例 3 2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类智慧的胜利,也有许多人持反对意见,有网友为此在某大学进行了调查,参加调查的共80位学生,调查数据的22⨯列联表如下所示: 持反对意见 赟同 总计男40 女 5总计2580(1)①请将列联表补充完整;②请根据表中数据判断,能否有的99.9%把握认为是否持反对意见与性别有关; (2)若表中持反对意见的5个女学生中,3个是大三学生,2个是大四学生.现从这5个学生中随机选2个学生进行进一步调查,求这2个学生是同一年级的概率.附参考公式及数据:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.()20P K k ≥ 0.40 0.25 0.10 0.010 0.005 0.001 0k7.879 1.3232.7066.6357.87910.828【答案】(1)①列联表见解析,②有99.9%的把握认为是否持反对意见与性别有关;(2)25.【分析】()1①由已知数据得出列联表;②由题可知,计算2K 的观测值013.09110.828k ≈>,可得出结论;()2记3个大三学生分别为,123,,,2A A A 个大四学生分别为12,B B 、运用列举法列出所有事件,由古典概率公式可得答案. 【详解】()1①②由题可知,2K 的观测值2080203552013.09110.828404055(25)k ⨯-⨯=≈>⨯⨯⨯所以有99.9%的把握认为是否持反对意见与性别有关.()2记3个大三学生分别为,123,,,2A A A 个大四学生分别为12,B B 、则从中抽取2个的基本事件有:1213231213112223212,,,,,,,,,A A A A A A AB A B A B A B A B A B B B ,共10个,其中抽取的2人是同一年级的基本事件有12132312,,,A A A A A A B B 共4个, 则这2个学生是同一年级的概率为42105P ==.这一年来人类与新型冠状病毒的“战争”让人们逐渐明白一个道理,人类社会组织模式的差异只是小事情,病毒在地球上存在了三四十亿年,而人类的文明史不过只有几千年而已,人类无法消灭病毒,只能与之共存,或者病毒自然消亡,在病毒面前,个体自由要服从于集体或者群体生命的价值.在传染病学中,通常把从致病刺激物侵入机体内或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期,因此我们应该注意做好良好的防护措施和隔离措施.某研究团队统计了某地区10000名患者的相关信息,得到如表表格: 潜伏期(天)(]0,2(]2,4(]4,6(]6,8(]8,10 (]10,12 (]12,14人数6001900300025001600250150(1)新冠肺炎的潜伏期受诸多因素的影响,为研究潜伏期与年龄的关系,通过分层抽样从10000名患者中抽取200人进行研究,完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关?潜伏期8≤天潜伏期8>天总计 60岁以上(含60岁)150 60岁以下 30 总计200(2)依据上述数据,将频率作为概率,且每名患者的潜伏期是否超过8天相互独立.为了深入研究,该团队在这一地区抽取了20名患者,其中潜伏期不超过8天的人数最有巩固练习可能是多少?附:()()()()()22n ad bcKa b c d a c b d-=++++.【答案】(1)表格见解析,能;(2)16名.【分析】(1)由表中数据可知,求得潜伏期大于8天的人数,列出2×2列联表,利用公式求得2K的值,结合附表,即可得到结论;(2)求得该地区10000名患者中潜伏期不超过8天的人数,求得潜伏期不超过8天的概率,进而抽取的20名患者中潜伏期不超过8天的人数.【详解】(1)由表中数据可知,潜伏期大于8天的人数为16002501502004010000++⨯=人,补充完整的2×2列联表如下,所以()2220013*********.66710.8281505016040K ⨯⨯-⨯=≈>⨯⨯⨯, 故能在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关.(2)该地区10000名患者中潜伏期不超过8天的人数为6001900300025008000+++=名,将频率视为概率,潜伏期不超过8天的概率为80004100005=, 所以抽取的20名患者中潜伏期不超过8天的人数最有可能是420165⨯=名.1、为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算得x 2=7.01,则认为“喜欢乡村音乐与性别有关系”的把握约为( )A .0.1%B .1%C .99%D .99.9%【答案】C 【分析】由x 2=7.01>6.635,对照临界值表求解即可.巩固提升【详解】易知x2=7.01>6.635,对照临界值表知,有99%的把握认为喜欢乡村音乐与性别有关系.故选:C2、某班主任对全班50名学生进行了作业量的评价调查,所得数据如表所示:则认为作业量的大小与学生的性别有关的犯错误的概率不超过()A.0.01 B.0.05C.0.10 D.无充分证据【答案】B【分析】计算2K,再进行判断.【详解】因为2250(181598)5.059 3.84127232624K⨯⨯-⨯=≈>⨯⨯⨯,又()2 3.8410.05P K≥=所以认为作业量的大小与学生的性别有关的犯错误的概率不超过0.05. 故选:B3、(多选)有关独立性检验的四个命题,其中正确的是()A.两个变量的2×2列联表中,对角线上数据的乘积相差越大,说明两个变量有关系成立的可能性就越大B.对分类变量X与Y的随机变量2K的观测值k来说,k越小,“X与Y有关系”的可信程度越小C.从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,我们说某人秃顶,那么他有95%的可能患有心脏病D.从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关【答案】ABD【分析】根据独立性检验的原理与知识,对选项中的命题判断正误即可.【详解】选项A,两个变量的2×2列联表中,对角线上数据的乘积相差越大,则2K观测值越大,两个变量有关系的可能性越大,所以选项A正确;选项B,根据2K的观测值k越小,原假设“X与Y没关系”成立的可能性越大,则“X与Y有关系”的可信度越小,所以选项B正确;选项C,从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,不表示某人秃顶他有95%的可能患有心脏病,所以选项C不正确;选项D,从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关,是独立性检验的解释,所以选项D正确.故选:ABD.4、为了判断某高中学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:已知P (x 2≥3.841)≈0.05,P (x 2≥6.635)≈0.01.根据表中数据,得到x 2=250(1320107)23272030⨯⨯-⨯⨯⨯⨯≈4.844,则认为选修文科与性别有关系出错的概率约为________.【答案】0.05 【分析】直接根据表中数据计算的x 2值与P (x 2≥3.841)≈0.05比较判断,即得结果. 【详解】因为x 2≈4.844>3.841,而P (x 2≥3.841)≈0.05,故认为选修文科与性别有关系出错的概率约为0.05. 故答案为:0.05.5、调查者通过询问72名男、女大学生在购买食品时是否看营养说明得到的数据如下表所示:大学生的性别和是否看营养说明之间___(填“有”或“没有”)关系.【答案】有【分析】由表中的数据直接计算卡方,从而可得结论【详解】解:因为22722820168)=8.4167.879 44283636χ⨯⨯-⨯≈>⨯⨯⨯(,所以有的把握认为大学生性别与购买食品时是否看营养说明之间有关,故答案为:有6、某高校《统计》课程的教师随机调查了选该课的一些学生情况,具体数据如下表: 为了判断主修统计专业是否与性别有关系,根据表中的数据,得到k=2 50(1320-107) 23272030⨯⨯⨯⨯⨯⨯=4.844>3.841,所以有_____的把握判定主修统计专业与性别有关系.附:【答案】95%【分析】根据独立性检验的基本思想,因为2K的观测值k=4.844>3.841,参考临界值表即可得出【详解】根据表格数据得2K的观测值k=250(1320-107)23272030⨯⨯⨯⨯⨯⨯≈4.844 3.841>,所以有95%的把握判定主修统计专业与性别有关系.故答案为:95%.7、某学生对其30名亲属的饮食习惯进行了一次调查,依据统计所得数据可得到如下的22⨯列联表:根据以上列联表中的数据,可得2K 的观测值k =__________,__________(填“有”或“没有”)99%的把握认为其亲属的饮食习惯与年龄有关.参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:【答案】10 有 【分析】根据列联表,求得a b c d ,,,的值,利用公式,求得2K 的值,结合附表,即可得到结论. 【详解】由列联表可得20a =,10b =,12c =,4d =,可得2230(8128)10 6.63512182010K ⨯-==>⨯⨯⨯, 所以有99%的把握认为其亲属的饮食习惯与年龄有关. 故答案为:10;有.8、2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2018届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为35.(1)请将上述列联表补充完整;(2)判断是否有99.9%的把握认为喜欢游泳与性别有关.附:x2=2()()()()()n ad bca b c d a c b d-++++【答案】(1)表格见解析;(2)有. 【分析】(1)根据概率补全列联表即可;(2)计算2x,再进行判断即可.【详解】(1)因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为3 5所以喜欢游泳的学生人数为3 100605⨯=.其中女生有20人,男生有40人,列联表补充如下:(2)因为22100(40302010)16.6710.82860405050x⨯⨯-⨯=≈>⨯⨯⨯所以有99.9%的把握认为喜欢游泳与性别有关.9、某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,得出以下22⨯列联表:如果随机抽查该班的一名学生,那么抽到积极参加班级工作的学生的概率是12 25.(1)求a,b,c,d的值.(2)试运用独立性检验的思想方法分析:能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.参考数据:【答案】(1)6a =,19b =,24c =,26d =;(2)有. 【分析】(1)由抽到积极参加班级工作的学生的概率是1225,可求出c 的值,然后根据表中的数据可求出,,a b d 的值;(2)直接利用22()()()()()n ad bc K a b c d a c b d -=++++公式求解,然后根临界值表判断即可【详解】解:(1)积极参加班级工作的学生有c 人,总人数为50, 由抽到积极参加班级工作的学生的概率1125025c P ==, 解得24c =,所以6a =.所以2525619b a =-=-=,50502426d c =-=-=.(2)由列联表知,2250(181967)11.53825252426K ⨯⨯-⨯=≈⨯⨯⨯, 由11.53810.828>,可得有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系.。
独立性检验-高中数学知识点讲解(含答案)

独立性检验(北京习题集)(教师版)一.选择题(共5小题)1.(2017春•东城区校级期末)某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是()表1表2表3表4A.成绩B.视力C.智商D.阅读量2.(2016春•海淀区校级期末)在检验吸烟与患肺炎是否有关的一次统计中,根据22⨯列联表中数据计算得2 6.234x≈,则下列说法正确的是()A .有99%的把握认为吸烟与患肺炎有关B .有99%的把握认为吸烟与患肺炎无关C .有95%的把握认为吸烟与患肺炎有关D .有95%的把握认为吸烟与患肺炎无关3.(2015秋•昌平区期末)某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示:下列叙述一定正确的是( )A .甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前B .乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前C .甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前D .乙同学的总成绩排名比丙同学的总成绩排名更靠前4.(2014•海淀区校级模拟)在对吸烟与患肺病这两个分类变量的独立性检验中,下列说法正确的是( ) (参考数据:2( 6.635)0.01)P k =①若2k 的观测值满足2 6.635k ,我们有99%的把握认为吸烟与患肺病有关系. ②若2k 的观测值满足2 6.635k ,那么在100个吸烟的人中约有99人患有肺病.③从独立性检验可知,如果有99%的把握认为吸烟与患肺病有关系时,那么我们就认为:每个吸烟的人有99%的可能性会患肺病.④从统计量中得知有99%的把握认为吸烟与患肺病有关系时,是指有1%的可能性使推断出现错误. A .①B .①④C .②③D .①②③④5.(2014•海淀区校级模拟)经过对2K 的统计量的研究,得到了若干个临界值,当2K 的观测值 3.841K >时,我们()2)k0.500.455A .在错误的概率不超过0.05的前提下可认为A 与B 有关 B .在错误的概率不超过0.05的前提下可认为A 与B 无关 C .在错误的概率不超过0.01的前提下可认为A 与B 有关D .没有充分理由说明事件A 与B 有关 二.填空题(共7小题)6.(2019春•东城区期末)吃零食是中学生中普遍存在的现象.长期吃零食对学生身体发育有诸多不利影响,影响学生的健康成长.下表给出性别与吃零食的列联表根据下面2K 的计算结果,试回答,有 的把握认为“吃零食与性别有关”.参考数据与参考公式:222()85(140480)9826000 4.722()()()()176845402080800n ad bc K a b c d a c b d --===≈++++⨯⨯⨯0)k7.(2013•西湖区校级模拟)给出下列说法:①从匀速传递的产品生产线上每隔20分钟抽取一件产品进行某种检测,这样的抽样为系统抽样; ②若随机变量若(1,4)N ξ-,(0)P m ξ=,则1(01)2P m ξ<<=-; ③在回归直线?0.22y x =+中,当变量x 每增加1个单位时,?y 平均增加2个单位; ④在22⨯列联表中,213.079K =,则有99.9%的把握认为两个变量有关系. 附表:0)k0.050k3.841其中正确说法的序号为 (把所有正确说法的序号都写上)8.(2010春•海淀区校级期中)在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):物理成绩好物理成绩不好合计数学成绩好622385数学成绩不好282250合计9045135根据以上数据求得2X=;所以有(填百分数)以上的把握认为数学成绩与物理成绩有关.9.(2010春•怀柔区期末)为了了解某地母亲身高x与女儿身高Y的相关关系,随机测得10对母女的身高如下表所示:母亲身()x cm159160160163159154159158159157女儿身()Y cm158159160161161155162157162156计算x与Y的相关系数0.71r≈,通过查表得r的临界值0.050.632r=,从而有的把握认为x与Y之间具有线性相关关系,因而求回归直线方程是有意义的.通过计算得到回归直线方程为ˆ34.920.78y x==+,因此,当母亲的身高为161cm时,可以估计女儿的身高大致为.10.(2009春•北京校级期末)某校为提高教学质量进行教改实验,设有试验班和对照班.经过两个月的教学试验,进行了一次检测,试验班与对照班成绩统计如下的22⨯列联表所示(单位:人),则其中m=,n=.80及80分以下80分以上合计试验班321850对照班12m50合计4456n11.(2009春•北京校级期末)若由一个2*2列联表中的数据计算得2 4.013X=,那么有把握认为两个变量有关系.附:2X临界值表:12.(2009春•房山区期中)为了调查高中生的性别与是否喜欢足球之间有无关系,一般需要收集以下数据.三.解答题(共3小题)13.(2019•西城区校级模拟)已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:)h ,汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:(1)求抽取的女职工的人数;(2)①根据频率分布表,求出m 、n 、p 的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h 的概率;②若在样本数据中,有60名女职工每周的平均运动时间不低于4h ,请完成以下22⨯列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h 与性别有关”. 附:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.0)k14.(2019•海淀区校级三模)手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下: 女性用户 分值区间[50,60)[60,70)[70,80)[80,90)[90,100] 频数20 40 80 50 10男性用户 分值区间[50,60)[60,70)[70,80)[80,90)[90,100] 频数 45 75 90 60 30(Ⅰ)完成下列频率分布直方图,计算女性用户评分的平均值,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);(Ⅱ)把评分不低于70分的用户称为“评分良好用户”,能否有90%的把握认为“评分良好用户”与性别有关? 参考附表:20()P K k 0.100.050 0.010 0.0010k2.7063.841 6.635 10.828参考公式:2()2()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++15.(2019•西城区校级模拟)近年电子商务蓬勃发展,2017年某网购平台“双11”一天的销售业绩高达1682亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.(1)根据已知条件完成下面的22⨯列联表,并回答能否有99%的把握认为“网购者对商品满意与对快递满意之间有关系”?(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.附:22()()()()()n ad bc K a b c d a c b d -=++++(其中n a b c d =+++为样本容量)2)kk独立性检验(北京习题集)(教师版)参考答案与试题解析一.选择题(共5小题)1.(2017春•东城区校级期末)某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是()表1表2表3表4A.成绩B.视力C.智商D.阅读量【分析】根据表中数据,利用公式,求出2K,即可得出结论.【解答】解:表2252(6221014)1:0.00916363220K⨯-⨯=≈⨯⨯⨯;表2252(4201216)2: 1.76916363220K⨯-⨯=≈⨯⨯⨯;表2252(824812)3: 1.316363220K⨯-⨯=≈⨯⨯⨯;表2252(143062)4:23.4816363220K⨯-⨯=≈⨯⨯⨯,∴阅读量与性别有关联的可能性最大,故选:D.【点评】本题考查独立性检验的应用,考查学生的计算能力,属于中档题.2.(2016春•海淀区校级期末)在检验吸烟与患肺炎是否有关的一次统计中,根据22⨯列联表中数据计算得2 6.234x≈,则下列说法正确的是()A.有99%的把握认为吸烟与患肺炎有关B.有99%的把握认为吸烟与患肺炎无关C.有95%的把握认为吸烟与患肺炎有关D.有95%的把握认为吸烟与患肺炎无关【分析】由2 6.234 3.841x≈>,对照表格,可知有95%的把握认为吸烟与患肺炎有关.【解答】解:由2 6.234 3.841x≈>,∴有95%的把握认为吸烟与患肺炎有关,故选:C.【点评】本题考查独立性检验的应用,考查学生的计算能力,属于基础题.3.(2015秋•昌平区期末)某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示:下列叙述一定正确的是( )A .甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前B .乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前C .甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前D .乙同学的总成绩排名比丙同学的总成绩排名更靠前【分析】根据图示,可得甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前. 【解答】解:根据图示,可得甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前, 故选:C .【点评】本题考查利用数学知识解决实际问题,考查数形结合的数学思想,考查学生分析解决问题的能力,比较基础.4.(2014•海淀区校级模拟)在对吸烟与患肺病这两个分类变量的独立性检验中,下列说法正确的是( ) (参考数据:2( 6.635)0.01)P k =①若2k 的观测值满足2 6.635k ,我们有99%的把握认为吸烟与患肺病有关系. ②若2k 的观测值满足2 6.635k ,那么在100个吸烟的人中约有99人患有肺病.③从独立性检验可知,如果有99%的把握认为吸烟与患肺病有关系时,那么我们就认为:每个吸烟的人有99%的可能性会患肺病.④从统计量中得知有99%的把握认为吸烟与患肺病有关系时,是指有1%的可能性使推断出现错误. A .①B .①④C .②③D .①②③④【分析】若2 6.635k >,我们有99%的把握认为吸烟与患肺病有关系,表示有1%的可能性使推断出现错误,不表示有99%的可能患有肺病,也不表示在100个吸烟的人中必有99人患有肺病,故可得结论.【解答】解:若2 6.635k >,我们有99%的把握认为吸烟与患肺病有关系,不表示有99%的可能患有肺病,故①正确.不表示在100个吸烟的人中必有99人患有肺病,故②不正确. 不表示有每个吸烟的人有99%的可能性会患肺病,故③不正确.从统计量中得知有99%的把握认为吸烟与患肺病有关系时,是指有1%的可能性使推断出现错误,④正确. 故选:B .【点评】本题的考点是独立性检验的应用,根据独立性检测考查两个变量是否有关系的方法进行判断,准确的理解判断方法及2k 的含义是解决本题的关键.5.(2014•海淀区校级模拟)经过对2K 的统计量的研究,得到了若干个临界值,当2K 的观测值 3.841K >时,我们()2)k0.500.455A .在错误的概率不超过0.05的前提下可认为A 与B 有关 B .在错误的概率不超过0.05的前提下可认为A 与B 无关 C .在错误的概率不超过0.01的前提下可认为A 与B 有关D .没有充分理由说明事件A 与B 有关【分析】根据所给的观测值,同临界值表中的临界值进行比较,根据2( 3.841)0.05P K >=,得到我们有10.0595%-=的把握认为A 与B 有关系. 【解答】解:依据下表:2)k2 3.841K >,2( 3.841)0.05P K >=∴我们在错误的概率不超过0.05的前提下可认为A 与B 有关,故选:A .【点评】本题考查独立性检验的应用,本题解题的关键是正确理解临界值对应的概率的意义,本题不用运算只要理解概率的意义即可. 二.填空题(共7小题)6.(2019春•东城区期末)吃零食是中学生中普遍存在的现象.长期吃零食对学生身体发育有诸多不利影响,影响学生的健康成长.下表给出性别与吃零食的列联表根据下面2K 的计算结果,试回答,有 95% 的把握认为“吃零食与性别有关”. 参考数据与参考公式:222()85(140480)9826000 4.722)176845402080800n ad bc K b d --===≈+⨯⨯⨯0)k【分析】根据题意得出观测值的大小,对照临界值得出结论. 【解答】解:根据题意知2 4.722 3.841K ≈>, 所以有95%的把握认为“吃零食与性别有关”. 故答案为:95%.【点评】本题考查了列联表与独立性检验的应用问题,是基础题. 7.(2013•西湖区校级模拟)给出下列说法:①从匀速传递的产品生产线上每隔20分钟抽取一件产品进行某种检测,这样的抽样为系统抽样; ②若随机变量若(1,4)N ξ-,(0)P m ξ=,则1(01)2P m ξ<<=-; ③在回归直线?0.22y x =+中,当变量x 每增加1个单位时,?y 平均增加2个单位; ④在22⨯列联表中,213.079K =,则有99.9%的把握认为两个变量有关系. 附表:0)k0.050k3.841其中正确说法的序号为 ①②④ (把所有正确说法的序号都写上)【分析】对于①,从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样系统抽样;对于②,根据随机变量~(1,4)x N ,得到正态曲线的对称轴是1x =,得到(0)(2)P x P x =,根据所给的条件(0)P x m =,得到(2)P x m =,又根据概率之和是1,得到要求的结果;对;对于③在回归直线方程 ?0.22y x =+中,当解释变量x 每增加一个单位时,预报变量 ?y 平均增加0.1个单位;不对;对于④,通过所给的观测值,同临界值表中的数据进行比较,发现13.07910.828>,得到结论. 【解答】解:①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件 产品进行某项指标检测,这样的抽样是系统抽样,故①正确, ②:随机变量~(1,4)x N ,∴正态曲线的对称轴是1x =,(0)(2)P x P x ∴= (0)P x m =,(02)112P x m m m ∴<<=--=-,1(01)2P m ξ∴<<=-,故③正确, ③在回归直线方程 ?0.22y x =+中,当解释变量x 每增加一个单位时, 预报变量 ?y 平均增加0.2个单位,故④不正确, 对于④,一个2*2列联表中的数据计算得213.079K =,213.07910.828K =>,∴有999%的把握说这两个变量有关系,故答案为:①②④.【点评】本题考查独立性检验,考查系统抽样方法,考查线性回归方程,考查判断两个相关变量之间的关系等,是一个综合题目,这种题考查的知识点比较多,需要认真分析.8.(2010春•海淀区校级期中)在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):根据以上数据求得2X = 4.066 ;所以有 (填百分数)以上的把握认为数学成绩与物理成绩有关.【分析】根据表中所给的数据,利用所给的求观测值的公式,代入公式22()()()()()n ad bc K a b c d a c b d -=++++,计算出k 值,把观测值同临界值进行比较,得到有95%的把握数学成绩与物理成绩有关. 【解答】解:提出假设0H :学生数学成绩与物理成绩之间没有关系.根据列联表可以求得22135(62222823) 4.066 3.841904585110K ⨯⨯-⨯=≈>⨯⨯⨯当0H 成立时,2( 3.841)0.05P K >=.所以我们有10.0595%-=的把握认为:学生的数学成绩与物理成绩之间有关系, 故答案为:4.066;95%【点评】本题考查独立性检验的应用,考查数据处理能力、运算求解能力和应用意识,本题解题的关键是正确运算出观测值,理解临界值对应的概率的意义,本题是一个基础题.9.(2010春•怀柔区期末)为了了解某地母亲身高x 与女儿身高Y 的相关关系,随机测得10对母女的身高如下表所示:计算x 与Y 的相关系数0.71r ≈,通过查表得r 的临界值0.050.632r =,从而有 95% 的把握认为x 与Y 之间具有线性相关关系,因而求回归直线方程是有意义的.通过计算得到回归直线方程为ˆ34.920.78yx ==+,因此,当母亲的身高为161cm 时,可以估计女儿的身高大致为 .【分析】查对临界值表,可得结论,利用回归直线方程,代入计算可估计女儿的身高.【解答】解:查对临界值表,由临界值0.050.632r =,可得有95%的把握认为x 与Y 之间具有线性相关关系,回归直线方程为ˆ34.920.78yx =+,因此,当161x cm =时,ˆ34.920.7834.920.78161161y x cm =+=+⨯= 故答案为:95%,161cm .【点评】本题考查独立性检验的应用,考查学生的计算能力,属于基础题.10.(2009春•北京校级期末)某校为提高教学质量进行教改实验,设有试验班和对照班.经过两个月的教学试验,进行了一次检测,试验班与对照班成绩统计如下的22⨯列联表所示(单位:人),则其中m = 38 ,n = .80及80分以下80分以上合计 试验班 32 1850 对照班 12 m50合计4456n【分析】根据22⨯列联表的规律对应的横行与竖行的和应该等于合计,故可求 【解答】解:由题意,1856m +=,5050n +=,38m ∴=.100n =, 故答案为38,010.【点评】利用随机变量 来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.独立性检验的基本思想类似于反证法11.(2009春•北京校级期末)若由一个2*2列联表中的数据计算得2 4.013X =,那么有 95% 把握认为两个变量有关系. 附:2X 临界值表:【分析】通过所给的观测值,同临界值表中的数据进行比较,发现4.013 3.841>,得到结论有95%的把握说这两个变量有关系.【解答】解:一个2*2列联表中的数据计算得2 4.013X =, 4.013 3.841>,∴有95%的把握说这两个变量有关系,故答案为:95%【点评】本题考查独立性检验,考查判断两个变量之间有没有关系,一般题目需要自己做出观测值,再拿着观测值同临界值进行比较,得到结论,本题给出了观测值,只剩下一个比较过程.12.(2009春•房山区期中)为了调查高中生的性别与是否喜欢足球之间有无关系,一般需要收集以下数据 男女生中喜欢或不喜欢足球的人数 .【分析】根据调查目的:为了调查高中生的性别与是否喜欢足球之间有无关系,一般需要收集男女生中喜欢或不喜欢足球的人数,通过计算得到结果,【解答】解:为了调查高中生的性别与是否喜欢足球之间有无关系,一般需要收集男女生中喜欢或不喜欢足球的人数,再得出22 列联表,最后代入随机变量的观测值公式,得出结果. 故答案为:男女生中喜欢或不喜欢足球的人数.【点评】本题考查独立性检验的应用,考查独立性检验的基本思想和应用意识, 三.解答题(共3小题)13.(2019•西城区校级模拟)已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:)h ,汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:(1)求抽取的女职工的人数;(2)①根据频率分布表,求出m 、n 、p 的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h 的概率;②若在样本数据中,有60名女职工每周的平均运动时间不低于4h,请完成以下22⨯列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”.附:22()()()()()n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.2()P K k0.250.150.100.050.025 0k 1.323 2.072 2.706 3.841 5.024【分析】(1)直接由分层抽样中每层所占比例相等求得抽取的女职工的人数;(2)①由图表数据及频率和为1求得n,然后依次求p与m的值,并完成频率分布直方图;②填写22⨯列联表,再由公式求得2K,则结论可求.【解答】解:(1)抽取的女职工的人数为1500 300905000⨯=;(2)①10.050.20.150.250.30.05n=-----=,15p=,300154575901560m=-----=;直方图如图:估计该企业职工每周的平均运动时间不低于4h的概率为:30.150.250.30.050.754P =+++==; ②22⨯列联表如图:22()300(456030165) 4.762 3.841()()()()7522521090n ad bc K a b c d a c b d -⨯-⨯==≈>++++⨯⨯⨯.∴有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h 与性别有关”.【点评】本题考查独立性检验,考查由频率分布直方图求概率的估计值,考查计算能力,是中档题.14.(2019•海淀区校级三模)手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:(Ⅰ)完成下列频率分布直方图,计算女性用户评分的平均值,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);(Ⅱ)把评分不低于70分的用户称为“评分良好用户”,能否有90%的把握认为“评分良好用户”与性别有关? 参考附表:20()P K k 0.100.050 0.010 0.0010k2.7063.841 6.635 10.828参考公式:2()2()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++【分析】(Ⅰ)利用所给数据,可得频率分布直方图,并比较女性用户和男性用户评分的波动大小; (Ⅱ)求出2K ,与临界值比较,即可得出结论.【解答】解:(Ⅰ)女性用户和男性用户的频率分布表分别如下左、右图:由图可得女性用户的波动小,男性用户的波动大. ⋯(4分) (Ⅱ)22⨯列联表如下图:女性用户 男性用户 合计 “认可”手机 140 180 320 “不认可”手机60 120 180 合计200300500500(14012018060)2 5.208 2.706200300320180K ⨯-⨯=≈>⨯⨯⨯,所以有95%的把握认为性别和对手机的“认可”有关.【点评】本题考查频率分布直方图的作法及应用,考查独立检验的应用,考查频率分布直方图等基础知识,考查运算求解能力,是基础题.15.(2019•西城区校级模拟)近年电子商务蓬勃发展,2017年某网购平台“双11”一天的销售业绩高达1682亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.(1)根据已知条件完成下面的22⨯列联表,并回答能否有99%的把握认为“网购者对商品满意与对快递满意之间有关系”?(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.附:22()n ad bcK-=(其中n a b c d=+++为样本容量)2)kk【分析】(1)由题意填写列联表,计算观测值,对照临界值得出结论;(2)根据题意,用列举法求出基本事件数,计算所求的概率值.【解答】解:(1)由题意,填写22⨯列联表,如下:计算2200(80204060)1001.59140601208063K⨯⨯-⨯==≈⨯⨯⨯,由于1.59 6.635<,所以没有99%的把握认为“网购者对商品满意与对快递满意之间有关系”;(2)根据题意,抽取的10次交易中,对商品和快递都满意的交易有4次,记为A、B、C、D,其余6次不是都满意的交易记为1、2、3、4、5、6,那么抽取2次交易一共有45种可能:AB 、AC 、AD 、1A 、2A 、3A 、4A 、5A 、6A 、BC 、BD 、1B 、2B 、⋯⋯、56, 其中2次交易对商品和快递不是都满意的有15种: 12、13、14、15、16、⋯⋯、56;所以,在抽取的2次交易中,至少一次对商品和快递都满意的概率是 45152453P -==. 【点评】本题考查了列联表与独立性检验的应用问题,也考查了列举法求古典概型的概率问题.。
2023年高考数学一轮复习精讲精练(新高考专用)专题52:列联表独立性检验(讲解版)
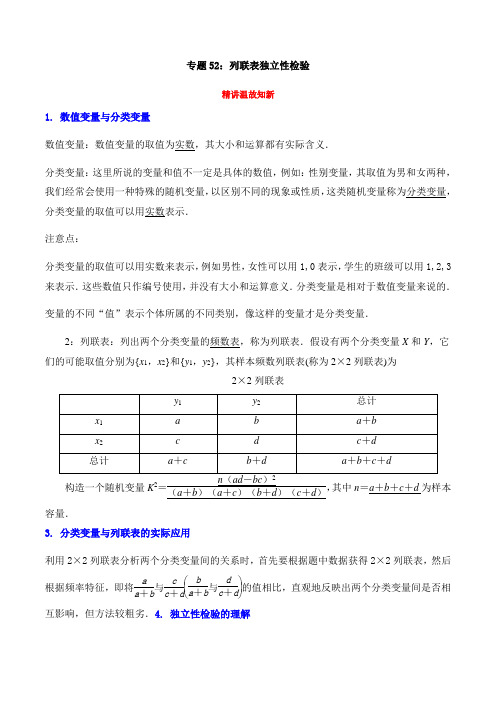
专题52:列联表独立性检验精讲温故知新1. 数值变量与分类变量数值变量:数值变量的取值为实数,其大小和运算都有实际含义.分类变量:这里所说的变量和值不一定是具体的数值,例如:性别变量,其取值为男和女两种,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量,分类变量的取值可以用实数表示.注意点:分类变量的取值可以用实数来表示,例如男性,女性可以用1,0表示,学生的班级可以用1,2,3来表示.这些数值只作编号使用,并没有大小和运算意义.分类变量是相对于数值变量来说的.变量的不同“值”表示个体所属的不同类别,像这样的变量才是分类变量.2:列联表:列出两个分类变量的频数表,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为2×2列联表构造一个随机变量K2=n(ad-bc)(a+b)(a+c)(b+d)(c+d),其中n=a+b+c+d为样本容量.3. 分类变量与列联表的实际应用利用2×2列联表分析两个分类变量间的关系时,首先要根据题中数据获得2×2列联表,然后根据频率特征,即将aa+b与cc+d⎝⎛⎭⎪⎫ba+b与dc+d的值相比,直观地反映出两个分类变量间是否相互影响,但方法较粗劣.4. 独立性检验的理解1.独立性检验:利用χ2的取值推断分类变量X 和Y 是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验. 2.χ2=n ad -bc 2a +bc +d a +cb +d,其中n =a +b +c +d .注意点:(1)卡方越小,独立性越强,相关性越弱;卡方越大,独立性越弱,相关性越强.(2)当χ2≥x α时,我们就推断H 0不成立,即认为X 和Y 不独立,该推断犯错误的概率不超过α;当χ2<x α时,我们没有充分证据推断H 0不成立 ,可以认为X 和Y 独立. 根据所给的观测值,与所给的临界值表中的数据进行比较,即可得出结论. 5. 有关“相关的检验” 用χ2进行“相关的检验”步骤 (1)零假设:即先假设两变量间没关系. (2)计算χ2:套用χ2的公式求得χ2值.(3)查临界值:结合所给小概率值α查得相应的临界值x α. (4)下结论:比较χ2与x α的大小,并作出结论. 6. 有关“无关的检验” 运用独立性检验的方法(1)列出2×2列联表,根据公式计算χ2. (2)比较χ2与x α的大小作出结论题型一:列联表例1:假设有两个变量X 和Y ,他们的取值分别为1x ,2x 和1y ,2y ,其列联表为:则表中a ,b 的值分别是( ) A .94,96 B .54,52C .52,50D .52,60【答案】D【详解】根据列联表知,=732152a -=,又8a b +=,所以60b =, 故选:D举一反三下列是关于出生男婴与女婴调查的22⨯列联表那么D __________.【答案】82【详解】解:由题意,4598E +=,35A D +=,45A B +=,35E C +=,180B C +=47A ∴=,92B =,88C =,82D =,53E =故答案为: 82.题型二:等高条形图例2:为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为100的调查样本,其中城镇户籍与农村户籍各50人,男性40人,女性60人,绘制不同群体中倾向选择生育二胎与选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则关于样本下列叙述中正确的是( )A .是否倾向选择生育二胎与户籍无关B .是否倾向选择生育二胎与性别有关C .倾向选择生育二胎的人员中,男性人数与女性人数相同D .倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数 【答案】D【详解】对于A ,城镇户籍中40%选择生育二胎,农村户籍中80%选择生育二胎,相差较大,则是否倾向选择生育二胎与户籍有关,A 错误;对于B ,男性和女性中均有60%选择生育二胎,则是否倾向选择生育二胎与性别无关,B 错误; 对于C ,由于男性和女性中均有60%选择生育二胎,但样本中男性40人,女性60人,则倾向选择生育二胎的人员中,男性人数与女性人数不同,C 错误;对于D ,倾向选择不生育二胎的人员中,农村户籍有5020%10⨯=人,城镇户籍有5060%30⨯=人,农村户籍人数少于城镇户籍人数,D 正确.故选:D.举一反三为了解某高校学生使用手机支付和现金支付的情况,抽取了部分学生作为样本,统计其喜欢的支付方式,并制作出如等高条形图:根据图中的信息,下列结论中不正确的是()A.样本中多数男生喜欢手机支付B.样本中的女生数量少于男生数量C.样本中多数女生喜欢现金支付D.样本中喜欢现金支付的数量少于喜欢手机支付的数量【答案】C【详解】对于A,由右图可知,样本中多数男生喜欢手机支付,A对;对于B,由左图可知,样本中的男生数量多于女生数量,B对;对于C,由右图可知,样本中多数女生喜欢手机支付,C错;对于D,由右图可知,样本中喜欢现金支付的数量少于喜欢手机支付的数量,D对.故选:C.题型三:独立性检验的概念及计算例3:(2022·湖北武汉·模拟预测)通过随机询问某中学110名中学生是否爱好跳绳,得到如下列联表:跳绳性别合计男女爱好40 20 60 不爱好20 30 50已知()()()()()22n ad bcKa b c d a c b d-=++++,则以下结论正确的是()A.根据小概率值0.001α=的独立性检验,爱好跳绳与性别无关B.根据小概率值0.001α=的独立性检验,爱好跳绳与性别无关,这个结论犯错误的概率不超过0.001 C.根据小概率值0.01α=的独立性检验,有99%以上的把握认为“爱好跳绳与性别无关”D.根据小概率值0.01α=的独立性检验,在犯错误的概率不超过1%的前提下,认为“爱好跳绳与性别无关”【答案】A【详解】由题知()()()()()22 2110(40302020)7.82260506050n ad bcKa b c d a c b d-⨯-⨯==≈++++⨯⨯⨯因为7.82210.828<,所以爱好跳绳与性别无关且这个结论犯错误的概率超过0.001,故A正确,B错误,又因为7.822 6.635>,所以有99%以上的把握认为“爱好跳绳与性别有关,或在犯错误的概率不超过1%的前提下,认为“爱好跳绳与性别有关.故C和D错误.故选:A.举一反三1.(2022·江西南昌·一模(理))根据分类变量x与y的观察数据,计算得到2 2.974K=,依据下表给出的2K 独立性检验中的小概率值和相应的临界值,作出下列判断,正确的是()A.有95%的把握认为变量x与y独立B.有95%的把握认为变量x与y不独立C.变量x与y独立,这个结论犯错误的概率不超过10%D.变量x与y不独立,这个结论犯错误的概率不超过10%【答案】D【详解】因为2 2.974 2.706K=>,所以变量x与y不相互独立,这个结论犯错误的概率不超过10%.故选:D 2.(2022·四川雅安·三模(文))为考察一种新药预防疾病的效果,某科研小组进行动物实验,收集整理数据后将所得结果填入相应的22K≈.参照附表,下列结论正确⨯列联表中,由列联表中的数据计算得29.616的是()附表:A.在犯错误的概率不超过0.1%的前提下,认为“药物有效”B.在犯错误的概率不超过0.1%的前提下,认为“药物无效”C.有99%以上的把握认为“药物有效”D.有99%以上的把握认为“药物无效”【答案】C解:因为29.616<<,所以有99%以上的把握认为“药物有效”.K7.87910.828K≈,即2故选:C.题型四:独立性检验的基本思想例4:(2022·江西·二模(文))千百年来,我国劳动人民在生产实践中根据云的形状、走向速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩销云,地上雨淋林”“日落云里走,雨在半夜后”……小明同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下22⨯列联表:并计算得到219.05K=,下列小明对地区天气判断正确的是()A.夜晚下雨的概率约为1 5B.未出现“日落云里走”,但夜晚下雨的概率约为12C.出现“日落云里走”,有99.9%的把握认为夜晚会下雨D.有99.9%的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关【答案】D【详解】根据表中数据可知,夜晚下雨的概率约为252511002P+==,所以A错.未出现“日落云里走”,但夜晚下雨的概率约为255254514P==+,故B错.219.0510.828K=>,对照临界值表可知,有99.9%的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关,但不能说有99.9%的把握认为夜晚会下雨,故C错,D对.故选:D举一反三(2022·安徽省芜湖市教育局模拟预测(理))为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设0H :“这种血清不能起到预防感冒的作用”,利用22⨯列联表计算的结果,认为0H 成立的可能性不足1%,那么2K 的一个可能取值为( )A .7.879B .6.635C .5.024D .3.841【答案】A【详解】若0H 成立的可能性不足1%,则2 6.635K >,由选项知:27.879K =. 故选:A.题型五:独立性检验解决实际问题例5:(2022·全国·高考真题)一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?(2)从该地的人群中任选一人,A 表示事件“选到的人卫生习惯不够良好”,B 表示事件“选到的人患有该疾病”.(|)(|)P B A P B A 与(|)(|)P B A P B A 的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R .(ⅰ)证明:(|)(|)(|)(|)P A B P A B R P A B P A B =⋅;(ⅱ)利用该调查数据,给出(|),(|)P A B P A B 的估计值,并利用(ⅰ)的结果给出R 的估计值.附22()()()()()n ad bc K a b c d a c b d -=++++,【解析】(1)由已知222()200(40906010)=24()()()()50150100100n ad bc K a b c d a c b d -⨯-⨯==++++⨯⨯⨯, 又2( 6.635)=0.01P K ≥,24 6.635>,所以有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异. (2)(i)因为(|)(|)()()()()=(|)(|)()()()()P B A P B A P AB P A P AB P A R P B A P B A P A P AB P A P AB =⋅⋅⋅⋅,所以()()()()()()()()P AB P B P AB P B R P B P AB P B P AB =⋅⋅⋅ 所以(|)(|)(|)(|)P A B P A B R P A B P A B =⋅,(ii) 由已知40(|)100P A B =,10(|)100P A B =,又60(|)100P A B =,90(|)100P A B =, 所以(|)(|)=6(|)(|)P A B P A B R P A B P A B =⋅举一反三(2021·全国·高考真题(文))甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:22()()()()()n ad bcKa b c d a c b d-=++++【详解】(1)甲机床生产的产品中的一级品的频率为15075% 200=,乙机床生产的产品中的一级品的频率为12060% 200=.(2)()22400150801205040010 6.63527013020020039K⨯-⨯==>>⨯⨯⨯,故能有99%的把握认为甲机床的产品与乙机床的产品质量有差异.精练巩固提升一、单选题1.(2022·全国·模拟预测)某初级中学有700名学生,在2021年秋季运动会中,为响应全民健身运动的号召,要求每名学生都必须在“立定跳远”与“坐位体前屈”中选择一项参加比赛.根据报名结果知道,有12的男生选择“立定跳远”,有34的女生选择“坐位体前屈”,且选择“立定跳远”的学生中女生占25,则参照附表,下列结论正确的是()附:()()()()()22n ad bc K a b c d a c b d -=++++,n =a +b +c +d .A .在犯错误的概率不超过2.5%的前提下,认为选择运动项目与性别无关B .在犯错误的概率不超过5%的前提下,认为选择运动项目与性别无关C .有97.5%的把握认为选择运动项目与性别有关D .有95%的把握认为选择运动项目与性别有关【答案】C 【详解】解:由题意得:设该校男生人数为x ,女生人数为y ,则可得如下表格:由题意知12411524y x y =+,即43y x =,又x +y =700,解得300,400,x y =⎧⎨=⎩则()2270015030015010046.67 5.024300400250450K ⨯⨯-⨯=≈>⨯⨯⨯,所以有97.5%的把握认为选择运动项目与性别有关.故选C . 2.(2022·四川成都·三模(理))在某大学一食品超市,随机询问了70名不同性别的大学生在购买食物时是否查看营养说明,得到如下的列联表:附:()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.根据列联表的独立性检验,则下列说法正确的是().A.在犯错误的概率不超过0.05的前提下认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多B.在犯错误的概率不超过0.010的前提下认为该校女大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比为3 4C.在犯错误的概率不超过0.025的前提下认为性别与是否查看营养说明有关系D.在犯错误的概率不超过0.010的前提下认为性别与是否查看营养说明有关系【答案】C【详解】由题可得2270(15102025)= 5.83 5.02435353040K⨯⨯-⨯≈>⨯⨯⨯,∴在犯错误的概率不超过0.025的前提下认为性别与是否查看营养说明有关系.故选:C.3.(2021·全国·模拟预测(理))为了丰富教职工业余文化生活,某校计划在假期组织70名老师外出旅游,并给出了两种方案(方案一和方案二),每位老师均选择且只选择一种方案,其中有50%的男老师选择方案一,有75%的女老师选择方案二,且选择方案一的老师中女老师占40%,则参照附表,得到的正确结论是( )附:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.A .在犯错误的概率不超过2.5%的前提下,认为“选择方案与性别有关”B .在犯错误的概率不超过2.5%的前提下,认为“选择方案与性别无关”C .有95%以上的把握认为“选择方案与性别有关”D .有95%以上的把握认为“选择方案与性别无关”【答案】C【详解】设该校男老师的人数为x ,女老师的人数为y ,则可得如下表格:由题意0.40.50.25x y =+,可得43y x =,可得30x =,40y =, 则()227015301510 4.667 3.84125453040K ⨯-⨯=≈>⨯⨯⨯, 但4.667 5.024<,所以无97.5%以上有95%以上的把握认为“选择方案与性别有关”.故选:C.4.(2021·安徽黄山·二模(理))下列命题:①在线性回归模型中,相关指数2R 表示解释变量x 对于预报变量y 的贡献率,2R 越接近于0,表示回归效果越好;②两个变量相关性越强,则相关系数的绝对值就越接近于1;③两个模型中残差平方和越小的模型拟合的效果越好;④对分类变量X 与Y ,它们的随机变量2K 的观测值k 来说,k 越大,“X 与Y 有关系”的把握程度越大. 其中正确命题的个数是( )A .1个B .2个C .3个D .4个【答案】C解:①在线性回归模型中,相关指数2R 表示解释变量x 对于预报变量y 的贡献率,2R 越接近于0,表示回归效果越不好,①错误;②两个变量相关性越强,则相关系数的绝对值就越接近于1,②正确;③两个模型中残差平方和越小的模型拟合的效果越好,③正确;④对分类变量X 与Y ,它们的随机变量2K 的观测值k 来说,k 越大,“X 与Y 有关系”的把握程度越大,④正确.故选:C .5.(2022·河南·长葛市第一高级中学模拟预测(理))某校计划在课外活动中新增攀岩项目,为了解学生喜欢攀岩和性别是否有关,面向全体学生开展了一次随机调查,其中参加调查的男、女生人数相同,并绘制成等高条形图(如图所示),则下列说法正确的是( ) ()20P K k ≥ 0.05 0.010k 3.841 6.635参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.A .参与调查的学生中喜欢攀岩的女生人数比喜欢攀岩的男生人数多B .参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数多C .若参与调查的男、女生人数均为100人,则能在犯错误的概率不超过0.01的前提下认为喜欢攀岩和性别有关D .无论参与调查的男、女生人数为多少,都能在犯错误的概率不超过0.01的前提下认为喜欢攀岩和性别有关【答案】C【详解】对于选项A :因为参加调查的男、女生人数相同,而男生中喜欢攀岩的占80%,女生中喜欢攀岩的占30%,所以参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多,所以选项A 错误;对于选项B :参与调查的女生中喜欢攀岩的人数占30%,不喜欢攀岩的人数占70%,所以参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数少,所以选项B 错误;对于选项C :若参与调查的男、女生人数均为100人,根据图表,列出2×2列联表如下:所以()2220080702030500050.505 6.6351109010010099K ⨯⨯-⨯==≈>⨯⨯⨯, 所以在犯错误的概率不超过0.01的前提下认为喜欢攀岩和性别有关,C 正确;对于选项D :如果不确定参与调查的男、女生人数,无法计算2K ,D 错误.故选:C .6.(2022·山东聊城·一模)根据分类变量x 与y 的成对样本数据,计算得到2 6.147χ=.依据0.01α=的独立性检验()0.01 6.635x =,结论为( )A .变量x 与y 不独立B .变量x 与y 不独立,这个结论犯错误的概率不超过0.01C .变量x 与y 独立D .变量x 与y 独立,这个结论犯错误的概率不超过0.01【答案】C【详解】按照独立性检验的知识及比对的参数值,当2 6.147χ=,我们可以下结论变量x 与y 独立.故排除选项A,B;依据0.01α=的独立性检验()0.01 6.635x =,6.147<6.635,所以我们不能得到“变量x 与y 独立,这个结论犯错误的概率不超过0.01”这个结论.故C 正确,D 错误.故选:C7.(2022·天津·模拟预测)下列说法错误的是( )A .线性相关系数0r >时,两变量正相关 B .两个随机变量的线性相关性越强,则相关系数r 的值就越接近于1C .在回归直线方程ˆ0.20.8yx =+中,当解释变量x 每增加1个单位时,预报变量ˆy 平增加0.2个单位 D .对分类变量X 与Y ,随机变量2χ的观测值越大,则判断“X 与Y 有关系”的把握程度越大【答案】B【详解】A :线性相关系数0r >时,变量为正相关,正确;B :两个随机变量的线性相关性越强,则相关系数||r 的值就越接近于1,错误;C :在回归直线方程ˆ0.20.8yx =+中,当1x ∆=时,ˆ0.2y ∆=,正确; D :对分类变量X 与Y ,随机变量2χ的观测值越大,变量间的关系把握程度越大,正确.故选:B8.(2020·河南·模拟预测(文))2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )附:()()()()()2n ad bc a b c d a c b d -++++,其中n a b c d =+++.A .130B .190C .240D .250【答案】B 【解析】【分析】设男、女学生的人数都为5x ,则男、女学生的总人数为10x ,建立22⨯列联表,由独立性检验算出2K ,结合观测值和选项可得答案.【详解】依题意,设男、女学生的人数都为5x ,则男、女学生的总人数为10x ,建立22⨯列联表如下,故()2222108310553721⋅-==⋅⋅⋅x x x x K x x x x ,由题意可得106.63510.82821x <<, 所以139.33510227.388x <<,结合选项可知,只有B 符合题意.故选:B.二、多选题9.(2021·福建福州·一模)“一粥一饭,当思来之不易”,道理虽简单,但每年我国还是有2000多亿元的餐桌浪费,被倒掉的食物相当于2亿多人一年的口粮.为营造“节约光荣,浪费可耻”的氛围,某市发起了“光盘行动”.某机构为调研民众对“光盘行动”的认可情况,在某大型餐厅中随机调查了90位来店就餐的客人,制成如下所示的列联表,通过计算得到K 2的观测值为已知()2 6.6350.010P K =,()210.8280.001P K =,则下列判断正确的是( )A .在该餐厅用餐的客人中大约有66.7%的客人认可“光盘行动”B .在该餐厅用餐的客人中大约有99%的客人认可“光盘行动”C .有99%的把握认为“光盘行动”的认可情况与年龄有关D .在犯错误的概率不超过0.001的前提下,认为“光盘行动”的认可情况与年龄有关【答案】AC【详解】∵K 2的观测值为9,且P (K 2≥6.635)=0.010,P (K 2≥10.828)=0.001,又∵9>6.635,但9<10.828,∴有99%的把握认为“光盘行动”的认可情况与年龄有关,或者说,在犯错误的概率不超过0.010的前提下,认为“光盘行动”的认可情况与年龄有关,所以选项C 正确,选项D 错误,由表可知认可“光盘行动”的人数为60人,所以在该餐厅用餐的客人中认可“光盘行动”的比例为6010090⨯%≈66.7%, 故选项A 正确,选项B 错误.故选:AC.10.(2022·湖南岳阳·三模)下列说法正确的是( )A .线性回归方程y bx a =+必过(,)x yB .设具有线性相关关系的两个变量x ,y 的相关系数为r ,则r 越接近于0,x 和y 之间的线性相关程度越强C .在一个22⨯列联表中,由计算得2K 的值,则2K 的值越小,判断两个变量有关的把握越大D .若()2~1,X N σ,()20.2P X >=,则()010.3P X <<= 【答案】AD【详解】因为线性回归方程y bx a =+必过样本中心点(,)x y ,所以选项A 正确; 因为r 越接近于0,x 和y 之间的线性相关程度越弱,所以选项B 不正确;因为2K 的值越小,确定两个变量有关的把握的程度越小,所以选项C 不正确;因为()2~1,X N σ,所以()()()1011220.32P X P X P X <<=<<=->=,因此选项D 正确,故选:AD 三、填空题11.(2020·宁夏·固原一中模拟预测(文))在独立性检验中,统计量K 2有两个临界值:3.841和6.635.当K 2>3.841时,有95%的把握说明两个事件有关,当K 2>6.635时,有99%的把握说明两个事件有关,当K 2≤3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算K 2=20.87.根据这一数据分析,我们有理由认为打鼾与患心脏病之间是________的(有关、无关).【答案】有关【详解】K 2=20.87>6.635时,有99%的把握说明打鼾与患心脏病有关.故答案为:有关12.(2022·全国·模拟预测)某大学为了解喜欢看篮球赛是否与性别有关,随机调查了部分学生,在被调查的学生中,男生人数是女生人数的2倍,男生喜欢看篮球赛的人数占男生人数的56,女生喜欢看篮球赛的人数占女生人数的13.若被调查的男生人数为n ,且有95%的把握认为喜欢看篮球赛与性别有关,则n 的最小值为______.【答案】12【详解】由题意得到如下列联表:所以2235263663822n n n n n n n n n n χ⎛⎫⋅-⋅⎪ ⎭⎝==⋅⋅⋅. 因为有95%的把握认为喜欢看篮球赛与性别有关,所以2 3.841χ≥,即3 3.8418n ≥, 3.841810.243n ⨯≥≈. 又2n ,3n ,6n 为整数,所以n 的最小值为12.故答案为:12 13.(2020·山西·大同一中模拟预测(理))某班主任对全班30名男生进行了作业量多少的调查,数据如下表:该班主任据此推断男生认为作业多与喜欢玩电脑游戏有关系,则这种推断犯错误的概率不超过________. 附表及公式:参考公式:K 2=2()()()()()n ad bc a b c d a c b d -++++. 【答案】0.05【详解】计算得K 2的观测值k =230(12828)14162010⨯⨯-⨯⨯⨯⨯≈4.286>3.841,则推断犯错误的概率不超过0.05.故答案为:0.05.14.(2022·辽宁葫芦岛·二模(理))下列说法:①线性回归方程y bx a =+必过(),x y ;②命题“21,34x x ∀≥+≥”的否定是“21,34x x ∃<+<”③相关系数r 越小,表明两个变量相关性越弱;④在一个22⨯列联表中,由计算得28.079K =,则有99%的把握认为这两个变量间有关系;其中正确..的说法是__________.(把你认为正确的结论都写在横线上) 本题可参考独立性检验临界值表: 【答案】①④详解:线性回归方程ˆˆˆybx a =+必过样本中心点(),x y ,故①正确. 命题“21,34x x ∀≥+≥”的否定是“21,34x x ∃≥+<” 故②错误③相关系数r 绝对值越小,表明两个变量相关性越弱,故不正确;④在一个22⨯列联表中,由计算得28.079K =,则有99%的把握认为这两个变量间有关系,正确.故答案为①④.四、解答题15.(2022·全国·高考真题(文))甲、乙两城之间的长途客车均由A 和B 两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?附:22()()()()()n ad bcKa b c d a c b d-=++++,()2P K k0.100 0.050 0.010k 2.706 3.841 6.635【解析】(1)根据表中数据,A共有班次260次,准点班次有240次,设A家公司长途客车准点事件为M,则24012 ()26013==P M;B共有班次240次,准点班次有210次,设B家公司长途客车准点事件为N,则210()27840==P N.A家公司长途客车准点的概率为12 13;B家公司长途客车准点的概率为7 8 .(2)列联表22()()()()()n ad bc K a b c d a c b d -=++++=2500(2403021020) 3.205 2.70626024045050⨯⨯-⨯≈>⨯⨯⨯, 根据临界值表可知,有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关. 16.(2020·全国·高考真题(文))某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?附:22()()()()()n ad bcKa b c d a c b d-=++++,【详解】(1)由频数分布表可知,该市一天的空气质量等级为1的概率为216250.43100++=,等级为2的概率为510120.27100++=,等级为3的概率为6780.21100++=,等级为4的概率为7200.09100++=;(2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为100203003550045350100⨯+⨯+⨯=(3)22⨯列联表如下:()221003383722 5.820 3.84155457030K ⨯⨯-⨯=≈>⨯⨯⨯, 因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.。
独立性检验高考真题(2017年-2018年))
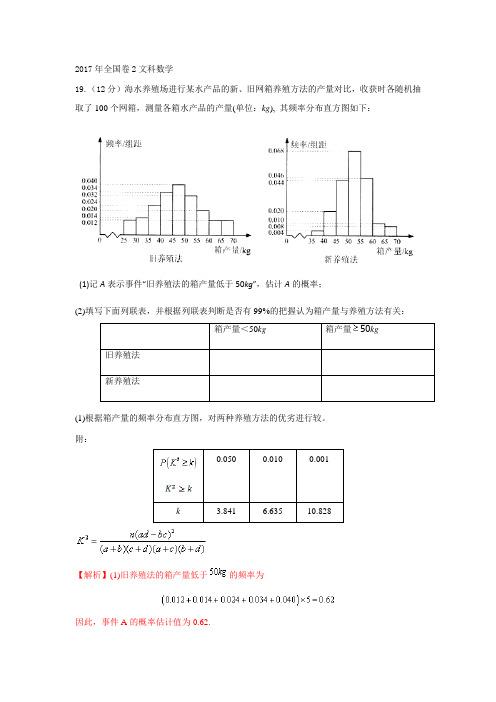
2017年全国卷2文科数学19.(12分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:箱产量(1)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:【解析】(1)旧养殖法的箱产量低于的频率为因此,事件A的概率估计值为0.62.(2)根据箱产量的频率分布直方图得列联表K2=由于15.705>6.635,故有99%的把握认为箱产量与养殖方法有关.(3)箱产量的频率分布直方图平均值(或中位数)在45kg到50kg之间,且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.2018全国卷318.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时同(单位:min)绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由:(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不?解:(1)第二种生产方式的效率更高.理由如下:(i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.(ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.(iii)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.(iv)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分.(2)由茎叶图知.列联表如下:超过不超过(3)由于,所以有99%的把握认为两种生产方式的效率有差异.。
高考数学一轮复习专题04 独立性检验(解析版)
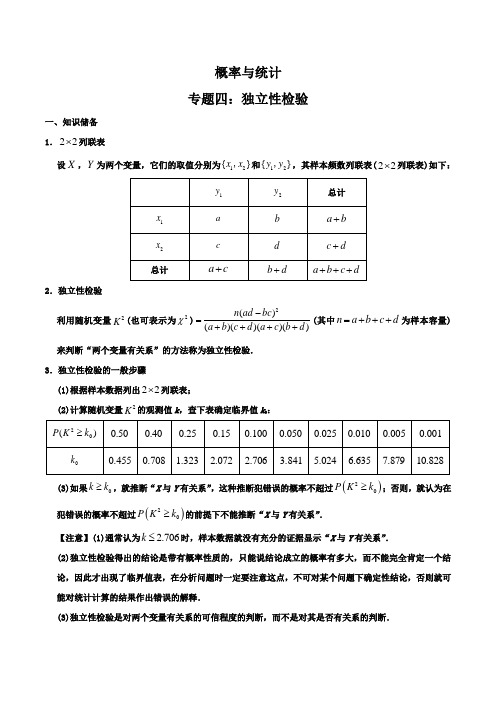
概率与统计 专题四:独立性检验一、知识储备 1.22⨯列联表设X ,Y 为两个变量,它们的取值分别为12{}x x ,和12{}y y ,,其样本频数列联表(22⨯列联表)如下:2.独立性检验利用随机变量2K (也可表示为2χ)2()()()()()n ad bc a b c d a c b d -=++++(其中n a b c d =+++为样本容量)来判断“两个变量有关系”的方法称为独立性检验. 3.独立性检验的一般步骤(1)根据样本数据列出22⨯列联表;(2)计算随机变量2K 的观测值k ,查下表确定临界值k 0:(3)如果0k k ≥,就推断“X 与Y 有关系”,这种推断犯错误的概率不超过()20P K k ≥;否则,就认为在犯错误的概率不超过()20P K k ≥的前提下不能推断“X 与Y 有关系”.【注意】(1)通常认为 2.706k ≤时,样本数据就没有充分的证据显示“X 与Y 有关系”.(2)独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论,因此才出现了临界值表,在分析问题时一定要注意这点,不可对某个问题下确定性结论,否则就可能对统计计算的结果作出错误的解释.(3)独立性检验是对两个变量有关系的可信程度的判断,而不是对其是否有关系的判断.二、例题讲解1.(2022·榆林市第十中学高三月考(文))随着经济的发展,人们的生活水平显著提高,健康意识不断增强,健康管理理念深入人心,人们参加体育锻炼的次数与时间在逐渐增加.某校一个课外学习小组为研究居民参加体育锻炼的时长(时长不超过60分钟)是否与性别有关,对某小区居民进行调查,并随机抽取了100名居民的调查结果,其中男性有55人,根据调查结果绘制了居民日均锻炼时间的频率分布直方图如下:(1)求样本中居民日均锻炼时间的中位数;(2)将日均锻炼时间不低于40分钟的居民称为“健生达人”(健康生活达人),已知样本中“健生达人”中有10名女性,根据已知条件完成下面22⨯列联表,并据此资料判断是否有95%的把握认为“健生达人”与性别有关.附:()()()()()22n ad bcKa b c d a c b d-=++++,n a b c d=+++.【答案】(1)32.8分钟;(2)表格见解析,没有95%的把握认为“健生达人”与性别有关. 【分析】(1)根据中位数的定义求样本中居民日均锻炼时间的中位数;(2)分析数据,完成列联表,计算2K ,通过比较其与临界值的大小,确定是否接受假设. 【详解】解:本题考查独立性检验.(1)由频率分布直方图知日均锻炼时间在[)0,30对应的频率为0.050.180.20.43++=,则中位数位于[)30,40,且中位数为0.500.43301032.80.25-+⨯=(分钟)(2)由频率分布直方图可知在抽取的100人中,“健生达人”有32人,从而22⨯列联表如下:得()210033103522 3.595 3.84155456832K ⨯-⨯=≈<⨯⨯⨯,所以没有95%的把握认为“健生达人”与性别有关2.(2022·江苏南京市·高三开学考试)科研小组为提高某种水果的果径,设计了一套实验方案,并在两片果园中进行对比实验.其中实验园采用实验方案,对照园未采用.实验周期结束后,分别在两片果园中各随机选取100个果实,按果径分成5组进行统计:[)21,26,[)26,31,[)31,36,[)36,41,[]41,46(单位:mm ).统计后分别制成如下的频率分布直方图,并规定果径达到36mm 及以上的为“大果”.(1)请根据题中信息完成下面的列联表,并判断是否有99.9%的把握认为“大果”与“采用实验方案”有关;(2)根据长期种植经验,可以认为对照园中的果径X 服从正态分布()2,N μσ,其中μ近似为样本平均数x ,5.5σ≈,请估计对照园中果径落在区间()39,50内的概率.(同一组中的数据以这组数据所在区间中点的值作代表)附:①()()()()()22n ad bc K a b c d a c b d -=++++;②若X 服从正态分布()2,N μσ,则()0.683P X μσμσ-<<+=,()220.954P X μσμσ-<<+=,()330.997P X μσμσ-<<+=.【答案】(1)列联表见解析,有99.9%的把握认为两者有关;(2)0.157. 【分析】(1)根据频率分布直方图分别求出采用实验方案大果和非大果数量及未采用实验方案大果和非大果数量,从而可得出列联表,再根据公式求出2K ,对照临界值表即可得出结论;(2)求出样本平均数x ,再根据正态分布的性质即可得出答案. 【详解】解:(1)由频率分布直方图可得:采用实验方案大果的数量为()50.1100.01010060⨯+⨯=个, 则非大果数量为1006040-=个,未采用实验方案大果的数量为()50.0400.02010030⨯+⨯=个, 则非大果数量为1003070-=个, 列联表如下:22006070304020010.8281001009011011K ⨯-⨯==⨯⨯⨯>,所以有99.9%的把握认为两者有关; (2)由题中数据,23.50.128.50.233.50.438.50.243.50.133.5x =⨯+⨯+⨯+⨯+⨯=, 则33.5μ=,则()()0.9970.683395030.157P X P X μσμσ-=++==<<<<.三、实战练习1.(2022·定远县育才学校高三开学考试(文))微信是腾讯公司推出的一种手机通信软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人.为了调查微信用户每天使用微信的时间,某经销化妆品的店家在一广场随机采访男性、女性用户各50名,将男性、女性平均每天使用微信的时间(单位:h )分成5组:(0,2],(2,4],(4,6],(6,8],(8,10]分别加以统计,得到如图所示的频率分布直方图.(1)根据频率分布直方图估计女性平均每天使用微信的时间;(2)若每天玩微信超过4h 的用户称为“微信控”,否则称为“非微信控”,判断是否有90%的把握认为“微信控”与性别有关. 附表:(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)【答案】(1)4.76()h ;(2)有90%的把握认为“微信控”与性别有关. 【分析】(1)用每个小矩形的面积乘以对应小矩形底边的中点,然后求和即可得到答案;(2)先通过频率分布直方图面积为1求出a ,进而根据参考公式求出K 2,然后将数据进行对比即可得到答案. 【详解】(1)由女性的频率分布直方图,可知女性用户平均每天使用微信的时间为0.1610.2430.2850.2070.129 4.76()h ⨯+⨯+⨯+⨯+⨯=.(2)由男性的频率分布直方图,可得2(0.040.1420.12)1a +++⨯=,解得0.08a =.由两个频率分布直方图,可得22⨯列联表如下:2K的观测值2100(38203012)2.941 2.70650506832k⨯⨯-⨯=≈>⨯⨯⨯,所以有90%的把握认为“微信控”与性别有关.2.(2022·河北唐山·高三开学考试)数字人民币是由央行发行的法定数字货币,它由指定运营机构参与运营并向公众兑换,与纸钞和硬币等价.截至2022年6月30日,数字人民币试点场景已超132万个,覆盖生活缴费、餐饮服务、交通出行、购物消费、政务服务等领域.为了进一步了解普通大众对数字人民币的感知以及接受情况,某机构进行了-次问卷调查,部分结果如下:(1)如果将高中及高中以下的学历称为“低学历”,大学专科及以上学历称为“高学历”,根据所给数据,完成下面的22⨯列联表;(2)若从低学历的被调查者中,按对数字人民币的了解程度用分层抽样的方法抽取8人,然后从这8人中抽取2人进行进一步调查,求被选中的2人中至少有1人对数字人民币不了解的概率;(3)根据列联表,判断是否有95%的把握认为“是否了解数字人民币”与“学历高低”有关? 附:()()()()()22n ad bc K a b c d a c b d -=++++【答案】(1)列联表答案见解析;(2)914;(3)没有95%的把握认为“是否了解数字人民币”与“学历高低”有关. 【分析】(1)根据题中所给数据完成22⨯列联表即可;(2)根据分层抽样分别求出不了解数字人民币和了解数字人民币的人数,再根据古典概型公式即可得解; (3)根据公式求出2K ,在参照临界值表即可得出结论. 【详解】解:(1)22⨯列联表如下:(2)从低学历被调查者中按对数字人民币的了解程度用分层抽样的方法抽取8人,抽取的8人中,不了解数字人民币的有81503400⨯=人, 了解数字人民币的有82505400⨯=人, 从这8人中抽取2人进行进一步调查,求被选中的2人中至少有1人对数字人民币不了解的概率2528C 91C 14P =-=.(3)根据列联表得()22800125250150275800 3.463 3.841275525400400231K ⨯⨯-⨯==≈<⨯⨯⨯.故没有95%的把握认为“是否了解数字人民币”与“学历高低”有关.3.(2022·广东实验中学高三月考)在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:(1)求这1000名患者的潜伏期的样本平均值x (同一组中的数据用该组区间的中点值作代表); (2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表请将列联表补充完整,并根据列联表判断是否有95%的把捏认为潜伏期与息者年龄有关;(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)...........是多少? 附:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.【答案】(1)5.4天;(2)列联表见解析,没有95%的把捏认为潜伏期与息者年龄有关.(3)潜伏期超过6天最有可能....是8人.【分析】(1)根据频率直方表求平均值即可.(2)由题设写出列联表,根据卡方检验公式计算卡方值,比照参考值即可知是否有95%的把捏认为潜伏期与息者年龄有关;(3)由题意知潜伏期超过6天的人数2(20,)5X B ,则202032()()()55k k kP X k C -==,应用不等法求最大概率时的k 值即可. 【详解】(1)10.08530.20550.3170.2590.13110.015130.005x =⨯+⨯+⨯+⨯+⨯+⨯+⨯ 5.4=天.(2)由题设知:[0,6]的频率为0.6,(6,14]的频率为0.4,故200人中潜伏期在[0,6]上有120人,在(6,14]上有80人. 列联表如下:∴22200(65453555) 2.083 3.84110010012080K ⨯⨯-⨯=≈<⨯⨯⨯,故没有95%的把捏认为潜伏期与息者年龄有关.(3)由患者潜伏期超过6天发生的概率400210005=, 设潜伏期超过6天的人数为X ,则2(20,)5XB ,∴202032()()()55k k kP X k C -==且020k ≤≤,*k N ∈,由题意,()(1)()(1)P X k P X k P X k P X k =≥=+⎧⎨=≥=-⎩,即2019112020202111202032325555{32325555k k k k k k k k k k k k C C C C --++----⎛⎫⎛⎫⎛⎫⎛⎫≥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫≥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,化简得3(1)2(20)2(21)3k k k k +≥-⎧⎨-≥⎩,解得374255k ≤≤, ∴8k ,即潜伏期超过6天最有可能....是8人. 4.(2022·黑龙江高三其他模拟(文))据有关部门统计,2021年本科生的平均签约薪酬为每月4300元.2021年某高校毕业生就业指导中心为了分析本校本科毕业生的专业课成绩优秀与否与本科毕业生就业后获得薪酬的关系,随机调查了从学校毕业的200名本科毕业学进行研究.研究结果表明:在专业课成绩优秀的120名本科毕业生中有90人每月工资超过人民币4300元,另30人每月工资低于人民币4300元;在专业课成绩不优秀的80名本科毕业生中有20人每月工资超过人民币4300元,另60人每月工资低于人民币4300元. (1)试根据上述数据完成22⨯列联表;(2)能否在犯错误的概率不超过0.001的前提下认为“该高校本科毕业生的专业课成绩优秀”与“每月工资超过当年本科生的平均签约薪酬”有关系?参考公式:()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.【答案】(1)列联表见解析;(2)能. 【分析】(1)根据题目已知数据完成22⨯列联表;(2)计算2K,根据临界值表判断即可【详解】(1)22⨯列联表如下:(2)因为()22009060302016004810.828 120801109033K⨯⨯-⨯==>>⨯⨯⨯.所以能在犯错误的概率不超过0.001的前提下认为“该校毕业生的专业课成绩优秀”与“每月工资超过当年本科生的平均签约薪酬”有关系.【点睛】方法点睛:本题考查22⨯联表判断相关性,独立性检验的一般步骤:第一步,提出假设0H:两个分类变量A和B没有关系;第二步,根据22⨯列联表和公式计算2K统计量;第三步,查对课本中临界值表,作出判断。
高中高考考点难点常见题型(带答案解析) 独立性检验(解析版)
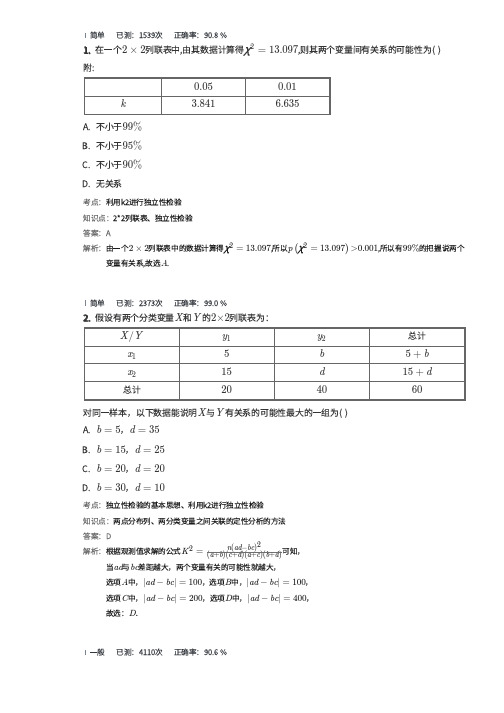
D.有以上的把握认为“爱好该项运动与性别⽆关”
考点:利⽤k2进⾏独⽴性检验
知识点:2*2列联表、两分类变量之间关联的定性分析的⽅法答案:C 解析:,在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”
即有以上的把握认为“爱好该项运动与性别有关”故选:.
⼀般已测:4499次正确率:71.9 %
9.现⾏普通⾼中学⽣在⾼⼀升⾼⼆时⾯临着选⽂理科的问题,学校抽取了部分男、⼥学⽣意愿的⼀份样本,制作出如下两个等⾼堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的是( ).
A.样本中的⼥⽣数量多于男⽣数量
B.样本中有理科意愿的学⽣数量多于有⽂科意愿的学⽣数量
C.样本中的男⽣偏爱理科
D.样本中的⼥⽣偏爱⽂科
考点:列联表与等⾼条形图的应⽤知识点:等⾼条形图答案:D
解析:由图可知,男、⼥⽣均偏爱理科,故错误.故选.
简单已测:4267次正确率:96.0 %
10.如图的等⾼条形图可以说明的问题是( )
99%∵K = ≈7.8>6.6352
60×50×60×50
110×(40×30−20×20)2
∴0.01=1%99%C D D。
高考数学专题复习:独立性检验

高考数学专题复习:独立性检验一、单选题1.某学校食堂对高三学生偏爱蔬菜还是肉类与性别的关系进行了一次调查,根据独立性检验原理,处理所得数据之后发现,有97.5%的把握但没有99%的把握认为偏爱蔬菜还是肉类与性别有关,则2K 的观测值可能为( ) k 2.706 A .2 3.206K =B .2 6.625K =C .27.869K =D .211.208K =2.某校为了解学生“玩手机游戏”和“学习成绩”是否有关,随机抽取了100名学生,运用2×2列联表进行独立性检验,经计算得到2 3.936K =,所以判定玩手机游戏与学习成绩有关系,那么这种判断出错的可能性为( )A .1%B .5%C .95%D .99%3.某校为了调查喜欢语文与性别的关系,随机调查了一些学生,数据如下表,由此判断喜欢语文与性别有关系,那么这种判断出错的可能性为( )()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.A .99.5%B .5%C .0.5%D .95%4.以下四个命题,其中正确的个数有( )①在独立性检验中,随机变量2K 的观测值越大,“认为两个分类变量有关”,这种判断犯错误的概率越小.②在线性回归方程ˆ0.80.35yx =-时,变量x 与y 具有负的线性相关关系; ③随机变量X 服从正态分布2(3,)N σ,若(4)0.64P X ≤=,则(23)0.07P X ≤≤=; ④两个随机变量相关性越强,则相关系数r 的值越接近于1. A .1个B .2个C .3个D .4个5.两个分类变量X 和Y ,它们的取值分别为{}12,x x 和{}12,y y ,其样本频数列联表如下表所示:则下列四组数据中,分类变量X 和Y 之间关系最强的是( ) A .4a =,2b =,3c =,6d = B .2a =,1b =,3c =,5d = C .4a =,5b =,6c =,8d =D .2a =,3b =,4c =,6d =6.为了丰富教职工业余文化生活,某校计划在假期组织70名老师外出旅游,并给出了两种方案(方案一和方案二),每位老师均选择且只选择一种方案,其中有50%的男老师选择方案一,有75%的女老师选择方案二,且选择方案一的老师中女老师占40%,则参照附表,得到的正确结论是( )附:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.A .在犯错误的概率不超过2.5%的前提下,认为“选择方案与性别有关”B .在犯错误的概率不超过2.5%的前提下,认为“选择方案与性别无关”C .有95%以上的把握认为“选择方案与性别有关”D .有95%以上的把握认为“选择方案与性别无关”7.利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用22⨯列联表,由计算可得27.236K =,参照下表:得到的正确结论是( )A .有99%以上的把握认为“爱好该项运动与性别无关”B .有99%以上的把握认为“爱好该项运动与性别有关”C .在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关"D .在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”8.如果根据性别与是否爱好运动的列联表得到2 3.852 3.841x ≈>,所以判断性别与运动有关,那么这种判断犯错的可能性不超过( ) A .2.5%B .0.5%C .1%D .5%9.某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用22⨯列联表进行独立性检验.经计算2 6.058K =,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”A .0.025%B .97.5%C .99%D .99.9%10.根据分类变量x 与y 的观测数据,计算得到2 2.974χ=.依据0.05α=的独立性检验,结论为( )A .变量x 与y 不独立B.变量x与y不独立,这个结论犯错误的概率不超过0.05C.变量x与y独立D.变量x与y独立,这个结论犯错误的概率不超过0.05二、填空题11.为了调查高中学生参加课外兴趣活动选篮球和舞蹈是否与性别有关,现随机调查了30名学生,得到如下22⨯列联表:根据表中的数据,及观测值2K(其中22()()()()()n ad bcKa b c d a c b d-=++++),参考数据:则在犯错误的概率不超过__________前提下,认为选择舞蹈与性别有关.12.某工厂为了调查工人文化程度与月收入的关系,随机抽取了部分工人,得到如下列联表:(单位:人)由上表中数据计算得2K的观测值22105(10302045)6.10955503075K⨯⨯-⨯=≈⨯⨯⨯,请估计在犯错误的概率不超过__________的前提下认为“文化程度与月收入有关系”.13.利用独立性检验的方法调查高中性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用22⨯列联表,由计算可得27.245K≈,参照下表2.706 至少有__________以上的把握认为“爱好该项运动与性别有关”.14.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:已知P (K 2≥3.841)≈0.05,P (K 2≥5.024)≈0.025.根据表中数据,得到K 2的观测值k =250(1320107)23272030⨯⨯-⨯⨯⨯⨯≈4.844.则认为选修文科与性别有关系出错的可能性为__________.三、解答题15.为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频率分布直方图如下:(1)求该市市民平均月收入的估计值(每组数据以区间中点值为代表).(2)将月收入不低于7500元称为“高收入”,否则称为“非高收入”,根据已知条件完成下面的22⨯列联表,并判断能否有99%的把握认为市民对楼市限购令的态度与收入有关.参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.16.为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果: 表1:男生上网时间与频数分布表表2:女生上网时间与频数分布表(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数; (2)完成联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”.附:()()()()22()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++为样本容量.0.45517.某大学为鼓励学生进行体育锻炼,购买了一批健身器材供学生使用,并从该校大一学生中随机抽取了100名学生调查使用健身器材的情况,得到数据如表所示:(1)设每周使用健身器材的次数不低于3次为“爱好健身”,根据上表数据,填写22⨯列联表,并判断能否在犯错误的概率不超过0.10的前提下认为“男生和女生在使用健身器材的爱好方面有差异”;(2)从上述每周使用健身器材3次的学生中,利用分层抽样的方法抽取5名学生,再从抽取的5名学生中随机抽取3人,求3人中至多有一名女生的概率.18.在对人们休闲方式的一次调查中,仅就看电视与运动这两种休闲方式比较喜欢哪一种进行了调查.调查结果:接受调查总人数110人,其中男、女各55人;受调查者中,女性有30人比较喜欢看电视,男性有35人比较喜欢运动.(1)请根据题目所提供的调查结果填写下列22⨯列联表:(2)能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”?注:22()()()()()n ad bcKa b c d a c b d-=++++,(其中n a b c d=+++为样本容量)参考答案1.B【分析】根据把握率确定2K的观测值区间范围即可选择.【详解】∵有97.5%的把握但没有99%的把握,∴2K的观测值区间范围为[5.024,6.635),结合选项可知,2K的观测值可能为6.625.故选:B2.B【分析】根据2K的值,对照附表即可得解.【详解】由题得2 3.936 3.841K=>,所以判定玩手机游戏与学习成绩有关系,这种判断出错的可能性为5%. 故选:B3.C【分析】计算出2K的值可得答案.【详解】因为()22501520510258.33320307.89225753K⨯⨯-⨯==≈>⨯⨯⨯,所有这种判断出错的可能性0.5%.故选:C.4.A【分析】利用随机变量2K的观测值越大,说明两个变量有关系的可能性越大判断①;根据回归方程一次项系数的正负判断②;根据正态分布的性质判断③; 利用线性相关的概念判断④. 【详解】①:在独立性检验中,因为随机变量2K 的观测值越大,说明两个变量有关系的可能性越大,即犯错误的概率越大,故①错误;②:回归方程ˆ0.80.35yx =-的一次项系数为-0.35<0,故变量x 与y 具有负的线性相关关系,故②正确;③:随机变量X 服从正态分布2(3)N σ,,则(34)(4)(3)0.640.50.14P X P X P X <≤=≤-<=-=, 由对称性可知,(23)0.14P X ≤≤=,故③错误;④:两个随机变量的线性相关关系越强,则相关系数r 的绝对值越接近于1,故④错误. 正确的选项有1个. 故选:A 5.A 【分析】逐项求出ad bc -的值并加以对比,最大值对应的分类变量之间关系最强. 【详解】我们可以用ad bc -的大小近似的判断两个分类变量之间关系的强弱,ad bc -的值越小,关系越弱,越大,关系越强.这四组数据中ad bc -的值分别为18、7、2、0, 所以A 组数据的ad bc -的值最大,相比较而言这组数据反应的X 和Y 的关系最强. 故选:A. 6.C 【分析】设该校男老师的人数为x ,女老师的人数为y ,根据条件,得到22⨯列联表,求出x ,y 的值,利用公式计算2K 的值,再与表中临界值比较可得结果. 【详解】设该校男老师的人数为x ,女老师的人数为y ,则可得如下表格:由题意0.40.50.25x y =+,可得43y x =,可得30x =,40y =,则()227015301510 4.667 3.84125453040K ⨯-⨯=≈>⨯⨯⨯, 但4.667 5.024<,所以无97.5%以上有95%以上的把握认为“选择方案与性别有关”. 故选:C. 7.B 【分析】由已知的27.236K =,对比临界值表可得答案 【详解】解:因为27.236 6.635K =>,所以有99%以上的把握认为“爱好该项运动与性别有关”. 故选:B. 8.D 【分析】根据临界值附表比较,即得结论. 【详解】根据以下临界值附表可知这种判断犯错的可能性不超过5%. 故选:D 9.B【分析】将2K 的值与表中数据比较大小可知5.024 6.058 6.635<<,由此确定出相应的把握有多少.【详解】因为2 6.058K =,对照表格:5.024 6.058 6.635<<,所以有10.0250.97597.5%-==的把握认为“学生性别与是否支持该活动有关系”. 故选:B.10.C【分析】由表中数据以及独立性检验的思想即可得出结果.【详解】0.05α=时,2 3.841 2.974χ=>,所以在犯错概率不超过0.1时变量x 与y 有关.故选:C11.0.025【分析】由列联表中的数据,根据公式计算出2K 的值,再对照临界表即可得答案.【详解】 解:由列联表中的数据可得,2230(13827)27 5.4 5.024*********K ⨯⨯-⨯===>⨯⨯⨯, 所以在犯错误的概率不超过0.025的前提下,认为选择舞蹈与性别有关.故答案为:0.025.12.0.025【分析】根据2K ,对比临界值即可得出结论.【详解】∵6.109 5.024>,故能在犯错误的概率不超过0.025的前提下认为“文化程度与月收入有关系”.故答案为:0.025.13.99%【分析】根据卡方的值与参考数据比较即可判断;【详解】解:因为27.245K ≈,6.6357.2457.879<<,所以10.0199%-=故至少有99%以上的把握认为“爱好该项运动与性别有关”,故答案为:99%14.5%【分析】根据观测值k ≈4.844以及独立性检验的基本思想即可得出结果.【详解】K 2的观测值k ≈4.844,这表明小概率事件发生.根据假设检验的基本原理,应该断定“是否选修文科与性别之间有关系”成立,并且这种判断出错的可能性约为5%.故答案为:5%15.(1)63;(2)表格见解析,有.【分析】(1)每组数据区间中点值乘以该组的频率求和可得答案;(2)根据每组频率乘以50可得每组的人数可完成列联表,计算2K 可得答案.【详解】(1)该市市民平均月收入的估计值为400.1500.2600.3700.2800.1900.163⨯+⨯+⨯+⨯+⨯+⨯=.(2)根据频率分布直方图知每组的人数分别为5,10,15,10,5,5.可得22⨯列联表如下:所以()22502882128.33340103020K ⨯⨯-⨯=≈⨯⨯⨯,因为8.333 6.635>,所以有99%的把握认为市民对楼市限购令的态度与收入有关.16.(1)225;(2)列联表答案见解析,没有90%的把握认为“大学生上网时间与性别有关”.【分析】(1)设上网时间不少于60分钟的人数为x ,依题意有30750100x =,计算即可; (2)填写列联表,计算2K ,对照临界值得出结论.【详解】(1)设上网时间不少于60分钟的人数为x ,依题意有30750100x =,解得225x =,所以估计其中上网时间不少于60分钟的人数是225.(2)塻22⨯列联表如下:由表中数据可得到22200(60304070) 2.20 2.70610010013070K ⨯-⨯=≈<⨯⨯⨯, 故没有90%的把握认为“大学生上网时间与性别有关”.17.(1)表格见解析,不能;(2)710. 【分析】(1)根据已知数据统计列联表中的各项的人数,填写列联表,进而计算2K 并与0.1的临界值进行比较,得到论断;(2)利用分层抽样的等比例原则求得抽取的5人中男女生的人数,利用符号表示每个学生,利用列举法计数,得到所求概率.【详解】解:(1)填写的列联表如下所示:()2210222422320.506 2.70644565446K ⨯⨯-⨯=≈<⨯⨯⨯.所以不能在犯错误的概率不超过0.1的前提下认为“男生和女生在使用健身器材的爱好方面有差异”.(2)从每周使用健身器材3次的学生中,利用分层抽样的方法抽取5名学生,则抽取男生3名,抽取女生2名.将抽取的3名男生分别记为a ,b ,c ,2名女生分别记为m ,n ,则从5人中随机抽取3人的不同情况有abc ,abm ,abn ,acm ,acn ,amn ,bcm ,bcn ,bmn ,cmn ,共10种, 其中至多有一名女生的情况有abc ,abm ,abn ,acm ,acn ,bcm ,bcn ,共7种. 所以从抽取的5名学生中随机抽取3人,至多有一名女生的概率为710. 18.(1)答案见解析;(2)不能.【分析】(1)由题意填写列联表即可;(2)代入数据计算2K 的观测值,比较观测值与3.841的大小,判断能否在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系” .【详解】解.(1)根据题目所提供的调查结果,可得下列22⨯列联表:(2)根据列联表中的数据,可计算()2211030352025 3.66750605555K ⨯⨯-⨯=≈⨯⨯⨯,因为03.667 3.841k k ≈<=,所以不能在犯错误的概率不超过0.05的前提下认为“性别与休闲方式有关系”.。
【高考数学总复习】:回归性分析与独立性检验(知识点讲解+真题演练+详细解答)
量,例如某同学的数学成绩与化学成绩。
2.线性回归分析 (1) 散点图:将样本中的各对数据在直角坐标系中描点而得到的图形叫做散点图,它直观地 描述了两个变量之间是否有相关关系,是判断两个变量相关性的重要依据。 (2) 回归直线:散点图中点的整体分布在一条直线左右,则称这两个变量之间具有线性相关
(a b)(c d)(a c)(b d )
通过对统计量 K2 的研究,一般情况下认为:
①当 K 2 ≤3.841 时,认为变量 X 与 Y 是无关的。
②当 K 2 >3.841 时,有 95%的把握说变量 X 与 Y 有关;
④ 当 K 2 >6.635 时,有 99%的把握说变量 X 与 Y 有关;
定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。
2.分类变量的理解: 分类变量是说明事物类别的一个名称,其取值是分类数据。如“性别”就是一个分类变 量,其变量值为“男”或“女”;“行业”也是一个分类变量,其变量值可以为“零售 业”,说明 X 与 Y 无关的把握越小
6. 右表是对与喜欢足球与否的统计列联表依据表中的数据,得到( )
A. K 2 9.564 B. K 2 3.564 C. K 2 2.706 D. K 2 3.841
7. 对两个分类变量 A、B 的下列说法中正确的个数为( ). ①A 与 B 无关,即 A 与 B 互不影响;②A 与 B 关系越密切,则 K2 的值就越大;③K2
x yw
46.6 563 6.8
8
(xi x )2
i 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4节 独立性检验基础巩固题组(建议用时:40分钟)一、单项选择题1.在一次独立性检验中,其把握性超过但不超过,则的可能值为 99%99.5%2χ 参考数据:独立性检验临界值表20()≥P k χ0.10 0.05 0.025 0.010 0.005 0.0010k 2.706 3.841 5.024 6.635 7.87910.828A .5.424B .6.765C .7.897D .11.8972.独立性检验显示:在犯错误的概率不超过0.1的前提下认为性别与是否喜爱喝酒有关,那么下列说法中正确的是A .在100个男性中约有90人喜爱喝酒B .若某人喜爱喝酒,那么此人为女性的可能性为10%C .认为性别与是否喜爱喝酒有关判断出错的可能性至少为10%D .认为性別与是否喜爱喝酒有关判断正确的可能性至少为90%3.为了判定两个分类变量和是否有关系,应用独立性检验法算得的观测值为5,X Y 2χ又已知,,则下列说法正确的是 2( 3.841)0.05P χ=≥2( 6.635)0.01P χ=≥A .有以上的把握认为“和有关系” 99%X Y B .有99%以上的把握认为“和没有关系” X Y C .有95%以上的把握认为“和有关系” X Y D .有95%以上的把握认为“和没有关系”X Y 4.利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关,通过随机询问110名不同的大学生是否爱好某项运动,利用列联表,由计算可得,22⨯28.806χ≈20()P k χ≥0.15 0.10 0.05 0.025 0.010 0.005 0.0010k 2.0722.7063.8415.024 6.635 7.87910.828参照附表,得到的正确结论是A .有99.5%以上的把握认为“爱好该项运动与性别无关”B .有99.5%以上的把握认为“爱好该项运动与性别有关”C .在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别有关”D .在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别无关” 5.某市政府调查市民收入与旅游欲望时,采用独立性检验法抽取3000人,计算发现k 2=6.023,则根据这一数据查阅下表,市政府断言市民收入增减与旅游欲望有关系的把握是20()P k ≥0.15 0.10 0.05 0.025 0.010 0.0050k 2.072 2.7063.841 5.024 6.635 7.879 A .90% B .95% C .97.5%D .99.5%6.假设两个分类变量X 与Y ,它们的可能取值分别为{x 1,x 2}和{y 1,y 2},其列联表为y 1 y 2 总计 x 1 a b a +b x 2 c d c +d 总计a +cb +da +b +c +d对于同一样本的以下各组数据,能说明X 与Y 有关的可能性最大的一组为( ) A .a =5,b =4,c =3,d =2 B .a =5,b =3,c =4,d =2 C .a =2,b =3,c =4,d =5 D .a =2,b =3,c =5,d =4 二、多项选择题7. 下列说法正确的是____________.(填序号) A . 对事件A 与B 的检验无关,即两个事件的相关性较小; B . 对事件A 与B 关系越密切,就越大;2χC . 的大小是判断事件A 与B 是否相关的唯一数据;2χD . 若判断两事件A 与B 有关,则A 发生B 一定发生.8. 在调查中发现480名男人中有38名患有色盲,520名女人中有6名患有色盲,则下列说法正确的是A . 男人、女人中患色盲的频率分别为0.038,0.006;B . 男、女患色盲的概率分别为;193240260,C . 男人中患色盲的比例比女人中患色盲的比例大,患色盲与性别有关; D . 能说明患色盲与性别是否有关. 三、填空题9.在公式中,若则22()()()()()n ad bc a b c d a c b d χ-=++++87935,,,,a b d n ====c =______________.10.博鳌亚洲论坛2018年年会于4月8日至11日在海南博鳌举行,为了搞好对外宣传工作,会务组选聘了50名记者担任对外翻译工作,在下面“性别与会俄语”的列联22⨯表中,______________.a b d ++= 会俄语 不会俄语总计 男 a b 20 女 6 d 总计185011.某高校“统计初步”课程的教师随机调查了该选修课的一些学生情况,具体数据如下表:非统计专业统计专业男 13 10 女720为了检验主修专业是否与性别有关系,根据表中的数据,得到2χ.因为,所以断定主修统计专业与性别有关250(1320107)= 4.8423272030⨯⨯-⨯≈⨯⨯⨯2 3.841≥χ系.这种判断出错的可能性为______________.20()P k χ≥0.15 0.10 0.05 0.025 0.010 0.005 0.0010k 2.0722.7063.8415.024 6.635 7.87910.82812.某校学生会为研究该校学生的性别与语文、数学、英语成绩这3个变量之间的关系,随机抽查了100名学生,得到某次期末考试的成绩数据如表1至表3,根据表中数据可知该校学生语文、数学、英语这三门学科中表1(语文)表2(数学)表3(英语)不及格及格总计不及格及格总计不及格及格总计男14 36 50 男10 40 50 男25 25 50 女16 34 50 女20 30 50 女 5 45 50 总计30 70 100总计30 70 100总计30 70 100A.语文成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小B.数学成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小C.英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小D.英语成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小能力提升题组(建议用时:20分钟)13.某县对在职的71名高中数学教师就支持新的数学教材还是支持旧的数学教材做了调查,结果如下表所示:支持新教材支持旧教材合计具有15年以上教龄的教师122537教龄在15以下的教师102434合计224971 根据此资料,你是否认为教龄的长短与支持新的数学教材有关?14.某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样的方法(按A类、B类分两层)从该工厂的工人中抽取100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数),结果如表.表1:A 类工人生产能力的频数分布表生产能力分组[110,120)[120,130)[130,140)[140,150)人数8x32表2:B 类工人生产能力的频数分布表生产能力分组[110,120)[120,130)[130,140) [140,150) 人数6y2718(1)确定x ,y 的值;(2)完成2×2列联表,并回答能否在犯错误的概率不超过0.001的前提下认为工人的生产能力与工人的类别有关系? 生产能力分组 工人类别[110,130)[130,150)总计 A 类工人 B 类工人 总计附:22()()()()()n ad bc a b c d a c b d χ-=++++20()P k χ≥0.050 0.010 0.001k 03.841 6.635 10.82815.为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了2018年下半年该市100名农民工(其中技术工、非技术工各50名)的月工资,得到这100名农民工的月工资均在(百元)内,且月工资收入在(百元)内的人数为,并根据调查[2555],[4550),15结果画出如图所示的频率分布直方图:(1)求n 的值;(2)已知这100名农民工中月工资高于平均数的技术工有31名,非技术工有19名.①完成如下所示列联表22⨯技术工 非技术工总计 月工资不高于平均数 50 月工资高于平均数50 总计5050100②则能否在犯错误的概率不超过0.001的前提下认为是不是技术工与月工资是否高于平均数有关系?参考公式及数据:,其中.22()()()()()n ad bc a b c d a c b d χ-=++++n a b c d =+++20()P k χ≥0.15 0.10 0.05 0.025 0.010 0.005 0.0010k 2.0722.7063.8415.024 6.635 7.87910.828第4节 独立性检验1.B 2.D 3.C 4.B 5.C 6. D 7.A B对于A ,事件A 与B 检验无关,只是说两事件的相关性较小,故 A 对.B 是正确的.对于C ,判断A 与B 是否相关的方式很多,可以用列联表,也可以借助于概率运算,故C 错.对于D ,两事件A 与B 有关,说明两者同时发生的可能性相对来说较大,但并不是A 发生B 定发生,故D 错. 8.C D男人中患色盲的比例为≈0.079,女人中患色盲的比例,故3848060.012520≈,又38×(520-6)-6×(480-38)=16880,相差较大,说明患色盲与性别有关,故选386480520>C ,D 9.11若则故答案为11. 87935,,,,a b d n ====11c n a b d =---=10.44由于总人数为50,可得出,解得. 650a b d +++=44a b d ++=11.5%(或0.05)根据临界值表: ,223.841( 3.841)0.050≥≥,P χχ=所以断定主修统计专业与性别有关系.这种判断出错的可能性为0.05. 故答案为5%(或0.05) 12. C因为,222100(14341636)100(10302040)100(2545525)307050503070505030705050⨯⨯-⨯⨯⨯-⨯⨯⨯-⨯<<⨯⨯⨯⨯⨯⨯⨯⨯⨯所以英语成绩与性别有关联性的可能性最大,。
