2017唐山一模数学理科
河北省唐山市迁安市2017年中考数学一模试卷及参考答案

20. 按照如下步骤计算:6﹣2÷( + ﹣ ﹣ ). (1) 计算:( + ﹣ ﹣ )÷6﹣2; (2) 根据两个算式的关系,直接写出6﹣2÷( + ﹣ ﹣ )的结果. 21. 如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度 移动,过点E作BC的垂线交直线CD于点F.
(1) 求证:∠A=∠BCD; (2) 点E运动多长时间,CF=AB?并说明理由. 22. 在一个多边形中,一个内角相邻的外角与其他各内角的和为600°. (1) 如果这个多边形是五边形,请求出这个外角的度数; (2) 是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由. 23. 小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和
(2) 如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩
形铁片切割成两个全等的直角梯形铁片;
①当BE=DF= 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由; ②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围. 26. 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x= 1,直线BC与抛物线的对称轴交于点D.
(1)
求抛物线的函数表达式;
(2) 求直线BC的函数表达式; (3) 点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ= AB时,求tan∠CED的值; ②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答. 参考答案 1. 2. 3. 4. 5. 6. 7.
河北省唐山一中2017届高三高考仿真(四)(理科数学)(含答案)word版

唐山一中2011年高考模拟试卷(四)数 学(理科)说明:1.本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至6页。
全卷150分,考试时间120分钟。
2. 将Ⅰ卷答案用2B 铅笔涂在答题卡上,卷Ⅱ用蓝黑钢笔或圆珠笔答在试卷上。
第Ⅰ卷 (共60分)一、选择题 (本大题共12小题,每小题5分,共60分.) 1.设复数2221,z i z z=-+则等于A .1i -+B .1i +C .12i -+D .12i +2.已知0m >,命题:p 函数()log m f x x =是()0,+∞的增函数,命题2:()ln(q g x mx =-2)3x m +的值域为R ,且p q ∧是假命题,p q ∨是真命题,则实数m 的范围是A .1,3⎛⎫+∞ ⎪⎝⎭B .103m <≤C.()10,1,3⎛⎤+∞ ⎥⎝⎦D .1,13⎛⎫ ⎪⎝⎭3.“1a =-”是“直线260a x y -+=与直线4(3)90x a y --+=互相垂直”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 4. 函数ln xy x=的图像大致是A B C D 5.函数1ln(1),(1)2x y x -+-=>的反函数是( )A .211(0)x y e x +=->B .211(0)x y e x +=+>C .211(R)x y e x +=-∈ D.211(R)x y e x +=+∈6. 已知P 是双曲线22143x y -=上的动点,12,F F 分别是双曲线的左、右焦点,Q 是21PF F ∠的平分线上的一点,且20F Q QP ⋅=,O 为坐标原点,则||OQ =A .1B .3C .2 D7. 设(132)n x y -+的展开式中含y 的一次项为01(),n n a a x a x y +++则01a a +n a ++=A .(2)n n --B .(2)n n -C .12--n n D .1(2)n n ---8.已知非零向量,,a b c 满足++=a b c 0,向量,a b 的夹角为120,且||2||=b a , 则向量a 与c 的夹角为A .︒60 B .︒90 C .︒120D . ︒1509.直线20x y m -+=与圆225x y +=交于A 、B ,O 为坐标原点,若OB OA ⊥,则m 的值A .5±B .52±C .±D .10.某运输公司有7个车队,每个车队的车多于4辆,先从这7个车队中抽取10辆,且每个车队至少抽一辆组成运输队,则不同的抽法有A. 84种B. 120种C. 63种D. 301种11. 如图,将45°直角三角板和30°直角三角板拼在一起,其中45°直角三角板的斜边与30°直角三角板的30°角所对的直角边重合.若DB x DC y DA =⋅+⋅,则x ,y 等于A .1x y =B .1x y =C .2,x y =D .1x y ==12.已知抛物线)0(2:2>=p px y C 过点)0,(p A 的直线与抛物线C 交于M ,N 两点,且AN MA 2=,过点M ,N 向直线x p =-作垂线,垂足分别为Q P ,,,MAP NAQ ∆∆的面积分别为记为1S 与2S ,A .21:S S =2:1B .21:S S =5:2C .21:S S =4:1D .21:S S =7:1第Ⅱ卷注意事项:1. 用钢笔或圆珠笔直接答在试题卷中。
2017年河北省唐山市路北区中考一模数学试卷(解析版)
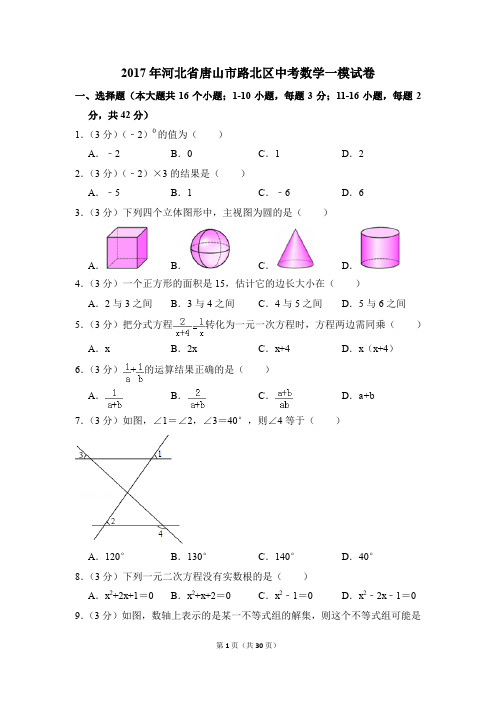
2017年河北省唐山市路北区中考数学一模试卷一、选择题(本大题共16个小题;1-10小题,每题3分;11-16小题,每题2分,共42分)1.(3分)(﹣2)0的值为()A.﹣2B.0C.1D.22.(3分)(﹣2)×3的结果是()A.﹣5B.1C.﹣6D.63.(3分)下列四个立体图形中,主视图为圆的是()A.B.C.D.4.(3分)一个正方形的面积是15,估计它的边长大小在()A.2与3之间B.3与4之间C.4与5之间D.5与6之间5.(3分)把分式方程转化为一元一次方程时,方程两边需同乘()A.x B.2x C.x+4D.x(x+4)6.(3分)+的运算结果正确的是()A.B.C.D.a+b7.(3分)如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°8.(3分)下列一元二次方程没有实数根的是()A.x2+2x+1=0B.x2+x+2=0C.x2﹣1=0D.x2﹣2x﹣1=0 9.(3分)如图,数轴上表示的是某一不等式组的解集,则这个不等式组可能是()A.B.C.D.10.(3分)自来水公司为了解居民某月用水量,随机抽取了20户居民的月用水量x(单位:立方米),绘制出表格,则月用水量x<3的频率是()A.0.15B.0.3C.0.8D.0.911.(2分)如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?()A.∠1<∠2B.∠1>∠2C.∠3<∠4D.∠3>∠412.(2分)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是()A.8B.6C.4D.213.(2分)如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:(甲)作AB的中垂线,交BC于P点,则P即为所求(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求对于两人的作法,下列判断何者正确?()A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确14.(2分)如图,坐标平面上有A(0,a)、B(﹣9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在()A.第一象限B.第二象限C.第三象限D.第四象限15.(2分)如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F 两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为何?()A.10B.11C.D.16.(2分)在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B →C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为()A.B.C.D.二、填空题(本大题共3个小题;17-18每小题3分,19题每空2分,共10分)17.(3分)据报道,2015年某市城镇非私营单位就业人员年平均工资超过60500元,将数60500用科学记数法表示为.18.(3分)甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小明打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小明抽出的两颗求颜色相同的概率为.19.(4分)如图,已知点A(0,2)、B(2,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.(1)当AB∥PQ时,点P的横坐标是;(2)当BP∥QA时,点P的横坐标是.三、解答题(本大题共7个小题,共68分)20.(9分)先化简,再求值:,其中x满足方程:x2+x ﹣6=0.21.(9分)国家环保局统一规定,空气质量分为5级:1级质量为优;2级质量为良;3级质量为轻度污染;4级质量为中度污染;5级质量为重度污染.某城市随机抽取了一年中某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:(1)本次调查共抽取了天的空气质量检测结果进行统计;(2)补全条形统计图;(3)扇形统计图中3级空气质量所对应的圆心角为°;(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计该年该城市只有多少天适宜户外活动.(一年天数按365天计)22.(9分)如图,已知边长为6的等边△ABC内接于⊙O.(1)求⊙O半径;(2)求的长和弓形BC的面积.23.(9分)如图,已知一次函数y1=kx+b的图象与反比例函数y2=的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B(1)求m的值;(2)求一次函数的表达式;(3)根据图象,当y1<y2<0时,写出x的取值范围.24.(10分)如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)延长MP交CN于点E(如图2).①求证:△BPM≌△CPE;②求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.25.(10分)某高新企业员工的工资由基础工资、绩效工资和工龄工资三部分组成,其中工龄工资的制定充分了考虑员工对企业发展的贡献,同时提高员工的积极性,控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案.Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;Ⅱ.社会工龄=参加本企业工作时年龄﹣18,企业工龄=现年年龄﹣参加本企业工作时年龄.Ⅲ.当年工作时间计入当年工龄Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.请解决以下问题(1)求出y1、y2与工龄x之间的函数关系式;(2)现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?(3)已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?26.(12分)如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.(1)点B的坐标为;用含t的式子表示点P的坐标为;(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求t为何值时,S有最大值?(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC 分割成三角形和四边形两部分,且三角形的面积是△ONC面积的?若存在,求出点T的坐标;若不存在,请说明理由.2017年河北省唐山市路北区中考数学一模试卷参考答案与试题解析一、选择题(本大题共16个小题;1-10小题,每题3分;11-16小题,每题2分,共42分)1.(3分)(﹣2)0的值为()A.﹣2B.0C.1D.2【解答】解:(﹣2)0=1.故选:C.2.(3分)(﹣2)×3的结果是()A.﹣5B.1C.﹣6D.6【解答】解:原式=﹣2×3=﹣6.故选:C.3.(3分)下列四个立体图形中,主视图为圆的是()A.B.C.D.【解答】解:A、主视图是正方形,故此选项错误;B、主视图是圆,故此选项正确;C、主视图是三角形,故此选项错误;D、主视图是长方形,故此选项错误;故选:B.4.(3分)一个正方形的面积是15,估计它的边长大小在()A.2与3之间B.3与4之间C.4与5之间D.5与6之间【解答】解:∵一个正方形的面积是15,∴该正方形的边长为,∵9<15<16,∴3<<4.故选:B.5.(3分)把分式方程转化为一元一次方程时,方程两边需同乘()A.x B.2x C.x+4D.x(x+4)【解答】解:由两个分母(x+4)和x可得最简公分母为x(x+4),所以方程两边应同时乘x(x+4).故选:D.6.(3分)+的运算结果正确的是()A.B.C.D.a+b【解答】解:+=+=故+的运算结果正确的是.故选:C.7.(3分)如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°【解答】解:∵∠1=∠2,∴a∥b,∴∠3=∠5,∵∠3=40°,∴∠5=40°,∴∠4=180°﹣40°=140°,故选:C.8.(3分)下列一元二次方程没有实数根的是()A.x2+2x+1=0B.x2+x+2=0C.x2﹣1=0D.x2﹣2x﹣1=0【解答】解:A、△=22﹣4×1×1=0,方程有两个相等实数根,此选项错误;B、△=12﹣4×1×2=﹣7<0,方程没有实数根,此选项正确;C、△=0﹣4×1×(﹣1)=4>0,方程有两个不等的实数根,此选项错误;D、△=(﹣2)2﹣4×1×(﹣1)=8>0,方程有两个不等的实数根,此选项错误;故选:B.9.(3分)如图,数轴上表示的是某一不等式组的解集,则这个不等式组可能是()A.B.C.D.【解答】解:∵,∴这个不等式组的解集为:﹣1<x≤2,A、解不等式组得:x>1,故本选项错误;B、解不等式组得:﹣2<x≤1,故本选项错误;C、解不等式组得:﹣1≤x<2,故本选项错误;D、解不等式组得:﹣1<x≤2,故本选项正确.故选:D.10.(3分)自来水公司为了解居民某月用水量,随机抽取了20户居民的月用水量x(单位:立方米),绘制出表格,则月用水量x<3的频率是()A.0.15B.0.3C.0.8D.0.9【解答】解:由图可得,月用水量x<3的总户数为:1+2+3+4+3+3=16,则频率==0.8.故选:C.11.(2分)如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?()A.∠1<∠2B.∠1>∠2C.∠3<∠4D.∠3>∠4【解答】解:∵四边形ABCD、AEFG均为正方形,∴∠BAD=∠EAG=90°,∵∠BAD=∠1+∠DAE=90°,∠EAG=∠2+∠DAE=90°,∴∠1=∠2,在Rt△ABE中,AE>AB,∵四边形AEFG是正方形,∴AE=AG,∴AG>AB,∴∠3>∠4.故选:D.12.(2分)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是()A.8B.6C.4D.2【解答】解:过点P作PE⊥BC于E,∵AB∥CD,P A⊥AB,∴PD⊥CD,∵BP和CP分别平分∠ABC和∠DCB,∴P A=PE,PD=PE,∴PE=P A=PD,∵P A+PD=AD=8,∴P A=PD=4,∴PE=4.故选:C.13.(2分)如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:(甲)作AB的中垂线,交BC于P点,则P即为所求(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求对于两人的作法,下列判断何者正确?()A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确【解答】解:甲:如图1,∵MN是AB的垂直平分线,∴AP=BP,∴∠ABC=∠BAP,∵∠APC=∠ABC+∠BAP,∴∠APC=2∠ABC,∴甲正确;乙:如图2,∵AB=BP,∴∠BAP=∠APB,∵∠APC=∠BAP+∠ABC,∴∠APC≠2∠ABC,∴乙错误;故选:C.14.(2分)如图,坐标平面上有A(0,a)、B(﹣9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵B(﹣9,0)、C(10,0),∴△ABC的外心在直线x=上.∵∠BAC=100°,∴△ABC的外心在三角形的外部,∴△ABC的外心在第四象限.故选:D.15.(2分)如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F 两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为何?()A.10B.11C.D.【解答】解:∵四边形ABCD,BEFG是正方形,∴BC=CD=AB=5,GF=BG=3,∠C=∠BGF=∠GFE=∠CGF=∠GFH=90°,∵四边形DGHI是矩形,∴∠DGH=90°,∴∠DGC+∠CGH=∠FGH+∠HGC=90°,∴∠DGC=∠FGH,∴△DGC∽△HGF,∴=,∴FH===,=GF•FH=,∴S△FHG故选:D.16.(2分)在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B →C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为()A.B.C.D.【解答】解:∵AB=2,BC=1,动点P从点B出发,P点在BC上时,BP=x,AB=2,∴△ABP的面积S=×AB×BP=×2x=x;动点P从点B出发,P点在CD上时,△ABP的高是1,底边是2,所以面积是1,即s=1;∴S=x时是正比例函数,且S随x的增大而增大,S=1时,是一个常数函数,是一条平行于x轴的直线.所以只有C符合要求.故选:C.二、填空题(本大题共3个小题;17-18每小题3分,19题每空2分,共10分)17.(3分)据报道,2015年某市城镇非私营单位就业人员年平均工资超过60500元,将数60500用科学记数法表示为 6.05×104.【解答】解:60500=6.05×104.故答案为:6.05×104.18.(3分)甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小明打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小明抽出的两颗求颜色相同的概率为.【解答】解:画树状图为:共有12可等可能的结果数,其中抽出的两颗求颜色相同的结果数为2,所以小明抽出的两颗求颜色相同的概率==.故答案为.19.(4分)如图,已知点A(0,2)、B(2,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.(1)当AB∥PQ时,点P的横坐标是;(2)当BP∥QA时,点P的横坐标是0或2.【解答】解:(1)如图1:当AB为梯形的底时,PQ∥AB,∴Q在CP上,∵△APQ是等边三角形,CP∥x轴,∴AC垂直平分PQ,∵A(0,2),C(0,4),∴AC=2,∴PC=AC•tan30°=2×=,∴当AB为梯形的底时,点P的横坐标是:;(2)如图2,当AB为梯形的腰时,AQ∥BP,∴Q在y轴上,∴BP∥y轴,∵CP∥x轴,∴四边形ABPC是平行四边形,∴CP=AB=2,如图3,当C与P重合时,∵A(0,2)、B(2,2),∴tan∠APB==,∴∠APB=60°,∵△APQ是等边三角形,∴∠P AQ=60°,∴∠ACB=∠P AQ,∴AQ∥BP,∴当C与P重合时,四边形ABPQ以AB为腰的梯形,此时点P的横坐标为0;∴当AB为梯形的腰时,点P的横坐标是:0或2.故答案为:(1);(2)0或2.三、解答题(本大题共7个小题,共68分)20.(9分)先化简,再求值:,其中x满足方程:x2+x ﹣6=0.【解答】解:(x+1﹣)÷=÷=•=,∵x满足方程x2+x﹣6=0,∴(x﹣2)(x+3)=0,解得:x1=2,x2=﹣3,当x=2时,原式的分母为0,故舍去;当x=﹣3时,原式==.21.(9分)国家环保局统一规定,空气质量分为5级:1级质量为优;2级质量为良;3级质量为轻度污染;4级质量为中度污染;5级质量为重度污染.某城市随机抽取了一年中某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:(1)本次调查共抽取了200天的空气质量检测结果进行统计;(2)补全条形统计图;(3)扇形统计图中3级空气质量所对应的圆心角为72°;(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计该年该城市只有多少天适宜户外活动.(一年天数按365天计)【解答】解:(1)抽查的总天数是24÷48%=50(天),故答案是:50;(2)是5级的天数是50﹣3﹣7﹣10﹣24=6(天),;(3)扇形统计图中3级空气质量所对应的圆心角为×360=72°,故答案是:72;(4)估计该年该城市适宜户外活动的天数是×365=146(天).答:估计该年该城市适宜户外活动的天数是146天.22.(9分)如图,已知边长为6的等边△ABC内接于⊙O.(1)求⊙O半径;(2)求的长和弓形BC的面积.【解答】解:(1)连结OB,OC,作OM⊥BC于M,∵△ABC是等边三角形,∴∠A=60°,∴∠BOC=120°.又∵OM⊥BC,∴BM=CM=3.又∵OB=OC,∴∠OBC=∠OCB=30°.∴⊙O半径==2;(2)∵由(1)知∠BOC=120°,OB=2,∴弧BC的长==弓形BC的面积=S扇形BOC ﹣S△BOC=﹣×6×3=4π﹣3.23.(9分)如图,已知一次函数y1=kx+b的图象与反比例函数y2=的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B(1)求m的值;(2)求一次函数的表达式;(3)根据图象,当y1<y2<0时,写出x的取值范围.【解答】解:(1)把点A(﹣4,m)的坐标代入y2=,则m==﹣1,得m=﹣1;(2)连接CB,CD,∵⊙C与x轴,y轴相切于点D,B,∴∠CBO=∠CDO=90°=∠BOD,BC=CD,∴四边形BODC是正方形,∴BO=OD=DC=CB,∴设C(a,a)代入y2=得:a2=4,∵a>0,∴a=2,∴C(2,2),B(0,2),把A(﹣4,﹣1)和(0,2)的坐标代入y1=kx+b中,得:,解得:,∴一次函数的表达式为:y1=x+2;(3)∵A(﹣4,﹣1),∴当y1<y2<0时,x的取值范围是:x<﹣4.24.(10分)如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)延长MP交CN于点E(如图2).①求证:△BPM≌△CPE;②求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.【解答】(1)证明:①如图2:∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMA=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE,②∵△BPM≌△CPE,∴PM=PE∴PM=ME,∴在Rt△MNE中,PN=ME,∴PM=PN.(2)解:成立,如图3.证明:延长MP与NC的延长线相交于点E,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,又∵P为BC中点,∴BP=CP,又∵∠BPM=∠CPE,在△BPM和△CPE中,,∴△BPM≌△CPE,∴PM=PE,∴PM=ME,则Rt△MNE中,PN=ME∴PM=PN.(3)解:如图4,四边形BMNC是矩形,理由:∵MN∥BC,BM⊥AM,CN⊥MN,∴∠AMB=∠ANC=90°,∠AMB+∠CBM=180°,∴∠CBM=∠AMB=∠CNA=90°,∴四边形BMNC是矩形.∵BM=CN,∠PBM=∠PCN,BP=CP,∴△PBM≌△PCN(SAS)∴PM=PN.25.(10分)某高新企业员工的工资由基础工资、绩效工资和工龄工资三部分组成,其中工龄工资的制定充分了考虑员工对企业发展的贡献,同时提高员工的积极性,控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案.Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;Ⅱ.社会工龄=参加本企业工作时年龄﹣18,企业工龄=现年年龄﹣参加本企业工作时年龄.Ⅲ.当年工作时间计入当年工龄Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.请解决以下问题(1)求出y1、y2与工龄x之间的函数关系式;(2)现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?(3)已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?【解答】解:(1)设y1与x之间的函数关系式为y1=kx,由题意,得100=10k,解得:k=10∴y1=10x(x≥0,x为整数);当0≤x≤3时,y2与x之间的函数关系式为y2=k2x,由题意,得60=3k2.∴k2=20,∴y2=20x,当3<x≤32时,设y2=a(x﹣23)2+860,由题意,得698=a(32﹣23)2+860,解得:a=﹣2,∴y2=﹣2(x﹣23)2+860,当32<x≤42时,由图象,得y2=698.∴y2=;(2)小张在原厂的社会工龄为:28﹣18=10年,企业工龄为:28﹣28=0年,y1=0,y2=522,∴在小张在原厂的工龄工资为:0+522=522元,当小张回家乡到后进该企业,小张的社会工龄为:28﹣18=10年,企业工龄为:28﹣28=0年∴小张的工龄工资为;y1+y2=10×10+20×0=100∴小张的第一年工龄工资每月下降了:522﹣100=422元,答:第一年每月工龄工资下降422元;(3)依题知要李程师的总工龄为:48﹣18=30,设李工程师的工龄工资为y,在本企业工作x年,由题意,得3<x≤30∴y=y1+y2=10(30﹣x)+[﹣2(x﹣23)2+860]=﹣2(x﹣20.5)2+942.5,∵a=﹣2<0,∴抛物线开口向下,对称轴是x=20.5,∵x为整数,∴当x=20或21时,y最大,且最大值为942,∴李工程师的工龄工资最高为942元/月.26.(12分)如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO 向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.(1)点B的坐标为(6,4);用含t的式子表示点P的坐标为(t,t);(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求t为何值时,S有最大值?(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC 分割成三角形和四边形两部分,且三角形的面积是△ONC面积的?若存在,求出点T的坐标;若不存在,请说明理由.【解答】解:(1)延长NP交OA于H,如图1所示:∵矩形OABC,∴BC∥OA,∠OCB=90°,∵PN⊥BC,∴NH∥OC,∴四边形CNHO是平行四边形,∴OH=CN,∵OA=6,AB=4,∴点B的坐标为(6,4);由图可得,点P的横坐标=0H=CN=t,纵坐标=4﹣NP,∵NP⊥BC,∴NP∥OC,∴NP:OC=BN:CB,即NP:4=(6﹣t):6,∴NP=4﹣t,∴点P的纵坐标=4﹣NP=t,则点P的坐标为(t,t);故答案为:(6,4);(t,t);(2)∵S=×OM×t,△OMP∴S=×(6﹣t)×t=﹣t2+2t=﹣(t﹣3)2+3(0<t<6).∴当t=3时,S有最大值.(3)存在.理由如下:由(2)得,当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),则直线ON的函数关系式为:y=x.设点T的坐标为(0,b),则直线MT的函数关系式为:y=﹣x+b,解方程组得,∴直线ON与MT的交点R的坐标为(,),∵S △OCN =×4×3=6,∴S △ORT = S △OCN =2,①当点T 在点O 、C 之间时,分割出的三角形是△OR 1T 1, 如图2所示,作R 1D 1⊥y 轴,D 1为垂足,则S △OR 1T 1=RD 1•OT =••b =2. ∴3b 2﹣4b ﹣16=0,解得:b =(负值舍去). ∴b =,此时点T 1的坐标为(0,). ②当点T 在OC 的延长线上时,分割出的三角形是△R 2NE ,如图,设MT 交CN于点E ,由①得点E 的横坐标为,作R 2D 2⊥CN 交CN 于点D 2,则 S △R 2NE =•EN •R 2D 2=•(3﹣)•(4﹣==2. ∴b 2+4b ﹣48=0,解得:b =±2﹣2(负值舍去). ∴b =2﹣2.∴此时点T 2的坐标为(0,2).综上所述,在y 轴上存在点T 1(0,),T 2(0,2﹣2)符合条件.。
2017届河北省唐山一中高三12月月考理科数学试题及答案 精品

唐山一中2016—2017学年高三年级12月份调研考试数学试题(理科)注意事项:1.本试卷分第Ⅰ卷(选择题)和II 卷(非选择题)两部分,满分150分,考试时间120分钟。
2.答题前请仔细阅读答题卡(纸)上的“注意事项”,按照“注意事项”的规定答题。
3.选择题答案涂在答题卡上,非选择题答案写在答题卡上相应位置,在试卷和草稿纸上作答无效。
第Ⅰ卷 选择题(共60分)一.选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项符合题目要求,将正确答案填涂在答题卡上。
1.不等式21ax <解集为Q ,{}0p x x =≤,若104R Q C P x x ⎧⎫=<<⎨⎬⎩⎭,则a 等于( ) A.14 B.12C.4D. 2 2.设S n 为等比数列{a n }的前n 项和,若0852=-a a ,则=24S S ( ) A.8- B.5 C. 8 D. 153. 已知直线l ⊥平面α,直线m ⊂平面β,则“α∥β”是“l ⊥m ”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件4.已知命题p :∀x ∈(0,∞+),3x>2x,命题q :∃x ∈(∞-,0),x x ->2,则下列命题为真命题的是( )A . p ∧qB .(¬p )∧q C.(¬p )∧(¬q ) D.p ∧(¬q )5. 直线x -2y -3=0与圆C :(x -2)2+(y+3)2=9交于E 、F 两点,则△ECF 的面积为( )A .23B.52C.553 D. 436.已知向量(sin(),1),(4,4cos 6παα=+=a b ,若⊥a b ,则4sin()3πα+等于( )A.14- D. 147. 已知双曲线22221x y a b-= (0,0)a b >>的左、右焦点分别为12,F F ,以12||F F 为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( )A .221916x y -=B .22134x y -=C . 221169x y -=D .22143x y -=8. 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为9.函数3sin(2)3y x π=-的图像为C ,如下结论中错误的是( ) A .图像C 关于直线1112x π=对称B .图像C 关于点2(,0)3π对称 C .函数()f x 在区间)127,12(ππ-内是增函数D .由x y 2cos 3=得图像向右平移125π个单位长度可以得到图像C10. 已知函数()(f x x ∈R)是偶函数,且(2)(2)f x f x +=-,当[0,2]x ∈时,()1f x x =-,则方程1()1||f x x =-在区间[10,10]-上的解的个数是 ( ) A .8 B .9 C .10 D .11 11. △ABC 内接于以O 为圆心,1为半径的圆,且02=-+OC OB OA ,则的值为( )A.1-B.1C. 2-D. 2 12.定义在(0,)上的函数)(),(/x f x f 是它的导函数,且恒有x x f x f tan )()(/<成立,则( ) A.)3(2)4(3ππf f >B. 1sin )6(2)1(πf f <C. )4()6(2ππf f >D. )3()6(3ππf f <第Ⅱ卷 非选择题(共90分)二.填空题:本大题共4小题,每小题5分,共20分,将答案填在答题卡上相应位置。
河北省唐山一中2017届高三高考冲刺热身考试(一)(数学理)(含答案)word版

唐山一中2017届高考冲刺热身试卷(一)数 学(理科)说明:1. 本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至6页。
全卷150分,考试时间120分钟。
2. 将Ⅰ卷答案用2B 铅笔涂在答题卡上,卷Ⅱ用蓝黑钢笔或圆珠笔答在试卷上。
第Ⅰ卷(选择题 共60分)一、选择题:(本大题共12小题,每小题5分,共60分。
每小题只有一个选项符合题目要求,请将正确答案的序号填在答题卡相应空格内。
)1. 复数1ii +在复平面内的对应点到原点的距离为( )A .12B .2C .1D 2.已知集合B A B x Z x A 则集合},,2,1,0{},2|3||{=<-∈=为( )A .{2}B .{1,2}C .{1,2,3}D .{0,1,2,3} 3.下列四个命题中的真命题为( )A .∠∠若sinA=sinB ,则A=B B .01x ==2若lgx ,则C .1a b1若a>b,且ab>0,则〈 D .若2b ac =,则a 、b 、c 成等比数列4. 若P 为双曲线221445x y -=的右支上一点,且P 到左焦点1F 与到右焦点2F 的距离之比为4:3,则P 点的横坐标x=( )A. 2B. 4C. 4.5D. 55、将边长为1的正方形 ABCD 沿对角线BD 折起,使得点A 到点A '的位置,且1A C '=,则折起后二面角A DC B '--的大小 ( )A. arctan2B. 4πC.arctan 3π6.已知函数2()f x ax bx c =++,当x=1时有最大值1。
当[,](0)x m n m n ∈<<时,函数()f x 的值域为11[,]n m ,则()()f m f n 的值为A .1mn B .11m n -- C .m n D .nm7.若不等式x>0,24x y +≤与24x y +≥所确定的平面区域被直线2y kx =+分为面积相等的两部分,则k 的值是( ) A . 1 B . 2 C .12D . 1-8.曲线)0,0(2sin >>+=N M N x M y ω在区间],0[ωπ上截直线y=4,与y=-2所得的弦长相等且不为0,则下列描述中正确的是( )A .3,1>=M NB .3,1≤=M NC .23,2>=M N D .23,2≤=M N 9. 已知)(x f 为偶函数,且)2()2(x f x f -=+,当02≤≤-x 时,x x f 2)(=,若),(,*n f a N n n =∈则=2009a ( )A . 2009B . 2009-C .41D .2110. 一个三位数,其十位上的数字既小于百位上的数字也小于个位上的数字(735,414等),那么这样的三位数共有 ( ) A. 240 个 B. 249 个 C.285 个 D. 330个11. F 1、F 2分别是双曲线12222=-by a x 的左、右焦点,A 是其右顶点,过F 2作x 轴的垂线与双曲线的一个交点为P ,G 是0,2121=⋅∆F F F PF 若的重心,则双曲线的离心率是A .2B .23D .312. 在三棱锥A —BCD 中,侧棱AB 、AC 、AD 两两垂直,△ABC 、△ACD 、△ADB 的面积分别为2A —BCD 的外接球的体积为AB .D .第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.点P 在焦点为12(0,1),(0,1)F F -,一条准线为4y =的椭圆上,且12||||1PFPF -=,12tan F PF ∠____________。
河北省唐山市第一中学2017届高三12月调研考试数学(理)试题Word版含答案

数学(理)试题 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若集合 {}1,2,3,4,5A =,集合 (){}|40B x x x =-<,则图中阴影部分表示 ( ) A .{}1,2,3,4 B .{}1,2,3 C .{}4,5 D .{}1,42. 等比数列 {}n a 满足 2379a a π=,则5cos a = ( )A .12-B .12C .12± D .3. 设为i 虚数单位且z 的共轭复数是 z ,若48z z z z +==,则z 的虚部为 ( ) A .2± B .2i ± C .2 D .2- 4. 下列关于命题的说法错误的是 ( )A .命题“ 若 2320x x -+=,则2x = ” 的逆否命题为“ 若 2x ≠,则2320x x -+≠” B .“3a =” 是“ 函数 ()log a f x x = 在定义域上为增函数” 的充分不必要条件 C. 若命题 :,3100p n N n ∃∈>,则:,3100p n N n ⌝∀∈≤ D .命题 “(),0,35x x x ∃∈-∞<” 是真命题5.在ABC ∆中,6,AC AC =的垂直平分线交AB 边所在直线于N 点,则AC CN 的值 为 ( )A .-.-9- D .18- 6. 某几何体的三视图及其尺寸如图所示,则该几何体的各侧面中最大的侧面的面积为 ( )A .4B .8 C. D .7. 一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为()(),,,0,1c a b c ∈, 已知他投篮一次得分的数学期望是2,则213a b+的最小值为( )A .323B .283C.143 D .1638. 阅读如下程序框图,如果输出 5i =,那么在空白矩形框中应填入的语句为 ( )A .22s i =*-B .21s i =*- C.2s i =* D .24s i =*+ 9. 已知函数()f x 定义在R 上的奇函数,当0x <时,()()1xf x ex =+,给出下列命题:①当0x >时,()()1xf x e x =-;②函数()f x 有2个零点;③()0f x >的解集为()()1,01,-⋃+∞;④12,x x R ∀∈,都有()()122f x f x -<,其中正确命题个数是 ( ) A .1 B .2 C. 3 D .4 10. 如图,将绘有函数 ()()2sin 0,2f x x πωϕωϕπ⎛⎫=+><< ⎪⎝⎭部分图象的纸片沿x 轴折成直二面角后,若,A B 两点之间的距离为,则()1f -= ( )A .2-B .2 C.11. 已知双曲线 ()2222:10x y C a b a b-=>>右支上非顶点的一点A 关于原点O 的对称点为,B F 为其右焦点,若AF FB ⊥,设ABF θ∠=且,124ππθ⎛⎫∈ ⎪⎝⎭,则双曲线离心率的取值范围是( ) A.2⎤⎦ B.(C.)+∞ D .()2,+∞12. 把曲线 3:sin cos 44C y x x ππ⎛⎫⎛⎫=-+⎪ ⎪⎝⎭⎝⎭上所有点向右平移 ()0a a >个单位,得到曲线'C ,且曲线'C 关于点()0,0中心对称.当11,(84b b x b ππ++⎡⎤∈⎢⎥⎣⎦为正整数)时,过曲线'C 上任意两点的直线的斜率恒小于零,则b 的值为( )A .1B .2 C. 3 D .1或 2第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13. 若()()12f x x f t dt =+⎰,则()()ln x f x x ϕ=-的零点个数为__________.14. 已知实数,x y 满足约束条件0401x y x y y -≥⎧⎪+-≤⎨⎪≥⎩,则212x yz -+⎛⎫= ⎪⎝⎭的最小值为 __________.15.2nx x ⎛⎫- ⎪⎝⎭ 的展开式中只有第5项的二项式系数最大,则它的展开式中常数项是_________.16. 设函数 ()22ln (x e f x k x k x x ⎛⎫=-+ ⎪⎝⎭为常数, 2.71828...e =是自然对数的底数), 若函数 ()f x 在()0,2内存在两个极值点, 则k 的取值范围 _________.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)若向量()()3sin ,sin ,cos ,sin a x x b x x ωωωω==,其中0ω>,记函数()12f x a b =-,若函数()f x 的图象上相邻两个极值点之间的距离是2.(1) 求 ()f x 的表达式;(2)设ABC ∆ 三内角,,A B C 的对应边分别为,,a b c ,若()3,1a b c f C +===,求ABC ∆的面积.18.(本小题满分12分)设等差数列{}n a 的前n 项和为n S ,且4224,21n n S S a a ==+. (1)求数列{}n a 的通项公式n a ; (2)设数列{}n b 的前n 项和为 n T ,且132n n na T ++=,又令()2n n cb n N *=∈,求数列 {}nc 的前n 项和n R .19.(本小题满分12分)生产甲乙两种元件,其质量按检测指标划分为:指标大于或者等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:(1)试分别估计元件甲、乙为正品的概率;(2)生产一件元件甲,若是正品可盈利40元,若是次品则亏损5元;生产一件元件乙,若是正品可盈利50元,若是次品则亏损10元. 在( 1)的前提下: ①记X 为生产1件甲和1件乙所得的总利润,求随机变量X 的分布列和数学期望; ② 求生产5件元件乙所获得的利润不少于140元的概率.20.(本小题满分12分)如图 1 在Rt ABC ∆中,90,,ABC D E ∠=分别为线段,AB AC 的中点,4,AB BC ==以DE 为折痕,将Rt ADE ∆折起到图 2 的位置,使平面'A DE ⊥平面DBCE ,连接',',A C A B ,设F 是线段'A C 上的动点,满足'CF CA λ=. (1)证明:平面 FBE ⊥平面'A DC ;(2)若二面角 F BE C -- 的大小为45,求λ的值.21.(本小题满分12分)已知椭圆()222210x y a b c a b+=>>>的左、右焦点分别为12,F F ,若以2F 为圆心,b c -为半径作圆2F ,过椭圆上一点P 作此圆的切线,切点为T ,且PT 的最)a c -. (1)求椭圆的离心率e 的取值范围;(2)设椭圆的短半轴长为1,圆2F 与x 轴的右交点为Q ,过 点 Q 作斜率为()0k k >的直线l 与椭圆相交于,A B 两点,若以AB 为直径的圆过坐标原点,求直线l 被圆2F 截得的弦长的最大值.22.(本小题满分12分)设函数()2ln f x x bx a x =-+.(1)若2b =,函数()f x 有两个极值点12,x x ,且12x x <,求实数a 的取值范围; (2) 在(1)的条件下,证明:()232ln 24f x +>-; (3)若对任意实数 []1,2b ∈,都存在实数 ()1,(x e e ∈ 为自然对数的底数),使得:()0f x <成立,求实数a 的取值范围.河北省唐山市第一中学2017届高三12月调研考试数学(理)试题参考答案一、选择题(每小题5分,共60分)1-5. ABADD 6-10.DDCBB 11-12. CD 二、填空题(每小题5分,共20分)13.1 14. 2 15. 1120 16. 2,2e e ⎛⎫⎪⎝⎭三、解答题 17.解:(1)()()3sin ,sin ,cos ,sin a x x b x x ωωωω==,()2113cos sin sin 2226f x a b x x x x πωωωω⎛⎫∴=-=+-=- ⎪⎝⎭, 由题意可知其周期为π,故1ω=,则()sin 26f x x π⎛⎫=- ⎪⎝⎭.(2)由()1f C =,得11sin 21,0,2,2666662C C C C πππππππ⎛⎫-=<<∴-<-<∴-= ⎪⎝⎭,解得3C π=,又3,a b c +==()22222cos ,333c a b ab a b ab π=+-∴+-=,即2ab =,由面积公式得ABC ∆面积为1sin 2ab C =可得1131494n n n R -+⎛⎫=- ⎪⎝⎭. 19.解:(1)元件甲为正品的概率约为:4032841005++=; 元件乙为正品的概率约为:4029631004++=.(2)①随机变量X 的所有取值为 90,45,30,15-.而且()()43313390;455455420P X P X ==⨯===⨯=; ()()41111130;1520P X P X ==⨯==-=⨯=,所以随机变量X 的分布列为:所以:()19045301566520520E X =⨯+⨯+⨯-⨯=.②设生产的5件元件乙中正品有n 件,则次品有5n -件,依题意,()50105140n n --≥,解得:19,46n n ≥∴=或5n =,设“生产5件元件乙所获得的利润不少于140元”为事件A ,则:()454531381444128P A C ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭.20.解:(1)平面'A DE ⊥平面,','DBCE A D DE A D ⊥∴⊥平面,'.,DBCE A DBE D E ∴分别为中点,11222DE BC BD AB ∴====. 在直角三角形DEB 中,tan tan tan tan 12BD BD BED CDE BED CDE DE CB ∠==∠==∴∠∠=. 90BED CDE ∴∠+∠=,可得,BE DC BE ⊥∴⊥平面'A DC ,又BE ⊂平面.FEB ∴平面FBE ⊥平面'A DC .(2)以D 为坐标原点,,'DB DE DA 分别为,,OX OY OZ 轴建立空间直角坐标系,各点坐标分别为()()()()()0,0,0,'0,0,2,2,0,0,,D A B C E .()()()'2,22,2,',2,2,22,2CA CF CA CF F λλλλ--=∴=---∴-,设平面 BEF 的法向量为()()(),,,2,2,0,2,2n x yz BE BF λλ==-=-,()20220x x y z λλ⎧-=⎪∴⎨-++=⎪⎩,取(),2,32n λλλ=-,又平面BEC 的法向量为()0,0,1n =,cos 452∴==,化为23620λλ-+=,解得13λ=±,又01,13λλ<<∴=-. 21.解:(1)依题意设切线长 PT =∴ 当且仅当2PF 取得最小值时PT 取得最小值,而)2min 1,,022b c PF a ca c a c -=-≥-∴<≤-,从而解得352e ≤<,故离心率e 的取值范围是352e ≤<. (2)依题意Q 点的坐标为()1,0,则直线的方程为()1y k x =-,联立方程组()22211y k x x y a⎧=-⎪⎨+=⎪⎩,得()22222222120a k x a k x a k a +-+-=,设()()1122,,,A x y B x y ,则有22222121222222,11a k a k a x x x x a k a k -+==++,代入直线方程得()()2212121222111k a y y x x x x a k -=-++=⎡⎤⎣⎦+, 221212221k a x x y y a k -+=+,又221212,0,0,,OA OB OA OB x x y y k a k a ⊥∴=+=∴=∴=,直线的方程为0ax y a --=,圆心()2,0F c到直线l的距离d =,由图象可得max 3351,213,0,,52424141l e c c s s ⎛==∴≤<∴≤<≤+<∴∈∴= ⎝⎦.22.解:(1)由已知, 2b =时,()()22ln ,f x x x a x f x =-+的定义域为()0,+∞,求导数得:()()222',x x af x f x x-+=有两个极值点12,x x ,故方程()'0f x =有两个不同的正根12,x x ,故2220x x a -+=的判别式480a ∆=->,即12a <,且12121,02ax x x x +==>,所以a 的取值范围为10,2⎛⎫ ⎪⎝⎭. (2)由(1)得:2112x <<且()2'0f x =,得()()2222222222222,222ln a x x f x x x x x x =-∴=-+-,令()()221222ln ,12F t t t t t t t ⎛⎫=-+-<< ⎪⎝⎭,则()()'212ln F t t t =-,当1,12t ⎛⎫∈ ⎪⎝⎭时,()()'0,F t F t >∴在1,12⎛⎫⎪⎝⎭上是增函数,()()2132ln 232ln 2,244F t F f x --+⎛⎫∴>=∴>- ⎪⎝⎭.(3)令()[]2ln ,1,2g b xb x a x b =-++∈,由于()1,x e ∈,所以()g b 为关于b 的递减的一次函数,根据题意,对任意[]1,2b ∈,都存在()1,(x e e ∈为自然对数的底数),使得()0f x <成立,则()1,x e ∈上()()2max 1ln 0g b g x x a x ==-++<有解,令()2ln h x x x a x =-++,则只需存在()01,x e ∈,使得()00h x <即可,由于()22'x x ah x x-+=,令()()()()22,1,,'410,x x x a x e x x x ωωω=-+∈=->∴在()1,e 上单调递增,()(1)1x a ωω∴>=+.①当10a +≥,即1a ≥-时,()()()0,'0,x h x h x ω>∴>∴在()1,e 上是增函数, ()()10h x h ∴>=,不符合题意. ②当10a +<,即1a <-时,()()2110,2a e e e a ωω=+<=-+.(i )若()0e ω<,即221a e e ≤-<-时,在()1,x e ∈上()0x ω>恒成立,即()'0h x <恒成立, ()h x ∴在()1,e 上单调递减.(ii )若()0e ω>,即221e e a -<<-时,在()1,e 上存在实数m ,使得()0,m ω=∴在()1,m 上()0x ω<恒成立,即()'0h x <恒成立,()h x ∴在()1,e 上单调递减,∴存在()01,x e ∈,使得()()010h x h <=,符合题意,综上所述,当1a <-时,对任意[]1,2b ∈,都存在()1,x e ∈,使得()0f x <成立.。
河北省唐山市2017届高三上学期第一次调研统考理数试题Word版含解析

河北省唐山市2017届高三上学期第一次调研统考理数试题一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}5,4,3,2,1⊆A ,且{}{}2,13,2,1= A ,则满足条件的集合A 的个数是( ) A .2 B .4 C .8 D .16 【答案】B 【解析】试题分析:因为{}{}1,2,31,2A=,所以A 中有1,2没有3,故可能性有{}{}{}{}1,21,2,41,2,51,2,4,5共四种.考点:子集,交集.【易错点晴】集合的三要素是:确定性、互异性和无序性.研究一个集合,我们首先要看清楚它的研究对象,是实数还是点的坐标还是其它的一些元素,这是很关键的一步.第二步常常是解一元二次不等式,我们首先用十字相乘法分解因式,求得不等式的解集.在解分式不等式的过程中,要注意分母不能为零.元素与集合之间是属于和不属于的关系,集合与集合间有包含关系. 在求交集时注意区间端点的取舍. 熟练画数轴来解交集、并集和补集的题目. 2.已知复数z 满足i z i 3)31(=+,则=z ( )A .i 2323+ B .i 2323- C .i 4343+ D .i 4343- 【答案】C考点:复数运算.3.某班学生一次数学考试成绩频率分布直方图如图所示,数据分组依次为90,110,[,若成绩大于等于90分的人数为36,则成绩在70[),90[),150]110,130,130[),[的人数110130,)为()A.12 B.9 C.15D.18【答案】A考点:频率分布直方图.4.设函数R x x f y ∈=),(,“)(x f y =是偶函数”是“)(x f y =的图像关于原点对称”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 【答案】B 【解析】试题分析:设:p “)(x f y =是偶函数”,:q “)(x f y =的图象关于原点对称”.p 不能推出q ,因为()f x 有可能是偶函数,图象关于y 轴对称.q 可以推出p ,因为原来图象关于原点对称,加绝对值之后就关于y 轴对称,所以p 是q 的必要不充分条件. 考点:函数的奇偶性,充要条件.5.设21,F F 是双曲线1422=-y x 的两个焦点,P 在双曲线上,且9021=∠PF F ,则21PF F ∆的面积为( )A .1B .2C .25D .5 【答案】A 【解析】试题分析:双曲线焦点三角形面积公式为2tan2b S θ=,其中12F PF θ∠=,所以本题面积为11tan 45=.考点:双曲线焦点三角形.6.要得到函数R x x x x f ∈=,cos sin 2)(,只需将函数R x x x g ∈-=,1cos 2)(2的图像( )A .向左平移2π个单位 B .向右平移2π个单位 C .向左平移4π个单位 D .向右平移4π个单位【答案】D考点:三角函数图象变换.7.执行如图所示的程序框图,若输入2,1==b a ,则输出的=x ( )A .25.1B .375.1C .4375.1D .40625.1【答案】C 【解析】试题分析:运行程序,32x =,判断否,32b =,判断否, 1.25x =,判断是, 1.25a =,判断否, 1.375x =,判断是, 1.375a =,判断否, 1.4375x =,判断否 1.4375b =,判断是,输出 1.4375x =. 考点:算法与程序框图. 8.设0x 是方程x x=)31(的解,则0x 所在的范围是( )A .)31,0( B .)21,31( C .)32,21( D .)1,32( 【答案】B考点:函数的图象与性质,二分法.9.某几何体的三视图如图所示,则此几何体的体积为( )A .6226++B .226+C .3D .38【答案】D 【解析】试题分析:该几何体是上面一个三棱锥,下面一个三棱柱,故体积为11182212212323⨯⨯⨯+⨯⨯⨯⨯=. 考点:三视图.10.把长为cm 80的铁丝随机截成三段,则每段铁丝长度都不小于cm 20的概率是( ) A .161B .81C .41D .163【答案】A考点:几何概型.11.在四棱锥ABCD P -中,底面ABCD 是正方形,⊥PA 底面ABCD ,H F E AB PA ,,,4==分别是棱PD BC PB ,,的中点,则过H F E ,,的平面截四棱锥ABCD P -所得截面面积为( )A .62B .64C .65D .6432+ 【答案】C 【解析】试题分析:取CD 中点K ,连接HK ,根据三角形中位线的性质有//EF HK .取PA 的中点J ,取PJ 的中点I ,根据三角形中位线的性质有////HF BJ EI ,所以EFKHI共面,面积为12EFKH EHI S S S =+=⨯=DF考点:立体几何.【思路点晴】本题主要考查立体几何点线面的位置关系,考查多点共面的证明方法,考查空间想象能力,考查动手能力.先画出题目给定的四棱锥,标出中点,,E F H ,并将三点连接起来,然后在几何体中平移,,EF EH HF 到四棱锥的表面.利用中位线将EF 平移到HK ,由此可得//EH FK .现将//HF JB ,然后将//JB EI ,经过以上步骤,就将平面扩展到几何体的表面了,进而得出截面.12.设函数a x a x x x f ---+-=5)8(331)(23,若存在唯一的正整数0x ,使得0)(0<x f ,则a 的取值范围是( )A .]61,151(B .]41,151(C .]41,61( D .]158,41(【答案】A 【解析】考点:函数导数与不等式.【思路点晴】题考查函数导数与单调性.确定零点的个数问题:可利用数 形结合的办法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理.选择题可以采用代入法的策略,选项中的特殊值代入,验证来得出结果.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.已知向量)75sin ,75(cos ),15sin ,15(cos ==b a =-_______. 【答案】3 【解析】试题分析:依题意有,11,1,2sin15cos15sin 302a b a b ==⋅===,所以 222443a b a a b b -=-⋅+=.考点:向量运算.14.在nxx )12(3-的展开式中,各二项式系数的和为128,则常数项是_______. 【答案】14 【解析】试题分析:依题意有721282,7n n ===,37(2x-展开式的通项为 ()()173721 3.5277212rrr r r r r C xx C x ----⎛⎫-=- ⎪⎝⎭,21 3.50,6r r -==,故常数项为()676671214C --=.考点:二项式.15.已知抛物线y x 42=与圆)0()2()1(:222>=-+-r r y x C 有公共点P ,若抛物线在P 点处的切线与圆C 也相切,则=r ______. 【答案】2考点:抛物线与圆.【思路点晴】本题考查圆和抛物线的位置关系,考查圆锥曲线的切线.由题意可知,两条曲线相交于切点,对于抛物线来说,先设出切点,就可以利用导数求得切线的斜率和切线方程,对于圆来说,圆心和切点的连线是和切线垂直的,转化为数学的式子就是两直线斜率乘积等于1-,解方程就可以求出切点坐标,然后利用两点间的距离公式求出半径.16.一艘海监船在某海域实施巡航监视,由A 岛向正北方向行驶80海里至M 处,然后沿东偏南30方向行驶50海里至N 处,再沿南偏东30方向行驶330海里至B 岛,则B A ,两岛之间距离是_____海 里. 【答案】70 【解析】试题分析:以M 为坐标原点建立平面直角坐标系,由图可知()()0,80,70A B --,故70AB ==.考点:解三角形.【思路点晴】本题主要考查解三角形、方位角、数形结合的数学思想方法.利用解三角形知识解决实际问题要注意 根据条件画出示意图,结合示意图构造三角形,然后转化为解三角形的问题进行求解.本题由于涉及方位,所以可以建立平面直角坐标系来求,也就是在M 点建立坐标系,然后求出想关点的坐标,最后利用两点间的距离公式来求.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分12分)设n S 为等差数列{}n a 的前n 项和,240,1101510==S S . (1)求数列{}n a 的通项公式; (2)令11+++=n nn n n a a a a b ,求数列{}n b 的前n 项和n T . 【答案】(1)n a n 2=;(2)21n nn n T =++.(2)211111222222++-=+++=+++=n n n n n n n n n n b n , n n nn n n T n 21211141313121211++=++-+⋅⋅⋅+-+-+-=.考点:数列基本概念,裂项求和法. 18.(本小题满分12分)如图,在四棱锥ABCD P -中,⊥PA 底面ABCD ,PB BC ⊥,BCD ∆为等边三角形,3==BD PA ,AD AB =,E 为PC 的中点.(1)求AB ;(2)求平面BDE 与平面ABP 所成二面角的正弦值.【答案】(1)1=AB ;(2)47. 【解析】试题分析:(1)连接AC ,因为⊥PA 底面ABCD ,ABCD ,所以BC PA ⊥,所以⊥BC 平面PAB .所以BC AB ⊥,因为BCD ∆为等边三角形,所以30=∠ABD .又已知AD AB =,3=BD ,可得1=AB ;(2)分别以BA BC ,所在直线为y x ,轴,过B 且平行PA 的直线为z轴建立空间直角坐标系,计算得平面PAB 的法向量为)0,0,1(=m ,平面BDE 的法向量为)2,3,3(--=,所以3cos ,4m n <>=.(2)分别以BA BC ,所在直线为y x ,轴,过B 且平行PA 的直线为z 轴建立空间直角坐标系,)0,23,23(),23,21,23(),0,0,3(),3,1,0(D E C P . 由题意可知平面PAB 的法向量为)0,0,1(=. 设平面BDE 的法向量为),,(z y x =,则⎪⎩⎪⎨⎧=⋅=⋅,0,0即⎪⎪⎩⎪⎪⎨⎧=+=++,02323,0232123y x z y x 则)2,3,3(--=, 43)2()3(3020313,cos 222=-+-+⨯-⨯-⨯>=<. 所以平面BDE 与平面ABP 所成二面角的正弦值为47.考点:空间向量与立体几何. 19.(本小题满分12分)甲将要参加某决赛,赛前D C B A ,,,四位同学对冠军得主进行竞猜,每人选择一名选手,已知B A ,选择甲的概率均为m ,D C ,选择甲的概率均为)(n m n >,且四人同时选择甲的概率为1009,四人均未选择 甲的概率为251. (1)求n m ,的值;(2)设四位同学中选择甲的人数为X ,求X 的分布列和数学期望.【答案】(1)⎪⎩⎪⎨⎧==.21,53n m ;(2)分布列见解析,2.2.试题解析:(1)由已知可得:⎪⎪⎪⎩⎪⎪⎪⎨⎧>=--=,,251)1()1(,10092222n m n m n m 解得⎪⎩⎪⎨⎧==.21,53n m (2)X 可取4,3,2,1,0.251)0(==X P ,51)211(21)531()211()531(53)1(122212=-⨯⨯⨯-+-⨯-⨯⨯==C C X P , 10037)211()531()211()53()211(21)531(53)2(22221212=-⨯-+-⨯+-⨯⨯⨯-⨯⨯==C C X P , 103)211(21)53()21()531(53)3(122212=-⨯⨯⨯+⨯-⨯⨯==C C X P ,1009)4(==X P . X 的分布列为2.21004103100251250)(=⨯+⨯+⨯+⨯+⨯=X E .考点:相互独立事件与二项分布. 20.(本小题满分12分)如图,过椭圆)0(1:2222>>=+b a by a x E 上一点P 向x 轴作垂线,垂足为左焦点F ,B A ,分别为E 的右顶点,上顶点,且OP AB ∥,12+=AF .(1)求椭圆E 的方程;(2)过原点O 做斜率为)0(>k k 的直线,交E 于D C ,两点,求四边形ACBD 面积S 的最大值.【答案】(1)1222=+y x ;(2)2. 【解析】试题分析:(1)设焦距为c 2,则),(2a b c P -,由//AB OP 得a bac b =2,则c a c b 2,==,由1AF =解得2,1,1===a b c ,椭圆E 的方程为1222=+y x ;(2)设),(),,(2211y x D y x C ,CD 的方程为kx y =,代入1222=+y x 解得2221212,212kx kx +-=+=,直线AB 的方程为0x =,故12d d ==,利用面积公式求得222(1)12S k =++,利用基本不等式求得最大值为2.(2)kx y CD =:,设),(),,(2211y x D y x C ,到AB 的距离分别为21,d d ,将kx y =代入1222=+y x 得22212k x +=,则2221212,212kx k x +-=+=, 由)1,0(),0,2(B A 得3=AB ,且022:=-+y x AB ,322,322222111-+=-+=y x d y x d ,)](2)[(21)(21212121y y x x d d AB S -+-=+=2212122))(21(21kkx x k ++=-+=, )21221(222kkS ++=,因为k k 22212≥+,当且仅当122=k 时取等号, 所以当22=k 时,四边形ACBD 的面积S 取得最大值2. 考点:直线与圆锥曲线位置关系.【方法点晴】直线和圆锥曲线的位置关系一方面要体现方程思想,另一方面要结合已知条件,从图形角度求解.联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解是一个常用的方法. 涉及弦长的问题中,应熟练地利用根与系数关系、设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解. 21.(本小题满分12分) 已知函数2ln )(-+=xax x f . (1)讨论)(x f 的单调性;(2)若函数)(x f y =的两个零点为)(,2121x x x x <,证明:a x x 221>+.【答案】(1)当0≤a 时,)(x f 在),0(+∞上单调递增,当0>a 时,)(x f 在),0(a 上单调递减,在),(+∞a 上单调递增;(2)证明见解析.试题解析:(1))0(,1)(22>-=-='x xax x a x x f , 所以当0≤a 时,0)(>'x f ,)(x f 在),0(+∞上单调递增; 当0>a 时,)(x f 在),0(a 上单调递减,在),(+∞a 上单调递增.(2)若函数)(x f y =的两个零点为)(,2121x x x x <,由(1)可得210x a x <<<, 令)0(),2()()(a x x a f x f x g <<--=, 则0])2(11)[()2()()(22<---=-'+'='x a x a x x a f x f x g , 所以)(x g 在),0(a 上单调递减,0)()(=>a g x g ,即)2()(x a f x f ->. 令a x x <=1,则)2()(11x a f x f ->,所以)2()()(112x a f x f x f ->=, 由(1)可得)(x f 在),(+∞a 上单调递增,所以122x a x ->,故a x x 221>+. 考点:函数导数与不等式.【方法点晴】本题主要考查利用导数求函数的单调区间,构造函数证明不等式.第一问是一个常见的求导后对参数进行分类讨论的题,求导通分后分子是一个一次函数,则只需要分成两类,结合图像来讨论即可.第二问是极点偏移问题.构造函数()g x 后,利用导数求得函数()g x 是一个减函数,然后根据单调性就可以证明原不等式成立.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.解答时请写清题号.22.(本小题满分10分)选修4-1:几何证明选讲如图,ABC ∆与ABD ∆都是以AB 为斜边的直角三角形,O 为线段AB 上一点,BD 平分ABC ∠,且 BC OD ∥.(1)证明:D C B A ,,,四点共圆,且O 为圆心;(2)AC 与BD 相交于点F ,若62==CF BC ,求D C ,之间的距离.【答案】(1)证明见解析;(2)试题解析:(1)因为ABC ∆与ABD ∆都是以AB 为斜边的直角三角形, 所以D C B A ,,,四点都在以AB 为直径的圆上.因为BD 平分ABC ∠,且BC OD ∥,所以OD OB ODB CBD OBD =∠=∠=∠,. 又90,90=∠+∠=∠+∠ODB ODA OBD OAD ,所以OD OA ODA OAD =∠=∠,. 所以OB OA =,O 是AB 的中点,O 为圆心. (2)由62==CF BC ,得53=BF , 由BCF RT ADF RT ∆∆~得2==CFBCDF AD . 设x DF AD 22==,则x AF 5=,由BD 平分ABC ∠得2==CFBCDA BD , 所以2253=+xx,解得5=x ,即52=AD , 连接CD ,由(1),52==AD CD . 考点:几何证明选讲.23.(本小题满分10分)选修4-4:坐标系与参数方程以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系.曲线1C 的极坐标方程是2=ρ.矩形ABCD 内接于曲线1C ,B A ,两点的极坐标分别为)6,2(π和)65,2(π.将曲线1C 上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线2C .(1)写出D C ,的直角坐标及曲线2C 的参数方程;(2)设M 为2C 上任意一点,求2222MD MC MB MA +++的取值范围. 【答案】(1))1,3(),1,3(---D C ,曲线2C 的参数方程为θθθ(sin ,cos 2⎩⎨⎧==y x 为参数);(2)]32,20[.【解析】试题分析:(1)先利用公式求得(A B ,利用对称性可求得)1,3(),1,3(---D C .C 的直角坐标方程为224x y +=,参数方程为2cos 2sin x y θθ=⎧⎨=⎩(θ为参数)横坐标不变,纵坐标缩短为原来的一半,即2cos sin x y θθ=⎧⎨=⎩(θ为参数);(2)设)sin ,cos 2(θθM ,利用两点间的距离公式,化简2222MA MB MC MD +++得212cos 20θ+,故所求的取值范围是]32,20[.(2)设)sin ,cos 2(θθM ,则2222MDMC MB MA +++22222222(2cos (sin 1)(2cos (sin 1)(2cos (sin 1)(2cos (sin 1)θθθθθθθθ=+-+++-++++++20cos 1216sin 4cos 16222+=++=θθθ,则所求的取值范围是]32,20[.考点:坐标系与参数方程.24.(本小题满分10分)选修4-5:不等式选讲 已知函数11)(-++=mx x x f .(1)若1=m ,求)(x f 的最小值,并指出此时x 的取值范围;(2)若x x f 2)(≥,求m 的取值范围.【答案】(1))(x f 的最小值为2,此时x 的取值范围是]1,1[-;(2)),1[]1,(+∞--∞ .【解析】试题分析:(1)1m =时2)1()1(11)(=--+≥-++=x x x x x f ,当且仅当0)1)(1(≤-+x x 时取等号,解得[1,1]x ∈-;(2)0≤x 时,x x f 2)(≥显然成立;0>x 时,由x mx x x f 211)(≥-++=,得11-≥-x mx ,由1-=mx y 及1-=x y 的图象可得1≥m 且11≤m,解得(,1][1,)m ∈-∞-+∞. 试题解析:考点:不等式选讲.。
2017年河北省唐山市滦县中考数学一模试卷

2017年河北省唐山市滦县中考数学一模试卷一、选择题:本大题共16小题,共42分,1-10小题各3分,11-16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(3分)计算:﹣(﹣1)=()A.±1 B.﹣2 C.﹣1 D.12.(3分)下列运算正确的是()A.﹣a(a﹣b)=﹣a2﹣ab B.(2ab)2÷a2b=4ab C.2ab×3a=6a2b D.(a ﹣1)(1﹣a)=a23.(3分)下列各数中,为不等式组解的是()A.﹣1 B.0 C.2 D.44.(3分)如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b 相交所成的锐角是()A.20°B.30°C.70°D.80°5.(3分)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为()A.10 B.17 C.20 D.21.56.(3分)某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为()A.﹣=5 B.+5=C.﹣=5 D.﹣=57.(3分)有五张背面完全相同的卡片,正面分别写有,()0,,,2﹣2,把卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是无理数的概率是()A.B.C.D.8.(3分)如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于()A.40°B.50°C.60°D.70°9.(3分)如图,△ABC的项点都在正方形网格的格点上,则cosC的值为()A.B.C.D.10.(3分)甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A 城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有()①甲车的速度为50km/h ②乙车用了3h到达B城③甲车出发4h时,乙车追上甲车④乙车出发后经过1h或3h两车相距50km.A.1个 B.2个 C.3个 D.4个11.(2分)如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A、B不重合),连结AP、PB,过点O分别作OE⊥AP于点E,OF⊥AP于点E,OF⊥PB于点F,则EF=()A.4 B.5 C.5.5 D.612.(2分)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),其对称轴为直线x=1,下面结论中正确的是()A.abc>0 B.2a﹣b=0 C.4a+2b+c<0 D.9a+3b+c=013.(2分)如图,点A、C为反比例函数y=图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB 于点E,点E恰好为OC的中点,当△AEC的面积为时,k的值为()A.4 B.6 C.﹣4 D.﹣614.(2分)如图,△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为()A.3 B.C.3或D.4或15.(2分)如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O 逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为()A.(1,﹣1)B.(﹣1,﹣1)C.(,0)D.(0,﹣)16.(2分)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的()A.B.C.D.二、填空题:本大题共3小题,共10分,17-18题各3分,19小题有2个空,每空2分,把答案写在题中横线上.17.(3分)关于x的方程kx2﹣4x﹣4=0有两个不相等的实数根,则k的最小整数值为.18.(3分)如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是cm(计算结果保留π).19.(4分)如图,∠ACD是△ABC的外角,第1次操作:∠ABC的平分线与∠ACD的平分线交于点A1;第2次操作:∠A1BC的平分线与∠A1CD的平分线交于BC的平分线与∠A n﹣1CD的平分线交于点A n,则∠点A2,…第n次操作:∠A n﹣1A2与∠A之间的数量关系是;若∠A=64°,∠A n≤4°,则n的取值范围是.三、解答题:本大题共7小题,共68分,解答应写出文字说明、证明过程或演算步骤.20.(9分)计算:(3.14﹣π)0+﹣2sin45°+()﹣1﹣|1﹣|.21.(9分)某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前四次单价变化的情况,绘制了如下统计表:A,B产品单价变化统计表并求得了A产品四次单价的平均数和方差:2=14[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2+(5.9﹣5.9)2]==5.9,s(1)B产品第四次的单价比第二次的单价减少了%;(2)A产品四次单价的中位数是;B产品四次单价的众数是;(3)求B产品四次单价的方差,并比较哪种产品的单价波动小.22.(9分)如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.(1)求证:△ABD≌△ACE;(2)求∠ACE的度数;(3)求证:四边形ABFE是菱形.23.(9分)如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y 轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.(1)当t=3时,求l的解析式;(2)若点M,N位于l的异侧,确定t的取值范围;(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.24.(10分)某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.(1)请直接写出y与x的函数关系式;(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?25.(10分)图1和图2,半圆O的直径AB=2,点P(不与点A,B重合)为半圆上一点,将图形延BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.(1)当α=15°时,过点A′作A′C∥AB,如图1,判断A′C与半圆O的位置关系,并说明理由.(2)如图2,当α=°时,BA′与半圆O相切.当α=°时,点O′落在上.(3)当线段BO′与半圆O只有一个公共点B时,求α的取值范围.26.(12分)如图1和图2,在△ABC中,AB=13,BC=14,cos∠ABC=.=.探究:如图1,AH⊥BC于点H,则AH=,AC=,△ABC的面积S△ABC拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为S △ABD=0).(1)用含x、m或n的代数式表示S△ABD 及S△CBD;(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.2017年河北省唐山市滦县中考数学一模试卷参考答案与试题解析一、选择题:本大题共16小题,共42分,1-10小题各3分,11-16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(3分)(2016•河北)计算:﹣(﹣1)=()A.±1 B.﹣2 C.﹣1 D.1【解答】解:﹣(﹣1)=1.故选:D.2.(3分)(2017•滦县一模)下列运算正确的是()A.﹣a(a﹣b)=﹣a2﹣ab B.(2ab)2÷a2b=4ab C.2ab×3a=6a2b D.(a ﹣1)(1﹣a)=a2【解答】解:A、原式=﹣a2+ab,不符合题意;B、原式=4a2b2÷a2b=4b,不符合题意;C、原式=6a2b,符合题意;D、原式=﹣(a﹣1)2=﹣a2+2a﹣1,不符合题意,故选C3.(3分)(2012•河北)下列各数中,为不等式组解的是()A.﹣1 B.0 C.2 D.4【解答】解:,由①得,x>,由②得,x<4,∴不等式组的解集为<x<4.四个选项中在<x<4中的只有2.故选:C.4.(3分)(2014•河北)如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是()A.20°B.30°C.70°D.80°【解答】解:a,b相交所成的锐角=100°﹣70°=30°.故选:B.5.(3分)(2017•滦县一模)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为()A.10 B.17 C.20 D.21.5【解答】解:∵根据题意得出MN是线段AB的垂直平分线,∴AD=BD,∴AD+CD=BC.∵△ABC的周长为24,AB=7,∴△ADC的周长=AC+BC=△ABC的周长﹣AB=24﹣7=17.故选B.6.(3分)(2017•滦县一模)某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为()A.﹣=5 B.+5=C.﹣=5 D.﹣=5【解答】解:因客户的要求每天的工作效率应该为:(48+x)件,所用的时间为:,根据“因客户要求提前5天交货”,用原有完成时间减去提前完成时间,可以列出方程:﹣=5.故选:D.7.(3分)(2016•本溪)有五张背面完全相同的卡片,正面分别写有,(),,,2﹣2,把卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是无理数的概率是()A.B.C.D.【解答】解:=3,()0=1,=2,2﹣2=,,无理数为:,所以抽到无理数的概率为:,故选A.8.(3分)(2012•山西)如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于()A.40°B.50°C.60°D.70°【解答】解:连接OC,如图所示:∵圆心角∠BOC与圆周角∠CDB都对,∴∠BOC=2∠CDB,又∠CDB=20°,∴∠BOC=40°,又∵CE为圆O的切线,∴OC⊥CE,即∠OCE=90°,则∠E=90°﹣40°=50°.故选B9.(3分)(2017•滦县一模)如图,△ABC的项点都在正方形网格的格点上,则cosC的值为()A.B.C.D.【解答】解:在格点三角形ADC中,AD=2,CD=4,∴AC===2,∴cosC===.故选B.10.(3分)(2016•葫芦岛)甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有()①甲车的速度为50km/h ②乙车用了3h到达B城③甲车出发4h时,乙车追上甲车④乙车出发后经过1h或3h两车相距50km.A.1个 B.2个 C.3个 D.4个【解答】解:①甲车的速度为=50km/h,故本选项正确;②乙车到达B城用的时间为:5﹣2=3h,故本选项正确;③甲车出发4h,所走路程是:50×4=200(km),甲车出发4h时,乙走的路程是:×2=200(km),则乙车追上甲车,故本选项正确;④当乙车出发1h时,两车相距:50×3﹣100=50(km),当乙车出发3h时,两车相距:100×3﹣50×5=50(km),故本选项正确;故选D.11.(2分)(2017•滦县一模)如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A、B不重合),连结AP、PB,过点O分别作OE⊥AP于点E,OF⊥AP于点E,OF⊥PB于点F,则EF=()A.4 B.5 C.5.5 D.6【解答】解:∵OE⊥AP于E,OF⊥PB于F,∴AE=PE,PF=BF,∴EF是△APB的中位线,∴EF∥AB,EF=AB=5;故选B.12.(2分)(2016•本溪)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),其对称轴为直线x=1,下面结论中正确的是()A.abc>0 B.2a﹣b=0 C.4a+2b+c<0 D.9a+3b+c=0【解答】解:∵抛物线的开口向下,则a<0,对称轴在y轴的右侧,∴b>0,图象与y轴交于正半轴上,∴c>0,∴abc<0,:∵对称轴为x=1,∴x=﹣=1,∴﹣b=2a,∴2a+b=0,当x=2时,4a+2b+c>0,当x=3时,9a+3b+c=0,故选D.13.(2分)(2016•本溪)如图,点A、C为反比例函数y=图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为时,k的值为()A.4 B.6 C.﹣4 D.﹣6【解答】解:设点C的坐标为(m,),则点E(m,),A(m,),=BD•AE=(m﹣m)•(﹣)=﹣k=,∵S△AEC∴k=﹣4.故选C.14.(2分)(2017•滦县一模)如图,△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为()A.3 B.C.3或D.4或【解答】解:∵△DCE和△ABC相似,∠ACD=∠ABC,AC=6,AB=4,CD=2,∴∠A=∠DCE,∴=或=,即=或=解得,CE=3或CE=故选C.15.(2分)(2016•河南)如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D 的坐标为()A.(1,﹣1)B.(﹣1,﹣1)C.(,0)D.(0,﹣)【解答】解:菱形OABC的顶点O(0,0),B(2,2),得D点坐标为(1,1).每秒旋转45°,则第60秒时,得45°×60=2700°,2700°÷360=7.5周,OD旋转了7周半,菱形的对角线交点D的坐标为(﹣1,﹣1),故选:B.16.(2分)(2009•临沂)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y 与x之间的函数关系用图象表示大致是下图中的()A.B.C.D.【解答】解:此题在读懂题意的基础上,分两种情况讨论:当x≤4时,y=6×8﹣(x•2x)=﹣2x2+48,此时函数的图象为抛物线的一部分,它的最上点抛物线的顶点(0,48),最下点为(4,16);当4<x≤6时,点E停留在B点处,故y=48﹣8x=﹣8x+48,此时函数的图象为直线y=﹣8x+48的一部分,它的最上点可以为(4,16),它的最下点为(6,0).结合四个选项的图象知选A项.故选:A.二、填空题:本大题共3小题,共10分,17-18题各3分,19小题有2个空,每空2分,把答案写在题中横线上.17.(3分)(2016•本溪)关于x的方程kx2﹣4x﹣4=0有两个不相等的实数根,则k的最小整数值为1.【解答】解:∵关于x的方程kx2﹣4x﹣4=0有两个不相等的实数根,∴k≠0且b2﹣4ac>0,即,解得k>﹣1且k≠0,∴k的最小整数值为:1.故答案为:1.18.(3分)(2016•广东)如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是10πcm (计算结果保留π).【解答】解:∵圆锥的高h为12cm,OA=13cm,∴圆锥的底面半径为=5cm,∴圆锥的底面周长为10πcm,∴扇形AOC中的长是10πcm,故答案为:10π.19.(4分)(2017•滦县一模)如图,∠ACD是△ABC的外角,第1次操作:∠ABC的平分线与∠ACD的平分线交于点A1;第2次操作:∠A1BC的平分线与∠A1CD的平分线交于点A2,…第n次操作:∠A n﹣1BC的平分线与∠A n﹣1CD的平分线交于点A n,则∠A2与∠A之间的数量关系是∠A2=∠A;若∠A=64°,∠A n≤4°,则n的取值范围是n≥4.【解答】解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=∠ABC,∠A1CD=∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,∴(∠A+∠ABC)=∠ABC+∠A1,∴∠A1=∠A,同理可得∠A2=∠A1=∠A;根据以上规律可得∠A n=∠A,当∠A=64°,∠A n≤4°时,∠A≤4°,解得n≥4,故答案为:∠A2=∠A,n≥4.三、解答题:本大题共7小题,共68分,解答应写出文字说明、证明过程或演算步骤.20.(9分)(2017•滦县一模)计算:(3.14﹣π)0+﹣2sin45°+()﹣1﹣|1﹣|.【解答】解:(3.14﹣π)0+﹣2sin45°+()﹣1﹣|1﹣|=1+2﹣2×+3﹣(﹣1)=1+2﹣+3﹣+1=5.21.(9分)(2017•滦县一模)某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前四次单价变化的情况,绘制了如下统计表:A,B产品单价变化统计表并求得了A产品四次单价的平均数和方差:2=14[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2+(5.9﹣5.9)2]==5.9,s(1)B产品第四次的单价比第二次的单价减少了12.5%;(2)A产品四次单价的中位数是 5.95;B产品四次单价的众数是 3.5;(3)求B产品四次单价的方差,并比较哪种产品的单价波动小.【解答】解:(1)B产品第四次的单价比第二次的单价减少了:×100%=12.5%;故答案为:12.5;(2)把这组数从小到大排列为:5.2,5.9,6,6.5,最中间两个数的平均数是:=5.95,则A产品四次单价的中位数是5.95;B产品四次单价的众数是3.5;故答案为:5.95,3.5;(3)B产品四次的平均数是:(3.5+4+3+3.5)÷4=3.5,则B产品四次单价的方差是:[(3.5﹣3.5)2+(4﹣3.5)2+(3﹣3.5)2+(3.5﹣3.5)2]=,因为B的方差比A的方差小,所以B的波动小.22.(9分)(2014•河北)如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A 按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.(1)求证:△ABD≌△ACE;(2)求∠ACE的度数;(3)求证:四边形ABFE是菱形.【解答】(1)证明:∵△ABC绕点A按逆时针方向旋转100°,∴∠BAC=∠DAE=40°,∴∠BAD=∠CAE=100°,又∵AB=AC,∴AB=AC=AD=AE,在△ABD与△ACE中∴△ABD≌△ACE(SAS).(2)解:∵∠CAE=100°,AC=AE,∴∠ACE=(180°﹣∠CAE)=(180°﹣100°)=40°;(3)证明:∵∠BAD=∠CAE=100°AB=AC=AD=AE,∴∠ABD=∠ADB=∠ACE=∠AEC=40°.∵∠BAE=∠BAD+∠DAE=140°,∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°,∴∠BAE=∠BFE,∴四边形ABFE是平行四边形,∵AB=AE,∴平行四边形ABFE是菱形.23.(9分)(2013•河北)如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b 也随之移动,设移动时间为t秒.(1)当t=3时,求l的解析式;(2)若点M,N位于l的异侧,确定t的取值范围;(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.【解答】解:(1)直线y=﹣x+b交y轴于点P(0,b),由题意,得b>0,t≥0,b=1+t.当t=3时,b=4,故y=﹣x+4.(2)当直线y=﹣x+b过点M(3,2)时,2=﹣3+b,解得:b=5,5=1+t,解得t=4.当直线y=﹣x+b过点N(4,4)时,4=﹣4+b,解得:b=8,8=1+t,解得t=7.故若点M,N位于l的异侧,t的取值范围是:4<t<7.(3)如右图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F 为点M在坐标轴上的对称点.过点M作MD⊥x轴于点D,则OD=3,MD=2.已知∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,∴DE=MD=2,OE=OF=1,∴E(1,0),F(0,﹣1).∵M(3,2),F(0,﹣1),∴线段MF中点坐标为(,).直线y=﹣x+b过点(,),则=﹣+b,解得:b=2,2=1+t,解得t=1.∵M(3,2),E(1,0),∴线段ME中点坐标为(2,1).直线y=﹣x+b过点(2,1),则1=﹣2+b,解得:b=3,3=1+t,解得t=2.故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上.24.(10分)(2016•葫芦岛)某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.(1)请直接写出y与x的函数关系式;(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?【解答】解:(1)设y=kx+b,把(22,36)与(24,32)代入得:,解得:,则y=﹣2x+80;(2)设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x元,根据题意得:(x﹣20)y=150,则(x﹣20)(﹣2x+80)=150,整理得:x2﹣60x+875=0,(x﹣25)(x﹣35)=0,解得:x1=25,x2=35(不合题意舍去),答:每本纪念册的销售单价是25元;(3)由题意可得:w=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,此时当x=30时,w最大,又∵售价不低于20元且不高于28元,=﹣2(28﹣30)2+200=192∴x<30时,y随x的增大而增大,即当x=28时,w最大(元),答:该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元.25.(10分)(2014•葫芦岛)图1和图2,半圆O的直径AB=2,点P(不与点A,B重合)为半圆上一点,将图形延BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.(1)当α=15°时,过点A′作A′C∥AB,如图1,判断A′C与半圆O的位置关系,并说明理由.(2)如图2,当α=45°时,BA′与半圆O相切.当α=30°时,点O′落在上.(3)当线段BO′与半圆O只有一个公共点B时,求α的取值范围.【解答】解:(1)相切,理由如下:如图1,过O作OD过O作OD⊥A′C于点D,交A′B于点E,∵α=15°,A′C∥AB,∴∠ABA′=∠CA′B=30°,∴DE=A′E,OE=BE,∴DO=DE+OE=(A′E+BE)=AB=OA,∴A′C与半圆O相切;(2)当BA′与半圆O相切时,则OB⊥BA′,∴∠OBA′=2α=90°,∴α=45°,当O′在上时,如图2,连接AO′,则可知BO′=AB,∴∠O′AB=30°,∴∠ABO′=60°,∴α=30°,故答案为:45;30;(3)∵点P,A不重合,∴α>0,由(2)可知当α增大到30°时,点O′在半圆上,∴当0°<α<30°时点O′在半圆内,线段BO′与半圆只有一个公共点B;当α增大到45°时BA′与半圆相切,即线段BO′与半圆只有一个公共点B.当α继续增大时,点P逐渐靠近点B,但是点P,B不重合,∴α<90°,∴当45°≤α<90°线段BO′与半圆只有一个公共点B.综上所述0°<α<30°或45°≤α<90°.26.(12分)(2017•滦县一模)如图1和图2,在△ABC中,AB=13,BC=14,cos ∠ABC=.探究:如图1,AH⊥BC于点H,则AH=12,AC=15,△ABC的面积S△ABC= 84.拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为S △ABD=0).(1)用含x、m或n的代数式表示S△ABD 及S△CBD;(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.【解答】探究:解:∵在△ABC中,AB=13,BC=14,cos∠ABC=,∴=,∴BH=5,∴AH==12,∴HC=9,AC==15,∴△ABC的面积S=×12×14=84;△ABC故答案为:12,15,84;拓展:=mx,S△CBD=nx;解:(1)由三角形面积公式得出:S△ABD(2)∵m=,n=,∴m+n=+=,∵AC边上的高为:==,∴x的取值范围为:≤x≤14,∵(m+n)随x的增大而减小,∴x=时,(m+n)的最大值为:15;当x=14时,(m+n)的最小值为12;(3)x的取值范围是x=或13<x≤14,发现:解:∵AC>BC>AB,∴过A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线,AC边上的高的长为.参与本试卷答题和审题的老师有:gbl210;sks;CJX;星期八;ZJX;HLing;tcm123;gsls;lantin;733599;王学峰;曹先生;2300680618;hbxglhl;lf2﹣9;sjzx;szl;sd2011;守拙;未来;Ldt;家有儿女(排名不分先后)菁优网2017年6月4日。
